Abstract
We use the principle of maximum entropy to propose a parsimonious model for the generation of simulated rainfall during the wettest three-month season at a typical location on the east coast of Australia. The model uses a checkerboard copula of maximum entropy to model the joint probability distribution for total seasonal rainfall and a set of two-parameter gamma distributions to model each of the marginal monthly rainfall totals. The model allows us to match the grade correlation coefficients for the checkerboard copula to the observed Spearman rank correlation coefficients for the monthly rainfalls and, hence, provides a model that correctly describes the mean and variance for each of the monthly totals and also for the overall seasonal total. Thus, we avoid the need for a posteriori adjustment of simulated monthly totals in order to correctly simulate the observed seasonal statistics. Detailed results are presented for the modelling and simulation of seasonal rainfall in the town of Kempsey on the mid-north coast of New South Wales. Empirical evidence from extensive simulations is used to validate this application of the model. A similar analysis for Sydney is also described.1. Introduction
We propose a model for seasonal rainfall using the principle of maximum entropy. To demonstrate our model, we used official records from the Australian Bureau of Meteorology for station 059017 (Wide Street) in Kempsey in New South Wales during the period 1889 to 2011. The town of Kempsey is a typical location on the east coast of Australia with a humid sub-tropical or temperate climate and no pronounced dry season. The Köppen classification [1] is Cfa. Although the annual rainfall is relatively high and is generally regarded as reliable, there is ample historical evidence of extended periods with well below average rainfall.
There is consensus amongst climate scientists that summer and autumn rainfall in eastern Australia is influenced on a recurring basis by the quasi-periodic seasonal climatic events, El Niño and La Niña. During El Niño, rainfall is inhibited, and during La Niña, it is enhanced. It is therefore not especially surprising to find a positive correlation for monthly rainfall in Kempsey during the period February-March-April—the wettest time of the year. Our aim is to construct a parsimonious model for a vector-valued random variable X = (X1, X2, X3) ∈ ℝ3 that can be used to simulate typical monthly rainfall time series for February-March-April in Kempsey. We will show that the key observed seasonal statistics lie well within the commonly accepted empirical confidence intervals established by repeated simulations with our proposed model. Our results also show that even seemingly significant trends in the observed data could be due to chance alone.
2. A Brief Literature Review
A comprehensive review of the vast array of the relevant literature is neither feasible nor helpful. Instead, we shall be content to refer only to articles of fundamental historical significance or to those that are directly relevant to the methods used in this paper.
The topic of entropy has a long and distinguished research history dating back to the fundamental principles of thermodynamics proposed by Rudolf Clausius in 1855. The principle of maximum entropy, enunciated much later by the physicist E. T. Jaynes [2,3] in 1957, is a recurring theme in our discussion. We apply this principle to both discrete and continuous entropy. The modern notion of discrete entropy [4] was introduced by John von Neumann in his 1927 treatise on quantum mechanics in which he defined the entropy of a statistical operator ρ = {pn, ψn}n, where pn > 0 and ∑n pn = 1 and where {ψn} is a complete orthonormal system of basis vectors as the weighted ensemble average S(ρ) = −k⟨ρ loge⟩n = −k Tr(ρ loge ρ) = −k ∑n pn loge pn. See [5] (pp. 348–353) for more details.
This measure was adopted in 1948 by C. E. Shannon [6] as a measure of information in the theory of communication systems. Shannon also introduced the analogous notion of continuous or differential entropy S(f) = −∫Ωf(x) loge f(x)dx, where f(x) ≥ 0 and ∫Ωf(x)dx = 1 for continuous probability distributions. The entropy of a system is commonly described as a measure of the inherent disorder within the system. Entropy is maximized when the system is in the highest possible state of disorder. For a system with a finite number of possible states, the entropy is maximized when all probabilities are equal.
By contrast, the topic of rainfall modelling has a much more recent research history. The early work, such as the paper by Stern and Coe [7], follows a classical style that is typical of the physical sciences. However, the focus has shifted in recent times to a more pragmatic approach that is less concerned with a logical axiomatic basis and more concerned with a positive utilitarian outcome. The most relevant recent paper in relation to our work is the comprehensive 2005 report to the Australian Cooperative Research Centre for Catchment Hydrology by Srikanthan [8]. We shall discuss this paper in some detail. Although the report describes a successful scheme for the generation of daily rainfall data at multiple sites, a substantive difficulty emerges in the accumulation of simulated daily rainfall totals. This difficulty lies at the very heart of the problem that we will address. At each site, Srikanthan uses a simple two-by-two Markov chain to generate realistic sequences of wet and dry days. On the designated wet days, a two-parameter gamma distribution is invoked to generate rainfall depths. However, Srikanthan makes the following critical observation.
The generated daily rainfall amounts when aggregated into monthly and annual totals will not, in general, preserve the monthly and annual characteristics.
Hence, it is necessary to implement a nested correction process. In the first place, the generated monthly total, , for the current month, i, obtained by summing the daily totals is modified to produce a corrected monthly total, Xi, according to the iterative formula:
While this is an eminently sensible correction process, effectively a top-down approach based on the primary importance of the annual distribution, it also recognises a fundamental problem with the original model in which correlations in the daily rainfall, although undoubtedly very small, are apparently ignored. It is known that the introduction of a single correlation parameter allows one to adjust the standard deviation for the sum of the daily totals in a month, so that it matches the observed monthly standard deviation. See, for instance, the correlative coherence analysis proposed by Getz [9], which, incidentally, makes direct use of the Shannon entropy, and the model proposed by Hasan and Dunn [10], which uses a Tweedie distribution. In the overall modelling context, we see it as somewhat logically perverse to select a gamma distribution that will generate realistic daily rainfall depths and then to systematically modify the data generated by it. This inevitably means that the modified daily rainfall depth distributions will be biased relative to the observed distributions.
While we acknowledge the utility and undoubted practicality of the Srikanthan model, we are concerned about what appears to be an ad hoc theoretical basis. There is no clear statement about the relationship between the sample measurements and the a priori criteria that will be used to judge the goodness-of-fit. In this regard, there is one further point we wish to make. In order to embed spatial correlation into the rainfall generation process, Srikanthan uses a multivariate normal distribution to generate appropriately correlated sequences of random numbers at the various sites. This is equivalent to using a multivariate normal copula to construct a joint distribution that preserves the marginal single site distributions. Srikanthan points out that there is no known theoretical method to calculate the corresponding grade correlation coefficients from the correlation matrix and, hence, concedes that it is necessary to use a process of iterative adjustment to find the correct correlation matrix. This is one more reason why the calculation of a checkerboard copula of maximum entropy, as we propose in this paper, may be a more computationally efficient way to generate the required correlations. Since there are many other copulas that could be chosen for this task, it would also seem to be good practice to provide some rationale for the choice.
There is a large number of other papers that we could legitimately cite, but we mention only a few. For a more comprehensive review, we refer to Srikanthan and McMahon [11] and to an earlier review by Wilks and Wilby [12]. The over-dispersion phenomenon that bedevils the Srikanthan model was studied by Katz and Parlange [13], who suggested that higher order Markov models can reduce apparent discrepancies in the number of generated wet days and the number of observed wet days. Rosenberg et al. [14] constructed a joint density using a Laguerre series to incorporate the correlation between successive months and, hence, to correct the seasonal variance, but the optimal parametric structure of this model is unclear. Hasan and Dunn [10] have recently used a Tweedie distribution to model monthly rainfall. The model combines a Poisson process to generate wet and dry days and a collection of correlated gamma distributions to model daily rainfall depth. There is insufficient freedom in this model to match individual daily correlations, but it is possible to adjust the correlation parameters, so as to avoid the over-dispersion problem.
3. First Experiment: Comparing the Observed Seasonal Rainfalls with Simulated Observations for a Stationary Time Series at Various Timescales
In practice, it may be possible to observe only a finite number of terms in a doubly-infinite time series . In such cases, we may define the moving average , where Nk = N − k + 1 at scale k by:
If the time series, is stationary in the wide sense, then:
- (1)
E[μs(k)] = μ for all k = 1, . . . , Ns; and
- (2)
E[σs(k)2] = Rs(k) for all k = 1, . . . , Ns
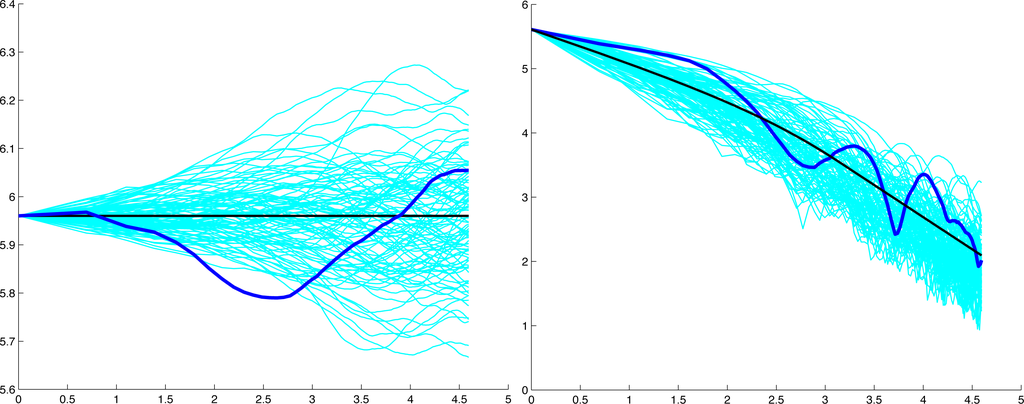
Consequently, we compared the observed time series of seasonal rainfall totals in Kempsey, where N = 123 years, with a large number of independently generated simulated observed time series of uniformly distributed uncorrelated pseudo-random numbers. For a time frame of s = 25 years, we compared the graphs of the log mean and log standard deviation at scale k against loge k for the observed rainfall to the corresponding graphs of the adjusted log mean , where cs = μs(1)/νs(1), and adjusted the log standard deviation , where ds = σs(1)/τs(1) for the pseudo-random numbers. The pseudo-random numbers were generated in Matlab.
If the partially observed time series of seasonal rainfall is a wide sense stationary time series of independent random numbers with mean μ and standard deviation σ, then for time frame s, the expected values, E[μs(k)] and E[σs(k)2], at scale k are given by:
The graphs in Figure 1 show that the mean and standard deviation at scale k for the series of seasonal rainfall totals exhibit similar behaviour to that of the corresponding adjusted mean and standard deviation for the simulated observations of a stationary time series of uncorrelated pseudo-random numbers. We conclude that it is reasonable to model the observed seasonal rainfall as a stationary time series and, hence, deduce that the distribution of observed values can be modelled by a real-valued random variable.
4. First Theoretical Principle: The Gamma Distribution Is the Maximum Entropy Model for a Random Variable Defined only by a Finite Number of Strictly Positive Observations
In his influential 1957 papers, the physicist E. T. Jaynes [2,3] wrote down the following general principle, now known as the principle of maximum entropy.
In making inferences on the basis of partial information we must use that probability distribution which has maximum entropy subject to whatever is known. This is the only unbiased assignment we can make; to use any other would amount to arbitrary assumption of information which, by hypothesis, we do not have.
We will use this principle to argue that the gamma distribution is the best model to represent the distribution of a random variable, X, provided the means of the partially observed totals and of the natural logarithm of the partially observed totals are both well-defined and finite. This is true if we assume that the observed totals are strictly positive.
It is useful to outline the mathematical argument. We wish to find a probability density f : (0, ∞) → [0, ∞), such that the differential entropy:
We can formulate this problem as a convex optimization with linear constraints. From the theory of Fenchel duality [16] (pp. 33–63) and the Fenchel–Young inequality [17] (pp. 171–178), we have:
We conclude that the gamma distribution with parameters α and β determined by solving (5) is the least ordered or least prescriptive probability distribution on (0, ∞) satisfying the nominated constraints. It is pleasing that Equation (5) is also the maximum likelihood equation used to estimate α and β if one has decided a priori to fit a gamma distribution to the observed values .
Remark 4.1. There are various other maximum entropy distributions that can be obtained by imposing constraints based on the observed data. The normal distribution uses constraints on the observed mean and variance. A normal distribution is not appropriate here, because it allows negative values. The exponential distribution uses a single constraint on the mean, but is unsuitable for monthly rainfall, because the maximum probability density is always at zero. The beta distribution requires an a priori choice of the allowed finite interval, which is difficult. The log-normal distribution is a maximum entropy normal distribution for the logarithm of the observed data, while the Weibull distribution is a maximum entropy exponential distribution for an appropriately chosen power of the observed data. The constraints used for the maximum entropy gamma distribution—that the distribution should be constrained by the mean of the observed data and the mean of the logarithm of the observed data—seem to be more basic.
Remark 4.2. There are other methods that have been proposed for selecting an appropriate distribution to model observed data. One such principle is the method of estimation by minimum description length proposed by Rissanen [18,19]. The method extends the principle of maximum likelihood and permits the estimation of the number of parameters required for a statistical model, their role in the model and their values. It rests on the derivation of a universal prior distribution for the integers, which, in turn, relies on classical notions of entropy. The Akaike information criterion [20] provides a similar basis for model selection. A recent paper by Weijs et al. [21] uses a restricted form of estimation by minimum description to show that a two parameter gamma distribution is the best model for daily rainfall depth.
5. Second Experiment: A Comparison of the Trend-Slopes for the Observed Time Series of Monthly Rainfall Totals and the Trend-Slopes for Simulated Time Series of Monthly Rainfall Totals Generated by the Appropriate Maximum Likelihood Gamma Distributions
The observed monthly rainfall totals for February, March and April in Kempsey for the period 1889 to 2011 are all strictly positive. Our tests so far suggest that we may reasonably propose the following null hypothesis: that the observed monthly rainfall totals in Kempsey in February, March and April can be modelled as independently and successively generated outcomes of independent stationary random variables with the respective gamma distributions Xi ∼ Γ(αi, βi) for each i = 1, 2, 3, where:
Although these models are clearly stationary, it is nevertheless true that finite samples of successively and independently generated random outcomes collated as a simulated time series may exhibit phantom trends. Our aim is to compare the trends (if any) in the series of observed monthly rainfalls for each month with the phantom trends in a large number of simulated data series of the same length generated by the corresponding gamma distribution. We will show that the trends in observed monthly rainfall are so small that they could reasonably be regarded as phantom trends, due to chance alone.
We tested the null hypothesis by a linear regression on the observed time series of monthly rainfall totals and on each of 20, 000 simulated time series of monthly rainfall totals over the same period of 123 years with each simulated series independently and successively generated by the proposed gamma distributions. Let {ri(t)} denote the rainfall in month i and year t. We used MATLAB to find (pi, qi), such that is minimized. The slope, pi, of this line is the trend-slope. In each case, we found that the trend-slope of the observed rainfall datasets lay well within the empirical 95% confidence intervals for the trend-slopes of the simulated rainfall datasets. The trend-slopes for the observed datasets and the corresponding 95% confidence intervals for the trend-slopes of the simulated datasets were p1 = 0.22 ∈ [−0.63, 0.63] in February, p2 = 0.19 ∈ [−0.55, 0.55] in March and p3 = 0.14 ∈ [−0.52, 0.52] in April. We conclude that there is insufficient evidence to reject the hypothesis that the observed monthly rainfall totals {xi,j}j=1,...,N are the outcomes of a stationary random variable Xi ∼ Γ(αi, βi) for each i = 1, 2, 3. This means that the apparent observed trends could reasonably be regarded as due to chance alone. The results of our simulations are shown in Figure 2.
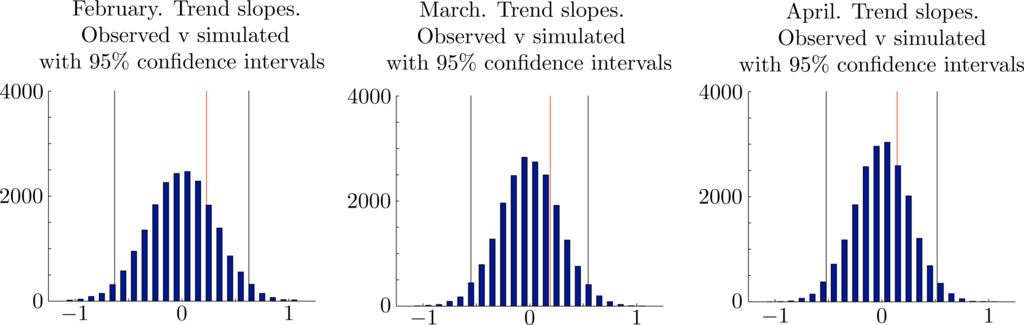
Since ri(t) ≈ pit + qi and since pi > 0 for each observed series, one could possibly argue that all observed trend-slopes are positive and that a null hypothesis of a positive trend slope in each case is more appropriate. If so, a more complex time-dependent model for both monthly and seasonal rainfall would be required. Although most climate scientists expect rainfall events in eastern Australia to become more extreme and although such changes could conceivably lead to more extreme monthly rainfall distributions, we believe there is currently no firm agreement about such rainfall trends.
6. Third Experiment: Using Q-Q Plots to Test the Goodness-of-Fit for the Simulated Time Series of Monthly Rainfalls Generated by the Maximum Likelihood Gamma Distributions to the Observed Time Series of Monthly Rainfall
We demonstrate the goodness-of-fit for the observed monthly rainfall data to the designated gamma distributions using Q-Q plots.
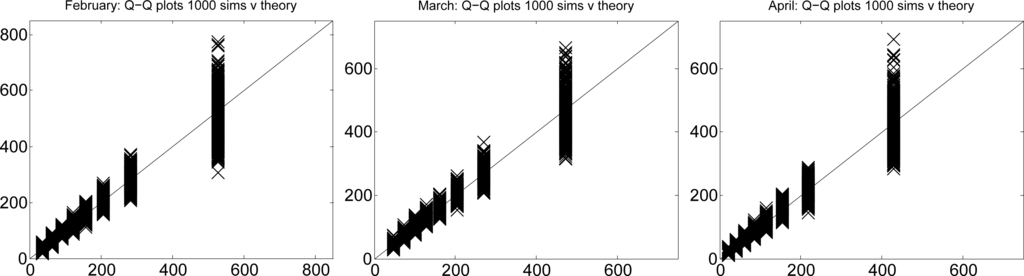
Firstly, we used the designated gamma distribution to generate 1000 simulated datasets. Then, we plotted the simulated quantiles against the theoretical quantiles. The results are shown in Figure 3. These plots show the full range of random variation that one should expect from observations of the designated gamma random variable from 1000 samples, each of size N = 123. By discarding the bottom 25 and top 25 values for each quantile from the simulated datasets, we found empirical 95% confidence intervals.
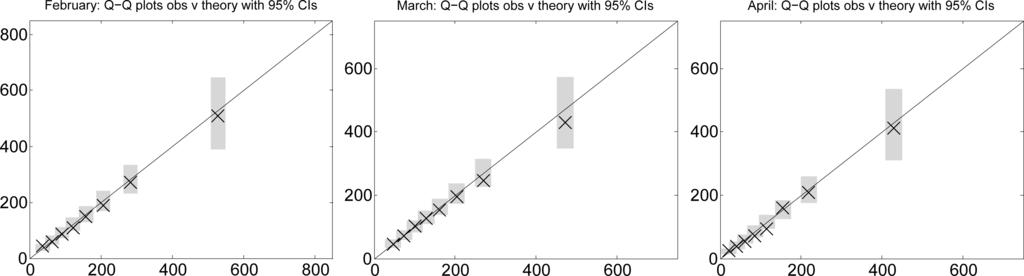
Secondly, we plotted the observed quantiles against the theoretical quantiles for the gamma distribution. The results are shown in Figure 4. We used grey bars on these plots to show the empirical 95% confidence intervals for the simulated quantiles. In all but one of twenty four cases, the observed values lie within the desired intervals. Thus, on the basis of the Q-Q plots, there are no recognised statistical grounds to reject the hypothesis that the monthly rainfall totals can be modelled by the designated gamma distributions.
Remark 6.1. We have been taken to task by some in the engineering community for not comparing our proposed model to other models currently in popular use. Nevertheless, our model is based on well-established scientific methodology. We use the principle of maximum entropy to argue that the maximum likelihood gamma distribution is the most appropriate model for rainfall accumulations in which the observed totals are strictly positive. While it is true that we make an arbitrary decision to use the sample means of the observed data and log-data as axiomatic constraints, we note that in any modelling process, some assumptions are necessary. At the very least, in our model, the assumptions and the subsequent logic are clearly defined.
Once the model is established, we use maximum likelihood to calculate the relevant parameter values and then test our model rigorously and impartially against the observed values according to accepted statistical wisdom. The conclusion is clear: there are no reasonable statistical grounds for rejecting the model. The argument that other models may provide a better fit to the observed data is essentially irrelevant. Indeed, this criticism embraces a fundamental misconception that an observed sample is always a true representation of the entire population. Moreover, the suggested iterative correction methods used by Srikanthan and others are subject to concerns about overfitting [22].
A legitimate criticism of our model would need to argue either that the principle of maximum entropy is inappropriate or else that we should incorporate more suitable constraints on the observed data.
7. Second Theoretical Principle: Finding a Checkerboard Copula of Maximum Entropy to Construct a Joint Density for Seasonal Rainfall that Matches the Observed Marginal Rank Correlation Coefficients and Preserves the Desired Marginal Monthly Distributions
The next step in the modelling process is to construct a joint probability distribution for the entire three-month time period. We will do this in what we believe is the most natural way: by using the principle of maximum entropy. Past studies of rainfall accumulations over several months [13,14] have concluded that the variance of the simulated time series of seasonal rainfall totals generated by models with independent marginal distributions is often not consistent with the observed variance. Since the observed data in Kempsey shows a positive correlation for February-March-April, we expect the observed variance in seasonal rainfall to be higher than one would find with independent marginal monthly distributions.
Our aim will be to construct a joint distribution that not only preserves the desired monthly rainfall characteristics, but also replicates the observed variance in the seasonal rainfall totals. We will do this using a checkerboard copula of maximum entropy. Once again, we will proceed on the basis that our model should satisfy the fundamental physical requirements (that the marginal distributions are preserved and that the joint distribution is constrained by the observed rank correlation coefficients), and that we should test the model against the observed data using accepted statistical principles. In the first instance, we need to show that the model satisfies the required constraints. In the second instance, we wish to show that the variance of the simulated seasonal rainfall totals is consistent with the observed variance.
7.1. Copulas with Prescribed Grade Correlation Coefficients
An m-dimensional copula, where m ≥ 2 is a cumulative probability distribution C(u) ∈ [0, ∞) defined on the m-dimensional unit hypercube u = (u1, u2, . . . , um) ∈ [0, 1]m for a vector-valued random variable U = (U1, U2, . . . , Um) with uniform marginal distributions for U1, U2, . . . , Um. We refer to [23,24] for further discussion. The correlation coefficients for the joint distribution are defined by:
For our proposed application, we make the following observation. Once it has been decided that the monthly rainfall, Xi, can be modelled by a gamma distribution Xi ∼ Γ(αi, βi) with Fi(x) = Fαi,βi (x), then we can define transformed random variables Ui = Fi(Xi) for each i = 1, 2, 3, which will be uniformly distributed on (0, 1). The original observed dataset {xi,j}j=1,2,...,N for the random variable Xi ∼ Γ(αi, βi) can be transformed into a corresponding dataset {ui,j = Fi(xi,j)}j=1,2,...,N for the uniformly distributed random variable Ui ∼ U([0, 1]) for each i = 1, 2, 3. This transformation is also important insofar as it removes seasonal factors from the observed data.
7.2. Problem Formulation and Solution for the Checkerboard Copula of Maximum Entropy with Prescribed Grade Correlation Coefficients
We now outline the basic ideas. An m-dimensional multivariate checkerboard copula is a probability distribution on the unit hypercube [0, 1]m defined by subdividing the hypercube into nm congruent small hypercubes with constant density on each one. If the density on Ii, where i = (i1, i2, . . . , im) is defined by nm−1hi ≥ 0, then the marginal distributions will be uniform if:
The principle of maximum entropy means that the best such distribution is the most disordered or least prescriptive solution: the multiply-stochastic hypermatrix h ∈ ℝℓ, which has the most equal subdivision of probabilities, but still allows the required correlations. In mathematical terminology, this is the hypermatrix that satisfies the grade correlation constraints and has the highest possible entropy.
We have the following formal statement of the problem.
Problem 7.1 (The primal problem). Find the hypermatrix h = [hi] ∈ ℝℓ, where i = (i1, . . . , im) and ℓ = nm to maximize the entropy:
The problem can be neatly and rigorously solved using the theory of Fenchel duality. The solution and a full description of the construction process for the trivariate checkerboard copula of maximum entropy can be found elsewhere [25,26]. We note that Matlab algorithms to construct the copula in three dimensions can be found on the website [27] for the Centre for Computer Assisted Research Mathematics and its Applications (CARMA). The m-dimensional copula of maximum entropy is determined by m(m − 1)/2 real parameters—the grade correlation coefficients—defined in Equation (7).
7.3. The Checkerboard Copula of Maximum Entropy for Seasonal Rainfall in February-March-April at Kempsey
We set m = 3 and n = 4. The triply-stochastic hypermatrix h ∈ ℝ4×4×4 describing the trivariate checkerboard copula of maximum entropy for February-March-April rainfall in Kempsey is shown below to four decimal place accuracy. We set ρ12 = ρ̂12 = 0.202, ρ13 = ρ̂13 = 0.112 and ρ23 = ρ̂23 = 0.152 and calculate:
8. Fifth Experiment: Simulations for Seasonal Rainfall in Kempsey
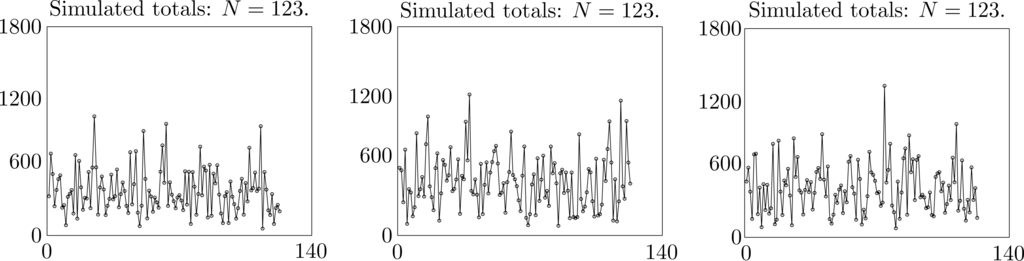
We used the copula of maximum entropy to generate numerous simulated datasets each spanning a period of N = 123 years. The simulation finds the monthly rainfalls in each year, draws a histogram of the total seasonal rainfall and plots the corresponding time series. The simulations show that sample statistics are quite variable. Selected results in Figures 5 and 6 from 15 successively generated simulated datasets illustrate the typical range of variation in samples of this size. Consequently, it is not unreasonable to believe that the statistics for an observed sample taken over a period of 123 years may exhibit similar variation. In view of these observations, we suggest that it is prudent to regard minor changes in statistical parameters from the observed values during the 30-year standard period 1961 to 1990 as random fluctuations. To obtain more reliable observed samples, it would be necessary to take observations over a much larger time span than 123 years.
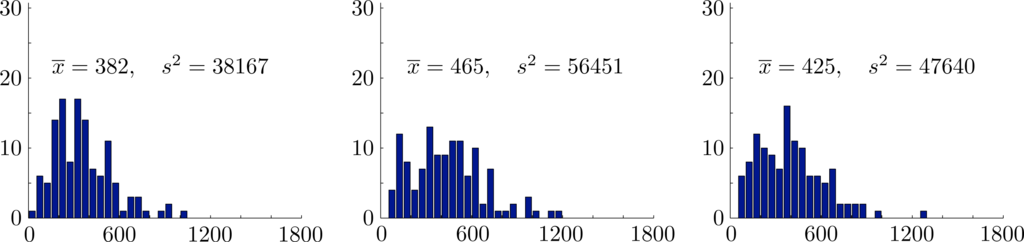
In Figure 7, we compare the observed frequencies for total rainfall with the probability density of the maximum likelihood gamma distribution X ∼ Γ(3.6524, 116.9983) for total rainfall and also show generated frequencies from a typical simulation using the copula of maximum entropy spanning a period of 12300 years. Summary statistics for both models are shown in Figure 7. Note that the maximum likelihood gamma distribution generates simulated seasonal rainfall totals directly and does not generate individual monthly rainfall totals.
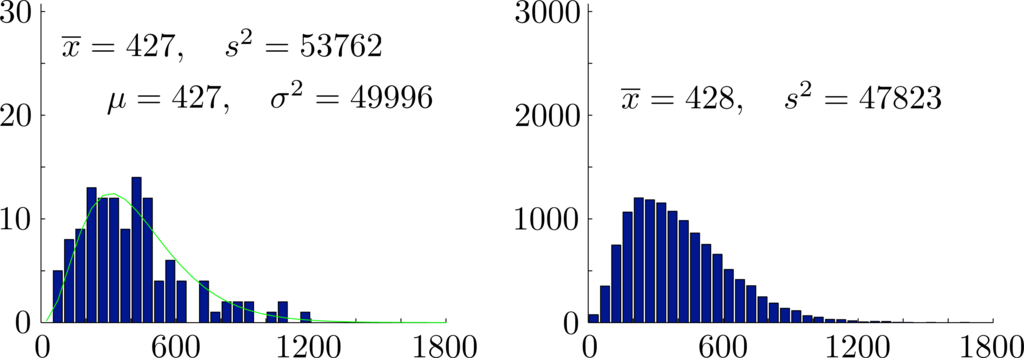
In Figures 8 and 10, we show histograms of sample means for monthly rainfall, sample means and variances for seasonal rainfall and corresponding values for the rank correlation coefficients from 10000 independently generated simulated datasets. Each dataset covers a period of N = 123 years. In each case, the empirical 95% confidence intervals established by the simulations are also shown. The mean values over all samples and the corresponding empirical 95% confidence intervals were , and for the monthly rainfalls, x̄ = 427 ∈ [396, 459] and s2 = 47467 ∈ [36403, 60266] for the seasonal rainfall and seasonal variance and ρ̂12 = 0.201 ∈ [0.055, 0.340], ρ̂13 = 0.111 ∈ [−0.037, 0.258] and ρ̂23 = 0.152 ∈ [0.004, 0.297] for the rank correlation coefficients. Importantly, we see that the observed overall variance 53762 ∈ [36403, 60266] lies well within the empirical 95% confidence intervals for the proposed model. We conclude that there are no reasonable statistical grounds to reject the proposed model.
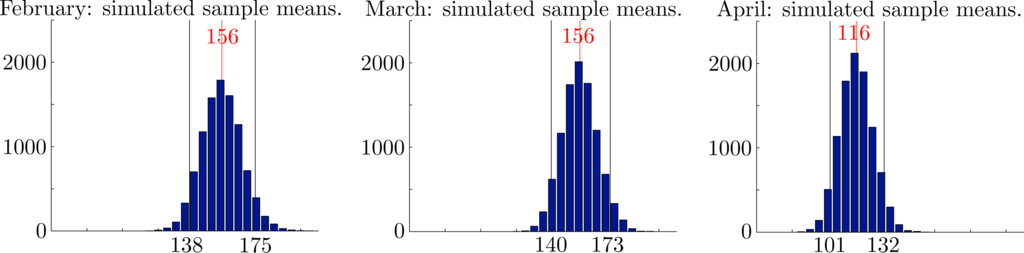
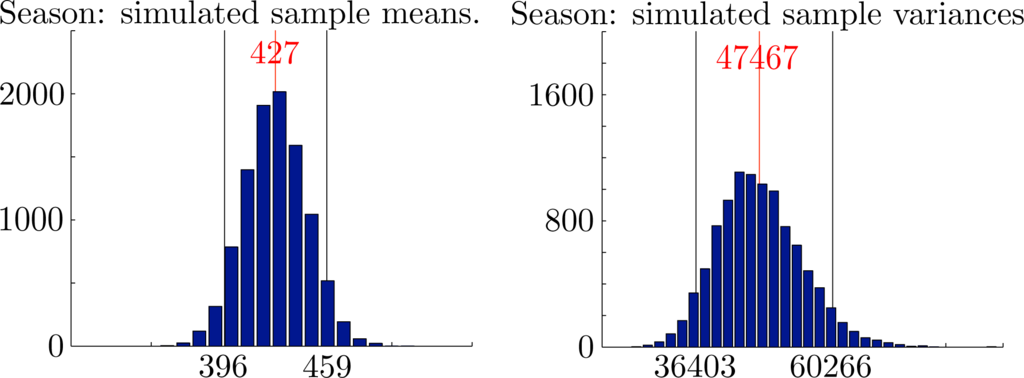
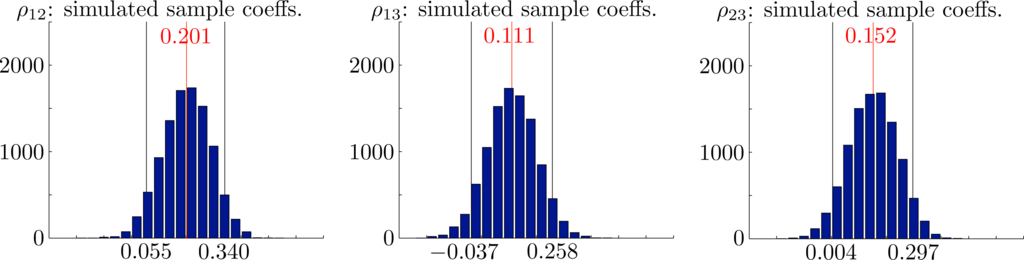
It is one thing to argue that the observed statistics lie within the empirical 95% confidence intervals generated by the proposed model. It is another thing altogether to turn this statement around and imagine that the observed statistics were actually generated by the model. If so, one might ponder on what should be expected from the next set of generated statistics. The answer is that one should not be unduly surprised by a change of ±7% in the average seasonal rainfall. In purely statistical terms, such changes lie within the empirical 95% confidence intervals and, as such, could be regarded as fluctuations, due to chance alone.
9. Sixth Experiment: An Alternative Joint Distribution, The Checkerboard Normal Copula
The normal distribution is popular and is generally regarded as easy to apply. Hence, we decided to compare the copula of maximum entropy to a copula defined by a multivariate normal distribution.
9.1. Constructing a Normal Checkerboard Copula with the Prescribed Grade Correlation Coefficients
The m-dimensional normal distribution φ : ℝm → [0, ∞) for the vector-valued random variable Z = (Z1, . . . , Zm)T ∈ ℝm with unit normal marginal distributions is defined by the density:
If we define Ur = Φ(Zr) for each r = 1, 2, . . . , m, then the random variables Ur are uniformly distributed on the interval [0, 1], and the function c : [0, 1]m → [0, ∞) defined by:
In practice, the normal copula is approximated by a checkerboard normal copula. The idea is simple. We assume that the positive definite symmetric matrix, Σ, is known. The unit hypercube I = [0, 1]m is divided into ℓ = nm congruent hypercubes Ii, where i = (i1, . . . , in), and we construct the corresponding multiply-stochastic hypermatrix k = [ki] ∈ ℝℓ where ℓ = nm by defining:
Write Σ = PΛPT ⇔ Λ = PTΣP, where P is orthogonal and Λ is diagonal. Now, consider the successive transformations w = Φ−1(v) ⇔ wr = Φ−1(vr) for each r = 1, . . . , m, followed by the length distortion y = Λ1/2w, the orthogonal transformation z = P y and, finally, the transformation u = Φ(z) ⇔ ur = Φ(zr) for each r = 1, . . . , m. It has been shown [26] that the collective transformation u = Φ[Λ−1/2PT Φ−1(v)] maps v ∈ [0, 1]m into u ∈ [0, 1]m. If we define the region Ji = Φ[Λ−1/2PT Φ−1(Ii) ⊂ [0, 1]m, then:
This means that the positive definite symmetric matrix, Σ, must be iteratively adjusted in order to satisfy the equations ρr,s = ρ̂r,s.
9.2. The Normal Checkerboard Copula for Kempsey
We set m = 3 and n = 4. The triply-stochastic hypermatrix k ∈ ℝ4×4×4 describing the trivariate checkerboard normal copula for February-March-April rainfall in Kempsey is shown below to four decimal place accuracy. We define Σ by setting θ12 = 1.3179, θ13 = 1.4309, θ23 = 1.3813 to give ρ1,2 = ρ̂1,2 = 0.202, ρ1,3 = ρ̂1,3 = 0.112 and ρ2,3 = ρ̂2,3 = 0.152 and calculate:
The simulation results are very similar to those obtained using the checkerboard copula of maximum entropy. It is necessary to search for the values of θr,s. For given values, θr,s, a Matlab program to find the necessary volumes by counting the transformed distribution of 643 equally spaced points in (0, 1)3 took 31 s to run and calculated the corresponding k to only a two-decimal place accuracy. This program was used to iteratively adjust θr,s. For the final adjustment, the program used 2563 points and took 1970 s to run. This shows that the calculation of the checkerboard normal copula is considerably more difficult than the calculation of the checkerboard copula of maximum entropy.
10. Commentary: The Modelling Process and Model Evaluation
In this section, we wish to comment on the modelling process. Thus, we compare our proposed model with two elementary models in order to highlight the key points. We will not compare our model directly with any of the more sophisticated models, such as the model proposed by Srikanthan, because it is not our intention to reach a conclusion about which model is best. Our intention is to examine the difficulties that arise when modelling rainfall accumulations and to examine the physical and theoretical basis for various assumptions. Our objective is to build a model based on the measurement of certain key statistics and to decide, on the basis of standard statistical performance criteria, whether the model should be rejected or accepted.
The question of which population model is best depends on the measurements that have been made and on the selection criteria. In our case, we argue that if we have a single sample of independently generated monthly rainfall totals and if only the sample mean of the observed values and the sample mean of the logarithm of the observed values are used as constraints on the model, then the principle of maximum entropy tells us that the maximum likelihood gamma distribution is the best model for the random generation of monthly totals. For the joint distribution of seasonal rainfall, we show that if a piecewise constant joint probability density is used on a subdivision of the unit cube, such that the marginal distributions are uniform and the grade correlation coefficients are equal to the observed rank correlation coefficients, then the principle of maximum entropy shows that the checkerboard copula of maximum entropy is the best solution. Thus, in a purely theoretical sense, on that axiomatic basis, there is no point in trying to compare our model to another model based on different measurement constraints and different selection criteria. A much more sensible debate is to argue about the most appropriate constraints and the best selection criteria to be used.
We understand why hydrologists have focussed on model outputs. The problems of catchment hydrology are real, and they require a solution. The simulation of realistic rainfall and run-off regimes over an entire river basin is vital for the planning of sustainable agricultural practice and for the implementation and operation of effective flood mitigation infrastructure. There is ample recent evidence in Australia of failures to understand and appreciate both the sustainability of agriculture and the management of the flood mitigation infrastructure. The failure of water supplies for irrigation in the Murray-Darling basin during an extended period of below average rainfall in eastern Australia from 2003–2008 and the flooding of Brisbane in January, 2011, are prime examples.
The main modelling motivations in catchment management are to understand long-term behaviour and to cope with the management of extreme events. Thus, the model construction should reflect the most appropriate data collection processes and the best statistical design in relation to the desired objectives. These issues are addressed in the study by Srikanthan [8], but the approach is somewhat informal and is general, rather than particular. Despite the acknowledged practical imperatives of catchment management, which seem to have captured the attention of engineers in recent times, we argue that it is both necessary and beneficial to continue investigating more basic modelling questions for which the answers are less tangible and the benefits less clear.
In the first place, there is the apparent contradiction in the process of modelling rainfall accumulations at a single site over different timescales. For each fixed timescale, there is general agreement that a mixed gamma distribution with cumulative distribution F (x) = P [0 ≤ X < x] for x ≥ 0 given by:
The same dilemma arises in the relationship between monthly and seasonal rainfall. This is the problem that we have tried to address. To test the utilitarian value of our model, we must test the properties of the seasonal rainfall totals. By contrast, the Srikanthan model [8] at an individual site is essentially a disaggregation model, since the model is ultimately adjusted at the monthly and daily level to match the annual characteristics. Hence, it was tested, with generally positive results, at a monthly and daily level. The model will be acceptable, in our view, if it can be shown that the bias introduced by modifying the monthly and daily rainfall totals is not significant. Incidentally, it can be seen that if the generated rainfall for a particular day at some given site is X̃ ∼ Γ(α, β), then the modified rainfall in the Srikanthan model will take the form X = kX̃ ∼ Γ(α, kβ). Thus, both the daily mean and daily standard deviation will be multiplied by the correction factor, k.
There are other important modelling issues. We use a model in which monthly rainfall distribution does not depend on the year. We have tested samples generated by our model and have concluded, using established statistical procedures, that the apparent trend-slopes in the observed data are well within the 95% confidence intervals for the randomly generated trend-slopes in the simulated data from our time-independent model. This means that the trends in the observed data could have been generated by chance alone. This does not mean that the observed data is time independent, and it does not mean that a time-dependent model would be unsuitable. Indeed, we noted earlier in the paper that a linear regression against time showed a positive trend-slope for the observations in each month. Thus, one could argue that an unbiased model should incorporate those observed trends and that one should expect random fluctuations in these base trend-slopes during simulation. The only clear reason to prefer a time-independent model is that it will be simpler.
The checkerboard copula uses a piecewise constant density on the unit hypercube. Although the maximum entropy criterion keeps the different densities as close to equal as possible, subject to the required grade correlations, the discontinuities are clearly an artefact of the model. An increase in the number of subdivisions will reduce the magnitude of these jumps, but also increase the complexity of the model. Since the grade correlation coefficients do not change, it is essentially a matter of judgement as to how many subdivisions should be used. See [23] for further comment.
The final point we wish to address is the issue of parameter estimation. Perhaps the most contentious estimation is that of the rank correlation coefficients. In each case, subsequent simulations with the proposed model showed the observed values and the empirical 95% confidence intervals as ρ̂12 = 0.201 ∈ [0.055, 0.340], ρ̂13 = 0.111 ∈ [−0.037, 0.258] and ρ̂23 = 0.152 ∈ [0.004, 0.297]. This suggests that one could legitimately argue that a model with ρ13 = 0 would be simpler and would possibly also fit the observed data. Nor is it entirely clear, on the basis of one sample, that all correlations are truly positive. Indeed, the strongest argument for assuming that there is positive monthly correlation is probably that a model with independent marginals will seriously underestimate the seasonal variance. Even this argument is not entirely certain, since the calculated variance of 38236 for the model with independent marginals lies within the empirical 95% confidence interval [36403, 60266] for the simulated variance obtained from our model.
In Table 1, the summary statistics for: (a) observed total rainfall in February-March-April in Kempsey are compared to the summary population statistics for models using; (b) the maximum likelihood gamma distribution; (c) the checkerboard copula of maximum entropy with marginal gamma distributions ; and (d) the joint distribution with independent marginal gamma distributions. Note that details of the theoretical calculation procedures for (c) can be found in [25,26].

11. Seventh Experiment: Simulations for Seasonal Rainfall in Sydney
We also successfully simulated seasonal rainfall in March-April-May in Sydney. We used official records from the Australian Bureau of Meteorology for Station 066062 (Observatory Hill) in Sydney in NSW during the period 1859 to 2008. The monthly rainfall totals were again modelled by gamma distributions Xi ∼ Γ(αi, βi) with the respective parameters defined by:
The copula of maximum entropy is shown below to four decimal place accuracy. We set ρ12 = ρ̂12 = 0.112, ρ13 = ρ̂13 = 0.043 and ρ23 = ρ̂23 = 0.183 and calculate:

12. Conclusions
The problem of seasonal rainfall modelling has no obvious solution. Our model is derived on a solid theoretical basis, and the standard tests of simulated data generated by the model against observed data showed there was insufficient evidence to reject the model on statistical grounds. There are many other models that have been proposed recently for the purpose of modelling catchment hydrology. In most cases, researchers report on the successful use of these models in the simulation of catchment rainfall. Although such models are tested extensively to ensure that the simulated data is a good approximation to the observed data, it seems there is often no clear axiomatic model structure, no explicit a priori measurement strategy for parameter estimation and no coherent testing procedure. It is more like measure everything you can, use as many parameters as you like and test every statistical parameter that comes to mind. See [22] for a relevant discussion of the backtest overfitting problem.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci 2007, 11, 1633–1644. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev 1957a, 106, 620–630. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev 1957b, 108, 171–190. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
- Ziedler, E. Applied Functional Analysis, Applications to Mathematical Physics (Applied Mathematical Sciences); Springer: New York, NY, USA, 1997; Volume 108. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
- Stern, R.D.; Coe, R. A model fitting analysis of daily rainfall. J. Roy. Stat. Soc. A 1984, 147, 1–34. [Google Scholar]
- Srikanthan, R. Stochastic Generation of Daily Rainfall at a Number of Sites; Technical Report 05/7; Cooperative Research Centre for Catchment Hydrology: Melbourne, Australia,, 2005. [Google Scholar]
- Getz, W.M. Correlative coherence analysis: Variation from intrinsic and extrinsic sources in competing populations. Theor. Popul. Biol 2003, 64, 89–99. [Google Scholar]
- Hasan, M.M.; Dunn, P.K. Two Tweedie distributions that are near optimal for modelling monthly rainfall in Australia. Int. J. Climatol 2011, 31, 1389–1397. [Google Scholar]
- Srikanthan, R.; McMahon, T.A. Stochastic generation of annual, monthly and daily climate data: A review. Hydrol. Earth Syst. Sci 2001, 5, 633–670. [Google Scholar]
- Wilks, D.S.; Wilby, R.L. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr 1999, 23, 329–357. [Google Scholar]
- Katz, R.W.; Parlange, M.B. Overdispersion phenomenon in stochastic modelling of precipitation. J. Clim 1998, 11, 591–601. [Google Scholar]
- Rosenberg, K.; Boland, J.; Howlett, P.G. Simulation of monthly rainfall totals. ANZIAM J 2004, 46, E85–E104. [Google Scholar]
- Koutsoyiannis, D. Hurst-Kolmogorov dynamics and uncertainty. J. Am. Water Resour. Assoc 2011, 47, 481–495. [Google Scholar]
- Borwein, J.M.; Lewis, A.S. Convex Analysis and Nonlinear Optimization, Theory and Examples, 2nd ed.; Springer-Verlag Inc.: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Borwein, J.M.; Vanderwerff, J.D. Convex Functions: Constructions, Characterizations and Counterexamples; Cambridge University Press: Cambridge, UK, 2010; Volume 109. [Google Scholar]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar]
- Rissanen, J. A universal prior for integers and estimation by minimum description length. Ann. Stat 1983, 11, 416–431. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar]
- Weijs, S.V.; van de Giesen, N.; Parlange, M.B. HydroZIP: How hydrological knowledge can be used to improve compression of hydrological data. Entropy 2013, 15, 1289–1310. [Google Scholar]
- Bailey, D.H.; Borwein, J.M.; de Prado, M.L.; Zhu, Q. Pseudo Mathematics and Financial Charlatanism: The Effects of Backtest Overfitting on out-of-Sample Performance. Available online: http://www.carma.newcastle.edu.au/jon/backtest.pdf (accessed on 24 December 2013).
- Kulpa, T. On approximation of copulas. Int. J. Math. Math. Sci 1999, 22, 259–269. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Lecture Notes in Statistics; Springer-Verlag: New York, NY, USA, 1999; Volume 139. [Google Scholar]
- Piantadosi, J.; Howlett, P.G.; Borwein, J.M. Copulas of maximum entropy. Optim. Lett 2012, 6, 99–125. [Google Scholar]
- Piantadosi, J.; Howlett, P.G.; Borwein, J.M.; Henstridge, J. Maximum entropy methods for generating simulated rainfall. Numer. Algebra Control Optim 2012, 2, 233–256. [Google Scholar]
- Centre for Computer Assisted Research Mathematics and its Applications (CARMA) website. Available online: http://www.carma.newcastle.edu.au/hydro/ (accessed on 7 December 2013).
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).