Abstract
In dyadic communication, both interlocutors adapt to each other linguistically, that is, they align interpersonally. In this article, we develop a framework for modeling interpersonal alignment in terms of the structural similarity of the interlocutors’ dialog lexica. This is done by means of so-called two-layer time-aligned network series, that is, a time-adjusted graph model. The graph model is partitioned into two layers, so that the interlocutors’ lexica are captured as subgraphs of an encompassing dialog graph. Each constituent network of the series is updated utterance-wise. Thus, both the inherent bipartition of dyadic conversations and their gradual development are modeled. The notion of alignment is then operationalized within a quantitative model of structure formation based on the mutual information of the subgraphs that represent the interlocutor’s dialog lexica. By adapting and further developing several models of complex network theory, we show that dialog lexica evolve as a novel class of graphs that have not been considered before in the area of complex (linguistic) networks. Additionally, we show that our framework allows for classifying dialogs according to their alignment status. To the best of our knowledge, this is the first approach to measuring alignment in communication that explores the similarities of graph-like cognitive representations.
1. Introduction
Talking to others seems to be a natural and easy thing. How is that? An answer to this question has recently been given by [1]. They argue that human dialog involves a mechanistic component that automatically brings about similar mental representations within interlocutors. Without further ado by the dialog partners, their representations on the linguistic levels involved in speech processing and understanding become aligned. The respective psycholinguistic model of language use is known as the Interactive Alignment Model (IAM). The model name is headed interactive since it is expressis verbis concerned with dialog. The basic setting of dialog is a two person, face to face conversation called a dyad. In a dyad, two interlocutors interact with each other in various ways, verbally and non-verbally. By their interaction, the interlocutors become coordinated with respect to their behaviors [2], or (structurally) coupled, to borrow a term from system theory [3].
In what follows, we briefly introduce the core statements of the IAM. We start with its significance for theory construction in research on human communication. Thereupon, priming is described as the basic mechanism of alignment according to the IAM. In this context, the notion of paired primes is introduced, which plays a decisive role in this article. Finally, we explicate the widely excepted explanation that alignment is a matter of degree of the similarity of mental representations. This is a main proposition of the IAM and the starting point of the modeling and measuring framework of two-layer time-aligned network series introduced in this article.
In the production as well as the comprehension of speech, interlocutors make use of mental representations of, so to speak, the meanings conveyed and the word forms encoding those meanings. These linguistic representations are, according to standard theories of speech processing following the hierarchical model of [4], organized into levels, reflecting the linguistic layers involved “from intention to articulation”. Accordingly, in dialog, alignment is found to take place in representations on all linguistic levels as, for example, the phonetic/phonological [5], the lexical [6], the syntactic [7], the semantic [8] level and on the level of situation models [9].
Since the linguistic levels are interconnected, alignment is, according to the IAM, supposed to percolate through these levels. Via this spreading of alignment, global alignment, that is, alignment of situation models—which are part and parcel of understanding—can be a result of local alignment on lower levels. In sum, the conception of alignment according to the IAM provides an account to the ease and efficiency of dialogical communication and therefore is a pivotal aspect of human communication. It supplements, though not substitutes, approaches to dialog that rest on higher level, resource-intensive cognitive acts such as coordination, negotiation, or maintenance of explicit common ground [10,11,12].
The central mechanism that is acknowledged within the IAM to bring about aligned representations is priming. Priming is typically understood and modeled as spreading activation within neural networks like the ones displayed in Figure 1. Given a linguistic form /a/ as input, that is, the so-called prime, we have to distinguish two scenarios of priming [13]:
- Firstly, the linguistic form /a/ activates or primes its representation a in the mind of the recipient.
- Secondly, by the priming of the mental representation a by its manifestation /a/, items that are, for example, phonetically, syntactically or semantically related to a may be co-activated, that is, primed in the mind of the recipient, too. Take the word form /cat/ as an example for a prime. Evidently, this word form primes the form /mat/ phonetically, while it primes the concept dog semantically.
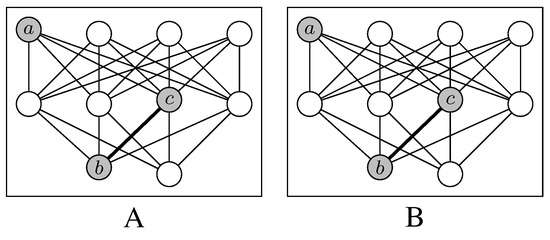
Figure 1.
Priming of representations within two networks of mental representations of an interlocutor A and B, respectively.
In this article, we focus on semantic priming among lexical units. Generally speaking, in a dyad, the linguistic representations of one dialog partner are primed by the utterances of his interlocutor and vice versa. This ongoing mutual priming may finally lead to the inter-personal alignment of the mental representations of both interlocutors. As [1](p.173) put it: “[A]n utterance that activates a particular representation makes it more likely that the person will subsequently produce an utterance that uses that representation.” On the lexico-semantical level, lexical alignment leads to the generation of a dialog lexicon, that is, a routinization of an unambiguous usage of certain word forms that are associated in a similar way by both interlocutors. Note that due to self-monitoring, priming also operates as a reflexive mechanism so that alignment occurs inter- and intra-personally. Each linguistic input, thus, co-primes representations within both interlocutors of a “dyadic conversational system”. As a result of this, their mental networks of linguistic representations become structurally coupled starting from paired primes that simultaneously operate within both interlocutors. Henceforth, we call lexical items that are produced by both interlocutors during a conversation, paired primes.
In a nutshell, we say that alignment is manifested by co-activated sub-networks of the interlocutors’ mental representations. In this sense, alignment can be conceived as a sort of graph similarity according to graph theory: the more similar the mental sub-networks of both interlocutors, which are co-activated during their conversation by using more and more paired primes, the more they are aligned. This is the approach followed here, that is, we measure alignment in terms of the similarity of graphs that represent networks of linguistic units as manifestations of conceptual units that are activated during a conversation.
Let us illustrate the phenomenological core aspects of alignment in communication by means of an empirical example in the area of route directions. In this example, which has been taken from the Speech and Gesture Alignment Corpus [14], a speaker A describes to his addressee B the windows of two churches B has to pass. In this scenario, the following dialogical interaction appears:
- A:
- both churches have those typical church windows, to the bottom angular, to the top just thus (pauses and performs a wedge-like gesture)
- B:
- gothically
- A:
- (slightly nodding) gothically tapering
This sample dialog extract involves two alignment phenomena. The first is B’s completion of A’s unfinished utterance. B proposes a word form that is associated with a concept that matches A’s description of a church window. The second one is A’s uptake of B’s proposal (throughout this article we ignore non-verbal information like the gesture in the above-given dialog extract; accounting for cross-modal alignment is left for future work—see [15] for first steps into this direction). B can only be up to complete A’s utterance if the gestalt A describes is, in an ecclesiastical context, related to the concept gothically. That is, a certain partial description triggers the representation for the word form /gothically/. When the word form in question is produced by B in the second turn, it triggers its representation in A and enables A to use it herself.
This sample datum illustrates two ways in which interpersonal alignment of representations is brought about. On the one hand, representations can become aligned via an association between them (e.g., gestalt ↔ gothically). On the other hand, alignment also occurs through identity (as the strongest form of similarity) of utterances or utterance features (e.g., gothically ↔ gothically).
When are representations said to be aligned at all? [1] base their notion of aligned representations on a similarity between them. Similarity is a matter of degree. Related by priming processes, two representations become more and more similar (“many aspects of the representation will be shared” [1](p.172)) right up to identity (“interlocutors share the same representation at some level” [1](p.172)). However, as the church window datum attests, it is not only similarity of representations that furnishes alignment, but also similarity of the links between these representations. In line with this conception, we distinguish two reference points of alignment (measurement):
- Firstly, alignment by the coupling or linkage of interlocutors due to the usage of paired primes, that is, by linguistic units which both are used to express certain meanings and which connect their mental representations interpersonally.
- Secondly, alignment by the structural similarity of the networks of representations that are possibly co-activated by these paired primes.
We call the first reference point alignment by linkage and the second one alignment by similarity. Both of them are at the core of our approach to alignment. Note that whereas alignment by linkage can be measured by counting shared items (that define paired primes), alignment by similarity is more demanding as its measurement requires to compute graph similarities as explained above. We propose an approach that integrates these two notions in a single framework. This is done with the help of a network model of dialog lexica that overcomes the notion of similarity in the sense of identity of mental representations as mainly acknowledged within the IAM. Alignment cannot be assessed properly by counting repeated elements on whatever linguistic levels. Rather, the relations between these elements have to be captured, too. We present a model that fulfills this requirement with a focus on lexical data in order to assess alignment of dialog lexica that are built by interlocutors as a result of their conversation.
What we come up with in this article is threefold:
- We develop a framework in which the notion of alignment, that we take to be essential for the understanding of natural language dialog, is operationalized and made measurable. That is, we provide a formal, quantitative model for assessing alignment in dialog.
- This model, and thereby the notion of alignment, is exposed to falsifiability; it is applied to natural language data collected in studies on lexical alignment. Our evaluation indeed yields evidence for alignment in dialog.
- Our framework also implements a developmental model that captures the procedural character of alignment in dialog. Thus, it takes the time-bounded nature of alignment serious and, again, makes it expressible within a formal model and, as a result, measurable.
The article is organized as follows: Section 2 overviews related work in the context of alignment measurement. Section 3 describes the experimental framework that we have developed to explore empirical data by which lexical alignment can be analyzed. This empirical basis is used throughout the article to formalize so-called Two-layer Time-Aligned Network (TiTAN) series as a network representation model of dialog lexica (Section 4.1) whose quantification in terms of alignment measures is provided by Section 4.2 and whose randomization is carried out in Section 5. The main empirical part of the article is presented in Section 6. Based on our network model, we first show in Section 6.1 that dialog lexica are naturally distinguished from their random correspondents described in Section 5. Secondly, in Section 6.2, we present a classification model of alignment by which we can automatically separate dialog lexica that manifest alignment from those that do not. Finally, in Section 8 we conclude and give prospect on future work.
2. Related Work
Although not concerned explicitly with alignment, there are some approaches of counting repeated elements over the time course of dialog in order to assess the influence of priming within and between interlocutors. The earliest work on assessing alignment-related properties of (written) texts in quantitative terms is the lexical adaption model proposed by [16]. [16] measured the frequency of primed words in comparison to unprimed ones in the second half of split documents. He found that the probability of occurrence of these primed words was higher in the second half of the documents than in the first half. A related measurement of the recurrence of syntactic patterns was conducted by [17], who account for the repetition of phrase structure rule instances within the Switchboard corpus [18] and Map Task corpus [19], in both the within-speaker (PP) and the between-speakers (CP) case. Their model additionally includes a delay parameter, ruling out long-distance primes as coincidental. [17] found positive priming effects in both corpora. However, PP priming is stronger than CP priming, and CP priming is much stronger in Map Task than in Switchboard.
A priming assessment that relates counting repeated elements to task achievement was implemented by [20]. They train a Support Vector Machine (SVM) to predict task success from lexical and syntactic repetition in the HCRC Map Task corpus. The SVM is applied to time stamps in the data, indicating the proportion of variance that can be explained by the model. The resulting coefficient was , indicating that “linguistic information alone will not explain the majority of the task-solving abilities” [20](p.182).
In addition to these approaches, there are two accounts that rely on an experimental setting that is not part of the dialog proper, i.e., part of the “linguistic information [...] encoded in sound.” [1](p.177). The assessment of priming effects in the work of [21] is embedded in psychological experiments. For example, in the card description experiment reported in [21] the prime is a two-stage factor varying over prepositional object (PO) vs. double object (DO) constructions, that is, either sentences of the form The X verbing the Y to the Z or of the form The X verbing the Z the Y. Experiments are recorded and transcribed, specifying the type of the prime and of subsequent descriptions. The authors found that the type of the prime had a significant effect, i.e., they found evidence for syntactic priming.
Yet another approach is followed by researchers around Nicholas Fay and Simon Garrod that are concerned with the evolution of symbol systems from iconic representations to symbols conventionalized by interactive usage. Their work is based on a series of empirical studies within the Pictionary framework: a concept has to be drawn by a so-called director and understood by a so-called matcher. [22] found that establishing a symbol is a matter of feedback-driven grounding rather than of mere repetition. [23] observe that the graphical representations of a concept become more and more aligned in dyads as well as in larger-scale communities. However, they give no explication of “graphical alignment” beyond mere visual inspection of the researchers themselves.
In a nutshell, assessing alignment so far is primarily based on approaches that count repetitions of (linguistic) items shared among interlocutors. To date, there is no model of alignment that measures the structural similarity of cognitive networks in terms of the similarities of their manifestations in the form of linguistic networks. The present article aims to fill this gap.
3. An Experimental Setting of Alignment Measurement
How to make alignment an object of empirical measurement? How to get insights into the degree to which interlocutors are aligned cognitively as a result of their conversation? Because of the fundamental openness of dialogical communication (regarding its thematic and verbal diversity), it seems to be impossible to answer questions of this sort. However, there is a way out of this impasse, that is, via controlled dialogs by which the thematic universe of conversations can be constrained as their course of events can be sharpened so that alignment can be focused by measurement operations. In this section, we describe the so-called Jigsaw Map Game (JMG) as an experimental framework for alignment measurement by which we get dialogical data that is controlled in the latter sense. This section describes the design of the JMG and the corpus being derived from its conduction.
The empirical investigation of language processing in communication has developed around a relatively small number of experimental settings [24]. As language use in natural conversations cannot readily be controlled, some experimental designs have been developed to elicit semi-spontaneous dialog situations where some degree of control over the topic of conversation is possible. The most important paradigms are the referential communication task [25], the maze game [8] and the map task [19].
Though the referential communication task allows for a detailed analysis of referential processes, there is always a fixed role allocation between the communicating partners. Maze game studies highlight some of the ways in which language processing in a task allowing relatively free verbal interaction is affected by the demand of consensus in dialog. But with both players sitting alone in different rooms, each of them presented with the maze on his/her monitor, no real face to face situation is created. In the spatial map task again there is a clear role allocation of the partners. Due to these considerations it became evident that for the examination of basic processes in natural face to face dialogs none of these paradigms was sufficient on its own. Consequently, with the Jigsaw Map Game (JMG) [26] we developed a flexible design, which permits us to investigate language processing in interactive conversation in a natural but controlled way.
The setting is based on the referential communication task, but also includes some elements of the maze game and the map task. It allows for naturalizing experimental dialogs by encouraging face to face interaction with naïve participants mutually perceiving their behavior while communicating in a multimodal way. At the same time, one can control important dialog parameters such as dialog organization and task-relevant knowledge by regulating the flow of the game and balancing the roles of the partners.
The scenario of the game is as follows: two participants cooperatively position real objects like cuboids, cones or buttons on a table, which serves as common interaction space, until all objects are placed on the table according to a predefined object arrangement (see Figure 3). The arrangement is designed in such a way that some objects stand out because of size. These objects define so-called critical objects as there are normally at least two possible object names in the underlying language (in our case German) to name them (e.g., ball vs. bowl) as has been verified by a pre-study [26]. The variation of the critical object names is realized by adopting some elements of the confederate priming paradigm [7]. The first participant plays the game with a confederate (confederate dialog) who was instructed to use specific object names so that the participant acquired them implicitly through lexical priming. Then, this participant meets up with a second naïve participant playing the game again (experimental dialog). The cooperative character of the game emerges because each partner gets, via instruction cards, only partial information about the final arrangement. These instruction cards contain in each case the constellation of exactly three objects at a time: two already positioned and one new object that has to be placed by the partner in the next step. Guided by these instruction cards, partners communicate in turns which object the other should pick next from a personal object box (object identification) and where it has to be placed on the table (object placement) until the whole arrangement is completed. Further corrections or specifications are possible. For data analysis regarding, for example, alignment on the lexical level, we can record how interlocutors name the objects and how this naming gets aligned or not during the course of a dialog.
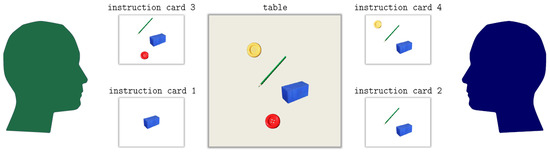
Figure 3.
Schematic depiction of an object arrangement in the JMG: agent A (left side) plays two instruction cards as does agent B (right side). Numbers indicate the order of the cards being played. The map in the middle shows the object arrangement after these for cards have been processed.
In the present study, we consider three critical and three uncritical objects (see Figure 2). Figure 3 depicts a sample series of four instruction cards equally distributed among the interlocutors. The numbers indicate the order by which the cards are processed. Each instruction card defines a target object to be placed on the table. A single round of the JMG is defined by the processing of such a card whose focal topic is defined by the object to be located. Obviously, the interlocutors may, but do not need to align in using critical terms for naming the objects or in using any other lexical items when performing the game cooperatively. Thus, they may, but do not need to bring about aligned dialog lexica as a result of their controlled conversation. In Section 6 we use this data to measure alignment by example of the JMG.
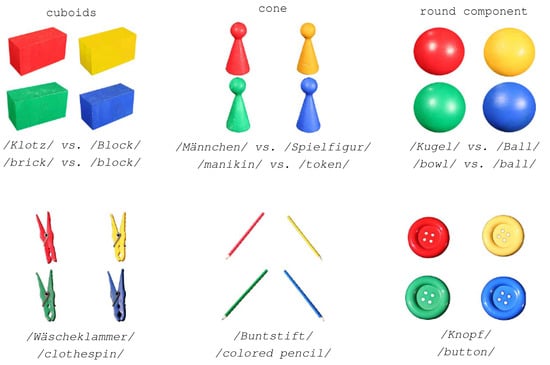
Figure 2.
Critical (upper row) and uncritical (lower row) objects and their naming (/in diagonal slashes/) in the JMG.
In order to successfully identify the objects that have to be arranged on the table, the participants have to agree on how to refer to these objects. Part of this agreement is plainly due to the fact that the participants share a language. However, in the case of the critical objects, language does not provide unique terms. Thus, participants have to choose between several alternatives. Their choice may or may not fall onto the same term their partner has used previously. It is only in the positive but not the negative case that we observe a necessary condition of lexical alignment. The reason is that using the same term the same way for denoting the same object is what we mean by lexical alignment. Thus, our measurement procedure goes beyond simply counting shared items: it also looks for common usages, which will be represented by means of networks. Since this scenario holds for each critical object and for each card displaying a critical object, a spectrum of (non-)aligned lexical choices over the time of a JMG round is possible and to be expected. In this sense, the experimental design of the JMG provides a controlled setting for studying paths of lexical alignment in task-oriented dialog.
An overview of the corpus of dialogs that have been derived from the JMG is given by Table 1. Note that in this study, we analyze experimental dialogs as well as confederate dialogs. This is only done in the experimental classification as described in Section 6.2. Using dialogs with confederates is due to the problem of data sparseness. As we do not provide a supervised classification that uses them for any training and as we do not make any claim about the causes of alignment in a dialog when being successfully classified by our algorithm, we are convinced that using dialogs including confederates is unproblematic in the present scenario. In any event, in Section 6.1 where we discus the temporal dynamics of alignment, we only explore experimental dialogs.

Table 1.
Overview of the corpus of 24 dialogs based on the JMG played by 24 naïve participants and 13 confederates. Asterisks code experimental dialogs in which only naïve interlocutors participated (in contrast to confederate dialogs). Column 2 codes whether the dialog manifests alignment or not according to a manual annotation as explained in Section 6.2. The corpus belongs to a larger corpus of 32 dialogs (in preparation). Data has been partly annotated using the Ariadne system [27]. is the lexicon size, and are the sizes of the interlocutors’ sublexica. is the number of associations (edges) that have been induced by the algorithm of Section 4. #events is the number of nominal word forms in referential function and #turns is the number of turns.
4. A Network Model of Alignment in Communication
Generally speaking, in order to model interpersonal alignment in dialogical communication, we need at least two ingredients: firstly, a graph model that is expressive enough to capture the specifics of dyadic communication (see Section 4.1), that is, its characteristic distribution over two interlocutors as a result of their turn-taking. Secondly, we need a quantification of this graph model (see Section 4.2) that gives insights into the temporal dynamics of alignment according to its time course. At the same time, this model should allow us to separate aligned from non-aligned conversations. Obviously, models based on simple graphs that have traditionally been used to represent linguistic networks ([28,29,30,31,32,33,34]) are not expressive enough to capture dialogical communication, its inherent bipartition and gradual development. Rather, we need to develop a novel graph model in conjunction with topological indices to capture the specifics of dialogical communication.
4.1. Two-Layer Time-Aligned Network Series
If dyadic, dialogical communication is structured by the turn-taking of two interlocutors and thus happens in time. That is, bipartition and time reference are reference points of any network model of dialogical communication. In order to capture both of them, we invent the notion of a two-layer time series of lexical networks as illustrated in Figure 4(1-3). It presents the gradual build-up of the dialog lexica of two interlocutors A and B as a result of their conversation. Vertices in Figure 4 denote types of lexical items uttered by A or B, respectively, while edges represent associations among these types as a result of their co-activation during the conversation. At the beginning of the conversation, at time point 1, each agent starts with a specific set and of unlinked lexical items. For a single agent, this set represents the subset of items of his overall lexicon that he activates during his conversation. From this perspective, interpersonal alignment of dialog lexica includes two networked networks: the one representing the sub-lexicon of agent A and the other representing the sub-lexicon of his interlocutor B where both networks are connected by edges that represent interpersonal associations. This is a significant departure from many linguistic networks ([28,29]) of written communication in which edges denote associations among linguistic items that have been produced by authors separately. In contrast to this, our focus is on intra- and interpersonal (lexical) associations in spoken communication. In other words, we deal with a sort of statistics of association ([35,36]) that is also based on paired primes. Note further that while linguistic networks generally cover several communication events (on a larger time scale as, for example, a corpus of texts written at different days), in our case networks are always induced by single conversations (on a very short time scale).
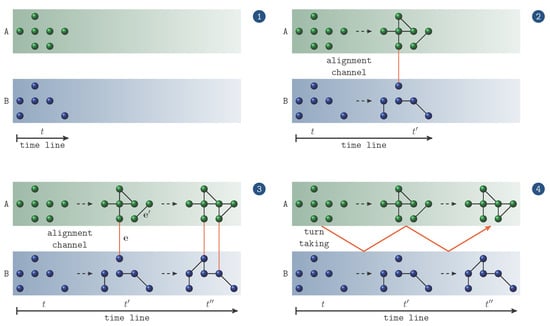
Figure 4.
Schematic representation of a Two-layer Time-Aligned Network (TiTAN) series starting with two initially unlinked lexica of interlocutor A and B (upper left). Both interlocutor lexica are networked step by step (upper right) till, finally, a dialog lexicon emerges that is spanned by intra- and interpersonal links across the alignment channel (lower left). The lower right part of the figure highlights the role of turn-taking as the means by which dialog lexica (represented as TiTAN series) gradually evolve.
Obviously, this scenario goes beyond graph models based on simple bipartite graphs that still predominate in the analysis of complex linguistic networks (see [37] for an overview): although we can separate two parts in the dialog lexicon of a conversation, both interlocutors’ lexica are structured in themselves so that we better speak of a two-layer graph [30]. On the other hand, a dialog lexicon is an emergent entity that gradually evolves during a conversation so that we get for each of its time points a snapshot of the development of this lexicon. Thus, a dialog lexicon can be conceived as a time series that emits two-layer networks at each time point. We now present a graph model that captures these specifics in terms of a TiTAN series. In order to distinguish the constituents of such time series terminologically, we speak of the (overall) dialog lexicon of the conversation of two interlocutors A and B that is induced by edges between both interlocutor lexica and of agent A and B, respectively.
Generally speaking, two-layer networks—as separately depicted for the different time points in Figure 4—remind one of bipartite graphs whose vertex set V is partitioned into non-empty disjunct subsets so that every edge ends at vertices and , respectively [38]. However, two-layer networks are different. These are networks in which both parts are networked in themselves. In case of our application area this linkage is due to intrapersonal associations among lexical items. That is, two-layer networks are graphs in which the vertex set V is partitioned—by analogy to bipartite graphs—into non-empty disjunct subsets and such that the edge set E is additionally partitioned into three non-empty disjunct subsets so that all edges end at vertices , while all other edges end at vertices (for a generalization of this notion see [30]). The subgraphs and are called the A- and B-layer of the two-layer graph and are denoted by the projection function
In order to denote the vertex and edge sets of any such projection we write and for . In terms of our application area, layer A represents the interlocutor lexicon of agent A, layer B the lexicon of agent B and G represents the overall dialog lexicon of the conversation of both interlocutors (see Figure 4 for a depiction of this scenario).
In order to complete our model of a TiTAN series we have to consider that dialog lexica are weighted labeled graphs that are indexed by the point in time at which they are built. We assume that vertices are labeled by the surjective function for the set of labels (e.g., lemmata). Each time an interlocutor produces an output of the linguistic type (e.g., nominal or verbal) under consideration, the series proceeds to the next time point. As a two-layer graph, is divided into two subgraphs
according to the distribution of over the agents A and B at time t. In Figure 4(3), this corresponds to a column of the TiTAN series. Note that is the bijective restriction of to , while the weighting function is the restriction of to . , , weights the intrapersonal strength of association among the items x and y that are interlinked in the lexicon of interlocutor X. For two items , , , weights the interpersonal strength of association among the items x and y that are interlinked in the dialog lexicon of A and B at time t. Throughout this article we only consider two-layer graphs for which , , is a bijective function. That is, there are no different vertices of the same layer that are equally labeled.
By continuing their conversation, both interlocutors A and B gradually introduce new associations or reinforce associations that are already established in the dialog lexicon. The sources of this process are at least threefold: interlocutors may continue to reuse items in similar contexts or to use them in novel contexts. Further, they may introduce items that they did not use before in their conversation. In the present framework, we model these processes by inducing new edges or by strengthen the weights of already given ones. As we deal with dyads, we have to distinguish inter- from intrapersonal edges. In order to ensure the referential semantic background of lexicon induction (see Section 3), these edges are built subject to the focus of the conversation on certain topics. In the JMG, this is reflected by its division into rounds, each of which corresponds to a target object (e.g., cone or ball) to be positioned on the table, where different rounds may deal with the same topic, that is, object. Thus, for each time point t of a JMG we can identify the topic that is focal at t. In this way, we get a reference point to demarcate thematically homogeneous dialog units as constituents of a dialog above the level of turns. This is needed to establish co-occurrence statistics where lexical items are said to co-occur in certain frames—in our case these are the latter dialog units. In principle, we may consider two variants to induce intra- and interpersonal links:
- Variant I—unlimited memory span:
- −
- Interpersonal links: if at time t, agent uses the item to express the topic that has been expressed by in the same round of the game or in any preceding round on the same topic T by the same item, we span an interpersonal link between and for which , given that e does not already exist. Otherwise, if , its weight is increased by 1. The initial weight of any edge is 1.
- −
- Intrapersonal links: if at time t, agent uses item l to express , we generate intrapersonal links between , , and all other vertices labeled by items that X has used in the same round of the game or in any preceding round on the same topic T. Once more, if the links already exist, their weights are augmented by 1.
Variant I models an unlimited memory where both interlocutors always remember, so to speak, every usage of any item in any preceding round of the game irrespective how long ago it occurred. Obviously, this is an unrealistic scenario that may serve as a borderline case of network induction. A more realistic scenario is given by the following variant that simulates a limited memory. - Variant II—limited memory span:
- −
- Interpersonal links: if at time t, agent uses to express topic that has been expressed by in the same or preceding round on the same topic by the same item, we span an interpersonal link between and for which , given that e does not already exist. Otherwise, e’s weight is adapted as before.
- −
- Intrapersonal links: if at time t, agent uses item l to express , we generate intrapersonal links between , , and all other vertices labeled by items that X has used in the same round or in the preceding round on the same topic T. If the links already exist, their weights are augmented by 1.
The latter scenario models a limited memory span where (co-)occurrences affect lexical associations only within the same or successive rounds. Otherwise, this effect fails to appear—regarding the induction of new associations and the update of already activated associations. In more technical terms, this can be explained as follows: suppose that time points t are represented by triples of agents X, topics T and lexical items l. In Variant I, an interpersonal link is generated (or updated) at for any pair of time points , , , where . In Variant II, this only happens if there is no time point such that .
Note that there are strong linguistic arguments in favor of Variant II: [39] found that syntactic priming is subject to decay: it has a close time-limited effect that diminishes rapidly. Besides this short-term priming, [40] identified a long-term effect they called adaptation. [41] argued that the long-term and the short-term priming involve different cognitive processes. Though [1] do not distinguish these two kinds of priming explicitly, the IAM most likely rests on a short-term mechanism as reflected by the turn restriction of Variant II. For this reason, we only implement this variant to span intra- and interpersonal links in dialog lexica. This is done for nouns so that lexical items l in triples of the sort always stand for nominal units. In principle, the model introduced here is open to additionally consider items of other part of speeches. However, as we focus on referential descriptions we consider vertices that are labeled by nouns.
In Figure 4(3), interpersonal links are exemplified by edge e, while intrapersonal links are exemplified by edge . Interpersonal links are said to cross the alignment channel between A and B. Obviously, without turn-taking no interpersonal links would exist in this model. Thus, turn-taking as depicted in Figure 4(4) is constitutive for TiTAN series. The more such interpersonal links exist, the more the interlocutors tend to express the same topics by the same items. Analogously, the more intrapersonal links exist, the more the corresponding agent tends to use the same group of items to express the same topic. Variant II transfers the notion of a usage-based semantics ([36,43,44]) onto the level of dialog lexica: associations are established among lexical items that are used in similar contexts where the strength of their associations is a function of the frequency of the items’ common usages.
One advantage of our graph model is that it directly allows for representing turning points of alignment as shown in Figure 5: on the left side, a dialog lexicon is depicted with no interpersonal links across the alignment channel. Such a lexicon results from a conversation in which neither of the interlocutors use the same items to speak about the same topic (though they may use the same items to speak about different topics). That is, both agents use different words or the same words differently so that their lexica are nonaligned. In other words, missing interpersonal links or few interpersonal links of low weights indicate non-alignment. The right part of Figure 5 demonstrates the opposite case in which both interlocutors use exactly the same words the same way so that their dialog lexica are completely aligned. Obviously, dialog lexica as emerging from real conversations appear somewhere between these extreme points. This is depicted in Figure 6. It shows the final dialog network of a dyadic conversation of which it is known that they manifest lexical alignment (see Section 3). Obviously, this network is far from the extreme case of an unaligned two-layer network as it has many, highly weighted links across the alignment channel. At the same time, this network is also very different from the idealistic scenario of completely aligned lexica of two interlocutors. A central hypothesis of this article is that the position of real lexica regarding this spectrum of two-layer networks (as spanned by the turning points of minimal and maximal alignment) is law-like. If this is true it should be possible to classify aligned and non-aligned lexica only by means of their topology. In other words, TiTAN series that are induced from natural dyadic conversations should be both distinguishable from their random counterparts and separable in terms of aligned and non-aligned dialogs. We now present a quantitative model of TiTAN series that allows this classification only by virtue of the topology of two-layer networks.
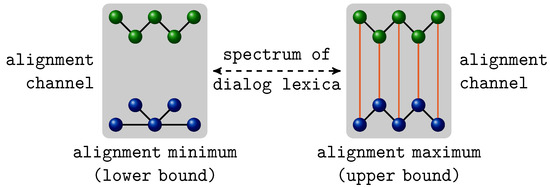
Figure 5.
A graph-theoretical model of turning points of lexical alignment (cf. [42]). On the left side, a two-layer dialog lexicon is shown whose layers are completely separated as there are no links crossing the alignment channel. The right side depicts the opposite case where both interlocutor lexica are identical and where each item is linked across the alignment channel with its correspondent in the lexicon of the opposite interlocutor.
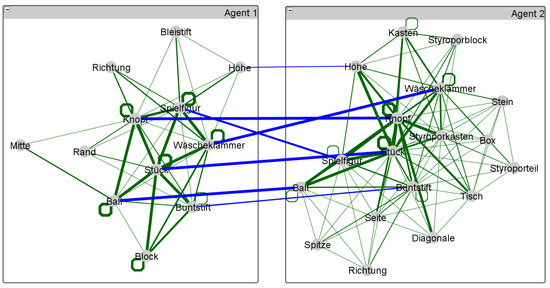
Figure 6.
The final two-layer network of a TiTAN series that represents a gradually evolving dialog lexicon of two interlocutors. Initially, no items are interlinked. From turn to turn, more and more associations are established intra- and interpersonally so that the dialog lexicon is finally structured as depicted by the network. Edge weights are represented by the thickness of lines.
4.2. Mutual Information of Two-Layer Networks
Our aim is to quantify dialogical alignment of two interlocutors as a function of topological commonalities of their dialog lexica represented as the layers of a two-layer network. In Section 1, we have explained that alignment can in principle be conceived as a sort of structural coupling that results from interlinking similar cognitive structures. Thus, linkage and similarity of cognitive systems are major reference points of our search for alignment measures.
By representing dialog lexica as networks, we are in a position to apply the wide range of topological indices that have been invented to describe complex networks ([45,46,47,48]) in general as well as linguistic networks ([29,30,31,33]) in particular. We will use some of these indices to characterize the topology of two-layer networks in TiTAN series. However, we also face the fact that the majority of indices have been developed to describe unipartite graphs. Therefore, we put special emphasis on measures that focus on the topological characteristics of two-layer networks in terms of their inherent bipartition. A natural way to do this is to compute the classical indices of network theory separately for both layers and of a two-layer graph G. This approach will be adopted here—however, only as one of several alternatives.
As we are interested in measuring alignment in terms of the linkage and the structural similarity of the dialog lexica of conversational partners, it seems promising to apply the apparatus of graph similarity measurement [49]. We may say, for example, that two interlocutors are the more lexically aligned, the more similar the graphs that represent their dialog lexica. It is well known that many algorithms for computing graph similarities are NP-hard [50]. Thus, we face a dilemma: we want to measure alignment in terms of structural similarity, but this seems to be infeasible.
To find a way out of this impasse, we now introduce a graph similarity measure based on the notion of mutual information of two graphs (as, e.g., the projections and of a two-layer graph G) (see [51] and [52] for related approaches to information-theoretical indices of graphs; see also [53] for a classical approach in this research branch). Our idea is to integrate the notion of MI-based distance measurement in the sense of Kraskov & Grassberger [54] with the notion of vertex probabilities leading to the structural information content in the sense of Dehmer ([52,55,56]). More specifically, [54] prove that for two random variables X and Y the quantity
is a metric where is the Mutual Information (MI) of X and Y. Intuitively, if is low in relation to , that is, if X and Y tend to be statistically independent (so that knowing X does not inform very much about Y, and vice versa), then X and Y are highly distant. Conversely, if knowing X reduces much of the uncertainty about Y and vice versa, then both variables are less distant, that is, is low.
Regarding the underlying notion of MI these are well known concepts. But how to apply them to measuring the distance of graphs? How to derive a notion of alignment measurement based on D? In order to answer these questions, has to be defined in graph-theoretical terms. This can be done with the help of the notion of local graph entropy. Generally speaking, a graph entropy is defined by means of an equivalence relation over the set of vertices or edges of a graph G such that for the set of classes a probability distribution is defined by the quantities , [53]. [52] uses a different approach in that he captures more of the topological information of a graph by analyzing patterns of geodesic distances of their vertices. Based on this work, [56] define the entropy of a graph G by the following quantity:
where
is called an information functional operating on vertex , is the geodesic distance of v and w in G, is a vector of weights , , that bias the so-called j-spheres of v, and is the diameter of G. By Graph in Figure 7, for example, we see that , , and . By varying the vector , one gets different instances of the class of entropy measures in Equation 4. Intuitively, high values of indicate shared patterns of geodesic distance among the vertices of G, while low values hint at unequally distributed patterns of this kind. This is in the line of what we seek, but with a focus on complete graphs. That is, we need a measure of the (dis-)similarity of two graphs that tells us something about the patterns of the geodesic distances of their vertices.
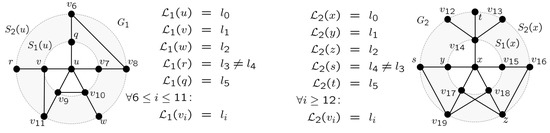
Figure 7.
Two labeled graphs and as the projections and of a graph such that and . and share, for example, an equally labeled vertex in the 1-sphere of and , respectively.
As we deal with labeled graphs, we use a different definition of j-spheres. More specifically, we assume that j-spheres are defined on uniquely labeled graphs or on some appropriately delimited subgraph , where  , that fulfills this condition of unique labeling. In this case, we define for any the j-sphere of v in G as the set:
If the denotation of G is clear from the context, the superscript G is omitted.
, that fulfills this condition of unique labeling. In this case, we define for any the j-sphere of v in G as the set:
If the denotation of G is clear from the context, the superscript G is omitted.
 , that fulfills this condition of unique labeling. In this case, we define for any the j-sphere of v in G as the set:
, that fulfills this condition of unique labeling. In this case, we define for any the j-sphere of v in G as the set:As operates on unipartite graphs, it cannot be used to derive a measure of the MI of graphs. However, its underlying notion of a j-sphere has this potential. Suppose that we have two labeled graphs and as exemplified in Figure 7. Intuitively, we say that the MI of both equally labeled vertices and in Figure 7, for which , is high, if by knowing the neighborhood of u in we gain much information about the neighborhood of x in , and vice versa, where vertices are identified by their labels. Note that in this case, neighborhood is defined in terms of j-spheres. Once more, this is exemplified in Figure 7, where u and x have an equally labeled vertex in their 1-sphere. More specifically, v in and y in are equally labeled by such that and . Thus, u and y share this label in the same sphere. Information of this sort can be explored to measure alignment if u and y form paired primes (see Section 1).
Obviously, we straightforwardly get an entropy measure that operates on the distribution of properly normalized MI values of all pairs of equally labeled vertices shared among and . Notwithstanding its attractiveness, this approach disregards the fundamental law of semiological preference [57], according to which occurrences of linguistic units obey a very skewed distribution such that, for example, lexical networks probably coincide in sharing highly frequent words (even nouns), while they are much less likely to share highly focused content words. When measuring lexical alignment, such content words are of high interest as it is less likely that, for example, in the JMG two interlocutors share the specific term ball than that they share the general noun thing. Thus, one should carefully select commonly used words for exploring their neighborhoods. This holds all the more for dialogical communication as exemplified by the JMG where a small set of “uncritical” content words tends to be used by all interlocutors. It seems natural to explore the special role of such thematically focused, though commonly used, words to implement the notion of MI among graphs in the present application area. The reason is that linguistic networks as analyzed here are association networks in which such seed words play the role of inter-subjectively controllable primes whose patterns of spreading activation inform us about the topological commonalities of the networks in which they are activated. That is, they provide comparability among interlocutors of the same conversation as well as between different dialogs. Along this line of reasoning we now define the prime-based mutual information of two graphs as follows.
Definition 1. Mutual information of primes and of two-layer graphs. Let be a labeled two-layer graph with the projections and . Let further
be a subset of pairs of commonly labeled vertices, henceforth called paired primes, that belong to different layers of G.
We call the set  of order |
of order |  the lexicon of G. The Local Mutual Information (LMI) of the paired primes , , is defined by the quantity
where
and
is the -sphere of v and w in G, that is, the set of all labels assigned to vertices , with the normalized geodesic distance to v and to w. normalizes the geodesic distance δ in the sense that
where is the restriction of δ to , . Note that if x and y belong to different layers or if they are unconnected within the same layer (of course, these two cases may be handled separately—we save this variant for future work). Note further that a simple variant of is given by re-defining as follows:
In this case, edges that belong to the bipartition of G are additionally explored when measuring geodesic distances—this variant will not be considered here.
the lexicon of G. The Local Mutual Information (LMI) of the paired primes , , is defined by the quantity
where
and
is the -sphere of v and w in G, that is, the set of all labels assigned to vertices , with the normalized geodesic distance to v and to w. normalizes the geodesic distance δ in the sense that
where is the restriction of δ to , . Note that if x and y belong to different layers or if they are unconnected within the same layer (of course, these two cases may be handled separately—we save this variant for future work). Note further that a simple variant of is given by re-defining as follows:
In this case, edges that belong to the bipartition of G are additionally explored when measuring geodesic distances—this variant will not be considered here.
 of order |
of order |  the lexicon of G. The Local Mutual Information (LMI) of the paired primes , , is defined by the quantity
the lexicon of G. The Local Mutual Information (LMI) of the paired primes , , is defined by the quantity Now, the LMI-distance of and induced by the pair of vertices can be defined as
where the entropy of v is defined as
naturally induces a similarity measure by
Further, the Local Mutual Information of and is defined by the maximum of the local MI of paired primes in P:
By analogy to Equation 13, we finally get a distance measure of and by
with the corresponding similarity measure
In order to exemplify the computation of , look at Figure 7. Suppose that the vertices are labeled by so that some of these vertices are equally labeled, while all other vertices of and are labeled by some for which . Suppose further that the pair of equally labeled vertices u and x is our focal pair of primes . In this case, we observe that
- ; by definition, paired primes are both located in the zero sphere.
- ; starting from u and x, respectively, is directly associated to in both interlocutor lexica.
- ; exemplifies a word that is mediately associated to their respective primes in both interlocutor lexica the same way.
- is the subset of words in used by speaker A, but not by speaker B.
- is the subset of words in used by speaker A, but not by speaker B.
- is the subset of words in used by speaker B, but not by speaker A.
- is the subset of words in used by speaker B, but not by speaker A.
- ; exemplifies a word that is used by both interlocutors but in a different way from the point of view of the paired primes u and x.
- ; note that 18 = |
 | − 1 where
| − 1 where  .
. - .
By this example, we get the complete range of sets that we need to know to compute in the case of the graphs and in Figure 7.
Remark: remember that above we have made the assumption that the labeling function on vertices is bijective so that there is no label which does not label any vertex in or in . Thus, for any label there is a vertex in labeled by l while there is either no vertex in labeled by l or this vertex is equal to w. In this way, we deal with words that are used only by one interlocutor. (An alternative to handle such words is to define that they have a constant distance of |  | + 1 to any item in the lexicon of the interlocutor who does not use them.)
| + 1 to any item in the lexicon of the interlocutor who does not use them.)
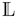 | + 1 to any item in the lexicon of the interlocutor who does not use them.)
| + 1 to any item in the lexicon of the interlocutor who does not use them.)Theorem 1. Equation 8 is a measure of mutual information (i.e., Equation 8 defines a measure for estimating MI by means of the -sphere ).
Proof. We start by showing the symmetry of I, that is, . Without loss of generality, we assume that and . Then, the symmetry of I simply follows from the fact that for every , , in Equation 8, there exists exactly one such that . Further, and hence . Analogously, we see that .
We continue with showing that . Note that this means to focus on one of the projections of G, that is, either or . Without loss of generality, we assume that . Thus, we can concentrate on subsets of the sort . By Equation 9 we directly get . That is, and, thus, for . As a consequence, the sum over j in Equation 8 reduces to
so that we can conclude in the usual way that . Finally, starting from the sum , it straightforwardly follows that [58]. ☐
By the work of [54] we know that measures like D become a metric for an appropriately defined set M of objects supposed that D is based on a measure of mutual information. For I we have shown this property. However, what we miss is such a set M as D is only defined for layers of the same conversation. Of course, we may say that is a metric space, where . But that would leave out any applicability of the triangle inequality and, thus, a realistic scenario of a metric space of dialogs and their components. We leave this elaboration of a metric dialog space—by analogy to a metric semantic space of textual units—to future work.
Intuitively, what does mean? In order to explain this, it is easier to look at . We suppose that among all paired primes of , the pair maximizes I. So what does it mean to get a zero distance, that is, ? This equals the value of and as D is a metric. Thus, for any two graphs , a value indicates that both graphs are equally organized in terms of the (im-)mediate neighborhoods of the paired primes v and w in and , respectively. In other words, by knowing the i-sphere of v in we get a great deal of information about the corresponding spheres around w in which the correspondents of the vertices in are located in , and vice versa. An extreme case would be that by knowing the sphere in we know exactly the composition of the sphere in —by analogy to . From this perspective, is a measure that indicates a kind of topological dissimilarity of and —from the point of view of the paired primes v and w. For small values of D near to zero it tells us that by knowing the i-sphere of a vertex in we know the corresponding j-sphere of its equally labeled vertex in (note that in this case it does not necessarily hold that as I is a measure of mutual information). This is exactly the notion of alignment that we address in this article: the dialog lexica of two interlocutors are said to be aligned if they manifest alike patterns of spreading activation. In the present context, this spreading activation is modeled by both the paired primes and their neighborhoods. Obviously, this notion integrates the notion of alignment in terms of linkage with that of alignment in terms of structural similarity:
- On the one hand, both interlocutors are aligned in the sense that they activate a common sub-lexicon during their conversation out of which they recruit paired primes by expressing, for example, the same topic of conversation by the same word. Without such a larger sub-lexicon, the value of could be hardly near to zero as word usages of one interlocutor would tell us nothing about the word usages of the other. Thus, for higher values of it is necessary that the sub-lexicon shared among the interlocutors covers a bigger part of the overall dialog lexicon—note that this notion relates to the notion of graph distance of [59] as explained below. As seen by example of the JMG, there are hardly many paired primes in our study that are common to all pairs of interlocutors. Thus, in order to secure comparability among different pairs of interlocutors, it makes sense to focus on a single lexeme that is actually used by all pairs of interlocutors. In our present study this is exemplified by the lexeme button (see Figure 2 in Section 3).
- On the other hand, both interlocutors are additionally aligned in the sense that the focal primes v and w induce similar patterns of spreading activation [60] within their respective dialog lexica. That is, by commonly using the lexeme that equally labels the vertices v and w, their neighborhoods are activated in a way that is mutually predictable. In terms of geodesic distances, this means that both interlocutors have built dialog lexica that are similarly organized from the point of view of the paired primes v and w.
At least theoretically, S and D as defined here indicate by their application to graph-theoretical representations of dialog lexica the (non-)alignment of interlocutors by two reference points, that is, by the linkage and the similarity of their dialog lexica. This makes these quantities interesting candidates for measuring alignment as studied empirically in Section 6.
The measures discussed so far explore the complete spectrum of -spheres. A simple variant that focuses on spheres for which is defined as follows:
where
Obviously, this measure is based on an information-related function that relates the common neighborhood of two vertices to the overall set of vertices. Note that implies that there is only one such w and that this w belongs to the opposite layer of G. Note further that in this case . is 0, if both layers of G do not have commonly labeled vertices, that is, if both interlocutors use different vocabularies (e.g., because of speaking different languages). In the opposite case, that is, if both layers share commonly labeled vertices, higher values of indicate that these vertices are integrated into their respective layers in similar ways. In terms of our application area this means that both interlocutors are aligned in terms of the topological relations of their common sub-lexicon. Below we will see that this variant also has a potential in classifying dialog lexica for manifesting alignment or non-alignment.
So far, we have introduced measures of mutual information (and entropy) to capture the similarity of lexical systems as dialog lexica represented by two-layer networks. Now, we complement these candidates by instances of three additional classes of graph-theoretical indices:
- First and foremost, we calculate classical indices of complex network theory separately for each of the layers of two-layer networks and aggregate them by a mean value to describe, for example, the average cluster value of interlocutor lexica in dyadic conversations. This is done for the cluster value C1 [61], its weighted correspondents and [62], the normalized average geodesic distance and the closeness centrality of graphs [30,63]. For an undirected graph , is defined as follows:where is the number of vertices in G andpenalizes, so to speak, pairs of unconnected vertices by the theoretical maximum of the diameter of G. measures the proportion of the average geodesic distances of the vertices in relation to the sum of their penalties in the latter sense: the more vertices are connected by the shorter paths, the smaller this proportion such that for completely connected graphs , while for a completely unconnected graph . Computing the normalized variant of the average geodesic distance is indispensable. The reason is that at their beginning, dialog lexica are mainly disconnected so that computing L for their largest connected component would get unrealistically small values.
- The latter group of indices simply adapts classical notions of complex network theory to the area of two-layer networks. That is, they do not measure the dissimilarity of graphs as done, for example, by . As an alternative to D, we utilize two graph distance measures [64,65,66]. More specifically, [59] consider the following quantity to measure the distance of two (labeled) graphs :where is the maximum common subgraph of and and is the order of . This measure has very interesting properties: firstly, if and are uniquely labeled and if the computation of reflects this labeling, it is efficiently computable. Further is a metric and, thus, computes easily interpretable graph distances [60]. In this line of research, [67] propose a graph distance measure based on graph union:Both of these measures compute graph distances and are therefore applicable to measuring the dissimilarity of dialog lexica distributed among interlocutors. Consequently, we apply them in addition to D and S, respectively, to extend our tertium comparationis.
- Last but not least, we consider an index of modularity that, for a given network, measures the independence of its candidate modules. As we consider networks with two modules, we use the following variant of the index of [68]:where is the number of links within the ith part of the network and is the number of links across the alignment channel.
Except for the classical indices of complex network theory as adapted here, all other indices that are newly invented in this article go beyond existing approaches to measuring alignment that basically count repetitions of shared (e.g., lexical) items (see Section 2). In contrast to this, our approach takes the structure of dialog lexica into account as represented by two-layer networks. In this sense, we do not perform a set-based but a structure-based measurement of alignment that focuses on structural similarity and coupling.
5. Random Models of Two-Layer Networks
In order to show that dialog lexica span two-layer time-aligned network series in a law-like manner, we have to show that their topology differs from that of corresponding random graphs. In other words, we consider random networks in order to identify topological characteristics of TiTAN series that are non-random in the sense that they cannot be reconstructed by means of the former. If a topological characteristic of the dialogs considered here characterizes their random counterparts the same way, it is judged to be linguistically uninformative as it does not separate linguistic TiTAN series from random ones. This also means that the random networks introduced in the following subsections are non-linguistic artefacts even if they reflect structural constraints of their linguistic counterparts. From this point of view, we do not aim at reinterpreting the random networks linguistically, but always motivate our decisions on how to span them. As a result we get a tertium comparationis of artificial units for delimiting characteristics of dialogs that are linguistically relevant. This procedure is indispensable as corpora of dialogs are rare because of the tremendous effort to annotate them appropriately. Random networks provide a first way out of this problem of data sparseness.
An obvious way to introduce random models of a TiTAN series is to compare each network of each of its time points with a corresponding random network according to the Erdős–Rényi–model [69] (Section 5.1). However, this approach focuses on unipartite graphs. Thus, a random model is needed that reflects the topological peculiarities of two-layer networks. In this section, we introduce such models that extend the random model of simple graphs in a self-evident way by rewiring the layers of two-layer networks separately (Section 5.2 and Section 5.3).
Another way to look at randomized counterparts of networks is not to rewire the output of networking directly, but to shuffle the input data from which these networks are induced. This way to look at randomized two-layer graphs is inspired by [70] who analyze random models of annotation networks. Basically, [70] shuffle the input sets of heterogeneous relations (over artefacts, annotators, and their tags) by which they induce hypergraphs. We adapt this idea to get two additional types of randomized two-layer networks based on shuffled input (Section 5.4 and Section 5.5).
Altogether, we analyze five approaches to randomized networks whose topological characteristics will be compared with those of two-layer networks of equal order and size to get first insights into the question whether dialog lexica as represented by TiTAN series manifest a law-like dynamic that is characteristic of dialogical communication.
| Algorithm 1: Binomial case I: computing a set of randomized TiTAN series. |
| Data: TiTAN series ; number of iterations n Result: Set of n randomized TiTAN series for do rewire at random to get ; for do randomly delete edges from to get ; ; end ; ; end |
| Algorithm 2: Binomial case II: computing a set of layer-sensitive randomized TiTAN series. |
| Data: TiTAN series ; number of iterations n Result: Set of n randomized TiTAN series for do rewire , and at random to build where such that , and ; for do randomly delete edges from to get ; randomly delete edges from to get ; randomly delete edges from to get ; set such that and , and ; end ; ; end |
5.1. The Binomial Model (BM-I)
To introduce random models of TiTAN series we begin with the binomial case. Algorithm 1 computes a series of random networks of equal size and order as their two-layer correspondents. It gets a TiTAN series as input and outputs a set of randomized series. This is done by rewiring the last link of the input series at random and then by randomly deleting edges till the first link of the input series is reached. As all input networks have the same order, a random graph is distinguished from its natural correspondent only by its edge set. In linguistic terms, the BM-I approach models a sort of “unnatural” dialog in which turn-taking is completely disregarded. Note that Algorithm 1 does not generate a single randomized TiTAN series but a set of n such series. The reason is that topological characteristics of random networks are averaged over this set separately for each time point.
5.2. The Partition-Sensitive Binomial Model (BM-II)
As mentioned above, the binomial model handles two-layer networks as unipartite graphs so that layer-internal links (e.g., intrapersonal in dialog networks) may be rewired as layer-external links and vice versa. In order to overcome this deficiency, we extend the binomial model by restricting the rewiring to the layers , and its bipartition . This is done by Algorithm 2. In terms of our application area, it rewires the interlocutor lexica and their bipartition across the alignment channel independently of each other so that their sizes (i.e. numbers of edges) are unaffected. The BM-II approach models a sort of unnatural dialog in which turns and topical references are randomly reorganized, that is, a sort of conversation in which each interlocutor generates turns by randomly selecting lexical constituents and by randomly selecting the topic of this turn. As before, deletion of edges in the BM-II is done at random when approaching the first link of the input series. This means that an edge may be deleted at time point i that has been generated at time , , while it has been updated several times during the span . Obviously, such a deletion rule may disadvantageously affect the computation of typological indices that explore weighted graphs.
5.3. The Partition- and Edge-Identity-Sensitive Binomial Model (BM-III)
In order to overcome the deficit of variant BM-II, we introduce variant BM-III that replaces the mode of edge deletion of variant BM-II by reflecting the time of birth of edges and of their updates. More specifically, when backtracking the input series only those edges are deleted at time point i that have been generated at time point . Likewise, the weights of those edges are decremented by 1 that have been augmented by the same value at time point . In this way, a randomized series of two-layer networks is generated, which at each time point t has exactly the same order, size and sum of weights as its natural correspondent within the input series. Obviously, this makes it much harder for dialog lexica to show significant differences to such randomized series than to its alternatives based on variant BM-I or BM-II.
5.4. The Event-Related Shuffle Model (SM-I)
As described in Section 4.1, TiTAN series of dialog lexica are basically induced by exploring three data sources: at time t, which interlocutor has uttered which lexical item to express which topic? That is, TiTAN series can be conceived of as being induced from a time series of triples , …, indexed by their time point of generation. From this perspective it is easy to generate a model that shuffles these data sources independently of each other at random. This is done by SM-I, which makes the shuffled data sources an input to generating TiTAN series in the usual manner. From a linguistic point of view, this is an attractive model as it randomizes directly the utterances of the interlocutors. The SM-I approach focuses on a sort of unnatural conversation in which the overall dialog lexicon is randomly distributed over both interlocutors—note that the original distribution of this dialog lexicon is retained by the BM-I, -II and -III. Thus, the SM-I provides a further perspective on assessing the peculiarities of dialog lexica.
5.5. The Time Point-Related Shuffle Model (SM-II)
A simple variant of SM-I is given by shuffling not the constituents of the triples , but their indices, that is, time points. In this way, we retain the events as basic building blocks of dialogs while shuffling their temporal order. The SM-II approach models a sort of unnatural conversation which disregards any natural order of turns and their constituents as if the interlocutors would select in advance any of their utterances while randomly selecting their time points.
5.6. Summary Attributes of Randomized Two-Layer Networks
A TiTAN series that results from one of the latter five variants of network randomization cannot be compared directly with its natural counterpart. Rather, we compute the topological indices of each network of such a random series to finally average them over the corresponding set of series of the same type. Below, we will produce 100 random series of each type to compute these summary attributes. Thus, it does not make sense to depict a single such random network as characteristics are always averaged over any such series of 100 networks. In this way, we get for each topological index of Section 4.2 an estimator of the corresponding expected value under the condition that the networking of the lexicon is at random. This provides a tertium comparationis for rating the peculiarities of the temporal dynamics of dialog lexica.
6. Experimentation
We are now in a position to analyze the regularities of TiTAN series as representations of dialog lexica. This is done with respect to their temporal dynamics (Section 6.1) and their classification into the classes of aligned and non-aligned dialog lexica (Section 6.2).
6.1. On the Temporal Dynamics of Lexical Alignment
The structure of a dialog lexicon that, as a two-layer network, integrates co-evolving sublexica of two interlocutors, can be described with respect to several topological characteristics: regarding their transitivity we ask for the generation of micro clusters in terms of triads and triples of co-associated words. Under the notion of lexical closeness we examine the compactness of dialog lexica in terms of geodesic distances among indirectly associated items. Clustering and closeness can be examined regarding a dialog lexicon as a whole or separately for each of its sublexica. From the point of view of modularity, we examine a characteristic of dialog lexica that interrelates both of these sublexica directly. This is further examined at the end of this section where we investigate the time course of the similarity of the interlocutors’ sublexica in a dyadic conversation.
Lexical Clustering
In terms of (dialog) lexica, a high cluster coefficient means a high probability that if a lexical item a is associated with two items b and c, then these items are (semantically) associated, too. In this case, if the word form /a/ is processed, it probably primes b and c that, in turn, prime each other. This sort of mutual reinforcement of co-primed or co-activated items has the effect that if an interlocutor manifests a by a word form, say, /a/, then it is likely that in this context, the items b and c are manifested, too. This effect seems to be present in dialog lexica as indicated by the Figure 8, Figure 9, Figure 10 and Figure 11. The Figure 8, Figure 9 and Figure 10 do that by example of Dialog 19 (see Table 1) that in terms of its number of 201 events is the longest dialog examined here (i.e., this dialog covers more than 200 nominal word forms in referential function as defined by the JMG). Figure 8 shows the temporal dynamics of the cluster coefficient C1 [61] as a function of time in Dialog 19. In this example, clustering is very high (up to 80%) while in the corresponding randomized networks it is much lower: while the BM-II and BM-III converge in a cluster value of C1 , the BM-I rests below 20% of clustered items—both results coincide with general findings about random networks [61] that are known for small cluster values. This observation is at least not falsified by the SM-I and SM-II of Dialog 19: both models produce rather stable cluster values that rapidly converge below the corresponding values of the BM-II and BM-III. Thus, by example of Dialog 19, we get a first hint that clustering in dialog lexica is a likely phenomenon much beyond what can be expected by chance. In principle, the same relation holds in the case of the weighted variant of C1, that is, [62]. This is exemplified by Figure 9, which depicts a large gap between weighted clustering in natural in relation to randomized dialog lexica. Moreover, if we switch from the perspective of a dialog lexicon as a whole and compute separately for each of its sublexica before aggregating it by a mean value (see Section 4.2), we still see that this relation is retained as shown in Figure 10.
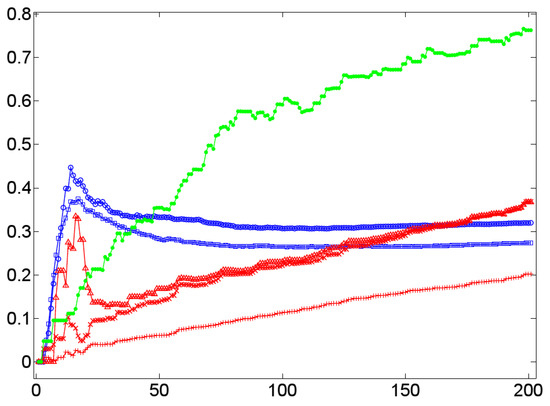
Figure 8.
The temporal dynamics of the cluster coefficient C1 [61] (y-axis) as a function of time (x-axis) by example of the TiTAN series induced from Dialog 19 (•) in relation to the corresponding BM-I (+), BM-II (×), BM-III (Δ), SM-I (□), and SM-II (∘) model.
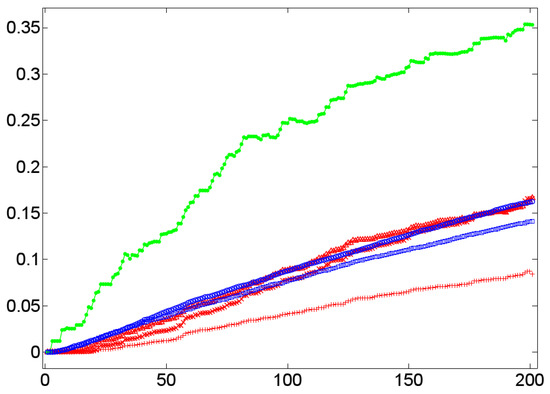
Figure 9.
The temporal dynamics of the weighted cluster coefficient [62] (y-axis) as a function of time (x-axis) by example of the TiTAN series induced from Dialog 19 (•) in relation to the corresponding BM-I (+), BM-II (×), BM-III (Δ), SM-I (□), and SM-II (∘) model.
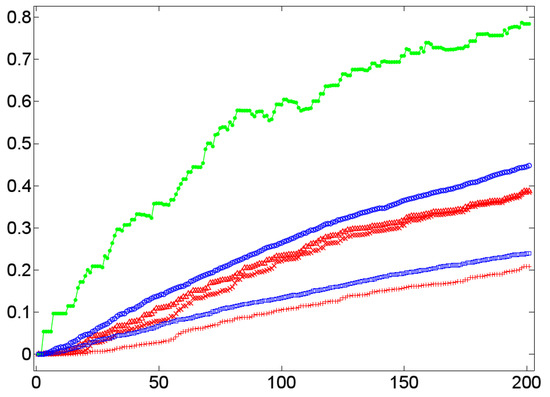
Figure 10.
The temporal dynamics of the average cluster coefficient C1 [61] (y-axis) as a function of time (x-axis) by example of both layers of the TiTAN series induced from Dialog 19 (•) in relation to the corresponding BM-I (+), BM-II (×), BM-III (Δ), SM-I (□), and SM-II (∘) model.
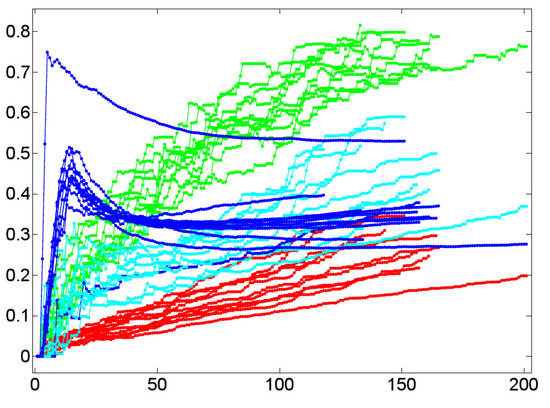
Figure 11.
The temporal dynamics of the cluster coefficient [61] (y-axis) as a function of time (x-axis) by example of 11 dialog lexica (green) in relation to the corresponding BM-I (red), BM-III (cyan), and SM-I (blue) models.
Based on these findings the question arises whether this is a stable result that is confirmed by the findings for the other lexica analyzed here. This question is addressed by Figure 11 that shows the temporal dynamics of as a function of the time course of 11 experimental dialogs (marked by an asterisk in Table 1). It supports the view that the cluster values of dialog lexica, which are generated by human communication, are predictable as they evolve in a well separated area of low dispersion that is distinguished from any of the random models considered here. In particular, we see that all experimental dialogs are separated from their counterparts in terms of the BM-I, while their BM-III- and SM-I-based correspondents are located between dialog networks (as an upper bound) and BM-I-based networks (as a lower bound of cluster formation). In a nutshell, clustering clearly distinguishes dialog networks from their random counterparts. As we only deal with 11 experimental dialogs, this finding is in support of a corresponding hypothesis whose testing has to be done by means of a much larger dialog corpus than has been accessible for this study.
What does this result mean in linguistic terms? It means that in conversations of the sort considered here, interlocutors tend to generate triples of lexical units that are associated due to their co-occurrence patterns. Irrespective of whether both interlocutors align lexically or not, that is, whether they use the same words to denote the same entities or not, they preferably use any lexical item in the context of other items that tend to co-occur for their part. Since all dialog lexica analyzed here are connected, this implies that the formation of triples does not depend on turn-taking nor on topic change. In other words, triples are not simply generated by turns that contain all their lexical constituents. Rather, triple formation is also due to the distribution of these constituents over different turns as, for example, in the case where a dialog partner uses ball and angle in one turn, ball and distance in another and, finally, angle and distance in a turn in which ball does not occur. Thus, in dialogs of the sort considered here, association is a local process that induces small, but highly connected, very dense networks. This outstanding position of high cluster values is underpinned if we look on linguistic networks that are known to form small worlds: clustering in Wikipedia, for example, is below 20% (see [71] and [72]); the same is true for many special wikis [30]. Only co-occurrence networks show a likewise large cluster value—though not that large as in dialog networks. This result corresponds to the small size of dialog networks. However, we do not yet know enough about the interplay of everyday dialogs and findings of this sort, simply because reference corpora are still out of reach in this area. In any event, all random networks considered here show much smaller cluster values so that our findings hint at a characteristic of dialogical communication.
Lexical Closeness
Under the notion of lexical closeness we briefly look at the statistics of geodesic distances in dialog lexica. We do that in terms of the normalized average geodesic distance (Equation (21) and the standardized closeness centrality of a graph [63]:
- A low value of for a graph G indicates short paths between any pair of vertices in G that tends to be connected without any two disconnected components. In terms of dialog lexica this is tantamount to a high probability that any prime may activate any other item in the lexicon even though to a low degree. In other words, when receiving a word form /a/, the dialog lexicon of an interlocutor allows, in principle, for activating the complete sublexicon that he has generated till the moment of processing /a/. Both of these assessments are confirmed by our corpus of 11 experimental dialogs. The upper left part of Figure 12 reports the temporal dynamics of in Dialog 19, while the upper right part of Figure 12 depicts the values of after being averaged over both interlocutor lexica. In both cases, we observe that short average geodesic distances emerge much more rapidly in the BM-I, the BM-II, and the BM-III. We also observe that all variants (whether natural or randomized) result in very low values of indicating the existence of the latter mechanism. However, we also observe that the SM-II (based on shuffling the time points of dialog events) perfectly approximates geodesic distances in natural dialogs. In any event, as dialog lexica finally produce short average geodesic distances, even though more slower than their binomial counterparts, they perfectly fit into the class of networks that have been called small-worlds ([61,73]) as they also have high cluster values. Note that the upper left and right part of Figure 12 hints at a constant drop of as the dialog evolves. In other words, nouns as considered here are not distinguished in their contribution to the decrease of as a function of the time of their utterance. This may explain why the SM-II approximates the dynamics of in natural dialogs.
 Figure 12. The temporal dynamics of the normalized average geodesic distance (upper left), its average over both interlocutor lexica (upper right), the standardized closeness centrality [63] (lower left) and its corresponding average (y-axis) by example of the TiTAN series induced from Dialog 19 (•) in relation to the corresponding BM-I (+), BM-II (×), BM-III (Δ), SM-I (□), and SM-II (∘) models.
Figure 12. The temporal dynamics of the normalized average geodesic distance (upper left), its average over both interlocutor lexica (upper right), the standardized closeness centrality [63] (lower left) and its corresponding average (y-axis) by example of the TiTAN series induced from Dialog 19 (•) in relation to the corresponding BM-I (+), BM-II (×), BM-III (Δ), SM-I (□), and SM-II (∘) models. - A high closeness centrality of a graph G indicates that its vertices coincide more or less regarding the sum of their geodesic distances to all other vertices of G [30]. In conjunction with a value of near to zero this means that all vertices operate on an equal footing as efficient entry points to the lexicon by which any other item is accessible with almost the same effort of spreading activation. This picture is only confirmed, if we average the standardized closeness centrality over both interlocutor lexica (depicted by the lower right part of Figure 12). Obviously, Dialog 19 has a much higher closeness centrality than its random counterparts.
These assessments of and are confirmed by the corpus of 11 experimental dialogs: the left part of Figure 13 supports the view that in dialogs, geodesic distances evolve above the range of values of BM-I-based networks (and BM-III) and below the values of SM-I-based networks. This special role of dialog is more manifest in the right part of Figure 13, which shows that the closeness centralities of these networks tend to be above the corresponding values of all other types of random networks. Thus, we conclude that a higher closeness centrality is characteristic of dialogs as higher cluster values. This also holds, though to a lower degree, for average geodesic distances—in accordance with the observation that random networks according to the binomial model generally tend to smaller average geodesic distances [73]. Note that the values of observed here are below those that have been observed for co-occurrence networks [30] and related lexical networks.
Figure 13.
The temporal dynamics of the normalized average geodesic distance and the standardized closeness centrality (y-axis) both averaged over the layers of two-layer networks by example of 11 dialog lexica (green) in relation to the corresponding BM-I (red), BM-III (cyan), and SM-I (blue) models.
What do these results mean in linguistic terms? In addition to the observation of remarkably high cluster values, we get the information that dialog lexica as considered here do not manifest a preference order among their constituents in terms of likely and less likely entry points. Rather, whatever nominal input has to be processed by an interlocutor, any items that may help to interpret this input are located in the near of it. This hints at a type of interlocutor who keeps constant a uniform activation level of her dialog lexicon so that any input can be rapidly contextualized appropriately. Likewise, language production operates—irrespective of its topic—in a single, densely structured, but small lexical context. It seems that interlocutors tend to save effort as they keep their dialog lexica small while they spend effort to organize them as tiny small worlds. This observation relates to the phenomenon of lexical-semantic diversification and its interpretation in terms of Zipfian forces [74], but with a focus on dialog lexica. Of course, this interpretation needs to be tested by subsequent studies. Note also that our findings relate to the sort of controlled communication manifested by the JMG. Thus, we are in need of further studies by means of larger corpora of more spontaneous dialogs in order to underpin these findings.
Lexical Modularity
Modularity [68] is an index that evaluates candidate modules for their overplus of module internal links in relation to module external ones. In terms of dialog lexica, this relates to intrapersonal associations in comparison to interpersonal ones (see Section 4.2). As depicted by example of Figure 6 such a relation is likely to occur in dialog lexica and their BM-II and BM-III-based variants, which both retain the modularity of the corresponding input lexicon (see Section 5) and, therefore, cannot be distinguished from the point of view of modularity from the latter. For this reason, Figure 14 only depicts dialogs in relation to their BM-I- and SM-I-based variants. Obviously, modularity in the sense just mentioned naturally occurs in these dialogs and clearly separates them from these two random counterparts.
Figure 14.
The temporal dynamics of the index of modularity [68] (y-axis) averaged over the layers of two-layer networks by example of 11 dialog lexica (green) in relation to the corresponding BM-I (red), and SM-I (blue) models.
Modularity of dialog lexica is in a sense obvious so that it does not need further interpretation in linguistic terms. Our findings just confirm this expectation. However, we see by all cases of dialog networks and their random counterparts depicted in Figure 14 that the respective degree of modularity keeps constant already after the first 20 time points (i.e., utterances of nouns). This hints at the fact that real dialogs, which have a near maximum degree of modularity, are very economical in establishing interpersonal links in relation to intrapersonal ones—they just establish a very small fraction of the former in relation to the latter and do not vary this relation throughout the conversation. Once again, this interpretation needs to be tested by means of a larger study based on a much larger dialog corpus.
Lexical Similarity
As a last snapshot of the temporal dynamics of dialog networks we consider the MI-based similarity measure (see Section 4.2) and the graph distance measure [67](see Section 4.2). The reason to select these two candidates of (dis-)similarity measuring is due to their special role in network classification as explained in the next section. As depicted by Figure 15, both measures fail to clearly separate dialog networks from their random counterparts. This is less clear in the case of where the values of dialogs are settled between the corresponding values of their variants in terms of the BM-III and SM-I, respectively. At the same time we observe that in relation to the range of possible dissimilarity values of , the sublexica of dialog networks tend to be rather dissimilar.
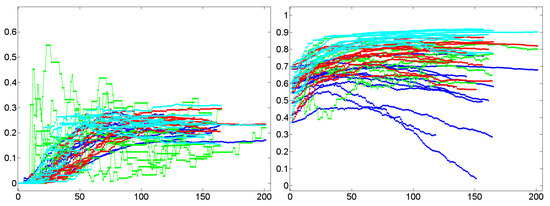
Figure 15.
The temporal dynamics of (left) and (right) (y-axis) by example of 11 dialog lexica (green) in relation to the corresponding BM-I (red), BM-III (cyan), and SM-I (blue) models.
So far, we have shown that dialog lexica are characterized by a high modularity in conjunction with a high cluster value, a low average geodesic distance and a higher value of closeness centrality. Although emerges in dialogs less rapidly than in their binomial variants, these features altogether clearly separate naturally evolving dialog lexica from their random counterparts. Thus, TiTAN series as induced from dyadic conversations can be seen to describe a novel class of time-aligned graphs. They manifest a sort of law-like structuring that is not captured by means of the random models considered above.
6.2. A Classification Model of Alignment
As we have shown that dialog lexica evolve differently than corresponding random models, we turn to the question of how to utilize the representation format provided by TiTAN series to automatically classify dialog lexica into aligned and non-aligned ones. This brings us back to the beginning of this article (see Section 1) where alignment has been defined (i) in terms of the similarity of cognitive representations on some level(s) of cognitive resolution and (ii) their coupling as a result of interpersonal priming manifested by the tendency to share lexical items in conversation.
In Section 4.2, we have introduced several measures that capture these two aspects of alignment. Now, we apply these measures to build a quantitative network model as input to network classification. This approach utilizes Quantitative Network Analysis (QNA) ([30,75]) with a focus on two-layer networks. QNA has been introduced to learn classes of networks solely by virtue of their structure, while disregarding any content units (i.e., any labels and attributes of vertices and edges). Generally speaking, QNA integrates vector representations of complex networks with hierarchical cluster analysis. The cluster analysis is complemented by a subsequent partitioning, where the number of classes is determined in advance. In this sense, QNA is semi-supervised. In order to instantiate QNA, we solely experiment with complete linkage in conjunction with the Mahalanobis distance to compute pairwise object distances. The reason to focus on the Mahalanobis distance is to handle correlations between different topological indices. Roughly speaking, QNA takes a space of input objects, where each object is represented by a vector of topological indices, to find the subset of indices that best separate the data space according to a corresponding gold standard [see [30] for a thorough explanation of this approach]. We use F-measure statistics (i.e., the harmonic mean of precision and recall also called F-score) to evaluate classification results. As we deal with two classes (i.e., the class of aligned and non-aligned dialogs), F is defined by the quantity
where R is the recall and P the precision of the target classification in relation to the gold standard. Note that indicates the best and the worst possible classification. Note further that QNA (optionally) integrates a genetic search for the best performing subset of topological indices that maximizes F. As a matter of fact, this search tries to find the optimal feature set, but may stop at a local maximum.
By applying QNA to the classification of labeled two-layer networks, we specialize it in one respect: as explained in Section 4.2, the Mutual Information (MI) of graphs as well as similarity measures based on maximum common subgraphs explore vertex labels. However, this is only done to identify commonly labeled vertices (e.g., paired primes) so that, finally, two-layer networks are represented by topological indices that abstract from any symbolic information.
As a gold standard, we use a human-based classification that has been performed by counting referential items shared among interlocutors. More specifically, a conversation is said to be aligned on the lexical level, if interlocutors name at least two of the three critical objects (see Section 3) in the same way, that is, by the same word, during a conversation. Conversely, it is said to be non-aligned lexically if they do not produce alike names for at least two of the three objects.
According to these criteria, 19 dialogs of our target corpus of 24 dialogs (see Section 3) manifest alignment, while 5 dialogs manifest non-alignment. Consequently, the first task in QNA is to learn these two classes where (non-)alignment is conceived as a property of the final outcome of a dyadic conversation, that is, of the two-layer network at the endpoint of the corresponding TiTAN series. This approach is unsatisfactory for two reasons:
- In spite of the fact that annotating dialogical data is very effortful so that even 24 dialogs can be seen to be a data set of medium size, any classification result based on such a small set is hardly expressive.
- On the other hand, alignment is a process variable that does not (necessarily) emerge suddenly at the endpoint of a conversation. Rather, alignment gradually evolves so that it is present at different stages of a conversation by different, possibly non-monotonic degrees. According to this view, we need to evaluate a larger interval of a conversation when measuring its alignment—ideally beginning with its end in a regressive manner.
To meet these requirements and to find a way out of the problem of data sparseness, we enlarge our corpus as follows: starting with the endpoints of all dialogs in our corpus, we regress event by event so that for each of the corresponding time points a set of 24 two-layer networks is induced that represent the state of the corresponding dialog lexicon at this point in time of the conversation. This is done for the last fifty events of each dialog so that 50 different classifications are performed that cover an overall set of 1,200 networks.
An obvious, but unrealistic classification hypothesis would be to say that the gold standard is predicted by QNA for any of the 50 time points of this regression. In this case, for each of the 50 classifications, a maximum F-measure of 1 would be expected—much beyond the F-scores that are usually computed in the area of computational linguistics [76]. This approach disregards the gradual nature of alignment which is more unlikely in early stages of a dialog while it is more likely in later stages. Remember that many of the dialogs analyzed here have a size of little more than 100 events so that a regression by 50 events stops at their middle where even dialogs that manifest alignment likely manifest it to a lower degree. From this point of view we have to expect a degression in F-score as a function of the number of regressions being made. To reflect this scenario, our revised cluster hypothesis runs as follows: it is possible to classify the two-layer networks at the endpoints of a set of TiTAN series in terms of (non-)alignment, while this is less likely for earlier stages of the corresponding conversations. Figure 16 summarizes the results of testing this hypothesis by means of the 50 classifications under consideration:
- Straight lines parallel to the x-axis denote the F-scores of two baselines: (i) the known-partition-scenario (with an F-score of ) that has knowledge about the cardinality of each target class, and (ii) the equi-partition-scenario (with an F-score of ) that assumes equally sized target classes. Computing these baselines is done 1,000 times so that Figure 16 shows their average F-scores. Roughly speaking, an F-score of means that about 70% of dialogs are correctly classified by randomly assigning them onto both target classes subject to knowing their cardinality—a remarkably high value.
- On the opposite range of the curves in Figure 16 we get the values of the best performing classification (denoted by bullets). In each of the 50 classifications, reported by Figure 16, this variant integrates a genetic search for the best performing subset of 50 topological features. This includes indices of complex network theory (as, for example, the cluster coefficient and the average geodesic distance [73]), graph centrality measures [63], entropy measures ([52,75]) as well as the graph similarity measures described in Section 4.2. According to Figure 16, this variant produces a maximal F-score of in the case of three different classifications—this holds especially for the endpoint of the time series under consideration (with the x-coordinate 1). On average, this variant reaches an F-score of . That is, nearly percent of the dialogs are correctly classified by this nearly optimal approach. Thus, using a wide range of topological indices together with an optimization algorithm seems to perform very well, but to the price of an optimization that runs the risk of overfitting.
- In order to shed light on this risk, we compute two additional alternatives. Firstly, Figure 16 shows the values of a genetic search (denoted by circles) on the subset of those 12 features that result in an F-score of for the dialogs’ endpoints. We observe a loss in F-score down to an average score of , which, at first glance, does not seem to be dramatic. But things are different if we apply the same subset of features in each of the fifty classifications without any additional optimization. In this case, the average F-score drops down to (i.e., below the upper baseline). Obviously, the optimized classifier performs very unreliably. That is, although we can classify two-layer networks according to (non-)alignment, the classifiers considered so far should be treated very carefully when processing heretofore unseen data.
- Figure 16 also shows that the latter assessment is preliminary. It presents the F-scores of a variant (denoted by squares) that has been produced by two features only, that is, (using the lexeme button as the single paired prime) and . On the one hand, we see that this variant produces an average F-score of only and, thus, outperforms the upper-bound of both baselines on a rather low level. Further, it also generates two outliers that fall below this upper-bound. However, we also observe that this variant produces very stable results by means of only two indices that according to Section 16, directly relate to alignment measurement. Moreover, the outlier on the right side of the corresponding curve may be due to a loss in the prominence of alignment at this earlier stage of conversation.
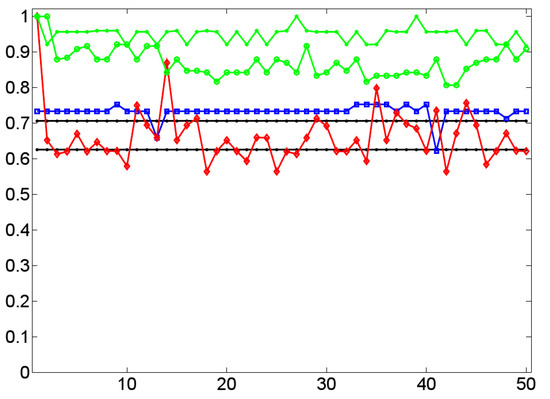
Figure 16.
Distribution of F-scores (y-axis) of 50 classifications (x-axis) each of which operates on 24 dialogs as represented by two-layer networks. The classification starts with the endpoints of the 24 dialogs (i.e., from the left on the x-axis) and then regresses event by event. The ordinate plots the corresponding F-scores. Bullets (•) denote the values of the best performing classification as a result of a genetic search for the best performing subset of 50 topological features. Circles (∘) denote the values of a genetic search for the best performing subset of 12 features that give an F-score of for the first classification (i.e., the endpoints of the dialogs). Diamonds are the corresponding F-scores that are produced by using all these 12 features without any additional optimization. Squares (□) denote the F-scores of only two features, and . Finally, the straight lines denote the F-scores of two baselines.
The results reported in Figure 16 can be discussed as follows: on the one hand, they shed light on the possibility of purely structural classifications of network data as manifested by dialog lexica. Under this perspective, we show that spoken communication is open to a kind of modeling that prior to this study has been applied only in the area of written communication. Moreover, in conjunction with the notions of graph distance measures as considered here, TiTAN series provide a way to operationalize the notion of alignment beyond simple models based on counting shared items. Other than all models of alignment considered so far, we apply a notion of alignment in terms of structural similarity based on graph theory that considers vertices (alignment by linkage) as well as their edges (alignment by structural similarity). However, we also hint at the fact that one should carefully select topological indices for representing dialog data as their reliability definitely correlates with their interpretability. Somehow low but stable classifications that are not generated by any additional optimization, are produced only by the pair of features and . In this sense, it seems worth continuing this research branch but with a focus on a small set of well interpreted graph-similarity measures while leaving the wider branch of network theory behind.
7. General Discussion
In this article we have developed a model of lexical alignment in dialogical communication. This has been done by starting from complex network theory and quantitative structure analysis. More specifically, we have identified a minimal set of two topological indices that compute the similarity of the dialog lexica of two interlocutors as a measure of their alignment at any point in time of their conversation. Although both features perform only slightly above the corresponding baselines, they produce stable results for the last 50 time points of the conversations analyzed here. In this sense, we have developed a first method to measure lexical alignment in structural terms. That is, other than the majority of approaches to alignment in dialogical communication, our approach additionally captures the structure of the dialog lexica under consideration. Thus, we cannot only state that two interlocutors are aligned because of using the same subset of words. Rather, we can attribute this alignment also to the way both interlocutors use these words in communication. In this sense, we provide a structural measure that captures a characteristic of mental structures, that is their alignment in dialog.
From a general point of view, one might say that our measurement procedure is trivial because speakers tend to use the same words in a similar way when speaking about the same topic. In this sense, lexical alignment is just a function of the topic of conversation. This is tantamount to saying that lexical alignment occurs by default as long as the topic of conversation does not change. However, if we have a closer look at lexical alignment, we see that this position is wrong. In our experiments, we have observed that interlocutors actually use a wider range of words when speaking about critical objects (as the topic of conversation) and even when speaking about those objects that have been judged to be uncritical. These are objects for which a pretest has shown that German speakers use exactly one term to refer to them. Take the example of colored pencils. In our experiments, test persons used any of three words to refer to them: Buntstift (colored pencil), Bleistift (lead pencil) and Stift (pen) (not to mention the general nouns, which test persons used to refer to colored pencils as, for example, Ding (thing) or Objekt (object) or Gegenstand (item)). Obviously, speakers have a range of choices even when speaking about topics that seem to be uniquely lexicalized. Moreover, lexical alignment by default contradicts linguistic knowledge about dialogical communication. The reason is that alignment by default implies a maximum level of lexical redundancy. Of course, this is not what we observe in general nor what we have observed in our experiments. As demonstrated in Figure 6, dialog lexica are different in a way that lexical redundancy is smaller than implied by the notion of alignment by default. Their difference may be due to many reasons, that is, stylistic differences of the interlocutors, their lexical non-alignment, their misunderstanding, differences in the linguistic competence of the interlocutors, their social relationships etc. In any event, we missed a measure of lexical alignment so far, a measure that captures the degree of alignment as well as the difference between lexical alignment and non-alignment. This article provided a first proposal of such a method.
Another objection to our method relates to the corpus of dialogs that we have used in this study. More specifically, we have evaluated TiTAN series by example of dialogs that keep control of turn-taking in such a way that a uniform distribution of turns is guaranteed among both interlocutors. Further, our corpus of 24 dialogs also keeps control of topic change. Obviously, the reason to proceed in this way is to guarantee interpretability of our results as there are uncountably many parameters of dialog organization in open, everyday conversations. Nevertheless, one may think about the effects of modeling uncontrolled conversations on our model. One question is, for example, whether there is a fundamental difference in the structure of dialog networks as a result of sudden changes of the topic of conversation. Although we cannot yet answer this question completely, a possible answer may look as follows: in the case of sudden topic changes that are reflected by both interlocutors, their sublexica get more and more clustered (as a function of the frequency of these changes) such that for any newly introduced topic there is a pair of subgraphs of both interlocutor lexica that are interlinked according the degree of their dialogical alignment (see Figure 17). Moreover, we expect that these paired sublexica show the sort of topological characteristics that we have analyzed in this article so that, finally, they may manifest alignment or non-alignment independently of each other. In this case, the clusters of the dialog lexicon of the same interlocutor are sparsely interlinked, typically by means of general nouns that tend to be used irrespective of the topic. Moreover, we expect that the shorter the time rates at which sudden topic changes occur, the smaller these clusters. Following this line of thinking, our approach may be further developed in order to arrive at a model of thematic segmentation of conversations.
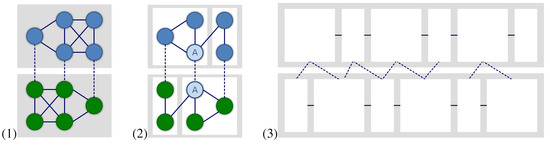
Figure 17.
Three scenarios of dialog network formation: (1) schematic depiction of a time point of a TiTAN series. (2) Formation of clusters at a certain time point of a TiTAN series. The vertices labeled by A denote a general noun that is used by both interlocutors in different thematic contexts. (3) Cluster formation with interlocutor lexica as a result of sudden topic changes.
8. Conclusions
In this article, we have developed two-layer time-aligned network series as a novel class of graphs to represent dialogical communication, its inherent bipartition and gradual development in time. We have adapted several quantities of complex network theory, which show that dialog lexica as represented by TiTAN series can be separated from several random counterparts. In this sense, dialog lexica form a kind of linguistic network that manifests a law-like structuring far from binomial random models. Moreover, we have developed a measure of graph similarity based on the notion of mutual information of graphs that together with related measures of graph distance measuring has a high potential in classifying two-layer networks. In this way, the article has formally presented and empirically tested a classification model of alignment in communication that—other than its predecessors—accounts for the networking of linguistic units beyond counting shared items. As the graph distance measure introduced in this article is a metric, this paves the way for building networks of dialogs by analogy to networks of texts in information retrieval. That is, we are now in a position to compute the distances of different dialogs as a whole so that for a given dialog we may ask for its most related “neighbor” that manifests a similar dialogical behavior. Another way to proceed would be to identify for a given interlocutor the partner that best fits to his conversational habits. Analogously, we may also explore roles or types of interlocutors according to their predominant alignment behavior. These are at least three points of departure that open novel tasks in machine learning in the area of dialogical communication. Future work will address these and related tasks.
Acknowledgement
Financial support of the German Federal Ministry of Education through the project Linguistic Networks, of the German Research Foundation through the Cluster of Excellence Cognitive Interaction Technology and the Collaborative Research Center Alignment in Communication is gratefully acknowledged. We also thank Tatjana Lokot for proof-reading the mathematical apparatus of this article and Sara Maria Hellmann for annotating the gold standard that we used in our classification experiment. Finally, we thank the anonymous reviewers for their helpful hints.
References
- Pickering, M.J.; Garrod, S. Toward a mechanistic psychology of dialogue. Behav. Brain. Sci. 2004, 27, 169–226. [Google Scholar] [CrossRef] [PubMed]
- Clark, H.H. Using Language; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Maturana, H.R.; Varela, F.J. Autopoiesis and Cognition. The Realization of the Living; Reidel: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Levelt, W.J.M. Speaking. From Intention to Articulation; MIT Press: Cambridge, MA, USA, 1989. [Google Scholar]
- Giles, H.; Powesland, P.F. Speech Styles and Social Evaluation; Academic Press: London, UK / New York, NY, USA, 1975. [Google Scholar]
- Clark, H.H.; Wilkes-Gibbs, D. Referring as a collaborative process. Cognition 1986, 22, 1–39. [Google Scholar] [CrossRef]
- Branigan, H.P.; Pickering, M.J.; Cleland, A.A. Syntactic coordination in dialogue. Cognition 2000, 25, B13–B25. [Google Scholar] [CrossRef]
- Garrod, S.; Anderson, A. Saying what you mean in dialogue: a study in conceptual and semantic co-ordination. Cognition 1987, 27, 181–218. [Google Scholar] [CrossRef]
- Watson, M.E.; Pickering, M.J.; Branigan, H.P. An empirical investigation into spatial reference frame taxonomy using dialogue. In Proceedings of the 26th Annual Conference of the Cognitive Science Society, Chicago, IL, USA, 2004; pp. 2353–2358.
- Kamp, H.; Reyle, U. From Discourse to Logic. Introduction to Modelltheoretic Semantics of Natural Language, Formal Logic and Discourse Representation Theory; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Lewis, D. Conventions. A Philosophical Study; Harvard University Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Stalnaker, R. Common ground. Linguist. Phil. 2002, 25, 701–721. [Google Scholar] [CrossRef]
- Collins, A.M.; Loftus, E.F. A spreading-activation theory of semantic processing. Psychol. Rev. 1975, 82, 407–428. [Google Scholar] [CrossRef]
- Kopp, S.; Rieser, H.; Wachsmuth, I.; Bergmann, K.; Lücking, A. Speech-Gesture alignment. In Project Panel at the 3rd International Conference of the International Society for Gesture Studies, Evanston, IL, USA, June, 2007.
- Lücking, A.; Mehler, A.; Menke, P. Taking fingerprints of speech-and-gesture ensembles: approaching empirical evidence of intrapersonal alignment in multimodal communication. In Proceedings of the 12th Workshop on the Semantics and Pragmatics of Dialogue, King’s College, London, UK, June 2008; pp. 157–164.
- Church, K.W. Empirical estimates of adaptation: the chance of two noriegas is closer to p/2 than p2. In Proceedings of Coling 2000, Saarbrücken, Germany, July-August 2000; pp. 180–186.
- Reitter, D.; Keller, F.; Moore, J.D. Computational modelling of structural priming in dialogue. In Proceedings of the Human Language Technology Conference of the North American Chapter of the Association for Computational Linguistics, New York, NY, USA, June 2006; pp. 121–124.
- Wheatley, B.; Doddington, G.; Hemphill, C.; Godfrey, J.; Holliman, E.; McDaniel, J.; Fisher, D. Robust automatic time alignment of orthographic transcriptions with unconstrained speech. In Proceedings of IEEE International Conference on Acoustics, Speechand Signal Processing (ICASSP-92), San Francisco, CA, USA, March 1992; pp. 533–536.
- Anderson, A.H.; Bader, M.; Gurman Bard, E.; Boyle, E.; Doherty, G.; Garrod, S. The HCRC map task corpus. Lang. Speech 1991, 34, 351–366. [Google Scholar]
- Reitter, D.; Moore, J.K. Predicting success in dialogue. In Proceedings of the 45th Annual Meeting of the Association of Computational Linguistics (ACL), Praque, Czech Republic, June 2007; pp. 808–815.
- Branigan, H.P.; Pickering, M.J.; McLean, J.F.; Cleland, A.A. Syntactic alignment and participant role in dialogue. Cognition 2007, 104, 163–197. [Google Scholar] [CrossRef] [PubMed]
- Garrod, S.; Fay, N.; Lee, J.; Oberlander, J.; MacLeod, T. Foundations of representations: where might graphical symbol systems come from? Cogn. Sci. 2007, 31, 961–987. [Google Scholar] [CrossRef] [PubMed]
- Fay, N.; Garrod, S.; Roberts, L. The fitness and functionality of culturally evolved communication systems. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2008, 363, 3553–3561. [Google Scholar] [CrossRef] [PubMed]
- Schober, M.F.; Brennan, S.E. Processes of interactive spoken discourse: the role of the partner. In Handbook of Discourse Processes; Erlbaum: Mahwah, NJ, USA, 2003. [Google Scholar]
- Krauss, R.M.; Weinheimer, S. Concurrent feedback, confirmation, and the encoding of referents in verbal communication. J. Pers. Soc. Psychol. 1966, 4, 343–346. [Google Scholar] [CrossRef] [PubMed]
- Weiß, P.; Pfeiffer, T.; Schaffranietz, G.; Rickheit, G. Coordination in dialog: alignment of object naming in the Jigsaw Map Game. In Proceedings of the 8th Annual Conference of the Cognitive Science Society of Germany, Saarbrücken, Germany, August 2007; pp. 4–20.
- Gleim, R.; Mehler, A.; Eikmeyer, H.J. Representing and maintaining large corpora. In Proceedings of the Corpus Linguistics 2007 Conference, Birmingham, UK, July 2007.
- Ferrer i Cancho, R.; Solé, R.V. The small-world of human language. Proc. R. Soc. Lond. B Biol. Sci. 2001, 268, 2261–2265. [Google Scholar] [CrossRef] [PubMed]
- Ferrer i Cancho, R.; Solé, R.V.; Köhler, R. Patterns in syntactic dependency-networks. Phys. Rev. E 2004, 69, 051915. [Google Scholar] [CrossRef] [PubMed]
- Mehler, A. Structural similarities of complex networks: a computational model by example of Wiki graphs. Appl. Artif. Intell. 2008, 22, 619–683. [Google Scholar] [CrossRef]
- Mehler, A. On the impact of community structure on self-organizing lexical networks. In Proceedings of the 7th Evolution of Language Conference (Evolang7), Barcelona, Spain, March 2008; pp. 227–234.
- Motter, A.E.; de Moura, A.P.S.; Lai, Y.C.; Dasgupta, P. Topology of the conceptual network of language. Phys. Rev. E 2002, 65. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Choudhury, M.; Basu, A.; Ganguly, N. Self-organization of the sound inventories: analysis and synthesis of the occurrence and co-occurrence networks of consonants. J. Quant. Linguist. 2009, 16, 157–184. [Google Scholar] [CrossRef]
- Steyvers, M.; Tenenbaum, J. The large-scale structure of semantic networks: Statistical analyses and a model of semantic growth. Cogn. Sci. 2005, 29, 41–78. [Google Scholar] [CrossRef] [PubMed]
- Church, K.W.; Hanks, P. Word association norms, mutual information, and lexicography. Comput. Linguist. 1990, 16, 22–29. [Google Scholar]
- Miller, G.A.; Charles, W.G. Contextual correlates of semantic similarity. Lang. Cogn. Process 1991, 6, 1–28. [Google Scholar] [CrossRef]
- Mehler, A. Large text networks as an object of corpus linguistic studies. In Corpus Linguistics. An International Handbook of the Science of Language and Society; De Gruyter: Berlin, Germany/New York, NY, USA, 2008; pp. 328–382. [Google Scholar]
- Diestel, R. Graph Theory; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Branigan, H.P.; Pickering, M.J.; Cleland, A.A. Syntactic priming in written production: evidence for rapid decay. Psychon. Bull. Rev. 1999, 6, 635–640. [Google Scholar] [CrossRef] [PubMed]
- Bock, K.; Griffin, Z.M. The persistence of structural priming: transient activation or implicit learning? J. Exp. Psychol. 2000, 129, 177–192. [Google Scholar] [CrossRef]
- Ferreira, V.S.; Bock, K. The functions of structural priming. Lang. Cogn. Process 2006, 21, 1011–1029. [Google Scholar] [CrossRef] [PubMed]
- Mehler, A.; Weiß, P.; Menke, P.; Lücking, A. Towards a simulation model of dialogical alignment. In Proceedings of the 8th International Conference on the Evolution of Language (Evolang8), Utrecht, The Netherlands, April 2010.
- Halliday, M.A.K. Lexis as a linguistic level. In In Memory of J. R. Firth; Longman: London, UK, 1966. [Google Scholar]
- Rieger, B.B. Semiotic cognitive information processing: learning to understand discourse. A systemic model of meaning constitution. In Adaptivity and Learning. An Interdisciplinary Debate; Springer: Berlin, Germany, 2003; pp. 347–403. [Google Scholar]
- Barrat, A.; Barthélemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Caldarelli, G. Scale-Free Networks. Complex Webs in Nature and Technology; Oxford Uiversity Press: Oxford, UK, 2008. [Google Scholar]
- Caldarelli, G.; Vespignani, A. Large Scale Structure and Dynamics of Complex Networks; World Scientific: Hackensack, NJ, USA, 2007. [Google Scholar]
- Pastor-Satorras, R.; Vespignani, A. Evolution and Structure of the Internet; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bunke, H. What is the distance between graphs? Bull. EATCS 1983, 20, 35–39. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Wilhelm, T.; Hollunder, J. Information theoretic description of networks. Phys. A 2007, 385. [Google Scholar] [CrossRef]
- Dehmer, M. Information processing in complex networks: graph entropy and information functionals. Appl. Math. Comput. 2008, 201, 82–94. [Google Scholar] [CrossRef]
- Bonchev, D. Information Theoretic Indices for Characterization of Chemical Structures; Research Studies Press: Chichester, UK, 1983. [Google Scholar]
- Kraskov, A.; Grassberger, P. MIC: mutual information based hierarchical clustering. In Information Theory and Statistical Learning; Springer: New York, NY, USA, 2008; pp. 101–123. [Google Scholar]
- Dehmer, M.; Varmuza, K.; Borgert, S.; Emmert-Streib, F. On entropy-based molecular descriptors: statistical analysis of real and synthetic chemical structures. J. Chem. Inf. Model. 2009, 49, 1655–1663. [Google Scholar] [CrossRef] [PubMed]
- Dehmer, M.; Barbarini, N.; Varmuza, K.; Graber, A. A large scale analysis of information-theoretic network complexity measures using chemical structures. PLoS One 2009, 4, e8057. [Google Scholar] [CrossRef] [PubMed]
- Tuldava, J. Methods in Quantitative Linguistics; Wissenschaftlicher Verlag: Trier, Germany, 1995. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NY, USA, 2006. [Google Scholar]
- Bunke, H.; Shearer, K. A graph distance metric based on the maximal common subgraph. Pattern Recogn. Lett. 1998, 19, 255–259. [Google Scholar] [CrossRef]
- Gärdenfors, P. Conceptual Spaces; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of `small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Serrano, M.Á.; Boguñá, M.; Pastor-Satorras, R. Correlations in weighted networks. Phys. Rev. E 2006, 74, 055101. [Google Scholar] [CrossRef] [PubMed]
- Feldman, R.; Sanger, J. The Text Mining Handbook. Advanced Approaches in Analyzing Unstructured Data; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bunke, H.; Günter, S. Weighted mean of a pair of graphs. Computing 2001, 67, 209–224. [Google Scholar] [CrossRef]
- Bunke, H.; Günter, S.; Jiang, X. Towards bridging the gap between statistical and structural pattern recognition: two new concepts in graph matching. In Proceedings of the Second International Conference on Advances in Pattern Recognition; Springer: Berlin, Germany/New York, NY, USA, 2001; pp. 1–11. [Google Scholar]
- Schenker, A.; Bunke, H.; Last, M.; Kandel, A. Graph-Theoretic Techniques for Web Content Mining; World Scientific: Hackensack, NJ, USA/London, UK, 2005. [Google Scholar]
- Wallis, W.D.; Shoubridge, P.; Kraetz, M.; Ray, D. Graph distances using graph union. Pattern Recogn. Lett. 2001, 22, 701–704. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Erdős, P.; Rényi, A. On random graphs. Publ. Math. 1959, 6, 290–297. [Google Scholar]
- Cattuto, C.; Barrat, A.; Baldassarri, A.; Schehr, G.; Loreto, V. Collective dynamics of social annotation. PNAS 2009, 106, 10511–10515. [Google Scholar] [CrossRef] [PubMed]
- Zlatic, V.; Bozicevic, M.; Stefancic, H.; Domazet, M. Wikipedias: Collaborative web-based encyclopedias as complex networks. Phys. Rev. E 2006, 74, 016115. [Google Scholar] [CrossRef] [PubMed]
- Mehler, A. Text linkage in the Wiki medium — a comparative study. In Proceedings of the EACL Workshop on New Text — Wikis and blogs and other dynamic text sources, Trento, Italy, April 2006; pp. 1–8.
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Altmann, G. Semantische diversifikation. Folia Linguist. 1985, 19, 177–200. [Google Scholar] [CrossRef]
- Mehler, A. A quantitative graph model of social ontologies by example of Wikipedia. In Towards an Information Theory of Complex Networks: Statistical Methods and Applications; Birkhäuser: Boston, MA, USA/Basel, Switzerland, 2009. [Google Scholar]
- Manning, C.D.; Schütze, H. Foundations of Statistical Natural Language Processing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.