Abstract
The work presents experimental confirmation of the author’s thermodynamic theory of the biological evolution and aging of living beings. It shows that using the law of temporal hierarchies and the second law of thermodynamics, it is easy to describe biological evolution (phylogeny) and ontogeny in terms of equilibrium hierarchical thermodynamics. This theory explains many known facts and makes it possible to formulate new practical recommendations in the sphere of medical and biological disciplines, for instance, dietology, gerontology, and geriatrics. Using the models of temporal hierarchies when studying living nature, researchers can go a long way towards understanding it.
"In addition to entropy there may well exist other "one-way" functions which add to the overall description of the world as temporal development."Kenneth G. Denbigh [1]
Introduction
Understanding the specifics of the biological evolution and aging of living organisms becomes much easier if these processes are considered in terms of phenomenological equilibrium thermodynamics of hierarchical systems [2,3].
Thanks to the law of temporal hierarchies and the existence of temporal hierarchical sequences in biological systems [4,5,6], it is possible to identify, at given time intervals, the quasi-closed biological systems in preset hierarchies and to build both stationary and non-stationary models of the evolution of these systems.
The theory of the evolution and aging of quasi-closed biological structures rests on the laws of thermodynamics of close-to-equilibrium systems and on equilibrium (quasi-equilibrium) dynamic models, e.g., the model of equilibrium molecular chromatography of flow systems. Let me note that such flow systems, while being open in principle, are easy to study using the methods of equilibrium thermodynamics [7].
The thermodynamic criterion of completeness of any particular evolution (evolution of the structure of biological systems at the given hierarchical level) can be constituted by the variation of the specific value of the Gibbs function (Gibbs energy) of the formation of suprastructures of the selected j-th hierarchy, 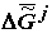 , which for a quasi-closed system tends to the most negative value (
, which for a quasi-closed system tends to the most negative value ( 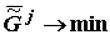 ).
).
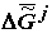 , which for a quasi-closed system tends to the most negative value (
, which for a quasi-closed system tends to the most negative value ( 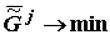 ).
). The models of biological evolution are best examined at the molecular and supramolecular levels. The findings of macrothermodynamics (supramolecular thermodynamics) of quasi-closed systems and the published data about the variation of the chemical composition of living organisms in ontogeny confirm the thermodynamic tendency of aging processes [8,9]. According to the thermodynamic theory the specific value of the Gibbs function of the formation of supramolecular structures of the organism, 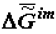 , tends to a minimum. That tendency explains the variation of the supramolecular and chemical composition and the morphology of tissues during aging. The theory makes it possible to define the principles upon which proper diets and medications can be devised to slow down aging. Such diets and medications are also useful in preventative care and in the treatment of various pathologies and among them those attending old age. The use of the Le Chatelier-Brown principle, as well as the other laws of equilibrium thermodynamics to describe quasi-closed systems, offers broad opportunities for the study of the biological world [3,4,6].
, tends to a minimum. That tendency explains the variation of the supramolecular and chemical composition and the morphology of tissues during aging. The theory makes it possible to define the principles upon which proper diets and medications can be devised to slow down aging. Such diets and medications are also useful in preventative care and in the treatment of various pathologies and among them those attending old age. The use of the Le Chatelier-Brown principle, as well as the other laws of equilibrium thermodynamics to describe quasi-closed systems, offers broad opportunities for the study of the biological world [3,4,6].
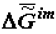 , tends to a minimum. That tendency explains the variation of the supramolecular and chemical composition and the morphology of tissues during aging. The theory makes it possible to define the principles upon which proper diets and medications can be devised to slow down aging. Such diets and medications are also useful in preventative care and in the treatment of various pathologies and among them those attending old age. The use of the Le Chatelier-Brown principle, as well as the other laws of equilibrium thermodynamics to describe quasi-closed systems, offers broad opportunities for the study of the biological world [3,4,6].
, tends to a minimum. That tendency explains the variation of the supramolecular and chemical composition and the morphology of tissues during aging. The theory makes it possible to define the principles upon which proper diets and medications can be devised to slow down aging. Such diets and medications are also useful in preventative care and in the treatment of various pathologies and among them those attending old age. The use of the Le Chatelier-Brown principle, as well as the other laws of equilibrium thermodynamics to describe quasi-closed systems, offers broad opportunities for the study of the biological world [3,4,6].The Model of Biological Evolution
The author maintains that life on the Earth (and in other parts of the Universe) originated and is evolving in conformity with the law of temporal hierarchies and the second law of thermodynamics.
Under the action of solar energy, the substances that are thermodynamically stable in conditions of primary Earth or some other heavenly body (H2O, CO2, N2, etc.) turn (as they do now) into various products of photosynthesis. Later, as a result of spontaneous «darkness reactions» these products are transformed into various substances in organic and inorganic systems under the laws of chemical thermodynamics. The selection of these substances is «performed» by kinetics, which obeys the same laws. Under the laws of local thermodynamics, due to the fact that the Gibbs function of the formation of supramolecular (intermolecular, im) structures, 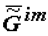 , tends to minimum, the substances that form the most stable supramolecular structures are selected. These structures are accumulated in micro- and macrovolumes of biological systems. Individual macromolecules and superstructures reduplicate in consequence of possible matrix mechanisms. The first to be selected are nucleic acids whose composition and structure (because of the thermodynamic factors) slowly adapt to the nature of the surroundings, including the nature of proteins, which, in turn, is determined by the DNA (RNA) itself. This explains the feedback in the reading off of information between protein structure and DNA. Under our model, this feedback has a thermodynamic nature. Let me note that in my view, there is thermodynamic feedback among all hierarchical levels: ecosystems ⇒ populations ⇒ organisms ⇒ cells ⇒ supramolecular structures ⇒ proteins and some other macromolecules ⇒ DNA.
, tends to minimum, the substances that form the most stable supramolecular structures are selected. These structures are accumulated in micro- and macrovolumes of biological systems. Individual macromolecules and superstructures reduplicate in consequence of possible matrix mechanisms. The first to be selected are nucleic acids whose composition and structure (because of the thermodynamic factors) slowly adapt to the nature of the surroundings, including the nature of proteins, which, in turn, is determined by the DNA (RNA) itself. This explains the feedback in the reading off of information between protein structure and DNA. Under our model, this feedback has a thermodynamic nature. Let me note that in my view, there is thermodynamic feedback among all hierarchical levels: ecosystems ⇒ populations ⇒ organisms ⇒ cells ⇒ supramolecular structures ⇒ proteins and some other macromolecules ⇒ DNA.
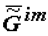 , tends to minimum, the substances that form the most stable supramolecular structures are selected. These structures are accumulated in micro- and macrovolumes of biological systems. Individual macromolecules and superstructures reduplicate in consequence of possible matrix mechanisms. The first to be selected are nucleic acids whose composition and structure (because of the thermodynamic factors) slowly adapt to the nature of the surroundings, including the nature of proteins, which, in turn, is determined by the DNA (RNA) itself. This explains the feedback in the reading off of information between protein structure and DNA. Under our model, this feedback has a thermodynamic nature. Let me note that in my view, there is thermodynamic feedback among all hierarchical levels: ecosystems ⇒ populations ⇒ organisms ⇒ cells ⇒ supramolecular structures ⇒ proteins and some other macromolecules ⇒ DNA.
, tends to minimum, the substances that form the most stable supramolecular structures are selected. These structures are accumulated in micro- and macrovolumes of biological systems. Individual macromolecules and superstructures reduplicate in consequence of possible matrix mechanisms. The first to be selected are nucleic acids whose composition and structure (because of the thermodynamic factors) slowly adapt to the nature of the surroundings, including the nature of proteins, which, in turn, is determined by the DNA (RNA) itself. This explains the feedback in the reading off of information between protein structure and DNA. Under our model, this feedback has a thermodynamic nature. Let me note that in my view, there is thermodynamic feedback among all hierarchical levels: ecosystems ⇒ populations ⇒ organisms ⇒ cells ⇒ supramolecular structures ⇒ proteins and some other macromolecules ⇒ DNA. In the final analysis, the DNA structure determines the structure of a population. At the same time, the existence of feedback makes it possible to «transcribe», for instance, the newly emergent behavioural reactions of a population (ones that are shaped in consequence of environmental changes) as new nucleotide sequences in DNA and RNA molecules. This should not be surprising if one bears in mind the existence of the law of temporal hierarchies and examines the processes of transcription of «thermodynamic information» (transmitted from one hierarchical level to another) on the given time scales. The principle of the stability of substance of all hierarchies (in particular, the principle of stability of chemical substances) [4,9] makes it possible to explain the reasons for the practically unlimitable evolution of the biological world in terms of the general laws of nature.
We see that the processes of direct reading off of information from DNA and its transmission to the level of population, on the one hand, and the reverse processes of adaptation of lower-lever structures to the nature of the structures located at a higher hierarchical level (i.e., the nature of the environment) have different development rates. These processes occur against the background of fluctuation of thermostatic parameters (natural environment), which, along with other factors, ensures the maintenance of life. Thermodynamic factors promote stabilization of all complex biological structures, causing the emergence of higher social, ecological, and other hierarchies of the biological world.
On the whole, one may assert that both internal factors (characteristics of the biosystem) and external factors (characteristics of the environment) determine the trend of biological evolution, whose progress is, of course, possible thanks to the inflow of solar energy and energy from other sources. All hierarchical levels of the biological world at certain time intervals obey the law of Le Chatelier—Brown (the principle of complementarity or the principle of least compulsion) because its operation extends not only to closed but, naturally enough, quasi-closed systems. The latter’s emergence in the biological world is connected, as was stated above, with the operation of the law of temporal hierarchies formulated by the author.
Thermodynamic Model of Ontogeny and the Aging of Living Organisms
The thermodynamic trend of the evolution of biosystems is the easiest to identify when studying an organism’s evolutionary development (ontogeny).
It is demonstrated that the motive force of ontogeny (as well as phylogeny) is the trend toward a minimum of the specific supramolecular component of the Gibbs function (e.g., biological tissue), 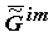 [2,3,4,5,6,10]:
[2,3,4,5,6,10]:
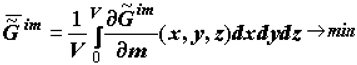 here V is the volume of the system, m is the mass of the selected microvolumes; x, y and z are coordinates; the symbol «-» means that we consider the specific value of Gim (
here V is the volume of the system, m is the mass of the selected microvolumes; x, y and z are coordinates; the symbol «-» means that we consider the specific value of Gim ( 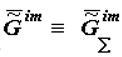 [4, p. 57]); the symbol «~ » stresses that the system is heterogeneous.
[4, p. 57]); the symbol «~ » stresses that the system is heterogeneous.
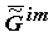 [2,3,4,5,6,10]:
[2,3,4,5,6,10]:
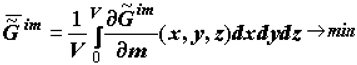
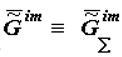 [4, p. 57]); the symbol «~ » stresses that the system is heterogeneous.
[4, p. 57]); the symbol «~ » stresses that the system is heterogeneous. This trend is presented in the bottom part of Figure 1.
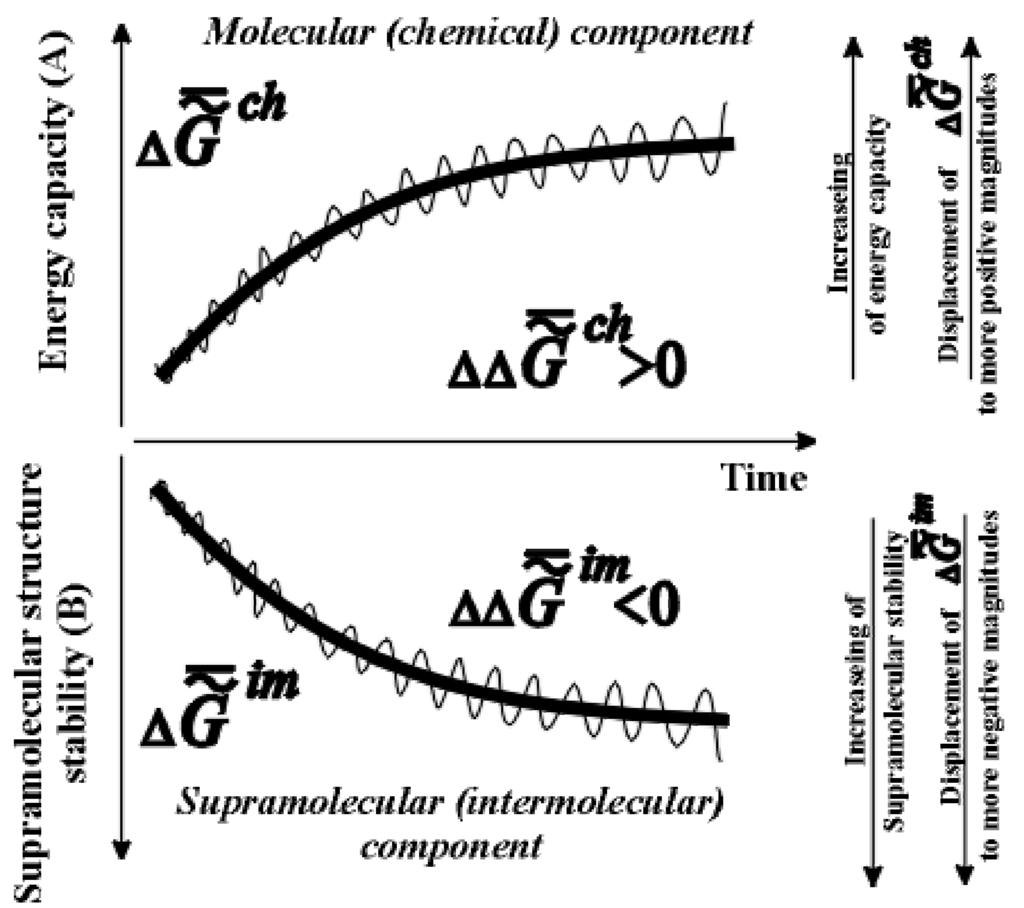
Figure 1.
Scheme of changes in specific chemical energy capacity of the biological mass (biological tissue) A ( 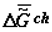 ) or (
) or ( 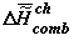 ) and thermodynamic stability of its supramolecular structures during ontogeny of living beings B (
) and thermodynamic stability of its supramolecular structures during ontogeny of living beings B ( 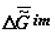 ).
).
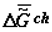 ) or (
) or ( 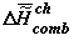 ) and thermodynamic stability of its supramolecular structures during ontogeny of living beings B (
) and thermodynamic stability of its supramolecular structures during ontogeny of living beings B ( 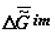 ).
).
Scales A and B are different ( 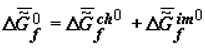 ,
, 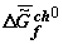 is much greater than
is much greater than 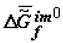 ). The time axis set by the second law of thermodynamics is scaleless. Jagged lines plotted onto the curves emphasize the fact that fluctuation of environmental parameters (temperature, pressure, diet, physical fields, time of day, season, etc.) change the levels
). The time axis set by the second law of thermodynamics is scaleless. Jagged lines plotted onto the curves emphasize the fact that fluctuation of environmental parameters (temperature, pressure, diet, physical fields, time of day, season, etc.) change the levels 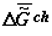 and
and 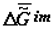 . Organisms adapt to these fluctuations only within the limits of the adaptive zone (range of tolerance).
. Organisms adapt to these fluctuations only within the limits of the adaptive zone (range of tolerance).
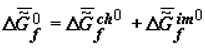 ,
, 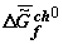 is much greater than
is much greater than 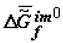 ). The time axis set by the second law of thermodynamics is scaleless. Jagged lines plotted onto the curves emphasize the fact that fluctuation of environmental parameters (temperature, pressure, diet, physical fields, time of day, season, etc.) change the levels
). The time axis set by the second law of thermodynamics is scaleless. Jagged lines plotted onto the curves emphasize the fact that fluctuation of environmental parameters (temperature, pressure, diet, physical fields, time of day, season, etc.) change the levels 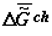 and
and 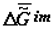 . Organisms adapt to these fluctuations only within the limits of the adaptive zone (range of tolerance).
. Organisms adapt to these fluctuations only within the limits of the adaptive zone (range of tolerance).The use of average integral value 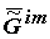 obliges one to refer to a new branch of physical chemistry, supramolecular thermodynamics, which studies complex supramolecular structures without any detailed analysis at molecular level. This approach does not contradict the methods of phenomenological thermodynamics and is, perhaps, currently the only effective approach to the study of the thermodynamic aspects of evolution, aging and behavior of living systems.
obliges one to refer to a new branch of physical chemistry, supramolecular thermodynamics, which studies complex supramolecular structures without any detailed analysis at molecular level. This approach does not contradict the methods of phenomenological thermodynamics and is, perhaps, currently the only effective approach to the study of the thermodynamic aspects of evolution, aging and behavior of living systems.
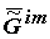 obliges one to refer to a new branch of physical chemistry, supramolecular thermodynamics, which studies complex supramolecular structures without any detailed analysis at molecular level. This approach does not contradict the methods of phenomenological thermodynamics and is, perhaps, currently the only effective approach to the study of the thermodynamic aspects of evolution, aging and behavior of living systems.
obliges one to refer to a new branch of physical chemistry, supramolecular thermodynamics, which studies complex supramolecular structures without any detailed analysis at molecular level. This approach does not contradict the methods of phenomenological thermodynamics and is, perhaps, currently the only effective approach to the study of the thermodynamic aspects of evolution, aging and behavior of living systems. As ontogeny progresses, one can observe the growth of the energy capacity of the biological mass (top part of Figure 1), that is, its specific chemical component, 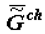 or
or 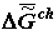 (as well as
(as well as 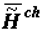 or
or 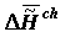 - change of the specific enthalpy of the chemical component), which is a secondary effect. According to the second law, the thermodynamics of supramolecular interactions (or supramolecular thermodynamics) «benefits» by the accumulation in a biological system of chemical substances with a high energy capacity (the reference is to the chemical component,
- change of the specific enthalpy of the chemical component), which is a secondary effect. According to the second law, the thermodynamics of supramolecular interactions (or supramolecular thermodynamics) «benefits» by the accumulation in a biological system of chemical substances with a high energy capacity (the reference is to the chemical component, 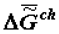 ), which oust water from this system. This can be explained by the fact that substances with a relatively high energy capacity have a heightened capacity for participation in the formation of supramolecular structures (the principle of the stability of a chemical substance [4,6]).
), which oust water from this system. This can be explained by the fact that substances with a relatively high energy capacity have a heightened capacity for participation in the formation of supramolecular structures (the principle of the stability of a chemical substance [4,6]).
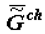 or
or 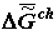 (as well as
(as well as 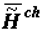 or
or 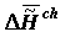 - change of the specific enthalpy of the chemical component), which is a secondary effect. According to the second law, the thermodynamics of supramolecular interactions (or supramolecular thermodynamics) «benefits» by the accumulation in a biological system of chemical substances with a high energy capacity (the reference is to the chemical component,
- change of the specific enthalpy of the chemical component), which is a secondary effect. According to the second law, the thermodynamics of supramolecular interactions (or supramolecular thermodynamics) «benefits» by the accumulation in a biological system of chemical substances with a high energy capacity (the reference is to the chemical component, 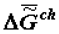 ), which oust water from this system. This can be explained by the fact that substances with a relatively high energy capacity have a heightened capacity for participation in the formation of supramolecular structures (the principle of the stability of a chemical substance [4,6]).
), which oust water from this system. This can be explained by the fact that substances with a relatively high energy capacity have a heightened capacity for participation in the formation of supramolecular structures (the principle of the stability of a chemical substance [4,6]). The chemical composition of the supramolecular structures of biosystems change slowly at the temporal segments commensurate with the duration of adaptive processes and ontogeny (as well as in phylogeny and at protracted stages of biological evolution generally). As biological tissue ages, supramolecular structures become more stable thermodynamically (needless to say, the reference is to the stability of the supramolecular structures themselves, not of the chemical substance forming them: the latter’s energy capacity rises, while stability decreases).
The selection of thermodynamically more stable supramolecular structures (structural stabilization of the phase) is determined by the thermodynamic factor: it is postulated that the time of retention or retention time (the term was borrowed from chromatography) of molecules (macromolecules) at the supramolecular phase, 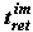 is connected with the value of the Gibbs function of the formation of supramolecular structures:
is connected with the value of the Gibbs function of the formation of supramolecular structures:
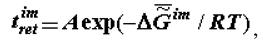 where A - coefficient, R - gas constant.
where A - coefficient, R - gas constant.
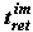 is connected with the value of the Gibbs function of the formation of supramolecular structures:
is connected with the value of the Gibbs function of the formation of supramolecular structures:
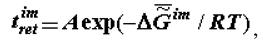
The longest-retained molecules (which are the products of biosynthesis or enter the biosystem from the external environment) located in supramolecular phase promote the selection of their own kind, which also changes the composition (and chemical nature) of the phase of supramolecular structures. As was noted above, this change is a consequence of the operation of the thermodynamic factor, although in this case it manifests itself through kinetics (Equation 2). Thus at the phase of supramolecular structures there occurs an accumulation of molecules (absorption and adsorption) whose self-assembly is the most advantageous in thermodynamic terms (these molecules have a heightened affinity with the phase of supramolecular structures). In the presence of the matrix synthesis mechanism, these molecules have advantages in reduplication (multiplication). As a result, the specific Gibbs function of the formation of supramolecular structures, 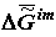 (or the specific value of the Helmholtz function, which practically coincides with it in the condensed phase) increases in absolute value becoming more negative as biological tissue evolves (ages).
(or the specific value of the Helmholtz function, which practically coincides with it in the condensed phase) increases in absolute value becoming more negative as biological tissue evolves (ages).
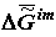 (or the specific value of the Helmholtz function, which practically coincides with it in the condensed phase) increases in absolute value becoming more negative as biological tissue evolves (ages).
(or the specific value of the Helmholtz function, which practically coincides with it in the condensed phase) increases in absolute value becoming more negative as biological tissue evolves (ages). The assessment of value 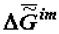 can be performed with the use of the approximated Gibbs-Helmholtz equation
can be performed with the use of the approximated Gibbs-Helmholtz equation
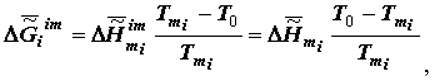 where
where 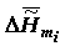 is the specific enthalpy variation due to melting (
is the specific enthalpy variation due to melting ( 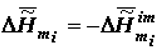 , crystallisation or self-assembly), T0 is the standard temperature (25oC) to which the calculations relate,
, crystallisation or self-assembly), T0 is the standard temperature (25oC) to which the calculations relate, 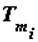 is the melting temperature of the i-th substance (or a phase consisting of i-th substances).
is the melting temperature of the i-th substance (or a phase consisting of i-th substances).
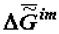 can be performed with the use of the approximated Gibbs-Helmholtz equation
can be performed with the use of the approximated Gibbs-Helmholtz equation
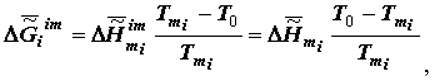
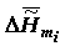 is the specific enthalpy variation due to melting (
is the specific enthalpy variation due to melting ( 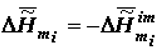 , crystallisation or self-assembly), T0 is the standard temperature (25oC) to which the calculations relate,
, crystallisation or self-assembly), T0 is the standard temperature (25oC) to which the calculations relate, 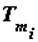 is the melting temperature of the i-th substance (or a phase consisting of i-th substances).
is the melting temperature of the i-th substance (or a phase consisting of i-th substances). The thermodynamic theory of ontogeny can help explain the phenomenon of adaptation of living organisms to the changes in the various environmental factors. Thus, a change in the temperature and chemical composition of food causes changes in the composition of the organism’s biological tissues. The necessary calculations are easy to make using the classical Gibbs-Helmholtz equation, this equation’s analogue (the author’s equation), and correlations of the following type:
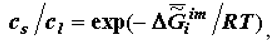 where cs and cl are concentrations of i-th metabolite in the volume V in the "solid" (aggregated, adsorbed) state and in the liquid phase, respectively.
where cs and cl are concentrations of i-th metabolite in the volume V in the "solid" (aggregated, adsorbed) state and in the liquid phase, respectively.
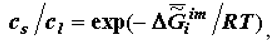
Let me note that the presented scheme of ontogeny is applicable to phylogeny and to biological evolution generally.
Experimental Confirmation of Theory
Let me point out some factors that directly confirm this theory.
Let us consider the main correlations and equations used in the author’s models and present some known experimental proof of their feasibility.
There is no doubt that the specific Gibbs function of the formation of supramolecular structures, 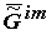 (Equation 1), characterizing the given volume of the biological mass (e.g., biological tissue) tends to a minimum in the case of quasi-closed biological systems (open systems functioning in constant conditions of the environment).
(Equation 1), characterizing the given volume of the biological mass (e.g., biological tissue) tends to a minimum in the case of quasi-closed biological systems (open systems functioning in constant conditions of the environment).
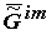 (Equation 1), characterizing the given volume of the biological mass (e.g., biological tissue) tends to a minimum in the case of quasi-closed biological systems (open systems functioning in constant conditions of the environment).
(Equation 1), characterizing the given volume of the biological mass (e.g., biological tissue) tends to a minimum in the case of quasi-closed biological systems (open systems functioning in constant conditions of the environment). Indeed, the practice of equilibrium molecular chromatography shows that the classical correlation (2) is executed with a high degree of precision for the various flow systems (open systems when the chemical composition of the substances entering the system is constant), which is precisely what chromatographic cells and columns are.
Equations of the type
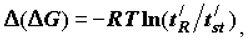 where
where 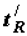 is the retention time of the examined substance,
is the retention time of the examined substance, 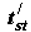 is the retention time of standard substance, are a consequence of equation (2) and have a wide practical application. I shall cite one of the hundreds of known examples is cited below.
is the retention time of standard substance, are a consequence of equation (2) and have a wide practical application. I shall cite one of the hundreds of known examples is cited below.
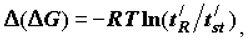
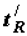 is the retention time of the examined substance,
is the retention time of the examined substance, 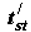 is the retention time of standard substance, are a consequence of equation (2) and have a wide practical application. I shall cite one of the hundreds of known examples is cited below.
is the retention time of standard substance, are a consequence of equation (2) and have a wide practical application. I shall cite one of the hundreds of known examples is cited below.
Table 1.
The retention time of the examined substance ( 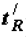 ) and the Gibbs function (Gibbs energy) of adsorption ∆(∆G) of benzene derivatives in relation to benzene on a column of silica gel with hydroxylated surface KSS-4 (s =650 m2/g) at 32° C, the consumption of water eluent is 2.5 cm3/min [7].
) and the Gibbs function (Gibbs energy) of adsorption ∆(∆G) of benzene derivatives in relation to benzene on a column of silica gel with hydroxylated surface KSS-4 (s =650 m2/g) at 32° C, the consumption of water eluent is 2.5 cm3/min [7].
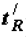 ) and the Gibbs function (Gibbs energy) of adsorption ∆(∆G) of benzene derivatives in relation to benzene on a column of silica gel with hydroxylated surface KSS-4 (s =650 m2/g) at 32° C, the consumption of water eluent is 2.5 cm3/min [7].
) and the Gibbs function (Gibbs energy) of adsorption ∆(∆G) of benzene derivatives in relation to benzene on a column of silica gel with hydroxylated surface KSS-4 (s =650 m2/g) at 32° C, the consumption of water eluent is 2.5 cm3/min [7].
| No | Adsorbate | 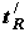 , s , s | ∆(∆G), J/mol |
| 1 | Benzene | 134 | - |
| 2 | Benzoic acid | 80 | + 1312 |
| 3 | Phenol | 100 | + 746 |
| 4 | Phloroglucinol | 120 | + 264 |
| 5 | Hydroquinone | 124 | + 195 |
| 6 | Resorcinol | 127 | + 127 |
| 7 | Benzoic alcohol | 157 | - 409 |
| 8 | o-Cresol | 179 | - 746 |
| 9 | p- Cresol | 181 | - 769 |
| 10 | m - Cresol | 187 | - 850 |
| 11 | Flurobenzene | 206 | - 1096 |
| 12 | o-Xylene | 269 | - 1774 |
| 13 | m - Xylene | 287 | - 1941 |
Table 1 and Figure 2 present experimental results which confirm the applicability of formula (5) and, consequently, (2) to one of the chromatographic systems. These results are in a good agreement with the results obtained from other different methods (calorimetric and isosteric methods). Let me note that in such a chromatographic column, the sorbent can be a biological material, including the biological mass of a vivid (alive) substance. Needless to say, equation (5) is just for any natural metabolite substances, provided corresponding chromatographic columns are used.
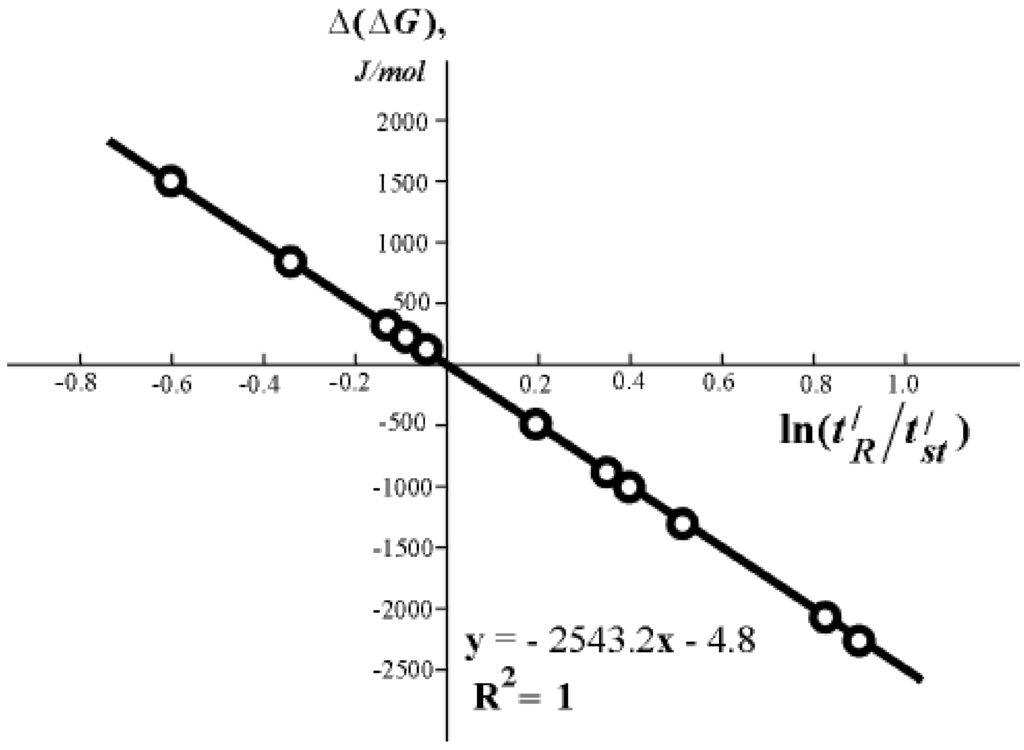
Figure 2.
Dependence of ∆(∆G) on the value of 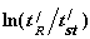 for different organic compounds on silica gel with hydroxylated surface.
for different organic compounds on silica gel with hydroxylated surface.
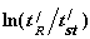 for different organic compounds on silica gel with hydroxylated surface.
for different organic compounds on silica gel with hydroxylated surface.
Further, comparisons of the theoretical scheme presented in Figure 1 with the numerous factual data show that theory and experiment fully coincide. Figure 3 and Figure 4 present data obtained by measuring the energy capacity ( 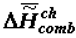 or
or 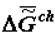 ) of biological tissue in the process of the organism’s aging and the trend of
) of biological tissue in the process of the organism’s aging and the trend of 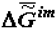 to the most negative value when forming supramolecular structures in ontogeny.
to the most negative value when forming supramolecular structures in ontogeny.
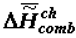 or
or 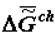 ) of biological tissue in the process of the organism’s aging and the trend of
) of biological tissue in the process of the organism’s aging and the trend of 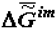 to the most negative value when forming supramolecular structures in ontogeny.
to the most negative value when forming supramolecular structures in ontogeny.Results of the type presented in Figure 3 are known to any educated person familiar with the concept of the calorific value of the biological mass (food).
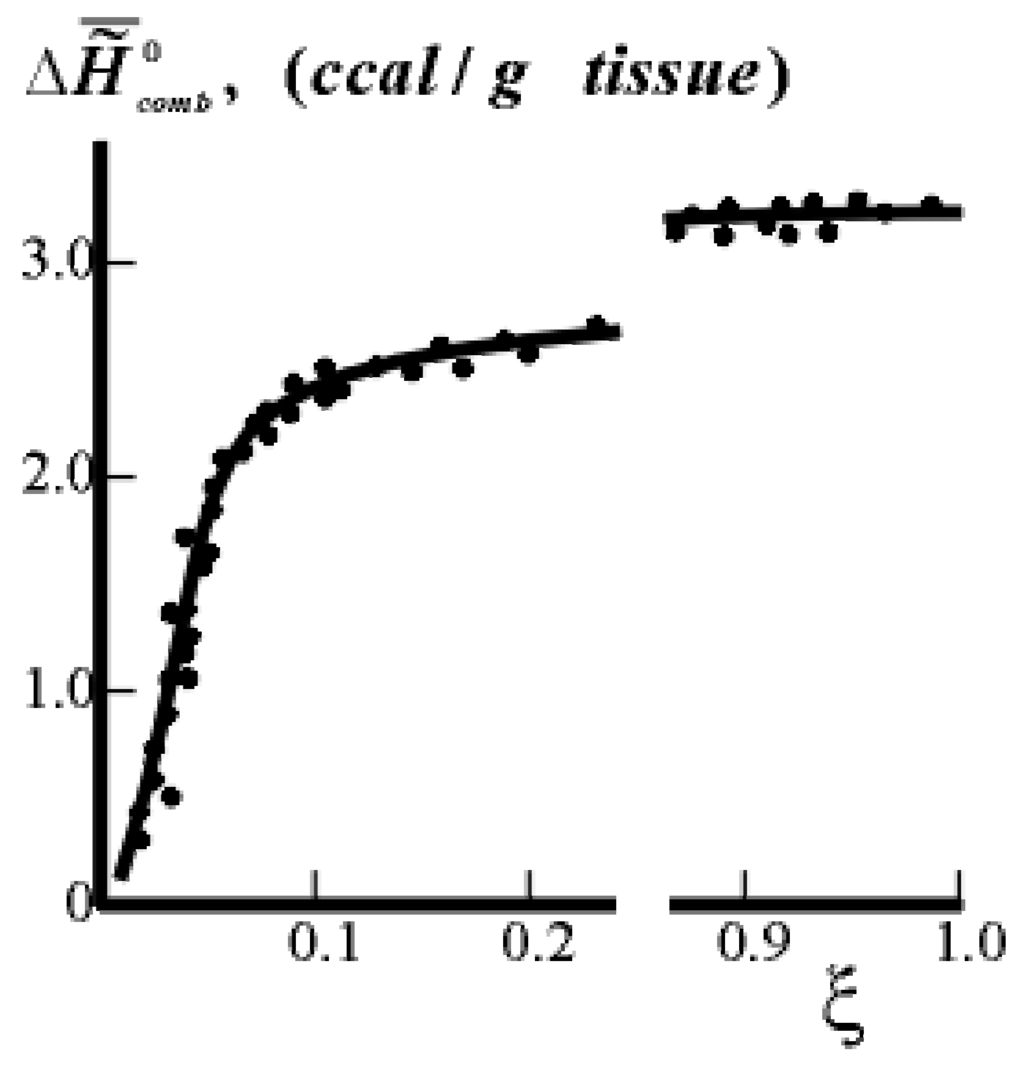
Figure 3.
Dependence of 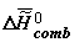 (caloric content) on the extent of ontogeny ξ (or time) for pig tissue. The values of
(caloric content) on the extent of ontogeny ξ (or time) for pig tissue. The values of 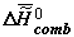 (points) were calculated on the basis of experimental data of the chemical composition of tissues (the heat of combustion of the components: fats - 9.2 ccal/g, proteins - 5.0 ccal/g). The curve shows the results of calorimetric experiments. ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue.
(points) were calculated on the basis of experimental data of the chemical composition of tissues (the heat of combustion of the components: fats - 9.2 ccal/g, proteins - 5.0 ccal/g). The curve shows the results of calorimetric experiments. ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue.
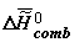 (caloric content) on the extent of ontogeny ξ (or time) for pig tissue. The values of
(caloric content) on the extent of ontogeny ξ (or time) for pig tissue. The values of 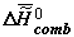 (points) were calculated on the basis of experimental data of the chemical composition of tissues (the heat of combustion of the components: fats - 9.2 ccal/g, proteins - 5.0 ccal/g). The curve shows the results of calorimetric experiments. ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue.
(points) were calculated on the basis of experimental data of the chemical composition of tissues (the heat of combustion of the components: fats - 9.2 ccal/g, proteins - 5.0 ccal/g). The curve shows the results of calorimetric experiments. ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue.
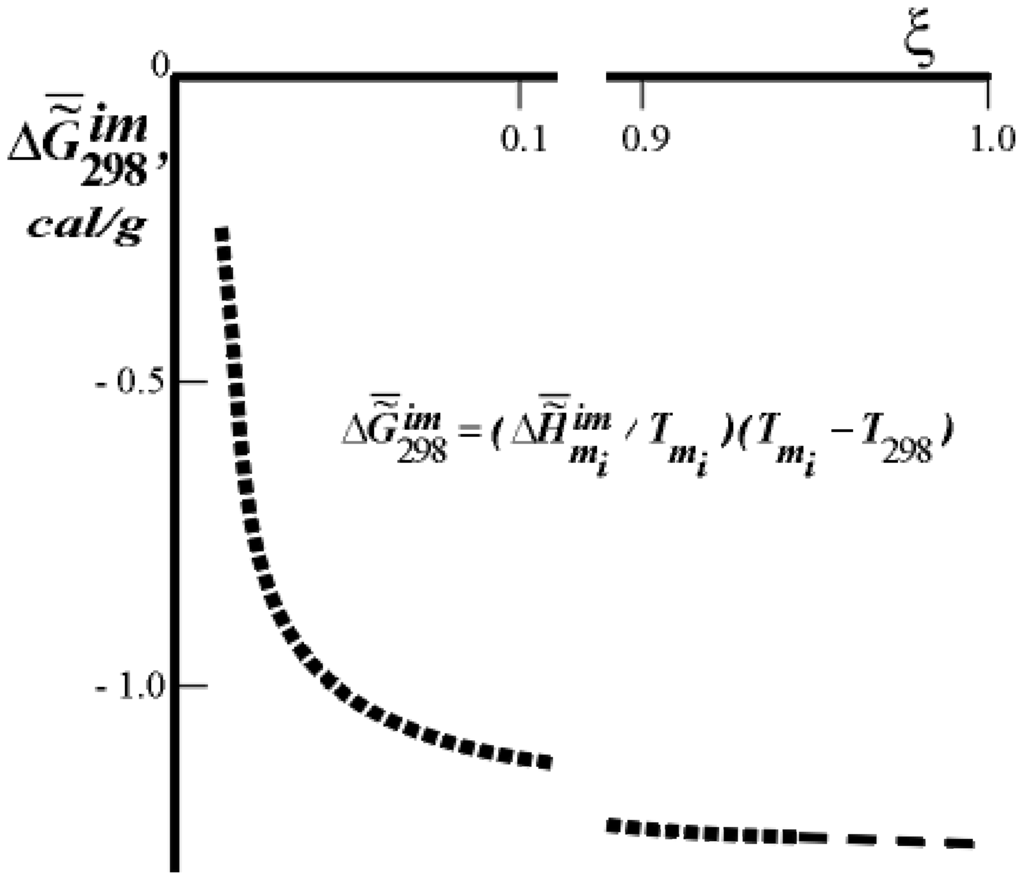
Figure 4.
Dependence of 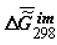 on the extent of ontogeny, ξ (or time). ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue, for rat skin collagen. The values of
on the extent of ontogeny, ξ (or time). ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue, for rat skin collagen. The values of 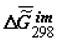 (cal/g collagen) were calculated from the data of F.Flandin et al. and Gladyshev.
(cal/g collagen) were calculated from the data of F.Flandin et al. and Gladyshev.
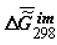 on the extent of ontogeny, ξ (or time). ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue, for rat skin collagen. The values of
on the extent of ontogeny, ξ (or time). ξ = 0.0 for 100% H2O in the tissue, ξ = 1.0 for 55% H2O in the tissue, for rat skin collagen. The values of 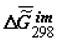 (cal/g collagen) were calculated from the data of F.Flandin et al. and Gladyshev.
(cal/g collagen) were calculated from the data of F.Flandin et al. and Gladyshev.
The data presented in Figure 4 (predicted by the author [10]) is less well-known. Presented here are the results obtained with the help of the method of differential scanning calorimetry (DSC method). By way of example, Figure 5 presents DSC thermograms of the skin of differently-aged rats [11]. Similar results have been obtained in several laboratories in the United States, Canada, and other countries.
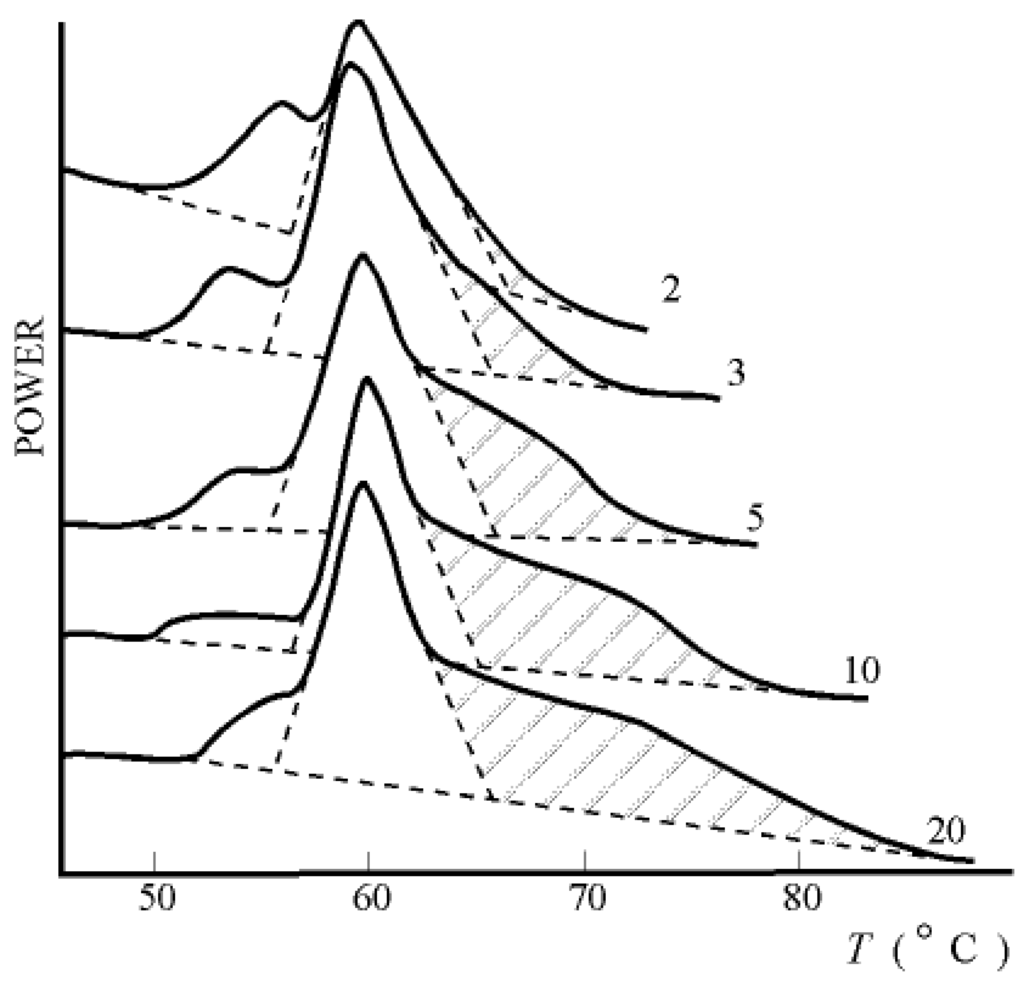
Figure 5.
DSC thermograms of the skin of rats of different ages (2-20 months). Data of F.Flandin et al.
Noteworthy are the measurements made in J. Lepock’s laboratory (Department of Physics, Waterloo University, Canada). Figure 6 shows "the thermograms of the aging" of Greenbottle fly larvae. Even a qualitative assessment of value 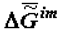 performed with the use of the approximated Gibbs-Helmholtz equation (3) shows that, indeed, values ∆H and
performed with the use of the approximated Gibbs-Helmholtz equation (3) shows that, indeed, values ∆H and 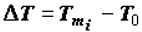 increase during ontogeny substantially, which makes value
increase during ontogeny substantially, which makes value 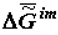 significantly more negative.
significantly more negative.
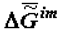 performed with the use of the approximated Gibbs-Helmholtz equation (3) shows that, indeed, values ∆H and
performed with the use of the approximated Gibbs-Helmholtz equation (3) shows that, indeed, values ∆H and 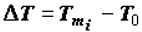 increase during ontogeny substantially, which makes value
increase during ontogeny substantially, which makes value 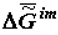 significantly more negative.
significantly more negative.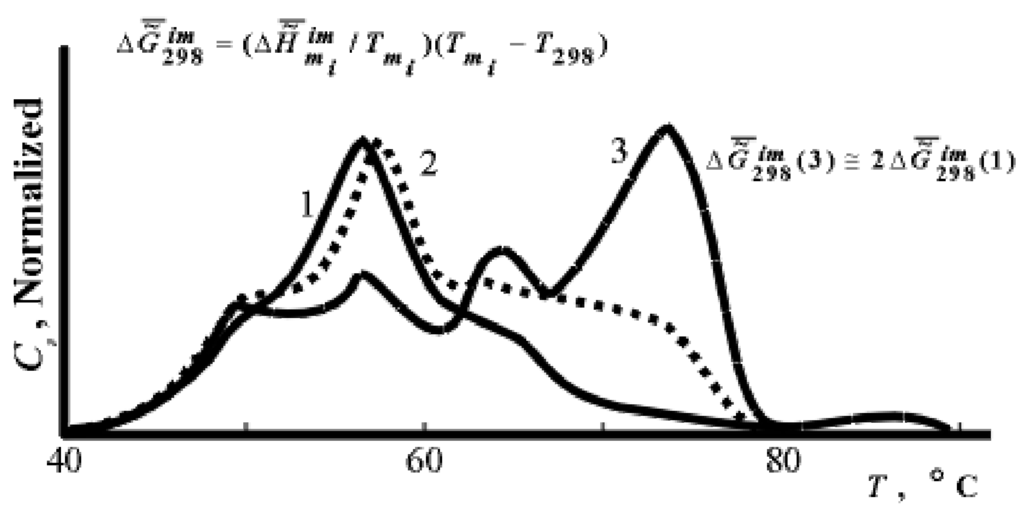
Figure 6.
DSC thermograms of Greenbottle flies (larvae). Ages: 1 - 1 day, 2 - 3 days, 3 - 5 days. Data of J.Lepock et al.
Note that, when necessary, the values of 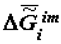 may be estimated more precisely by using the equation
may be estimated more precisely by using the equation
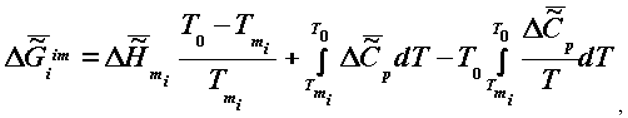 where
where 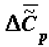 is the change of heat capacity of the corresponding supramolecular structures during phase transition.
is the change of heat capacity of the corresponding supramolecular structures during phase transition.
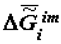 may be estimated more precisely by using the equation
may be estimated more precisely by using the equation
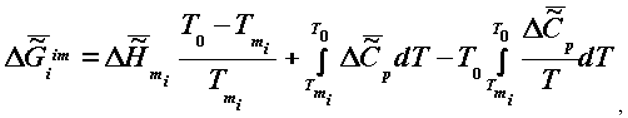
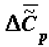 is the change of heat capacity of the corresponding supramolecular structures during phase transition.
is the change of heat capacity of the corresponding supramolecular structures during phase transition. I would like to note that the trend toward the increase of 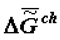 (
( 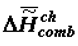 ) and decrease of
) and decrease of 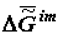 in ontogeny (as well as in phylogeny) is not likely to surprise physico-chemists, since it is qualitatively obvious that they are a consequence of the lower concentration of water in the biological mass as the latter ages.
in ontogeny (as well as in phylogeny) is not likely to surprise physico-chemists, since it is qualitatively obvious that they are a consequence of the lower concentration of water in the biological mass as the latter ages.
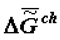 (
( 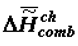 ) and decrease of
) and decrease of 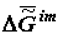 in ontogeny (as well as in phylogeny) is not likely to surprise physico-chemists, since it is qualitatively obvious that they are a consequence of the lower concentration of water in the biological mass as the latter ages.
in ontogeny (as well as in phylogeny) is not likely to surprise physico-chemists, since it is qualitatively obvious that they are a consequence of the lower concentration of water in the biological mass as the latter ages. As was noted above that, the use of the generally known correlation (4) makes it easy to calculate the changes in metabolite concentration under temperature changes. Works [4,6,12] compare the results of calculations and experimental data. The performed model calculations (to be convincing, they have a relatively high degree of accuracy) directly confirm the applicability of the macrothermodynamic model to the evolution of the organisms’ fatty tissue and explains the reasons for the variation of the composition of fatty acids (fats) during the organisms’ adaptation to the temperature of the environment.
A convincing illustration is also Frenckel’s and Hoppe’s classical data on the dependence of the iodine value of phosphatides (lipids) of fly larvae upon the temperature of their habitat [13]. When the temperature is high, the concentration of unsaturated acids drops. This agrees with the results of our calculations (when the temperature decreases by 10° C, the iodine value rises 1.21 ± 0.03 times).
The concept of the thermodynamic nature of adaptation of biosystems to the changes in the composition of the environment is confirmed by the well-known data regarding the binding of gaseous ligands with hemoglobin and other proteins.
One of the applications of our theory is connected with the problems of gerontology, nutrition, and several other medical and biological sciences. From the view point of nutrition it can be formulated in the form of the following principle by the author:
Diets including «thermodynamic evolutionary young» animal and vegetable foods stimulate longevity and improve the quality of human life. The degree of «evolutionary» youth of a food product is determined by its chemical composition and supramolecular structure. The chemical composition and supramolecular structure of a product depend, in their turn, on its ontogenetic and philogenetic ages. An important quantitative measure of the «gerontological efficiency» of a food product is its Gibbs function of supramolecular structure formation, which characterizes the thermodynamic stability of its supramolecular structure.
Work [9] gives examples of diets that promote a healthy way of life and the organism’s rejuvenation within the limits of its adaptive occasions (facility). Let me note that significant rejuvenating effects can be achieved when using mineral waters and other liquid foods whose salt composition is close to that of physiological liquids of a young organism. For example, it is known that the correlation of sodium and potassium salts in the biological mass of an organism changes significantly with aging [14]. There is no doubt that enrichment of the tissues with potassium salts (in adaptively acceptable quantities) helps rejuvenate the organism. In this connection, assessment of the gerontological value of mineral waters and other liquid products (pH, chemical composition) can be very useful.
Experiments in cloning (Dolly) show that the molecular environment of the genetic apparatus determines the character and the specifics of its functioning [15]. An old cell that finds itself in embryonic environment becomes rejuvenated and actively reduplicates. It would be interesting to conduct additional experiments to determine the influence of the nature of the nutrient medium (environment of old and young tissue) upon the cells’ capacity for division. Studies of the impact upon chromatin of chemical substances that reduce its supramolecular thermodynamic stability could be presented as of special interest. Such studies could be of importance for gene engineering and the investigation of adaptive evolution of DNA (RNA) [16].
The following can be said about the law of temporal hierarchies [2,3,4,5,6,9], which can be formulated as
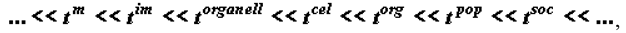 where t is the average time of the existence (life) of «free» metabolite molecules, supramolecular structures, organelles, and cells in biological tissue, as well as organisms, populations, and communities. This law, formulated by the author, is an outcome of observations and cannot be derived on the basis of any physical considerations. It is just nature-given.
where t is the average time of the existence (life) of «free» metabolite molecules, supramolecular structures, organelles, and cells in biological tissue, as well as organisms, populations, and communities. This law, formulated by the author, is an outcome of observations and cannot be derived on the basis of any physical considerations. It is just nature-given.
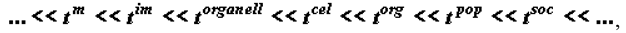
The series (7) was transcribed on the basis of factual data. Each biological species (population) is characterized by a series of figures of its own. However, for all biological systems, the life spans of the structures belonging to different hierarchies can be divided by a strong inequality. The series of type (7) make it possible to identify quasi-closed (thermodynamically and kinetically, see [4]) biosystems and use the apparatus of equilibrium hierarchical thermodynamics.
The applicability of the second law of thermodynamics in the definitions of R.Klausius, J.W.Gibbs, H.Helmholtz and other classics is not likely to arouse doubts in researchers working in physics, physical chemistry and many other fields.
Thus, in the author’s view, there is every reason to believe that his thermodynamic theory of biological evolution and the aging of living organisms has a right to existence and can prove useful to researchers working in different fields of science.
More detailed information can be found in the new works [17,18,19,20,21,22,23,24,25] and in the Internet [26].
References and Notes
- Denbigh, K.G. The Many Faces of Irreversibility. Brit. J. Phil. Sci. 1989, 40, 501–518. [Google Scholar] [CrossRef]
- Gladyshev, G.P. Termodinamika of the Ierarkhicheskikh Sistem (Thermodynamics of the Hierarchic Systems). In Khimicheskaya Enciklopedia (Chemical Encyclopedia); Bolshaya Rossiiskaya Enciklopedia: Moscow, 1995; Vol. 4, p. 535. [Google Scholar]
- Gladyshev, G.P. Termodinamika i Makrokinetika Prirodnykh Ierarkhicheskikh Processov (Thermodynamics and Macrokinetics of Natural Hierarchical Processes); Nauka: Moscow, 1988; p. 287. [Google Scholar]
- Gladyshev, G.P. Thermodynamic Theory of the Evolution of Living Beings; Nova Sci. Publ. Inc.: New York, 1997; p. 142. [Google Scholar]
- Gladyshev, G.P. On the Macrokinetics and Thermodynamics of Natural Hierarchic Processes. J. Phys. Chem. 1987, 61, 2289–2301. [Google Scholar]
- Gladyshev, G.P. Thermodynamic Theory of the Evolution of Living Beings; Luch: Moscow, 1996; p. 98. [Google Scholar]
- Kiselev, A.V.; Poshkus, D.P.; Yashin, Ya.I. Moleculyarnye osnovy adsorbcionnoi chromatografii; Chimiya: Moscow, 1986; p. 272. [Google Scholar]
- Gladyshev, G.P. In Thermodynamics of Aging. In AAAS Annual Meeting and Science Innovation Exhibition (150th Anniversary Celebration), Philadelphia, Pennsylvania, Track: Emerging Science: Transforming the Next Generation. 12-17 February 1998. A-30; S-26 (AAAS, Scope, 1997).
- Gladyshev, G.P. Thermodynamics of Aging. Biology Bulletin 1998, 25, 433–441. [Google Scholar]
- Gladyshev, G.P. On the Thermodynamics of Biological Evolution. J. Theoret. Biol. 1978, 75, 425–444. [Google Scholar] [CrossRef]
- Flandin, F.; Buffevant, Ch.; Herbage, D. A. Differential Scanning Calorimetry Analysis of the Age - Related Changes in the Thermal Stability of Rat Skin Collagen. Biochimica et Biophysica Acta 1984, 791, 205–211. [Google Scholar] [CrossRef]
- Gladyshev, G.P. A Motive Force of Biological Evolution. Herald of the Russian Academy of Sciences 1994, 64, 118–124. [Google Scholar]
- Aleksandrov, V.Ya. Kletki, Makromolekuly i temperatura (Cells, macromolecules, and temperature); Nauka: Leningrad, 1975; p. 330. [Google Scholar]
- Novak, L.P. Aging, Total Body Potassium, Fat-Free Mass, and Cell Mass in Males and Females Between 18 and 85 Years. Journal of Gerontology 1972, 27, 438–443. [Google Scholar] [CrossRef] [PubMed]
- Campbell, K.H.S.; McWhir, J.; Ritchie, W.A.; Wilmut, I. Sheep Cloned by Nuclear Transfer a Cultured Cell Line. Nature 1997, 385, 810–813. [Google Scholar] [CrossRef] [PubMed]
- Moxon, E.R.; Wills, Ch. DNA - Microsatellites: Agents of Evolution? Scientific American 1999, 72–77. [Google Scholar] [CrossRef]
- Lepock, J. Supramolecular Thermodynamics. In AAAS Annual Meeting and Science Innovation Exhibition (150th Anniversary Celebration), Philadelphia, Pennsylvania, Track: Emerging Science: Transforming the Next Generation. February 12-17, 1998. P. A-30, S-26.
- Gladyshev, G.P. The Motive Force of Evolution of Living Matter and Thermodynamic Theory of Aging. Abstract and Report. In Pan-American Congress-99, San Antonio, Texas, USA, February 21-24, 1999.
- Kurnakova, N.V.; Gazaev, M.A. The Mountains and the Theory of Aging. Abstract and Report. In Pan-American Congress-99, Aging in the Americas: Frontiers of Care, Policy and Research. San Antonio, Texas, USA, February 21-24, 1999.
- Gladyshev, G.P.; Kurnakova, N.V. Motive Force of Evolution of Living Matter and Thermodynamic Theory of Aging. Advances in Gerontology (Russian Academy of Sciences) 1999, 2, 49–58. [Google Scholar]
- Gladyshev, G.P. Thermodynamic Theory of Biological Evolution and Aging. Modern Development in Thermody-namics. In Materials for Third Gordon Research Conference. Report, II Ciocco, Tuscany, Italy, April 18-23, 1999.
- Hayflick, L. How and Why We Age; Ballantine Books: New York, 1996; p. 377. [Google Scholar]
- Gladyshev, G.P. On the Thermodynamics, Entropy and Evolution of Biological Systems: What is Life from a Physical Chemist's Viewpoint. Entropy 1999, 1, 9–20. [Google Scholar] [CrossRef]
- Gladyshev, G.P. Supramolecular Thermodynamics is a Key to Understanding Phenomena of Life. Abstract and Report. In 37th IUPAC Congress. 27th GDCh General Meeting, Berlin, Germany, August 14-19, 1999; p. 873.
- Gladyshev, G.P. Thermodynamics of Aging. Abstract and Report. In “′99 International Symposium on Aging and Antiaging Science & Technology”, Beijing, China, September 8-12, 1999; p. 26.
- See the http://www.endeav.org/evolut website.
© 1999 by MDPI (http://www.mdpi.org). Reproduction of this article, by any means, is permitted for noncommercial purposes.