Enhancing CMRR in Fully Differential Amplifiers via Power Supply Bootstrapping
Abstract
1. Introduction
2. Materials and Methods
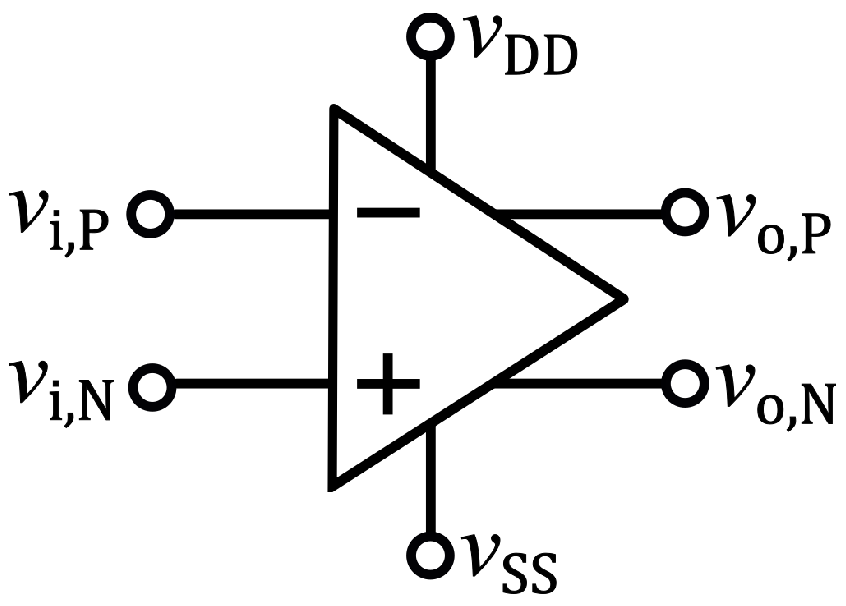
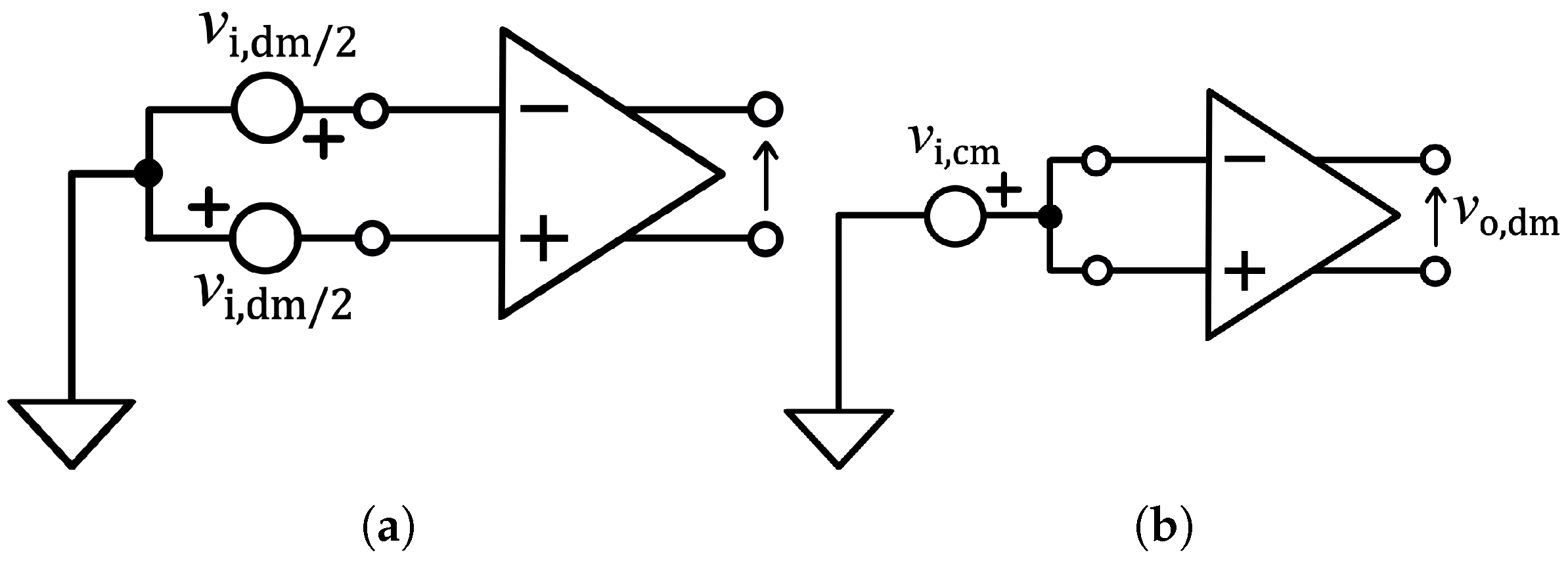
2.1. CMRR of a Fully Differential Active Circuit
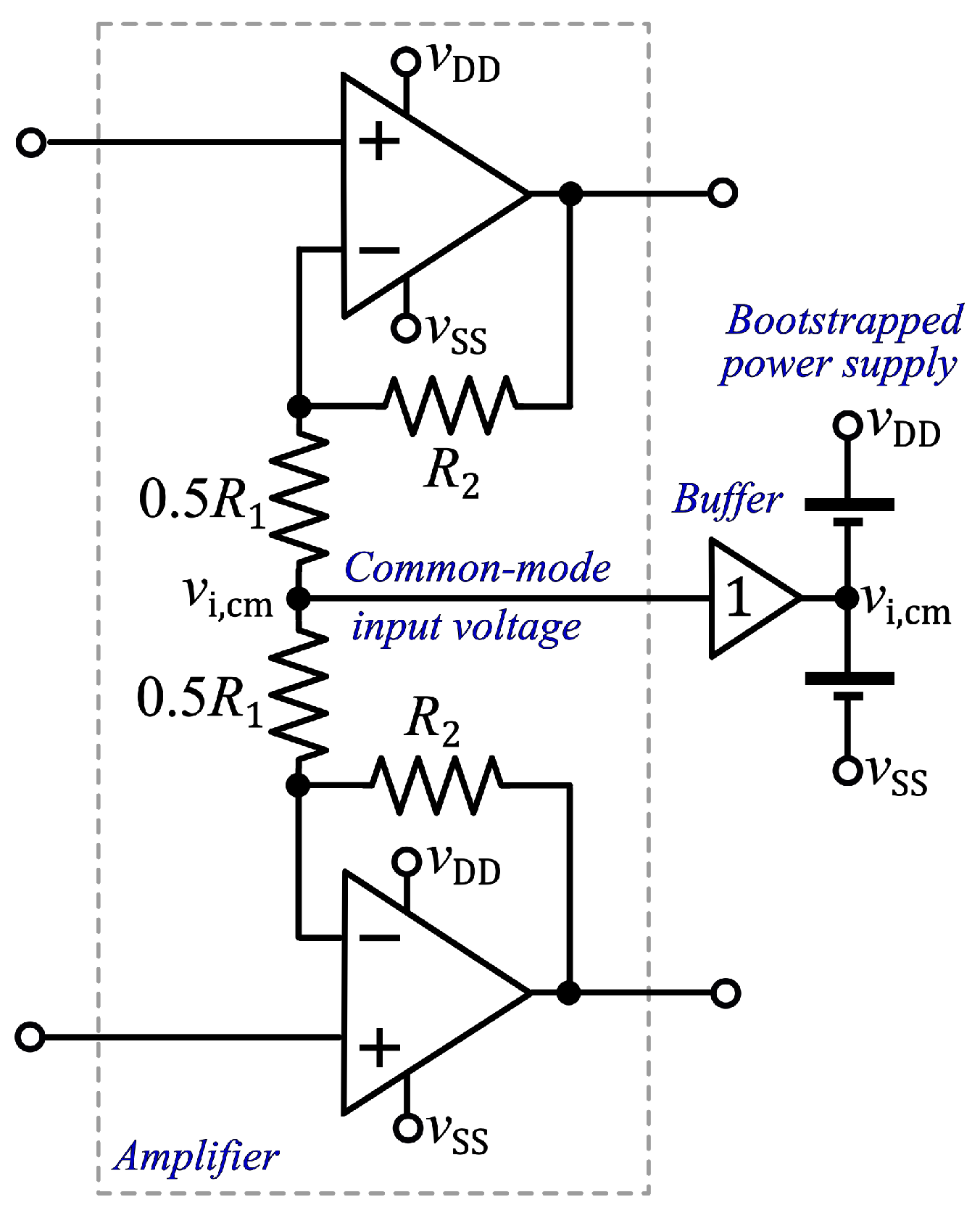
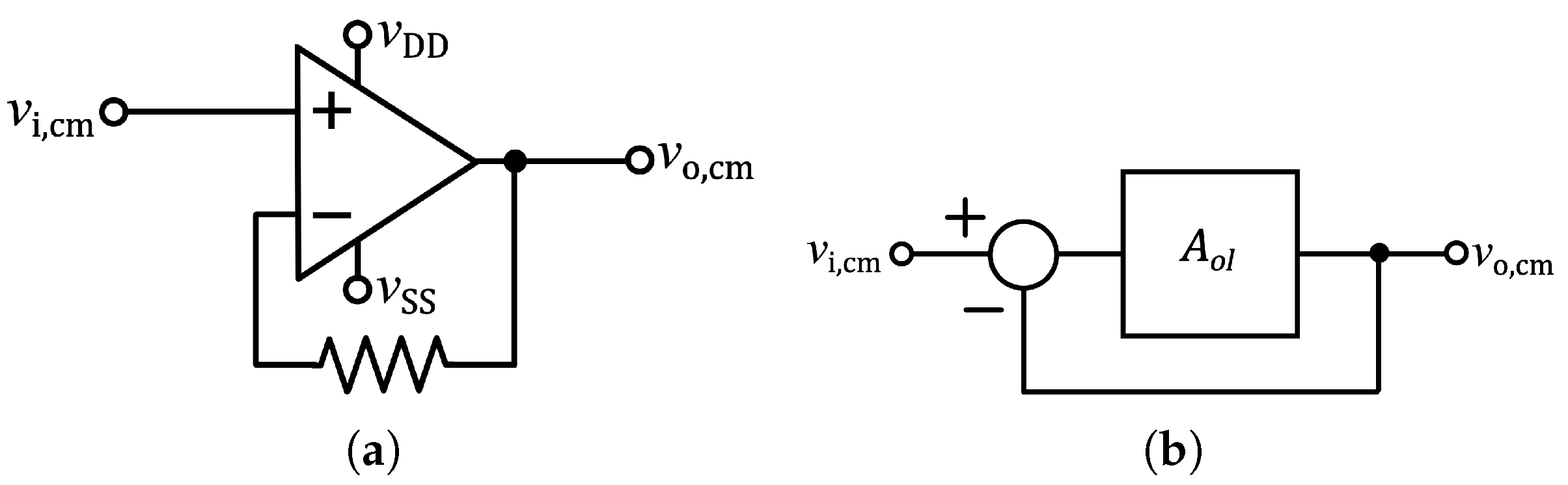
2.2. CMRR Enhancement by Power Supply Bootstrapping
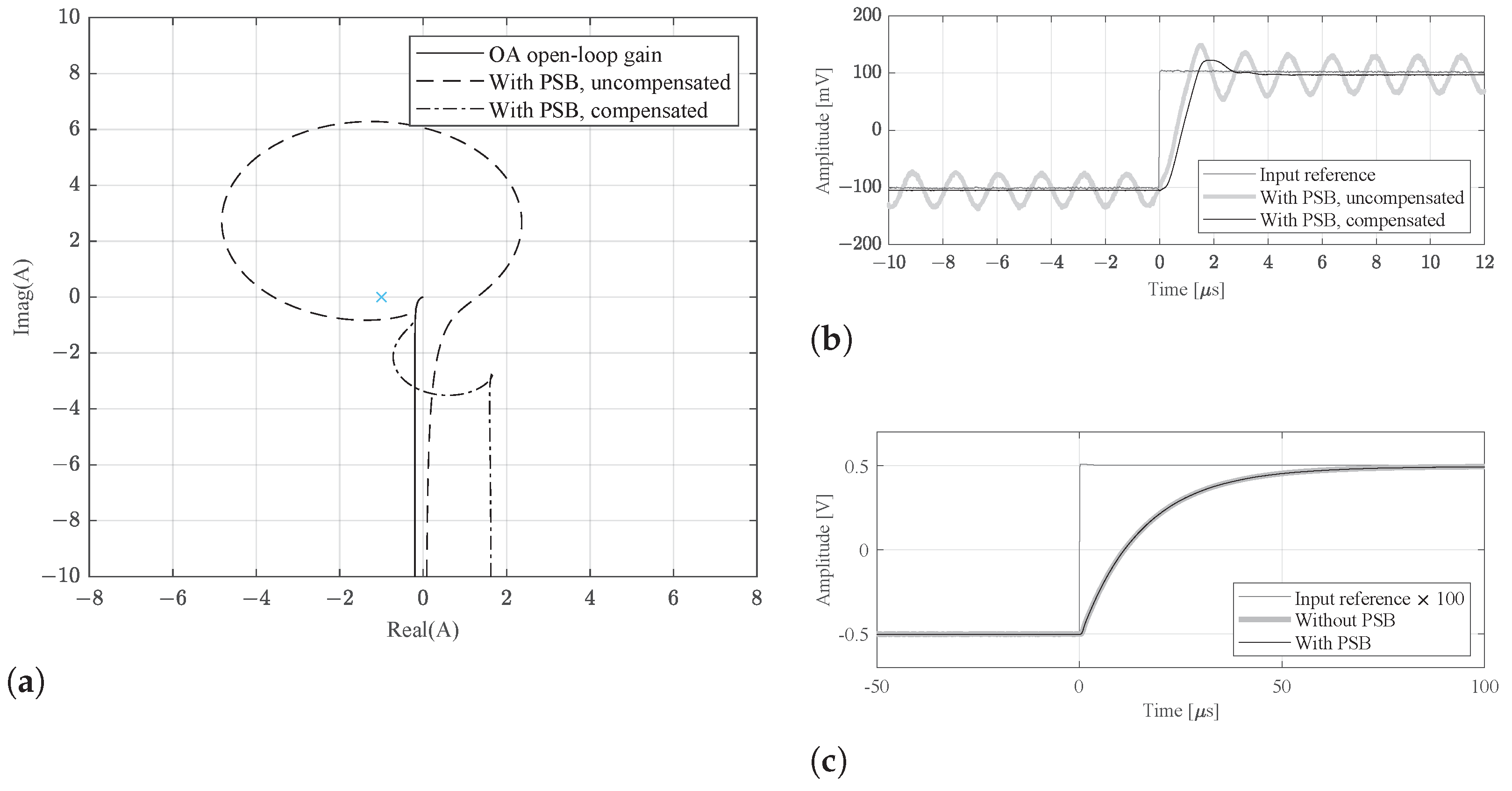
2.3. Stability Analysis
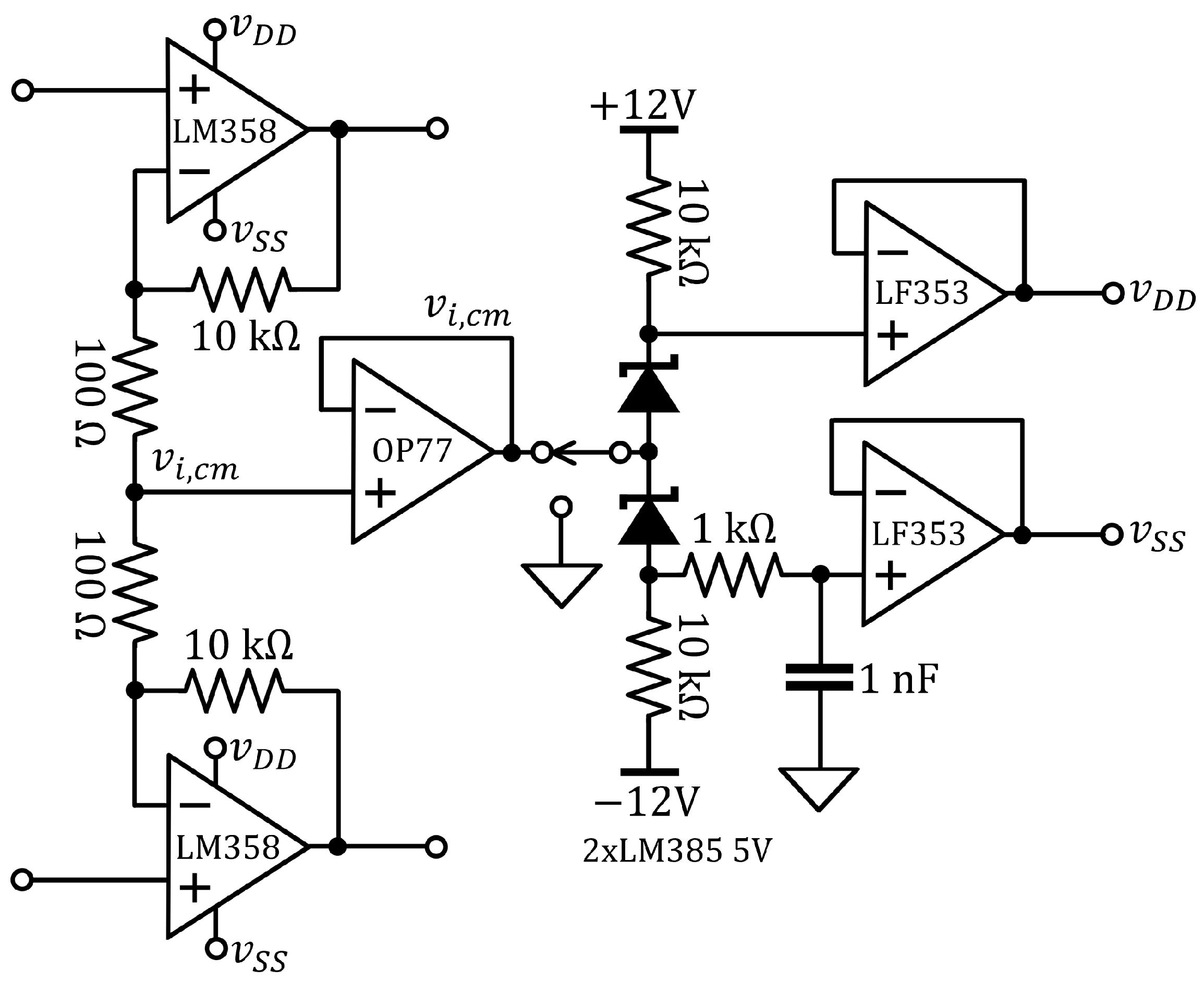
2.4. Experimental Setup
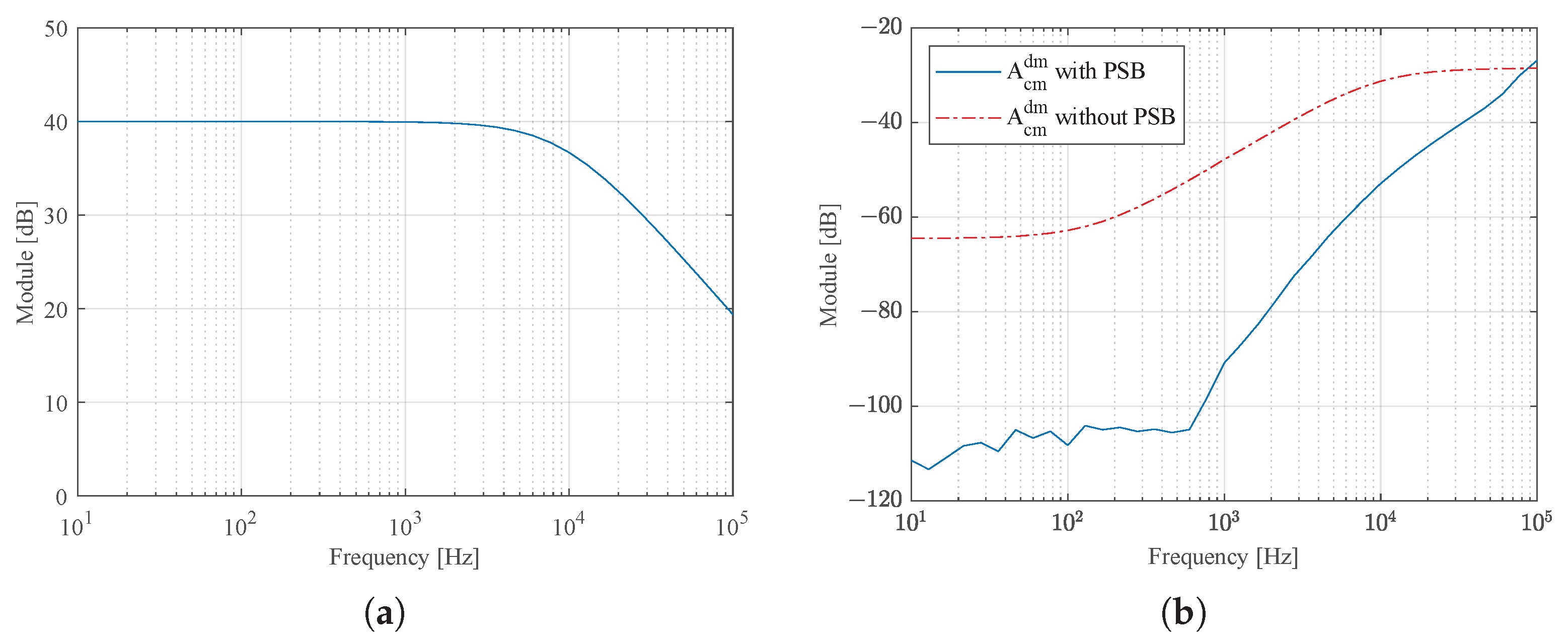
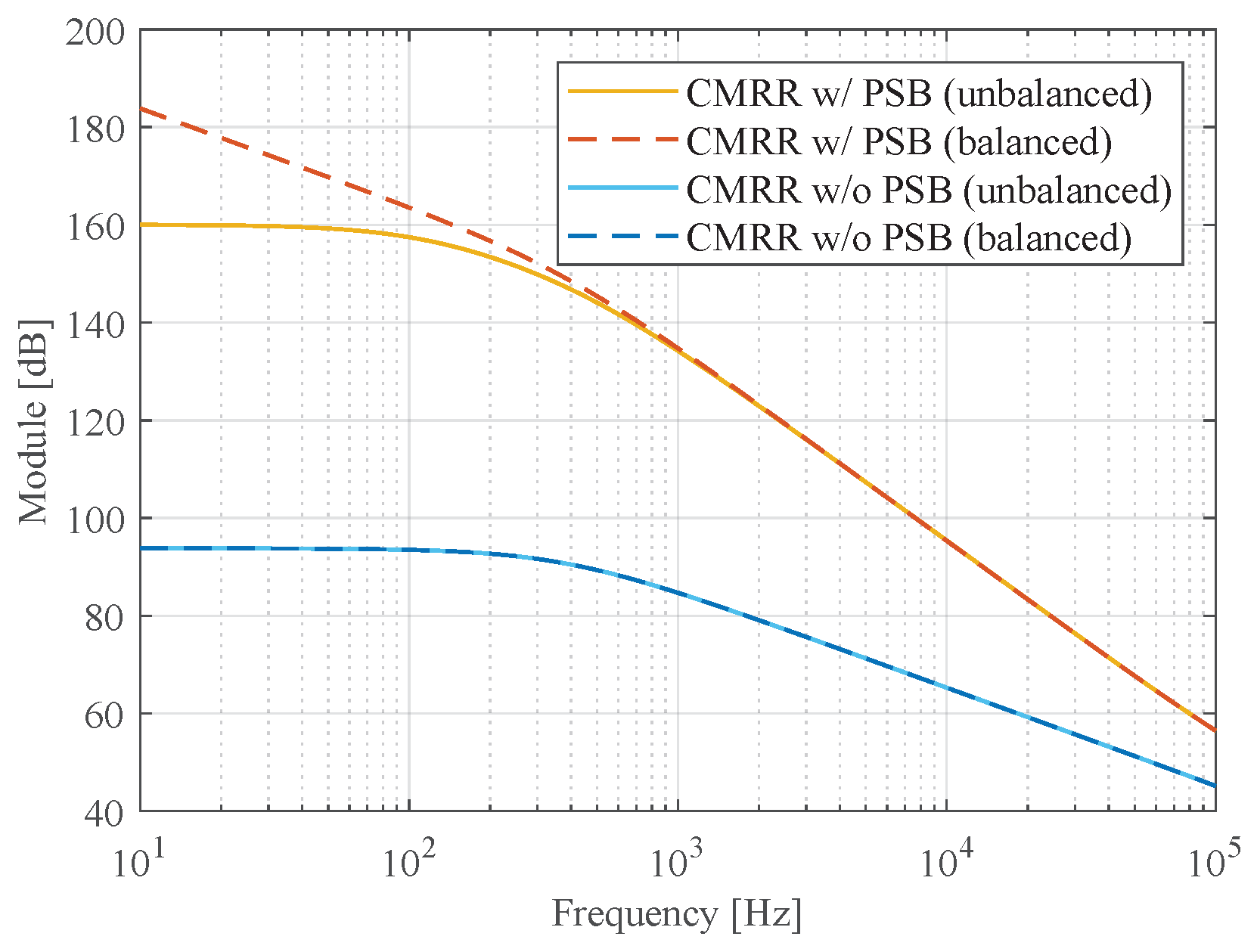
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
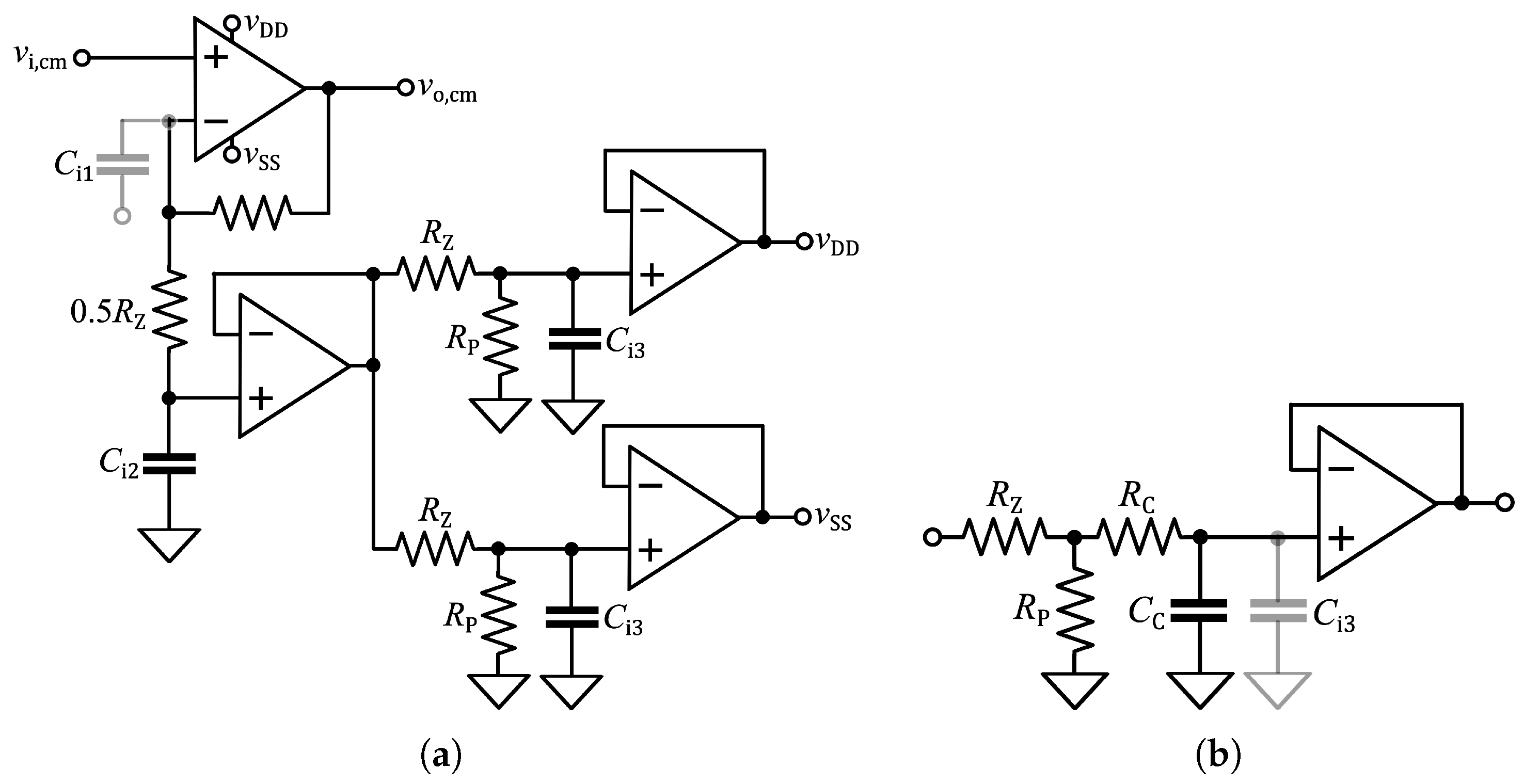
Appendix B
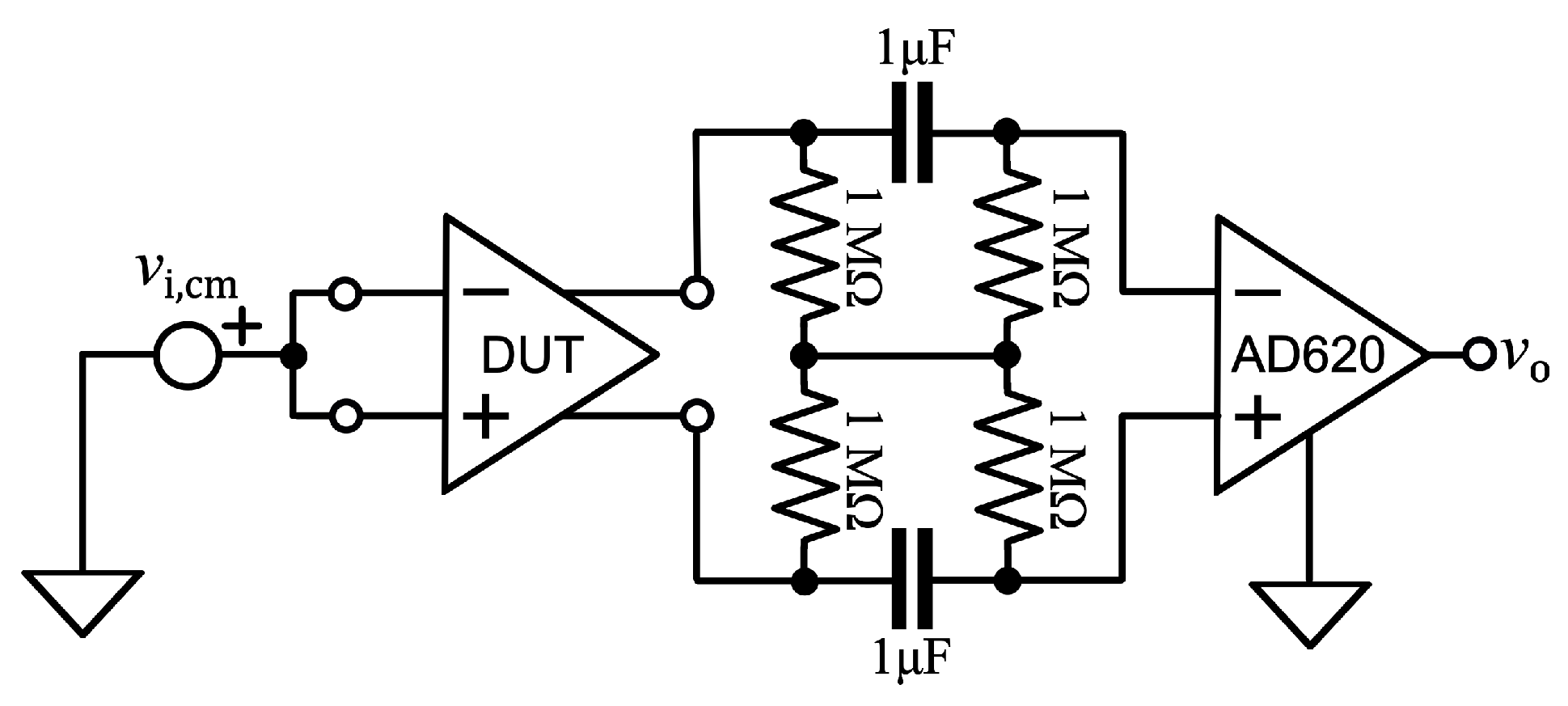
References
- Pallás-Areny, R.; Webster, J.G. Common mode rejection ratio in differential amplifiers. IEEE Trans. Instrum. Meas. 1991, 40, 669–676. [Google Scholar] [CrossRef]
- Casas, O.; Spinelli, E.M.; Pallas-Areny, R. Fully differential AC-coupling networks: A comparative study. IEEE Trans. Instrum. Meas. 2008, 58, 94–98. [Google Scholar] [CrossRef]
- Pallás-Areny, R.; Webster, J.G. Analog Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Spinelli, E.M.; Hornero, G.; Casas, O.; Haberman, M. A design method for active high–CMRR fully–differential circuits. Int. J. Instrum. Technol. 2012, 1, 103–113. [Google Scholar] [CrossRef]
- Spinelli, E.M.; Guerrero, F.N.; Garcia, P.A.; Catacora, V.A.; Haberman, M.A. A fully-differential biopotential amplifier with a reduced number of parts. IEEE Trans. Instrum. Meas. 2022, 71, 2006908. [Google Scholar] [CrossRef]
- Andrew, A.M. Differential amplifier design. Wirel. Eng. 1955, 33, 73–79. [Google Scholar]
- Blume, R.J. Bootstrapped Differential Amplifier with Reduced Common-Mode Effects. Rev. Sci. Instrum. 1958, 29, 122–124. [Google Scholar] [CrossRef]
- McClellan, A.D. Extracellular amplifier with bootstrapped input stage results in high common-mode rejection. Med. Biol. Eng. Comput. 1981, 19, 657–658. [Google Scholar] [CrossRef] [PubMed]
- Kootsey, J.M.; Johnson, E.A. Buffer amplifier with femtofarad input capacity using operational amplifiers. IEEE Trans. Biomed. Eng. 1973, BME-20, 389–391. [Google Scholar] [CrossRef] [PubMed]
- Bergveld, P. Alternative design of a unity-gain follower with buffer. IEEE Trans. Biomed. Eng. 1978, BME-25, 567–568. [Google Scholar] [CrossRef]
- Maji, S.; Burke, M.J. A bootstrapping technique to boost input impedance of ECG recording amplifiers. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Stitt, M. Boost Instrument Amp CMR with Common-Mode Driven Supplies; Technical report, Burr-Brown Application Bulletin SBOA014; Burr-Brown Corporation: Tucson, AZ, USA, 1997. [Google Scholar]
- Jooq, M.K.Q.; Behbahani, F.; Moaiyeri, M.H. An ultra-efficient recycling folded cascode OTA based on GAA-CNTFET technology for MEMS/NEMS capacitive readout applications. AEU-Int. J. Electron. Commun. 2021, 136, 153773. [Google Scholar] [CrossRef]
- Koo, N. Design of Low Power and Low Noise Instrumentation Amplifier for Biopotential Acquisition: A Review. IEEE Access 2025, 13, 23359–23370. [Google Scholar] [CrossRef]
- Fava, A.; Centurelli, F.; Monsurrò, P.; Scotti, G. A Compact Low-Power Chopper Low Noise Amplifier for High Density Neural Front-Ends. Sensors 2025, 25, 1157. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, X.; Gao, C.; Li, Q. A 130-dB CMRR instrumentation amplifier with common-mode replication. IEEE J. Solid-State Circuits 2021, 57, 278–289. [Google Scholar] [CrossRef]
- Yan, F.; Liu, J. Analog front-end input-impedance boosting techniques for bio-potential monitoring—A review. IEEE Trans. Instrum. Meas. 2024, 73, 2002214. [Google Scholar] [CrossRef]
- Säckinger, E.; Goette, J.; Guggenbühl, W. A general relationship between amplifier parameters, and its application to PSRR improvement. IEEE Trans. Circuits Syst. 1991, 38, 1173–1181. [Google Scholar] [CrossRef]
- Guerrero, F.N.; Spinelli, E.M. Stability of power supply bootstrapped unity-gain buffers. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4258–4262. [Google Scholar] [CrossRef]
- Midlebrook, R. Differential Amplifiers; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1963. [Google Scholar]
- Zhang, S.; Zhou, X.; Gao, C.; Li, Q. An AC-coupled instrumentation amplifier achieving 110-dB CMRR at 50 Hz with chopped pseudoresistors and successive-approximation-based capacitor trimming. IEEE J. Solid-State Circuits 2020, 56, 277–286. [Google Scholar] [CrossRef]
- Massarotto, M.; Casas, O.; Ferrari, V.; Pallas-Areny, R. Improved fully differential analog filters. IEEE Trans. Instrum. Meas. 2007, 56, 2464–2469. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spinelli, E.M.; Catacora, V.A.; Guerrero, F.N.; Haberman, M.A. Enhancing CMRR in Fully Differential Amplifiers via Power Supply Bootstrapping. Chips 2025, 4, 27. https://doi.org/10.3390/chips4020027
Spinelli EM, Catacora VA, Guerrero FN, Haberman MA. Enhancing CMRR in Fully Differential Amplifiers via Power Supply Bootstrapping. Chips. 2025; 4(2):27. https://doi.org/10.3390/chips4020027
Chicago/Turabian StyleSpinelli, Enrique M., Valentín A. Catacora, Federico N. Guerrero, and Marcelo A. Haberman. 2025. "Enhancing CMRR in Fully Differential Amplifiers via Power Supply Bootstrapping" Chips 4, no. 2: 27. https://doi.org/10.3390/chips4020027
APA StyleSpinelli, E. M., Catacora, V. A., Guerrero, F. N., & Haberman, M. A. (2025). Enhancing CMRR in Fully Differential Amplifiers via Power Supply Bootstrapping. Chips, 4(2), 27. https://doi.org/10.3390/chips4020027






