Extension of Quasi-Load Insensitive Generalized Class-E Doherty Operation with Complex Load Trajectories
Abstract
1. Introduction
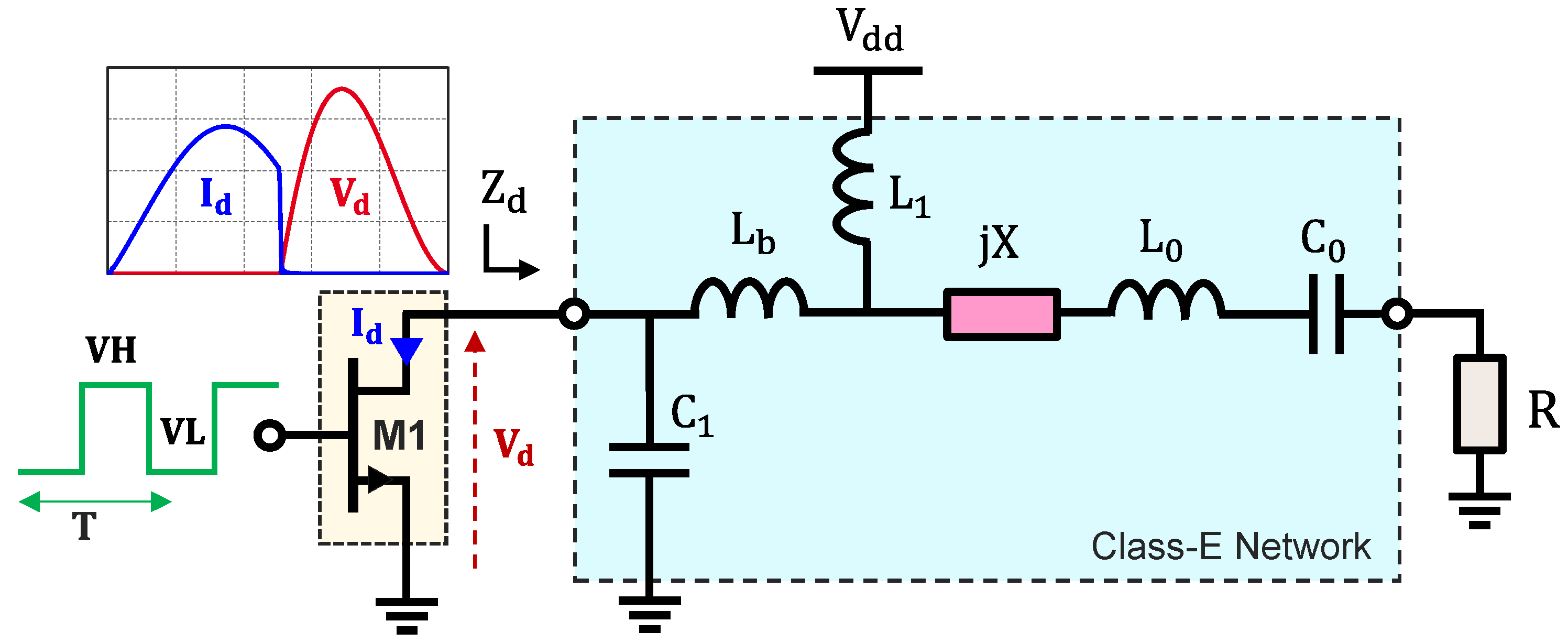
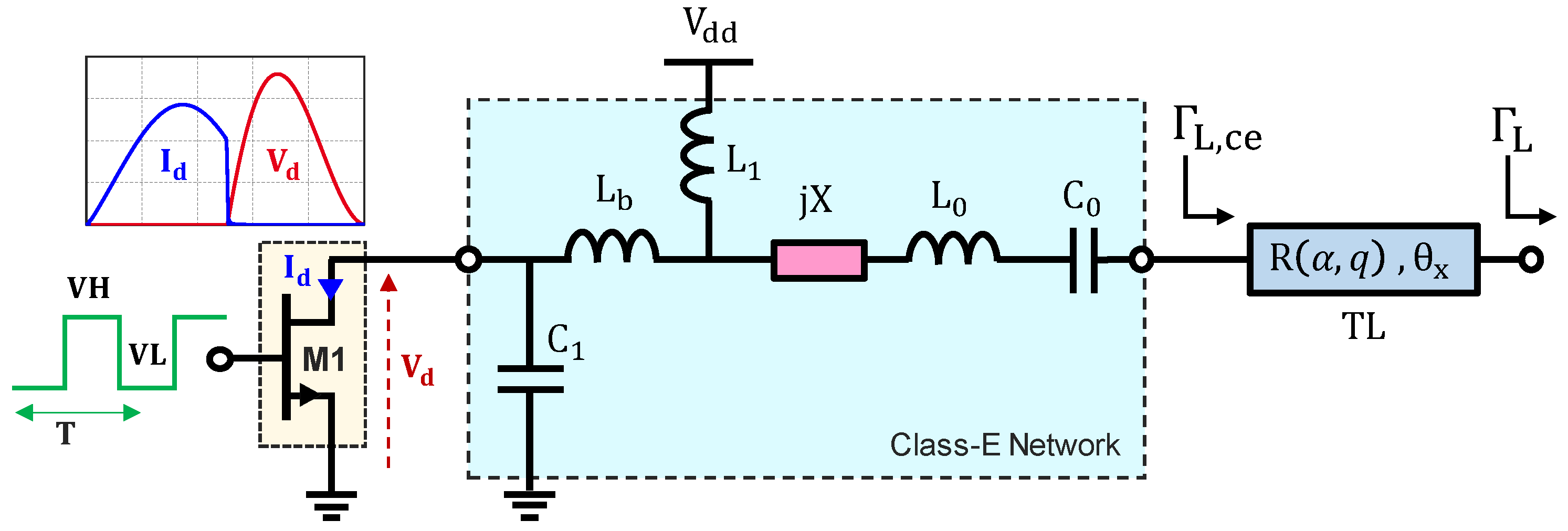
2. Generalized Class-E Output Network
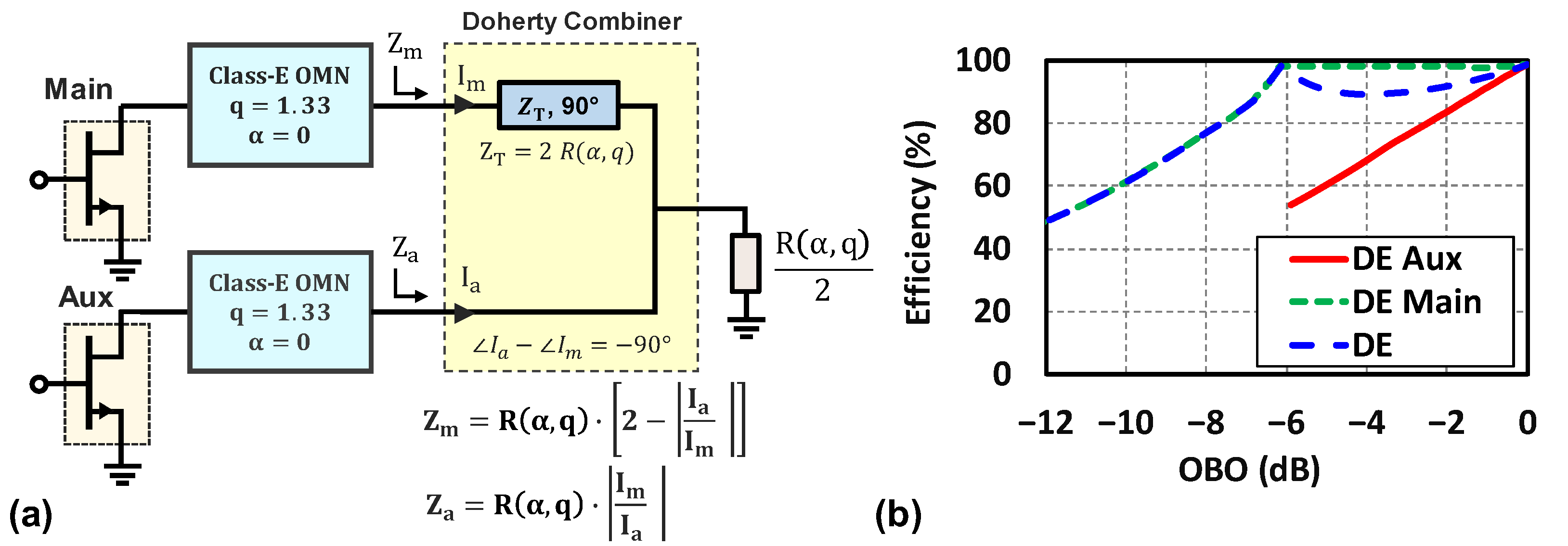
3. Quasi-Load Insensitive Class-E Doherty Operation
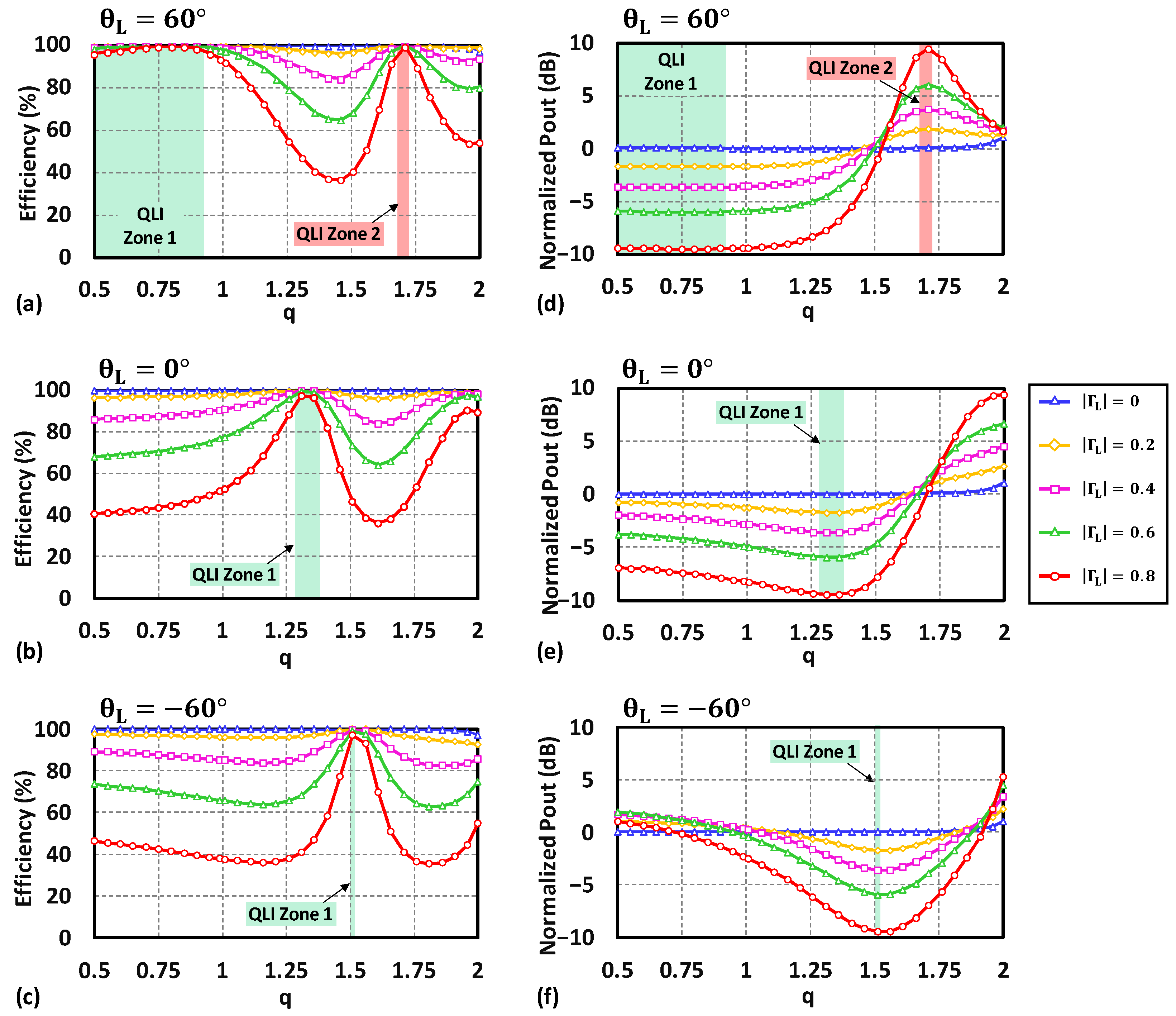
3.1. Original QLI Class-E ( and ) DPA Design Methodology
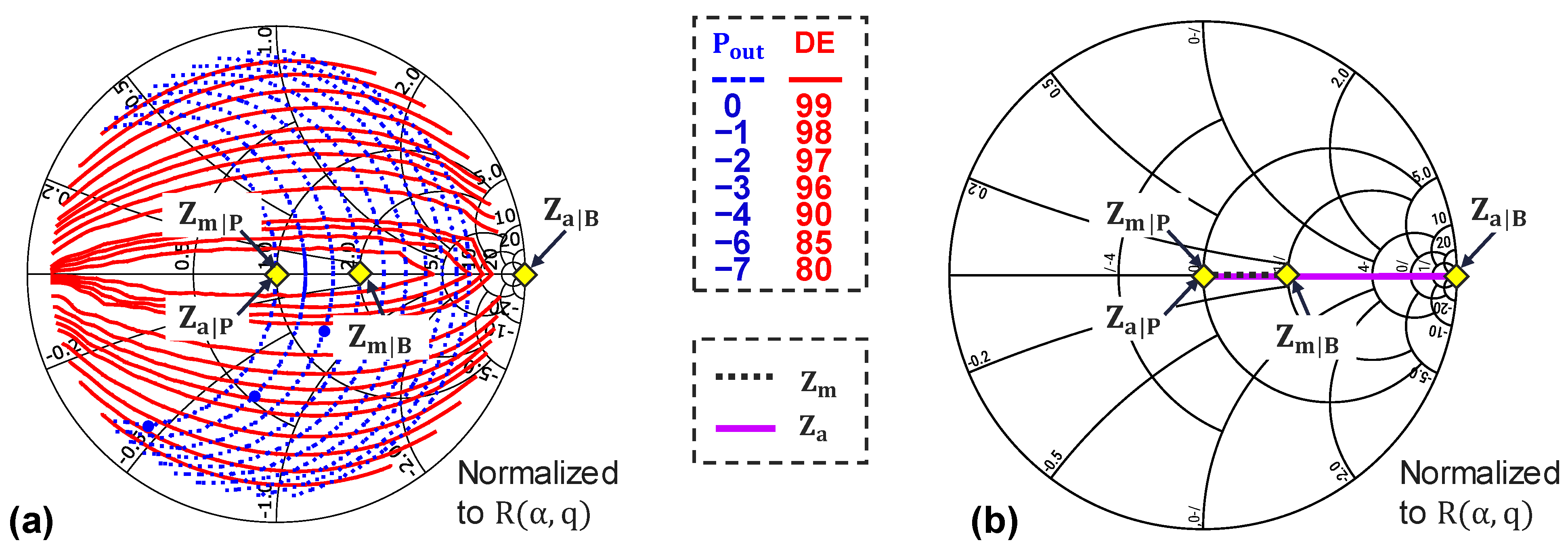
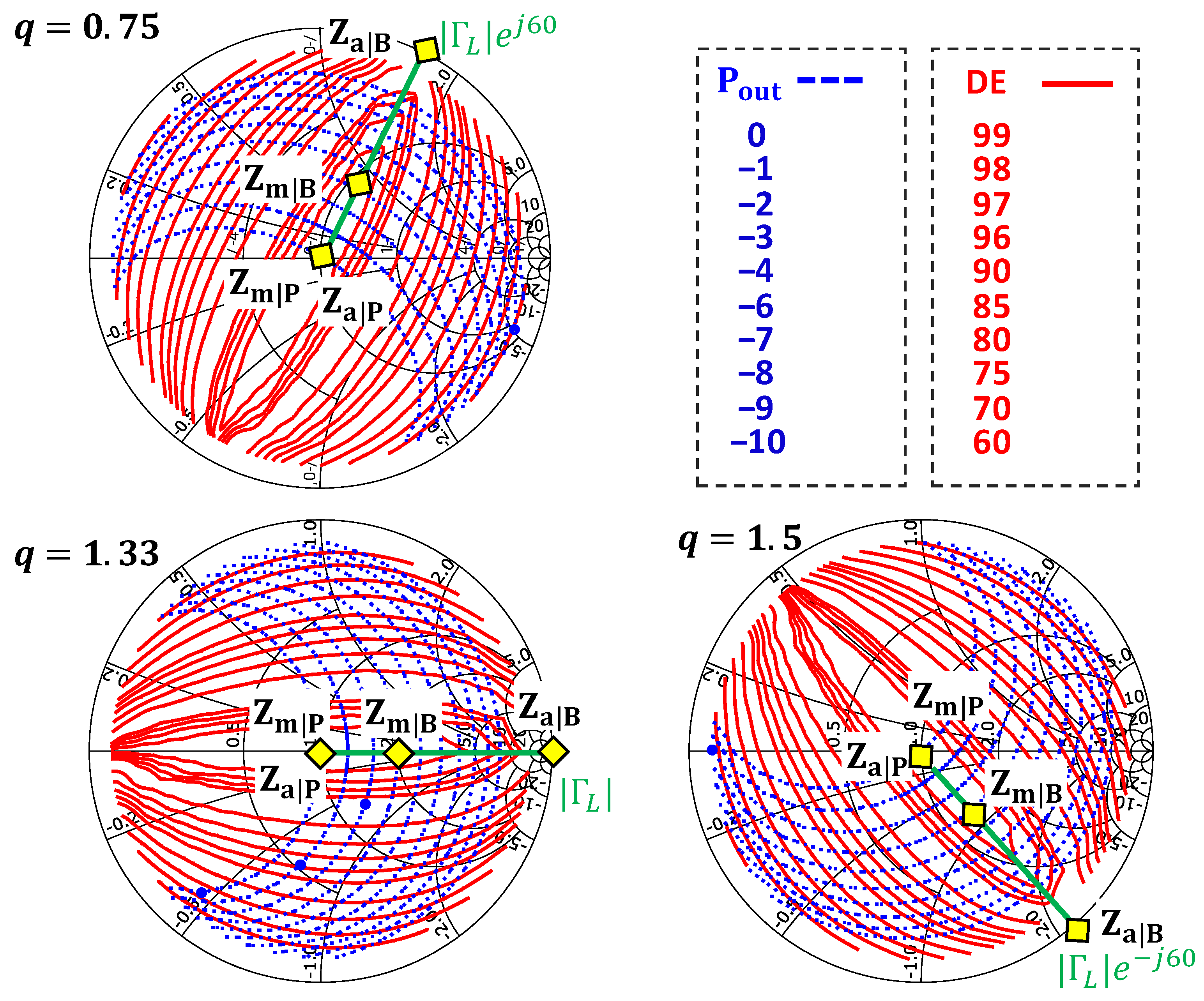
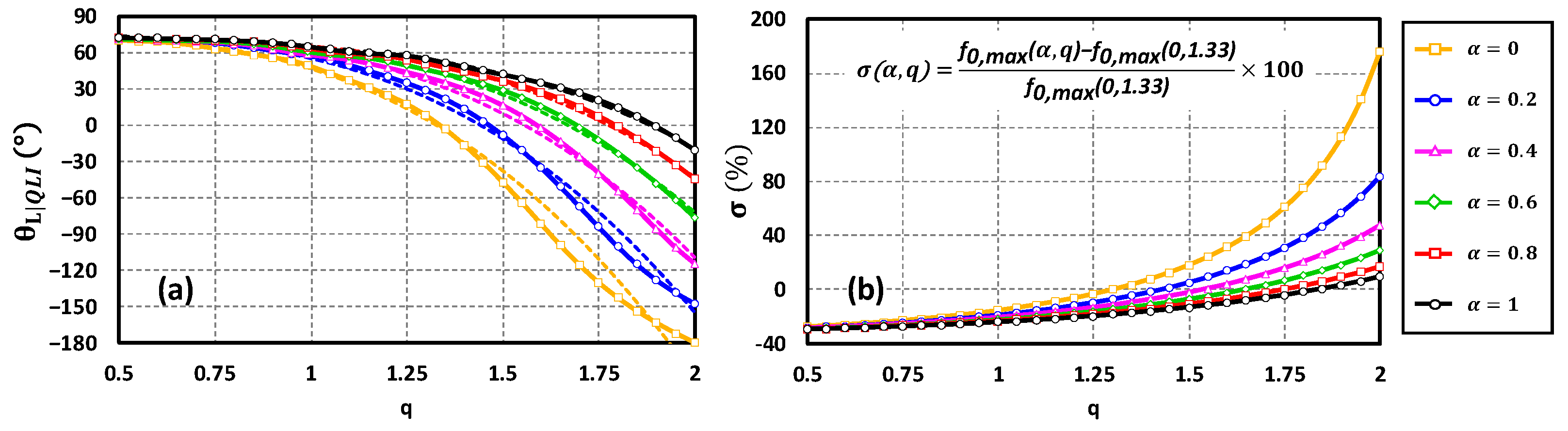
3.2. Extension of QLI Class-E DPA Methodology
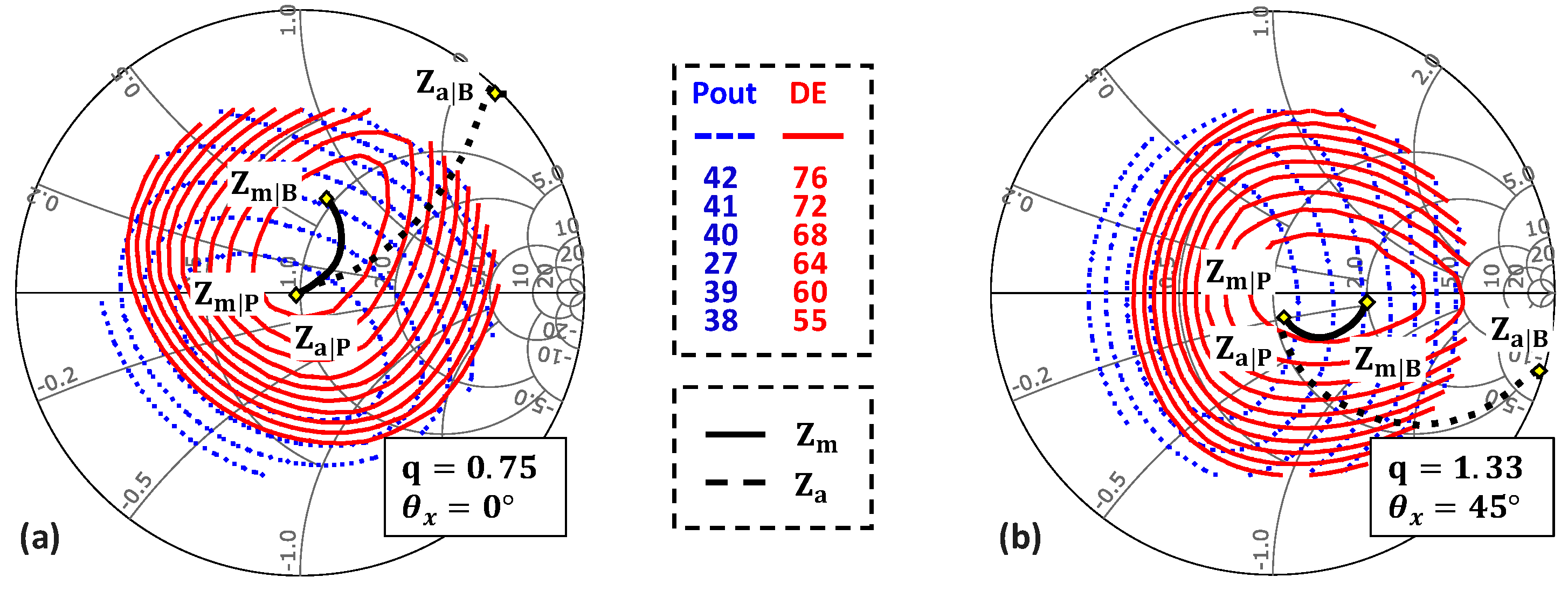
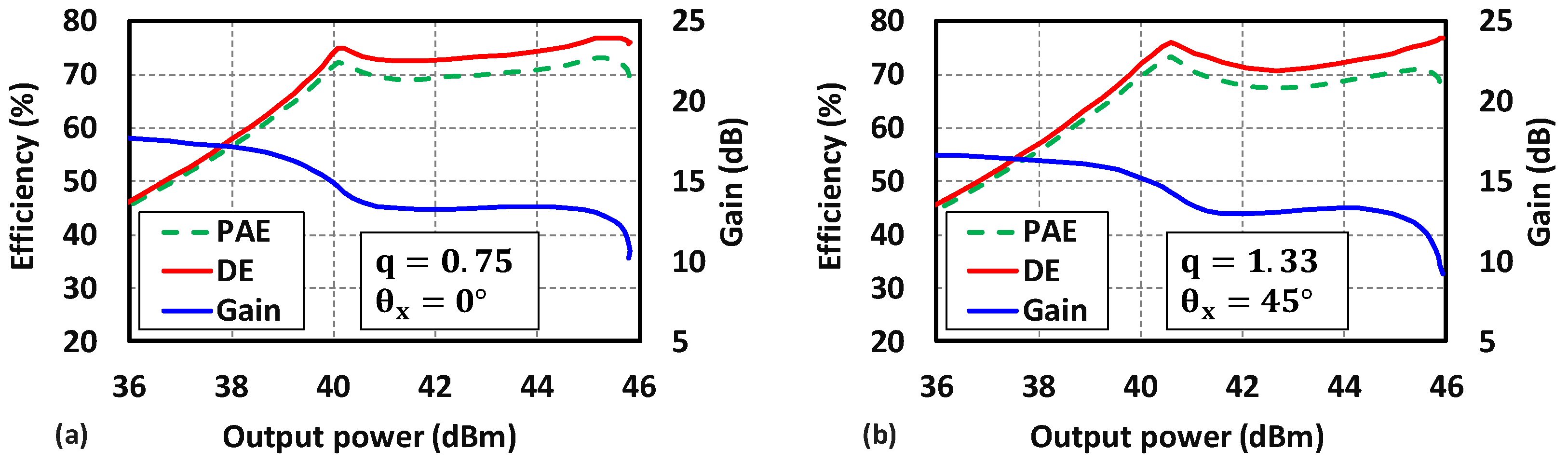
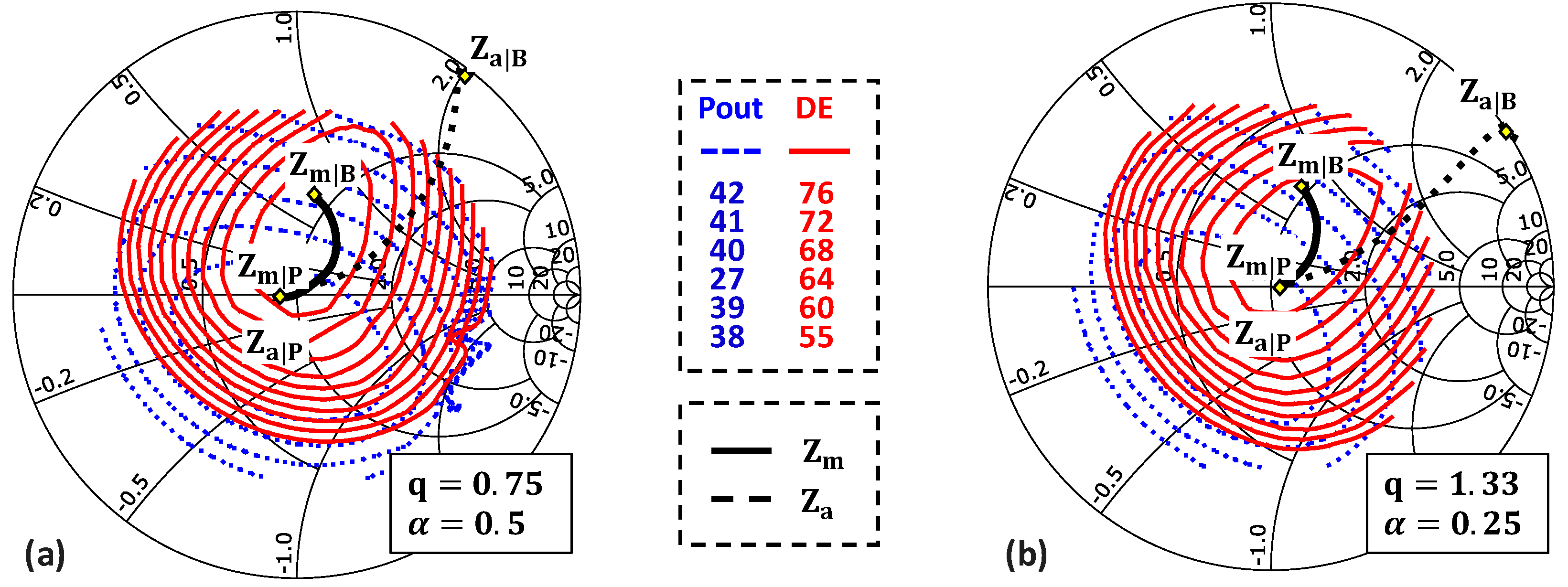
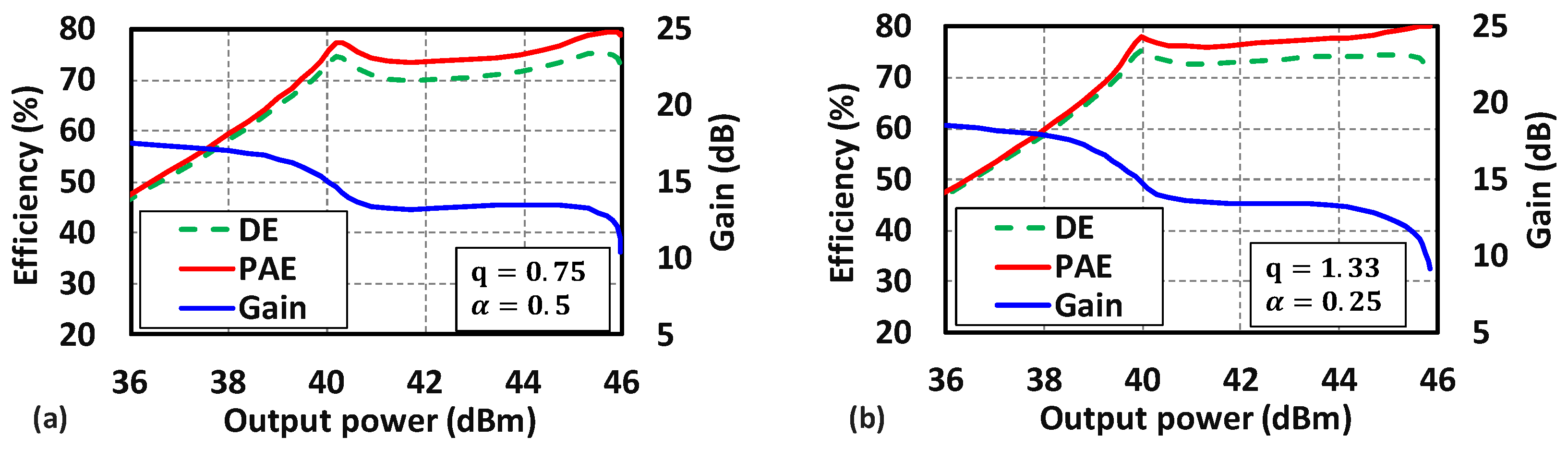
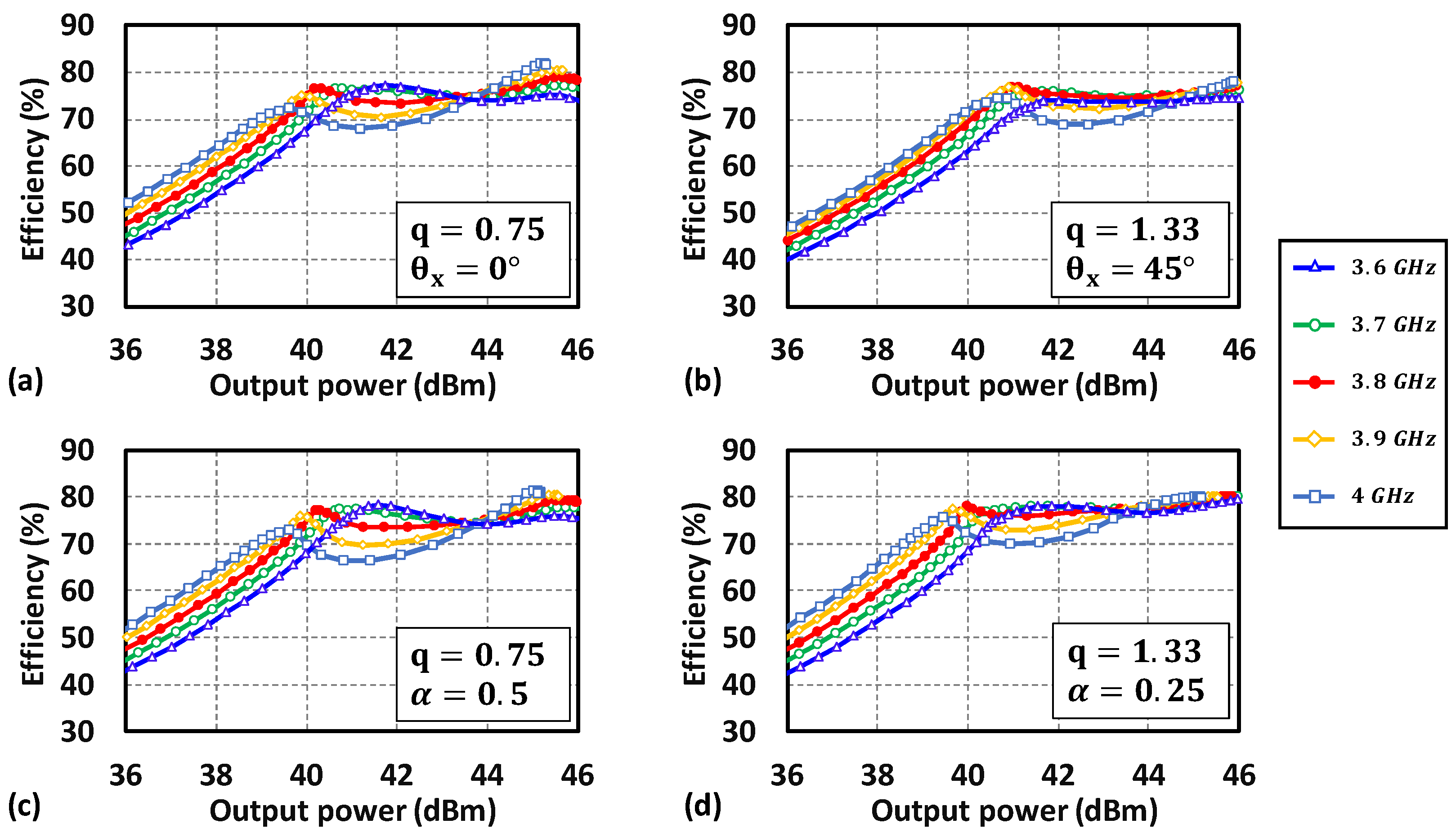
4. Application of the Proposed Design Methodology
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Giry, A.; Serhan, A.; Parat, D.; Reynier, P. Linear Power Amplifiers for Sub-6GHz Mobile Applications: Progress and Trends. In Proceedings of the 2020 18th IEEE International New Circuits and Systems Conference (NEWCAS), Montreal, QC, Canada, 16–19 June 2020; pp. 226–229. [Google Scholar]
- Doherty, W.H. A New High Efficiency Power Amplifier for Modulated Waves. Proc. IRE 1936, 24, 1163–1182. [Google Scholar] [CrossRef]
- Ozen, M.; van der Heijden, M.; Acar, M.; Jos, R.; Fager, C. A Generalized Combiner Synthesis Technique for Class-E Outphasing Transmitters. IEEE Trans. Circuits Syst. Regul. Pap. 2017, 64, 1126–1139. [Google Scholar] [CrossRef]
- Srirattana, N.; Raghavan, A.; Heo, D.; Allen, P.E.; Laskar, J. Analysis and design of a high-efficiency multistage Doherty power amplifier for wireless communications. IEEE Trans. Microw. Theory Tech. 2005, 53, 852–860. [Google Scholar] [CrossRef]
- Qureshi, J.H.; Sneijers, W.; Keenan, R.; deVreede, L.C.N.; van Rijs, F. A 700-W peak ultra-wideband broadcast Doherty amplifier. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar]
- Qureshi, A.R.; Acar, M.; Pires, S.C.; de Vreede, L.C.N. High Efficiency and Wide Bandwidth Quasi-Load Insensitive Class-E Operation Utilizing Package Integration. IEEE Trans. Microw. Theory Tech. 2018, 66, 5310–5321. [Google Scholar] [CrossRef]
- Nghiem, X.A.; Gajadharsing, J. Continuous Quasi-Load Insensitive Class-E Mode for Wideband Doherty Power Amplifiers. In Proceedings of the 2023 IEEE/MTT-S International Microwave Symposium—IMS 2023, San Diego, CA, USA, 11–16 June 2023; pp. 450–453. [Google Scholar]
- Bachi, J.; Serhan, A.; Pham, D.-K.G.; Parat, D.; Reynier, P.; Desgreys, P.; Giry, A. A Novel Approach for Doherty PA Design Using a Compact L-C Combiner. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4023–4027. [Google Scholar] [CrossRef]
- Rong, C.; Liu, X.; Xu, Y.; Xia, M. Analysis and Design of Class E Power Amplifier with Finite DC-Feed Inductance and Series Inductance Network. ACES J. Pap. 2017, 32, 455–462. [Google Scholar]
- Acar, M.; Annema, A.J.; Nauta, B. Analytical Design Equations for Class-E Power Amplifiers. IEEE Trans. Circuits Syst. Regul. Pap. 2007, 54, 2706–2717. [Google Scholar] [CrossRef]
- Takenaka, K.; Sato, T.; Matsumoto, H.; Kawashima, M.; Nakajima, N. New compact Doherty power amplifier design for handset applications. In Proceedings of the 2017 IEEE Topical Conference on RF/Microwave Power Amplifiers for Radio and Wireless Applications (PAWR), Phoenix, AZ, USA, 15–18 January 2017; pp. 81–83. [Google Scholar]
- Otmani, M.; Serhan, A.; Arnould, J.-D.; Lauga-Larroze, E.; Giry, A. Extension of Quasi-Load Insensitive Class-E Doherty Operation with Complex Load Trajectories. In Proceedings of the 2024 19th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Larnaca, Cyprus, 9–12 June 2024; pp. 1–4. [Google Scholar]





| Parameters | R | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Unit | pF | nH | nH | pF | nH | pF | ° | nH | pF | |
| 2.7 | 1.7 | 2.9 | 1.1 | 1.4 | 0 | 0 | 0 | 14.2 | ||
| 1 | 1 | 1.3 | 1.6 | 1.3 | 1.6 | 40 | 1.1 | 1.6 | 26 |
| Parameters | R | |||||||
|---|---|---|---|---|---|---|---|---|
| Unit | pF | nH | nH | nH | pF | nH | pF | |
| 0.8 | 0.7 | 2.8 | 0.8 | 2.9 | 0.4 | 1.7 | 9.5 | |
| 0.8 | 0.6 | 1.2 | 0.8 | 2.9 | 0.4 | 1.8 | 9 |
| Ref. | Frequency (GHz) | OBO (dB) | Efficiency @ Peak (%) | Efficiency @ OBO (%) | Psat (dBm) | Combiner Type |
|---|---|---|---|---|---|---|
| [6] | 1.4–2.6 | 6 | 73–68 | 56–41 | 48.2–45.2 | Inverter |
| [7] | 3.4–3.8 | 7.5 | 50–60 | 52.7–53.6 | 48–48.25 | Inverter |
| This work * q = 1.33, | 3.6–4 | 6 | 74.5–78 | 70.3–76.7 | 45.8–46.1 | L-C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otmani, M.; Serhan, A.; Arnould, J.-D.; Lauga-Larroze, E.; Reynier, P.; Giry, A. Extension of Quasi-Load Insensitive Generalized Class-E Doherty Operation with Complex Load Trajectories. Chips 2025, 4, 26. https://doi.org/10.3390/chips4020026
Otmani M, Serhan A, Arnould J-D, Lauga-Larroze E, Reynier P, Giry A. Extension of Quasi-Load Insensitive Generalized Class-E Doherty Operation with Complex Load Trajectories. Chips. 2025; 4(2):26. https://doi.org/10.3390/chips4020026
Chicago/Turabian StyleOtmani, Mehdi, Ayssar Serhan, Jean-Daniel Arnould, Estelle Lauga-Larroze, Pascal Reynier, and Alexandre Giry. 2025. "Extension of Quasi-Load Insensitive Generalized Class-E Doherty Operation with Complex Load Trajectories" Chips 4, no. 2: 26. https://doi.org/10.3390/chips4020026
APA StyleOtmani, M., Serhan, A., Arnould, J.-D., Lauga-Larroze, E., Reynier, P., & Giry, A. (2025). Extension of Quasi-Load Insensitive Generalized Class-E Doherty Operation with Complex Load Trajectories. Chips, 4(2), 26. https://doi.org/10.3390/chips4020026







