Abstract
Ramsey theory constitutes the dynamics of mechanical systems, which may be described as abstract complete graphs. We address a mechanical system which is completely interconnected by two kinds of ideal Hookean springs. The suggested system mechanically corresponds to cyclic molecules, in which functional groups are interconnected by two kinds of chemical bonds, represented mechanically with two springs and . In this paper, we consider a cyclic system (molecule) built of six equal masses m and two kinds of springs. We pose the following question: what is the minimal number of masses in such a system in which three masses are constrained to be connected cyclically with spring or three masses are constrained to be connected cyclically with spring ? The answer to this question is supplied by the Ramsey theory, formally stated as follows: what is the minimal number The result emerging from the Ramsey theory is . Thus, in the aforementioned interconnected mechanical system at least one triangle, built of masses and springs, must be present. This prediction constitutes the vibrational spectrum of the system. Thus, the Ramsey theory and symmetry considerations supply the selection rules for the vibrational spectra of the cyclic molecules. A symmetrical system built of six vibrating entities is addressed. The Ramsey approach works for 2D and 3D molecules, which may be described as abstract complete graphs. The extension of the proposed Ramsey approach to the systems, partially connected by ideal springs, viscoelastic systems and systems in which elasticity is of an entropic nature is discussed. “Multi-color systems” built of three kinds of ideal springs are addressed. The notion of the inverse Ramsey network is introduced and analyzed.
1. Introduction
Ramsey theory is a branch of mathematics/combinatorics that focuses on the appearance of ordered substructures within a structure of a known size. Ramsey theory states that any structure will necessarily contain an orderly substructure [1]. Ramsey’s theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colors) of a sufficiently large complete graph [2]. In graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent (vertices are considered as adjacent when both endpoints are connected by the same edge [2,3]).
To demonstrate the theorem for two colors (say, blue and orange), let p and q be any two positive integers. The Ramsey theorem states that there exists a least-positive integer for which every blue-orange link of the complete graph on vertices contains a blue clique on p vertices or an orange clique on q vertices. These integers are known as Ramsey numbers. The Schur Theorem, demonstrating that for any there is a natural number P such that any r-coloring of contains x, y, z having the same color such that , exemplifies the Ramsey theorem. One more example is supplied by the van der Waerden’s theorem: coloring of the integers by a finite number of colors must have long monochromatic arithmetic progressions [2,3]. Problems in Ramsey theory typically ask a question of the form: How big must some structure be to guarantee that a particular property holds? More specifically, Ron Graham described Ramsey theory as a “branch of combinatorics” [3,4,5,6]. A simple, popular introduction to the Ramsey theory is found in [4]. More advanced, rigorous mathematical approaches are presented in refs. [3,5,6]. Applications of the Ramsey theory for the theory of communication and decision making were discussed [7]. Interconnection between the Ramsey theory and statistical physics was also addressed [8]. A classical Hamiltonian system that favors configurations in a way to establish lower bounds on Ramsey numbers was demonstrated [8]. The application of the Ramsey theory to classical thermodynamics was demonstrated in [8]. Maps (graphs) built of distinct thermodynamic states were addressed [9]. The Ramsey theory supplies the answer to the following question: How large should be a graph describing connections between discrete thermodynamic states to guarantee the appearance of thermodynamic cycles [9]? The application of the Ramsey theory to physical systems, in which attraction and repulsion forces act between the bodies constituting the system, has been discussed [10]. The Ramsey theory explains why nature prefers cubic lattices over hexagonal ones for systems built of electric or magnetic dipoles [10].
In the present paper, we address the application of the Ramsey theory for the analysis of mechanical systems, which may be represented as complete graphs. Cyclic molecules may be seen as complete graphs [11,12]. Chemical bonds are seen on the edges (links) of the graph, which in a very crude approximation, may be considered as ideal springs. We demonstrate that the Ramsey theory introduces the “selection rules” for eigenmodes (eigenfrequencies) of the cyclic molecules, treated as completed graphs. Thus, the Ramsey approach to the vibrational spectra of the cyclic molecules becomes possible. The proposed Ramsey approach predicts the Ramsey modes, which are necessarily present in these spectra. One of the challenges of the Ramsey theory is the calculation of values of the Ramsey numbers for multiple-vertices systems. It takes an exponential amount of time to solve a Ramsey number problem with traditional electronic computers. DNA-based computing of Ramsey numbers was suggested recently [13]. In our paper, we restrict ourselves to the analysis of relatively small cyclic molecules, for which the Ramsey numbers are known. Our paper demonstrates that the Ramsey theory defines the kind of “selection rules” for the vibrational spectra of cyclic systems.
2. Ramsey Theory and Vibrations of Cyclic Molecules
2.1. Ramsey Theory for the System Interconnected by Two Kinds of Ideal Springs
Consider a cyclic mechanical system built of six identical masses m shown in Figure 1. These masses are connected by two ideal Hookean massless springs and as shown in Figure 1. The considered mechanical system corresponds to the cyclic chemical compound in which two kinds of chemical bonds are present. These bonds are represented schematically by the springs and . The bonds form the complete graph, i.e., a graph in which each pair of graph vertices (masses) is connected by an edge (representing the spring/chemical bond). We demonstrate that the Ramsey theory supplies predictions related to the eigenvalues of frequencies of vibrations in the system described in Figure 1. In other words, the Ramsey theory may predict the peculiarities of the vibrational spectrum of the cyclic chemical compound (molecule) corresponding to the mechanical system [14,15], shown in Figure 1. For the sake of simplicity, the masses of the vibrating bodies are taken as equal.
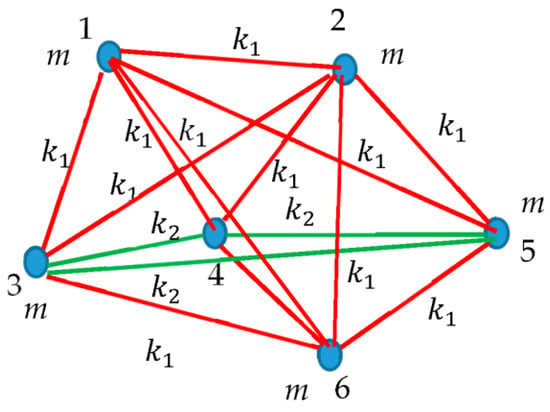
Figure 1.
Cyclic chemical compound represented by a mechanical system forming a complete graph. The system is built of identical masses m interconnected by two kinds of springs (red ones) and .
The complete graph depicted in Figure 1 is a graph typical of the Ramsey theory. The red lines connect those masses that are interconnected by the spring , while the green lines connect those masses interconnected by the spring .
We recognize a number of monochromatic triangles (namely one green and three red triangles) in the scheme. The vibrational spectrum of the considered system will crucially depend on the presence of triple cyclic chains of masses. Let us pose the following question: What is the minimal number of masses in the system in which three masses connected by spring or three masses connected by spring form a triangle? The answer to this question is supplied by the Ramsey theory, and it is formulated as follows: What is the minimal number The answer emerging from the Ramsey theory is: . Indeed, we recognize in the example illustrated in Figure 1, that in a molecule built of six point masses, in which the relationships “to be connected by spring ” and “to be connected by spring ” are necessarily present, we find triads of masses connected cyclically by the same kinds of springs (at least one triangle-shaped ring chain of masses will be necessarily present in the system of masses completely interconnected one to another). Of course, the quantitative prediction of the eigenfrequency corresponding to the triangle-shaped chain of masses for the asymmetric system, shown in Figure 1, presents an extremely challenging computational problem. This problem becomes solvable for the symmetric plane distribution of masses depicted in Figure 2 (the masses form a regular hexagon).
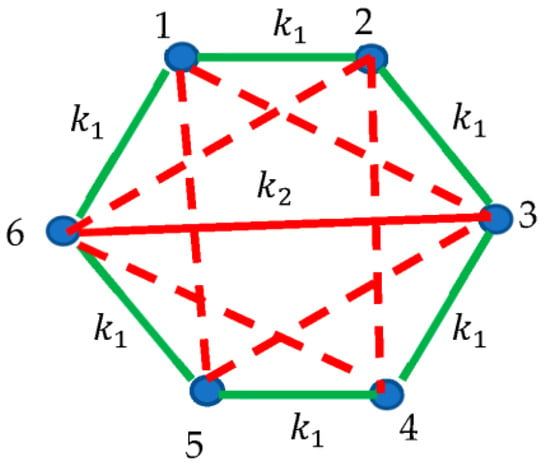
Figure 2.
Equal masses m forming a regular hexagon are interconnected by two kinds of ideal springs denoted, (green edges) and (red edges). Two equilateral triangles “153” and “246” are recognized.
Two equilateral triangles, namely “153” and “246” are present within the cyclic “molecule” depicted in Figure 2. These triangles built of the masses m and springs are shown with the red dashed lines. If harmonic oscillations of the masses connected by the green and red springs are decoupled (this will take place when is fulfilled), the eigenvalues of the vibrations occurring within the red dashed triangles are calculated with the standard methods of classical mechanics [15]. The full spectrum of the eigenfrequencies in this case is given by Equation (1):
Two of aforementioned trivial zero-eigenfrequencies correspond to the x and y translations of the entire system in the XY-plane, and the third one corresponds to the uniform rotation of the entire system about its center of mass (see Appendix A). The detailed treatment of the eigenmodes is supplied in Appendix A. In addition, the modes inherent for the ring of green springs should be considered [16,17]. We call these modes “the Ramsey modes”. It turns out that the Ramsey theory imposes restrictions on the vibrational spectrum of the cyclic mechanical systems, described by complete graphs. In other words, it supplies the “selection rules” for the vibrational spectra of the cyclic molecules, the chemical structure of which may be described with the complete graphs [13,14,15,16,17]. It is noteworthy that . Thus, if we have a molecule described by a complete graph, which is built of six functional groups, or two or six interconnected groups will necessarily be present in its structure; thus explaining the formation of the benzene-like ring structures (see Figure 2).
At the same time, the eigenfrequencies supplied by Equation (1) will not necessarily appear in the five-fold symmetrical molecule built of five point masses, shown in Figure 3. Indeed, the triangles built from the springs are not present in these structures, and this conclusion immediately follows from the Ramsey approach: .
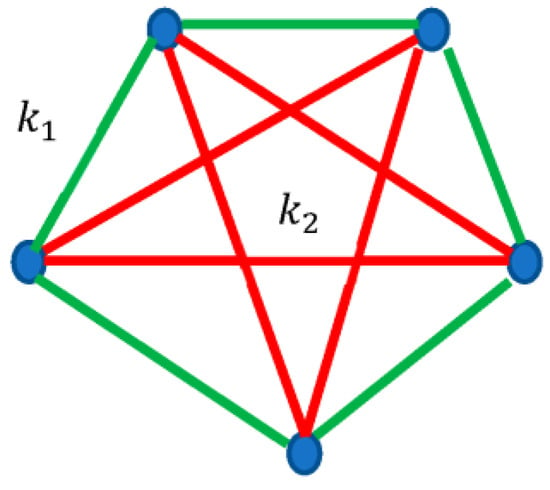
Figure 3.
Five equal masses m forming a regular pentagon are interconnected by two kinds of ideal springs denoted (green edges) and (red edges). No triangles are formed in the spring network. The Ramsey number .
Again, the Ramsey theorem works as a selection rule for the vibrational spectra of molecules.
The proposed Ramsey approach is easily extended for 3D vibrating systems/molecules such as those shown in Figure 4. The molecule shown in Figure 4 is built from two tetrahedrons, denoted “1234” and “1235”. Triangle “123” is located in the plane (see Figure 4). Masses placed in the vertices of the tetrahedron are connected by two kinds of springs, the green ( and red () ones.
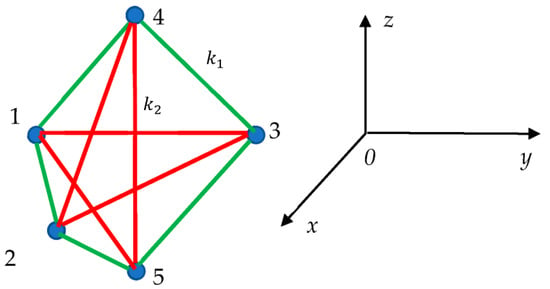
Figure 4.
3D systems built of two tetrahedrons “1234” and “1235” are depicted. Masses placed in the vertices of the tetrahedrons are connected by two kinds of springs. The green ( and red () links denote the springs. Triangle “123” is located in the plane .
Figure 4 depicts coloring of a 3D system in which no monochrome triangle is present. Thus, eigenmodes supplied by Equation (1) will not appear in the vibrating system/molecule built of five point masses, shown in Figure 4. This result conforms with the Ramsey approach: and it works for 3D systems. It is noteworthy that the springs connecting the masses may be classic or quantum ones [15].
2.2. Direct and Inverse Ramsey Networks of Ideal Springs
It is instructive to introduce the inverse Ramsey networks of ideal springs, i.e., to replace springs with springs , and springs to be replaced correspondingly with springs We call such a Ramsey network the “inverse graph”; introducing an inverse Ramsey network is possible for any complete source graph. Construction of the “inverse graph” results in replacement of the red links depicted in Figure 1 with the green links and vice versa. Consider the Ramsey structure built of six atoms, as depicted in Figure 1. Obviously, the total number of triangles in the “direct” (source) and “inverse” Ramsey graphs is the same, thus giving rise to Equation (2):
where are the numbers of red and green triangles in the source graph; are the numbers of red and green triangles in the inverse graph. Equation (2) represents the “conservation law” for the Ramsey complete networks built of six elements. It is noteworthy that direct and inverse graphs form the Abelian (commutative group), when the inversion of the color of the link is taken as an operation.
2.3. Ramsey Theory for the System of Vibrating Masses Partially Connected by the Ideal Springs
It seems from the first glance that the Ramsey theory will be useful only for systems completely interconnected by springs. Thus, the complete graphs, built of springs, depicted in Figure 1, Figure 2, Figure 3 and Figure 4 emerge.
We demonstrate that the Ramsey approach also works for the systems which are partially interconnected by the springs, such as those shown in Figure 5. Consider a two-fold symmetrical system built of six-point masses m connected by ideal springs k as depicted in Figure 5. It should be emphasized that the pairs of masses labeled “13”, ”14”, “45”, “35”, “46” and “36” are not connected by springs (see Figure 5).
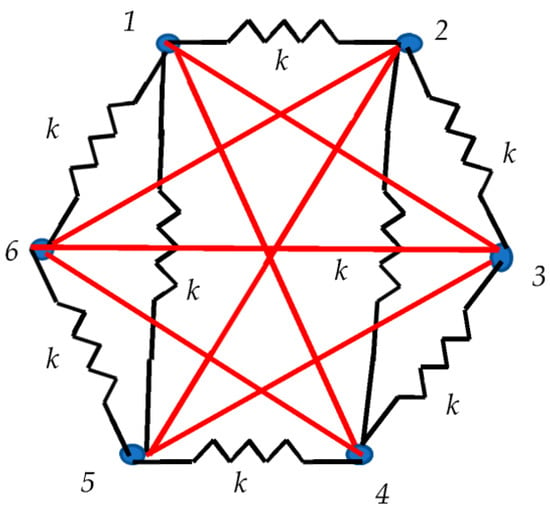
Figure 5.
Symmetrical system of six-point masses m partially interconnected by identical ideal springs k. Masses labeled ”14”, “45” and “36” are not connected by springs. Masses connected by springs are connected by black links; masses which are not joint with the springs are connected by red links. Black triangles “156” and “234” are present in the graph.
Let us connect the masses interacting via spring k with black links, and disconnected masses via red links as shown in Figure 5. Thus, the complete graph built of black and red links emerges. According to the Ramsey theory, at least one red or black triangle should necessarily appear within the graph. Indeed, black triangles “156” and “234” are present in the graph. The eigenfrequencies inherent for these triangles are . Thus, we come to the important conclusion, namely: vibrating systems partially interconnected with springs may be also described with the Ramsey approach.
2.4. Multi-Color Systems Built of Ideal Springs
The Ramsey approach enables the analysis of more complicated cyclic compounds interconnected by three kinds of ideal springs, denoted and . Thus, the analysis of the vibration of such a system is reduced to the Ramsey number . It was established that . If harmonic oscillations of the masses are decoupled (this will take place when is fulfilled), the eigenvalues of the vibrations occurring within the triangles are calculated by the standard methods of classical mechanics and they are given by: .
2.5. Ramsey Model of Viscoelasticity
It is also instructive to consider the Ramsey model of viscoelasticity presented in Figure 6 [16,17,18,19]. In this model point masses m are connected by ideal springs k or by viscous elements, quantified by viscosity denoted .
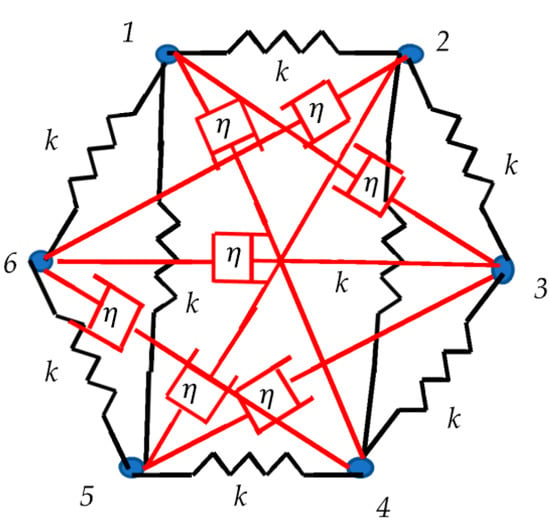
Figure 6.
The Ramsey model of viscoelastic body is presented. Point masses are connected by ideal springs k or with viscous elements, quantified by viscosity . Viscous joints are shown in red whereas elastic joints are connected by black links.
Elastic links are shown in black, whereas viscous connections are shown in red. For the sake of simplicity, we consider the complete graph, similar to that shown in Figure 5. For the Ramsey number = 6, a black (elastic) or red (viscous) triangle will necessarily appear in the graph. Indeed, elastic triangles labeled “156” and “234” are present in the graph.
The eigenfrequencies inherent for these triangles are . Thus, we conclude that the Ramsey approach is applicable for modeling of viscoelastic media [18,19,20,21], namely: vibrating systems partially interconnected by springs and partially with viscous elements may be described with the Ramsey approach. Of course, there exists the possibility that no “elastic” triangles will be present in the graph and only viscous ones will appear. In this case, only eigenvalues of frequencies inherent for pair oscillations of masses will appear in the vibration spectrum of the viscoelastic body.
2.6. Ramsey Theory for Vibrations of Systems in Which Entropy Elasticity Is Present
The approach presented in Section 2.1 is easily extended to the analysis of systems in which elasticity of an entropic nature, as it takes place for polymer molecules [22]. Entropic forces are also responsible for the contraction of cytoskeletal networks [23]. Consider a cyclic, 6-fold symmetrical interconnected system built of identical masses m, such as depicted in Figure 1, in which springs and represent elasticity of two kinds of ideal polymer chains. Assume that the red links correspond to ideal polymer chains built of Kuhn monomers; the Kuhn length of the monomer is denoted . In turn, the green links correspond to ideal polymer chains built of Kuhn monomers, the Kuhn length of the monomer is labeled . The entropic string constants of the chains are given by Equation (3) [22]:
where and T are the Boltzmann constant and the temperature of the polymer chains, correspondingly. In the simplest possible configuration of the symmetric polymer molecule, such as depicted in Figure 2 (again springs and represent entropic elasticity of ideal polymer chains), in the limiting case of, we obtain for the spectrum of
Remarkably all of the eigenfrequencies scale are: , thus, their values grow as square root from the temperature.
3. Conclusions
Our research is motivated by a search for physical applications of the Ramsey theory. Ramsey theory is a branch of combinatorics that predicts the appearance of ordered substructures within a structure of a known size [1,2,3,4,5,6]. Ramsey theory states, under addressing the properties of complete graphs, that any structure will necessarily contain an orderly substructure [1,2,3,4,5,6]. We applied the Ramsey theory for the analysis of cyclic mechanical systems, in which point masses m are connected by two kinds of ideal springs. Such systems may be seen as complete graphs, in which vertices (point masses) are connected by the edges colored with two colors (i.e., two kinds of springs). We applied the Ramsey theory for these kinds of graphs. These graphs also represent cyclic molecules in which functional groups are connected by two kinds of chemical bonds [11,12]. Two kinds of springs/chemical bonds in our case are colored with “green” and “red” correspondingly. The Ramsey number for the aforementioned systems is defined as the smallest value of n such that in a group of n point masses either a group of j masses forms a complete network of red springs or i masses form a complete network connected by the green springs. We formulated the following question: What is the minimal number of masses in the system in which three masses connected by spring or three masses connected by spring form a triangle? The answer to this question emerges from the Ramsey theory, and is mathematically formalized as follows: what is the minimal Ramsey number The Ramsey theory states that it is . Thus, within the interconnected mechanical system built of interconnected six point masses, the triangles (triangle), comprising masses and springs of the same kind will be necessarily present. This prediction constitutes the vibrational spectrum of the system. Thus, the Ramsey theory supplies selection rules for the vibrational spectra of the mechanical systems/cyclic molecules, which may be described by the complete graph. Consider also that . Thus, if we have a molecule described by a complete graph, which is built of six functional groups, either two or six interconnected groups will necessarily be present in its chemical structure; thus explaining the formation of the benzene-like ring structures.
The cyclic molecule built of five functional groups interconnected by two kinds of chemical bonds will not be necessarily characterized by the collective modes involving vibration of three-point entities. This fact is easily explained within the Ramsey approach . The calculation of the eigenfrequencies of these systems in the general case poses essential mathematical difficulties.
Symmetrical systems/molecules in turn may be analyzed explicitly. A six-fold symmetrical system built of six entities is addressed. The eigenfrequencies inherent for the vibrations of triangles are reported. We call these modes the Ramsey modes of the systems described by complete graphs [7,8]. The introduced approach is easily extended for 3D vibrating systems interconnected by classical/quantum springs, which may be described as abstract complete graphs. The extension of the proposed Ramsey approach to the systems partially connected by ideal springs, viscoelastic systems, and systems in which elasticity is of an entropic nature is discussed. Ramsey eigenfrequencies of the oscillations driven by entropic forces are calculated. “Multi-color systems” built of three kinds of springs are addressed. The notion of the inverse Ramsey network is introduced and analyzed. The total number of triangles in the direct (source) and inverse Ramsey graphs is the same. We emphasize the effectivity of the synthesis of the Ramsey and symmetry-based approaches for the analysis of complicated dynamic systems. Future work should consider k-partite-graph extensions of Ramsey theory, which correspond to graphs with k sets of nodes which cannot self-interact.
Author Contributions
Conceptualization, N.S. and E.B.; methodology, N.S. and E.B.; formal analysis, N.S., M.F., S.S. and E.B.; investigation, N.S., M.F., S.S. and E.B.; writing—original draft preparation, N.S., M.F., S.S. and E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Calculation of eigenmodes of system built of the point masses interconnected by ideal springs forming an equilateral triangle.
Consider three equal masses connected by ideal springs . Springs form an equilateral triangle (the side of the triangle is a), as shown in Figure A1. Assuming the center of the masses of the entire system is in rest yields:
where and denote the displacement of i-body from equilibrium.
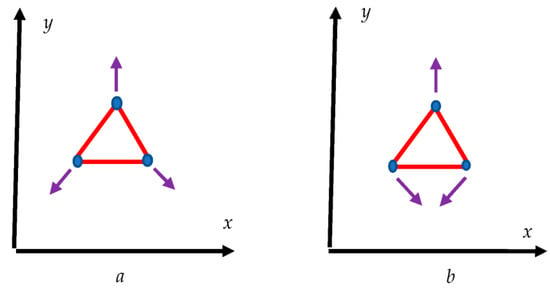
Figure A1.
Modes of the vibrations occurring within a system built from three equal masses m (a) and springs . (b) Springs form an equilateral triangle. Purple arrows show the displacement of the masses.
The addressed planar system is characterized by six degrees of freedom; hence it necessarily has six eigenfrequencies; three of these eigenfrequencies equal zero (see Equation (1)). Two of these trivial eigenfrequencies correspond to the x and y translations of the entire system in the XY-plane, and the third one corresponds to the uniform rotation of the entire system about its center of mass. The non-trivial modes are depicted in Figure A1. The mode shown in inset (a) corresponds to the situation when all of the bodies move along the bisectors of the triangle. The Lagrange function corresponding to this mode is supplied by Equation (A2):
Equation (A2) immediately yields (see Equation (1)):
One more mode, shown in inset (b), is found from the symmetry considerations. One of the nodes (the upper one in the inset (b)) moves along the bisector of the triangle. The movements of the remaining nodes in this case will be a mirror image of each other in the plane of symmetry of the triangle. The Lagrange function corresponding to this mode is supplied by Equation (A4) (is adopted):
The eigenfrequency emerging from this Lagrange function is given by Equation (A5):
The symmetry considerations yield (see Equation (1)):
References
- Ramsey, F.P. On a Problem of Formal Logic. In Classic Papers in Combinatorics. Modern Birkhäuser Classics; Gessel, I., Rota, G.C., Eds.; Birkhäuser: Boston, MA, USA, 2009; pp. 264–286. [Google Scholar] [CrossRef]
- Katz, M.; Reimann, J. An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics; Student Mathematical Library, American Mathematical Society: Providence, RI, USA, 2018; Volume 87, pp. 1–34. [Google Scholar]
- Di Nasso, M.; Goldbring, I.; Lupini, M. Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics; Springer-Verlag: Berlin, Germany, 2019; Volume 2239. [Google Scholar]
- Graham, R.L.; Spencer, J.H. Ramsey Theory. Sci. Am. 1990, 7, 112–117. [Google Scholar] [CrossRef]
- Graham, R.; Butler, S. Rudiments of Ramsey Theory, 2nd ed.; American Mathematical Society: Providence, RI, USA, 2015; pp. 7–46. [Google Scholar]
- Graham, R.L.; Rothschild, B.L.; Spencer, J.H. Ramsey Theory, 2nd ed.; Wiley-Interscience Series in Discrete Mathematics and Optimization; John Wiley & Sons, Inc.: New York, NY, USA, 1990; pp. 10–110. [Google Scholar]
- Roberts, F.S. Applications of Ramsey theory. Discret. Appl. Math. 1984, 9, 251–261. [Google Scholar] [CrossRef]
- Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 332. [Google Scholar] [CrossRef]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Ramsey theory and thermodynamics. Heliyon 2023, 9, e13561. [Google Scholar] [CrossRef] [PubMed]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems). World J. Phys. 2023, 1, 1–24. [Google Scholar]
- Randic, M. On Characterization of Cyclic Structures. J. Chem. Inf. Comput. Sci. 1997, 37, 1063–1071. [Google Scholar] [CrossRef]
- Garcia-Domenech, R.; Galvez, J.; de Julián-Ortiz, J.V.; Pogliani, L. Some New Trends in Chemical Graph Theory. Chem. Rev. 2008, 108, 1127–1169. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Li, K.; Goodman, M.; Sallam, A. A Novel Approach for the Classical Ramsey Number Problem on DNA-Based Supercomputing. Match Commun. Math. Comput. Chem. 2011, 66, 347–370. [Google Scholar]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics, 3rd ed.; Addison-Wesley: Menlo Park, CA, USA, 2001; Chapter 6. [Google Scholar]
- Collins, J.J.; Stewart, I. A group-theoretic approach to rings of coupled biological oscillators. Biol. Cybern. 1994, 71, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.-X.; Zhang, P.-L. Discrete rotating waves in a ring of coupled mechanical oscillators with strong damping. J. Math. Phys. 2009, 50, 52701. [Google Scholar] [CrossRef]
- Lievens, S.; Stoilova, N.I.; Van der Jeugt, J. A linear chain of interacting harmonic oscillators: Solutions as a Wigner Quantum System. J. Phys. Conf. Ser. 2008, 128, 12028. [Google Scholar] [CrossRef]
- Vinogradov, G.V.; Malkin, A.Y. Rheology of Polymers: Viscoelasticity and Flow of Polyme; USSR Mir: Moscow, Russia, 1980. [Google Scholar]
- Sánchez, M.A.G.; Giraldo-Vásquez, D.H.; Sánchez, R.M. Rheometric, transient, and cyclic tests to assess the viscoelastic behavior of natural rubber-based compounds used for rubber bearings. Mater. Today Commun. 2020, 22, 100815. [Google Scholar] [CrossRef]
- Breńkacz, L.; Bagiński, P.; Korbicz, J.K. Vibration damping of the anti-vibration platform intended for use in combination with audio/music devices. J. Vibroeng. 2020, 22, 578–593. [Google Scholar] [CrossRef]
- Christensen, R. Theory of Viscoelasticity: An Introduction; Elsevier: Amsterdam, The Netherlands, 2012; Chapter 1. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physcis; Oxford University Press: Oxford, UK, 2003; Chapter 2. [Google Scholar]
- Braun, M.; Lansky, Z.; Hilitski, F.; Dogic, Z.; Diez, S. Entropic forces drive contraction of cytoskeletal networks. BioEssays 2016, 38, 474–481. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).