Cooperative Operational Optimization of Water and Power Systems under Extreme Conditions ^†

Abstract

This research explores the integrated management of water distribution systems (WDS) and power distribution systems (PDS) to improve their resilience to extreme scenarios. This study delves into the dynamics of a locally managed PDS as an example of extreme operational conditions. The primary objective is to minimize load shedding (LS) in the PDS through strategic load shifting in the interconnected WDS, demonstrating the potential of cooperative decision making between the two critical systems. The optimization framework offers a novel approach to managing flexible resources during emergencies by utilizing the mutual links between a WDS and a PDS. Typically, WDSs and PDSs are operated by different operators such that cooperation is limited. This study presents how communication based on limited information sharing between the two systems is sufficient to increase resilience and improve the systems’ functionality, emphasizing the advantages of cooperative decision making. This paper highlights the significance of cross-sectoral collaboration, presenting a viable pathway for managing local infrastructure systems under extreme conditions while ensuring uninterrupted service delivery to communities.

1. Introduction

Water distribution systems (WDS) and power distribution systems (PDS) are intrinsically interconnected, with WDSs being substantial energy consumers. Nonetheless, WDS operation exhibits inherent flexibility due to water storage facilities. Consequently, WDSs have high potential for providing flexible demand response (DR) services to PDSs [1]. DR refers to the dynamic balancing of power loads (e.g., shifting power demand to lower demand periods) to align more closely with the availability of power supply. A crucial application of DR emerges when supply and demand are imbalanced, potentially leading to enforced power outages or suboptimal power system operation (e.g., bringing online expensive generators to meet the demand). Under such circumstances, power system operators may be tasked with making critical decisions about which loads to curtail (i.e., a process known as load shedding) to ensure the secure operation of the system if there is an inadequate generation capacity. Several studies have explored the potential of WDSs in the DR context [2,3]. However, these studies often assume non-communication between the systems, which is sub-optimal, or complete cooperative decision making, which is not realistic. This study presents a novel communication logic aimed at enabling decision making under extreme operational conditions based on an effective information exchange between the system operators.

2. Methodology

The method is designed to minimize load shedding (LS) in a PDS under extreme scenarios and limited power sources. For this, three different operational strategies are developed. First is a full cooperative approach, where both systems are optimized together under perfect knowledge assumption. The second approach considers separate decision making where WDS is not aware of the PDS emergency and does not adjust its pump scheduling (i.e., no DR services to the PDS). The third approach, which is the main contribution of this study, is a communicative approach where the PDS signals to the WDS about an emerging emergency, and the WDS responds with pump schedule adjustments, hence leveraging the flexible DR benefits from WDS to PDS. Optimization models were developed for each of these strategies and are presented below through a descriptive formulation. Let $f_{PDS}$ be the objective function that minimizes LS and let $g_{PDS}$ be the set of PDS constraints including power flow equations and operational constraints. Let $f_{WDS}$ be the objective function that minimizes WDS operational costs and let $g_{WDS}$ be the set of WDS constraints including hydraulics, satisfying demands, and maintaining tank levels in the allowed range. Let $x_{PDS}$ be the generator production and battery charging rate (kW) and $x_{WDS}$ be the pump status. With this notation, the first strategy of full cooperative optimization is presented in Equation (1):

$$\begin{array}{c}Min{f}_{PDS}\left(x_{PDS},x_{WDS}\right)\\ s.t.g_{PDS}\left(x_{PDS},x_{WDS}\right)\le 0\\ \hspace{1em}{g}_{WDS}\left(x_{WDS}\right)\le 0\end{array}$$

(1)

The second approach is individual decision making. Pump scheduling is determined as an inner optimization problem that minimizes WDS operational costs. The optimal solution to the inner problem is used in the power balance constraints as fixed loads.

$$\begin{array}{c}Min{f}_{PDS}\left(x_{PDS},x_{WDS}^{*}\right)\\ s.t.g_{PDS}\left(x_{PDS},x_{WDS}^{*}\right)\le 0\\ \hspace{1em}{x}_{WDS}^{*}=argmin{f}_{WDS}\left(x_{WDS}\right) s.t. g_{WDS}\left(x_{WDS}\right)\le 0\end{array}$$

(2)

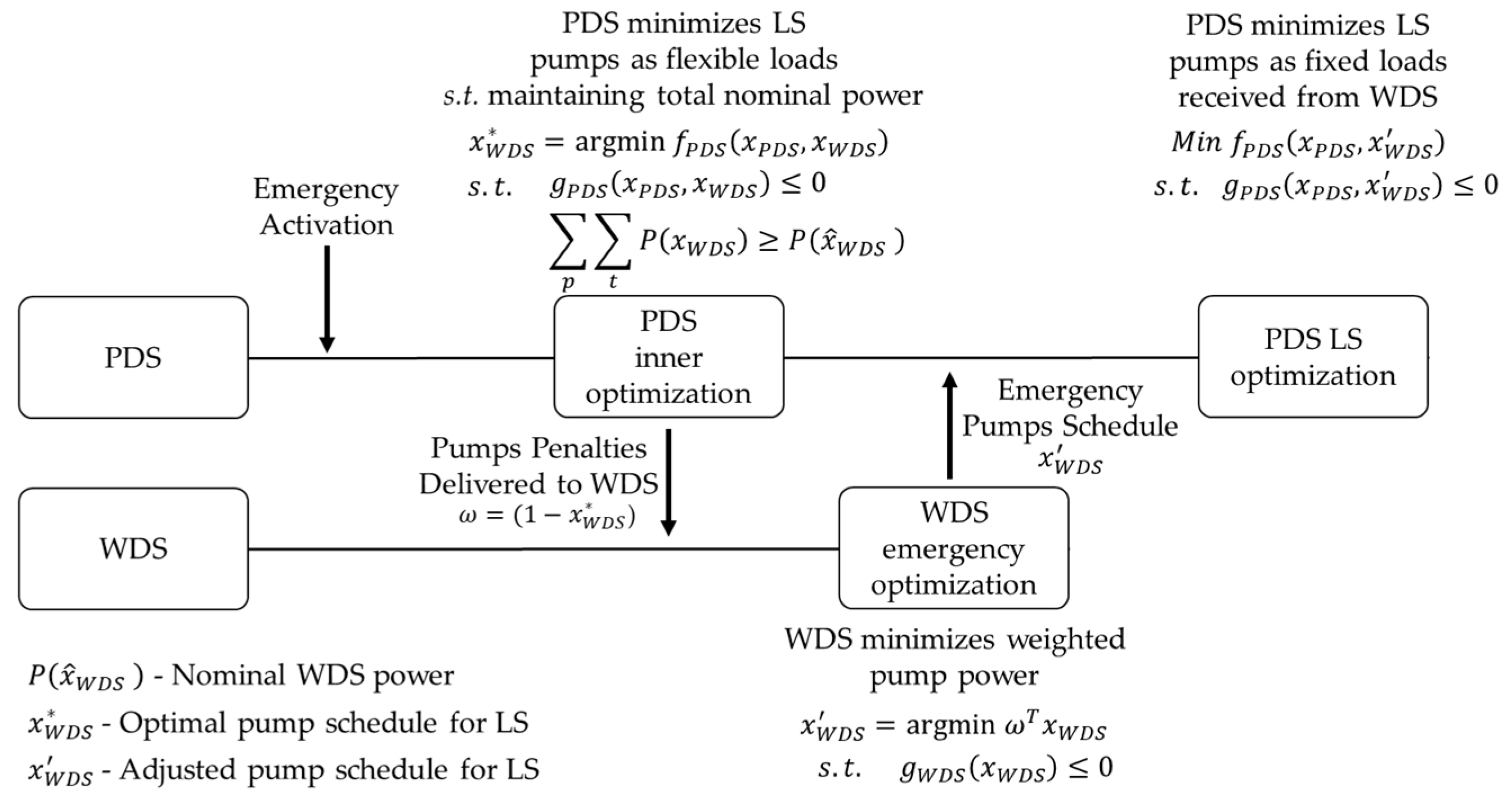
The third approach adopts minimal information exchange between the systems to achieve the common objective of LS minimization. Based on the bilevel optimization (BO) paradigm, the formulation involves a leader and a follower. Unlike the classic BO, here, the follower receives the opportunity to respond to the leader’s policy and ask for adoptions that serve the common objective. The leader is the WDS which, unless notified by the PDS, optimizes pump scheduling to minimize costs. The follower is the PDS, which adjusts the power generation schedule to the WDS operation. In the case of extreme scenarios where the PDS is disconnected from the main grid and loads need to be curtailed, the following procedure is taken. First, the PDS minimizes LS while considering WDS pumps as flexible loads. This is carried out to find the optimal pumping schedule from the PDS perspective. To ensure that the power operator allocates enough power for pumping, a constraint is added such that the total power consumed by the WDS is at least the nominal power consumed in routine times. Next, the PDS operator generates a penalties matrix, ω, based on the optimal pump schedule found in the previous step. The penalty matrix is delivered to the WDS which uses it to solve an inner “emergency” optimization problem with an objective function of minimizing weighted pump energy consumption. Another adoption taken by the WDS is the relaxation of the final tank volumes, allowing them to return to only 20% of their initial volume after a predefined period (e.g., 24 h). The solution of the WDS inner resilience optimization is then delivered as improved pump scheduling to the PDS. The process is depicted in Figure 1.

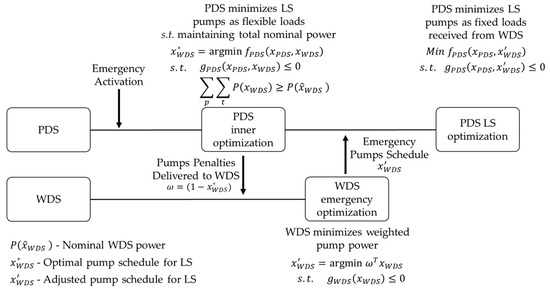
Figure 1. Communication logic.

Case Study

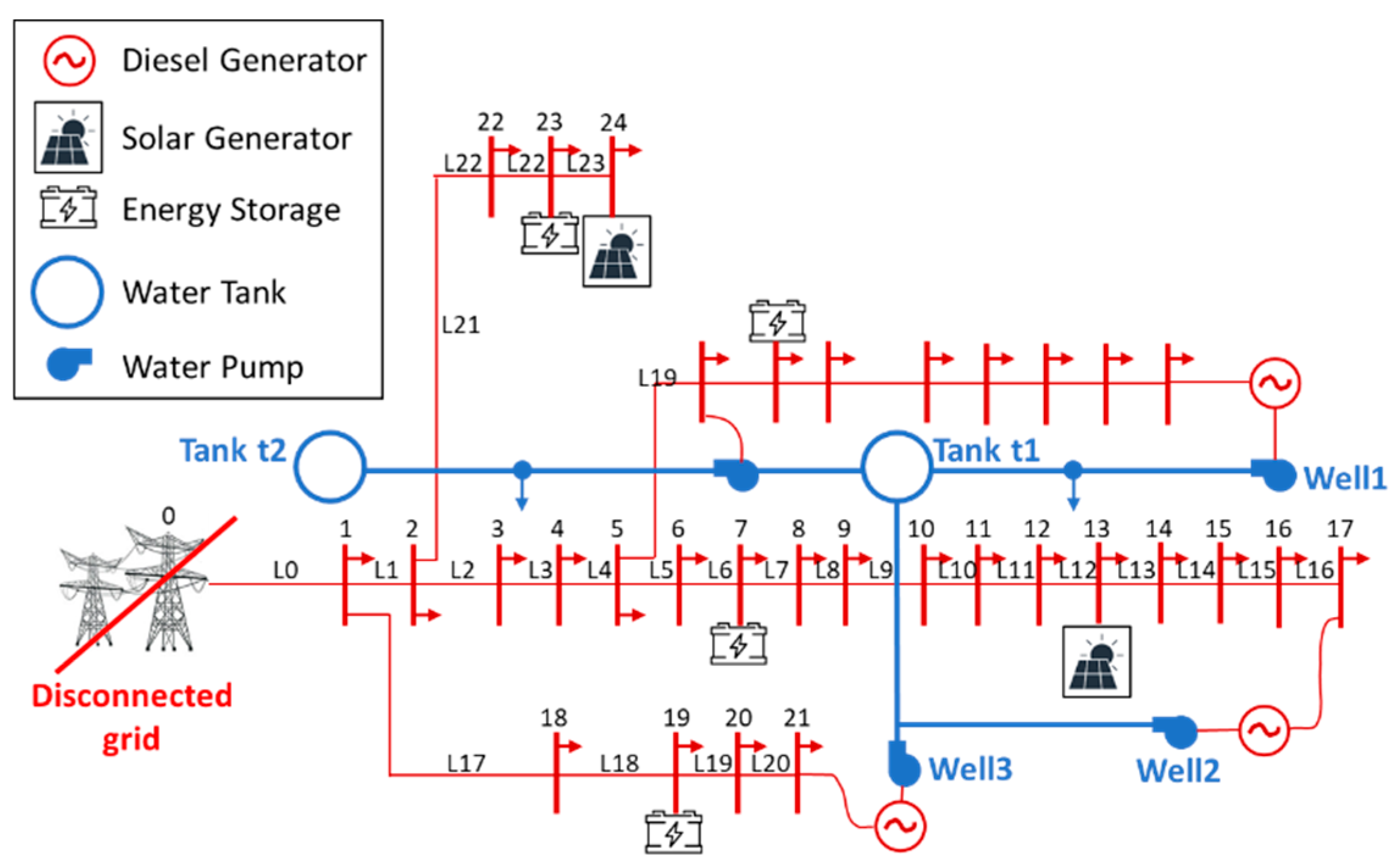
The proposed method was evaluated through a case study integrating a small WDS pumping water from three wells with the 33-bus system benchmark equipped with PV generators and energy storage facilities to simulate a local distribution microgrid. The case study layout is presented in Figure 2.

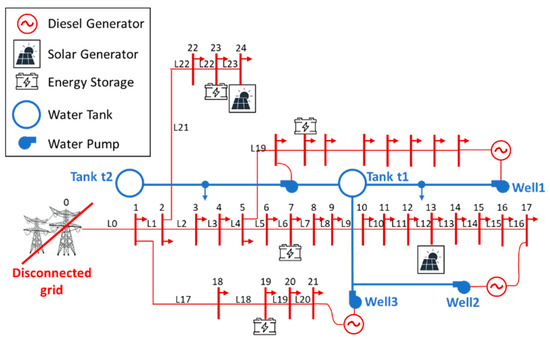
Figure 2. Case study layout.

To rigorously test the communicative strategy’s ability to reduce LS, a collection of 1000 random emergency scenarios was drawn. The random parameters in each scenario are emergency start time, duration, water demand factor, power load factor, PV availability, the number of outage lines, and tanks and batteries’ initial states.

3. Results

Each of the random scenarios was solved by the following three operational strategies: cooperative, independent, and communicative. The effectiveness of these strategies was statistically compared as presented in Table 1. The cooperative approach outperforms the other strategies, epitomizing the ideal of perfect knowledge and coordination between WDSs and PDSs. The independent approach resulted in a 9.53% increase in LS compared to the cooperative approach. Remarkably, the communicative approach showcased its effectiveness by limiting the increase in LS to a mere 1.37% above the cooperative one.

Table 1. LS statistical comparison between operational strategies across 1000 random scenarios.

	Cooperative	Communicative	Independent
Mean	7712.1	7817.7 (1.37%)	8447.1 (9.53%)
STD	3394.0	3438.0 (1.3%)	3629.8 (6.95%)

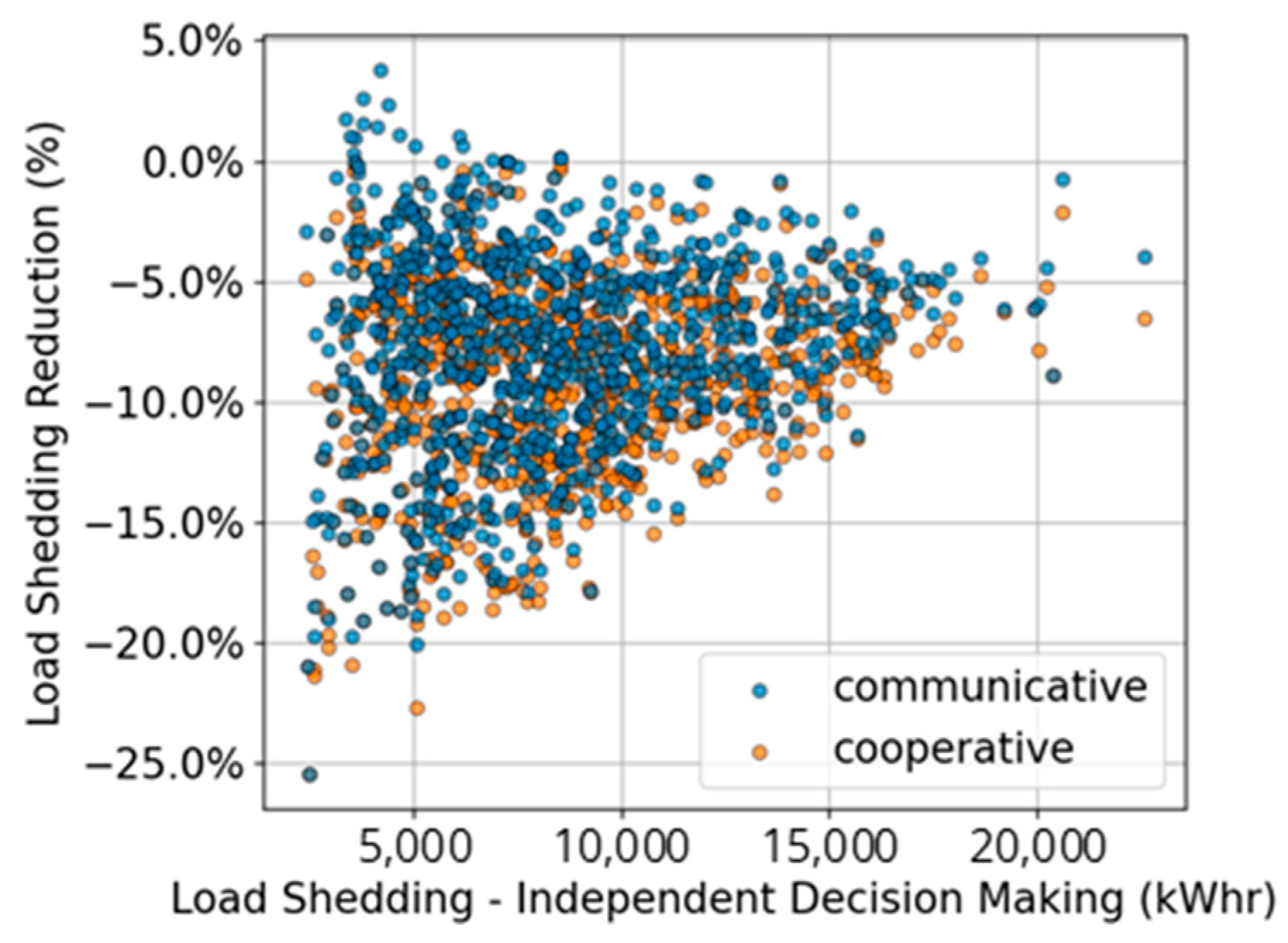
Figure 3 illustrates the relationship between the LS reduction achieved through the communicative strategy and the severity of the scenarios, as gauged by the LS levels under independent operation. This analysis suggests that while the communicative approach consistently mitigates LS, its relative benefit diminishes in scenarios of higher severity, as evidenced by a reduced LS reduction in these cases.

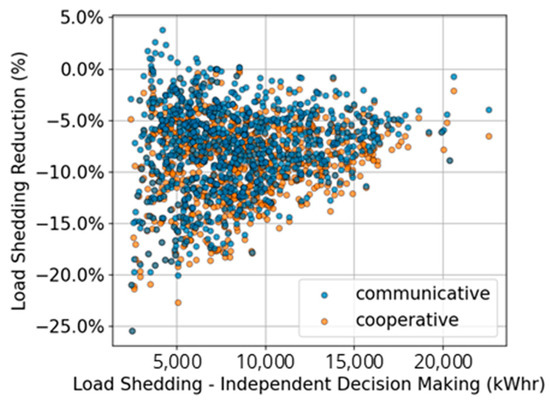
Figure 3. LS reduction by communicative strategy as a function of LS under independent strategy.

4. Summary

This study introduces a novel communicative approach to minimize LS. Through a comparative analysis, it is demonstrated that the presented approach reduces LS with only a slight increase compared to a fully cooperative strategy. Employing 1000 random scenarios, the communicative approach proves nearly as effective as perfect knowledge scenarios, highlighting its potential for enhancing system efficiency and resilience.