Analysis of Shrinkage Cracking of a Slab on the Ground Using a Probabilistic and Deterministic Approach †
Abstract
1. Introduction
2. Slabs Geometry and Parameters in Probabilistic Modeling
2.1. Properties of Slabs
2.2. Material Properties
3. FEM Modeling of the Slabs
3.1. FEM Model Description
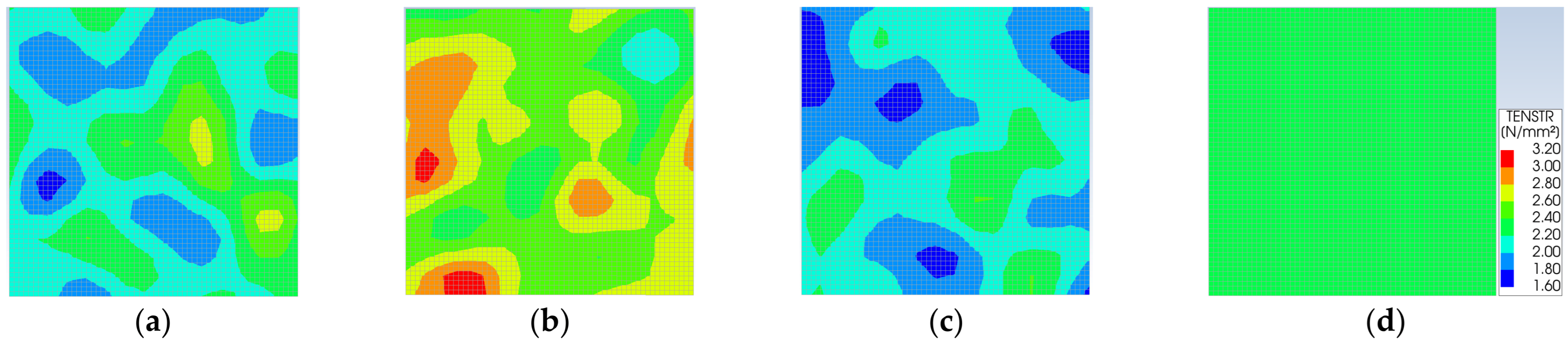
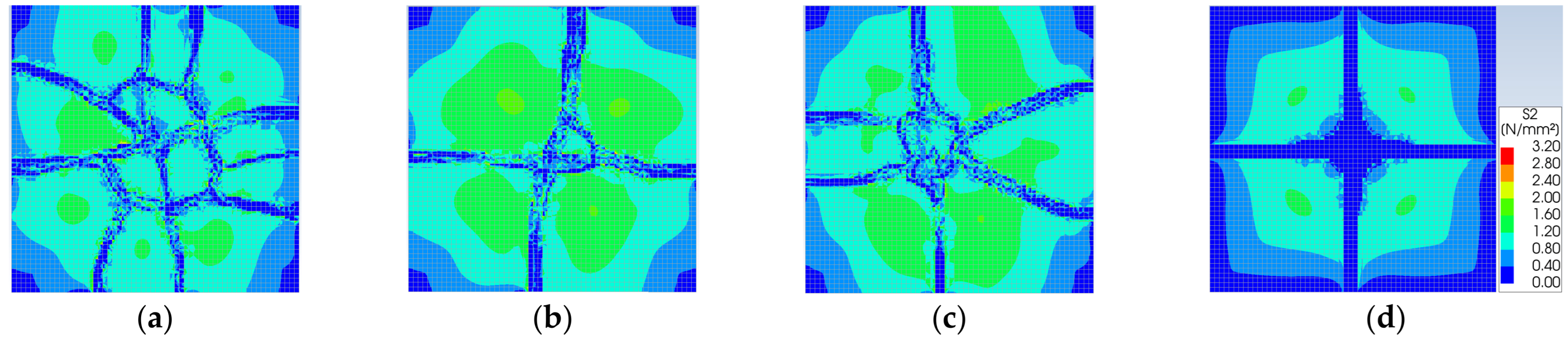
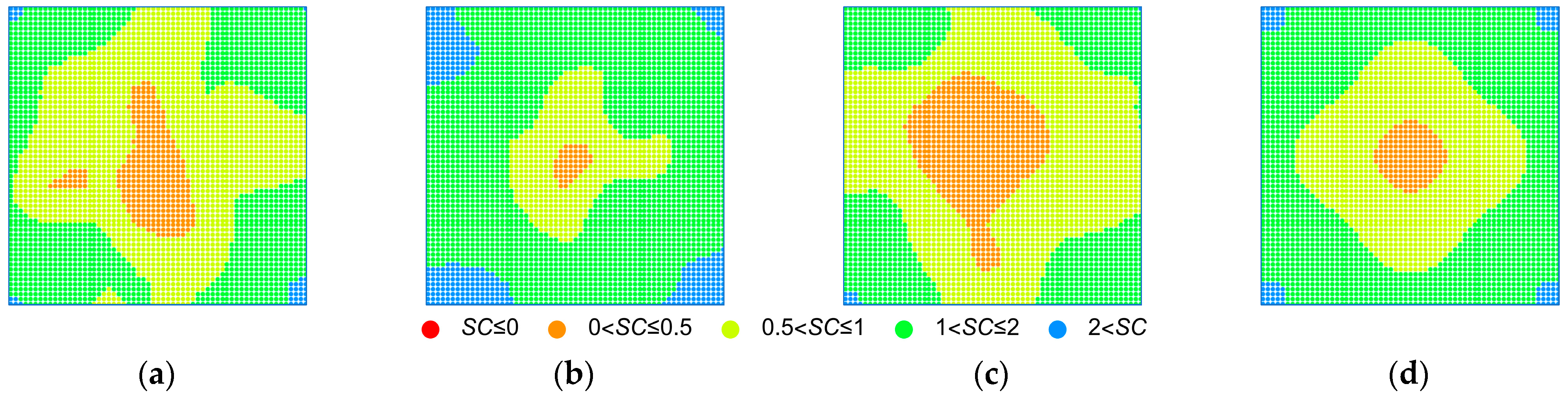
3.2. FEM Results
4. Comparison of the Probabilistic and Deterministic Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Botte, W.; Vereecken, E.; Caspeele, R. Random field modelling of spatial variability in concrete—A review. Struct. Infrastruct. Eng. 2023, 21, 1047–1060. [Google Scholar] [CrossRef]
- Vanmarcke, E. Random Fields: Analysis and Synthesis; The MIT Press: London, UK, 1983. [Google Scholar]
- Geyer, S.; Papaioannou, I.; Straub, D. Spatial modeling of concrete strength based on data. Struct. Saf. 2023, 103, 102345. [Google Scholar] [CrossRef]
- Botte, W.; Vereecken, E.; Caspeele, R. Numerical and experimental investigation of a correlation model to describe spatial variability of concrete properties. ASCE-ASME J. Risk Uncertain. Eng. Syst. A 2023, 9, 04023032. [Google Scholar] [CrossRef]
- Tao, J.; He, J.; Xiong, B.; Song, Y. Description of the spatial variability of concrete via composite random field and failure analysis of chimney. Probabilistic Eng. Mech. 2024, 77, 103677. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, T.; Liu, S.; Lin, W. Random Field-Based Time-Dependent Reliability Analyses of a PSC Box-Girder Bridge. Appl. Sci. 2019, 9, 4415. [Google Scholar] [CrossRef]
- Yi, G.; Ye, X.; Li, Q. Empirical Study of Surface Deterioration Analysis Based on Random Fields for Reinforced Concrete Structures in Marine Environment. Materials 2023, 16, 4150. [Google Scholar] [CrossRef] [PubMed]
- JCSS. Probabilistic Model Code. Joint Committee of Structural Safety. Available online: www.jcss-lc.org (accessed on 5 May 2025).
- Zhang, J.; Li, V.C. Influence of supporting base characteristics on shrinkage-induced stresses in concrete pavements. J. Transp. Eng. 2001, 127, 455–462. [Google Scholar] [CrossRef]
- Torrent, R.J. The log-normal distribution: A better fitness for the results of mechanical testing of materials. Mat. Constr. 1978, 11, 235–245. [Google Scholar] [CrossRef]
- Rackwitz, R. Predictive distribution of strength under control. Matér. Constr. 1983, 16, 259–267. [Google Scholar] [CrossRef]
- Sudret, B.; Der Kiureghian, A. Stochastic Finite Element Methods and Reliability: A State-of-the-Art Report; Technical Rep. UCB/SEMM-2000/08; University of California: Berkeley, CA, USA, 2000. [Google Scholar]
- Fenton, G.A. Error evaluation of three Random-Field Generators. J. Eng. Mech. 1995, 120, 2478–2497. [Google Scholar] [CrossRef]
- Fenton, G.A. Simulation and Analysis of Random Fields. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1990. [Google Scholar]
- Van der Have, R. Random Fields for Non-Linear Finite Element Analysis of Reinforced Concrete. Master’s Thesis, Delft University of Technology, Delft, The Netherland, 2015. [Google Scholar]
- de Vasconcellos, M.; Campos Filho, A.; Maestrini, S.R. Response variability in reinforced concrete structures with uncertain geometrical and material properties. Nucl. Eng. Des. 2003, 226, 205–220. [Google Scholar] [CrossRef]
- fib Model Code for Concrete Structures 2010; Ernst & Sohn: Hoboken, NJ, USA, 2010.
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures. Comité Européen de Normalisation: Brussels, Belgium, 2014.
- Landović, A.; Rožnjik, A. Optimization of Slabs-on-Ground Dimensions with Relation to Shrinkage Cracking. In Proceedings of the 33rd International Conference OTO 2024, Slavonski Brod, Croatia, 12 December 2024. [Google Scholar] [CrossRef]
- Narin, F.; Wiklund, O. Design of Slabs-on-Ground Regarding Shrinkage Cracking. Master’s Thesis, Department of Civil and Environmental Engineering, Chalmers University of Technology, Göteborg, Sweden, 2012. [Google Scholar]
- De Veaux, R.D.; Velleman, P.F.; Bock, D.E. Intro Stats, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2009. [Google Scholar]
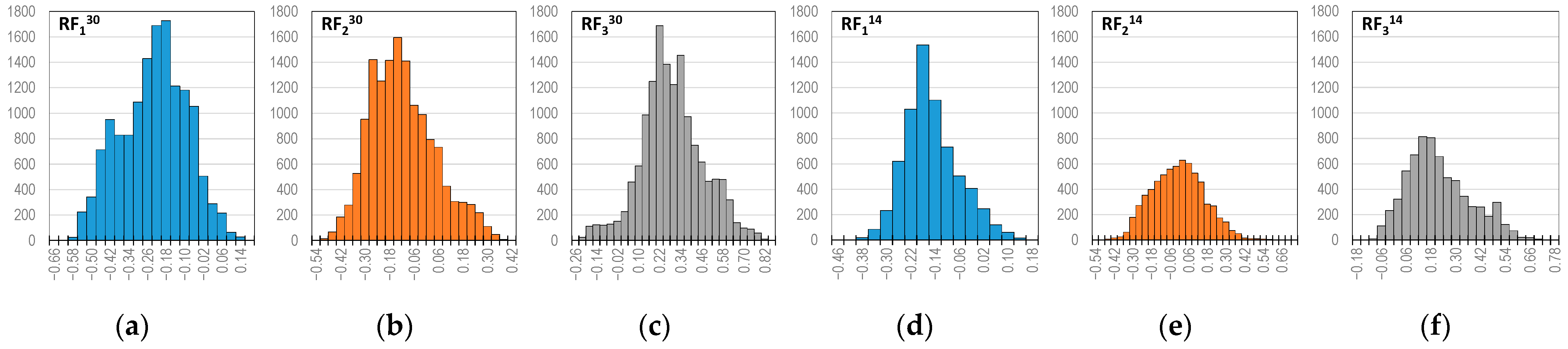
| Sample | n | Mean | Standard Deviation | p-Value | 99% Confidence Interval | |
|---|---|---|---|---|---|---|
| 14,400 | −0.2553 | 0.1417 | −216.18 | 0.0000 | (−0.2583, −0.2522) | |
| 14,400 | −0.1380 | 0.1589 | −104.29 | 0.0000 | (−0.1415, −0.1346) | |
| 14,400 | 0.2697 | 0.1768 | 183.05 | 0.0000 | (0.2659, 0.2735) | |
| 6720 | −0.1737 | 0.0887 | −160.54 | 0.0000 | (−0.1765, −0.1709) | |
| 6720 | −0.0280 | 0.1695 | −13.52 | 0.0000 | (−0.033, −0.0226) | |
| 6720 | 0.1956 | 0.1530 | 104.79 | 0.0000 | (0.1908, 0.2004) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Landović, A.; Rožnjik, A. Analysis of Shrinkage Cracking of a Slab on the Ground Using a Probabilistic and Deterministic Approach. Eng. Proc. 2026, 125, 6. https://doi.org/10.3390/engproc2026125006
Landović A, Rožnjik A. Analysis of Shrinkage Cracking of a Slab on the Ground Using a Probabilistic and Deterministic Approach. Engineering Proceedings. 2026; 125(1):6. https://doi.org/10.3390/engproc2026125006
Chicago/Turabian StyleLandović, Aleksandar, and Andrea Rožnjik. 2026. "Analysis of Shrinkage Cracking of a Slab on the Ground Using a Probabilistic and Deterministic Approach" Engineering Proceedings 125, no. 1: 6. https://doi.org/10.3390/engproc2026125006
APA StyleLandović, A., & Rožnjik, A. (2026). Analysis of Shrinkage Cracking of a Slab on the Ground Using a Probabilistic and Deterministic Approach. Engineering Proceedings, 125(1), 6. https://doi.org/10.3390/engproc2026125006






