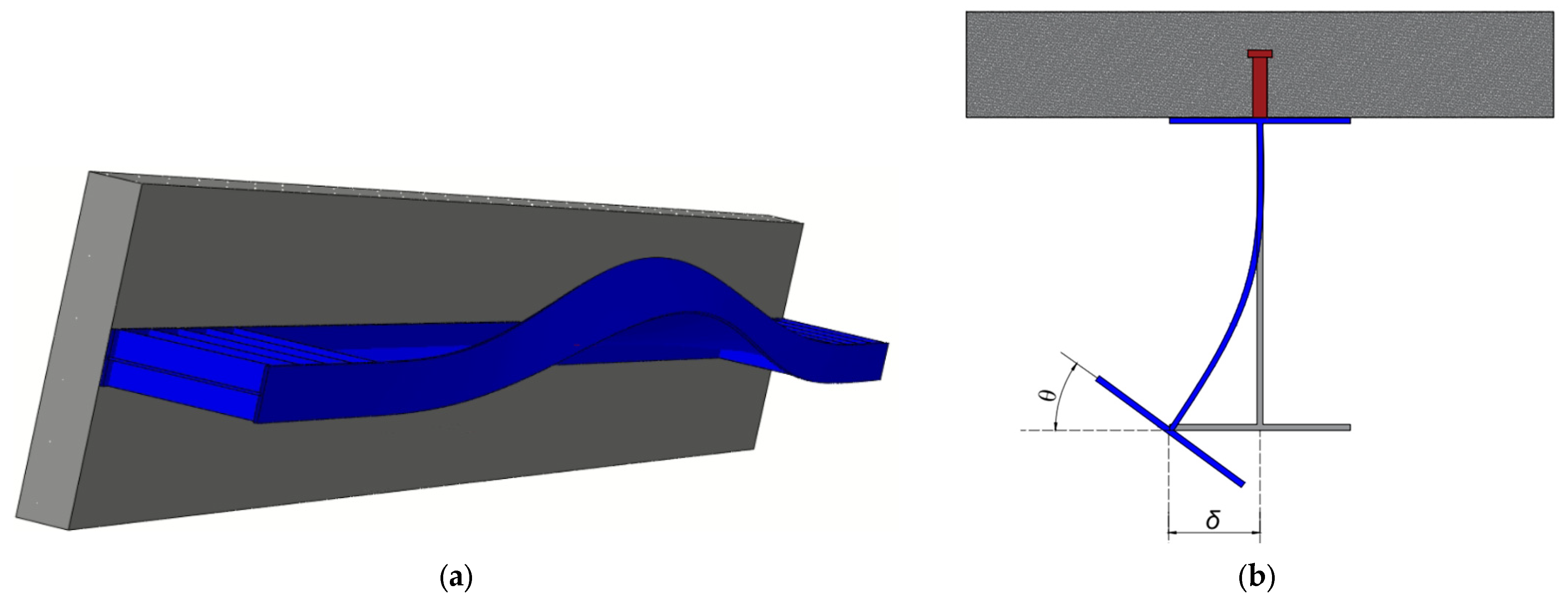
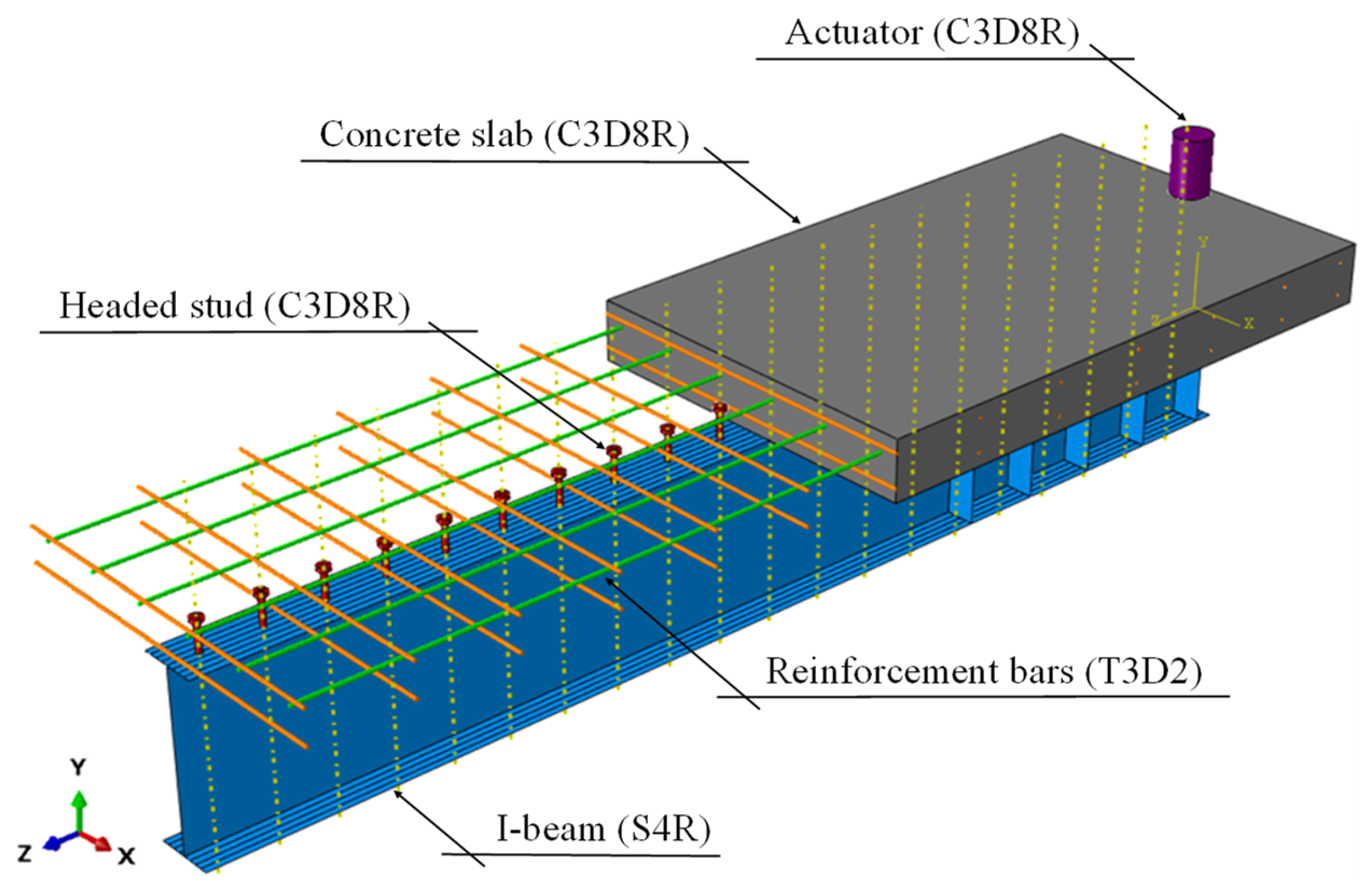
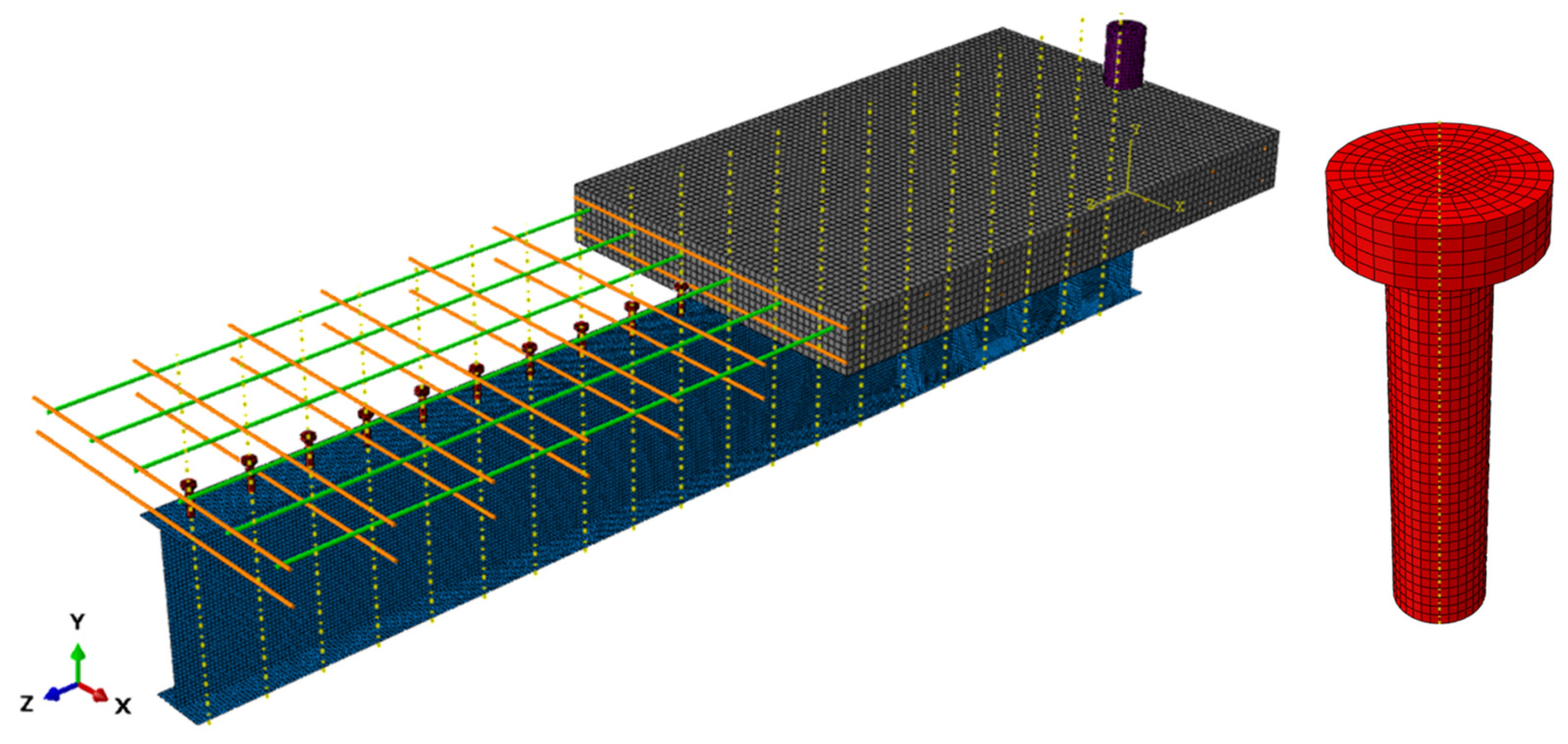
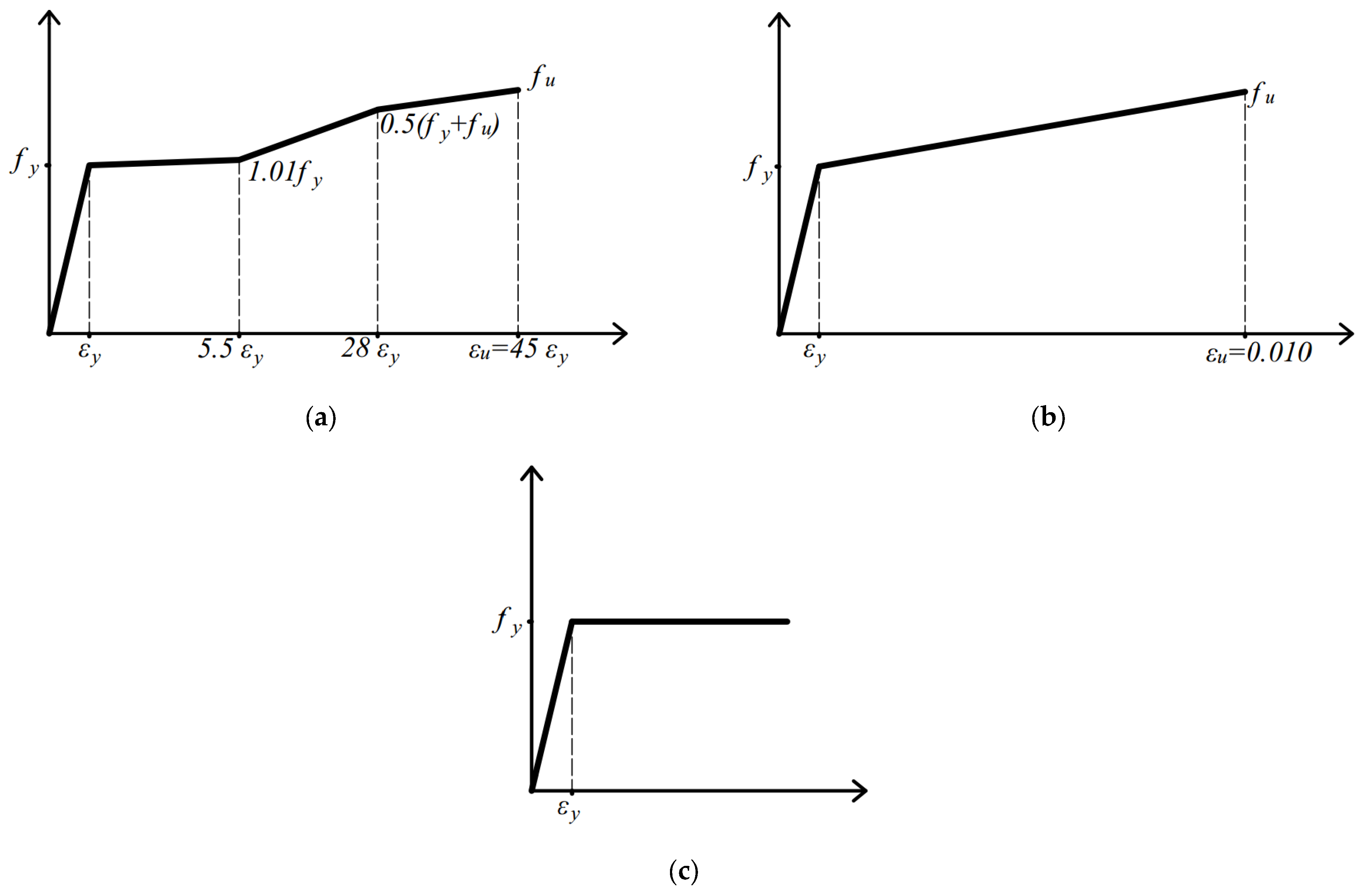
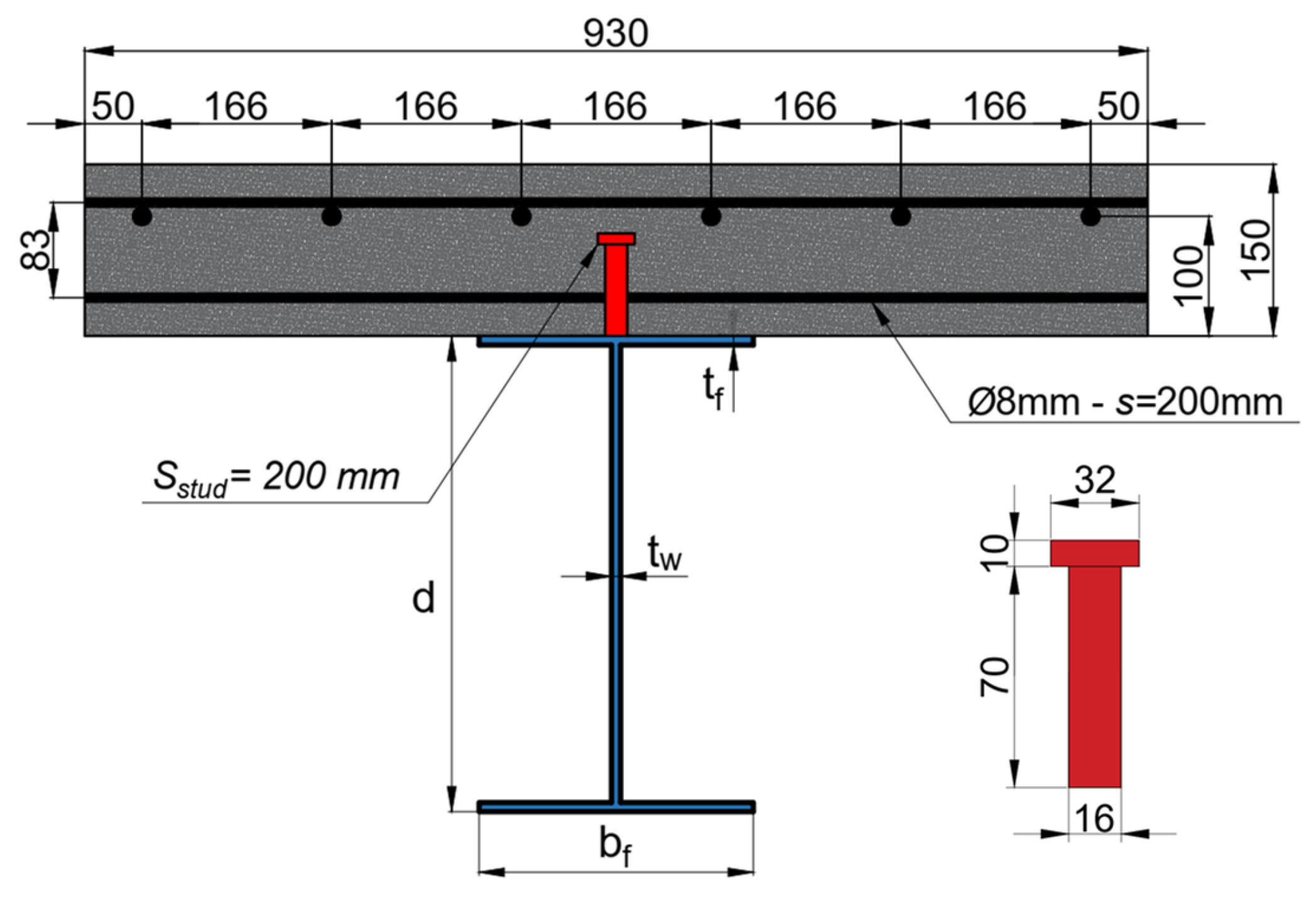
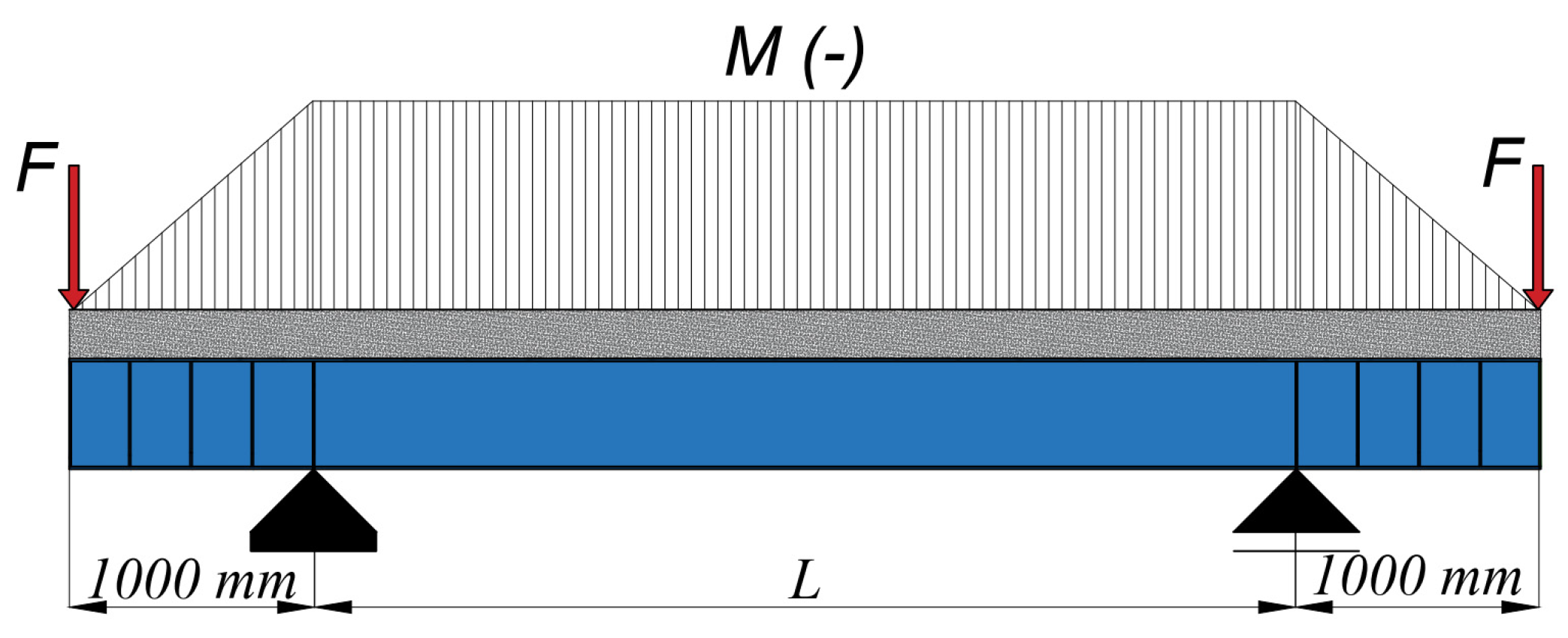
6.1. Steel Type Influence
In the parametric study developed, I-sections with mechanical properties of four different steel types were analyzed (
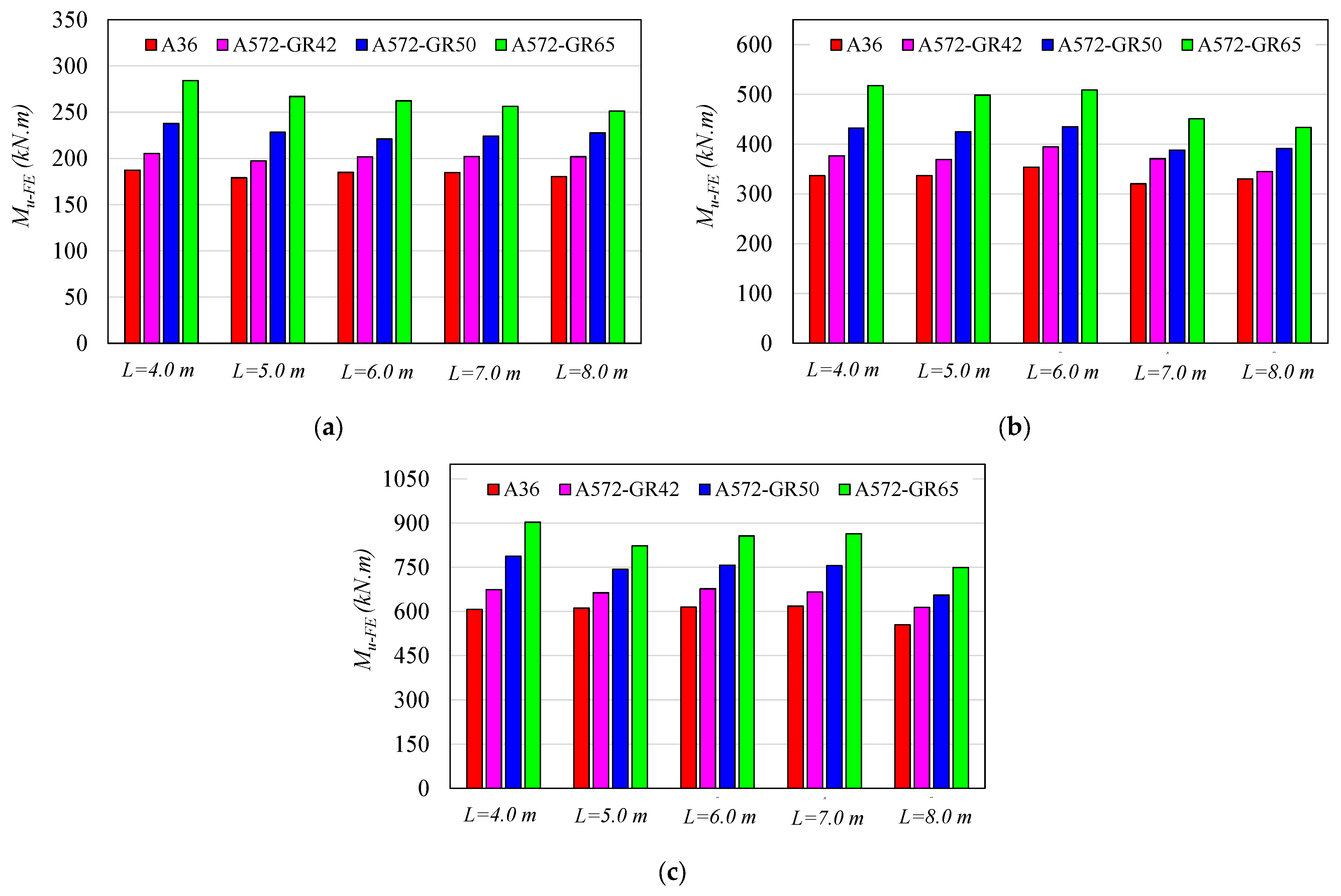
Table 4). The ultimate moment results for models with the I-sections CB350, CB450, and CB600 are shown in
Figure 14a–c, respectively. The results in
Figure 14 are for models with longitudinal reinforcements with 8 mm diameter.
As expected, the highest LDB strengths were obtained for the steel A572 GR65, which has a yield strength (
fy) of 450 MPa. It is also observed that with the increase in the yield strength (
fy), there is an increase in the LDB ultimate moment. Taking as reference the steel with a yield strength of 250 MPa, it is verified that for an increase of 16%, 40%, and 80% in the yield strength (
fy = 290 MPa;
fy = 350 MPa;
fy = 450 MPa), the variation of the LDB ultimate moment was 10.12%, 23.60%, and 42.43%, respectively. Another fact that can be observed in
Figure 14 is the small variation from the LDB ultimate moment due to the unrestricted length (
L) variation, which shows that the span length is not a predominant factor in the LDB strength of SCCB.
For the development of a general analysis of the mechanical properties’ (
fy) influence of different steel types on the LDB strength of SCCB,
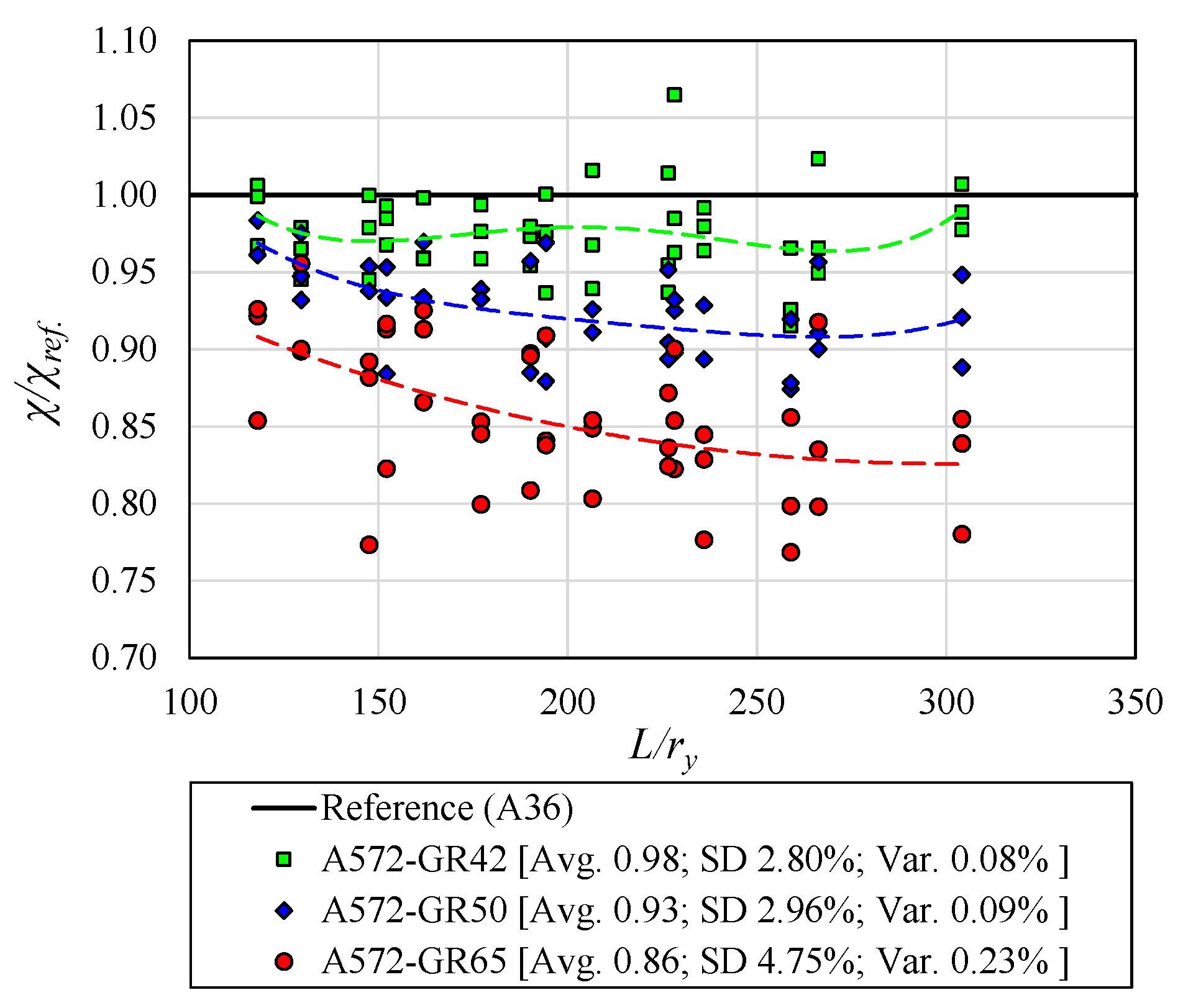
Figure 15 is presented. In
Figure 15, the reduction factor (
) calculated as a function of the ultimate moment values obtained in the FE analyses, and, as a function of the composite section plastic moment, calculated according to the plastic theory (EC4 [
13]), are compared for models with different steel types.
In
Figure 15, the reference values for the reduction factor (
χref.) were calculated as a function of the ultimate moment values obtained for the steel A36 (
fy = 250 MPa). The results in
Figure 15 show that the average value of the ratio (
χ/χref.) for the steel A572-GR65 is 0.86. This result is 14% lower when compared to the values obtained for the steel A36. This result shows that, although the LDB ultimate moment for A572-GR65 steel is higher than the value obtained with A36 steel, the value of the reduction factor (
χ) is 14% lower. That is, for steels with a value of higher yield strength (
fy), there is a greater difficulty for the composite section to reach the plastic moment, with LDB being responsible for reducing the sectional moment. It is also observed in
Figure 15 that the average value of the ratio (
χ/χref.) for A572-GR50 steel is 0.93, that is, 7% lower when compared to the values obtained for A36 steel. Finally, the reduction factor (
χ) values for models with A572-GR42 steel are compared with the reference values. The average value of the ratio (
χ/χref.) for A572-GR42 steel is 0.98, that is, only 2% lower than the values of A36 steel. This proximity occurs due to the yield strength (
fy) of the two types of steels are close: 250 MPa for A36 steel and 290 MPa for A572-GR42 steel.
In order to compare the values of the reduction factor (
χ), obtained through the FE analyses, with the values obtained through the standard procedures (ABNT NBR 8800:2008 [
15] and EC4 [
13]),
Table 5,
Table 6 and
Table 7 are shown. In standard procedures, the reduction factor (
χ) is obtained as a function of the relative slenderness factor (
) calculated as a function of the LDB elastic critical moment and the plastic moment of the composite section, which is dependent on the steel yield strength (
fy).
Table 5 presents the results for the models with 8 mm reinforcement bars, comparisons are made between the values of the reduction factor (
χ) obtained by the standard procedures and through the FE analyses for each type of steel used in the I-sections. In
Table 6 and
Table 7 the same comparisons are made, however, for models with 16 mm and 25 mm reinforcement bars, respectively. More information about the results obtained for each beam can be found on
Appendix A.
It is observed in
Table 5 that the values of the reduction factor (
χ) obtained by the standard procedures (NBR 8800:2008 [
15] and EC4 [
13]) are lower than the values obtained with the FE analyses. This situation shows a very conservative behavior of the Brazilian [
15], for models with 8 mm reinforcement bars, a situation also observed by Rossi et al. [
1], Zhou and Yan [
4], and Bradford [
29], in relation to the European procedure [
13].
Table 5 also presents the percentage error values of the standard procedures calculated in relation to the results obtained with the FE analyses. Percentage error values were calculated for models with different steel types. For the Brazilian standard procedure [
15], the average values of the percentage error for steels with a yield strength (
fy) of 250 MPa, 290 Mpa, 350 Mpa, and 450 MPa were −31.4%, −32.1%, −39.8%, and −35.1%, respectively. These results show that the LDB ultimate moment values obtained by the Brazilian standard procedure [
15] are inferior to the values obtained by the FE analyses, verifying a considerably conservative situation. When the results are compared with the values obtained by the European standard procedure [
13], there is an intensification of this conservative situation. The percentage error values for the European standard [
13] are −39.7%, −42.2%, −51.7%, and −51.5% for steels with a yield strength of 250 MPa, 290 MPa, 350 MPa, and 450 MPa, respectively. Therefore, the ultimate moment values obtained by the European procedure [
13] are up to 50% lower than the values obtained with the FE analyses for the models with reinforcement bars of 8mm.
Still in relation to
Table 5, observing the percentage error evolution for the different steel types, a growth tendency of the errors is verified with the yield strength (
fy) increase, except for the steel with a yield strength of 450 MPa. This situation shows that the use of steels with different mechanical characteristics has an impact on the LDB strength that is not captured by the design curves of SSRC (used by NBR 8800:2008 [
15]) and ECCS (used by EC3), which use the relative slenderness factor (
).
Table 6 presents the results for models with 16 mm reinforcement bars. The results of
Table 6 show a greater proximity between the LDB ultimate moment values obtained by the standard procedures and by the FE analyses. This situation can be explained by the plastic moment calculation of the composite section, which is dependent on the longitudinal reinforcement area present in the effective width of the concrete slab. Therefore, with the increase in the steel area, there is an increase in the plastic moment, and, therefore, a reduction in the relative slenderness factor (
), and, consequently, an increase in the reduction factor (
χ). Thus, with the increase in the plastic moment and the reduction factor, there is an increase in the value of the LDB ultimate moment, which leads to a closer approximation with the standard values. It is observed in
Table 6 that the average values of the percentage error for the Brazilian standard [
15] are 1.3%, 0.6%, 0.9%, and 0.5%, and for the European standard [
13] −2.8%, −4.2%, −4.9%, and −7.2%, for steels with a yield strength of 250 MPa, 290 MPa, 350 MPa, and 450 MPa, respectively. Regarding the steel type, it is verified, for the Brazilian procedure [
15] (curve 2P of the SSRC), that there is no great variation in the average values of the percentage errors for the different steel types. However, for the European standard [
13], there is an increase in divergences with the increase in the I-section steel yield strength.
Finally,
Table 7 shows the results for models with reinforced bars with 25 mm diameter. Contrary to the results observed in
Table 5,
Table 7 shows a non-conservative situation of the standard procedures; that is, the results of the FE analyses were lower than the ultimate moment values obtained by the standard procedures. The explanation for this situation is the same as that presented in the previous paragraph; that is, with the increase of the steel area in the effective width of the concrete slab, there is an increase in the plastic moment, and, therefore, a reduction in the relative slenderness factor (
), and, consequently, an increase in the reduction factor (
χ). Thus, with the increase in the plastic moment and the reduction factor, there is an increase in the LDB ultimate moment value, higher than those obtained in the FE analyses. In
Table 7, it is observed that the average values of the percentage error in relation to the Brazilian standard [
15] are 14.6%, 14.9%, 18.2%, and 20.5%, for the European standard [
13] these values are 12.3%, 12.3%, 15.1%, and 16.5%, for steels with a yield strength of 250 MPa, 290 MPa, 350 MPa, and 450 MPa, respectively. Analyzing the percentage error evolution, it is also observed a small influence of the yield strength variation on the LDB ultimate moment values that are not captured by the classic SSRC and ECCS curves.
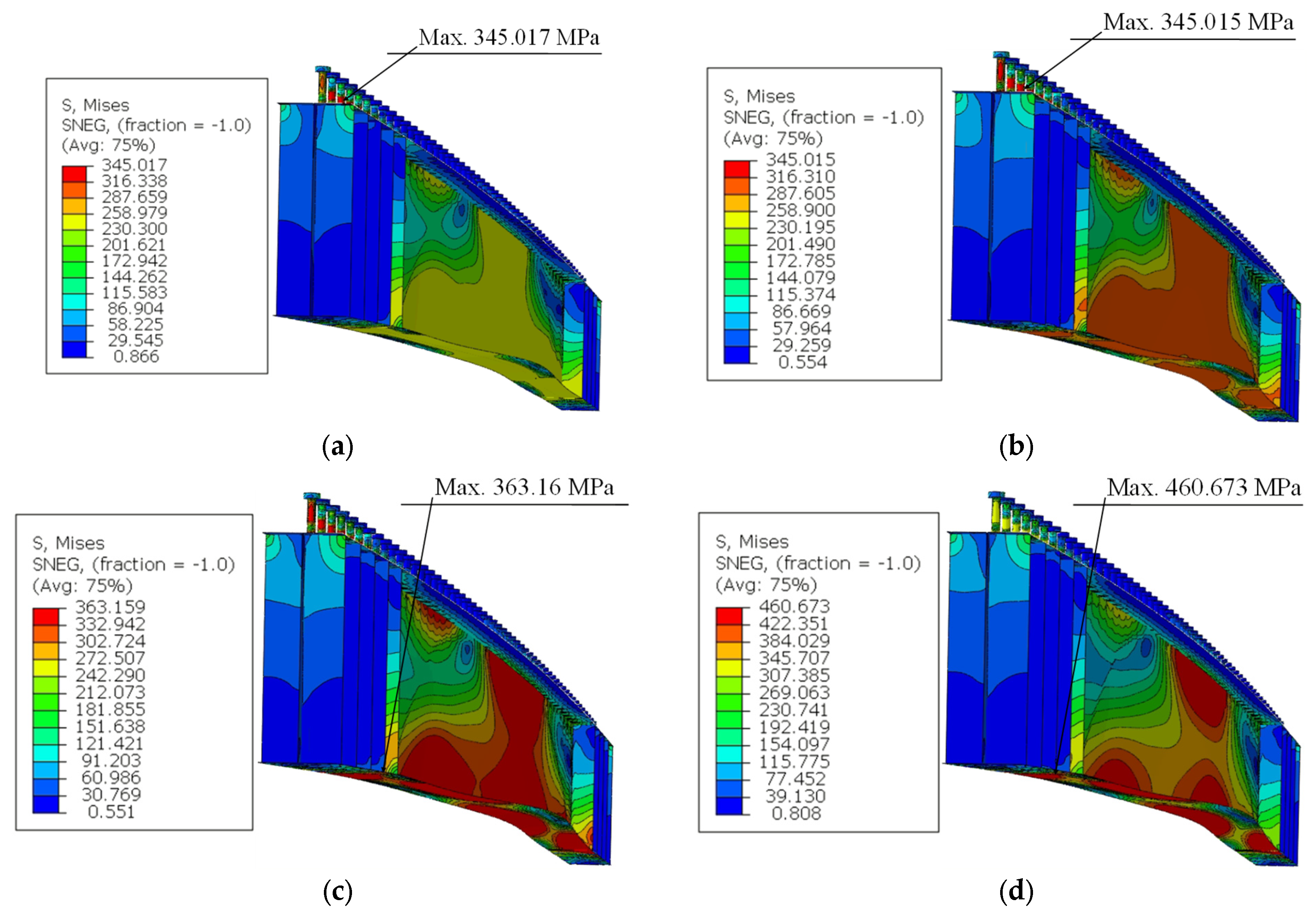
Figure 16 shows the deformed shape and von Mises stresses, for the CB450 model with a length of 6.0 m and reinforcement bars with 8 mm diameter for the four steel types analyzed. For the model with steel yield strength of 250 MPa (
Figure 16a), the maximum stress in the I-section web (middle of the span) varies from 230.30 to 258.98 MPa. For the model with 290 MPa yield strength (
Figure 16b), the maximum stress in the I-section web varies from 287.60 to 316.31 MPa. For the model in
Figure 16c, with a yield strength of 350 MPa, the maximum web stress ranges from 332.94 to 363.16 MPa, and finally, for the model with a yield strength of 450 MPa (
Figure 16d) the maximum web stress varies from 422.35 to 460.67 MPa.
6.2. Analytical Procedures and Other Parameters
The increase in the area of reinforcement bars present in the effective width of the concrete slab causes the increase in the plastic moment of the composite section calculated by plastic theory, which consequently leads to an increase in the LDB ultimate moment calculated by standard procedures such as EC4 [
13] and NBR 8800:2008 [
15]. However, the numerical analyses developed in this article show a small variation in LDB strength due to the increase in the area of reinforcement bars.
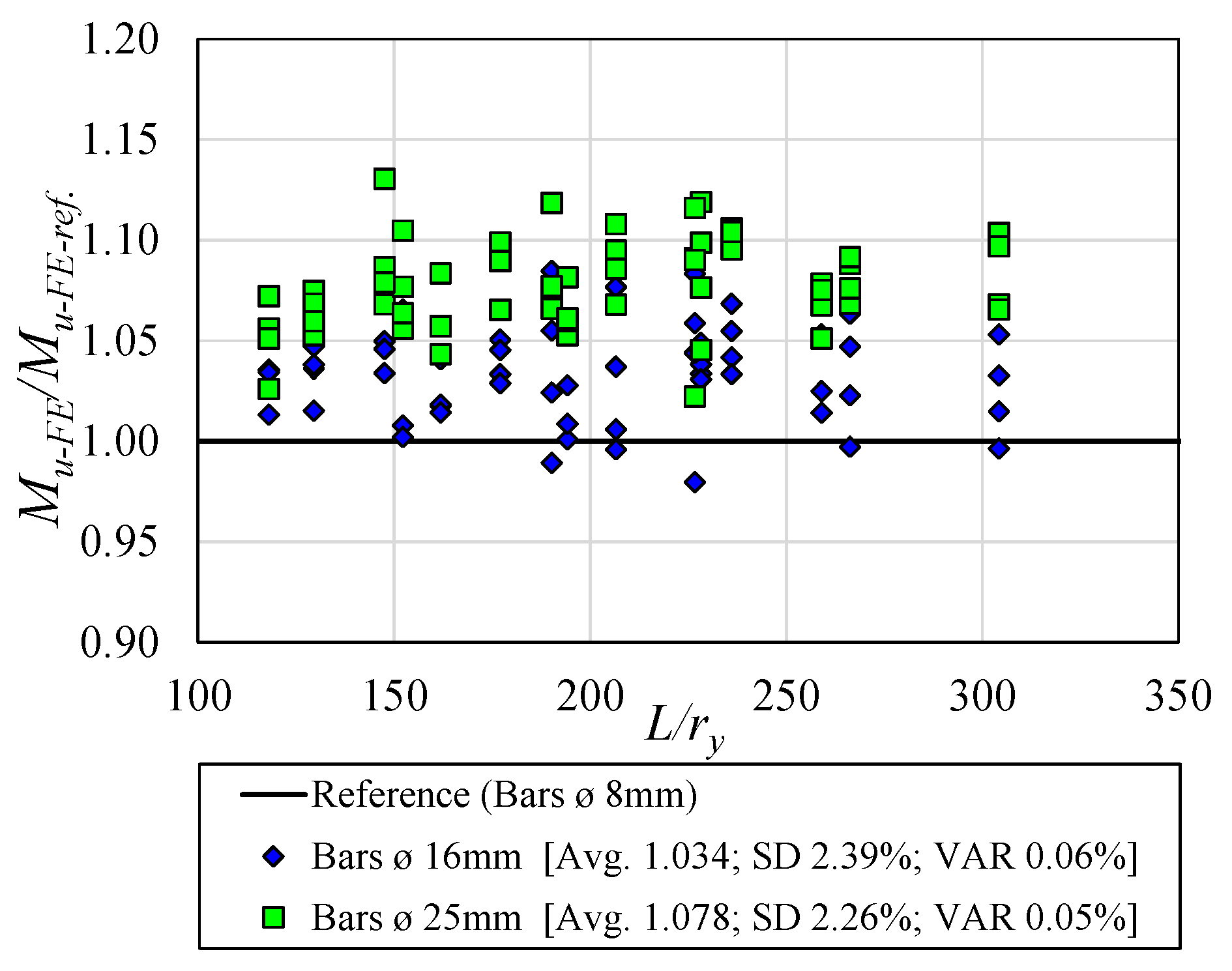
Figure 17 shows the LDB ultimate moment results for models with reinforcement bars with a diameter of 8 mm, 16 mm, and 25 mm. In
Figure 17 the reference values are those obtained by the models with 8 mm bars.
It is observed in
Figure 17 that the average value of the ratio (
Mu-FE/Mu-FE-ref.) for models with reinforcement bars with 16 mm diameter is 1.034; that is, there is an average gain in the ultimate moment value of about 3.4%. Regarding the models with 25 mm bars, the average value of the ratio (
Mu-FE/Mu-FE-ref.) is 1.078. This shows that the ultimate moment has an average gain of 7.8% compared with the models with 8 mm bars. This situation shows that, despite a considerable increase in the longitudinal reinforcement area, there is an insignificant increase in the value of the LDB ultimate moment.
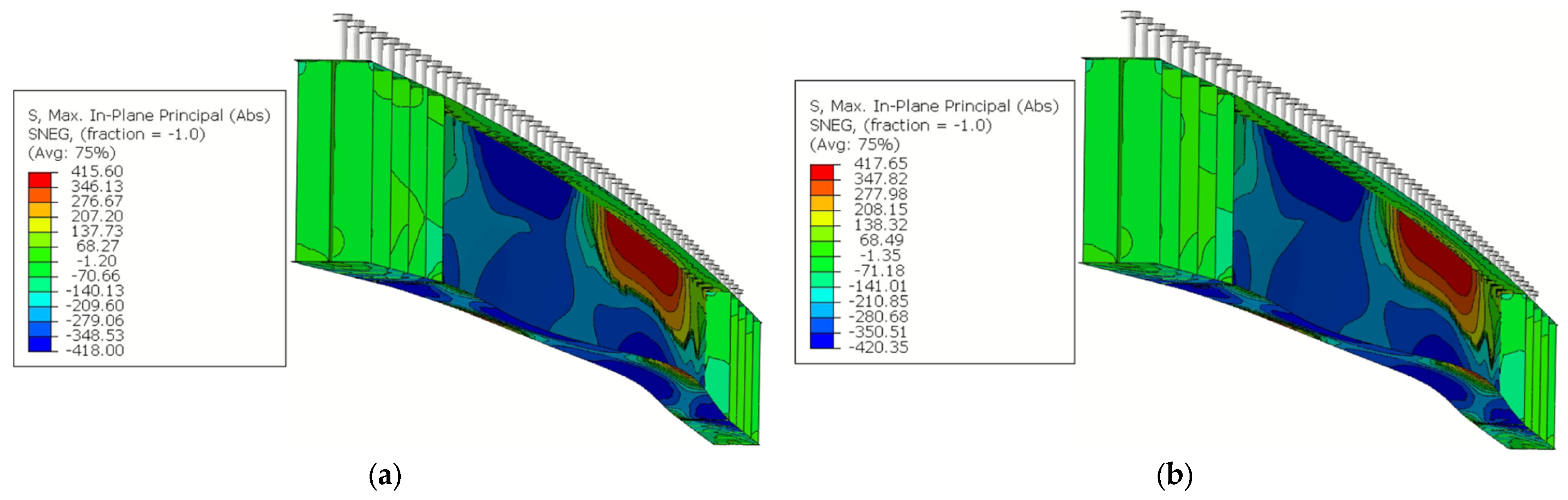
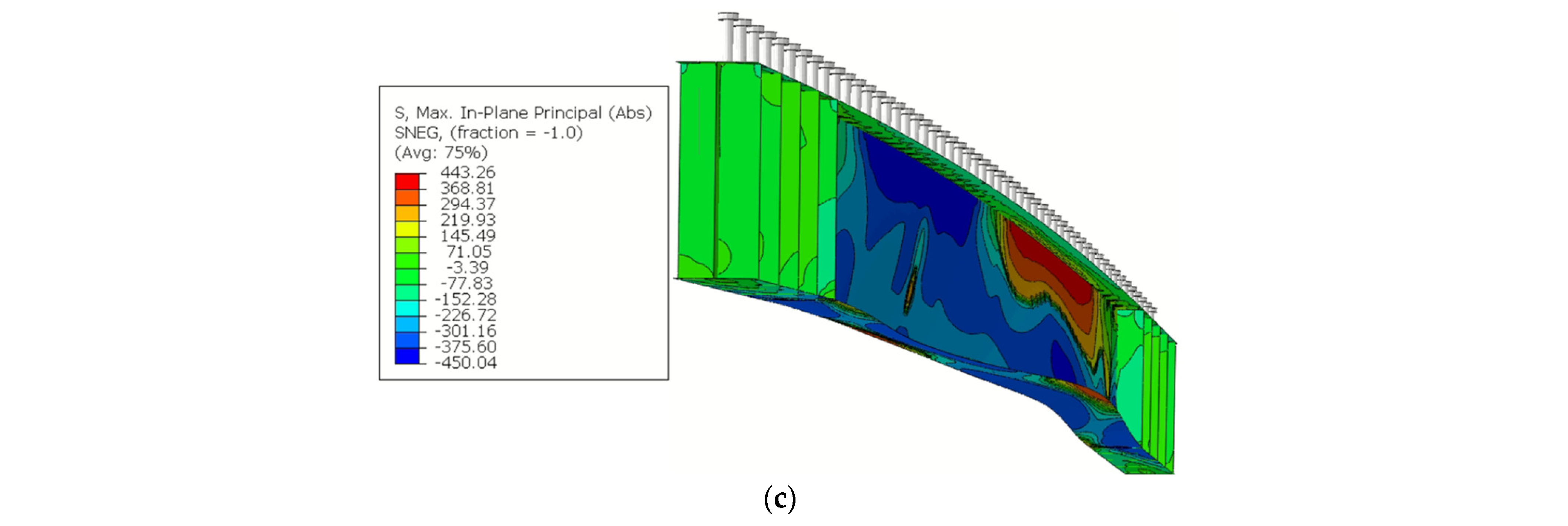
Figure 18 shows the deformed shape and the distribution of the absolute maximum stresses in the principal plane for models CB350 with a length of 6.0 m, A572-GR50 steel and with longitudinal reinforcements of 8 mm (
Figure 18a), 16 mm (
Figure 18b), and 25 mm (
Figure 18c). It is observed in
Figure 18 that the increase in the longitudinal reinforcement area in the effective width of the concrete slab causes an increase in the maximum tension and compression stresses, reflecting the increase in the LDB ultimate moment, a situation verified in the numerical models analyzed.
As seen in
Figure 17, the increase in the longitudinal reinforcement area in the effective width of the concrete slab leads to an insignificant increase in the LDB ultimate moment. However, this increase in the longitudinal reinforcement area causes a considerable increase in the plastic moment value calculated according to EC4 [
13] by plastic theory. This situation causes an increase in the LDB ultimate moment value, calculated according to the procedures of EC4 [
13] and NBR 8800:2008 [
15], as the longitudinal reinforcement area increases.
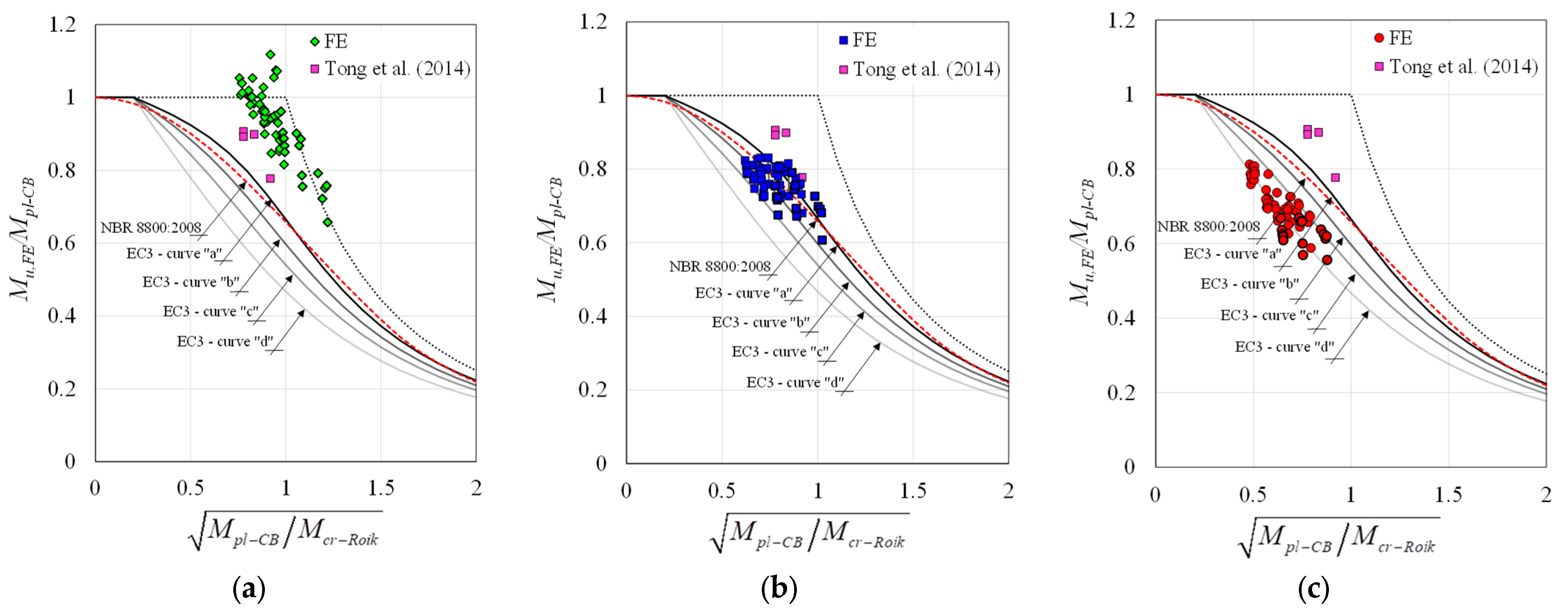
Figure 19 shows the comparison between the European [
13] and Brazilian [
15] standard design curves with the results of the FE analyses for models with 8 mm (
Figure 19a), 16 mm (
Figure 19b), and 25 mm (
Figure 19c). In addition,
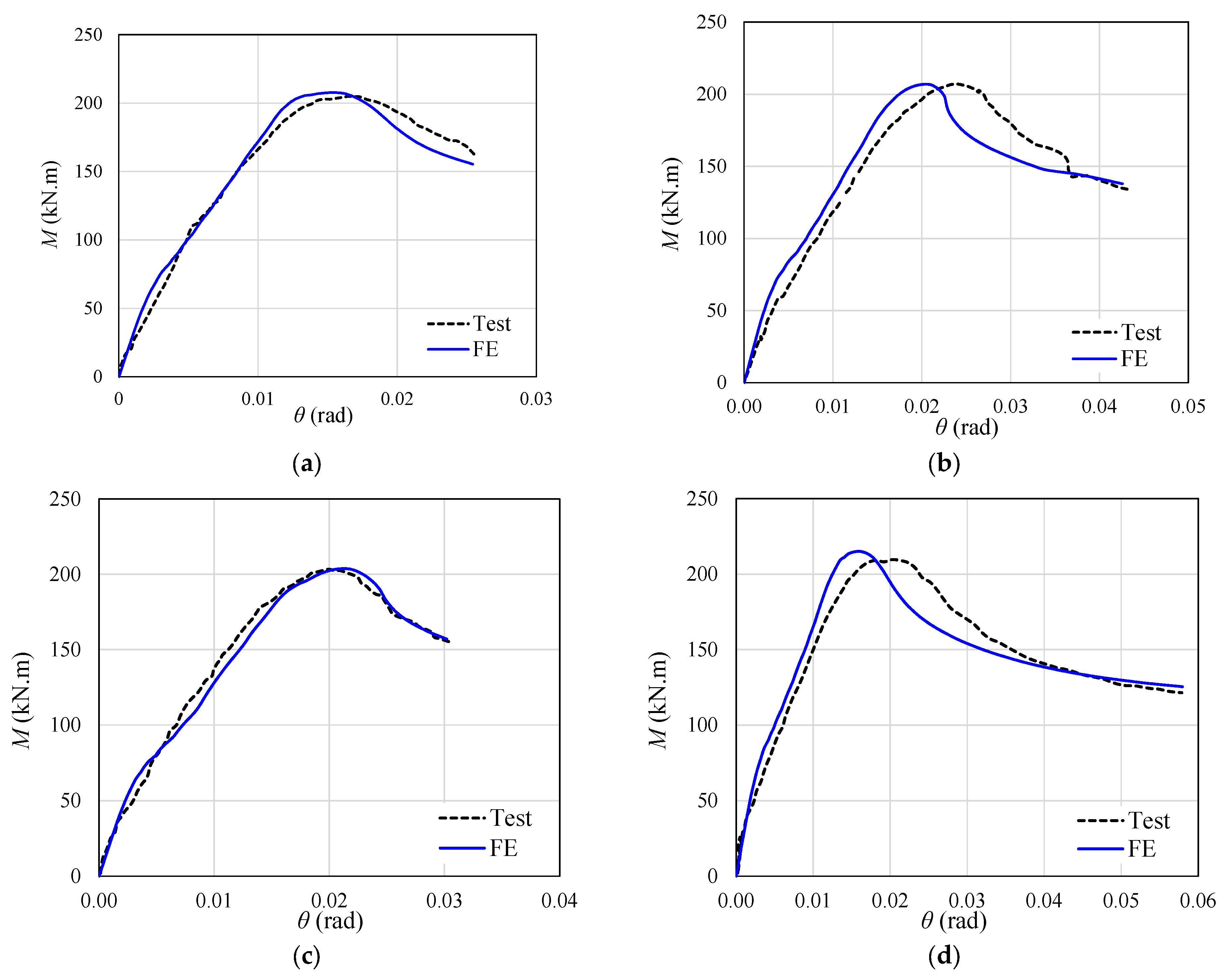
Figure 19 also shows the values of the experimental analysis of four beams tested by Tong et al. [
28], which served to validate the numerical model of this article.
It is observed in
Figure 19 three different situations. In
Figure 19a, the results of the FE analyses provided LDB ultimate moment values higher than those obtained by the Brazilian [
15] and European [
13] standard procedures. The average percentage error of the FE analyses results when compared to the European procedure [
13] was −46.28%, which shows considerable conservatism in the EC4 procedure [
13]. Regarding the Brazilian standard [
15], which is based on the SSRC 2P curve, the average percentage error was −34.60%, also showing conservatism.
Figure 19a also presents the results of four beams tested experimentally by Tong et al. [
28]. The results of these four beams are close to the values of the FE analyses developed in this article, since the longitudinal reinforcement area of the beams by Tong et al. [
28] is similar to the models with 8 mm bars analyzed in the present work.
In relation to
Figure 19b, which presents the results for the models with 16 mm diameter longitudinal reinforcement, a close proximity is observed between the results of the FE analyses and the standard procedures of EC4 [
13] and NBR 8800:2008 [
15]. The increase in the plastic moment of the composite section is the reason that leads to the greater proximity between the results of the standard procedures and those obtained through the FE analyses. For the results presented in
Figure 19b, the average percentage error of the numerical results compared with the standard procedures is 0.83% for the Brazilian standard [
15] and −4.78% for the European standard [
13]. Finally, in
Figure 19c, the results of the FE analyses are compared with the standard procedures for the models with 25 mm diameter longitudinal reinforcement. It is observed in
Figure 19c that the LDB ultimate moment values obtained by means of the FE analyses are inferior to the standard results, which leads to an unsafe situation of the European [
13] and Brazilian [
15] standards. As verified, the increase in the longitudinal reinforcement area does not cause a considerable gain in the LDB strength. However, for the EC4 [
13] and NBR 8800:2008 [
15] procedures, the increase in the longitudinal reinforcement area leads to a considerable gain from the LDB strength of SCCB, which leads to this unsafe situation for the European [
13] and Brazilian [
15] procedures. In
Figure 19c the average percentage error of the numerical results compared with the standard procedures is 17.05% for the Brazilian standard [
15] and 14.05% for the European standard [
13].
The results of the FE analyses were also compared with the analytical procedures presented by Zhou and Yan [
4] and Bradford [
29]. In
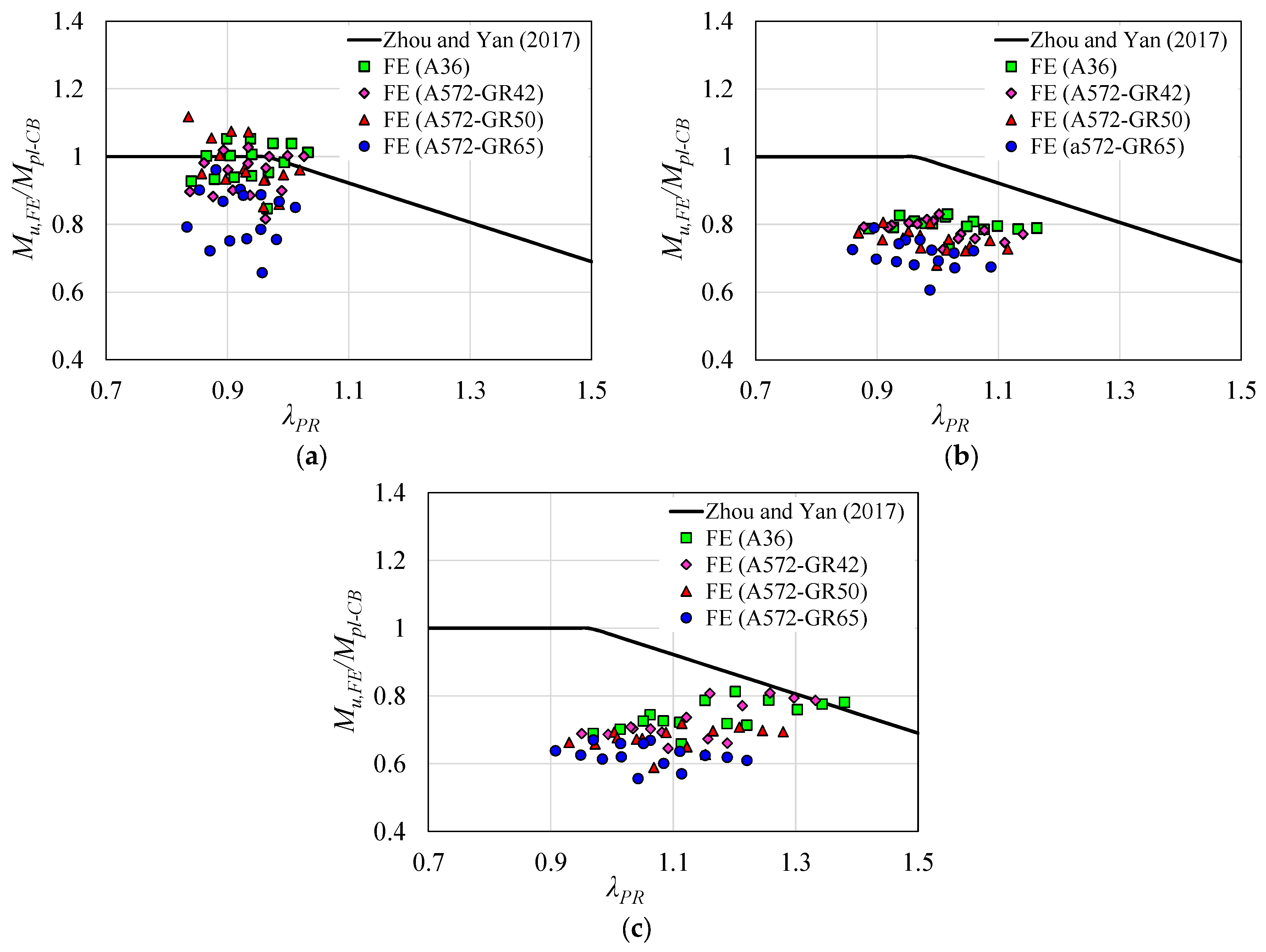
Figure 20, the results of the FE analyses are compared with the Zhou and Yan procedure [
4].
It is observed in
Figure 20 that the longitudinal reinforcement area variation in the concrete slab is also responsible for three different situations when the results of the FE analyses are compared with the Zhou and Yan procedure [
4]. For the models with 8 mm diameter longitudinal reinforcement (
Figure 20a) the results of the FE analyses show greater agreement with the Zhou and Yan [
4] procedure. The results analysis of the LDB ultimate moment shows that the average value of the ratio (
MZhou and Yan/Mu,FE) is 1.08, that is, the values obtained through the analytical procedure of Zhou and Yan [
4] are on average 8.0% higher than those obtained with the FE analyses.
Figure 20b presents the results obtained with the FE analyses for the models with 16 mm bars. It is verified that with the increase in the longitudinal reinforcement area there is also an increase in the divergence between the results of the FE analyses and the results of the Zhou and Yan procedure [
4]. The average value of the ratio (
MZhou and Yan/Mu,FE) is 1.28, that is, the results of the procedure developed by the authors [
4] are on average 28% higher than the results obtained in the numerical analysis, an unsafe situation. Finally,
Figure 20c shows the results for the models with 25 mm diameter longitudinal reinforcement bars. There is also a tendency to increase the divergence between the numerical results and the Zhou and Yan [
4] procedure as the longitudinal reinforcement area is increased. For the results in
Figure 20c, the average value of the ratio (
MZhou and Yan/Mu,FE) is 1.34, which shows an unsafe situation in the Zhou and Yan procedure [
4].
Figure 20 also presents the results for the models with the different steel types analyzed, it is verified that, as for the standard procedures, in the Zhou and Yan procedure [
4] the influence of the steel type is not captured properly.
Finally,
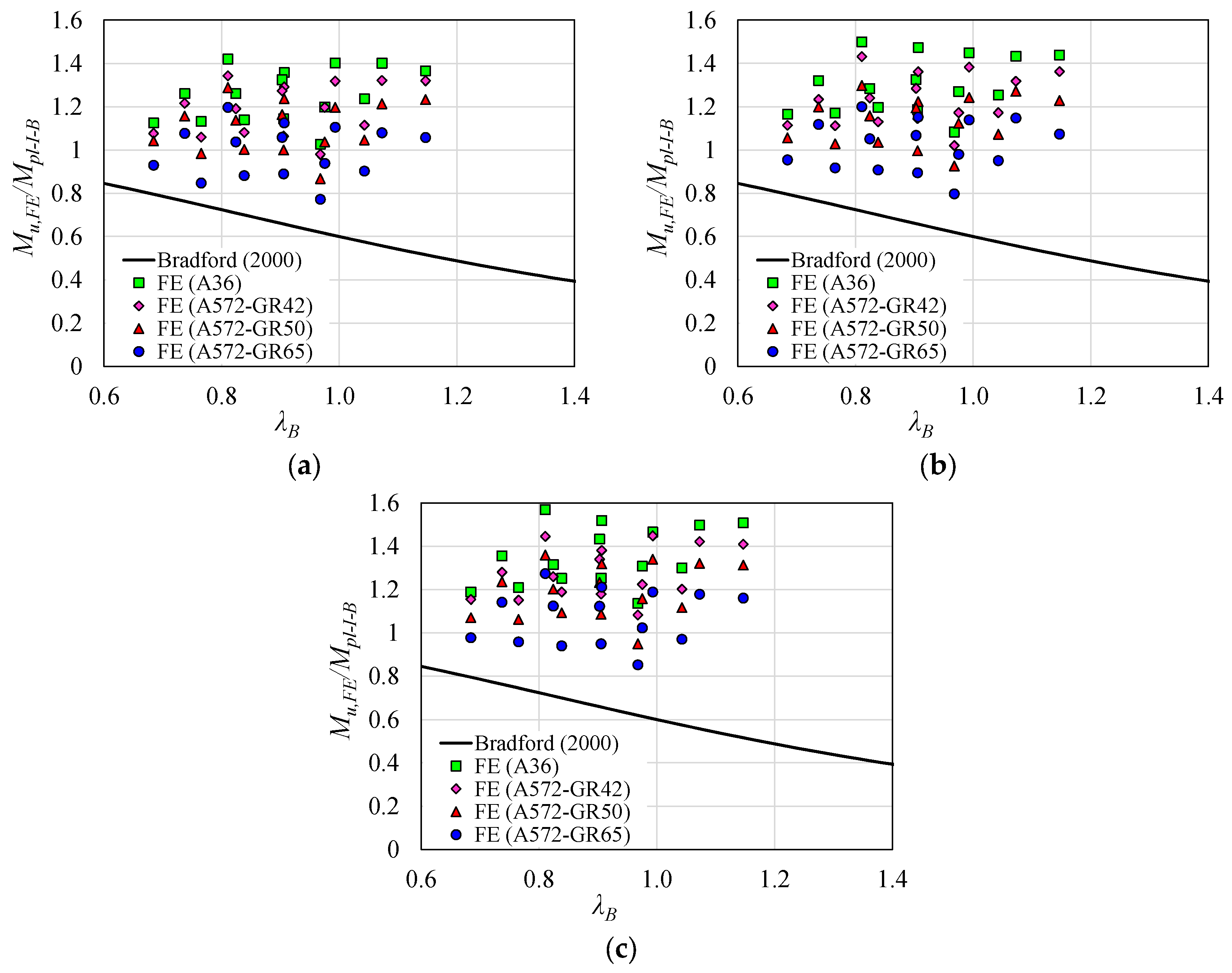
Figure 21 presents the comparison between the results obtained with the FE analyses and the Bradford [
29] procedure.
The results in
Figure 21 show a similar behavior of the Bradford procedure [
29] in comparison with the results of the FE analysis between the models with longitudinal reinforcement of 8 mm (
Figure 21a), 16 mm (
Figure 21b), and 25 mm (
Figure 21c). This situation is due to the fact that the Bradford procedure [
29] does not consider the plastic moment of the composite section, but only the I-section plastic moment to determine the LDB ultimate moment. This situation can be confirmed with the analysis of the average value of the ratio (
MBradford/Mu,FE) which provided values of 0.59, 0.57, and 0.55 for the models with reinforcement bars with a diameter of 8 mm, 16 mm, and 25 mm, respectively. However, despite providing safe results, the Bradford procedure [
29] is considerably conservative. Regarding the results for the different steel types analyzed, it is verified that for the models with greater steel yield strength, there is a greater proximity of the FE results with the author’s procedure [
29]. On the other hand, with the reduction in the steel yield strength, there is a tendency to increase the divergences between the FE results and the Bradford procedure [
29].
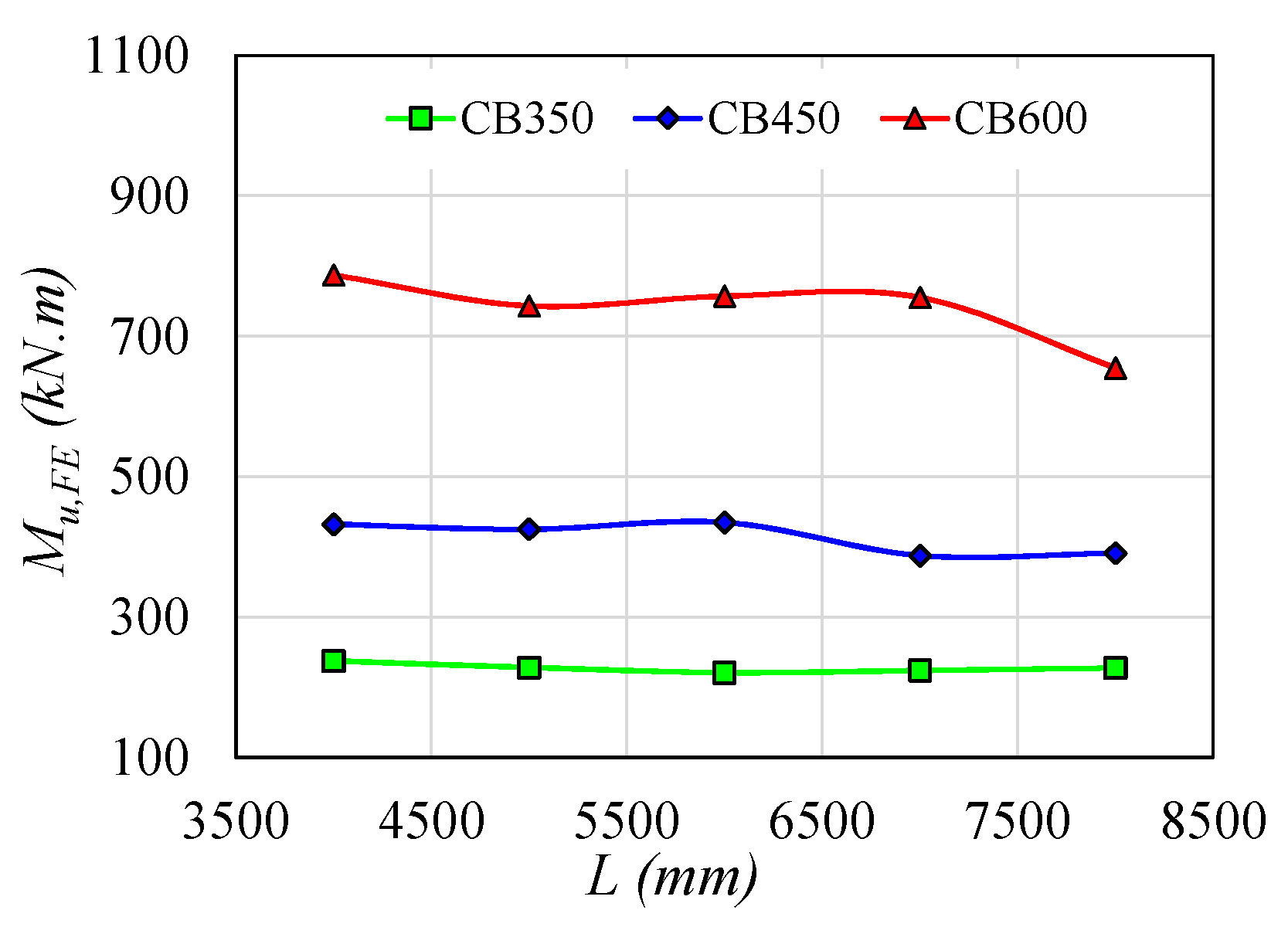
Finally,
Figure 22 shows the LDB ultimate moment values for models with A572-GR50 steel and 8 mm reinforcement bars. The results show that the unrestricted length variation does not significantly influence the LDB ultimate moment value, a situation also observed by Rossi et al. [
1]. It is verified in
Figure 22 that the preponderant factor in the LDB ultimate moment values is the I-section geometric properties.
The results presented show that the standard procedures are still flawed in determining the LDB strength of SCCB under the action of the hogging moment. The influence of parameters not previously investigated was presented, such as the I-section steel type and a considerable variation in the longitudinal reinforcement area in the effective width of the concrete slab. The investigation of these factors showed flaws until then not observed, in the standard procedures such as EC4 [
13] and NBR8800:2008 [
15]. The comparison between the FE results and the analytical procedures, such as Zhou and Yan [
4] and Bradford [
29], shows that further investigations are still needed to fully understand the LDB phenomenon in SCCB. Thus, the results presented in this article can provide a reference for future research and specification reviews.