Simulation Framework for Detection and Localization in Integrated Sensing and Communication Systems
Abstract
1. Introduction
- A background on PLA, emphasizing the rationale behind the approach and revitalizing key elements from the existing literature.
- A description of the proposed PLA method’s essential elements, focusing on those utilized in previous technologies, including channel generation and Signal to Noise Ratio (SNR).
- Two sensing services are considered, target location and detection, whose algorithms are formulated as examples of the PLA method.
- An evaluation of the sensing algorithms’ performance, offering quantitative insights.
- The mentioned evaluation is used to abstract the performance metrics of the algorithms.
2. ISAC Physical Layer Abstraction
- Position accuracy or error: This refers to the closeness of the measured position of the target or user to its true position value. In other words, the mean positioning error in the horizontal plane or 2D reference plane can also be considered the error on the vertical axis (i.e., the altitude). This KPI ensures that the data and results are trustworthy and can be used confidently.
- False alarm probability: This describes the conditional probability of falsely detecting the presence of a target object or environment when the target object or environment is not present.
- Detection probability: Conversely, the detection probability is the conditional probability of correctly detecting the presence of a target when the target is indeed present.
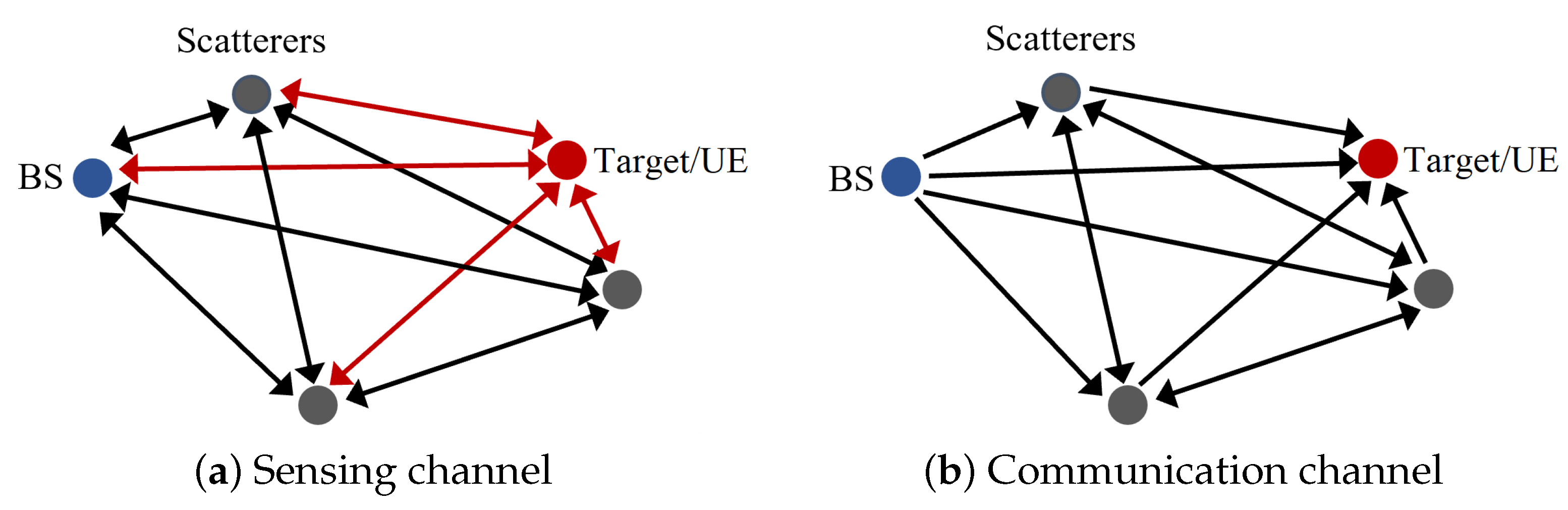
3. Main Elements of Abstraction: Channel and SNR Generation
4. Sensing Algorithms Generation: Target Detection and Localization
4.1. Effective Sensing Channel Estimation
4.2. Distance and Angular Direction Estimation Algorithm
| Algorithm 1 Distance and angle estimation algorithm |
| Input: , , , L Output: , ,
end for
|
4.3. Position Estimation Algorithm
4.4. Target Detection Algorithm
| Algorithm 2 Target detection algorithm |
| Input: , Output: withTarget
|
5. Evaluation and Abstraction
5.1. Distance and Positioning Abstraction
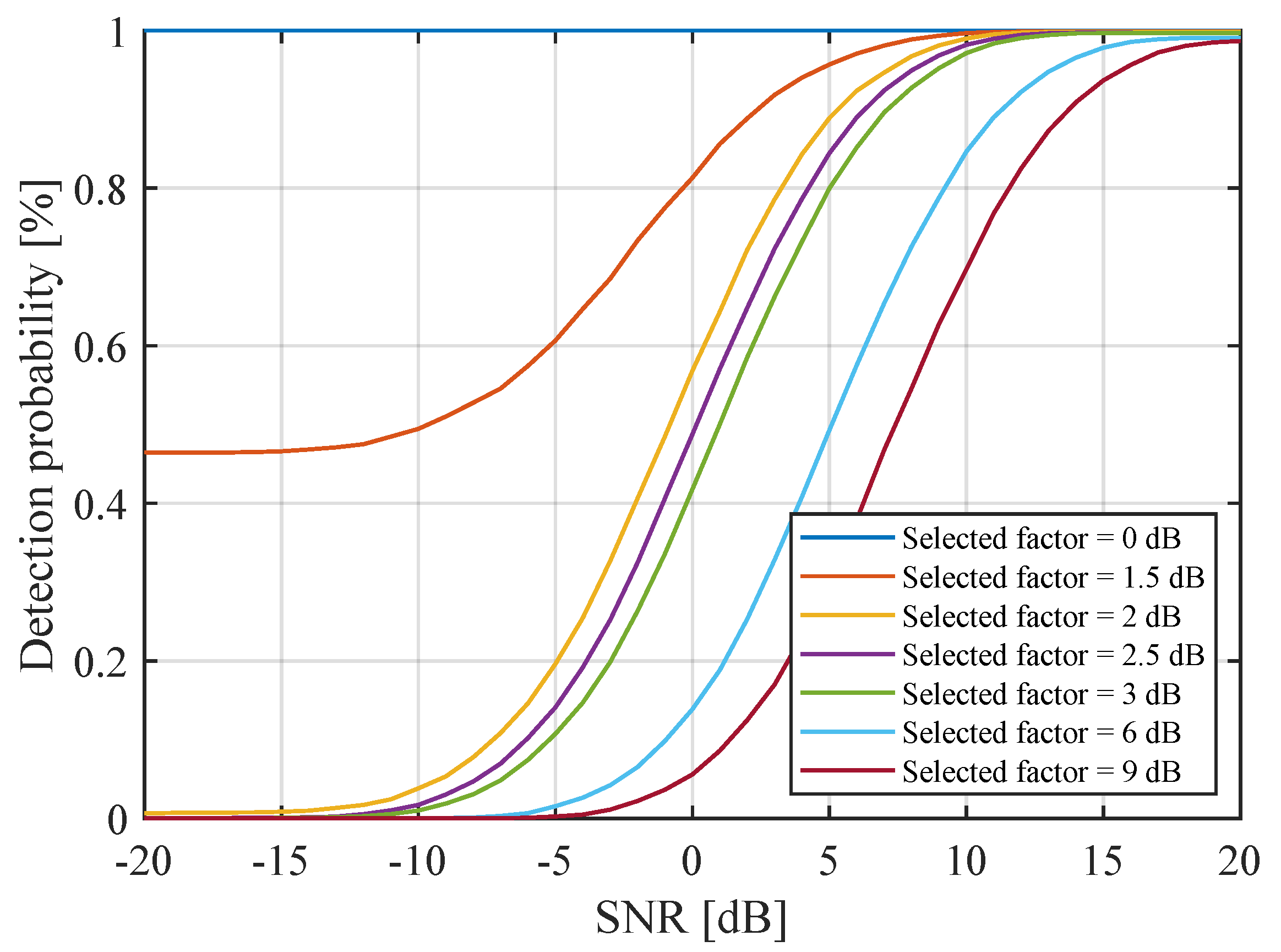
5.2. Target Detection Abstraction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pin Tan, D.K.; He, J.; Li, Y.; Bayesteh, A.; Chen, Y.; Zhu, P.; Tong, W. Integrated Sensing and Communication in 6G: Motivations, Use Cases, Requirements, Challenges and Future Directions. In Proceedings of the 2021 1st IEEE International Online Symposium on Joint Communications and Sensing, Dresden, Germany, 23–24 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, W.; Han, B.; Habibi, M.A.; Schotten, H.D. The road towards 6G: A comprehensive survey. IEEE Open J. Commun. Soc. 2021, 2, 334–366. [Google Scholar] [CrossRef]
- Ali, A.; Gonzalez-Prelcic, N.; Heath, R.W.; Ghosh, A. Leveraging Sensing at the Infrastructure for mmWave Communication. IEEE Commun. Mag. 2020, 58, 84–89. [Google Scholar] [CrossRef]
- Wei, Z.; Qu, H.; Jiang, W.; Han, K.; Wu, H.; Feng, Z. Iterative Signal Processing for Integrated Sensing and Communication Systems. IEEE Trans. Green Commun. Netw. 2023, 7, 401–412. [Google Scholar] [CrossRef]
- Rahman, M.L.; Zhang, J.A.; Huang, X.; Guo, Y.J.; Lu, Z. Joint communication and radar sensing in 5G mobile network by compressive sensing. IET Commun. 2020, 14, 3977–3988. [Google Scholar] [CrossRef]
- Zhang, Z.; He, R.; Ai, B.; Yang, M.; Li, C.; Mi, H.; Zhang, Z. A General Channel Model for Integrated Sensing and Communication Scenarios. IEEE Commun. Mag. 2023, 61, 68–74. [Google Scholar] [CrossRef]
- Calabuig, D.; Mrozowski, A.; Prado-Alvarez, D.; Monserrat, J.F.; Zhang, Y.; Yang, W.; Chen, Y.; Chen, Y. Stochastic Cluttered Environments for the Channel Modeling of ISAC Systems. In Proceedings of the 2023 IEEE Globecom Workshops (GC Wkshps), Lumpur, Malaysia, 4–8 December 2023; pp. 1195–1200. [Google Scholar] [CrossRef]
- Wang, H.; Hussain, F.; Wang, X.; Li, X.; Zhao, N.; Dev, K. Machine learning-enabled MIMO-FBMC communication channel parameter estimation in IIoT: A distributed CS approach. Digit. Commun. Netw. 2022, 9, 306–312. [Google Scholar] [CrossRef]
- Liu, Y.C.; Cheng, Y.B.; Pan, X.B.; Sun, Z.Z.; Pan, D.; Long, G.L. Quantum integrated sensing and communication via entanglement. Phys. Rev. Appl. 2024, 22, 034051. [Google Scholar] [CrossRef]
- ITU-R. Report ITU-R M.2516-0: Future Technology Trends of Terrestrial International Mobile Telecommunications Systems Towards 2030 and Beyond; Technical Report; ITU-R: Geneva, Switzerland, 2022. [Google Scholar]
- Ramos, A.; Mrozowski, A.; Prado-Alvarez, D.; Monserrat, J.F.; Zhang, Y.; Yu, Z.; Chen, Y. Evaluation Methodology for 6G Sensing-Assisted Communication System Performance. IEEE Access 2024, 12, 7841–7852. [Google Scholar] [CrossRef]
- ITU-R. Report ITU-R M.2412-0: Guidelines for Evaluation of Radio Interface Technologies for IMT-2020; Technical Report; ITU: Geneva, Switzerland, 2017. [Google Scholar]
- Chenand, L.; Chen, W.; Wang, B.; Zhang, X.; Chen, H.; Yang, D. System-level simulation methodology and platform for mobile cellular systems. IEEE Commun. Mag. 2011, 49, 148–155. [Google Scholar] [CrossRef]
- Lagen, S.; Wanuga, K.; Elkotby, H.; Goyal, S.; Patriciello, N.; Giupponi, L. New Radio Physical Layer Abstraction for System-Level Simulations of 5G Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- 3GPP. TS 22.137 (V1.0.0): Service Requirements for Integrated Sensing and Communication; Stage 1 (Release 19); Technical Report; 3GPP: Nice, France, 2023. [Google Scholar]
- Ramos, A.; Inca, S.; Ferrer, M.; Calabuig, D.; Roger, S.; Monserrat, J.F. Lookup Tables: “Physical Layer Abstraction of Detection and Localization Algorithms in ISAC Systems”. Repository Link. 2024. Available online: https://rb.gy/e9my7u (accessed on 1 October 2024).
- Olmos Bonafé, J.J.; Ruiz Boqué, S.; García Lozano, M.; Martín Sacristán, D. Link abstraction models based on mutual information for LTE downlink. In Proceedings of the 11th MCM of COST 2100, Athens, Greece, 31 May–1 June 2010. [Google Scholar]
- Hanzaz, Z.; Schotten, H.D. Performance evaluation of Link to system interface for Long Term Evolution system. In Proceedings of the 2011 7th International Wireless Communications and Mobile Computing Conference, Istanbul, Turkey, 4–8 July 2011; pp. 2168–2173. [Google Scholar] [CrossRef]
- Mezzavilla, M.; Miozzo, M.; Rossi, M.; Baldo, N.; Zorzi, M. A lightweight and accurate link abstraction model for the simulation of LTE networks in ns-3. In Proceedings of the 15th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems, New York, NY, USA, 21–22 October 2012; MSWiM’12. pp. 55–60. [Google Scholar] [CrossRef]
- Brueninghaus, K.; Astely, D.; Salzer, T.; Visuri, S.; Alexiou, A.; Karger, S.; Seraji, G.A. Link performance models for system level simulations of broadband radio access systems. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; Volume 4, pp. 2306–2311. [Google Scholar] [CrossRef]
- Ramos, A.; Keskin, M.F.; Wymeersch, H.; Inca, S.; Monserrat, J.F. Enhancing Sensing-Assisted Communications in Cluttered Indoor Environments Through Background Subtraction. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Huawei. 6G Integrated Sensing and Communication—Sensing-Assisted Environment Reconstruction and Channel Reconstruction; Technical Report 5; Communications of HUAWEI RESEARCH: Shenzhen, China, 2023. [Google Scholar]
- Huawei. Environment Reconstruction Based on Hybrid Aperture Sensing: Technologies and Applications; Technical Report 5; Communications of HUAWEI RESEARCH: Shenzhen, China, 2023. [Google Scholar]
- 3GPP. TR 38.901: Study on Channel Model for Frequencies from 0.5 to 100 GHz (Release 17); Technical Report; 3GPP: Nice, France, 2022. [Google Scholar]





| Simulation parameters | |
| Number of simulation seeds (J) | 30,000 |
| Number of scatterers | 30 |
| Number of OFDM symbols (L) | |
| Baseline evaluation configuration parameters | |
| Carrier frequency for evaluation | 30 GHz |
| Sampling frequency | 30.44 MHz |
| Number of sub-carriers (K) | 2048 |
| BS antenna height | 3 m |
| UE antenna height | 1.5 m |
| Total transmit power per TR × P | SNR dependent |
| SNR | |
| Additional parameters for system-level simulation | |
| Number of BS antenna elements (M) | 16 |
| Number of UE antenna elements | 1 |
| Hall size | 120 × 50 m |
| BS–UE distances (d) | 32 and 64 m |
| ISAC Channel model | Stochastic [7] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, A.; Inca, S.; Ferrer, M.; Calabuig, D.; Roger, S.; Monserrat, J.F. Simulation Framework for Detection and Localization in Integrated Sensing and Communication Systems. Telecom 2025, 6, 4. https://doi.org/10.3390/telecom6010004
Ramos A, Inca S, Ferrer M, Calabuig D, Roger S, Monserrat JF. Simulation Framework for Detection and Localization in Integrated Sensing and Communication Systems. Telecom. 2025; 6(1):4. https://doi.org/10.3390/telecom6010004
Chicago/Turabian StyleRamos, Andrea, Saúl Inca, Mireia Ferrer, Daniel Calabuig, Sandra Roger, and Jose F. Monserrat. 2025. "Simulation Framework for Detection and Localization in Integrated Sensing and Communication Systems" Telecom 6, no. 1: 4. https://doi.org/10.3390/telecom6010004
APA StyleRamos, A., Inca, S., Ferrer, M., Calabuig, D., Roger, S., & Monserrat, J. F. (2025). Simulation Framework for Detection and Localization in Integrated Sensing and Communication Systems. Telecom, 6(1), 4. https://doi.org/10.3390/telecom6010004







