The Classical Geometry of Chaotic Green Functions and Wigner Functions

Abstract

Semiclassical (SC) approximations for various representations of a quantum state are constructed on a single (Lagrangian) surface in the phase space but such surface is not available for chaotic systems. An analogous evolution surface underlies SC representations of the evolution operator, albeit in a doubled phase space. Here, it is shown that corresponding to the Fourier transform on a unitary operator, represented as a Green function or spectral Wigner function, a Legendre transform generates a resolvent surface as the classical basis for SC representations of the resolvent operator in the double-phase space, independently of the integrable or chaotic nature of the system. This surface coincides with derivatives of action functions (or generating functions) depending on the choice of appropriate coordinates, and its growth departs from the energy shell following trajectories in the double-phase space. In an initial study of the resolvent surface based on its caustics, its complex nature is revealed to be analogous to a multidimensional sponge. Resummation of the trace of the resolvent in terms of linear combinations of periodic orbits, known as pseudo orbits or composite orbits, provides a cutoff to the SC sum at the Heisenberg time. Here, it is shown that the corresponding actions for higher times can be approximately included within true secondary periodic orbits, in which heteroclinic orbits join multiple windings of relatively short periodic orbits into larger circuits.

1. Introduction

The semiclassical (SC) theory for unitary evolution of the states of a closed quantum system has quite a long continuing history, starting with studies by John Hasbrouck Van Vleck in 1928 [1] and proceeding to contemporary computations [2,3,4,5,6]. The SC theory is constructed on the corresponding evolution of privileged surfaces in the classical phase space. For instance, in the case of a position state $|\mathbf{q}\rangle$ with $\mathbf{q}=(q_1,...,q_L)$, the initial state $|{\mathbf{q}}_{-}\rangle$ corresponds to the L-dimensional plane $\mathbf{q}={\mathbf{q}}_{-}$ in the $2L$-dimensional phase space with points $\mathbf{x}=(\mathbf{q},\mathbf{p})$, where $\mathbf{p}$ denotes the state momentum. Driven by a Hamiltonian $\widehat{H}$, the initial state evolves in time (t) under the action of the evolution operator

$${\widehat{U}}_t=exp\left(-{\displaystyle \frac{it}{\hslash }}\widehat{H}\right),$$

(1)

(with ℏ the reduced Planck constant) corresponding to a continuous group of canonical transformations ${\mathbf{C}}_t$; that is, ${\mathbf{C}}_t:{\mathbf{x}}_{-}\mapsto {\mathbf{x}}_{+}$, generated by the classical Hamiltonian $H\left(\mathbf{x}\right)$ according to Hamilton’s equations.

The evolved classical surface ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{q}}_{-},{\mathbf{p}}_{-},t)$, corresponding to the evolved position state $|{\mathbf{q}}_{-}\left(t\right)\rangle$, is not generally considered to be a plane. However, even if the initial surface has a more complex topology, it preserves the Lagrangian property: the action for any reducible closed loop $\gamma$ on the surface is zero, i.e.,

$$S_{\gamma }={\oint }_{\gamma }\mathbf{p}·\mathrm{d}\mathbf{q}=0.$$

(2)

Furthermore, the surface is explicitly defined by the derivatives of a scalar generating function $S({\mathbf{q}}_{+},t)$:

$${\mathbf{p}}_{+}=\tilde{\mathbf{p}}({\mathbf{q}}_{-},{\mathbf{p}}_{-},t)={\displaystyle \frac{\partial S({\mathbf{q}}_{+},t)}{\partial {\mathbf{q}}_{+}}}.$$

(3)

Other examples are the eigenstates of integrable Hamiltonians, which, according to Arnold’s theorem, correspond to Lagrangian L-dimensional tori [7], so that the generating function and, hence, the projection (on the positioning plane $(\mathbf{p}=0)$ or any other Lagrangian plane) of those eigenstates are many-valued, with the sheets joined along caustics (see, e.g., [3]). On the other hand, no Lagrangian surface can be paired to the eigenstate of a classically chaotic system in the $2L$-dimensional phase space.

For this reason, the present SC theory reaches out into the double-phase space termed also the secondary phase space [8], whose elements are all ordered pairs of phase space points and, hence, encompasses all possible classical transitions. For example, a uniform translation of the regular phase space is represented by a Lagrangian plane in the double-phase space, which is transverse to the double-phase space plane that defines a canonical reflection through a phase space point. The points on these sets of planes can be used as conjugate coordinates for the double-phase space, which correspond, respectively, to the chord and center (Weyl) representations (see Appendix A). In contrast, planes $(\mathbf{q}={\mathbf{q}}_{+},\mathbf{q}={\mathbf{q}}_{-})$ and $(\mathbf{p}={\mathbf{p}}_{+},-\mathbf{q}={\mathbf{q}}_{-})$ are also Lagrangian coordinate planes, but they do not represent canonical transformations.

First, it is necessary to review the role of a general Lagrangian evolution surface in the double $4L$-dimensional phase space, which contains all pairs of points connected in a given time by the canonical transformation generated by the Hamiltonian. It is the backbone of SC approximations of the unitary evolution operator. Then, this paper goes on to present the Lagrangian resolvent surface in a doubled phase space, composed of all pairs of points connected by trajectory segments in a given energy shell $H\left(\mathbf{x}\right)=E$. This, in turn, corresponds to the energy-dependent resolvent operator

$${\widehat{U}}_E={[\widehat{H}-E\widehat{I}]}^{-1}=\sum _n{\displaystyle \frac{|n\rangle \langle n|}{E_n-E}}={\displaystyle \frac{1}{2\pi \hslash }}{\int }_{-\infty }^{\infty }\mathrm{d}texp\left({\displaystyle \frac{i}{\hslash }}Et\right){\widehat{U}}_t,$$

(4)

where n numbers the state and $\widehat{I}$ is the unity operator.

The poles of the resolvent operator lie on the eigenergies of $\widehat{H}$; that is,

$$\mathrm{tr}{\widehat{U}}_E=\sum _n{\displaystyle \frac{1}{E_n-E}},$$

(5)

and the residues are the projectors onto its eigenstates. Thus, all actually needed is to construct a SC approximation on this unexplored $2L$-dimensional Lagrangian surface, in analogy to the SC representations of states in terms of L-dimensional Lagrangian surfaces. Even though this is considerably more complex than the integrable case, this surface is obtained locally by $2L$ derivatives of various generating functions in related coordinate systems of the double-phase space.

Considering that the resolvent operator is the Fourier transform of the evolution operator, it is only natural that the resolvent surface arises in the SC theory through the Legendre transformation of the evolution surface. This is implicit in the local SC derivation of the phase of the resolvent operator as an action or generating function, but it does not seem to have yet been brought to the fore geometrically. Actually, the most straightforward grasp on the $2L$-dimensional resolvent surface is to follow of its growth from the $(2L-1)$-dimensional energy shell within the initial identity plane $H\left({\mathbf{x}}_{+}\right)=H\left({\mathbf{x}}_{-}\right)=E$ by following in time all its trajectories ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{q}}_{-},{\mathbf{p}}_{-},t)$. In spite of growing complexity of the surface, it is a single smooth surface for all time (the finite time cutoffs of the resolvent surface already support the SC approximation of energy-smoothed Green function and Wigner functions). In this paper, it is shown that the initially ’cylindrical extension’ of the energy shell into the double-phase space eventually develops folds along each of periodic orbits (POs) of the space.

Here and throughout the paper, all the POs of chaotic systems are assumed to be isolated and hyperbolic, endowed with stable and unstable manifolds composed of orbits, which approach the PO asymptotically as $t\to \infty$ or $t\to -\infty$, respectively. In reality, there often may exist tiny islands centered on elliptic orbits, but those islands are not considered here. The stable and unstable manifolds of the same PO (or different POs) intersect along homoclinic orbits (or heteroclinic orbits), forming a dense net of connections among the multitude of POs. It is argued here that each closed loop formed by these connections, joined to arbitrary numbers of windings among each of the internal POs in the given circuit, is quite close to a bona fide secondary periodic orbit. Each of these windings is also responsible for a fold in the resolvent surface as the period of a winding is reached. Furthermore, relatively short open orbits, which contribute to the Green function and the Wigner function, also come arbitrarily close to these circuits with their multiple windings, which can also be included in secondary open orbits.

In the limit of relatively large windings for all component POs of a secondary PO, the contribution to the total action from the secondary PO windings may be identified with the action of a pseudo orbit [9,10] or composite orbit [11,12] that, so far in the literature, has only been a construction for the resummation of the resolvent in terms of spectral determinants. Thus, one can now reinterpret these collective and apparently disjoint PO contributions to the resolvent as a resummation of secondary POs that are already present in representations of the resolvent operator and its trace.

Section 2 introduces the employment of double-phase space in the SC approximation of unitary operators, presenting the evolution surface. Then, the Legendre transform, corresponding hlsemiclassically to the Fourier transform between the evolution operator and the resolvent operator, generates the resolvent surface as shown in Section 3. Section 4 then discusses the various representations of the resolvent operator, corresponding semiclassically to different choices of canonical coordinate planes in double-phase space. Special attention is bestowed on the Wigner–Weyl representation (see Appendix A), in which the basic double-phase space coordinate plane coincides with the identity plane, from which the resolvent surface grows. Then, the example of a system with a single degree of freedom is examined in Section 5. While considering the special case of integrable systems in Appendix B, Section 6 then studies the multi-folded resolvent surface of a chaotic system. Finally, Section 7 and Section 8 present the secondary periodic orbits and their presence in representations of the resolvent operator and its trace.

2. Review of the Double-Phase Space Scenario for Unitary Operators

Time-dependent unitary operators that act on quantum states in Hilbert space correspond classically to evolving canonical phase space transformations. In the case of motion generated by a constant Hamiltonian operator, $\widehat{H}$, the continuous group of unitary operators (1) transport Hilbert space vectors $|{\psi }_t\rangle ={\widehat{U}}_t|{\psi }_0\rangle$ linearly. The various representations of unitary operators correspond semiclassically to different generating functions, which determine the phase of corresponding quantum propagators. The Schrödinger equation for ${\widehat{U}}_t$, for example, in either the position, momentum, or the Weyl–Wigner representations, are matched to corresponding versions of the Hamilton–Jacobi equation (see, e.g., [3]).

It might seem perverse to double the phase space of classical mechanics, which is already a doubling of the position space. Nonetheless, here, one is representing operators, commonly represented by both bra and ket spaces, so it is not unexpected that classical correspondence generally calls for a doubled classical space. Observables are deceptively simple in this sense (see, e.g., [13]; but, corresponding to unitary transformations, there arises an attractive and simple enough geometrical picture for canonical transformations, ${\mathbf{C}}_t:{\mathbf{x}}_{-}\to {\mathbf{x}}_{+}$, defined in the original phase space. Indeed, the canonical property demands that all closed curves, ${\gamma }_{-}$, be mapped onto closed curves, ${\gamma }_{+}$, such that

$${\oint }_{{\gamma }_{-}}{\mathbf{p}}_{-}·\mathrm{d}{\mathbf{q}}_{-}={\oint }_{{\gamma }_{+}}{\mathbf{p}}_{+}·\mathrm{d}{\mathbf{q}}_{+}.$$

(6)

Therefore, the definition of the double-momentum space, $\mathbf{P}=(-{\mathbf{p}}_{-},{\mathbf{p}}_{+})$, and double positions, $\mathbf{Q}=({\mathbf{q}}_{-},{\mathbf{q}}_{+})$, allows us to reinterpret the canonical condition as

$${\mathsf{\Xi }}_{\Gamma }\equiv {\oint }_{\Gamma }\mathbf{P}·\mathrm{d}\mathbf{Q}=0,$$

(7)

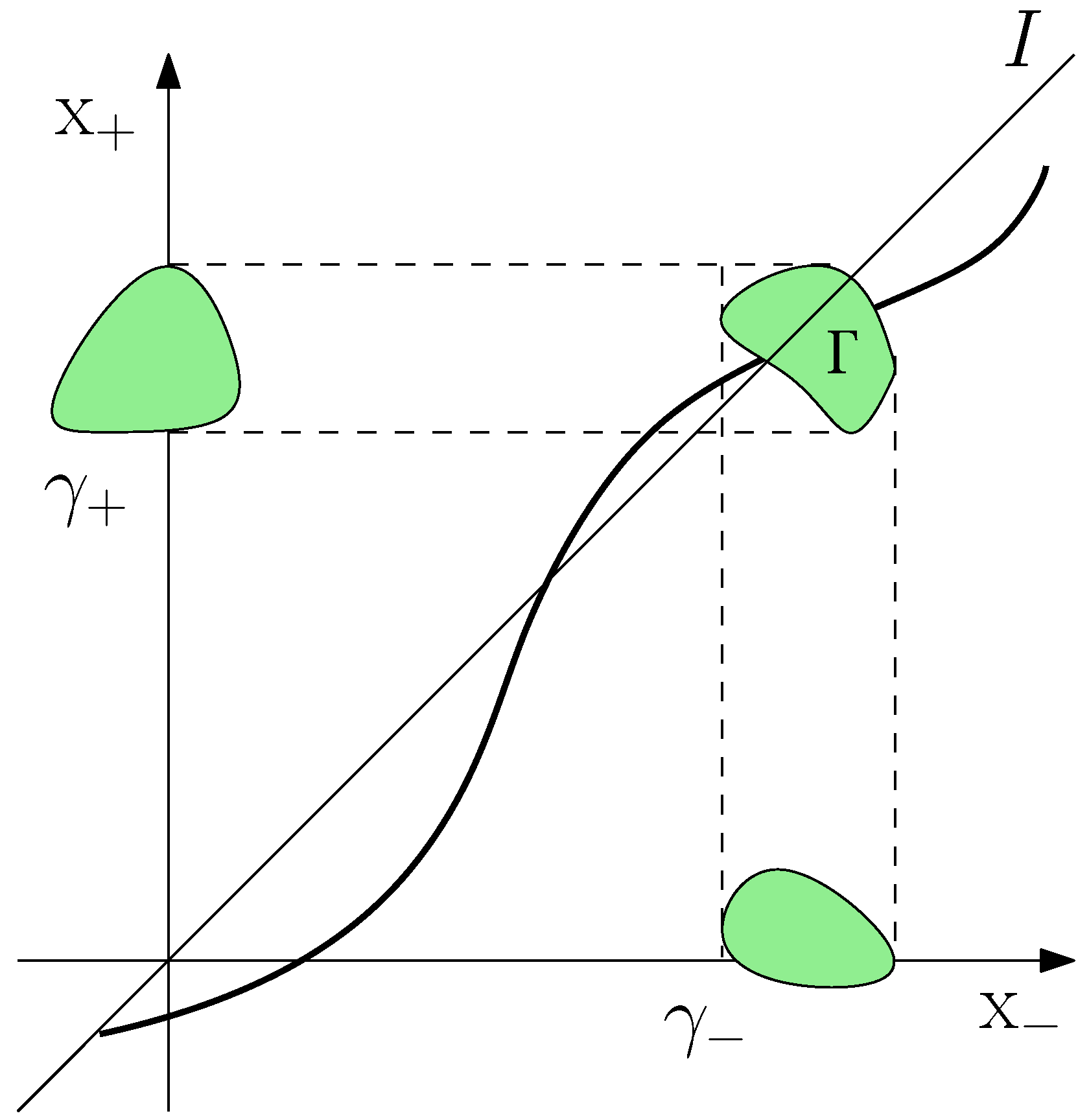
where $\Gamma =({\gamma }_{-},{\gamma }_{+})$. These are arbitrary closed curves on the $2L$-dimensional surface defined by the one-to-one function, ${\mathbf{x}}_{+}={\mathbf{C}}_t\left({\mathbf{x}}_{-}\right)$, within the $4L$-dimensional double-phase space $\mathbf{X}=(\mathbf{P},\mathbf{Q})$. Figure 1 provides a two-dimensional portrayal of the double-coordinate system.

The action (7) or symplectic area, ${\mathsf{\Xi }}_{\Gamma }=0$, for any closed curve drawn on the surface that defines the canonical transformation, ${\mathbf{C}}_t$, signifies that canonical transformations are described by $2L$-dimensional Lagrangian evolution surfaces [14] in the $4L$-dimensional double-phase space. This Lagrangian property allows us to define a function locally:

$$t\left(\mathbf{Q}\right)={\int }_{{\mathbf{Q}}_0}^{\mathbf{Q}}{\mathbf{P}}_t\left(\mathbf{Q}\right)·\mathrm{d}\mathbf{Q},$$

(8)

which is independent of the path followed in the $2L$-dimensional position–coordinate plane between ${\mathbf{Q}}_0$ and $\mathbf{Q}$, similar to the one-phase-space action

$$S\left(\mathbf{q}\right)={\int }_{{\mathbf{q}}_0}^{\mathbf{q}}\mathbf{p}\left(\mathbf{q}\right)·\mathrm{d}\mathbf{q}.$$

(9)

In turn, the generating Function (8) defines the given evolution surface by the following equations:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial {\mathsf{\Xi }}_t}{\partial \mathbf{Q}}}={\mathbf{P}}_t\left(\mathbf{Q}\right)\mathrm{or}{\displaystyle \frac{\partial {\mathsf{\Xi }}_t}{\partial {\mathbf{q}}_{+}}}={\mathbf{p}}_{+},{\displaystyle \frac{\partial {\mathsf{\Xi }}_t}{\partial \mathbf{q}-}}=-{\mathbf{p}}_{-},\end{array}$$

(10)

which implicitly determine the canonical transformation [7,15]. Furthermore, one obtains the energy of the trajectory segment as $\partial {\mathsf{\Xi }}_t/\partial t=E$.

Though the mapping ${\mathbf{C}}_t:{\mathbf{x}}_{-}\to {\mathbf{x}}_{+}={\mathbf{C}}_t\left({\mathbf{x}}_{-}\right)$ is necessarily univalued, no such restriction results on the function ${\mathbf{P}}_t\left(\mathbf{Q}\right)$, defined by the same evolution surface (generating functions using ${\mathbf{x}}_{-}$ or ${\mathbf{x}}_{+}$ cannot be defined as independent variables because neither of the planes ${\mathbf{x}}_{\pm }=0$ represent the Lagrangian in the double-phase space). What is allowed and often considered is to apply linear canonical transformation $\mathbf{X}\to {\mathbf{X}}^{\prime }$ to the double-phase space, which leaves the Lagrangian property invariant for any surface, including ${\mathbf{P}}^{\prime }=0$. Then, one may define a new generating function in the new variable, such that the invariant evolution surface is represented locally as ${\mathbf{P}}_t^{\prime }\left({\mathbf{Q}}^{\prime }\right)=\partial {\mathsf{\Xi }}_t^{\prime }/\partial {\mathbf{Q}}^{\prime }$.

All the commonly used generating functions [15] are obtained by the application of canonical ${90}^{\circ }$ rotations to single-phase spaces, ${\mathbf{q}}_{\pm }\to {\mathbf{p}}_{\pm }$, separately or in combination. There exist other unlimited possibilities in double-phase space [16], but, here, only special Wigner–Weyl canonical variables are concerned. So, recalling the skew product,

$$\mathbf{x}\wedge {\mathbf{x}}^{\prime }=\sum _{n=1}^L(p_l{q}_l^{\prime }-q_l{p}_l^{\prime })=J\mathbf{x}·{\mathbf{x}}^{\prime },$$

(11)

which also defines the skew symplectic matrix J. Then, the new canonical variables X → (Q’,P’) = (x,y) is constructed in the double-phase space:

$$\begin{array}{c}\hfill {\mathbf{Q}}^{\prime }=\mathbf{x}={\displaystyle \frac{{\mathbf{x}}_{+}+{\mathbf{x}}_{-}}{2}},{\mathbf{P}}^{\prime }=\mathbf{y}=J{\mathbf{x}}_{+}-{\mathbf{x}}_{-})=J\xi ,\end{array}$$

(12)

where x is the center and ξ is the chord of the transformation. Instead of the 90 ° rotations just above, Equation (12) describes rather a 45° rotation in the double-phase space. The plane y = 0 (or ξ = 0) specifies the identity transformation, I, which corresponds to the Lagrangian identity plane shown in Figure 1. Actually, all planes y = const. represent uniform translations T_ξ of the vector −Jy = ξ, whereas each plane defined by a constant x identifies the reflection R_x : x₋ → x₊ = −x₋ + 2x. Unlike the Lagrangian plane (q₋, q₊), the planes y = 0 and x = 0 can be considered as phase spaces on their own: the space of reflection centers (Weyl space) and the space of translation chords (there are definite advantages of defining ξ as a half chord, such as in Ref. [17], but that then involves an adaptation from most of the papers by the author).

However, one should remember that the planes are Lagrangian as far as the double-phase space action ${\mathsf{\Xi }}_t$ is concerned. Therefore, mapping ${\mathbf{C}}_t$ implicitly defines the local evolution surface as the function $\mathbf{y}(\mathbf{x},t)$ in terms of the generating function $\%S{\mathsf{\Xi }}_t\left(\mathbf{x}\right)$ (alternatively, the generating function $X{i}_t\left(\mathbf{y}\right)$ can be defined such that $\mathbf{x}(\mathbf{y},t)=\partial {\mathsf{\Xi }}_t/\partial \mathbf{y}$, corresponding to an analogously defined chord-generating function [13]):

$$\mathbf{y}(\mathbf{x},t)=J{\mathsf{\xi }}_t\left(\mathbf{x}\right)={\displaystyle \frac{\partial {\mathsf{\Xi }}_t}{\partial \mathbf{x}}}.$$

(13)

${\mathsf{\Xi }}_t\left(\mathbf{y}\right)$ can be defined ${\mathsf{\Xi }}_t/\partial \mathbf{y}$, corresponding to an analogously defined chord-generating function [13].

It is essential to point out that in this context, the Lagrangian $\mathbf{x}$-plane registers the centers of pairs of points ${\mathbf{x}}_{\pm }$, fully determined by the chord $\mathsf{\xi }\left(\mathbf{x}\right)$ according to Equation (12). For this reason, here, it is preferable to refer to the center plane rather than to the identity plane. In particular, a full return with $\mathsf{\xi }=0$; that is, $\mathbf{x}={\mathbf{x}}_{+}={\mathbf{x}}_{-}$ only occurs if ${\mathbf{x}}_{-}$ lies on a periodic trajectory.

The evolution surface is generated continuously by the Schrödinger double-phase space classical Hamiltonian [8]

$$IH\left(X\right)=IH(\mathbf{x},\mathbf{y})=H(\mathbf{x}-\mathrm{J}\mathbf{y}/2)=H\left(x_{+}\right),$$

(14)

which shifts ${\mathbf{x}}_{+}$ forward in time from the initial surface ${\mathbf{x}}_{+}=\mathbf{I}\left({\mathbf{x}}_{-}\right)={\mathbf{x}}_{-}=\mathbf{x}$, while keeping ${\mathbf{x}}_{-}$ fixed (earlier studies dealt with an alternative Heisenberg double-phase space Hamiltonian, corresponding to super-operators driving the evolution of quantum operators [17,18]). Hence, the trajectory from the initial to the final point is ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t)$, whereas the trajectory in the double-phase space is $\tilde{\mathbf{X}}\left(t\right)=(\tilde{\mathbf{x}}({\mathbf{x}}_{-},t),{\mathbf{x}}_{-})$. As noted just above, the initial surface is just the Weyl coordinate surface $\mathbf{y}=0$, that is, for quite short times, the evolution surface $\mathbf{y}(\mathbf{x},t)$ remains a one-to-one function. For long enough times, this surface may fold in various ways so that it is expressed in an action function ${\mathsf{\Xi }}_t\left(\mathbf{x}\right)$ with a number of branches, which also arise in other possible classical representations $\mathbf{P}(\mathbf{Q},t)$ of the evolution surface. On the other hand, the feature that the evolution surface is diffeomorphic to the identity plane ensures that no wrappings or handles develop on the evolution surface itself.

3. Extended Double-Phase Space

The evolution surface contains all pairs of points in the double-phase space, which are joined by a trajectory segment in the time t; that is, ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t)$. Since each segment has the constant energy $H\left({\mathbf{x}}_{-}\right)=H\left({\mathbf{x}}_{+}\right)=E$, one may consider that the evolution surface is the time slice of a full $(2L+1)$-dimensional extended evolution surface in the $2(2L+1)$-dimensional space by supplementing double phase space with the canonical variables t and E [7]. The extended evolution surface is defined by the trajectory segments of all durations t and all energies E.

It is then conceivable to choose the energy E as the free variable, with the dependent time $t=t({\mathbf{x}}_{-},E)$ for each point on the extended surface. Furthermore, one may then consider constant energy slices, even if the resulting surface, being composed of all pairs of points ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},E)$ irrespective of the time, need not have the simplified topology deduced for the evolution surface. Then, even if the surface has a number of branches, one can locally derive the energy action as a Legendre transform of the action (8) in time:

$${\mathsf{\Xi }}_E\left(\mathbf{Q}\right)={\mathsf{\Xi }}_t\left(\mathbf{Q}\right)-tE,$$

(15)

with $t\left(E\right)$ determined by

$${\displaystyle \frac{\partial {\mathsf{\Xi }}_t}{\partial t}}\left(\mathbf{Q}\right)=E$$

(16)

for each branch. Similar to Definition (8), the Expression (15) is also a generating function, implicitly defining the local transformation on the energy shell in the same form as Equation (10); that is, for $\mathbf{Q}=({\mathbf{q}}_{-},{\mathbf{q}}_{=})$, the derivatives of the energy action provide the corresponding momenta:

$$\mathbf{P}(\mathbf{Q},E)={\displaystyle \frac{\partial {\mathsf{\Xi }}_E}{\partial \mathbf{Q}}}\left(\mathbf{Q}\right).$$

(17)

Likewise, for the alternative choice ${\mathbf{Q}}^{\prime }=\mathbf{x}$, the derivative of the corresponding generating function is the chord $\xi (\mathbf{x},E)$ of the trajectory segment of energy E centered around $\mathbf{x}$. On the other hand, the duration of the same segment determined by $(\mathbf{Q},\mathbf{P})$ or $({\mathbf{Q}}^{\prime },{\mathbf{P}}^{\prime })$ reads

$${\displaystyle \frac{\partial {\mathsf{\Xi }}_E}{\partial E}}\left(\mathbf{Q}\right)=t\mathrm{or}{\displaystyle \frac{\partial {\mathsf{\Xi }}_E}{\partial E}}\left(\mathbf{x}\right)=t.$$

(18)

The $2L$-dimensional manifold, which is represented by Equation (17) in each Lagrangian coordinate system, to be referred to as the resolvent surface because of its quantum manifestation in in Section 4 to distinguish this manifold from the mere tensor product of the pair of energy shells, $H({\mathbf{x}}_{\pm }=E)$. The latter contains all pairs of points in the regular shell $H\left(\mathbf{x}\right)=E$ and is $2(2L-1)$-dimensional. Certainly, this includes the $2L$-dimensional resolvent surface of pairs of points connected by a trajectory segment of energy E. Indeed, given that all segments in the regular energy shell are included, one can follow the growing resolvent surface from the single $(2L-1)$-dimensional energy shell on the identity plane: $H\left({\mathbf{x}}_{+}\right)=H\left({\mathbf{x}}_{-}\right)=E$ at $t=0$. Then, for extremely short times $t^{\prime }$, the resolvent is a cylinder with a spherical base:

$${\mathbf{x}}_{+}={\mathbf{x}}_{-}+t^{\prime }{\dot{\mathbf{x}}}_{+}\left[H({\mathbf{x}}_{+}={\mathbf{x}}_{-}=\mathbf{x})=E\right]=t^{\prime }J\frac{\partial H}{\partial \mathbf{x}}{|}_{H\left(\mathbf{x}\right)=E},$$

(19)

where the dot on the top denotes the t-derivative. The smooth elongation over time of the continuum of trajectories that compose it cannot change this basic topology, regardless of how intricately the resolvent surface folds itself.

The development of the resolvent surface from this seed is given further in Section 5 and Section 6. For now, one just notes that the distinction with respect to the product of two shells becomes dramatic for the set of initial points lying on a periodic orbit: their participation in the resolvent surface is restricted to a two-dimensional torus, regardless of the number of degrees of freedom, that is, if ${\mathbf{x}}_{-}$ belongs to a periodic orbit, no point ${\mathbf{x}}_{+}$ outside this orbit can pair with the initial point in the resolvent surface.

A further general property of the resolvent surface is that it must touch the identity plane at all periodic points ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},k\tau )$; that is, even though a periodic orbit wanders off into the double-phase space, the orbit must return to the identity plane at multiples of its period $\tau$. Neighboring points that are not initially on this periodic orbit do not touch the identity plane any more unless their orbit is also periodic. In all cases, regardless of the complexity of the sheets of the resolvent surface, all its returns to the identity plane must lie on its energy shell $H({\mathbf{x}}_{+}={\mathbf{x}}_{-}=\mathbf{x})=E$. This special role of the identity plane provides the canonical center and chord variables $\mathbf{X}=(\mathbf{x},\mathsf{\xi })$, priviledged role in the description of the resolvent surface.

4. Propagators, Green Functions, and Wigner Functions

Quantum operators form a Hilbert space of Hilbert–Schmidt operators with the scalar product [19,20]

$$\langle \langle A|B\rangle \rangle =\mathrm{tr}{\widehat{A}}^{†}\widehat{B},$$

(20)

defined in terms of the adjoint operator, ${\widehat{A}}^{†}$. Then, in this notation, the trace of an operator is the scalar product with the identity operator $\widehat{I}$ is

$$\mathrm{tr}\widehat{A}=\langle \langle I|A\rangle \rangle .$$

(21)

Each foliation of the double-phase space by parallel Lagrangian planes corresponds to a possible operator representation. Perhaps the most common representation relies on dyadic operators, $\langle \langle \mathbf{Q}|=|{\mathbf{q}}_{-}\rangle \langle {\mathbf{q}}_{+}|$, so that

$$\langle \langle \mathbf{Q}|A\rangle \rangle =\langle {\mathbf{q}}_{+}|\widehat{A}|{\mathbf{q}}_{-}\rangle =\mathrm{tr}|{\mathbf{q}}_{-}\rangle \langle {\mathbf{q}}_{+}|\widehat{A},$$

(22)

where the Lagrangian planes are just $\mathbf{Q}=({\mathbf{q}}_{-},{\mathbf{q}}_{+})=\mathrm{const}$. From this, one turns to momentum or various mixed representations through Fourier transformations, corresponding to ${90}^{\circ }$ rotations in the double-phase space, $\{\mathbf{X}=(\mathbf{P},\mathbf{Q})\}\mapsto \{{\mathbf{X}}^{\prime }=({\mathbf{P}}^{\prime },{\mathbf{Q}}^{\prime })\}$. As described in Appendix A, the Wigner–Weyl representation, based on the self-adjoint operator, ${\widehat{R}}_{\mathbf{x}}$, then corresponds to the double-phase space rotation (12) so that, for ${\mathbf{Q}}^{\prime }=\mathbf{x}$,

$$\langle \langle {\mathbf{Q}}^{\prime }|A\rangle \rangle =2^L\mathrm{tr}{\widehat{R}}_{\mathbf{x}}\widehat{A}=A\left(\mathbf{x}\right),$$

(23)

and the Lagrangian basis in the double-phase space is the reflection plane, $\mathbf{x}=\mathrm{const}$. The Fourier transformation (A8) then introduces the translation operator, whose adjoint is ${\widehat{T}}_{-\mathsf{\xi }}$. This is represented in the double-phase space by the new Lagrangian plane, $P^{\prime }=\mathbf{y}=J\mathsf{\xi }=\mathrm{const}.$, so that

$$\langle \langle {\mathbf{P}}^{\prime }|A\rangle \rangle =\mathrm{tr}{\widehat{T}}_{-\mathsf{\xi }}\widehat{A}=A\left(\mathsf{\xi }\right).$$

(24)

In each case, the representation in terms of a set of Lagrangian planes, ${\mathbf{Q}}^{\prime }$, is complementary to the conjugate representation in terms of ${\mathbf{P}}^{\prime }$, which is obtained by a Fourier transform. Even though the trace (21) remains invariant, it assumes different forms in each representation. For example,

$$\begin{array}{cc}\hfill \mathrm{tr}\widehat{A}& =\int \mathrm{d}\mathbf{Q}\langle \langle I|\mathbf{Q}\rangle \rangle \langle \langle \mathbf{Q}|A\rangle \rangle =\int \mathrm{d}{\mathbf{q}}_{-}\mathrm{d}{\mathbf{q}}_{+}\delta ({\mathbf{q}}_{+}-{\mathbf{q}}_{-})\langle {\mathbf{q}}_{+}\left|A\right|{\mathbf{q}}_{-}\rangle \\ \hfill & =\int \mathrm{d}\mathbf{q}\langle \mathbf{q}\left|A\right|\mathbf{q}\rangle \mathrm{or}=\int \mathrm{d}\mathbf{x}A\left(\mathbf{x}\right),\end{array}$$

(25)

where $\delta (a-b)$ is the Dirac delta function. See further discussion in Ref. [21].

The evolution operator (1) is represented by various propagators, $\langle \langle {\mathbf{Q}}^{\prime }|U_t\rangle \rangle$. Each of these propagators is identified in terms of regular phase space variables, such as the position propagator $\langle \langle \mathbf{Q}|U_t\rangle \rangle =\langle {\mathbf{q}}_{+}|U_t|{\mathbf{q}}_{-}\rangle$ or the Weyl propagator $U_t\left(\mathbf{x}\right)$. For each propagator, the SC approximation assumes the standard form:

$$\langle \langle {\mathbf{Q}}^{\prime }|U_t\rangle \rangle \approx \sum _j{A}_{t,j}\left({\mathbf{Q}}^{\prime }\right)exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{t,j}\left({\mathbf{Q}}^{\prime }\right)+i\theta \right],$$

(26)

where the summation index j labels all the conjugate points in the possibly different branches of the evolution surface ${\mathbf{P}}_{t,j}^{\prime }\left({\mathbf{Q}}^{\prime }\right)$; for instance, all the pairs of momenta ${\mathbf{p}}_{\pm }$ for trajectory segments between ${\mathbf{Q}}^{\prime }={\mathbf{q}}_{\pm }$ or all $\mathbf{y}=J\mathsf{\xi }$ for trajectory chords with tips centered around ${\mathbf{Q}}^{\prime }=\mathbf{x}$. Generally, the phase also includes Maslov indices [2] independent of ℏ, which is denoted here just as $\theta$ in all the formulae to follow. The amplitude of each term depends on the stability matrix ${\mathbf{M}}_{t,j}$ for the relevant trajectory segment, for example, the SC Weyl propagator is

$$U_t\left(\mathbf{x}\right)\approx \sum _j{\displaystyle \frac{2^L}{|det(1+{\mathbf{M}}_{t,j}\left(\mathbf{x}\right)){|}^{1/2}}}exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{t,j}\left(\mathbf{x}\right)+i\theta \right],$$

(27)

as reviewed in Ref. [13]. On the other hand, the SC approximation for the trace of the evolution operator becomes [22]

$$\langle \langle I|U_t\rangle \rangle =\mathrm{tr}\widehat{U}\left(t\right)\approx \sum _j{\displaystyle \frac{2^L}{|det[1-{\mathbf{M}}_{t,j}]{|}^{1/2}}}exp\left[{\displaystyle \frac{i}{\hslash }}{S}_{t,j}+i\theta \right],$$

(28)

where the sum is now taken over periodic orbits of period t [22]. The action $S_{t,j}={\mathsf{\Xi }}_{t,j}$ of the orbits, while denoting the double-space action over ${\mathbf{x}}_{+}$, does not depend on the particular representation.

Just as the Fourier transform in time of the evolution operator provides the resolvent operator (4), the Fourier transform of various representations of evolution operators by propagators provides energy-dependent Green functions or spectral Wigner functions, which can be defined in the general form

$$\langle \langle {\mathbf{Q}}^{\prime }|U_E\rangle \rangle ={\displaystyle \frac{1}{2\pi \hslash }}{\int }_{-\infty }^{\infty }\mathrm{d}texp\left[{\displaystyle \frac{i}{\hslash }}Et\right]\langle \langle {\mathbf{Q}}^{\prime }|U_t\rangle \rangle .$$

(29)

Inserting the SC approximation for propagators, the stationary phase evaluation of the time integral leads to a corresponding SC evaluation,

$$\langle \langle {\mathbf{Q}}^{\prime }|U_E\rangle \rangle \approx \sum _j{B}_{EJ}\left({\mathbf{Q}}^{\prime }\right)exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{Ej}\left({\mathbf{Q}}^{\prime }\right)+i\theta \right],$$

(30)

of the representation of the resolvent in terms of the energy action (15) for all j-trajectory segments on the E-shell with endpoints ${\mathbf{x}}_{\pm ,j}\left(E\right)$, represented in Lagrangian coordinates as ${\mathbf{P}}_j({\mathbf{Q}}^{\prime },E)$. This holds for all representations of the resolvent operator corresponding to conjugate Lagrangian planes in the double-phase space, which amount to different perspectives of the same resolvent surface. Expressed locally by Equation (17), the surface does not have the open structure of the evolution surface, so a simplified case of a single degree of freedom is considered in Section 5.

Concerning the invariant trace of the resolvent operator, the SC approximation resulting from a stationary phase approximation of the Fourier transform has oscillatory terms of the form

$$\mathrm{tr}{\widehat{U}}_E=\langle \langle I|U_E\rangle \rangle \approx \sum _j{C}_{Ej}exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{Ej}+i\theta \right],$$

(31)

summing over the POs in the E-shell, with their double action ${\mathsf{\Xi }}_{Ej}$, which equals the regular PO action $S_{EJ}$ in all representations. There is also a contribution from the limit of extremely short orbits, which varies smoothly with energy (see, e.g., [13,23]), but this is not considered in the current paper.

5. Resolvent Surface for One Degree of Freedom

In the case of the one-degree-of-freedom resolvent surface, the energy shell, $H\left(\mathbf{x}\right)=E$, for a Hamiltonian describing bound motion is a closed curve $\gamma$ in the two-dimensional phase space, which topologically represents a circle. Then, the trajectory ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t)$ follows the $\gamma$-curve, closes it in the period $\tau \left(E\right)$, and retraces it infinitely. Therefore, there are infinite trajectory segments for each pair of points on the curve: ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t+j\tau )$. These trajectory segments differ in action by k times the PO action:

$${\mathsf{\Xi }}_{E\mathrm{PO}}=S_{E\mathrm{PO}}={\oint }_{\gamma }{\mathbf{p}}_{+}·\mathrm{d}{\mathbf{q}}_{+}.$$

(32)

Since the initial point ${\mathbf{x}}_{-}$ remains fixed, the circle in the double-phase space traced by $\tilde{\mathbf{X}}\left(t\right)=({\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},2t),{\mathbf{x}}_{-})$ projects onto the ${\mathbf{x}}_{+}$-phase plane exactly as an regular PO. One obtains the same projection for any initial point on the PO so that the full resolvent surface, which contains all pairs of points connected by a trajectory segment, is the product of the pair of circles in the ${\mathbf{x}}_{\pm }$ planes, i.e., a two-dimensional torus. If one considers the pair of curves in both the initial and the final phase spaces, their double action cancels out according to Equation (7). Indeed, this full double-phase space curve, $\Gamma =({\gamma }_{-}=\gamma ,{\gamma }_{+}=\gamma )$, lies on the intersection of the resolvent surface and the evolution surface, which is always topologically a plane, so all such circuits have zero double action as they wind around the torus that is the resolvent surface.

Depending on the choice of Lagrangian coordinates, this torus is described by a function ${\mathbf{P}}^{\prime }\left({\mathbf{Q}}^{\prime }\right)$, which is not univalued. Indeed, choosing the position representation $\mathbf{Q}=(q_{-},q_{+})$, the projection onto this plane is a rectangle with four sheets, bounded by sides at the turning points where the $q_{\pm }$-components of the respective phase space velocities are zero, for instance, where the potential $V\left(q_{\pm }\right)=E$ for a regular particle Hamiltonian $H\left(\mathbf{x}\right)=p^2/2m+V\left(q\right).$ This is also the projection in the momentum representation ${\mathbf{Q}}^{\prime }=\mathbf{P}=(-p_{-},p_{+})$, but there may be more sheets generated by extra internal folds, for instance, where $dV/dq=0$, if the potential does not increase monotonically, so that the energy shell has a (classical) guitar shape.

Any symplectic (linear canonical) transformation in the double-phase space, $(\mathbf{P},\mathbf{Q})\mapsto ({\mathbf{P}}^{\prime },{\mathbf{Q}}^{\prime })$, determines alternative views of the resolvent torus, in which the projection singularities separating the sheets generally unfold into fold caustics between pairs of sheets, as described in Ref. [24]. Remarkably, the global singularity structure for the Wigner function, resulting from the transformation $(\mathbf{P},\mathbf{Q})\mapsto (\mathbf{x},\mathsf{\xi })$ in (12), represents the resolvent surface $\mathsf{\xi }\left(\mathbf{x}\right)$ with only two sheets for $\mathbf{x}$ close to the energy shell. As noted in Section 2, the points $\mathbf{x}$ are centers of chords, which have a double role: as true geometrical chords between a pair of points in the regular phase space, along with that of the double phase space variable $\mathbf{y}=J^{\left(\mathsf{\xi }\right)}$. There are two geometric chords for each center by merely exchanging their endpoints ${\mathbf{x}}_{\pm }$. The chords only coincide for $\mathbf{y}=J^{\left(\mathsf{\xi }\right)}=0$ on the shell at the identity plane itself where ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},k\tau )$, with $\tau$ as the period of the orbit.

In the double-phase space coordinates, the energy surface within the center or identity plane is a projection singularity of the resolvent surface since ${\mathbf{x}}_E\left(\mathsf{\xi }\right)$ is an even function and $\mathsf{\xi }=0$ within this plane, according to Equation (12). Thus, the pair of chords centered around $\mathbf{x}$ coalesce as this point approaches the shell from its interior. Starting from any point $\mathbf{x}\left(0\right)={\mathbf{x}}_{+}={\mathbf{x}}_{-}$ on the shell, the center $\mathbf{x}\left(t\right)$ follows ${\mathbf{x}}_{+}\left(t\right)=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t)$ to the interior of the shell, also describing a closed curve as the period is completed, though the chord $\mathsf{\xi }(\mathbf{x},t)=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t)-{\mathbf{x}}_{-}$ reverses its sign. 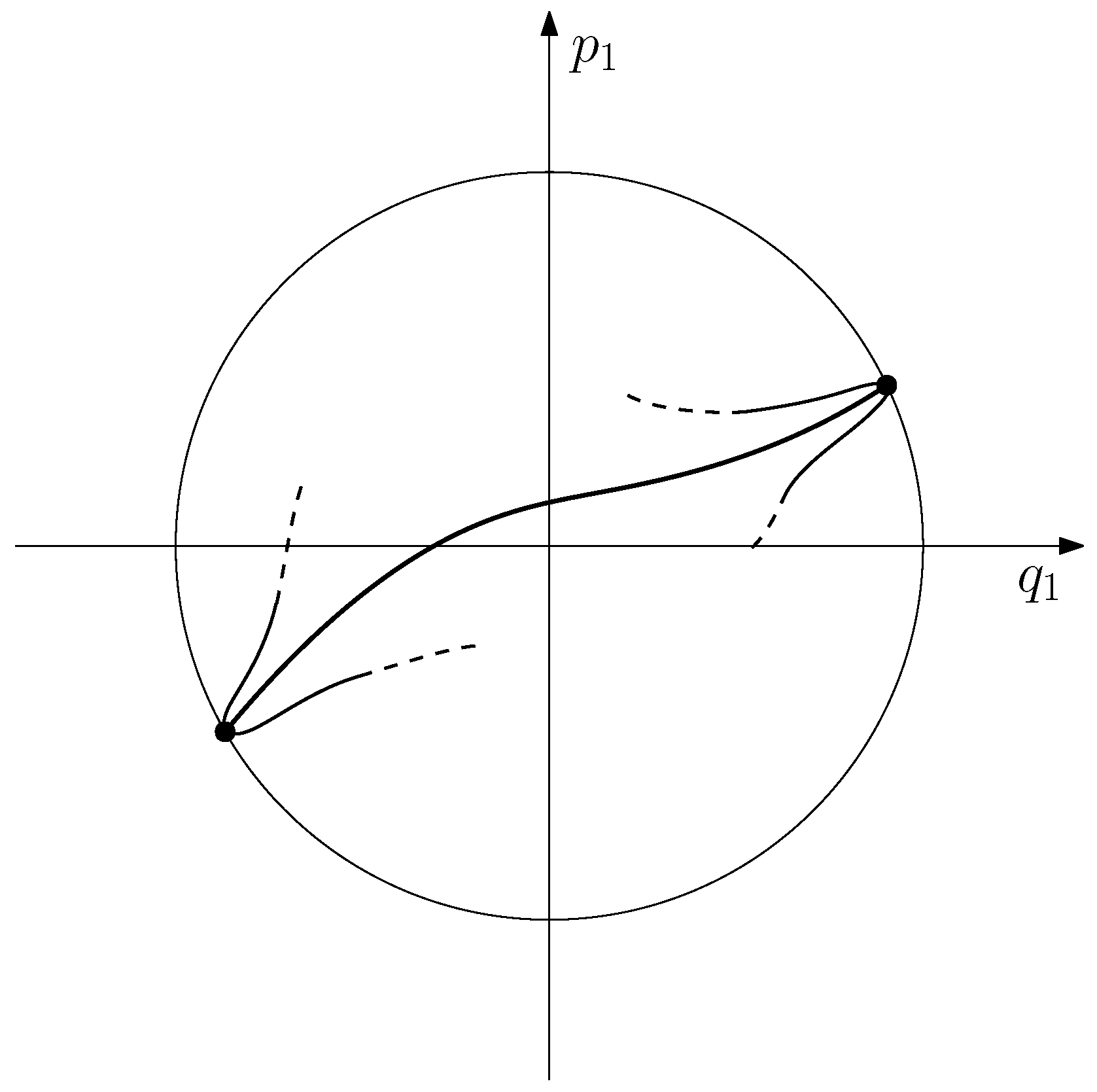For $\mathbf{x}$ far inside the shell, it becomes the center of relatively large chords stretching across this orbit and generically meets a cusped caustic island with three sheets in its interior. This configuration, shown in Figure 2, was not described in Ref. [24], but is present in Michael Berry’s original paper on SC Wigner functions [25].

Even though the resolvent torus has not been previously mentioned in the literature, its projection singularities are precisely the caustics where the SC approximation for various representations diverge; that is, an amplitude $B_{E,j}\left({\mathbf{Q}}^{\prime }\right)\to \infty$ in the sum (30). Strictly, these SC approximations concern representations of the resolvent, but the same formulae may be extended to a projector $|n\rangle \langle n|$, i.e., the residue of a pole in Equation (4). Heuristically, it is evident that only for an energy shell quantized by the SC Bohr–Sommerfeld rules can the sum over infinite repetitions of the trajectory segments add up in phase to produce the required pole. This argument can be further developed, though the final result, based just on single segments without repetitions, is rather straightforward in other approaches. In short, the SC caustic singularities of the representations of the resolvent for energies between its poles, as well as the residues at the poles, i.e., projectors, lie in the singularities of the projections of the resolvent surface onto each chosen Lagrangian coordinate system.

6. The Resolvent Surface as a Chaotic Sponge

Let us now proceed directly to a nonintegrable system with $L>1$ degrees of freedom since the integrable case described in Appendix B presents a completely different generalization in the case with $L=1$ in Section 5. The trajectories in the regular phase space for this more general scenario are not constrained to L-dimensional tori, and even if such exist, tori are generally nonresonant; that is, the trajectories are not families of periodic orbits, presumed to be isolated in each energy shell.

The conservation of energy along each trajectory ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},t)$ implies that the resolvent surface is the extension of the energy shell by all the trajectories that depart from the L-dimensional identity plane $H({\mathbf{x}}_{+}={\mathbf{x}}_{-}=\mathbf{x})=E$ over the course of positive and negative time. As noted in Section 3, for short enough times, the resolvent surface grows cylindrically according to Equation (19) in the directions of the double-phase space velocities generated by the double Hamiltonian (14). For somewhat longer positive times, the trajectories bend inwards if the shell is locally convex, with their (geometric) chords centered inside the shell like the string of a bow. Therefore, the shell on the identity plane is just a fold caustic of the resolvent surface as viewed from its center variables $\mathbf{x}$. Regardless of the number of degrees of freedom, this short-time behavior is entirely analogous to that discussed in Section 5.

However, this simplified structure of the growing cylinder lasts only until $\left|t\right|={\tau }_1$, the shortest period of a periodic orbit. Then, by the same argument as in the case of a single degree of freedom, which holds regardless of the dimension of the phase spaces, each point in this first PO generates a circle, and this continuum of circles forms a two-dimensional torus. The phase-space-action (32) has the same form as that of a single degree of freedom. Indeed, as it lies on a Lagrangian surface, the double-phase space action, including both the ${\mathbf{x}}_{-}$ circuit and the ${\mathbf{x}}_{+}$ circuit, cancels as in Section 2. Still, one must keep in mind that this two-dimensional torus is now embedded in the $2L$-dimensional resolvent surface. Thus, there is no inside or outside of this torus, and neighboring trajectory segments almost retrace themselves.

The crucial novelty imparted by the increased dimension is that each repetition of the PO is connected to an extension of the resolvent surface in its neighborhood. Indeed, the smoothness of this surface generated by a continuum of smooth trajectories demands that neighboring trajectories to the PO also almost touch the identity plane during this period. Furthermore, it is deduced in Ref. [13] that a fold caustic of the resolvent surface projected on the center plane touches the PO, which itself lies on the caustic along the entire energy shell, as sketched in Figure 3. The initially narrow PO caustic parts that form the energy shell broaden as they recede into the interior. This implies that, added to the quite short chords of centers within this narrow fold, there are chords of pairs of neighboring trajectory segments to the PO, which do not quite retrace themselves, so the chords approach the center plane without touching it again. Thus, one might say that a pair of thin tongues develop on the resolvent surface itself, which reaches down and licks the initial periodic orbit in the center plane precisely at $t=\pm {\tau }_1$. The symmetry of the trajectory growth for positive and negative times allows us to concentrate on positive times herein. This construction of the tongue of the resolvent surface at a particular point on the PO can be extended all the way around the PO so that a circular tongue is formed.

A new tongue is produced during each new period of the PO as a consequence of the deduction in Ref. [13] of its center caustic. (All trajectory segments contributing to the Weyl propagator for each center $\mathbf{x}$ have their tips lying in a particular Poincaré section. This is quite a small glancing section if this point is close enough to the energy shell so orbits that enter the section from the outside can coalesce at a caustic according to Ref. [13].) Even though the question of multiple windings was not treated explicitly in the literature, the linearized action difference $S\left(\mathbf{x}\right)-S\left({\mathbf{x}}_{\mathrm{PO}}\right)$ depends on the stability matrix for the Poincaré map of the PO, which has a power proportional to the number of windings. Therefore, there is a different action and, hence, a different chord for each winding; thus, a new lip of the resolvent surface is formed at each return to the PO.

In this way, the analysis of the caustics in Ref. [13] provides direct information about the growth of the resolvent surface with time. A first general picture is then that all trajectories depart vertically from the energy shell at the center plane. This includes each periodic orbit, which has no distinction before its first period. It is only as this period is reached that it touches the initial PO on the center plane, once more bringing along with it a narrow tongue of the resolvent surface. Then, this process repeats itself, bringing a new tongue to the initial orbit at each iteration. However, this is the first PO to complete its cycle, and the growth of narrow tongues of the resolvent surface that reach down to the center plane, as the period of each successive PO is reached, successively enriches its structure. It is an open question how these tongues broaden and blend into smooth folds of the resolvent surface over each center $\mathbf{x}$ deep inside the shell on the center plane. Nonetheless, the resultant multiple-layered structure may justly be described as a chaotic sponge.

7. Secondary Periodic Orbits

For a chaotic system, the isolated POs in each $(2L-1)$-dimensional energy shell are mostly hyperbolic. Then, there are $(L-1)$ directions of nearby points in the energy shell that approach the PO asymptotically in time and $(L-1)$ directions for which this approach occurs for $t\to -\infty$. These directions are tangent to stable L-dimensional and unstable manifolds, respectively, which are known to play an essential role in SC approximations [26]. Here, one points out that a local extension of the growing resolvent surface for all positive and negative iterations joins each double-phase space PO, for which ${\mathbf{x}}_{+}=\tilde{\mathbf{x}}({\mathbf{x}}_{-},{\tau }_j)={\mathbf{x}}_{-}$, to the PO’s stable and unstable manifolds.

The full extension of the resolvent surface for long positive and negative times generates a horribly convoluted $2L$–dimensional surface within the $2(2L-1)$-dimensional direct product of the pair of energy shells $H\left({\mathbf{x}}_{\pm }\right)=E$. Generally, one only needs to consider times up to the order of the Heisenberg time $t_{\mathrm{H}}\approx \hslash /\overline{(E_n-E_{n-1})}$, but this is insufficient to connect a PO to its stable and unstable manifolds. Therefore, one must place an initial point ${\mathbf{x}}_{-}$ on this manifold and propagate it infinitely so that it reaches its nearby PO. Further extensions of the resolvent surface beyond the Heisenberg time are not required in this paper.

The L-dimensional unstable manifold develops along ($L-1$) unstable directions that transverse each point of the PO, thus forming an L-dimensional cylinder. This topology is preserved despite eventually wrinkling in a complex manner. Being Lagrangian in the original phase space, the action around any irreducible circuit on this cylinder equals that of its parent PO [27], and an equivalent picture holds for the stable manifold in reverse time. The stable and unstable L-dimensional manifolds are allowed to intersect in the $(2L-1)$-dimensional energy shell, defining a homoclinic orbit, which is bi-asymptotic of the parent PO for $t\to \infty$. Likewise, an intersection of the unstable manifold of PO_j with the stable manifold of PO_j′ creates a heteroclinic orbit, originating in the neighborhood of PO_j and then winding infinitely around PO_j′.

Now, consider a path that winds $k\left(j\right)$ times around the parent PO_j then makes a relatively small step (across other trajectories) to the homoclinic orbit, and then another step so as to close itself at the initial point. This is not a trajectory, but a loose invocation of the shadowing lemma [28], which indicates that there exists a true PO that lies close enough to this path and, hence, winds $k\left(j\right)$ times around the j-PO. Indeed, the algorithm developed by Michel Baranger to converge periodic orbits [29] is applicable to the accurate computation of such secondary periodic orbits in Hamiltonian systems [30], as well as in canonical maps [31].

Similar steps can be followed for a departure from the PO_j after winding around it $k\left(j\right)$ times along a heteroclinic orbit and then winding $k^{\prime }\left(j^{\prime }\right)$ times around the PO_j′; then, one needs to return along a complementary heteroclinic orbit back to PO_j so as to close the circuit. This serves as a blueprin t for a sequence of secondary periodic orbits that accumulate on the pair of heteroclinic orbits as the windings $k\left(j\right)$ and $k^{\prime }\left(j^{\prime }\right)$ are increased. Indeed, there is no need to stop at two primitive POs: any number of POs are connected sequentially by various intersections of their stable and unstable manifolds. Infinite sequences of secondary POs, with higher and higher windings along each of these primitive POs, accumulate along the heteroclinic orbits in each of these constructions, and it is computationally observed that secondary POs become almost indistinguishable from parent POs, even for moderately low windings $k\left(j\right)$ [31].

Even though secondary POs are constructed as windings around the primitive POs, along with their heteroclinic excursions, secondary POs are true periodic orbits. Therefore, as each of their relatively large periods is completed, a thin tongue descends in the double-phase space onto this newly completed secondary PO on the identity plane, quite close to the tongues, which lick the primitive component POs. Thus, there may be a number of fold caustics in the vicinity of a relatively short PO, which delimit regions where longer and longer trajectory segments almost return to their initial point.

The emphasis on closed secondary periodic orbits should not obscure the presence of similar constructions that decorate open orbits. It is here assumed that a set of homoclinic orbits asymptotic to a single PO or a set of heteroclinic orbits is just as dense among the full set of trajectories as the set of POs themselves. (It may seem optimistic for a relatively simple open orbit to wander close to a homoclinic or heteroclinic orbit. However, in the case of a Bernoulli system [32], in which chaotic orbits are described in terms of a finite alphabet, it is shown that the set of homoclinic orbiting a single PO is dense among the full set of orbits.) Therefore, any considerably short open orbit may come close to a homoclinic or a heteroclinic orbit of primitive POs; hence, any number of cycles around primitive POs can be added to construct long open orbits, which satisfy the same boundary conditions, such as a pair of end-positions $\pm \mathbf{q}$ or a fixed center $\mathbf{x}$ between the endpoints $\pm \mathbf{x}$.

8. Secondary Orbits and Composite Orbits in the Semiclassical Scenario

A general secondary PO is characterized by its primitive POs, $j_1,j_2,...$, which are represented here by J, and the windings around each primitive PO, $k1\left(j_1\right),k2\left(j_2\right),...$, labeled generally just as $K\left(J\right)$. In the limit where all the $kn\left(j_n\right)\to \infty$, expressed as $K\left(J\right)\to \infty$, the windings around each primitive PO accumulate on it, and their connection to the windings around other POs approach heteroclinic orbits. In short, one may define ${\mathsf{\Xi }}_{EK\left(J\right)\mathrm{het}}$ as the action of the total heteroclinic circuit closed among primitive POs. (Indeed, there are various heteroclinic orbits joining a given pair of POs, ordered by the growing length of POs. Each of these orbits belongs to a different blueprint for a family of secondary periodic orbits). Thus, one obtains the limit of the total action of the secondary PO as follows:

$${\mathsf{\Xi }}_{EK\left(J\right)}\to {\mathsf{\Xi }}_{EK\left(J\right)\mathrm{het}}+\sum _{j,k\left(j\right)}k\left(j\right){\mathsf{\Xi }}_{Ej},$$

(33)

where the second term, a linear combination of the actions of a set of primitive POs, coincides with the action of a pseudo-orbit [9,10] or composite orbit [12],

$${\mathsf{\Xi }}_{EK\left(J\right)\mathrm{com}}=\sum _{j,k\left(j\right)}k\left(j\right){\mathsf{\Xi }}_{Ej},$$

(34)

which made its debut in the theory of quantum spectral determinants for individual states of chaotic systems.

A similar form describes the action of an open trajectory, which wraps many times around a circuit of primitive POs, neighboring a secondary PO on its way between two given endpoints. Along the way, a relatively short open orbit approaches a heteroclinic orbit of a circuit, allowing for a connection to it across a continuous set of trajectories. Then, in the limit $K\left(J\right)\to \infty$, the action for this ’dressed’ open orbit acquires the total action of the J-circuit, just as the secondary PO_K(J), so that the action of this secondary open orbit becomes

$${\mathsf{\Xi }}_{EK\left(J\right)}\left(\mathbf{Q}\right)\to {\mathsf{\Xi }}_{E,0}\left(\mathbf{Q}\right)+{\mathsf{\Xi }}_{EK\left(J\right)}$$

(35)

for any primitive open orbit with action ${\mathsf{\Xi }}_{E,0}\left(\mathbf{Q}\right)$, with the appropriate endpoints represented by the double-phase space variable $\mathbf{Q}$.

Therefore, the SC contribution of such simple primitive POs to the resolvent and its trace for relatively long times, beyond the Heisenberg time, can be approximately grouped within composite orbits. Starting with the oscillatory part of the trace of the resolvent, one can insert Equation (33) into Equation (31) to produce a sum over the long-time (LT) secondary orbits labled by J:

$$\begin{array}{c}\hfill {\left\{\mathrm{tr}{\widehat{U}}_{EK\left(J\right)}\right\}}_{\mathrm{LT}}\approx \sum _{K\left(J\right)}{C}_{EK\left(J\right)}exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{EK\left(J\right)}+i\theta \right].\end{array}$$

(36)

Note that. here, the special case of a single primitive orbit is included as a secondary orbit with only one non-zero j-entry.) The LT contribution of the relatively short primitive orbits can then be expressed as

$${\left\{\mathrm{tr}{\widehat{U}}_{EK\left(J\right)}\right\}}_{\mathrm{LT}}\approx \sum _{K\left(J\right)}{C}_{EK\left(J\right)}exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{\mathrm{het}EK\left(J\right)}\right]exp\left[{\displaystyle \frac{i}{\hslash }}\sum _{j,k\left(j\right)}k\left(j\right){\mathsf{\Xi }}_{Ej}+i\theta \right],$$

(37)

recalling that the amplitude of each secondary PO receives a complex phase from its heteroclinic excursions. From this point of view, the actions of all the composite orbits (or pseudo-orbits) with a long total period are already present in the trace of the resolvent. The resummation of the density of states consummated by spectral determinants [9,10,11,12] can then be considered to shift the contribution of compound orbits, already present in the trace, from relatively long total periods to those that are shorter than the Heisenbrg time.

Still, this is a bona fide periodic orbit, so it brings down a new tongue of the resolvent surface as its period is completed, thus forming a new layer of the chaotic sponge. In the LT limit, the amplitude of the contribution to the trace of each secondary orbit can also be derived from its primary components. Indeed, its main ingredient, already present in the amplitude of the trace of the evolution operator (28), is the stability matrix for the entire orbit. This is dominated by the product of primitive stability matrices

$${\mathbf{M}}_{t,K\left(J\right)}\approx \prod _{j,k\left(j\right)}{\mathbf{M}}_{t,j}^{k\left(j\right)},$$

(38)

if one neglects relatively short heteroclinic excursions (this decomposition does not apply to a secondary PO with few primary windings).

A similar decomposition holds for contributions to the representations of the resolvent of relatively short open orbits, which can be dressed by a secondary PO. Labeling the dressed open orbit as $K\left(J\right)$, i.e., by the added secondary orbit, one obtains its contribution by inserting Equation (35) into Equation (30):

$$\begin{array}{c}\hfill {\left\{\langle \langle {\mathbf{Q}}^{\prime }|U_{EK(J}\rangle \rangle \right\}}_{\mathrm{LT}}\approx B_{EK\left(J\right)}\left({\mathbf{Q}}^{\prime }\right)exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{EK\left(J\right)}\left({\mathbf{Q}}^{\prime }\right)+i\theta \right]\\ \hfill =B_{EK\left(J\right)}\left({\mathbf{Q}}^{\prime }\right)exp\left[{\displaystyle \frac{i}{\hslash }}{\mathsf{\Xi }}_{E0}\left({\mathbf{Q}}^{\prime }\right)\right]exp\left[{\displaystyle \frac{i}{\hslash }}\sum _{j,k\left(j\right)}k\left(j\right){\mathsf{\Xi }}_{Ej}\left({\mathbf{Q}}^{\prime }\right)+i\theta \right].\end{array}$$

(39)

Hence, again, just as with the trace of the resolvent, the resummation of the Green function or the Wigner function basically exchanges the contribution of extremely long open composite or pseudo-orbits with those of a period shorter than the Heisenberg time.

9. Discussion

The extraordinary complexity of the flow generated by an unintegrable Hamitonian was first put forward by the startling presentation of homoclinic intersections by Henri Poincaré [33]. Even though Poincaré did not emphasize this aspect, each unstable (stable) L-dimensional manifold emanates from each PO as an initially well-behaved cylinder, formed by helical trajectories. Further on, the cylinders become ever-more wrinkled, so that their folds eventually explore the entire energy shell. Nonetheless, the cylinders never lose their smoothness, just as their constituent trajectories and any circuit around them reproduces the action of the parent PO [27]. One-dimensional intersections of the cylinders with other stable (unstable) manifolds define homoclinic or heteroclinic orbits, which approach their respective POs bi-asymptotically as those manifolds wrap helically around the stable (unstable) cylinder. In this way, one achieves a quite a simple description of this exotic creature, the heteroclinic orbit, by sharing attention between both the initial unstable cylinder and the final stable cylinder.

There are some parallels between this microscopic picture of Hamiltonian chaotic motion and its macroscopic description in terms of the resolvent surface. Instead of picking a single isolated PO, it is the entire energy shell within the $2L$-dimensional identity plane in the $4L$-dimensional double-phase space that seeds a cylinder as each trajectory grows from its initial point. In contrast to the evolution of an L-dimensional unstable manifold from a relatively simple circuit, for example, a topological circle, one just adds one more dimension to the $(2L-1)$-dimensional shell in the doubled phase space. Notwithstanding its trivial projections onto the initial ${\mathbf{x}}_{-}$ plane and the final ${\mathbf{x}}_{+}$-plane, which are identical to the energy shell itself, the full resolvent surface develops smooth folds in the form of narrow tongues, which reach back onto the identity plane along each PO. The enormous multiplicity of smooth, narrow tongues, reaching back onto all the primary and secondary POs in the identity plane, admits the description of the resolvent surface as a multidimensional sponge, even if one cuts off the period of all the trajectories at the Heisenberg time.

Such is the complex geometrical structure that supports SC approximations of various representations of the resolvent operator. The approximations differ only by choice of Lagrangian coordinate planes for the description of the resolvent surface, which is itself Lagrangian in the double-phase space. In each of the chosen coordinates, the phase of the SC contribution of an orbit segment is integral along the resolvent surface, in strict analogy to the phase of a SC wave function in the regualr $2L$-dimensional phase space. Here, the existence of multiple folds generated by the POs is deduced from the caustics within the conjugate Wigner–Weyl coordinates of the center and chord, but it is not conceivable that projections of such an intricate structure onto other double phase space coordinates can avoid multiple projection singularities. In the neighborhood of each of these caustics, just the SC approximation for the corresponding representation of the resolvent operator breaks down and must be replaced with a more refined uniform approximation [34].

The feature that periodic orbits are dense within each energy shell may be claimed for the plausibility of their role in the SC approximation of the quantum density of states; that is, the trace of the resolvent. However, multiple families of secondary POs highlighted in this paper wind ever-more tightly around a relatively small set of primitive POs, even if their heteroclinic connections wander somewhat freely between them. The distinction between primary and secondary periodic orbits is robust with respect to any softening of the chaos, which allows for the presence of relatively small islands surrounding stable periodic orbits. These orbits form two-dimensional tori within the resolvent surface (just as in the integrable systems described in Appendix B), which in no way impede the heteroclinic connections and the formation of secondary POs in their neighborhood.

If one accepts that these high-period secondary PO’s are resummed in spectral determinants into composite orbits (with actions that are linear combinations of the actions of their primitive constituent POs), then it appears that only a relatively small set of primitive POs really matter as the classical skeleton of quantum mechanics. An indication that this conjecture may be correct is that, in the simple example of the spectral determinant for an integrable map (with no secondary POs) [35], resummation of the density of states produced inferior results to the straight SC trace. It is notable that a recent alternative scheme for building quantum states around quite a small set of hyperbolic POs showed promising computational results [36].