Characterizing Color Quality, Damage to Artwork, and Light Intensity of Multi-Primary LEDs for Museums
Abstract
:1. Introduction
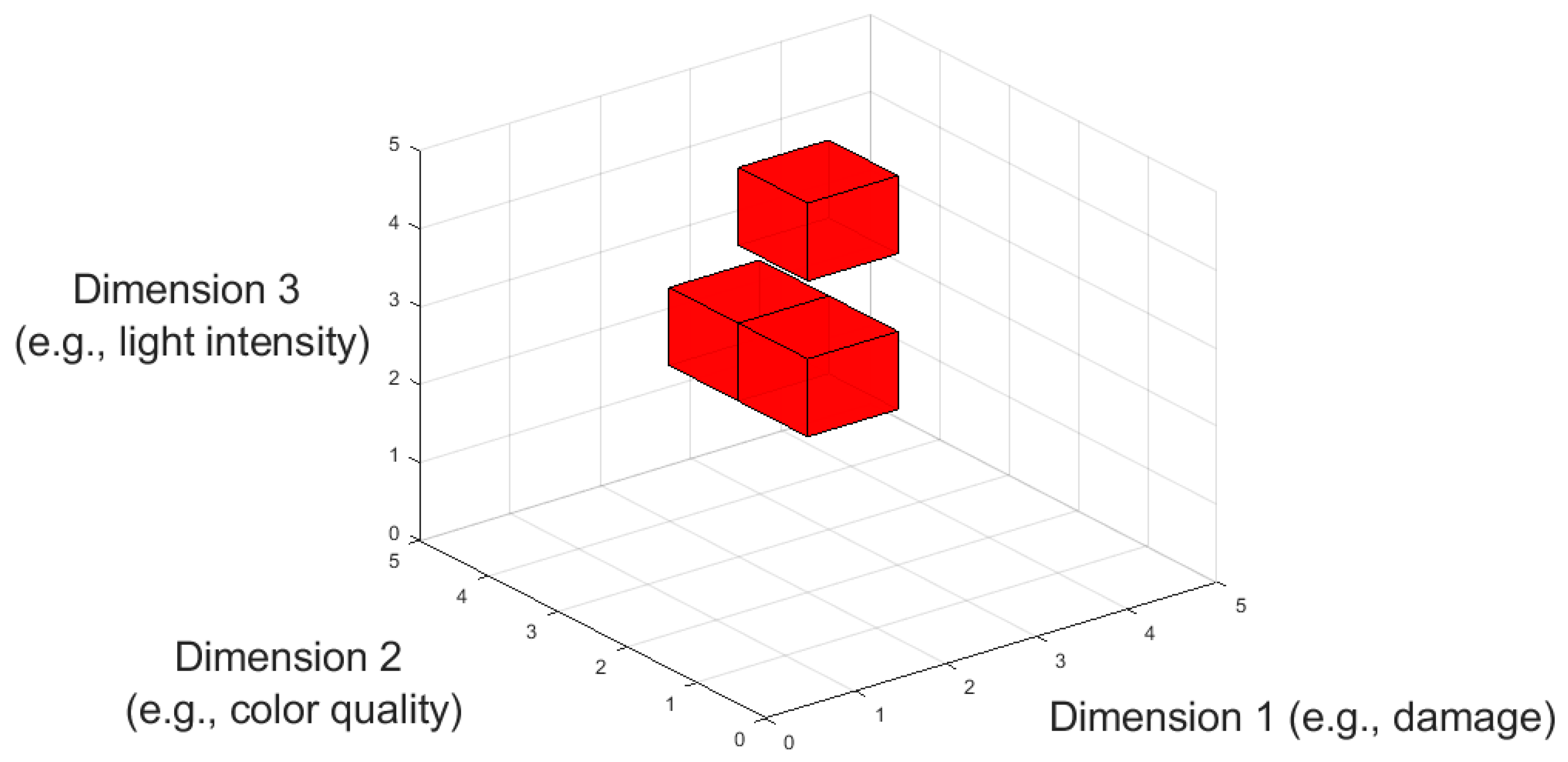
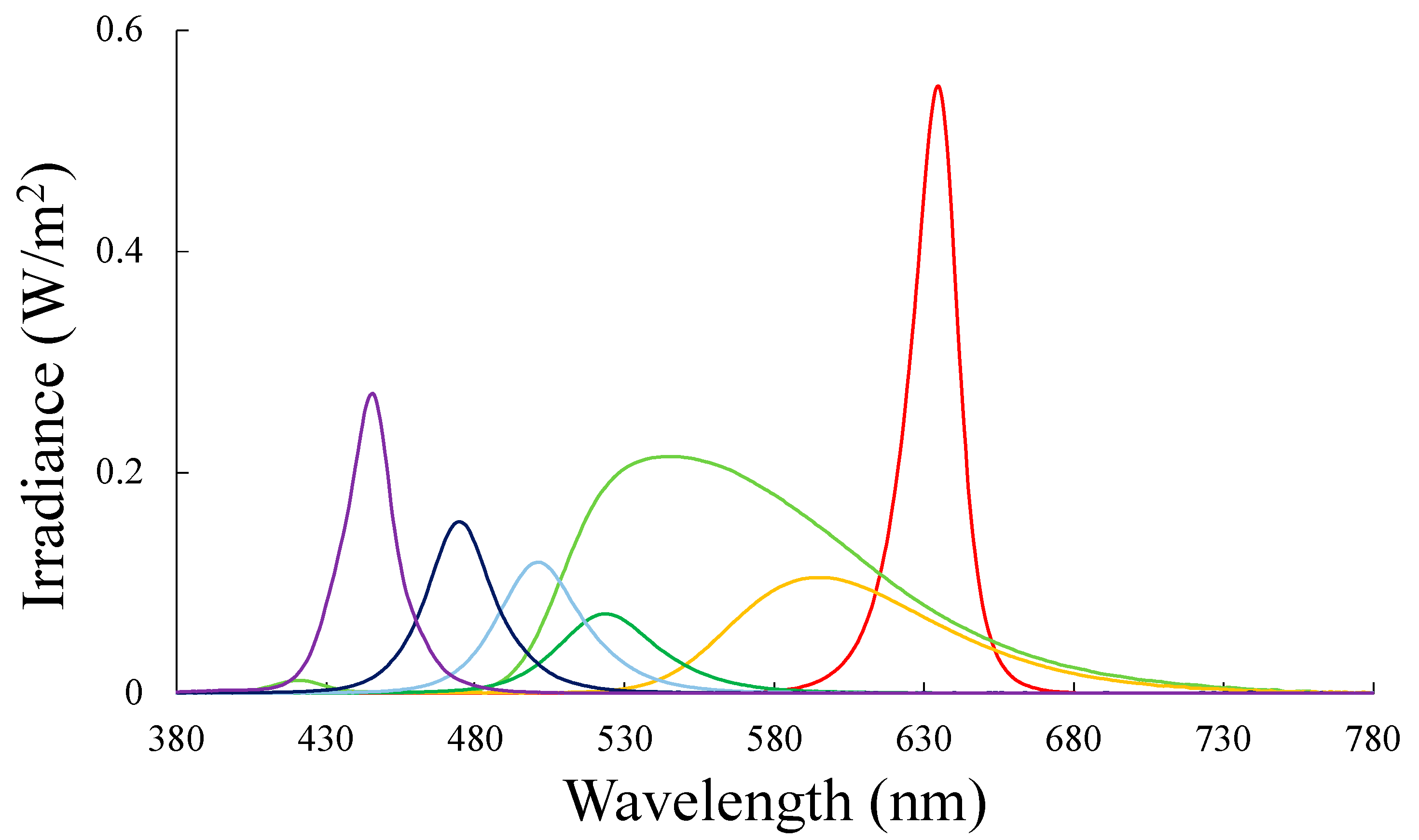
2. Methods
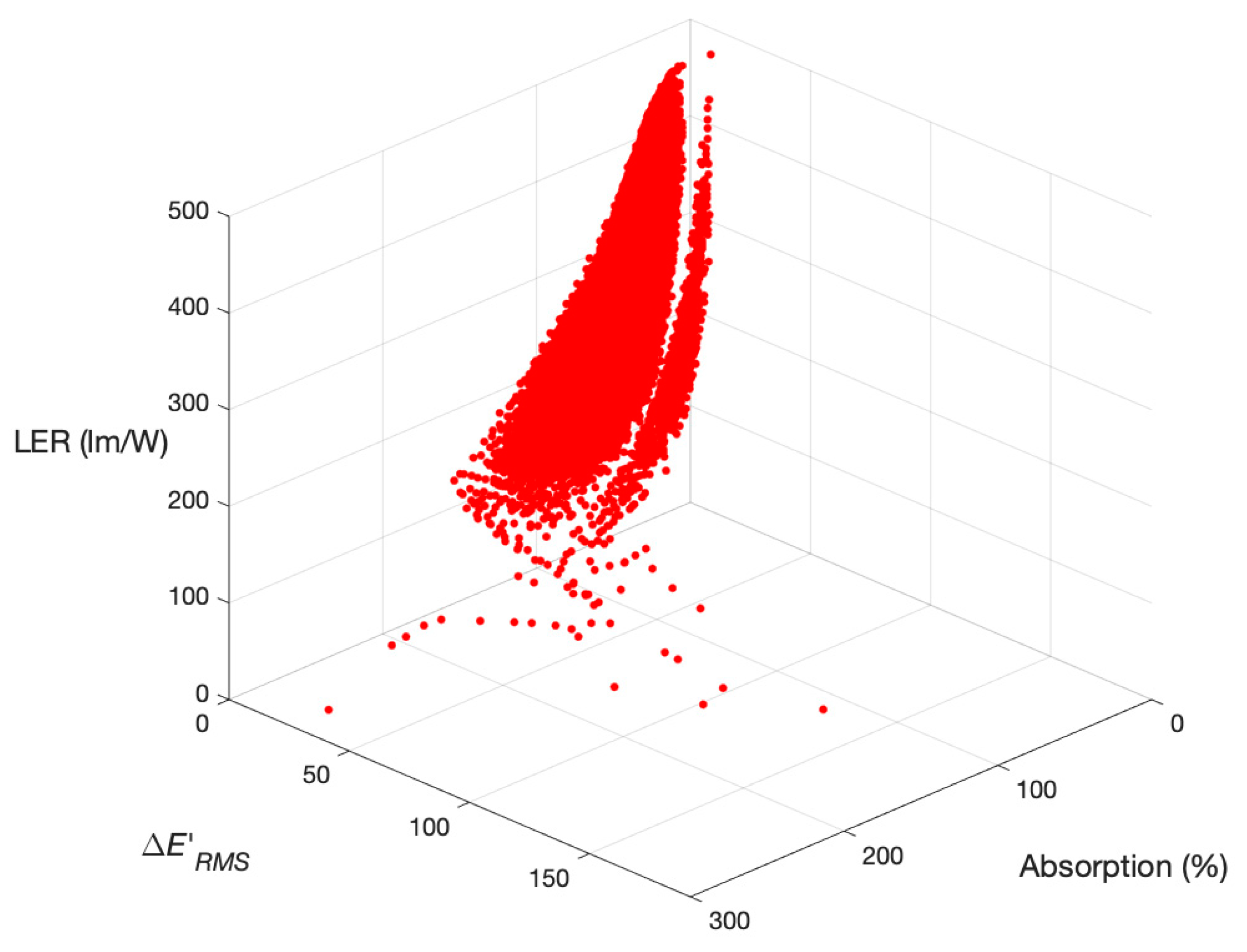
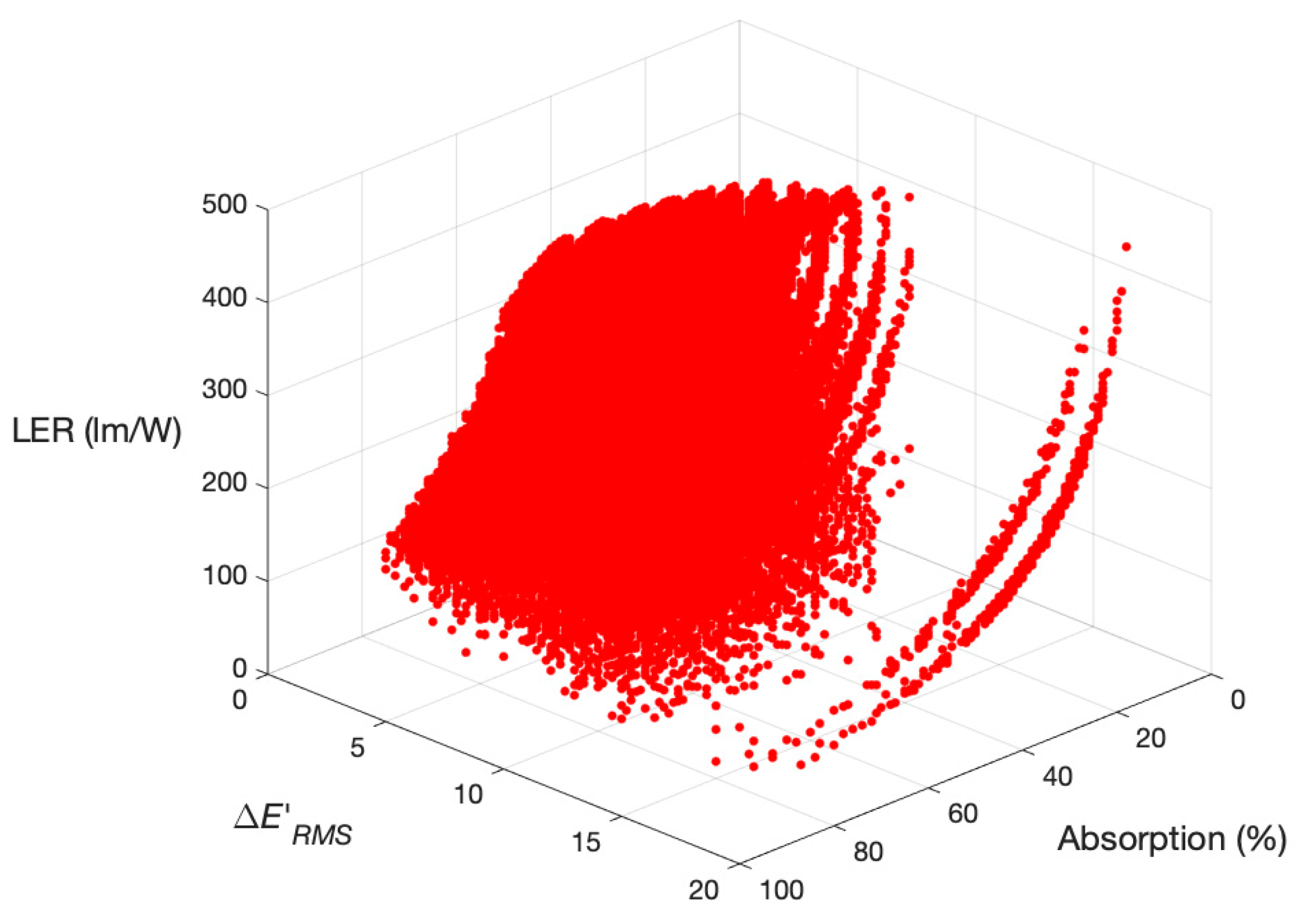
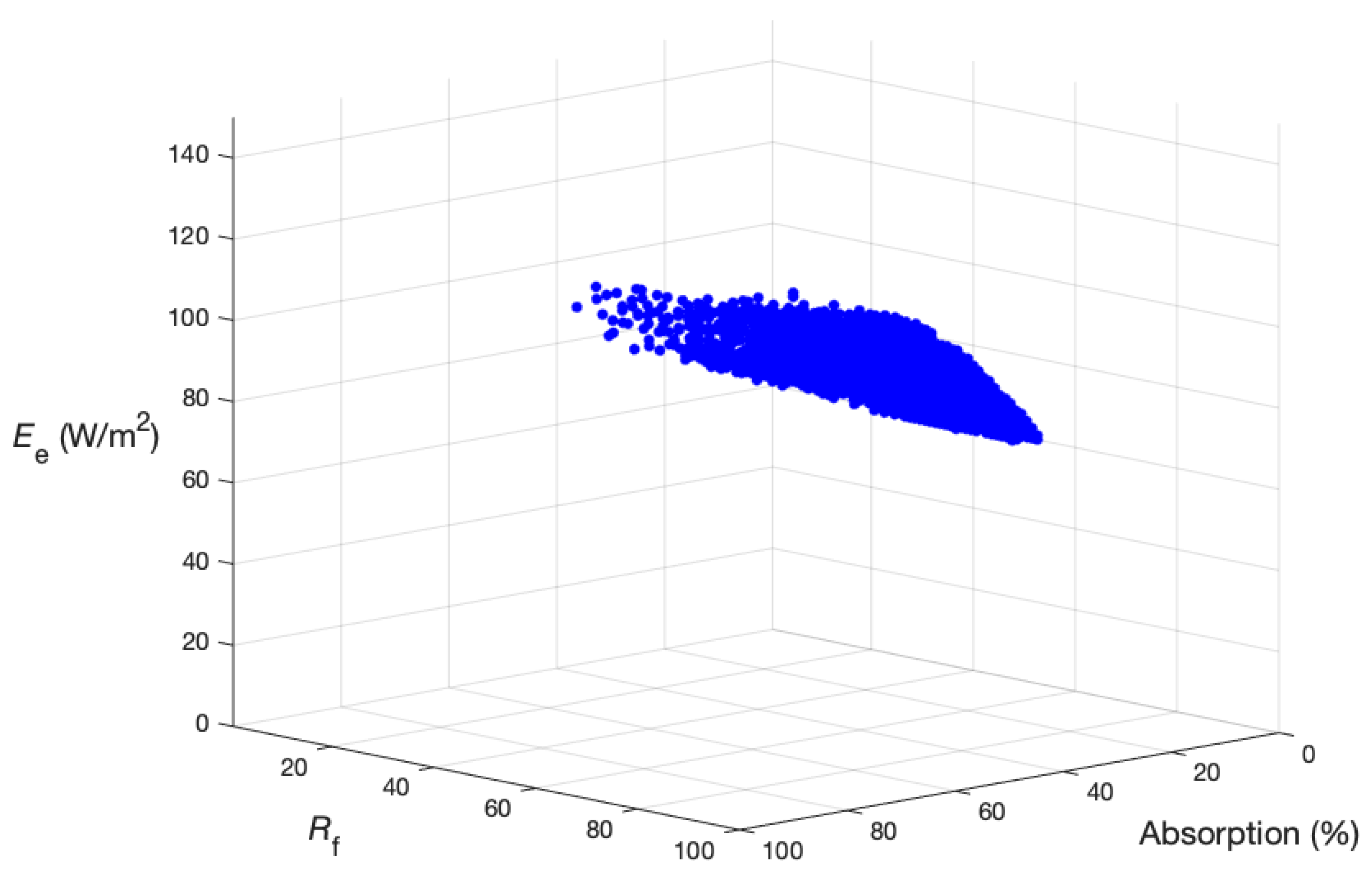
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schaeffer, T.T. Effects of Light on Materials in Collections: Data on Photoflash and Related Sources; Getty Publications: Los Angeles, CA, USA, 2001. [Google Scholar]
- Cuttle, C. Damage to museum objects due to light exposure. Light. Res. Technol. 1996, 28, 1–9. [Google Scholar] [CrossRef]
- CIE. 157:2004 Control of Damage to Museum Objects by Optical Radiation; CIE: Vienna, Austria, 2004. [Google Scholar]
- Harrison, L.S. Report on the Deteriorating Effects of Modern Light Sources; Metropolitan Museum of Art: New York, NY, USA, 1953. [Google Scholar]
- Feller, R.L. Control of deteriorating effects of light on museum objects: Heating effects of illumination by incandescent lamps. Mus. News 1968, 46, 39–47. [Google Scholar]
- Beek, H.V.; Heertjes, P.M. Fading by light of organic dyes on textiles and other materials. Stud. Conserv. 1966, 11, 123–132. [Google Scholar] [CrossRef]
- Michalski, S. Time’s Effects on Paintings. In Shared Responsibility; National Gallery of Canada: Ottowa, ON, Canada, 1990; pp. 39–52. [Google Scholar]
- Gupta, D.; Gulrajani, M.L.; Kumari, S. Light fastness of naturally occurring anthraquinone dyes on nylon. Color Technol. 2004, 120, 205–212. [Google Scholar] [CrossRef]
- Saunders, D.; Kirby, J. Wavelength-dependent fading of artists’ pigments. Stud. Conserv. 1994, 39, 190–194. [Google Scholar] [CrossRef]
- Nakagoshi, K.; Yoshizumi, K. Degradation of Japanese Lacquer under Wavelength Sensitivity of Light Radiation. Mater. Sci. Appl. 2011, 2, 1507–1515. [Google Scholar] [CrossRef] [Green Version]
- Lerwill, A.; Brookes, A.; Townsend, J.H.; Hackney, S.; Liang, H. Micro-fading spectrometry: Investigating the wavelength specificity of fading. Appl. Phys. A 2014, 118, 457–463. [Google Scholar] [CrossRef] [Green Version]
- Villmann, B.; Weickhardt, C. Wavelength Dependence of Light Induced Changes in Reflectance Spectra of Selected Dyes and Pigments. Stud. Conserv. 2017, 63, 104–112. [Google Scholar] [CrossRef]
- Scuello, M.; Abramov, I.; Gordon, J.; Weintraub, S. Museum lighting: Optimizing the illuminant. Color Res. Appl. 2004, 29, 121–127. [Google Scholar] [CrossRef]
- Abdalla, D.; Duis, A.; Durmus, D.; Davis, W. Customisation of light source spectrum to minimise light absorbed by artwork. In Proceedings of the CIE Lighting Quality Energy Efficiency, Melbourne, Australia, 7–9 March 2016; pp. 22–31. [Google Scholar]
- Lunz, M.; Talgorn, E.; Baken, J.; Wagemans, W.; Veldman, D. Can LEDs help with art conservation? Impact of different light spectra on paint pigment degradation. Stud. Conserv. 2016, 62, 294–303. [Google Scholar] [CrossRef]
- Delgado, M.F.; Dirk, C.W.; Druzik, J.; WestFall, N. Lighting the world’s treasures: Approaches to safer museum lighting. Color Res. Appl. 2011, 36, 238–254. [Google Scholar] [CrossRef]
- Dang, R.; Wang, N.; Liu, G.; Yuan, Y.; Liu, J.; Tan, H. Illumination in Museums: Four-Primary White LEDs to Optimize the Protective Effect and Color Quality. IEEE Photon J. 2019, 11, 1–15. [Google Scholar] [CrossRef]
- Vázquez, D.; Fernández-Balbuena, A.; Canabal, H.; Muro, C.; Durmus, D.; Davis, W.; Benítez, A.J.; Mayorga, S. Energy optimization of a light projection system for buildings that virtually restores artworks. Digit. Appl. Archaeol. Cult. Herit. 2020, 16, e00128. [Google Scholar] [CrossRef]
- Durmus, D.; Abdalla, D.; Duis, A.; Davis, W. Spectral Optimization to Minimize Light Absorbed by Artwork. LEUKOS 2018, 16, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Royer, M.P.; Durmus, D.; Baxter, D.J. Characterizing the color rendition performance of multi-primary LED lighting systems. In Proceeding of the IES Annual Conference, New Orleans, LA, USA, 6–8 August 2020. [Google Scholar]
- Hunt, R.W.G. Light and dark adaptation and the perception of color. JOSA 1952, 42, 190–199. [Google Scholar] [CrossRef]
- Smith, V.C.; Pokorny, J.; Cohen, J.; Perera, T. Luminance thresholds for the Bezold-Brücke hue shift. Percept. Psychophys. 1968, 3, 306–310. [Google Scholar] [CrossRef]
- Useful Color Data. Available online: https://www.rit.edu/cos/colorscience/rc_useful_data.php (accessed on 20 November 2020).
- Luo, M.R.; Li, C. CIECAM02 and Its Recent Developments. In Advanced Color Image Processing and Analysis; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2013; pp. 19–58. [Google Scholar]
- Perrin, T.E.; Druzik, J.R.; Miller, N.J. SSL Adoption by Museums: Survey Results, Analysis, and Recommendations; Office of Scientific and Technical Information (OSTI), Pacific Northwest National Laboratory: Richland, WA, USA, 2014. [Google Scholar]
- Durmus, D.; Davis, W. Appearance of Achromatic Colors under Optimized Light Source Spectrum. IEEE Photon J. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Liang, H.; Saunders, D.; Cupitt, J. A new multispectral imaging system for examining paintings. J. Imaging Sci. Technol. 2005, 49, 551–562. [Google Scholar]
- IES. ANSI/IES TM-30-20, IES Method for Evaluating Light Source Color Rendition; Illuminating Engineering Society: New York, NY, USA, 2020. [Google Scholar]
- Ohno, Y. Practical Use and Calculation of CCT and Duv. LEUKOS 2014, 10, 47–55. [Google Scholar] [CrossRef]
- Antunes, V.; Serrão, V.; Valadas, S.; Candeias, A.; Mirão, J.; Cardoso, A.; Manso, M.; Carvalho, M.L. A Painter in the Shadow: Unveiling Conservation, Materials and Techniques of the Unknown Luso-Flemish Master of Lourinhã. Heritage 2019, 2, 2725–2744. [Google Scholar] [CrossRef] [Green Version]
- Zalaffi, M.S.; Agostinelli, I.; Karimian, N.; Ugo, P. Ag-Nanostars for the Sensitive SERS Detection of Dyes in Artistic Cross-Sections—Madonna della Misericordia of the National Gallery of Parma: A Case Study. Heritage 2020, 3, 1344–1359. [Google Scholar] [CrossRef]
- Buse, J.; Otero, V.; Melo, M.J. New Insights into Synthetic Copper Greens: The Search for Specific Signatures by Raman and Infrared Spectroscopy for Their Characterization in Medieval Artworks. Heritage 2019, 2, 1614–1629. [Google Scholar] [CrossRef] [Green Version]
- Druzik, J.R. Evaluating the light sensitivity of paints in selected wall paintings at the Mogao Grottoes: Caves 217, 98, and 85. In Conservation of Ancient Sites on the Silk Road; Getty Conservation Institute: Los Angeles, CA, USA, 2010; pp. 457–463. [Google Scholar]
- Piccablotto, G.; Aghemo, C.; Pellegrino, A.; Iacomussi, P.; Radis, M. Study on Conservation Aspects Using LED Technology for Museum Lighting. Energy Procedia 2015, 78, 1347–1352. [Google Scholar] [CrossRef] [Green Version]
- Mayorga, S.; Vázquez, D.; Fernandez-Balbuena, A.A.; Muro, C.; Muñoz, J. Spectral damage model for lighted museum paintings: Oil, acrylic and gouache. J. Cult. Herit. 2016, 22, 931–939. [Google Scholar] [CrossRef] [Green Version]
- Farke, M.; Binetti, M.; Hahn, O. Light damage to selected organic materials in display cases: A study of different light sources. Stud. Conserv. 2016, 61, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Degani, L.; Gulmini, M.; Piccablotto, G.; Iacomussi, P.; Gastaldi, D.; Bello, F.D.; Chiantore, O. Stability of natural dyes under light emitting diode lamps. J. Cult. Herit. 2017, 26, 12–21. [Google Scholar] [CrossRef]
- Luo, H.-W.; Chou, C.-J.; Chen, H.-S.; Luo, M.R. Museum lighting with LEDs: Evaluation of lighting damage to contemporary photographic materials. Light. Res. Technol. 2018, 51, 417–431. [Google Scholar] [CrossRef]
- Jo, S.; Ryu, S.R.; Jang, W.; Kwon, O.-S.; Rhee, B.; Lee, Y.E.; Kim, D.; Kim, J.; Shin, K. LED illumination-induced fading of traditional Korean pigments. J. Cult. Herit. 2019, 37, 129–136. [Google Scholar] [CrossRef]
- Dang, R.; Tan, H.; Wang, N.; Liu, G.; Zhang, F.; Song, X. Raman spectroscopy-based method for evaluating LED illumination-induced damage to pigments in high-light-sensitivity art. Appl. Opt. 2020, 59, 4599–4605. [Google Scholar] [CrossRef]
- Liu, Y.; Shigley, J.; Fritsch, E.; Hemphill, S. Abnormal Hue-Angle change of the gemstone tanzanite between CIE illuminants d65 and a in CIELAB color space. Color Res. Appl. 1995, 20, 245–250. [Google Scholar] [CrossRef]
- Durmus, D.; Davis, W. Evaluation OF Hue Shift Formulae in CIELAB and CAM02. In Proceedings of the 29th Quadrennial Session of the CIE, Washington, DC, USA, 14–22 June 2019; International Commission on Illumination: Vienna, Austria, 2019; pp. 888–895. [Google Scholar]
- Sharma, G.; Rodríguez-Pardo, C.E. The dark side of CIELAB. In Color Imaging XVII: Displaying, Processing, Hardcopy, and Applications; International Society for Optics and Photonics; International Society for Optics and Photonics: Burlingame, CA, USA, 2012; Volume 8292, p. 82920D. [Google Scholar]
- Moroney, N. A hypothesis regarding the poor blue constancy of CIELAB. Color Res. Appl. 2003, 28, 371–378. [Google Scholar] [CrossRef]
- Lian, Y.; Liao, N.; Wang, J.; Tan, B.; Liu, Z. Evaluating the uniformity of color spaces and performance of color difference formulae. LED Disp. Technol. 2010, 7852, 785205. [Google Scholar] [CrossRef]
- Shamey, R.; Cao, R.; Sawatwarakul, W.; Lin, J. Performance of various color difference models in challenging regions of CIELAB color space. In 22nd Color and Imaging Conference; Society for Imaging Science and Technology: Springfield, VA, USA, 2014; Volume 2014, pp. 200–206. [Google Scholar]
- Saunders, D. Museum Lighting: A Guide for Conservators and Curators; Getty Publications: Los Angeles, CA, USA, 2020. [Google Scholar]
- Area, M.C.; Ceradame, H. Paper aging and degradation: Recent findings and research methods. BioResources 2011, 6, 5307–5337. [Google Scholar]
- Durmus, D.; Davis, W. Optimising Light Source Spectrum for Object Reflectance. Light Energy Environ. 2014, 23, 456. [Google Scholar] [CrossRef]
- Vázquez, D.; Alvarez, A.; Canabal, H.; Garcia, A.; Mayorga, S.; Muro, C.; Galan, T. Point to point multispectral light projec-tion applied to cultural heritage. In Nonimaging Optics: Efficient Design for Illumination and Solar Concentration XIV. Int. Soc. Opt. Photonics 2017, 10379, 103790K. [Google Scholar]
- Gómez Manzanares, Á.; Benítez, A.J.; Martínez Antón, J.C. Virtual Restoration and Visualization Changes through Light: A Review. Heritage 2020, 3, 1373–1384. [Google Scholar] [CrossRef]
- Durmus, D.; Davis, W. Blur perception and visual clarity in light projection systems. Opt. Express 2019, 27, A216–A223. [Google Scholar] [CrossRef]
- Khanh, T.; Bodrogi, P.; Guo, X.; Phan, Q.A. Towards a user preference model for interior lighting. Part 2: Experimental results and modelling. Light. Res. Technol. 2018, 51, 1030–1043. [Google Scholar] [CrossRef]
- Durmus, D. Spatial Frequency and the Performance of Image-Based Visual Complexity Metrics. IEEE Access 2020, 8, 100111–100119. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durmus, D. Characterizing Color Quality, Damage to Artwork, and Light Intensity of Multi-Primary LEDs for Museums. Heritage 2021, 4, 188-197. https://doi.org/10.3390/heritage4010011
Durmus D. Characterizing Color Quality, Damage to Artwork, and Light Intensity of Multi-Primary LEDs for Museums. Heritage. 2021; 4(1):188-197. https://doi.org/10.3390/heritage4010011
Chicago/Turabian StyleDurmus, Dorukalp. 2021. "Characterizing Color Quality, Damage to Artwork, and Light Intensity of Multi-Primary LEDs for Museums" Heritage 4, no. 1: 188-197. https://doi.org/10.3390/heritage4010011
APA StyleDurmus, D. (2021). Characterizing Color Quality, Damage to Artwork, and Light Intensity of Multi-Primary LEDs for Museums. Heritage, 4(1), 188-197. https://doi.org/10.3390/heritage4010011





