Generalized Cardioid Distributions for Circular Data Analysis

Abstract

The Cardioid (C) distribution is one of the most important models for modeling circular data. Although some of its structural properties have been derived, this distribution is not appropriate for asymmetry and multimodal phenomena in the circle, and then extensions are required. There are various general methods that can be used to produce circular distributions. This paper proposes four extensions of the C distribution based on the beta, Kumaraswamy, gamma, and Marshall–Olkin generators. We obtain a unique linear representation of their densities and some mathematical properties. Inference procedures for the parameters are also investigated. We perform two applications on real data, where the new models are compared to the C distribution and one of its extensions.

1. Introduction

Fitting densities to data has a long history. Statistical distributions are very useful in describing and predicting real world phenomena. Hundreds of extended distributions have been developed by introducing one or more parameters to a baseline distribution over the past decades for modeling data in several disciplines, in particular in reliability engineering [1], survival analysis [2], demography [3], actuarial science [4], etc.

Adding parameters to a well-established distribution is a time honored device for obtaining more flexible new families of distributions. In fact, several classes of distributions have been introduced by adding one or more parameters to generate new distributions in the statistical literature. Recent developments address definitions of new families that extend well-known distributions and, at the same time, provide great flexibility in modeling real data. The well-known generators are the Marshall–Olkin-G [5], beta-G [6], gamma-G [7], Kumaraswamy-G (Kw-G) [8], exponentiated generalized (EG) [9], type I half-logistic-G [10], Burr X-G [11], and exponentiated Weibull-H [12], among others. The applications of these generators have been made in the context of linear data, i.e., on the support of a subset of $\mathbb{R}$.

Several phenomena in practice provide angles (expressed in degrees or radians) as outputs called circular data, such as in the analysis of phase features obtained from radar imagery [13], time series analysis of wind speeds and directions [14], etc. As one of the most used circular distributions, the two-parameter Cardioid (C) law was pioneered by Jeffreys [15] for describing directional spectra of ocean waves. This model has a cumulative distribution function (cdf), $G\left(x\right)=G(x;\mu ,\rho )$, and probability density function (pdf), $g\left(x\right)=g(x;\mu ,\rho )$, given by (for $0<x\le 2\pi$)

$$G\left(x\right)=\frac{x}{2\pi }+\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]$$

(1)

and

$$g\left(x\right)=\frac{1}{2\pi }\left[1+2\rho cos(x-\mu )\right],$$

(2)

respectively, where $0<\mu \le 2\pi$ is a location parameter, and $\left|\rho \right|\le 0.5$ represents a concentration index. Some known competing distributions to the C distribution are the wrapped normal, wrapped Cauchy, wrapped Lévy, and Wrapped Lindley. A novel circular distribution introduced by Wang and Shimizu [16] applied the Möbius transformation to the C model. The Papakonstantinou family studied by Abe et al. [17] also extended (1). However, these extensions present hard analytic formulas for their densities. Recently, Paula et al. [18] introduced a simple extended C distribution, called the exponentiated Cardioid (EC), derived from the exponentiated G (exp-G) generator—after adapting the mapping linear to circular—that can describe asymmetric and some bimodal cases beyond those of the C model. The models mentioned and those that will be presented in this work are also classified as trigonometric distributions. In recent years, many trigonometric models have been proposed, such as the transformed Sin-G family [19] and Cos-G Class [20], thus highlighting their importance.

In this work, we derive four extensions of the C model through the adapted $\beta$-G, Kw-G, $\mathsf{\Gamma }$-G, and MO-G generators, which extend the exp-G family. We propose four new circular distributions called the beta Cardioid ($\beta$C), Kumaraswamy Cardioid (KwC), gamma Cardioid ($\mathsf{\Gamma }$C), and Marshall–Olkin Cardioid (MOC). Their densities are expressed in a unique linear representation, which is the result of weighting the term $\left[1+2\rho cos(x-\mu )\right]$ in Equation (2). Circular data phenomena often demand the proposal of tailored clustering structures. Abraham et al. [21] presented a discussion on an unsupervised clustering algorithm in circular data obtained from X-ray beam projectors. Based on mixtures of one-dimensional Langevin distributions, Qiu and Wu [22] derived a new information criterion to cluster circular data. We understand that these works motivate our proposals as the potential inputs for future clustering structures. Furthermore, some mathematical properties of the new models are derived, such as extensions and trigonometric moments [23]. A brief discussion about likelihood-based estimation procedures is provided. Finally, two applications to real data are performed to illustrate the flexibility of our proposals.

The remainder of this paper is organized as follows. New circular distributions are defined in Section 2. Section 3 provides some of their properties, and an estimation procedure is addressed in Section 4. Subsequently, two applications to real data are performed in Section 5, and some conclusions are offered in Section 6.

2. Generalized Cardioid Models

We provide some three- and four-parameter distributions by transforming the C distribution according to four well-known generators.

Let $G\left(x\right)$ be the cdf of a baseline distribution with p parameters:

(a)

The $\beta$-G cdf defined by Eugene et al. [6] is

$$F_{\beta -\mathrm{G}}\left(x\right)={\mathbb{I}}_{G\left(x\right)}(\theta ,\varphi )=\frac{1}{B(\theta ,\varphi )}{\int }_0^{G\left(x\right)}{\omega }^{\theta -1}{(1-\omega )}^{\varphi -1}\mathrm{d}\omega ,$$

(3)

where $\theta ,\varphi >0$ are two additional parameters, ${\mathbb{I}}_{G\left(x\right)}(\theta ,\varphi )$ is the incomplete beta function ratio evaluated at $G\left(x\right)$, and $B(\theta ,\varphi )={\int }_0^1{\omega }^{\theta -1}{(1-\omega )}^{\varphi -1}\mathrm{d}\omega$ is the complete beta function;

(b)

The Kw-G cdf pioneered by Cordeiro and Castro [8] is

$$F_{\mathrm{Kw}-\mathrm{G}}\left(x\right)=1-{\left\{1-G{\left(x\right)}^{\theta }\right\}}^{\varphi },$$

(4)

where $\theta ,\varphi >0$ are two additional parameters;

(c)

The $\mathsf{\Gamma }$-G cdf reported by Zografos and Balakrishnan [7] is

$$F_{\mathsf{\Gamma }-\mathrm{G}}\left(x\right)=\frac{{\displaystyle \gamma \left(\theta ,-log\left[1-G\left(x\right)\right]\right)}}{{\displaystyle \mathsf{\Gamma }\left(\theta \right)}},$$

(5)

where $\theta >0$, $\mathsf{\Gamma }\left(\theta \right)={\int }_0^{\infty }{t}^{\theta -1}{\mathrm{e}}^{-t}\mathrm{d}t$ is the gamma function, and $\gamma (\theta ,z)={\int }_0^z{t}^{\theta -1}{\mathrm{e}}^{-t}\mathrm{d}t$ is the incomplete gamma function;

(d)

The MO-G cdf defined by Marshal and Olkin [5] is

$$F_{\mathrm{MO}-\mathrm{G}}\left(x\right)=1-\frac{\theta [1-G(x\left)\right]}{1-(1-\theta )[1-G(x\left)\right]}=\frac{\theta [1-G(x\left)\right]}{G\left(x\right)+\theta [1-G(x\left)\right]},$$

(6)

where $\theta >0$ is a shape parameter.

For the first two generators, given a p-parameter baseline cdf as input, one has new $(p+2)$-parameter models, whereas for the remaining generators, $(p+1)$-parameter distributions are furnished.

Let $A\left(x\right)={\left(2\pi \right)}^{-1}[x-\mathrm{mod}(x,2\pi )]$, where $\mathrm{mod}(x,y)$ is the remainder after x is divided by y. In what follows, we will do an adaptation to the generators (3)–(6) in order to propose generalized Cardioid models with cdf $F(·)$ and pdf $f(·)$ that satisfy the conditions

• $f(x+2\pi )=f\left(x\right)$;
• $F(x+2\pi )-F\left(x\right)=1$.

The conditions are required for circular data studies (see Mardia and Sutton [24]). The new models present discontinuity in $\{2k\pi :k\in \mathbb{Z}\}$. This pattern also holds for other circular models in the literature such as wrapped exponential [25].

2.1. Beta Cardioid

By applying (1) to Equation (3), the cdf of the $\beta$C distribution is

$$F_1\left(x\right)=A\left(x\right)+{\mathbb{I}}_{\frac{\mathrm{mod}(x,2\pi )}{2\pi }+\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]}(\theta ,\varphi ),$$

for $x\in \mathbb{R}\setminus \{2\pi k:k\in \mathbb{Z}\}$. This case is denoted by $X\sim \beta C(\theta ,\varphi ,\mu ,\rho )$. By differentiating the last equation, the $\beta$C pdf, say $f_1\left(x\right)=f_1(x;\theta ,\varphi ,\mu ,\rho )$, has the form

$$f_1\left(x\right)=\underset{={\overline{h}}_1\left(x\right)}{\underbrace{\frac{h_1\left(x\right)}{2\pi B(\theta ,\varphi )}}}\left[1+2\rho cos(x-\mu )\right],$$

(7)

where ${\overline{h}}_1\left(x\right)=h_1\left(x\right)/\left[2\pi B\right(\theta ,\varphi \left)\right]$ and

$$h_1\left(x\right)=h_1(x;\theta ,\varphi ,\mu ,\rho )=\frac{{\left\{\frac{\mathrm{mod}(x,2\pi )}{2\pi }+\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}}^{\theta -1}}{{\left\{1-\frac{\mathrm{mod}(x,2\pi )}{2\pi }-\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}}^{1-\varphi }}.$$

For $\varphi =1$, the $\beta$C model reduces to the EC distribution discussed by Paula et al. (2020).

Figure 1a–d display $\beta$C densities for some parametric points.

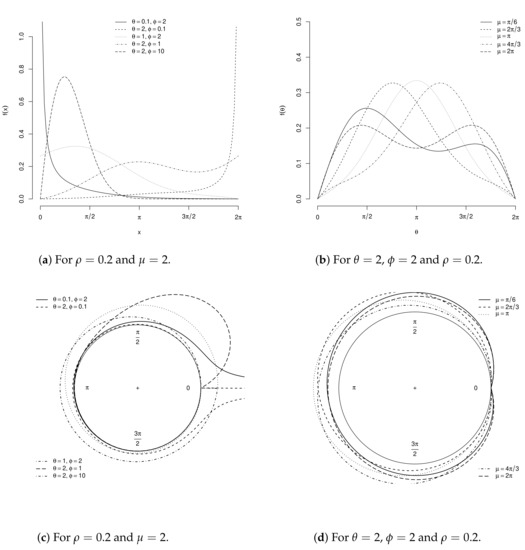
Figure 1. Cartesian and circular $\beta$C densities for some parametric points.

2.2. Kumaraswamy Cardioid

By inserting (1) in Equation (4), the Kw-C cdf, say $F_2\left(x\right)=F_2(x;\theta ,\varphi ,\mu ,\rho )$, can be expressed as

$$\begin{array}{c}\hfill F_2\left(x\right)=A\left(x\right)+1-{\left\{1-{\left\{\frac{\mathrm{mod}(x,2\pi )}{2\pi }+\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}}^{\theta }\right\}}^{\varphi }\end{array}$$

for $x\in \mathbb{R}\setminus \{2\pi k:k\in \mathbb{Z}\}$. This case is denoted by $X\sim KwC(\theta ,\varphi ,\mu ,\rho )$. The KwC pdf, $f_2\left(x\right)=f_2(x;\theta ,\varphi ,\mu ,\rho )$, can be reduced to

$$\begin{array}{c}\hfill f_2\left(x\right)=\underset{={\overline{h}}_2\left(x\right)}{\underbrace{\frac{\theta \varphi h_2\left(x\right)}{2\pi }}}\left[1+2\rho cos(x-\mu )\right],\end{array}$$

(8)

where ${\overline{h}}_2\left(x\right)=\theta \varphi h_2\left(x\right)/\left(2\pi \right)$ and

$$h_2\left(x\right)=h_2(x;\theta ,\varphi ,\mu ,\rho )=\frac{{\left\{\frac{\mathrm{mod}(x,2\pi )}{2\pi }+\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}}^{\theta -1}}{{\left\{1-{\left(\frac{\mathrm{mod}(x,2\pi )}{2\pi }+\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right)}^{\theta }\right\}}^{1-\varphi }}.$$

Figure 2a–d display KwC densities for some parametric points.

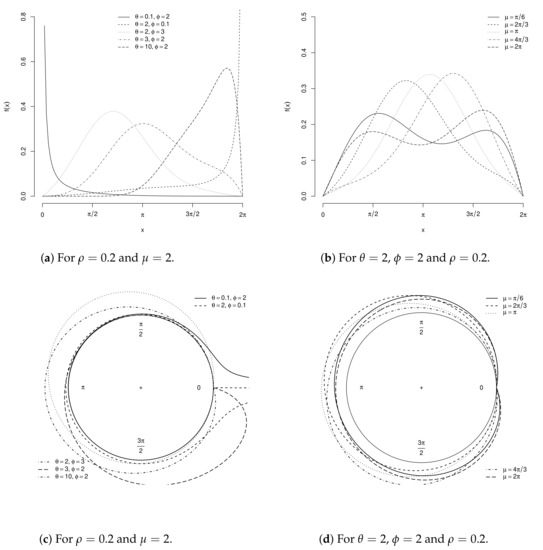
Figure 2. Cartesian and circular KwC densities for some parametric points.

2.3. Gamma Cardioid

By applying (1) in Equation (5), the $\mathsf{\Gamma }$C cdf, $F_3\left(x\right)=F_3(x;\theta ,\mu ,\rho )$, has the form

$$\begin{array}{c}\hfill F_3\left(x\right)=A\left(x\right)+\frac{{\displaystyle \gamma \left(\theta ,-log\left\{1-\frac{\mathrm{mod}(x,2\pi )}{2\pi }-\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}\right)}}{{\displaystyle \mathsf{\Gamma }\left(\theta \right)}},\end{array}$$

for $x\in \mathbb{R}\setminus \{2\pi k:k\in \mathbb{Z}\}$. This case is denoted by $X\sim \mathsf{\Gamma }C(\theta ,\mu ,\rho )$. By differentiating the last equation, the $\mathsf{\Gamma }$C pdf, $f_3\left(x\right)=f_3(x;\theta ,\mu ,\rho )$, reduces to   

$$\begin{array}{c}\hfill {\displaystyle f_3\left(x\right)=\underset{={\overline{h}}_3\left(x\right)}{\underbrace{\frac{{\displaystyle h_3\left(x\right)}}{{\displaystyle 2\pi \mathsf{\Gamma }\left(\theta \right)}}}}\left[1+2\rho cos(x-\mu )\right],}\end{array}$$

(9)

where ${\overline{h}}_3\left(x\right)={\displaystyle h_3\left(x\right)}/{\displaystyle \left[2\pi \mathsf{\Gamma }\right(\theta \left)\right]}$ and

$$h_3\left(x\right)=h_3(x;\theta ,\mu ,\rho )={\left(-log\left\{1-\frac{\mathrm{mod}(x,2\pi )}{2\pi }-\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}\right)}^{\theta -1}.$$

Figure 3a–d display $\mathsf{\Gamma }$C densities for some parametric points.

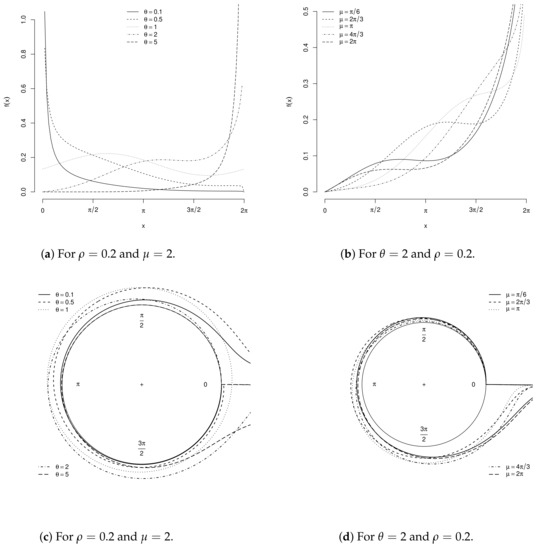
Figure 3. Cartesian and circular $\mathsf{\Gamma }$C densities for some parametric points.

2.4. Marshall–Olkin Cardioid

By inserting (1) in Equation (6), the MOC cdf, $F_4\left(x\right)=F_4(x;\theta ,\mu ,\rho )$, is given by

$$F_4\left(x\right)=A\left(x\right)+\frac{\theta \left\{1-\frac{\mathrm{mod}(x,2\pi )}{2\pi }-\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}}{\frac{\mathrm{mod}(x,2\pi )}{2\pi }+(1-\theta )\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]+\theta \left\{1-\frac{x}{2\pi }\right\}},$$

for $x\in \mathbb{R}\setminus \{2\pi k:k\in \mathbb{Z}\}$. This case is denoted by $X\sim MOC(\theta ,\mu ,\rho )$. Thus, the MOC pdf, $f_4\left(x\right)=f_4(x;\theta ,\mu ,\rho )$, becomes

$$\begin{array}{c}\hfill {\displaystyle f_4\left(x\right)=\underset{={\overline{h}}_4\left(x\right)}{\underbrace{\frac{{\displaystyle \theta h_4\left(x\right)}}{{\displaystyle 2\pi }}}}\left[1+2\rho cos(x-\mu )\right],}\end{array}$$

(10)

where ${\overline{h}}_4\left(x\right)=\theta h_4\left(x\right)/\left(2\pi \right)$ and

$$\begin{array}{cc}\hfill h_4\left(x\right)& =h_4(x;\theta ,\mu ,\rho )\hfill \\ \hfill & ={\left(1-(1-\theta )\left\{1-\frac{\mathrm{mod}(x,2\pi )}{2\pi }-\frac{\rho }{\pi }\left[sin(x-\mu )+sin\left(\mu \right)\right]\right\}\right)}^{-2}.\hfill \end{array}$$

Figure 4a–d display MOC densities for some parametric points.

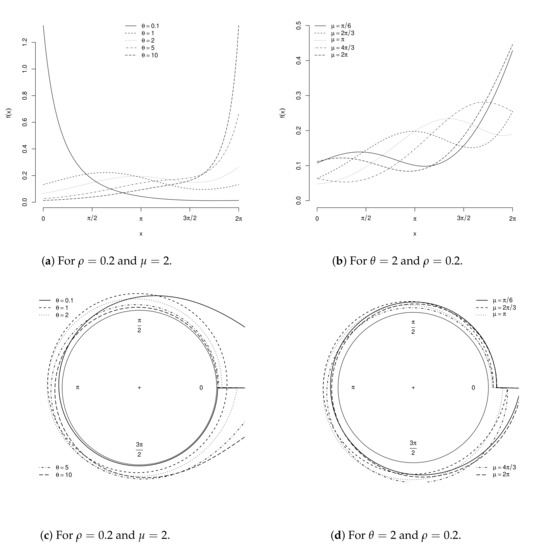
Figure 4. Cartesian and circular MOC densities for some parametric points.

2.5. A General Formula

All four extensions have the same support, and their densities can be expressed as

$$f_i\left(x\right)={\overline{h}}_i\left(x\right)\left[1+2\rho cos(x-\mu )\right],\mathrm{for}i=1,\dots ,4,$$

(11)

where ${\overline{h}}_i\left(x\right)$ is defined in Table 1.

Table 1. The weighted multipliers for the proposed models.

Model	C	$\mathit{\beta }\mathit{C}$	KwC	$\mathbf{\Gamma }$C	MOC
Index (i)	•	1	2	3	4
Expression	${\left(2\pi \right)}^{-1}$	${\overline{h}}_1\left(x\right)$	${\overline{h}}_2\left(x\right)$	${\overline{h}}_3\left(x\right)$	${\overline{h}}_4\left(x\right)$

The new densities can be interpreted as weighted multipliers for the baseline pdf kernel $\left[1+2\rho cos(x-\mu )\right]$. Thus, the behavior of ${\overline{h}}_i\left(x\right)$ in (11) has an important task for studying the flexibility of the new models. Figure 5 displays the weighted functions ${\overline{h}}_i\left(x\right)$. For these plots, we set $(\mu ,\rho )=(2,0.2)$ and consider $\theta =\varphi \in (0,100)$ and $x\in (0,2\pi )$. Note that although ${\overline{h}}_3\left(x\right)$ and ${\overline{h}}_4\left(x\right)$ have the highest values, ${\overline{h}}_1\left(x\right)$ and ${\overline{h}}_2\left(x\right)$ present larger domain regions, which lead to more flexible scenarios. Thus, we conclude that the $\beta$C and KwC can be more flexible among these models.

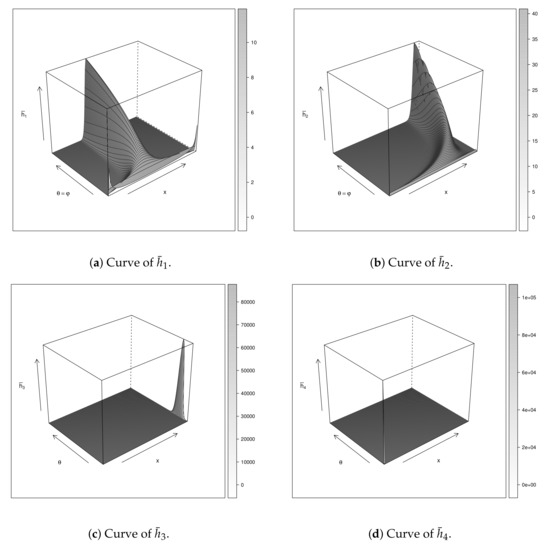
Figure 5. Weighted curves of $f_i\left(x\right)$.

3. Mathematical Properties

In this section, we obtain the trigonometric moments for the new models. First, we recall some concepts in the area of circular distributions. We follow the notation of Pewsey et al. [26].

Analogously as over the real line, a circular distribution can also be described by its characteristic function (cf). However, as random variables X considered in this paper are periodic, we can write

$${\varphi }_X\left(t\right)=\mathbb{E}\left({\mathrm{e}}^{itX}\right)=\mathbb{E}\left[{\mathrm{e}}^{it(X+2\pi )}\right]={\mathrm{e}}^{it2\pi }\mathbb{E}\left({\mathrm{e}}^{itX}\right),$$

where $i=\sqrt{-1}$, which implies ${\varphi }_X\left(t\right)=0$ or ${\mathrm{e}}^{it2\pi }=1$; i.e., the cf should be defined only at integer values.

The cf evaluated at an integer p is called the pth trigonometric moment of X defined by

$${\tau }_{p,0}=\mathbb{E}\left({\mathrm{e}}^{ipX}\right)=\underset{{\alpha }_p}{\underbrace{\mathbb{E}[cos(pX\left)\right]}}+i\underset{{\beta }_p}{\underbrace{\mathbb{E}[sin(pX\left)\right]}}.$$

The quantity ${\tau }_{p,0}$ is the mean resultant vector in the complex plane of length ${\rho }_p=\left|{\tau }_{p,0}\right|=\sqrt{{\alpha }_p^2+{\beta }_p^2}\in [0,1]$ and direction

$${\mu }_p=\left\{\begin{array}{c}\arctan ({\beta }_p/{\alpha }_p),{\alpha }_p>0,\hfill \\ \arctan ({\beta }_p/{\alpha }_p)+\pi ,{\beta }_p\ge 0,{\alpha }_p<0,\hfill \\ \arctan ({\beta }_p/{\alpha }_p)-\pi ,{\beta }_p<0,{\alpha }_p<0,\hfill \\ \pi /2,{\beta }_p>0,{\alpha }_p=0,\hfill \\ -\pi /2,{\beta }_p<0,{\alpha }_p=0,\hfill \\ \mathrm{undefined},{\beta }_p={\alpha }_p=0,\hfill \end{array}\right.$$

where $|·|$ is the norm of a complex argument. The quantities ${\rho }_1$ and ${\mu }_1$ are fundamental measures of concentration and location, respectively. The polar representation of ${\tau }_{p,0}$ is

$${\tau }_{p,0}={\rho }_p{\mathrm{e}}^{i{\mu }_p}=\underset{{\alpha }_p}{\underbrace{{\rho }_{p}cos\left({\mu }_p\right)}}+i\underset{{\beta }_p}{\underbrace{{\rho }_{p}sin\left({\mu }_p\right)}}.$$

Furthermore, the pth central trigonometric moment of a circular distribution is

$${\tau }_{p,{\mu }_1}=\underset{{\overline{\alpha }}_p}{\underbrace{\mathbb{E}\{cos\left[p(X-{\mu }_1)\right]\}}}+i\underset{{\overline{\beta }}_p}{\underbrace{\mathbb{E}\{sin\left[p(X-{\mu }_1)\right]\}}},$$

(12)

where ${\overline{\alpha }}_p$ and ${\overline{\beta }}_p$ are its real and imaginary parts. The polar representation of ${\tau }_{p,{\mu }_1}$ is given by

$${\tau }_{p,{\mu }_1}={\tau }_{p,0}{\mathrm{e}}^{-ip{\mu }_1}={\rho }_p[cos({\mu }_p-p{\mu }_1)+isin({\mu }_p-p{\mu }_1)].$$

Here, we are interested in finding expressions for ${\tau }_{p,{\mu }_1}$.

In what follows, $\mu$ refers to the parameter discussed previously in the models, while ${\mu }_1$ is the mean direction.

Furthermore, we derive expansions for $f_i\left(x\right)$ by means of the following results. First, consider a baseline distribution having cdf $G\left(x\right)$ and pdf $g\left(x\right)$. The exp-G family with power parameter $\theta >0$ has cdf and pdf given by

$${\mathsf{\Pi }}_{\theta }\left(x\right)=G{\left(x\right)}^{\theta }\mathrm{and}{\pi }_{\theta }\left(x\right)=\theta g\left(x\right)G{\left(x\right)}^{\theta -1},$$

respectively. Expansions for densities obtained from Equations (3)–(6) have often been given in terms of the last two functions:

• From Nadarajah et al. [27]:

  $$f_{\beta -\mathrm{G}}\left(x\right)=\sum _{i=0}^{\infty }\underset{w_i^{\left(1\right)}=w_i^{\left(1\right)}(\theta ,\varphi )}{\underbrace{\frac{{(-1)}^i}{(\theta +i)}\left(\genfrac{}{}{0pt}{}{\varphi -1}{i}\right){\left[B(\theta ,\varphi )\right]}^{-1}}}\underset{{\pi }_{\theta +i}\left(x\right)}{\underbrace{(\theta +i)g\left(x\right){\mathsf{\Pi }}_{\theta +i-1}\left(x\right)}}.$$

  (13)
• From Cordeiro and de Castro [8]:

  $$f_{\mathrm{Kw}-\mathrm{G}}\left(x\right)=\sum _{i=0}^{\infty }\underset{w_i^{\left(2\right)}=w_i^{\left(2\right)}(\theta ,\varphi )}{\underbrace{\frac{{(-1)}^i\theta \varphi }{\theta (i+1)}\left(\genfrac{}{}{0pt}{}{\varphi -1}{i}\right)}}\underset{{\pi }_{(i+1)\theta }\left(x\right)}{\underbrace{\theta (i+1)g\left(x\right){\mathsf{\Pi }}_{(i+1)\theta -1}\left(x\right)}}.$$

  (14)
• From Castellares and Lemonte [28]:

  $$f_{\mathsf{\Gamma }-\mathrm{G}}\left(x\right)=\sum _{i=0}^{\infty }\underset{w_i^{\left(3\right)}=w_i^{\left(3\right)}\left(\theta \right)}{\underbrace{\frac{{\phi }_i\left(\theta \right)}{(i+\theta )}}}{\pi }_{\theta +i}\left(x\right),$$

  (15)

  where

  $${\phi }_0\left(\theta \right)=\frac{1}{\mathsf{\Gamma }\left(\theta \right)},{\phi }_i\left(\theta \right)=\frac{{\rho }_i\left(\theta \right)}{\mathsf{\Gamma }\left(\theta \right)}=\frac{(\theta -1)}{\mathsf{\Gamma }\left(\theta \right)}{\psi }_{i-1}(i+\theta -2),i\ge 1,$$

  and ${\psi }_{i-1}(·)$ are the Stirling polynomials given in Castellares and Lemonte [28].
• From Cordeiro et al. [29]:

  $$f_{\mathrm{MO}-\mathrm{G}}\left(x\right)=\sum _{i=0}^{\infty }{w}_i^{\left(4\right)}{\pi }_{i+1}\left(x\right),$$

  (16)

  where the coefficients $w_i^{\left(4\right)}=w_i^{\left(4\right)}\left(\theta \right)$ are given by ($i=0,1,\dots$)

  $$w_i^{\left(4\right)}=\left\{\begin{array}{c}\frac{{(-1)}^i\theta }{(i+1)}\sum _{j=i}^{\infty }(j+1)\left(\genfrac{}{}{0pt}{}{j}{i}\right){\overline{\theta }}^j,\theta \in (0,1),\hfill \\ {\theta }^{-1}{(1-{\theta }^{-1})}^i,\theta >1,\hfill \end{array}\right.$$

  and $\overline{\theta }=1-\theta$.
• From Paula et al. [18]:  
  Let $X_{EC}\sim EC(\theta ,\mu ,\rho )$. The cdf of $X_{EC}$ is (Paula et al., 2020)

  $${\mathsf{\Pi }}_{\theta }(x;\mu ,\rho )=\sum _{k=0}^{\infty }\sum _{l=0}^k{b}_{k,l}(\theta ,\mu ,\rho )x^{\theta -k}{sin}^l(x-\mu ).$$

  (17)
  By simple differentiation, we can write

  $$\begin{array}{cc}\hfill {\pi }_{\theta }(x;\mu ,\rho )=& \sum _{k=0}^{\infty }\sum _{l=0}^k\sum _{q=0}^1[ql+(1-q)(\theta -k)]b_{k,l}(\theta ,\mu ,\rho )\hfill \\ \hfill & \times m_{\theta -k+q-1,q,l-q}(x;\mu ),\hfill \end{array}$$

  where $m_{p,q,r}(x;\mu )=x^p{cos}^q(x-\mu ){sin}^r(x-\mu )$,

  $$b_{k,l}(\theta ,\mu ,\rho )=\left(\genfrac{}{}{0pt}{}{\theta }{k}\right)\left(\genfrac{}{}{0pt}{}{k}{l}\right){\left(\frac{\rho }{\pi }\right)}^k\frac{{sin}^{k-l}\left(\mu \right)}{{\left(2\pi \right)}^{\theta -k}}.$$
  After some algebraic manipulations, the pth central circular trigonometric moment of $X_{EC}$, say ${\tau }_{p,{\mu }_1}^{EC\left(\theta \right)}$, with mean direction ${\mu }_1$, follows as

  $$\begin{array}{cc}\hfill {\tau }_{p,{\mu }_1}^{EC\left(\theta \right)}& ={\mathrm{e}}^{-ip{\mu }_1}+p\{{\int }_0^{2\pi }sin\left[p(x-{\mu }_1)\right]{\mathsf{\Pi }}_{\theta }(x;\mu ,\rho )\mathrm{d}x\hfill \\ \hfill & +i{\int }_0^{2\pi }cos\left[p(x-{\mu }_1)\right]{\mathsf{\Pi }}_{\theta }(x;\mu ,\rho )\mathrm{d}x\}\hfill \\ \hfill & ={\mathrm{e}}^{-ip{\mu }_1}+p\sum _{k=0}^{\infty }\sum _{l=0}^k{b}_{k,l}(\theta ,\mu ,\rho )\hfill \\ \hfill & \times [A_1(\theta -k,l,p)-i{A}_2(\theta -k,l,p)],\hfill \end{array}$$

  (18)

  where $A_1(a,b,c)={\int }_0^{2\pi }{x}^a{sin}^b(x-\mu )sin\left(c(x-{\mu }_1)\right)\mathrm{d}x$ and $A_2(a,b,c)={\int }_0^{2\pi }$$x^a$${sin}^b(x-\mu )cos\left(c(x-{\mu }_1)\right)\mathrm{d}x$. The functions $A_1(·,·,·)$ and $A_2(·,·,·)$ are easily handled both numerically and analytically.
  For example, Table 2 displays some special quantities using the symbolic computation software wxmaxima.
  Table 2. Some expressions for $A_1(·,·,·)$ and $A_2(·,·,·)$.

  $A_2(1,1,1)=-\frac{4\pi cos\left({\mu }_1+\mu \right)-8{\pi }^{2}sin\left({\mu }_1-\mu \right)}{8}$

  $A_1(1,1,1)=\frac{4\pi sin\left({\mu }_1+\mu \right)+8{\pi }^{2}cos\left({\mu }_1-\mu \right)}{8}$

  $A_2(2,2,2)=\frac{\left(96{\pi }^2-3\right)sin\left(2{\mu }_1+2\mu \right)-24\pi cos\left(2{\mu }_1+2\mu \right)-256{\pi }^{3}cos\left(2{\mu }_1-2\mu \right)+\left(48-384{\pi }^2\right)sin\left(2{\mu }_1\right)+192\pi cos\left(2{\mu }_1\right)}{384}$

  $+\frac{sin\left(2{\mu }_1+2\mu \right)-16sin\left(2{\mu }_1\right)}{128}$

  $A_1(2,2,2)=\frac{24\pi sin\left(2{\mu }_1+2\mu \right)+\left(96{\pi }^2-3\right)cos\left(2{\mu }_1+2\mu \right)+256{\pi }^{3}sin\left(2{\mu }_1-2\mu \right)-192\pi sin\left(2{\mu }_1\right)+\left(48-384{\pi }^2\right)cos\left(2{\mu }_1\right)}{384}$

  $+\frac{cos\left(2{\mu }_1+2\mu \right)-16cos\left(2{\mu }_1\right)}{128}$

By applying (17) to Equations (13)–(16), we obtain linear representations for (11), which hold for the four generalized C distributions.

Theorem 1.

The pdf (11) can be expanded as

$$f_i\left(x\right)=\frac{1}{2\pi }[1+2\rho cos(x-\mu )]\sum _{k=0}^{\infty }\sum _{l=0}^k\sum _{t=0}^{\infty }{b}_{k,l,t}^{\left(i\right)}{x}^{in{d}_i\left(t\right)-1-k}{sin}^l(x-\mu ),$$

(19)

where $b_{k,l,t}^{\left(i\right)}=in{d}_i\left(t\right)w_t^{\left(i\right)}(\theta ,\varphi )b_{k,l}(in{d}_i\left(t\right)-1,\mu ,\rho )$ for $i=1,\dots ,4$, $in{d}_1\left(t\right)=\theta +t$, $in{d}_2\left(t\right)=\theta (t+1)$, $in{d}_3\left(t\right)=\theta +t$ and $in{d}_4\left(t\right)=t$.

Equation (19) can be used to derive some mathematical properties (having intractable analytical forms) of $f_i\left(x\right)$ (for $i=1,\dots ,4$). Furthermore, as a consequence, we have expansions for the weights ${\overline{h}}_i\left(x\right)$ (which have complex forms) as linear combinations of $x^{l-v}{sin}^h(x-\mu )$. Proposing criteria for choosing the best $f_i\left(x\right)$ based on these expansions may be a promising research branch. In particular, we obtain expressions for the central trigonometric moments of distributions with pdf (11).

Corollary 1.

Let ${\tau }_{p,{\mu }_1}^{\left(j\right)}$ be the pth central trigonometric moment of the model $F_j$. We obtain

$$\begin{array}{cc}\hfill {\tau }_{p,{\mu }_1}^{\left(j\right)}={\mathrm{e}}^{-ip{\mu }_1}\left(\sum _{t=0}^{\infty }{w}_t^{\left(j\right)}(\theta ,\varphi )\right)+& p\sum _{k=0}^{\infty }\sum _{l=0}^k{d}_{k,l}^{\left(j\right)},\hfill \end{array}$$

where

$$d_{k,l}^{\left(j\right)}=\sum _{t=0}^{\infty }[A_1(in{d}_j\left(t\right)-k,l,p)-i{A}_2(in{d}_j\left(t\right)-k,l,p)]w_t^{\left(j\right)}(\theta ,\varphi )b_{k,l}(in{d}_j\left(t\right),\mu ,\rho ),$$

and $in{d}_j\left(t\right)$ is given in Theorem 1.

Proof of Corollary 1.

Let ${\tau }_{p,{\mu }_1}^{\left(j\right)}$ be the pth circular trigonometric moment of $X^{\left(j\right)}\sim F_j$.

Furthermore, let $in{d}_1\left(t\right)=\theta +t$, $in{d}_2\left(t\right)=\theta (t+1)$, $in{d}_3\left(t\right)=\theta +t$, and $in{d}_4\left(t\right)=t$. Thus, assuming ${\overline{\alpha }}_p^{EC\left(\theta \right)}$ and ${\overline{\beta }}_p^{EC\left(\theta \right)}$, similar to real and imaginary parts of ${\tau }_{p,{\mu }_1}^{EC\left(\theta \right)}$ in (18), it follows from Equations (13)–(16):

$$\begin{array}{cc}\hfill {\tau }_{p,{\mu }_1}^{\left(j\right)}& =\mathbb{E}\left\{cos\left[p\left(X^{\left(j\right)}-{\mu }_1\right)\right]\right\}+i\mathbb{E}\left\{sin\left[p\left(X^{\left(j\right)}-{\mu }_1\right)\right]\right\}\hfill \\ \hfill & =\sum _{t=0}^{\infty }{w}_t^{\left(j\right)}(\theta ,\varphi ){\overline{\alpha }}_p^{EC\left(in{d}_j\left(t\right)\right)}+i\sum _{t=0}^{\infty }{w}_t^{\left(j\right)}(\theta ,\varphi ){\overline{\beta }}_p^{EC\left(in{d}_j\left(t\right)\right)}\hfill \\ \hfill & =\sum _{t=0}^{\infty }{w}_t^{\left(j\right)}(\theta ,\varphi ){\tau }_{p,{\mu }_1}^{EC\left(in{d}_j\left(t\right)\right)}={\mathrm{e}}^{-ip{\mu }_1}\left(\sum _{t=0}^{\infty }{w}_t^{\left(j\right)}(\theta ,\varphi )\right)+p\sum _{k=0}^{\infty }\sum _{l=0}^k{d}_{k,l}^{\left(j\right)},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill d_{k,l}^{\left(j\right)}=\sum _{t=0}^{\infty }{w}_t^{\left(j\right)}(\theta ,\varphi )b_{k,l}(in{d}_j\left(t\right),\mu ,\rho )[A_1(in{d}_j\left(t\right)-k,l,p)-i{A}_2(in{d}_j\left(t\right)-k,l,p)].\end{array}$$

   □

4. Estimation

This section tackles a brief discussion about maximum likelihood estimation of the parameters of the pdf family (11). Several approaches for estimating the parameters have been proposed in the literature, but the maximum likelihood method is the most commonly employed. The maximum likelihood estimates (MLEs) present desirable properties for constructing confidence intervals for the parameters. They are easily computed by using well-known platforms such as the R (optim function), SAS (PROC NLMIXED), and Ox program (MaxBFGS sub-routine)..

Let $x_1,\dots ,x_n$ be an observed sample from a random variable having pdf (11). Thus, the associated log-likelihood function for $\mathbf{\delta }={(\theta ,\varphi ,\mu ,\rho )}^{\top }$ can be expressed as (for $i=1,\dots 4$)

$$\begin{array}{c}\hfill {\ell }_i\left(\mathbf{\delta }\right)=\sum _{j=1}^{n}log{f}_i\left(x_j\right)=\sum _{j=1}^n\{log{\overline{h}}_i\left(x_j\right)+log[1+2\rho cos(x_j-\mu )]\}.\end{array}$$

(20)

The score vector follows from ${\ell }_i\left(\mathbf{\delta }\right)$ as

$$(U_{\theta ,i},U_{\varphi ,i},U_{\mu ,i},U_{\rho ,i})=\left(\frac{\partial {\ell }_i\left(\mathbf{\delta }\right)}{\partial \theta },\frac{\partial {\ell }_i\left(\mathbf{\delta }\right)}{\partial \varphi },\frac{\partial {\ell }_i\left(\mathbf{\delta }\right)}{\partial \mu },\frac{\partial {\ell }_i\left(\mathbf{\delta }\right)}{\partial \rho }\right),$$

whose components are

$$U_{\theta ,i}=\sum _{j=1}^n\frac{1}{{\overline{h}}_i\left(x_j\right)}\frac{\partial {\overline{h}}_i\left(x_j\right)}{\partial \theta },U_{\varphi ,i}=\sum _{j=1}^n\frac{1}{{\overline{h}}_i\left(x_j\right)}\frac{\partial {\overline{h}}_i\left(x_j\right)}{\partial \varphi },$$

$$U_{\mu ,i}=\sum _{j=1}^n\left\{\frac{1}{{\overline{h}}_i\left(x_j\right)}\frac{\partial {\overline{h}}_i\left(x_j\right)}{\partial \mu }+\frac{2\rho sin(x_j-\mu )}{1+2\rho cos(x_j-\mu )}\right\},$$

and

$$U_{\rho ,i}=\sum _{j=1}^n\left\{\frac{1}{{\overline{h}}_i\left(x_j\right)}\frac{\partial {\overline{h}}_i\left(x_j\right)}{\partial \rho }+\frac{2cos(x_j-\mu )}{1+2\rho cos(x_j-\mu )}\right\}.$$

Thus, the MLE of $\mathbf{\delta }$ is $\widehat{\mathbf{\delta }}={\mathrm{argmax}}_{\mathbf{\delta }\in \mathsf{\Delta }}\left\{{\ell }_i\left(\mathbf{\delta }\right)\right\},$ where $\mathsf{\Delta }$ is the parametric space or, equivalently, the solution of the system of nonlinear equations $U_{\theta ,i}=U_{\varphi ,i}=U_{\mu ,i}=U_{\rho ,i}=0$. The compactness of the parameter space $\mathsf{\Delta }$ and the continuity of the log-likelihood function on $\mathsf{\Delta }$ are sufficient for the existence of the MLE.

The partitioned observed information matrix for the model $F_i\left(x\right)$ takes the form (for $i=1,\dots ,4$)

$$\begin{array}{cc}\hfill {\mathbf{J}}_i\left(\delta \right)& =-\left(\begin{array}{cccc}{U}_{\theta \theta ,i}& U_{\theta \varphi ,i}& U_{\theta \mu ,i}& U_{\theta \rho ,i}\\ U_{\varphi \theta ,i}& U_{\varphi \varphi ,i}& U_{\varphi \mu ,i}& U_{\varphi \rho ,i}\\ U_{\mu \theta ,i}& U_{\mu \varphi ,i}& U_{\mu \mu ,i}& U_{\mu \rho ,i}\\ U_{\rho \theta ,i}& U_{\rho \varphi ,i}& U_{\rho \mu ,i}& U_{\rho \rho ,i}\end{array}\right)\hfill \\ \hfill & =-\left\{U_{ab,i}=\frac{{\partial }^2{\ell }_i\left(\mathbf{\delta }\right)}{\partial a\partial b}\mathrm{for}a,b=\theta ,\varphi ,\mu ,\rho \right\},\hfill \end{array}$$

whose elements are

$$U_{\tau \nu ,i}=\sum _{j=1}^n{U}_{\tau \nu ,i}\left(j\right),$$

for $\{\tau ,\nu \in (\theta ,\varphi ,\mu ,\nu \left)\right\}-\left\{\right(\tau ,\nu ):\tau =\nu =\mu ,\rho \mathrm{and}(\tau ,\nu )=(\mu ,\rho ),(\rho ,\mu \left)\right\}$, where

$$U_{\tau \nu ,i}\left(j\right)=\frac{1}{{\overline{h}}_i\left(x_j\right)}\frac{{\partial }^2{\overline{h}}_i\left(x_j\right)}{\partial \tau \partial \nu }-\frac{1}{{\overline{h}}_i^2\left(x_j\right)}\frac{\partial {\overline{h}}_i\left(x_j\right)}{\partial \tau }\frac{\partial {\overline{h}}_i\left(x_j\right)}{\partial \nu },$$

$$U_{\mu \rho ,i}=\sum _{j=1}^n\left\{U_{\mu \rho ,i}\left(j\right)+\frac{2sin(x_j-\mu )}{{[1+2\rho cos(x_j-\mu )]}^2}\right\},$$

$$U_{\mu \mu ,i}=\sum _{j=1}^n\left\{U_{\mu \mu ,i}\left(j\right)+\frac{[4{\rho }^2-2\rho cos(x_j-\mu )-8{\rho }^2{cos}^2(x_j-\mu )]}{{[1+2\rho cos(x_j-\mu )]}^2}\right\},$$

and

$$U_{\rho \rho ,i}=\sum _{j=1}^n\left\{U_{\rho \rho ,i}\left(j\right)+\frac{4\rho sin(x_j-\mu )cos(x_j-\mu )}{{[1+2\rho cos(x_j-\mu )]}^2}\right\}.$$

For interval estimation of the parameters in $F_i\left(x\right)$, we obtain the Fisher information matrix (FIM) ${\mathbf{K}}_i\left(\mathbf{\delta }\right)=\mathbb{E}\left(J_i\left(\delta \right)\right)$ under standard regularity conditions.

For n sufficiently large, $\sqrt{n}(\widehat{\mathbf{\delta }}-\mathbf{\delta })\stackrel{\mathcal{D}}{\to }{N}_4(\mathbf{0},{\dot{\mathit{K}}}_i\left(\mathbf{\delta }\right))$ from a result in Casella and Berger [30], where ${\dot{\mathit{K}}}_i={\mathit{K}}_i/n$ is the unit FIM, “$N_k(\mathbf{\mu },\mathsf{\Sigma })$” denotes the k-dimensional multivariate normal distribution with parameters $\mathbf{\mu }$ and $\mathsf{\Sigma }$, and “$\stackrel{\mathcal{D}}{\to }$” means convergence in distribution.

However, the FIM is seldom tractable. As a solution, we can adopt ${\mathit{J}}_i$ instead of ${\mathit{K}}_i$. This last strategy will be used in the numerical results. In the next section, the last asymptotic result will be used to determine the standard errors associated with MLEs.

5. Applications

In this section, we provide two applications to illustrate the potentiality of the proposed models. The first dataset consists of 21 wind directions obtained by a Milwaukee weather station at 6:00 a.m. on consecutive days (see [31]). The second one corresponds to the directions taken by 76 turtles after treatment addressed by Stephens [32].

The Cartesian histograms of first and second datasets in Figure 6a and Figure 7a indicate positive ($0.4313$) and negative ($-0.0816$) skewness, respectively. Furthermore, these datasets have bimodal shapes.

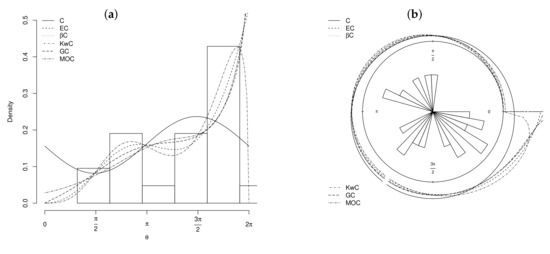
Figure 6. Fitted densities of the C, EC, $\beta$C, KwC, $\mathsf{\Gamma }$C, and MOC models to the first dataset. (a) histogram and (b) rose diagram.

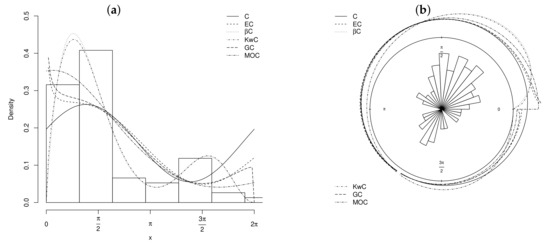
Figure 7. Fitted densities of the C, EC, $\beta$C, KwC, $\mathsf{\Gamma }$C, and MOC models to the second dataset. (a) histogram and (b) rose diagram.

First, the MLEs and their SEs (given in parentheses) are evaluated and, subsequently, the values of the Kuiper (K), Watson (W), Akaike information criterion (AIC), and Bayesian information criterion (BIC) statistics. The first two adherence measures are used in the context of circular statistics and can be found in Jammalamadaka and Sengupta [23]. All computations were performed using function maxLik of the R statistical software (see [33]).

The results for the first and second datasets are reported in Table 3 and Table 4, respectively. We note that all generalized models fit both datasets better than the Cardioid model according to these statistics. For the first dataset, the EC distribution stands out according to the K, AIC, and BIC measures, while the $\beta$C model yields the best fit to the dataset according to the W statistic. The $\beta$C model outperforms the other models for the second dataset.

Table 3. MLEs of the parameters for the first dataset, their standard errors (given in parentheses), and the Kuiper, Watson, AIC, and BIC statistics.

Model	$\mathit{\rho }$	$\mathit{\mu }$	$\mathit{\theta }$	$\mathit{\varphi }$	Kuiper	Watson	AIC	BIC
C	$0.2436$	$4.6708$	−	−	$1.1590$	$0.0711$	$76.5763$	$80.6654$
	($0.1463$)	($0.6835$)	−	−
EC	$0.2164$	$1.1780$	$2.8755$	−	$0.7367$	$0.0257$	$68.6317$	$74.7653$
	$\left(0.1465\right)$	$\left(0.6168\right)$	$\left(0.8929\right)$	−
$\beta$C	$0.2774$	$0.9093$	$3.9353$	$1.4044$	$0.8060$	$0.0247$	$68.8623$	$77.0404$
	($0.0980$)	($0.5030$)	($2.6919$)	($0.6641$)
KwC	$0.2767$	$0.9381$	$3.6511$	$1.4144$	$0.8038$	$0.0240$	$68.8919$	$77.0700$
	($0.0989$)	($0.4933$)	($2.1205$)	($1.1213$)
$\mathsf{\Gamma }$C	$0.1364$	$1.7274$	$1.8563$	−	$0.8289$	$0.0328$	$70.0159$	$76.1495$
	($0.1349$)	($0.6820$)	($0.2566$)	−
MOC	$0.2007$	$2.0632$	$4.5765$	−	$0.8134$	$0.0327$	$70.6394$	$76.7730$
	($0.1277$)	($0.7659$)	($1.8103$)	−

Table 4. MLEs of the parameters for the second dataset, their standard errors (given in parentheses), and the Kuiper, Watson, AIC, and BIC statistics.

Model	$\mathit{\rho }$	$\mathit{\mu }$	$\mathit{\theta }$	$\mathit{\varphi }$	Kuiper	Watson	AIC	BIC
C	$0.3259$	$1.2022$	−	−	$2.4852$	$0.4855$	$254.6554$	$261.3169$
	($0.0553$)	($0.3337$)	−	−
EC	$0.3067$	$1.6025$	$0.7688$	−	$2.3610$	$0.4443$	$251.9396$	$261.9318$
	$\left(0.1256\right)$	$\left(0.0829\right)$	$\left(0.5656\right)$	−
$\beta$C	$0.3978$	$0.1441$	$1.8836$	$3.1088$	$1.2683$	$0.0917$	$231.1254$	$244.4483$
	($0.0538$)	($0.1892$)	($0.4959$)	($1.0142$)
KwC	$0.3985$	$0.1712$	$1.6295$	$3.2205$	$1.3204$	$0.1007$	$231.9943$	$245.3172$
	($0.0543$)	($0.2713$)	($0.3180$)	($1.8769$)
$\mathsf{\Gamma }$C	$0.2829$	$1.5308$	$0.7788$	−	$2.3005$	$0.4006$	$249.8842$	$259.8764$
	($0.0776$)	($0.4744$)	($0.0760$)	−
MOC	$0.2160$	$1.9026$	$0.3880$	−	$1.9593$	$0.2614$	$242.0967$	$252.0889$
	($0.1088$)	($0.7594$)	($1.1475$)	−

Figure 6 and Figure 7 display plots of the empirical and fitted densities to these data. The plots support the indications from these tables.

6. Conclusions

We propose four new distributions with supports on the circle. These extensions of the Cardioid (C) distribution follow by inserting this distribution in the beta-G, gamma-G, Kumaraswamy-G (Kw-G), and Marshall–Olkin-G generators, considering a specific adaptation. We derive expansions for the densities and trigonometric moments of the new models. We also discuss the maximum likelihood estimation for their parameters. Two applications illustrate the flexibility of the proposed models to fit real data.