Spirally Confined Reinforcing Bar for Flexural Behavior of Glass Fiber-Reinforced Concrete Beam
Abstract
1. Introduction
2. Materials and Methods
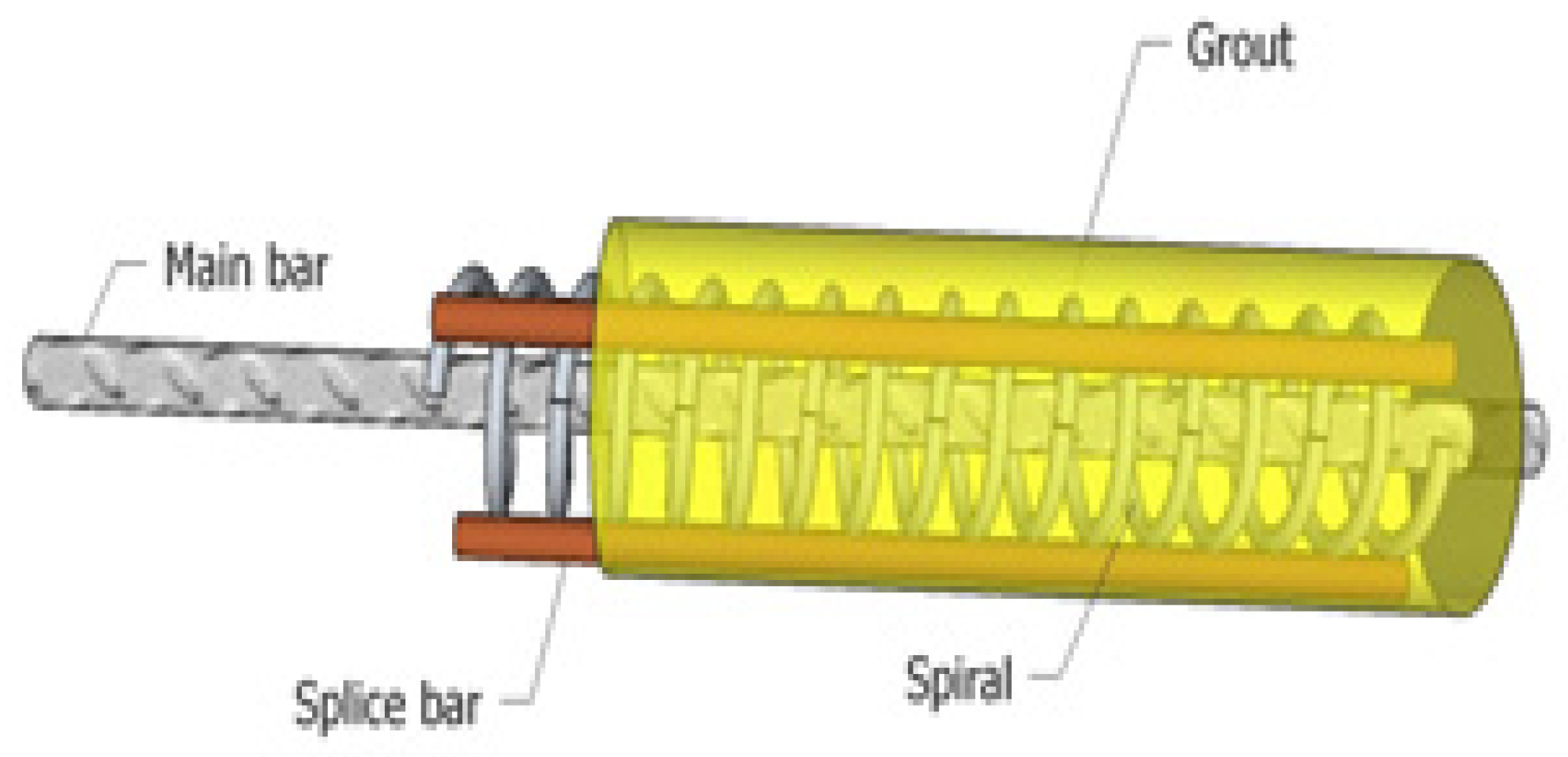
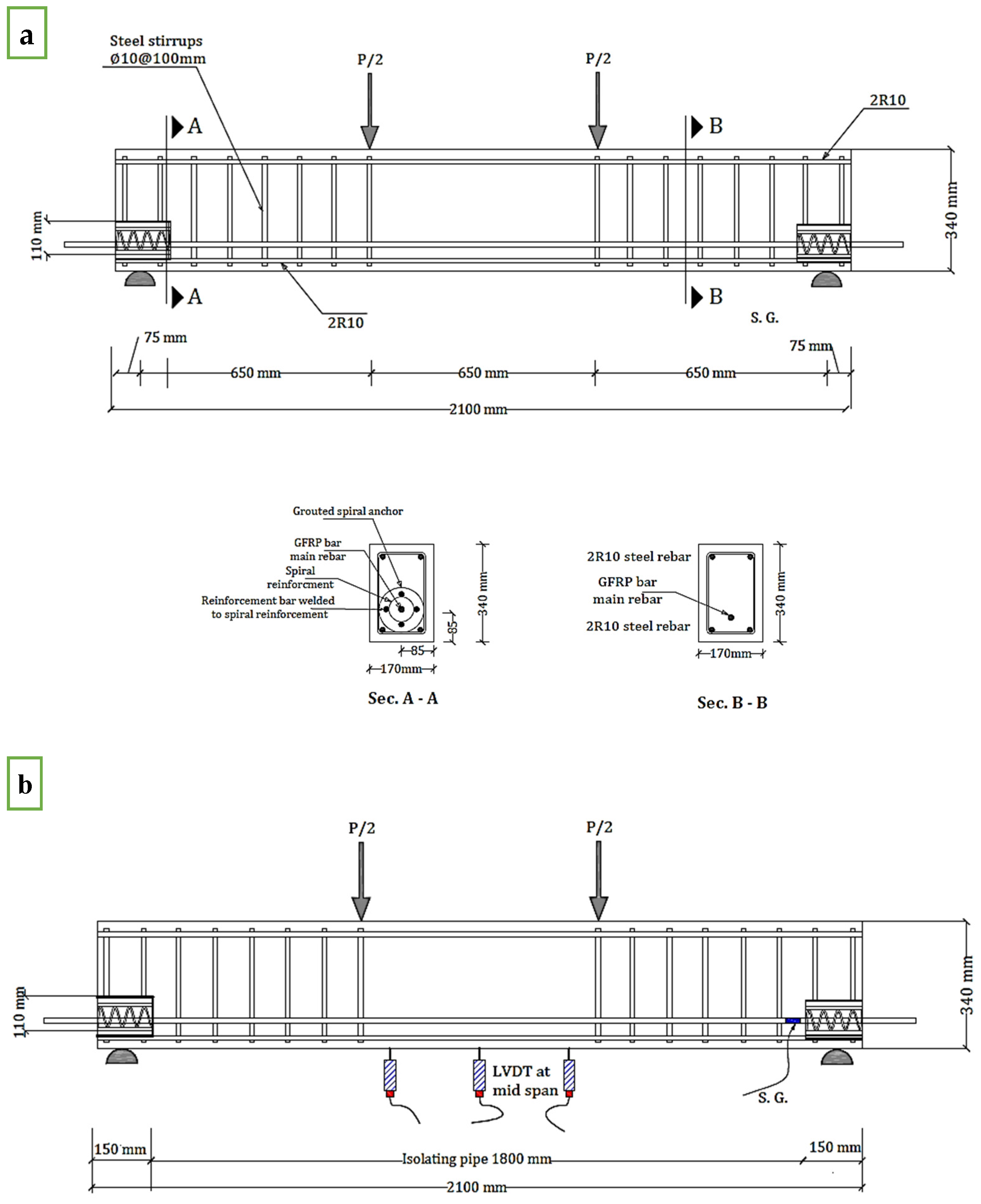
2.1. Beam Specimens and Materials
2.2. Test Setup and Test Procedures
3. Results and Discussions
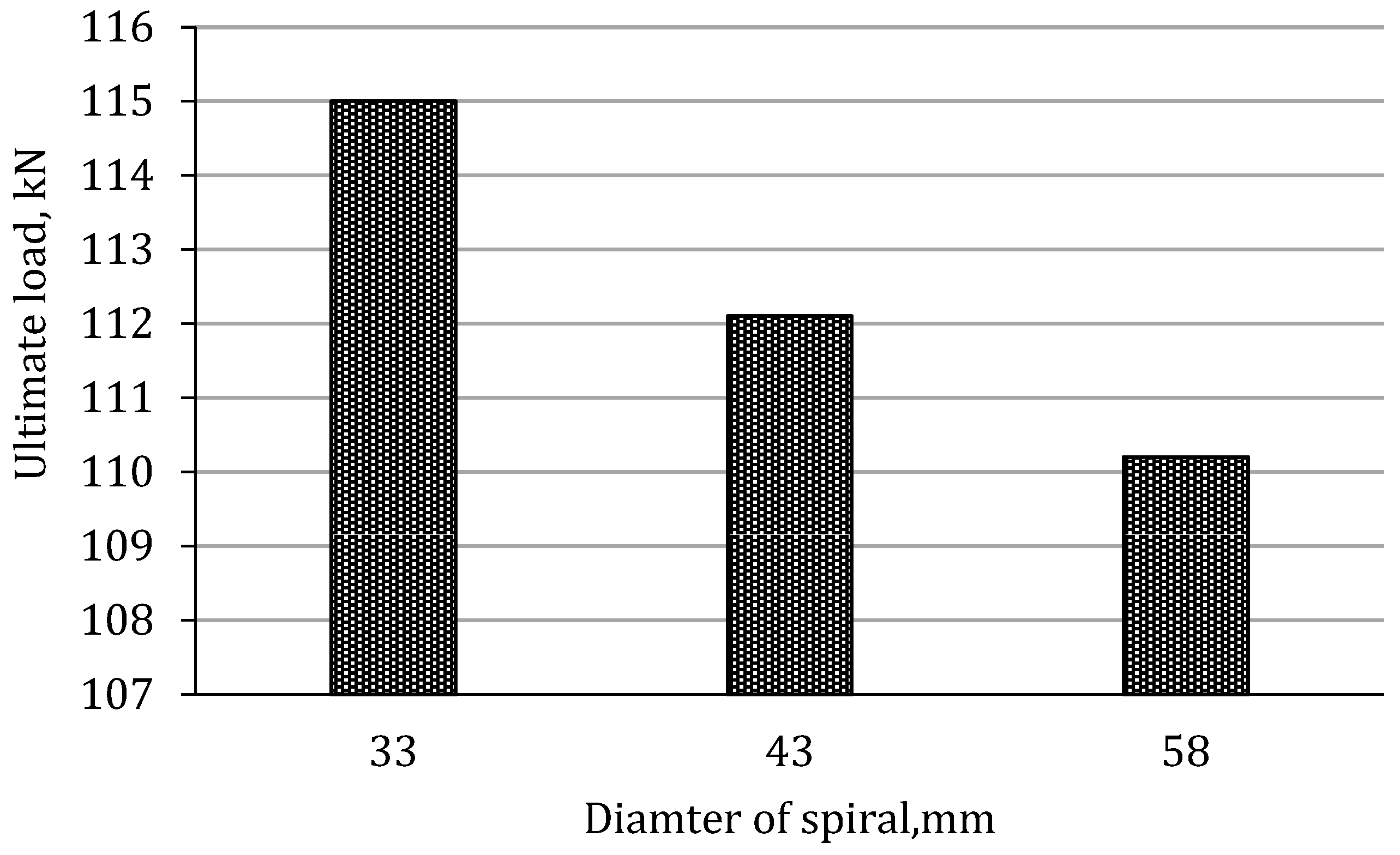
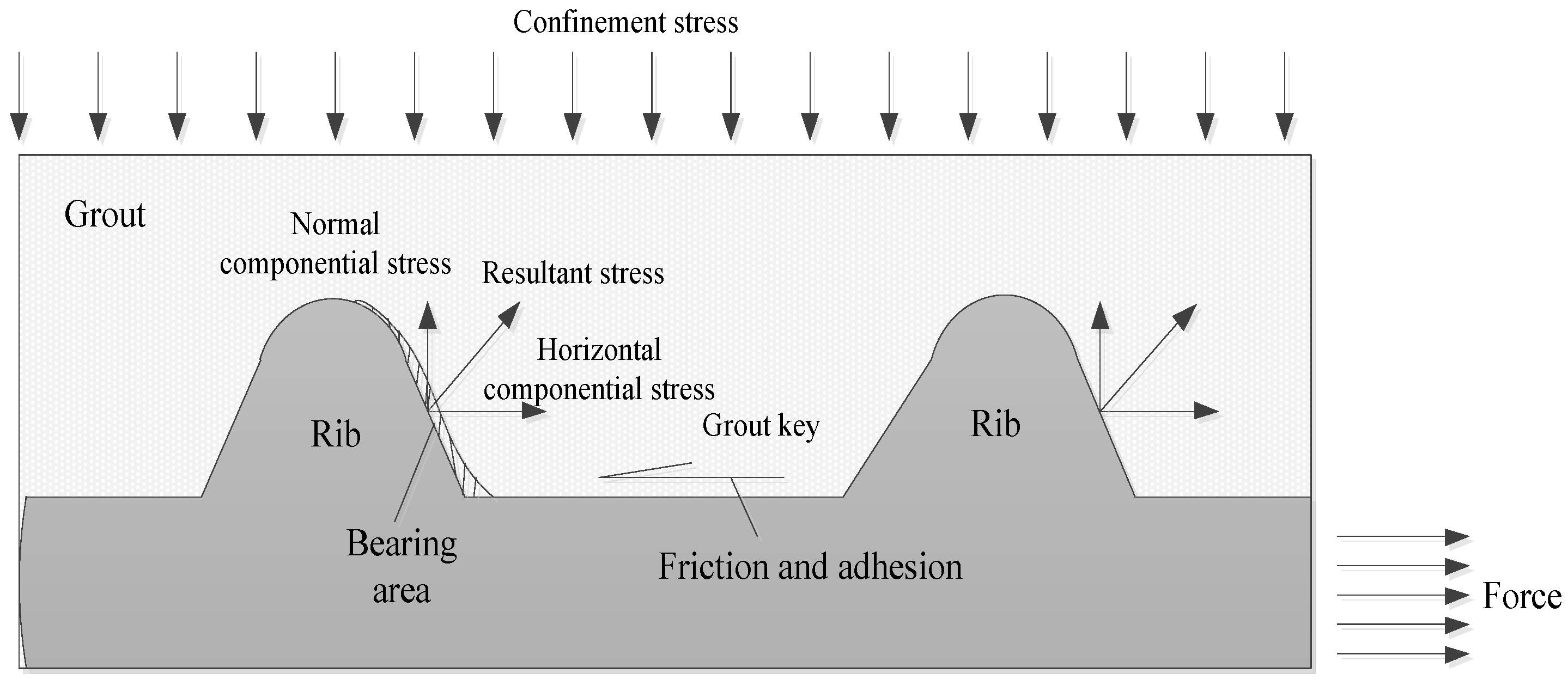
3.1. First-Crack Strength and Ultimate Loads
3.2. Load–Deflection Behavior
3.3. Strains in GFRP Bars
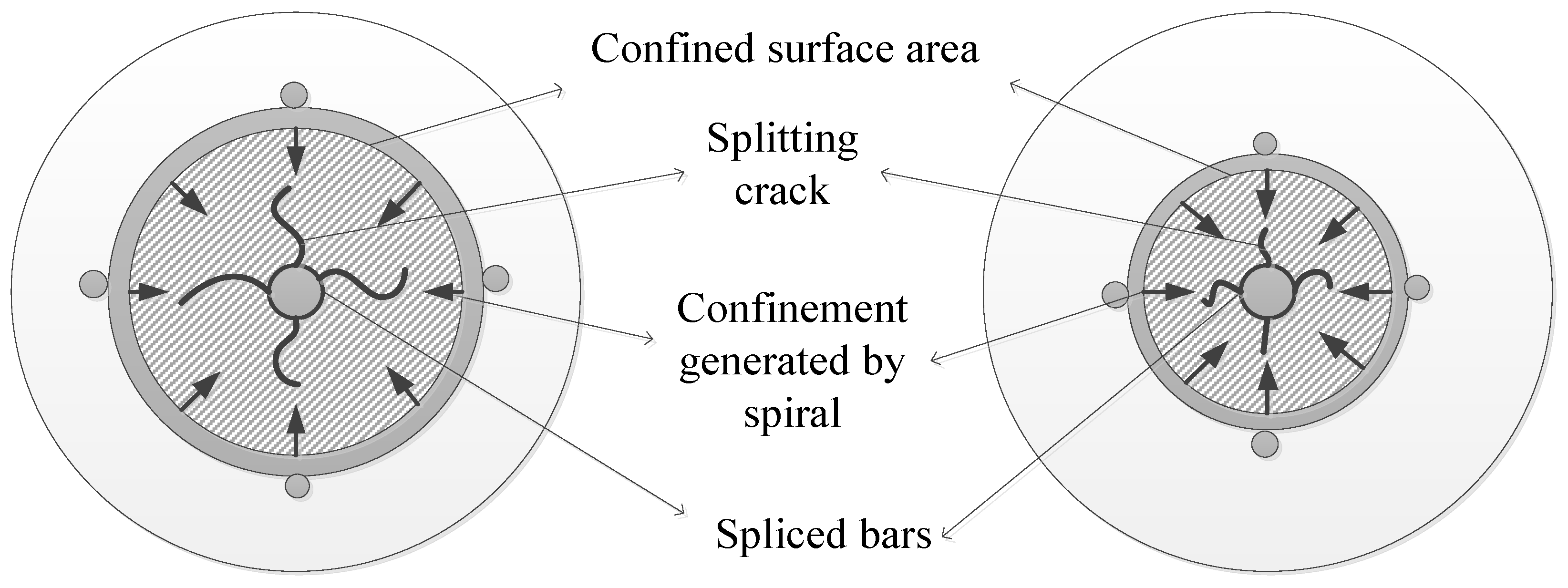
3.4. Failure Modes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ACI Committee440. Guide For the Design and Construction of Concrete Reinforced with FRP Bars, 440.1R-03; American Concrete Institute: Farmington Hills, MI, USA, 2003. [Google Scholar]
- Zhou, Z.; Ou, J.P.; Wang, B. Smart FRP-OFGB bars and their application in reinforced concrete beams. In Proceedings of the First International Conference on Structural Health Monitoring and Intelligent Structure, Tokyo, Japan, 13–15 November 2003; pp. 861–866. [Google Scholar]
- Tighiouart, B.; Benmokrane, B.; Gao, D. Investigation of Bond in Concrete Member with Fibre Reinforced Polymer (FRP) Bars. Constr. Build. Materials. 1998, 12, 453–462. [Google Scholar] [CrossRef]
- Lazorenko, G.; Kasprzhitskii, A.; Nazdracheva, T. Anti-corrosion coatings for protection of steel railway structures exposed to atmospheric environments: A review. Constr. Build. Mater. 2021, 288, 123115. [Google Scholar] [CrossRef]
- Keesler, R.J.; Powers, R.G. Corrosion of Epoxy Coated Rebars Keys Segmental Bridge Monroe County; Report No. 88-8A; Florida Department of Transportation, Materials Office, Corrosion Research Laboratories: Gainesville, FL, USA, 1988. [Google Scholar]
- Smith, J.L.; Virmani, Y.P. Materials and Methods for Corrosion Control of Reinforced and Prestressed Concrete Structures in New Construction; (No. FHWA-RD-00-081) United States; Federal Highway Administration: Washington, DC, USA, 2000. [Google Scholar]
- Aljibori, H.S.; Alamiery, A.; Kadhum, A.A.H. Advances in corrosion protection coatings: A comprehensive review. Int. J. Corros. Scale Inhib. 2023, 12, 1476–1520. [Google Scholar]
- Jerrett, C.V.; Ahmad, S.H. Bond Tests of Carbon Fibre Reinforced Plastic (CFRP) Rods. In Non-Metallic (FRP) Reinforcement for Concrete Structures: Proceedings of the Second RILEM International Symposium, Ghent, Belgium, 23–25 August 1995; CRC Press: Boca Raton, FL, USA, 1995; pp. 180–191. [Google Scholar]
- Acciai, A.; D’Ambrisi, A.; De Stefano, M.; Feo, L.; Focacci, F.; Nudo, R. Experimental Response of FRP Reinforced Members without Transverse Reinforcement: Failure Modes and Design Issues. Compos. Part B Eng. 2016, 89, 397–407. [Google Scholar] [CrossRef]
- Iyer, S.L.; Sen, R. (Eds.) Advanced Composite Materials in Civil Engineering Structures. In Proceedings of the Specialty Conference, Seattle, WA, USA, 25–27 June 1991; American Society of Civil Engineers: Reston, VA, USA, 1991. [Google Scholar]
- Neale, K.W.; Labossiere, P. Advanced Composite Materials in Bridges and Structures. In Proceedings of the First International Conference (ACMBS-I), Sherbrooke, QC, Canada; 1992. [Google Scholar]
- White, T.D. Composite Materials and Structural Plastics in Civil Engineering Construction. In Proceedings of the Materials Engineering Congress, New York, NY, USA, 10–12 August 1992; American Society of Civil Engineers: New York, NY, 1992; pp. 532–718. [Google Scholar]
- Taerwe, L. FRP Activities in Europe: Survey of Research and Applications. Proc. Third Int. Symp. Non Met. (FRP) Reinf. Concr. Struct. (FRPRCS-3) 1997, 1, 59–74. [Google Scholar]
- Benmokrane, B.; Rahman, H. Durability of Fiber Reinforced Polymer (FRP) Composites for Construction. In Proceedings of the First International Conference (CDCC ’98), Sherbrooke, QC, Canada, 5–7 August 1998. [Google Scholar]
- Saadatmanesh, H.; Ehsani, M.R. Fiber Composites in Infrastructure. In Proceedings of the Second International Conference on Composites in Infrastructure (ICCI-98), Tucson, AZ, USA, 12–14 January 1998. [Google Scholar]
- Dolan, C.W.; Rizkalla, S.H.; Nanni, A. Fiber reinforced polymer reinforcement for reinforced concrete structures. In Proceedings of the 4th International Symposium, Baltimore, MD, USA, 31 October–5 November 1999; American Concrete Institute: Farmington Hills, MI, USA, 1999. [Google Scholar]
- You, Y.J.; Park, K.T.; Seo, D.W.; Hwang, J.H. Tensile Strength of GFRP Reinforcing Bars with Hollow Section. Adv. Mater. Sci. Eng. 2015, 2015, 621546. [Google Scholar] [CrossRef]
- GangaRao, H.V.; Taly, N.; Vijay, P.V. Reinforced Concrete Design with FRP Composites; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Bank, L.C.; Puterman, M.; Katz, A. The Effect of Material Degradation on Bond Properties of Fiber Reinforced Plastic Reinforcing Bars in Concrete. ACI Mater. J. 1998, 95, 232–243. [Google Scholar]
- Harajli, M.; Abouniaj, M. Bond Performance of GFRP Bars In Tension: Experimental Evaluation and Assessment of ACI 440 Guidelines. J. Compos. Constr. 2010, 14, 659–668. [Google Scholar] [CrossRef]
- Schmidt, J.W.; Bennitz, A.; Täljsten, B.; Goltermann, P.; Pedersen, H. Mechanical anchorage of FRP tendons–a literature review. Constr. Build. Mater. 2012, 32, 110–121. [Google Scholar] [CrossRef]
- Hu, Z.; Shah, Y.I.; Yao, P. Experimental and numerical study on interface bond strength and anchorage performance of steel bars within prefabricated concrete. Materials 2021, 14, 3713. [Google Scholar] [CrossRef]
- Wang, Q.; Li, T.; Zhu, H.; Su, W.; Hu, X. Bond enhancement for NSM FRP bars in concrete using different anchorage systems. Constr. Build. Mater. 2020, 246, 118316. [Google Scholar]
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S. Feasibility Study of Grouted Splice Connector under Tensile Load. Constr. Build. Mater. 2014, 50, 530–539. [Google Scholar]
- Alias, A.; Sapawi, F.; Kusbiantoro, A.; Zubir, M.A.; Rahman, A.B.A. Performance of Grouted Splice Sleeve Connector under Tensile Load. J. Mech. Eng. Sci. 2014, 7, 1094–1102. [Google Scholar]
- Einea, A.; Yamane, T.; Tadros, M.K. Grout-Filled Pipe Splices for Precast Concrete Construction. PCI J. 1995, 40, 82–93. [Google Scholar] [CrossRef]
- Untrauer, R.E.; Henry, R.L. Influence of Normal Pressure on Bond Strength. ACI J. 1965, 62, 577–586. [Google Scholar]
- Robins, P.J.; Standish, I.G. The Influence of Lateral Pressure upon Anchorage Bond. Mag. Concr. Res. 1984, 36, 195–202. [Google Scholar]
- Moosavi, M.; Jafari, A.; Khosravi, A. Bond of Cement Grouted Reinforcing Bars Under Constant Radial Pressure. Cem. Concr. Compos. 2005, 27, 103–109. [Google Scholar]
- Xu, F.; Wu, Z.; Zheng, J.; Hu, Y.; Li, Q. Experimental Study on the Bond Behavior of Reinforcing Bars Embedded in Concrete Subjected to Lateral Pressure. J. Mater. Civ. Eng. 2011, 24, 125–133. [Google Scholar]
- Taniguchi, H.; Mutsuyoshi, H.; Kita, T.; Machida, A. Ductile behavior of beams using FRP as tendons and transverse reinforcement. In Proceedings of the International Symposium Fiber-Reinforced-Plastic Reinforcement for Concrete Structures, Vancouver, BC, Canada, 28–31 March 1993; Nanni, A., Dolan, C., Eds.; Special Publication: Vancouver, BC, Canada, 1993. [Google Scholar]
- Fam, A.; Cole, B.; Mandal, S. Composite Tubes as an Alternative to Steel Spirals for Concrete Members in Bending and Shear. Constr. Build. Mater. 2007, 21, 347–355. [Google Scholar]
- Loh, H.Y. Development of Grouted Splice Sleeve and Its Performance Under Axial Tension. Ph.D. Thesis, Universiti Teknologi Malaysia, ohor Darul Ta’zim, Malaysia, 2008. [Google Scholar]
- Loo, G.K. Parametric Study of Grout-Filled Splice Sleeve Integarated with Flexible Aluminium Tube for Precast Concrete Connection. Ph.D. Thesis, Universiti Teknologi Malaysia, ohor Darul Ta’zim, Malaysia, 2009. [Google Scholar]
- Ling, J.H.; Rahman, A.B.; Ibrahim, I.S.; Abd, Z. Tensile performance of ribbed hollow section splice sleeve connector under direct tensile load. In Proceedings of the 2nd Construction Industry Research Achievement International Conference (CIRAIC 2009), Kuala Lampur, Malaysia, 3–5 November 2009. [Google Scholar]
- Soroushian, P.; Choi, K.B.; Park, G.H.; Aslani, F. Bond of Deformed Bars to Concrete: Effects of Confinement and Strength of Concrete. ACI Mater. J. 1991, 88, 227–232. [Google Scholar]
- Lim, C.T. The Effect of Pitch Distance of Steel Spiral Reinforcement to the Performance of Grouted Sleeve Connector under Direct Tensile Load. Ph.D. Thesis, Universiti Teknologi Malaysia, ohor Darul Ta’zim, Malaysia, 2010. [Google Scholar]
- Lee, G.S. Parametric Studies of Sleeve Connector Using Steel Pipe with Spiral Steel for Precast Concrete Connection. Ph.D. Thesis, Universiti Teknologi Malaysia, ohor Darul Ta’zim, Malaysia, 2009. [Google Scholar]
- Hosseini, S.J.A.; Rahman, A.B.A. Effects of Spiral Confinement To The Bond Behavior of Deformed Reinforcement Bars Subjected to Axial Tension. Eng. Struct. 2016, 112, 1–13. [Google Scholar] [CrossRef]
- Guizani, L.; Chaallal, O. An Experimental Study on Bond-Slip in Moderately Confined Concrete Subjected to Monotonic and Cyclic Loading Using an Experimental Plan. Can. J. Civ. Eng. 2011, 38, 272–282. [Google Scholar]
- ACI Committee 408. Bond and Development of Straight Reinforcing Bars in Tension; ACI 408R-03; American Concrete Institute: Farmington Hills, MI, USA, 2003. [Google Scholar]
- Hamad, B.; Rteil, A. Comparison of roles of FRP sheets, stirrups, and steel fibers in confining bond critical regions. ASCE J. Compos. Constr. 2006, 10, 330–336. [Google Scholar] [CrossRef]
- Giuriani, E.; Plizzari, G.; Schumm, C. Role of Stirrups and Residual Tensile Strength of Cracked Concrete on Bond. J. Struct. Eng. 1991, 117, 1–18. [Google Scholar] [CrossRef]
- Rao, G.A. Parameters Influencing Bond Strength of Rebars in Reinforced Concrete. Int. J. Appl. Eng. Technol. 2014, 4, 72–81. [Google Scholar]
- Fadiel, A.; Mohammed, N.; Abdul Rahman, A.B.; Ali, E.A.B.; Abu-Lebdeh, T. Performance of Polyester Grouted Connector for Splicing of Reinforcement Bars. Am. J. Eng. Appl. Sci. 2024, 17, 46–50. [Google Scholar] [CrossRef]
- Fadiel, A.A.; Mohammed, N.S.; Rahman, A.B.A.; Ali, E.A.B.; Abu-Lebdeh, T.; Petrescu, F.I.T. Effect of Fly Ash on Mechanical Properties of Polymer Resin Grout. Biomimetics 2023, 8, 392. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, R.I.; Mickleborough, N.C. Design of Prestressed Concrete; CRC Press: Sydney, Australia, 1990. [Google Scholar]
- Cairns, J.; Zhao, Z. Behavior of concrete beams with exposed reinforcement. Proc. Inst. Civ. Eng. Struct. Build. 1993, 99, 141–154. [Google Scholar] [CrossRef]
- Mohammed, N.S. Behaviour and Performance of Non-Cement Polymer Grouted Spiral Connection. Ph.D. Thesis, Universiti Teknologi Malaysia, Skudai, Malaysia, 2019. [Google Scholar]
- Einea, A.; Yehia, S.; Tadros, M.K. Lap Splices in Confined Concrete. ACI Struct. J. 1999, 96, 937–994. [Google Scholar]
- Tastani, S.P.; Pantazopoulou, S.J. Experimental Evaluation of the Direct Tension-Pullout Bond Test. In Proceedings of the Symposium on “Bond in Concrete—From Research to Standards”, Budapest, Hungary, 20–22 November 2002; pp. 268–276. [Google Scholar]
- Brenes, F.J.; Wood, S.L.; Kreger, M.E. Anchorage Requirements for Grouted Vertical-Duct Connectors in Precast Bent Cap Systems; Project Summary Report 0-4176; Center for Transportation Research, The University of Texas at Austin: Austin, TX, USA, 2006; p. 252. [Google Scholar]
- Thompson, M.; Jirsa, J.; Breen, J.; Klingner, R. Anchorage Behaviour of Headed Reinforcement: Literature Review; University of Texas: Austin, TX, USA, 2002. [Google Scholar]
- Ling, J.H.; Rahman AB, A.; Ibrahim, I.S.; Hamid, Z.A. Tensile capacity of grouted splice sleeves. Eng. Struct. 2016, 111, 285–296. [Google Scholar]










| Tested Beam and Labels | Diameter of Spiral Reinforcement for the Anchor System | Types of Bond Along the GFRP Bar | |
|---|---|---|---|
| Series I: Beams reinforced with rough GFRP bars. | CR | No spiral | Bonded |
| D33-R-U | 33 mm | Unbonded | |
| D43-R-B | 43 mm | Bonded | |
| D43-R-U | 43 mm | Unbonded | |
| D58-R-U | 58 mm | Unbonded | |
| Series II: Beams reinforced with smooth GFRP bars. | CS | No spiral | Bonded |
| D33-S-U | 33 mm | Unbonded | |
| D43-S-B | 43 mm | Bonded | |
| D43-S-U | 43 mm | Unbonded | |
| D58-S-U | 58 mm | Unbonded | |
| Tested Beam | First-Crack Strength (kN) | Ultimate Load (kN) | Mid-Span Displacement at Ultimate Load (mm) | No. of Cracks at Failure | Maximum Crack Width (mm) | |
|---|---|---|---|---|---|---|
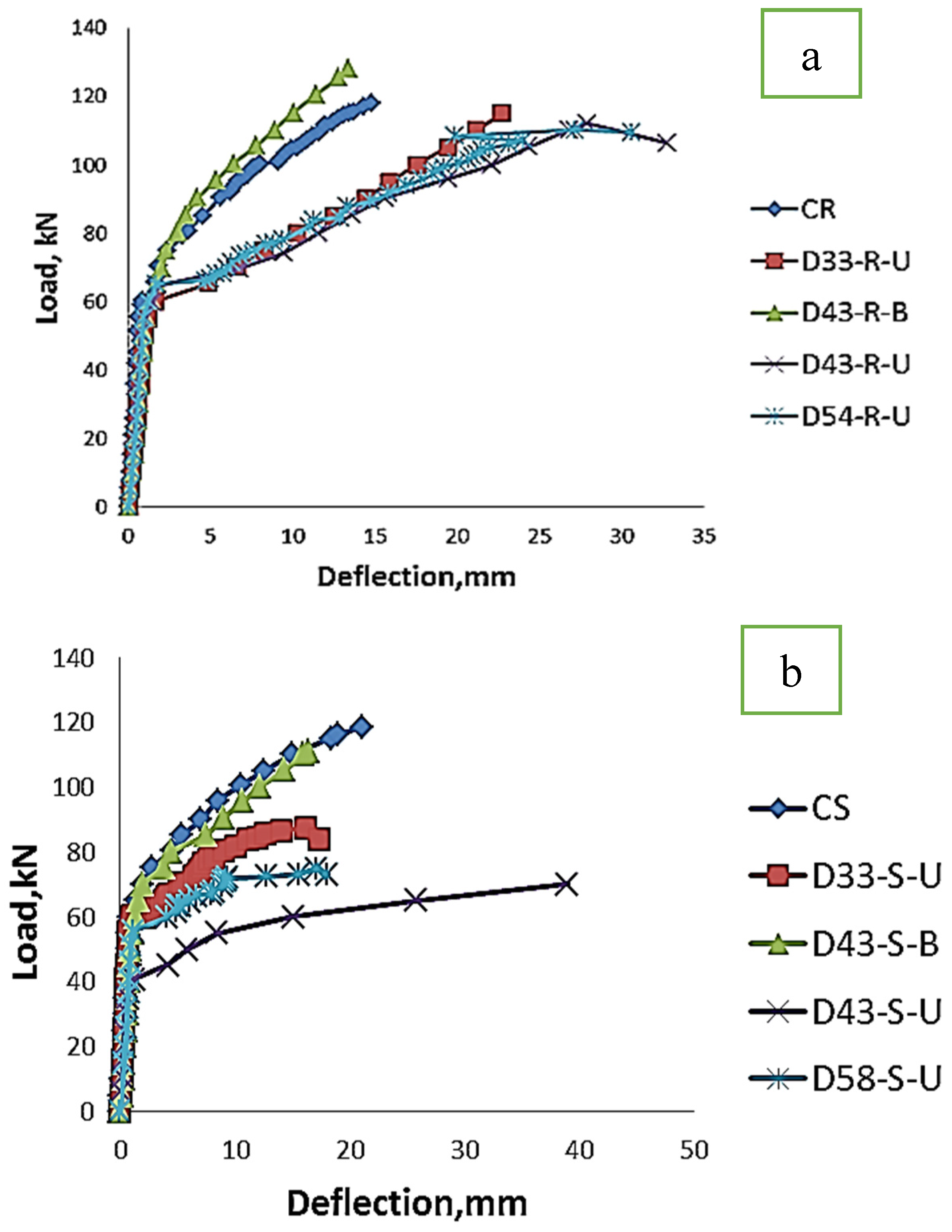
| Series I | CR | 65 | 117.9 | 14.8 | 6 | 10 |
| D33-R-U | 65 | 115 | 22.7 | 3 | 15 | |
| D43-R-B | 70 | 128.2 | 13.32 | 8 | 8 | |
| D43-R-U | 65 | 112.1 | 27.87 | 4 | 20 | |
| D58-R-U | 60 | 110.2 | 27.16 | 2 | 25 | |
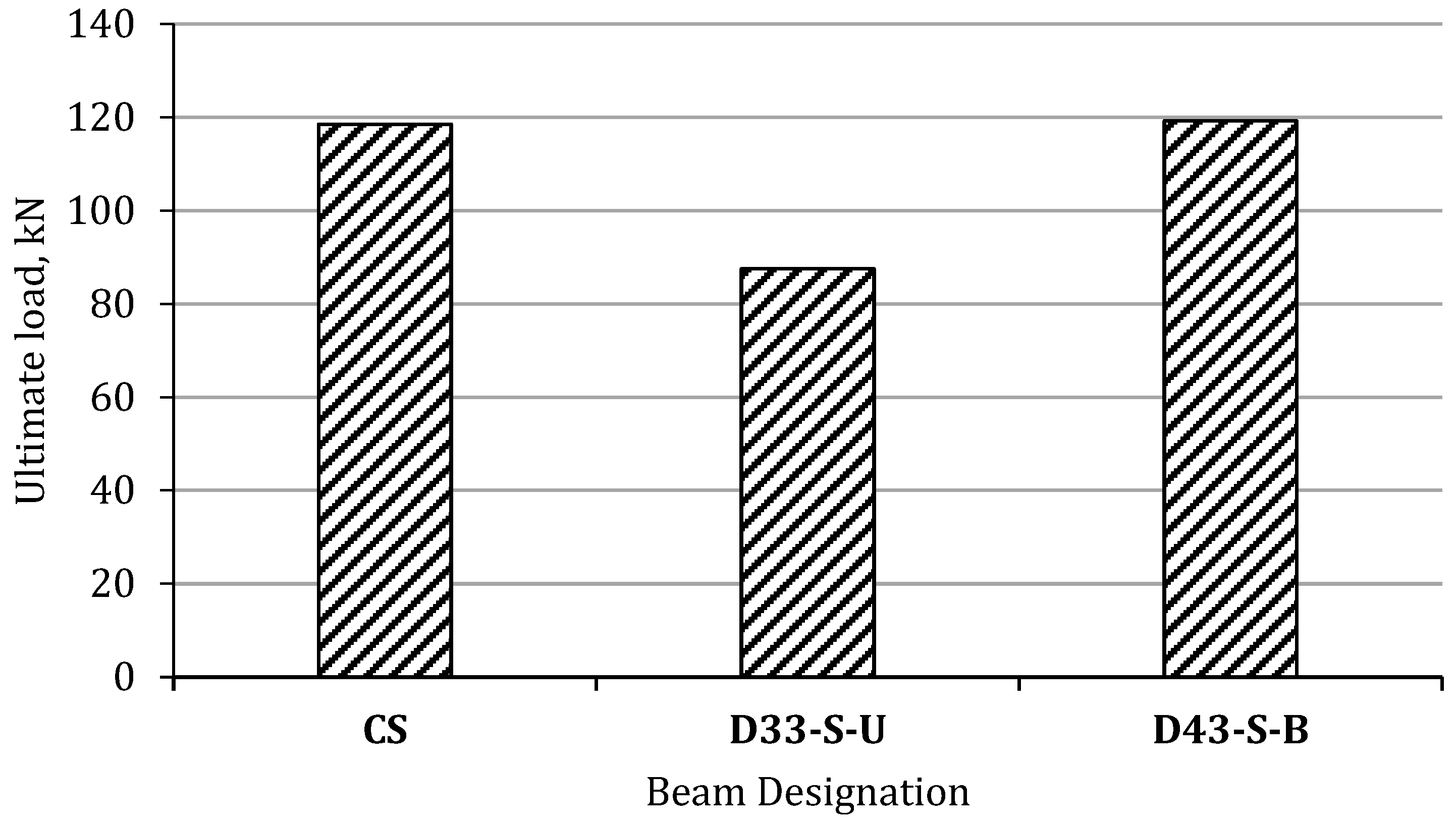
| Series II | CS | 60 | 118.5 | 21.08 | 2 | 20 |
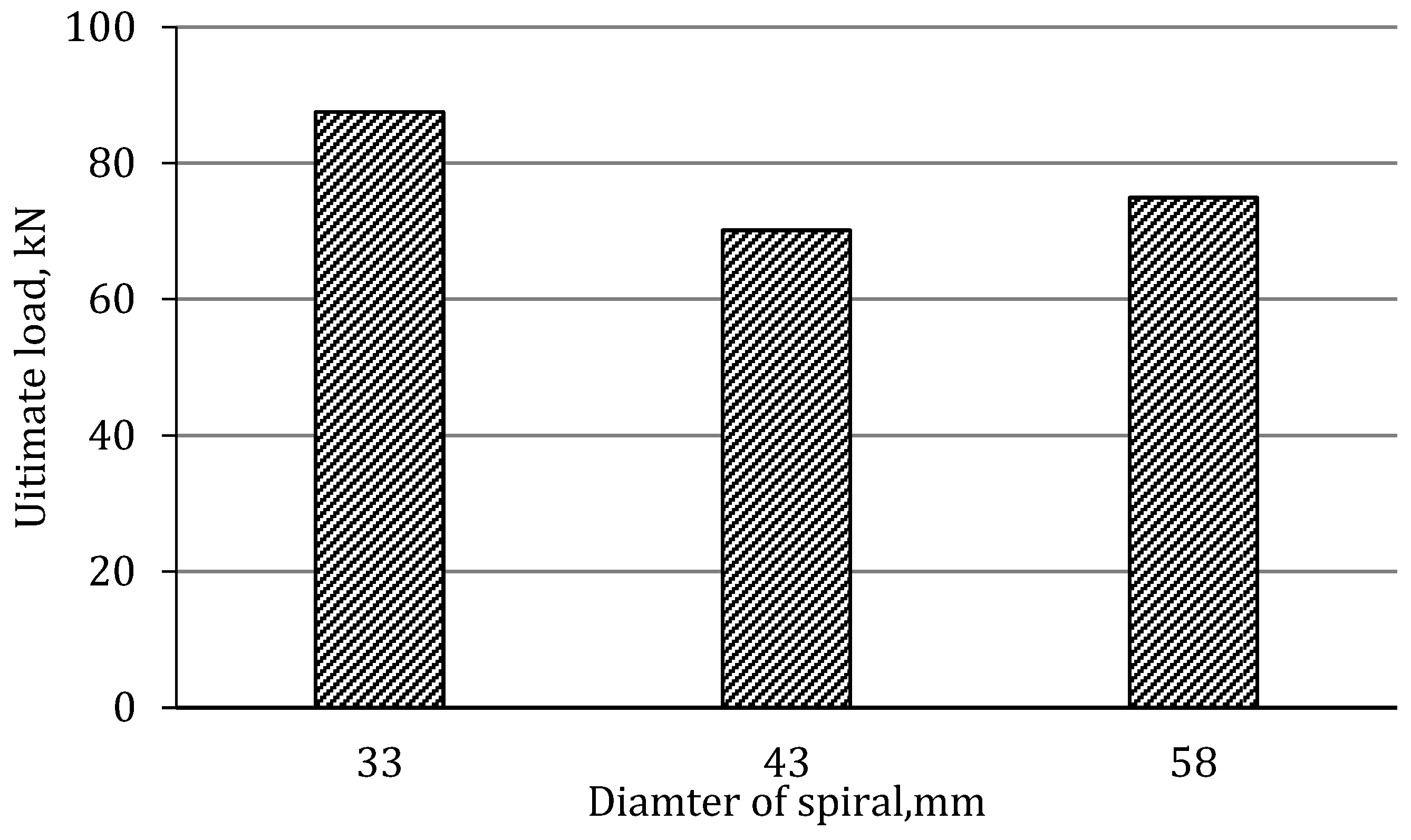
| D33-S-U | 60 | 87.5 | 16.18 | 3 | 12 | |
| D43-S-B | 60 | 119.2 | 20.43 | 3 | 5 | |
| D43-S-U | 55 | 70.1 | 29.01 | 3 | 20 | |
| D58-S-U | 60 | 74.9 | 17.07 | 1 | 30 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, N.S.; Fadiel, A.A.M.; Rahman, A.B.A.; Ali, E.A.B.; Abu-Lebdeh, T.; Kantaros, A.; Petrescu, F.I.T. Spirally Confined Reinforcing Bar for Flexural Behavior of Glass Fiber-Reinforced Concrete Beam. J. Compos. Sci. 2025, 9, 149. https://doi.org/10.3390/jcs9040149
Mohammed NS, Fadiel AAM, Rahman ABA, Ali EAB, Abu-Lebdeh T, Kantaros A, Petrescu FIT. Spirally Confined Reinforcing Bar for Flexural Behavior of Glass Fiber-Reinforced Concrete Beam. Journal of Composites Science. 2025; 9(4):149. https://doi.org/10.3390/jcs9040149
Chicago/Turabian StyleMohammed, Nuria S., Ashraf A. M. Fadiel, Ahmad Baharuddin Abdul Rahman, Esam Abu Baker Ali, Taher Abu-Lebdeh, Antreas Kantaros, and Florian Ion Tiberiu Petrescu. 2025. "Spirally Confined Reinforcing Bar for Flexural Behavior of Glass Fiber-Reinforced Concrete Beam" Journal of Composites Science 9, no. 4: 149. https://doi.org/10.3390/jcs9040149
APA StyleMohammed, N. S., Fadiel, A. A. M., Rahman, A. B. A., Ali, E. A. B., Abu-Lebdeh, T., Kantaros, A., & Petrescu, F. I. T. (2025). Spirally Confined Reinforcing Bar for Flexural Behavior of Glass Fiber-Reinforced Concrete Beam. Journal of Composites Science, 9(4), 149. https://doi.org/10.3390/jcs9040149











