Assessing the Shear Capacity of Screw Connectors in Composite Columns of Cold-Formed Steel and Concrete Infill
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Testing
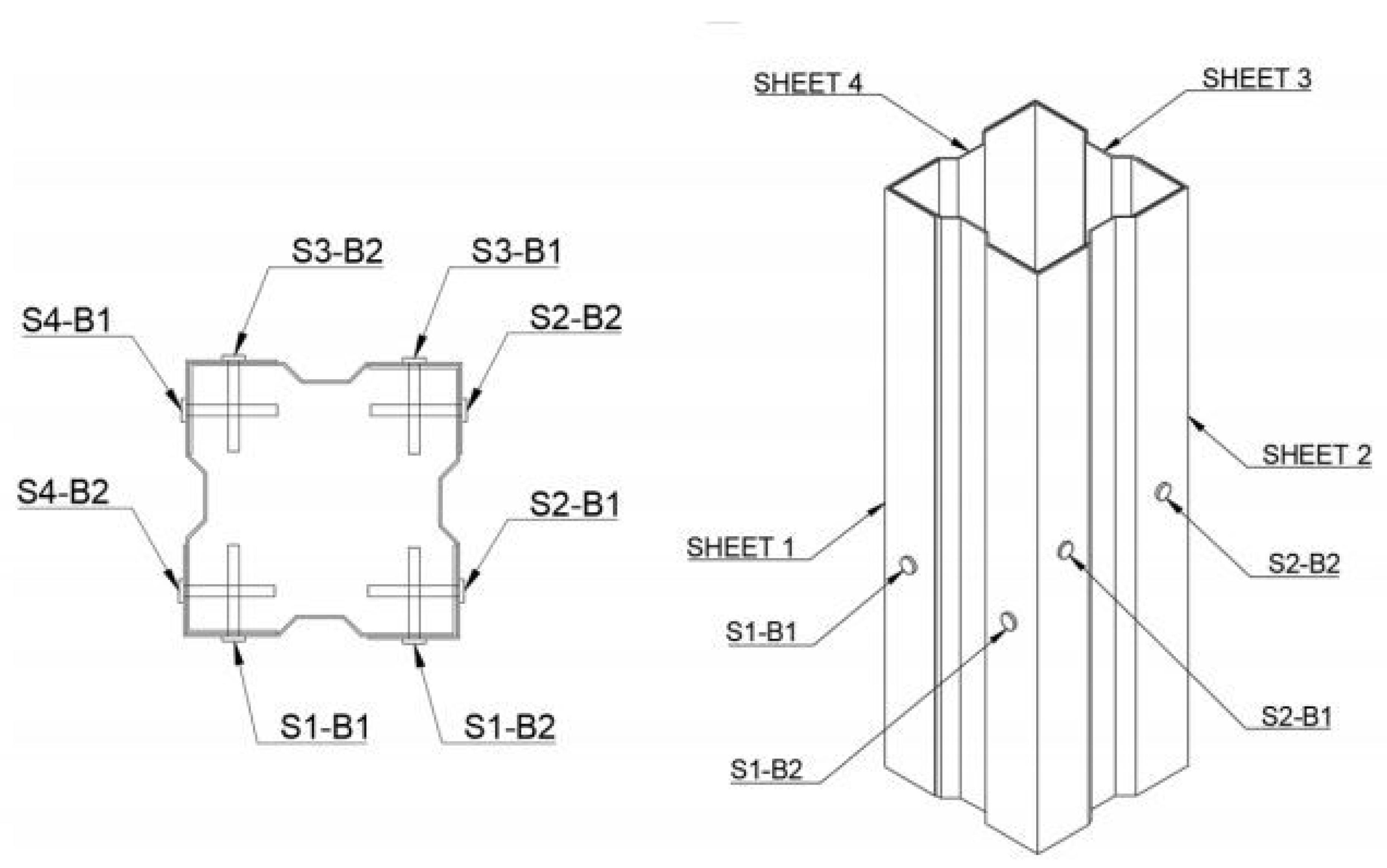
2.2. Specimen Fabrication
2.3. Test Setup
2.4. Test Instrumentation
2.5. Test Procedure
3. Results and Discussion
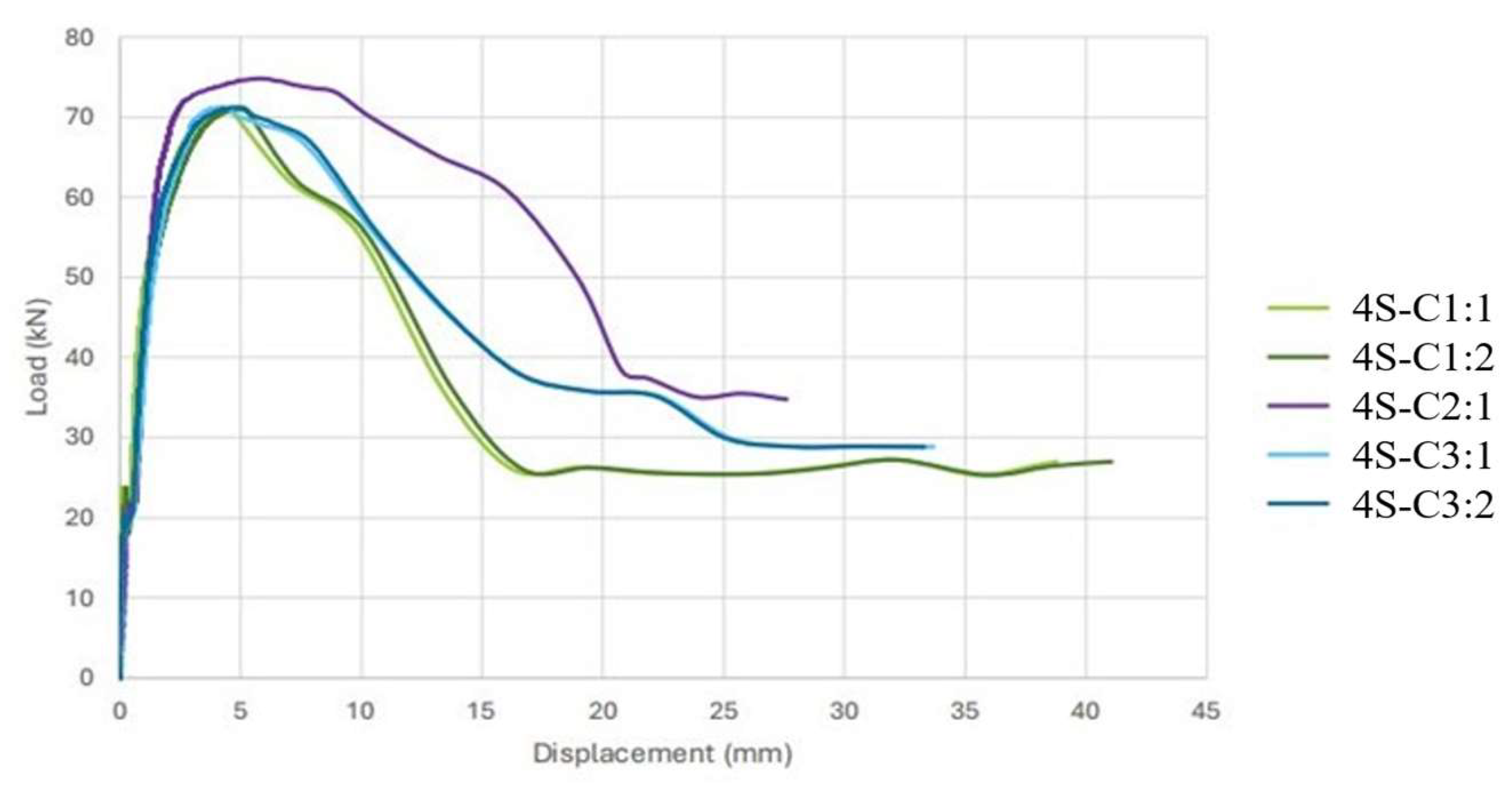
3.1. Push-Out Specimen Testing
3.2. Failure Modes
4. Mathematical Representation
5. Conclusions and Recommendations for Future Research
- The screw connectors exhibited an average shear strength of 9.041 kN per screw, as determined through axial compression push-out tests. Observations of the tests and specimen deconstruction revealed that the dominant failure mode was concrete crushing at the connection points.
- Experimental and theoretical comparisons showed that screw connectors performed within 10% of traditional shear connections, such as studs or bolts, as defined by AS 2327 [17]. However, the assumption of homogeneous concrete and uniform load distribution may have influenced the per-screw shear resistance values.
- Only three specimens were tested due to the scope of the study, and while all results fell within 10% of the mean, a larger sample size would provide a more accurate mean shear strength. The assumption of concrete homogeneity across the specimens could have affected the failure mode assessment, potentially exaggerating the concrete crushing failure mode.
- The study highlights the potential of self-tapping screw connections as a viable alternative to traditional shear connections in composite columns. Multi-sectional steel sections, such as the four-steel sigma section, can improve transport, construction, maintenance, and deconstruction phases. This innovative design presents a cost-effective, time-efficient, safe, and sustainable alternative to traditional composite columns.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, S.; Fang, Z.; Mosallam, A.S.; Ouyang, Y.; Zou, C. Behavior of CFSC-encased shear connectors in steel-concrete joints: Push-out tests. J. Struct. Eng. 2020, 146, 04020015. [Google Scholar] [CrossRef]
- Papavasileiou, G.S.; Charmpis, D.C.; Lagaros, N.D. Optimised seismic retrofit of steel-concrete composite buildings. Eng. Struct. 2020, 213, 110573. [Google Scholar] [CrossRef]
- Shariati, M.; Sulong, N.R.; Shariati, A.; Kueh, A. Comparative performance of channel and angle shear connectors in high strength concrete composites: An experimental study. Constr. Build. Mater. 2016, 120, 382–392. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Latour, M.; Monaco, A.; Rizzano, G. Analytical prediction of the shear connection capacity in composite steel–concrete trussed beams. Mater. Struct. 2017, 50, 1–18. [Google Scholar] [CrossRef]
- Jelčić Rukavina, M.; Skejić, D.; Kralj, A.; Ščapec, T.; Milovanović, B. Development of lightweight steel framed construction systems for nearly-zero energy buildings. Buildings 2022, 12, 929. [Google Scholar] [CrossRef]
- Pavlović, M.; Marković, Z.; Veljković, M.; Buđevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Constr. Steel Res. 2013, 88, 134–149. [Google Scholar] [CrossRef]
- Hosseini, M.; Mamun, M.S.; Mirza, O.; Mashiri, F. Behaviour of blind bolt shear connectors subjected to static and fatigue loading. Eng. Struct. 2020, 214, 110584. [Google Scholar] [CrossRef]
- Li, Z.; Li, H.; Zhou, X.-H.; Wang, Y.-H.; Li, X.-H.; Gan, D.; Zhu, R.-H. Damage detection of flange bolts in wind turbine towers using dynamic strain responses. J. Civ. Struct. Health Monit. 2023, 13, 67–81. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, J.; Li, Q.; Xu, S.; Shen, L. Application of High-Performance Cementitious Composites in Steel-Concrete Composite Bridge Deck Systems: A Review. J. Intell. Constr. 2024, 2, 1–23. [Google Scholar] [CrossRef]
- Viest, I.M. Investigation of stud shear connector for composite concrete and steel T-beam. ACI J. 1956, 27. [Google Scholar]
- Slutter, R.G.; Driscoll, G.C.J. Flexural strength of steel-concrete composite beams. J. Struct. Div. 1965, 91, 71–99. [Google Scholar] [CrossRef]
- Ollgaard, J.G.; Slutter, R.G.; Fisher, J.W. Shear strength of stud connectors in lightweight and normal-weight concrete. Eng. J. 1971, 8, 55–64. [Google Scholar] [CrossRef]
- Hussein, A.B.; Papp, F. State-of-the-Art: Integrating Fastener Technology and Design Guidelines for Enhanced Performance of Cold-Formed Steel Sections. Buildings 2023, 13, 2338. [Google Scholar] [CrossRef]
- De'nan, F.; Yeou, C.Y.; Salim, W.S.W.; Rahman, N.A.; Hashim, N.S. Assessing Cold-Formed Steel Section Performance in Fire: A Comprehensive Review of Numerical Models and Resistance Factors. Int. J. Steel Struct. 2024, 25, 125–143. [Google Scholar] [CrossRef]
- Lu, B.; Zhai, C.; Li, S.; Wen, W. Predicting ultimate shear capacities of shear connectors under monotonic and cyclic loadings. Thin-Walled Struct. 2019, 141, 47–61. [Google Scholar] [CrossRef]
- AS/NZS 4600:2018; Cold-Formed Steel Structures. Australian Standards: Sydney, Australia, 2005.
- AS/NZS 2327:2017; Composite Structures-Composite Steel-Concrete Construction in Buildings. Australian Standards: Sydney, Australia, 2017.
- EN 1994-1-1:2004; Eurocode 4: Design of Composite Steel and Concrete Structures, Part 1–1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Shen, M.H.; Chung, K.F.; Elghazouli, A.Y.; Tong, J.Z. Structural behaviour of stud shear connections in composite floors with various connector arrangements and profiled deck configurations. Eng. Struct. 2020, 210, 110370. [Google Scholar] [CrossRef]
- Rahnavard, R.; Craveiro, H.D.; Lopes, M.; Simões, R.A.; Laím, L.; Rebelo, C. Concrete-filled cold-formed steel (CF-CFS) built-up columns under compression: Test and design. Thin-Walled Struct. 2022, 179, 109603. [Google Scholar] [CrossRef]
- ASTM E8/E8M-21; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- AS 1391-2007; Metallic Materials—Tensile Testing at Ambient Temperature. Standards Australia: Sydney, Australia, 2007.
- Huang, Y.; Young, B. Experimental and numerical investigations of cold-formed steel columns with bolted end connections. Thin-Walled Struct. 2012, 61, 57–70. [Google Scholar] [CrossRef]
- Maleki, S.; Bagheri, S. Behavior of channel shear connectors, Part I: Experimental study. J. Constr. Steel Res. 2008, 64, 1333–1340. [Google Scholar] [CrossRef]
- Oeztuerk, F.; Mojtabaei, S.M.; Şentürk, M.; Pul, S.; Hajirasouliha, I. Buckling behaviour of cold-formed steel sigma and lipped channel beam–column members. Thin-Walled Struct. 2022, 173, 108963. [Google Scholar] [CrossRef]
- Antony, A.G. Study on cold formed steel sigma sections and the effect of stiffeners. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 16249–16255. [Google Scholar]
- Jeong, Y.J.; Kwon, Y.B.; Kim, S.H. Experimental study on interfacial shear resistance of steel–concrete composite members. J. Constr. Steel Res. 2005, 61, 1310–1331. [Google Scholar] [CrossRef]
- Pallarés, L.; Hajjar, J.F. Headed steel stud anchors in composite structures, Part I: Shear. J. Constr. Steel Research. 2010, 66, 198–212. [Google Scholar] [CrossRef]
- Roy, K.; Ting, T.C.H.; Lau, H.H.; Lim, J.B. Experimental and numerical investigations on the axial capacity of cold-formed steel built-up box sections. J. Constr. Steel Res. 2019, 160, 411–427. [Google Scholar] [CrossRef]
- Dos Santos, L.R.; Caldas, R.B.; Prates, J.A.; Rodrigues, F.C.; de Sousa Cardoso, H. Design procedure to bearing concrete failure in composite cold-formed steel columns with riveted bolt shear connectors. Eng. Struct. 2022, 256, 114003. [Google Scholar] [CrossRef]
- Dos Santos, L.R.; de Sousa Cardoso, H.; Caldas, R.B.; Grilo, L.F. Finite element model for bolted shear connectors in concrete-filled steel tubular columns. Eng. Struct. 2020, 203, 109863. [Google Scholar] [CrossRef]
- ANSI/AISC 360-05; Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2005.
- GB50017-2003; Code for Design of Steel Structure. China Planning Press, National Standards of People’s Republic of China: Beijing, China, 2003.
- Zheng, S.; Zhao, C.; Liu, Y. Analytical model for load–slip relationship of perfobond shear connector based on push-out test. Materials 2018, 12, 29. [Google Scholar] [CrossRef]
- Teoh, K.B.; Chua, Y.S.; Dai Pang, S.; Kong, S.Y. Experimental investigation of lightweight aggregate concrete-filled cold-formed built-up box section (CFBBS) stub columns under axial compression. Eng. Struct. 2023, 279, 115630. [Google Scholar] [CrossRef]
- Rahnavard, R.; Craveiro, H.D.; Simões, R.A.; Laím, L.; Santiago, A. Buckling resistance of concrete-filled cold-formed steel (CF-CFS) built-up short columns under compression. Thin-Walled Struct. 2022, 170, 108638. [Google Scholar] [CrossRef]
- Eghbali, N.B.; Andamnejad, P. Structural performance of rigid shear connectors in concrete encased steel composite columns. Structures 2023, 54, 348–368. [Google Scholar] [CrossRef]











| Properties | Value (MPa) |
|---|---|
| Compressive strength | 34.25 |
| Tensile strength | 2.43 |
| Modulus of Elasticity | 30,100 |
| Specimen | Shear Strength (kN) | Shear Strength Per Screw (kN) |
|---|---|---|
| 4S-C1 | 70.96 | 8.87 |
| 4S-C2 | 74.81 | 9.35 |
| 4S-C3 | 71.23 | 8.90 |
| Average | 72.33 | 9.04 |
| 4S-C1 | 4S-C2 | 4S-C3 | |||||
|---|---|---|---|---|---|---|---|
| Properties | Symbol | Laser 1 | Laser 2 | Laser 2 | Laser 1 | Laser 2 | Average |
| Interface Slip (mm) | SI | 0.004 | 0.256 | 0.342 | 0.197 | 0.187 | 0.197 |
| Interface Load (kN) | Vi | 23.724 | 23.639 | 21.810 | 20.489 | 20.064 | 21.945 |
| Yield Slip (mm) | Sy | 0.951 | 1.230 | 1.212 | 1.297 | 1.083 | 1.155 |
| Yield Strength (kN) | Vy | 48.225 | 47.716 | 50.703 | 48.307 | 47.169 | 48.442 |
| Shear Strength Slip (mm) | Su | 4.394 | 4.984 | 5.843 | 4.268 | 4.893 | 4.876 |
| Shear Strength (kN) | Vu | 70.961 | 70.961 | 74.808 | 71.225 | 71.225 | 71.336 |
| End Slip (mm) | SF | 16.237 | 16.659 | 20.704 | 16.621 | 16.561 | 17.607 |
| End Load (kN) | Vf | 26.075 | 26.075 | 38.365 | 37.889 | 37.889 | 33.259 |
| Screw ID | Screw Head Shearing | Failure Mode 1 | Failure Mode 2 | Notes |
|---|---|---|---|---|
| S1-B1 | Y | Screw shearing | Concrete crushing | The corner under the influence of S1-B1 and S4-B2 underwent severe concrete degradation. It is believed that due to the premature screw shearing of SB-B1, forces in this corner were transferred to S4-B2, leading to intense concrete crushing. It is evident as the S1-B1 screw was exposed and had undergone no bending, suggesting shearing at bolt heads early, in comparison to S4-B1, whose exposed screw was severely bent but did not shear off. |
| S1-B2 | N | Concrete crushing | - | As S1-B2 screw head did not shear off, concrete crushing was the evident failure mode. The screw remained lodged in the sample and, from what could be observed, sustained severe bending, local crushing surrounding the screw was considered mild as little concrete was displaced and a large crack had formed. |
| S2-B1 | Y | Concrete crushing | Screw head shearing | S2-B1 underwent both local concrete crushing and shearing of the bolt head. It was declared that concrete crushing was the initial failure mode. It was evident through the observation of the lodged screw (in comparison to that of S1-B1). It means the screw head sheared later in loading conditions. Moderate/severe concrete crushing was observed, with considerable cracking; however, there was slight material displacement. |
| S2-B2 | N | Concrete crushing | - | As the S2-B2 screw head did not shear off, concrete crushing was the evident failure mode. The screw remained lodged in the sample and, from what could be observed, sustained moderate bending. Local crushing surrounding the screw was considered mild as little concrete was displaced, and a large crack had formed. |
| S3- B1 | N | Concrete crushing | - | As the S2-B2 screw did not shear off, concrete crushing was the evident failure mode. The screw remained lodged in the sample and, from what could be observed, sustained moderate bending. Local crushing surrounding the screw was considered mild as little concrete was displaced, and a small crack had formed. |
| S3-B2 | N | Concrete crushing | - | As the S1-B2 screw head did not shear off, concrete crushing was the evident failure mode. The screw remained lodged in the sample, and from what could be observed, moderate to little concrete was displaced and minimal cracking. However, the bolt has undergone significant displacement close to the head of the bolt. |
| S4-BI | N | Concrete crushing | - | As the S1-B2 screw head did not shear off, concrete crushing was the evident failure mode. The screw remained lodged in the sample and, from what could be observed, sustained severe bending. Local crushing surrounding the screw was considered moderate as little concrete was displaced and minimal cracking. However, the bolt has undergone significant displacement close to the head of the bolt. Voids in concrete material homogeneity suggest a weakened area within the concrete. |
| S4-B2 | N | Concrete crushing | - | The corner under the influence of S1-B1 and S4-B2 underwent severe concrete degradation. It is believed that due to the premature screw shearing of S1-B1, forces in this corner were transferred to S4-B2, leading to intense concrete crushing. It is evident as the S1-B1 screw was exposed and bolted head in comparison to S4-B1, whose exposed screw was severely bent but did not shear off. |
| Name | Equation | Theoretical Shear Strength (kN) | Difference (%) | As | d | Ec | F′c | h | Rank |
|---|---|---|---|---|---|---|---|---|---|
| Australian Standards (AS 2327) [17] | 0.5 As f′c | 9.986 | 9.30 | X | X | X | X | X | 3 |
| American Institute of Steel Construction (AISC 2005) [32] | 0.5 As f′c | 9.986 | 9.30 | X | X | X | X | X | 3 |
| Eurocode 4 (EN 1994-1-1) [18] | 0.29 d2 f′c | 7.361 | −22.82 | X | X | X | X | X | 5 |
| Chinese Standard (GB50017) [33] | 0.4 As f′c | 8.573 | −5. 47 | X | X | X | X | X | 2 |
| Viest (1956) [10] | 9.068 | 0.29 | X | X | X | X | X | 1 | |
| Slutter and Driscoll (1961) [11] | 11.765 | 23.15 | X | X | X | X | X | 6 | |
| Ollgaard et al. (1971) [12] | 0.5 As | 9.986 | 9.30 | X | X | X | X | X | 3 |
| Pallarés (2009) [28] | 9λ(f′c)0.5(d)1.4(h)0.6 | 10.234 | 11.65 | X | X | X | X | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, S.S.; Colla, N.; Kafle, B.; Al-Ameri, R. Assessing the Shear Capacity of Screw Connectors in Composite Columns of Cold-Formed Steel and Concrete Infill. J. Compos. Sci. 2025, 9, 261. https://doi.org/10.3390/jcs9060261
Simon SS, Colla N, Kafle B, Al-Ameri R. Assessing the Shear Capacity of Screw Connectors in Composite Columns of Cold-Formed Steel and Concrete Infill. Journal of Composites Science. 2025; 9(6):261. https://doi.org/10.3390/jcs9060261
Chicago/Turabian StyleSimon, Serene Sara, Nathan Colla, Bidur Kafle, and Riyadh Al-Ameri. 2025. "Assessing the Shear Capacity of Screw Connectors in Composite Columns of Cold-Formed Steel and Concrete Infill" Journal of Composites Science 9, no. 6: 261. https://doi.org/10.3390/jcs9060261
APA StyleSimon, S. S., Colla, N., Kafle, B., & Al-Ameri, R. (2025). Assessing the Shear Capacity of Screw Connectors in Composite Columns of Cold-Formed Steel and Concrete Infill. Journal of Composites Science, 9(6), 261. https://doi.org/10.3390/jcs9060261







