Effect of Mixing Time on the Thermal Stability and Activation Energies of NiO/PMMA Nanocomposites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of PMMA/NiO Nanocomposites
2.3. Characterization Techniques
2.3.1. X-Ray Diffraction (XRD)
2.3.2. Scanning Electron Microscopy (SEM)
2.3.3. Differential Thermal Analysis (DTA)
2.4. Theoretical Background
3. Results
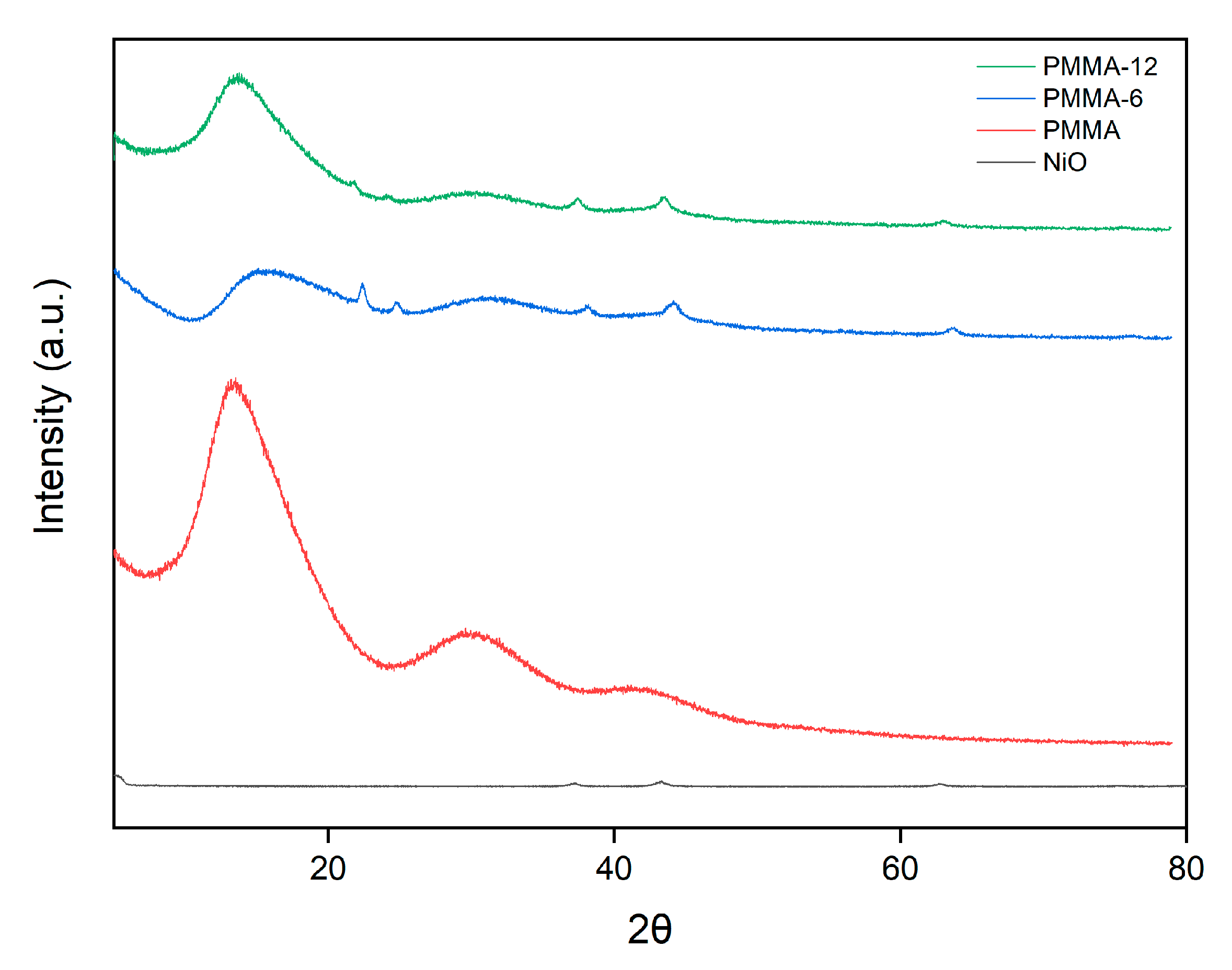
3.1. XRD Characterization
3.2. Morphology of PMMA and Nanocomposites
3.3. Differential Thermal Analysis (DTA)
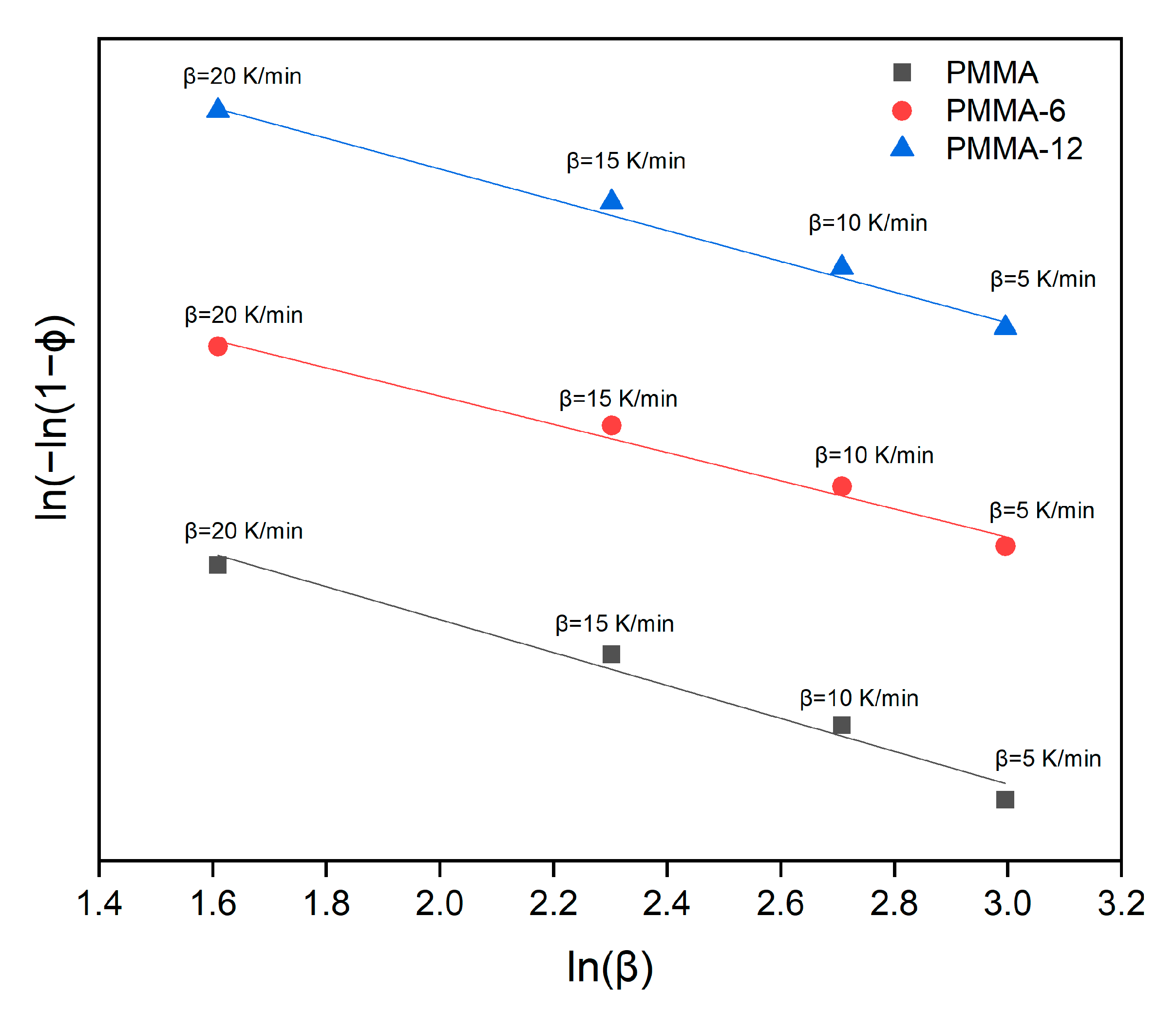
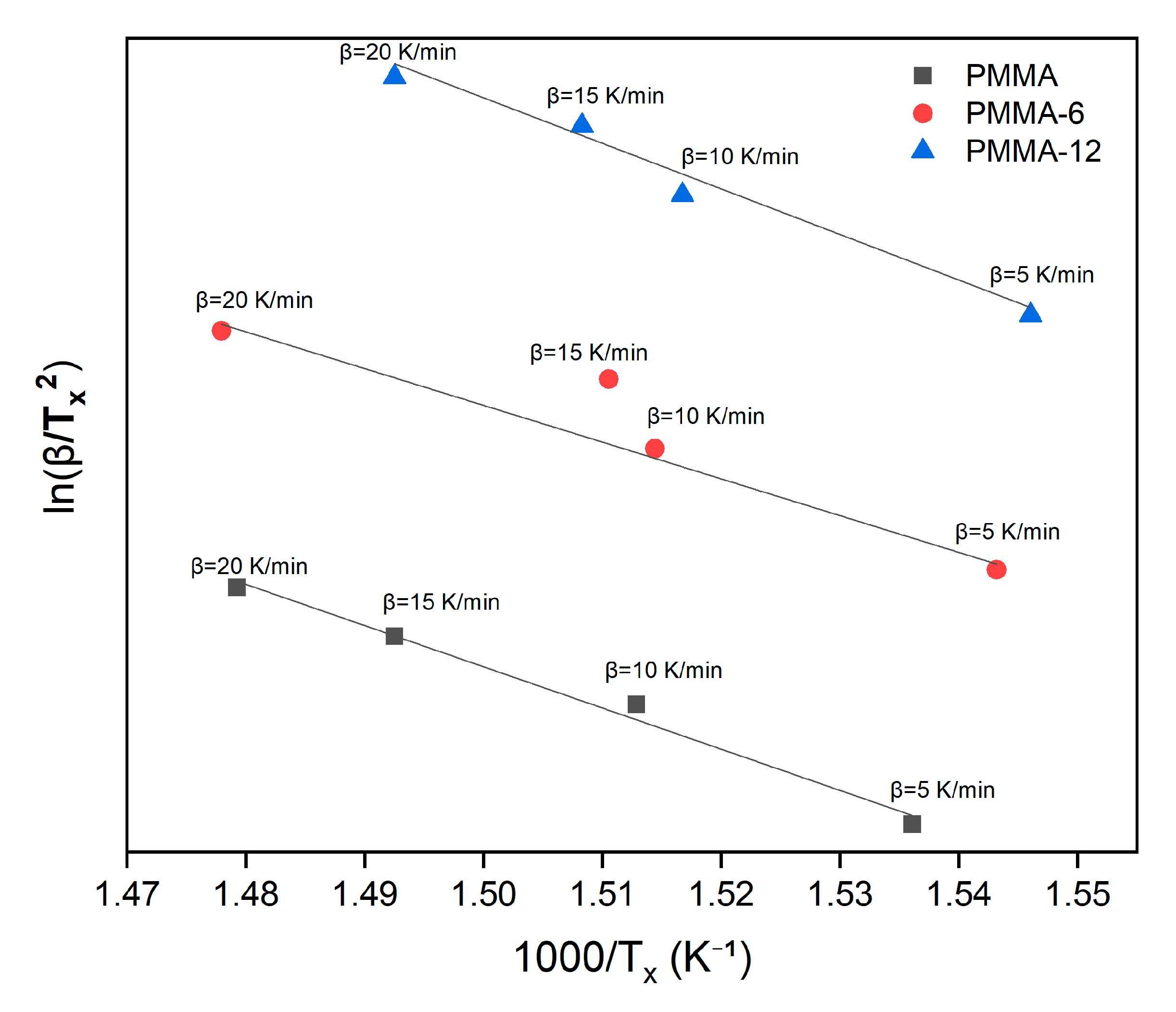
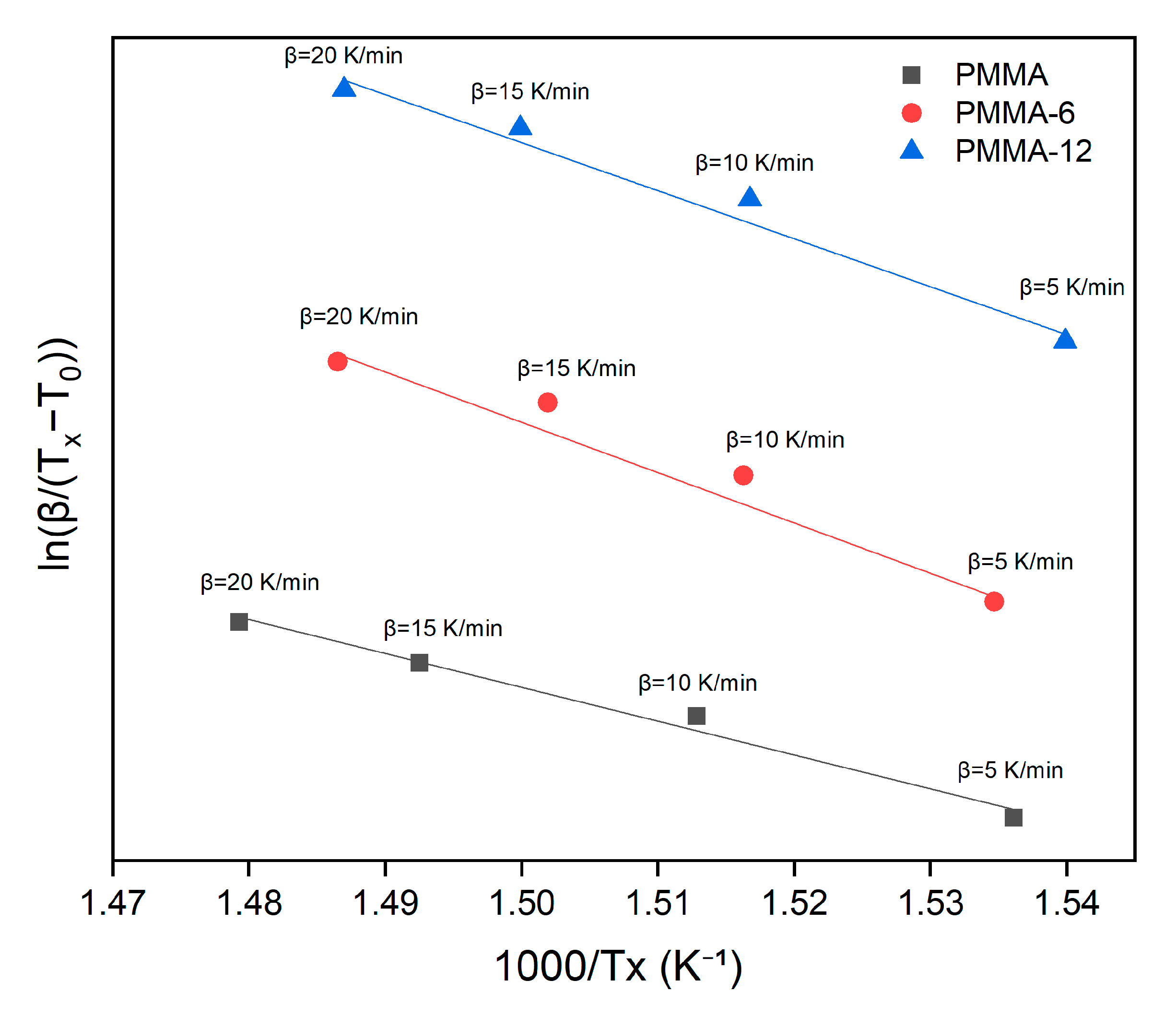
3.4. Thermal Activation Calculations
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PMMA | Poly(methyl methacrylate) |
| NiO | Nickel Oxide |
| NPs | Nanoparticles |
| XRD | X-ray Diffraction |
| SEM | Scanning Electron Microscopy |
| DTA | Differential Thermal Analysis |
| DSC | Differential Scanning Calorimetry |
| TGA | Thermogravimetric Analysis |
| UV | Ultraviolet |
| Ea | Activation Energy |
| Tx | Crystallization Peak Temperature |
| Tg | Glass Transition Temperature |
| β (Beta) | Heating Rate |
| JCPDS | Joint Committee on Powder Diffraction Standards |
| JEOL | Japan Electron Optics Laboratory |
| JSM | JEOL Scanning Microscope |
| MWCNT | Multi-Walled Carbon Nanotubes |
| PVC | Polyvinyl Chloride |
| DFT | Density Functional Theory |
| CAS | Chemical Abstracts Service |
References
- García-Cerda, L.A.; Romo-Mendoza, L.E.; Quevedo-López, M.A. Synthesis and Characterization of NiO Nanoparticles and Their PMMA Nanocomposites Obtained by in Situ Bulk Polymerization. J. Mater. Sci. 2009, 44, 4553–4556. [Google Scholar] [CrossRef]
- Bel, T.; Arslan, C.; Baydoğan, N. PMMA/Mikroküre/Montmorillonit Nanokompozit ve PMMA/Mikroküre/Halloysite Nanokompozitin Atom Transfer Radikal Polimerizasyon Tekniği Ile Üretilmesi ve Mekanik Özelliklerinin Karşılaştırmalı Olarak İncelenmesi. Gazi Univ. Muhendis.-Mimar. Fakültesi Derg. 2018, 2018, 688–700. [Google Scholar] [CrossRef]
- Çankaya, N.; Korcan, S.E.; Turan, N.; Aydin, B.; Tanış, E. First Report of the Synthesis, Characterization, DFT Calculations of the New Oxoethyl Methacrylate and o-Acetamide and Evaluation of Antimicrobial, Antibiofilm and Antioxidant Effect. Polycycl. Aromat. Compd. 2023, 43, 5139–5157. [Google Scholar] [CrossRef]
- Sudhakar, Y.; Selvakumar, M.; Bhat, D.K. Investigations on Thermo-Mechanical Properties of Organically Modified Polymer Clay Nanocomposites for Packaging Application. Polym. Polym. Compos. 2021, 29, 1191–1199. [Google Scholar] [CrossRef]
- Kroschwitz, J.I.; Mark, H.F. Encyclopedia of Polymer Science and Technology; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014. Available online: https://lccn.loc.gov/2013037237 (accessed on 5 May 2021).
- Khutia, M.; Joshi, G.M.; Thomas, P. Dielectric Relaxation of Nano Perovskite SrTiO3 Reinforced Polyester Resin/Styrene Blend for Electronic Applications. J. Mater. Sci. Mater. Electron. 2016, 27, 7685–7692. [Google Scholar] [CrossRef]
- Kong, T.; Yang, G.; Fan, P.; Yu, J. Solution-Processable NiOx:PMMA Hole Transport Layer for Efficient and Stable Inverted Organic Solar Cells. Polymers 2023, 15, 1875. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Dou, Q.; Wong, K.W.; Ng, K.M. Li7La3Zr2O12 Ceramic Nanofiber-Incorporated Composite Polymer Electrolytes for Lithium Metal Batteries. J. Mater. Chem. A Mater. 2019, 7, 3391–3398. [Google Scholar] [CrossRef]
- Soleimani, E.; Niavarzi, F.B. Preparation, Characterization and Properties of PMMA/NiO Polymer Nanocomposites. J. Mater. Sci. Mater. Electron. 2018, 29, 2392–2405. [Google Scholar] [CrossRef]
- El Sayed, A.M.; El-Gamal, S. Influence of NiO and La2O3 Nanoparticles on the Optical, Mechanical and Electrical Properties of PVAc–PMMA Blend: A Comparative Study. Phys. Scr. 2022, 97, 055814. [Google Scholar] [CrossRef]
- Basappa, M.; Ganesha, H.; Veeresh, S.; Nagaraju, Y.S.; Vandana, M.; Vijeth, H.; Devendrappa, H. Investigate the Optical, Structural and Electrochemical Properties of PVC/PMMA/NiO Blend Films. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1221, 012059. [Google Scholar] [CrossRef]
- Ninjbadgar, T.; Yamamoto, S.; Takano, M. Thermal Properties of the γ-Fe2O3/Poly(Methyl Methacrylate) Core/Shell Nanoparticles. Solid State Sci. 2005, 7, 33–36. [Google Scholar] [CrossRef]
- Genieva, S.D.; Vlaev, L.T.; Atanassov, A.N. Study of the Thermooxidative Degradation Kinetics of Poly(Tetrafluoroethene) Using Iso-Conversional Calculation Procedure. J. Therm. Anal. Calorim. 2010, 99, 551–561. [Google Scholar] [CrossRef]
- Koralay, H.; Yakuphanoglu, F.; Cavdar, S.; Günen, A.; Aksu, E. Crystallization Kinetics of Bi1.7V0.3Sr2Ca2Cu3Ox Glass-Ceramic. Phys. B Condens. Matter 2005, 355, 64–71. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of Peak Temperature with Heating Rate in Differential Thermal Analysis. J. Res. Natl. Bur. Stand. (1934) 1956, 57, 217. [Google Scholar] [CrossRef]
- Starink, M.J. Comments on “Precipitation Kinetics of Al–1.12Mg2Si–0.35Si and Al–1.07Mg2Si–0.33Cu Alloys”. J. Alloys Compd. 2007, 433, L4–L6. [Google Scholar] [CrossRef]
- Augis, J.A.; Bennett, J.E. Calculation of the Avrami Parameters for Heterogeneous Solid State Reactions Using a Modification of the Kissinger Method. J. Therm. Anal. 1978, 13, 283–292. [Google Scholar] [CrossRef]
- Ozturk, O.; Gokcen, T.; Cavdar, S.; Koralay, H.; Tasci, A.T. A Study on Nucleation, Crystallization Kinetics, Microstructure and Mechanical Properties of Ru–Bi Partial Substituted BSCCO Glass Ceramics. J. Therm. Anal. Calorim. 2016, 123, 1073–1082. [Google Scholar] [CrossRef]
- Xie, X.; Gao, H. Calorimetric Studies on the Crystallization of Li2S–B2O3 Glasses. J. Non Cryst. Solids 1998, 240, 166–176. [Google Scholar] [CrossRef]
- Sakharov, A.S.; Kolosov, A.E.; Sivetskii, V.I.; Sokolskii, A.L. Modeling of Polymer Melting Processes in Screw Extruder Channels. Chem. Pet. Eng. 2013, 49, 357–363. [Google Scholar] [CrossRef]
- Li, S.; Meng Lin, M.; Toprak, M.S.; Kim, D.K.; Muhammed, M. Nanocomposites of Polymer and Inorganic Nanoparticles for Optical and Magnetic Applications. Nano Rev. 2010, 1, 5214. [Google Scholar] [CrossRef] [PubMed]
- Gikarakis, T.; Pappas, I.; Arvanitaki, P.; Pantazi, E.; Mitsoni, E.; Roka, N.; Pitsikalis, M. Thermal Stability and Kinetics of Thermal Decomposition of Statistical Copolymers of N-Vinylpyrrolidone and Alkyl Methacrylates Synthesized via RAFT Polymerization. J. Chem. 2021, 2021, 6633052. [Google Scholar] [CrossRef]
- Freiman, S.W.; Hench, L.L. Effect of Crystallization on the Mechanical Properties of Li2O-SiO2 Glass-Ceramics. J. Am. Ceram. Soc. 1972, 55, 86–90. [Google Scholar] [CrossRef]
- Cheng, G.; Yan, Y.; Chen, R. From Ni-Based Nanoprecursors to NiO Nanostructures: Morphology-Controlled Synthesis and Structure-Dependent Electrochemical Behavior. New J. Chem. 2015, 39, 676–682. [Google Scholar] [CrossRef]
- Ayanoğlu, Z.G.; Doğan, M. Characterization and Thermal Kinetic Analysis of PMMA/Modified-MWCNT Nanocomposites. Diam. Relat. Mater. 2020, 108, 107950. [Google Scholar] [CrossRef]
- Lee, J.K.Y.; Chen, N.; Peng, S.; Li, L.; Tian, L.; Thakor, N.; Ramakrishna, S. Polymer-based Composites by Electrospinning: Preparation & Functionalization with Nanocarbons. Prog. Polym. Sci. 2018, 86, 40–84. [Google Scholar] [CrossRef]
- Campo, E.A. Polymeric Materials and Properties. In Selection of Polymeric Materials; Elsevier: Amsterdam, The Netherlands, 2008; pp. 1–39. [Google Scholar]
- Ozawa, T. Kinetic Analysis of Derivative Curves in Thermal Analysis. J. Therm. Anal. 1970, 2, 301–324. [Google Scholar] [CrossRef]
- Ul-Haq, Y.; Murtaza, I.; Mazhar, S.; Ullah, R.; Iqbal, M.; Zeeshan-ul-Huq; Qarni, A.A.; Amin, S. Dielectric, Thermal and Mechanical Properties of Hybrid PMMA/RGO/Fe2O3 Nanocomposites Fabricated by in-Situ Polymerization. Ceram. Int. 2020, 46, 5828–5840. [Google Scholar] [CrossRef]
- Salgansky, E.A.; Salganskaya, M.V.; Glushkov, D.O. Kinetics of Thermal Decomposition of Polymethylmethacrylate in a Carbon Dioxide Environment. Russ. J. Phys. Chem. B 2024, 18, 918–923. [Google Scholar] [CrossRef]
- Zeng, W.R.; Li, S.F.; Chow, W.K. Chemical Kinetics on Thermal Oxidative Degradation of PMMA. Chin. J. Chem. Phys. 2003, 16, 64–68. [Google Scholar]
- Holland, B.J.; Hay, J.N. The Effect of Polymerisation Conditions on the Kinetics and Mechanisms of Thermal Degradation of PMMA. Polym. Degrad. Stab. 2002, 77, 435–439. [Google Scholar] [CrossRef]
- Ponnamma, D.; Cabibihan, J.J.; Rajan, M.; Pethaiah, S.S.; Deshmukh, K.; Gogoi, J.P.; Pasha, S.K.K.; Ahamed, M.B.; Krishnegowda, J.; Chandrashekar, B.N.; et al. Synthesis, Optimization and Applications of ZnO/Polymer Nanocomposites. Mater. Sci. Eng. C 2019, 98, 1210–1240. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Li, Y.; Shi, Y.; Liu, J.; Xue, B.; Niu, M. Synergistic Effect of Activated Carbon, NiO and Al2O3 on Improving the Thermal Stability and Flame Retardancy of Polypropylene Composites. Polymers 2023, 15, 2135. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulou, K.; Tarani, E.; Ainali, N.M.; Chrissafis, K.; Wurzer, C.; Mašek, O.; Bikiaris, D.N. The Effect of Biochar Addition on Thermal Stability and Decomposition Mechanism of Poly(Butylene Succinate) Bionanocomposites. Molecules 2023, 28, 5330. [Google Scholar] [CrossRef]
- Wang, C.; Sheng, X.; Xie, D.; Zhang, X.; Zhang, H. High-Performance TiO2/Polyacrylate Nanocomposites with Enhanced Thermal and Excellent UV-Shielding Properties. Prog. Org. Coat. 2016, 101, 597–603. [Google Scholar] [CrossRef]
- Ogbonna, V.E.; Popoola, O.; Popoola, P. Effect of Titanium Dioxide Nanoparticles on the Dielectric, Thermal, and Corrosion Resistance Properties of Polyimide (PI) Nanocomposites. Int. J. Polym. Anal. Charact. 2024, 29, 533–546. [Google Scholar] [CrossRef]
- Asture, A.; Rawat, V.; Srivastava, C.; Vaya, D. Investigation of Properties and Applications of ZnO Polymer Nanocomposites. Polym. Bull. 2023, 80, 3507–3545. [Google Scholar] [CrossRef]




| Sample | Mean Area (px2) ± SD | CV (%) |
|---|---|---|
| PMMA-6 | 310 ± 740 | 240 |
| PMMA-12 | 400 ± 1100 | 275 |
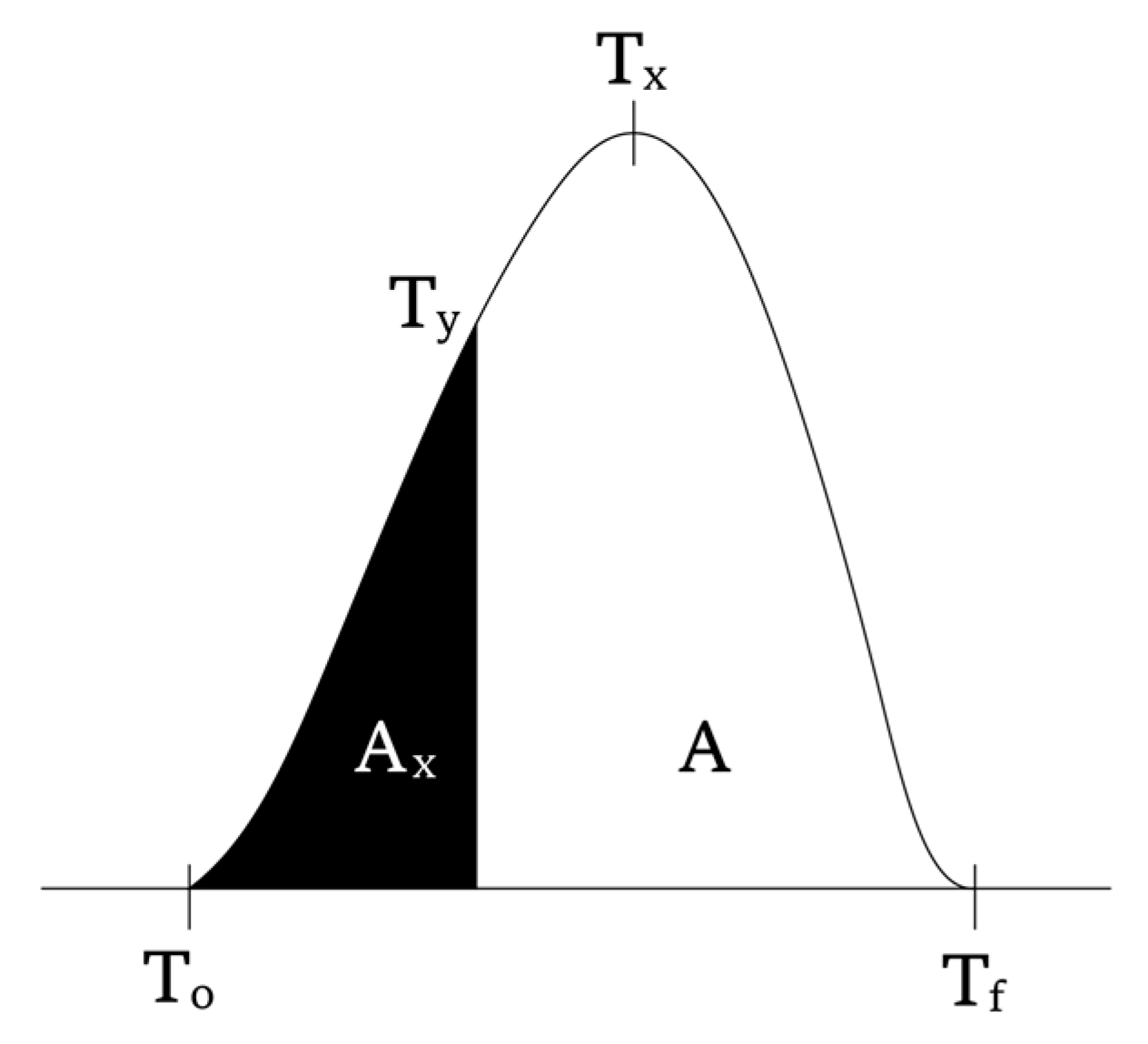
| Samples | Temp. Rate β (K/min) | To (K) | Tx (K) | A | Ax | ΔT (Tx-To) (K) |
|---|---|---|---|---|---|---|
| PMMA | 5 | 627 | 651 | 266 | 213 | 24 |
| 10 | 593 | 661 | 279 | 164 | 68 | |
| 15 | 595 | 670 | 311 | 132 | 75 | |
| 20 | 597 | 676 | 281 | 80,2 | 79 | |
| PMMA-6 | 5 | 594 | 652 | 332 | 276 | 58 |
| 10 | 604 | 660 | 310 | 201 | 56 | |
| 15 | 611 | 666 | 321 | 161 | 55 | |
| 20 | 615 | 673 | 292 | 109 | 58 | |
| PMMA-12 | 5 | 570 | 649 | 346 | 286 | 79 |
| 10 | 590 | 659 | 316 | 194 | 69 | |
| 15 | 597 | 667 | 323 | 148 | 70 | |
| 20 | 598 | 673 | 380 | 128 | 75 |
| Samples | Avrami Parameter | Kissinger Method (kJ/mol) | Takhor Method (kJ/mol) | Augis–Bennett Method (kJ/mol) |
|---|---|---|---|---|
| PMMA | 1 | 189 | 200 | 162 |
| PMMA-6 | 1 | 230 | 241 | 241 |
| PMMA-12 | 1 | 207 | 218 | 230 |
| System/Study | Mixing Time | Activation Energy (kJ/mol) | Notes |
|---|---|---|---|
| This Work (PMMA + NiO Nanocomposites) | 6 min | 230 | Higher dispersion, improved thermal stability |
| This Work (PMMA + NiO Nanocomposites) | 12 min | 210–220 | Agglomeration, reduced stability |
| Pure PMMA (in CO2, inert atmosphere) [30]. | – | ~206 | Average Ea using isoconversional methods in CO2 flow |
| Pure PMMA (radical polymerization) [32]. | – | ~200 | Two-step degradation under inert conditions |
| Pure PMMA (oxidative/air atmosphere) [31]. | – | 158.5/214.8 | Oxidative degradation—two mechanisms reported |
| Sample | Avrami (R2) | Kissinger (R2) | Takhor (R2) | Augis–Bennett (R2) |
|---|---|---|---|---|
| PMMA | 0.977 | 0.989 | 0.990 | 0.986 |
| PMMA-6 | 0.983 | 0.974 | 0.976 | 0.962 |
| PMMA-12 | 0.990 | 0.994 | 0.995 | 0.978 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulutaş, A. Effect of Mixing Time on the Thermal Stability and Activation Energies of NiO/PMMA Nanocomposites. J. Compos. Sci. 2025, 9, 557. https://doi.org/10.3390/jcs9100557
Ulutaş A. Effect of Mixing Time on the Thermal Stability and Activation Energies of NiO/PMMA Nanocomposites. Journal of Composites Science. 2025; 9(10):557. https://doi.org/10.3390/jcs9100557
Chicago/Turabian StyleUlutaş, Aytekin. 2025. "Effect of Mixing Time on the Thermal Stability and Activation Energies of NiO/PMMA Nanocomposites" Journal of Composites Science 9, no. 10: 557. https://doi.org/10.3390/jcs9100557
APA StyleUlutaş, A. (2025). Effect of Mixing Time on the Thermal Stability and Activation Energies of NiO/PMMA Nanocomposites. Journal of Composites Science, 9(10), 557. https://doi.org/10.3390/jcs9100557







