Coverage Path Planning of UAV Based on Linear Programming—Fuzzy C-Means with Pigeon-Inspired Optimization

Abstract

In contrast to rotorcraft, fixed-wing unmanned aerial vehicles (UAVs) encounter a unique challenge in path planning due to the necessity of accounting for the turning radius constraint. This research focuses on coverage path planning, aiming to determine optimal trajectories for fixed-wing UAVs to thoroughly explore designated areas of interest. To address this challenge, the Linear Programming—Fuzzy C-Means with Pigeon-Inspired Optimization algorithm (LP-FCMPIO) is proposed. Initially considering the turning radius constraint, a linear-programming-based model for fixed-wing UAV coverage path planning is established. Subsequently, to partition multiple areas effectively, an improved fuzzy clustering algorithm is introduced. Employing the pigeon-inspired optimization algorithm as the final step, an approximately optimal solution is sought. Simulation experiments demonstrate that the LP-FCMPIO, when compared to traditional FCM, achieves a more balanced clustering effect. Additionally, in contrast to traditional PIO, the planned flight paths display improved coverage of task areas, with an approximately 27.5% reduction in the number of large maneuvers. The experimental results provide validation for the effectiveness of the proposed algorithm.

1. Introduction

With the rapid evolution of automatic control and intelligent decision-making algorithms, unmanned aerial vehicles (UAVs) have emerged as formidable platforms for a range of tasks, encompassing reconnaissance and detection [1,2,3,4], traffic monitoring [5,6,7,8], disaster rescue [9,10,11,12], target tracking [13,14,15], and more. In contrast to manned aerial vehicles, UAVs are better suited for hazardous, repetitive, and heavy-duty tasks. Nevertheless, a single UAV’s computing power, task versatility, and operational scope often prove insufficient due to load constraints, falling short of meeting the intricate and interconnected requirements of tasks.

To address the escalating scale and complexity of practical applications, multi-UAV formations have gained substantial attention for their notable advantages in adaptability and scalability. Multi-UAV formations function collectively to enhance system performance through collaborative efforts. In large-scale search or scanning tasks, UAVs with diverse load-carrying capacities are widely employed to improve system cost-effectiveness and fault tolerance. For example, in agriculture, formations efficiently conduct short-term patrols of grasslands and farmland [16]. In the military domain, formations can achieve key target tracking [17,18], collaborative combat tasks [19], and more. While multi-UAV formations effectively reduce costs and enhance flexibility in various application areas, they pose challenges in executing tasks such as path planning [20], collaborative control [21], intelligent decision making [22], and performance optimization [23]. The multi-mission area coverage path-planning problem, in particular, is highly complex. This issue involves planning an optimal path from the start to the end waypoint, covering all mission areas in a given scenario while adhering to various constraints.

In response to the escalating numbers of UAVs and regions, researchers have conducted extensive studies. For instance, the expert system approach [24] has begun to provide effective paths to UAVs using decision-making tools. Heuristic intelligence algorithms, such as the particle swarm algorithm [25], pigeon swarm optimization algorithm [26], and ant colony algorithm [27], are appropriately applied to different constraints based on requirements. Despite the effectiveness of these approaches in generating reasonable flight paths, they often overlook the turning constraint, potentially leading to the irrationality of the planned path.

This paper tackles the coverage path-planning problem in multi-UAV multi-region scenarios, with the goal of identifying the optimal flight path for each UAV to traverse from the start to the end waypoint, covering all mission regions with the shortest distance. The primary focus of this work is on the region assignment and path optimization of UAVs, excluding considerations of obstacle avoidance, system faults, and other related issues. The contributions are as follows:

(1)

To illustrate this problem, this paper abstracts a linear programming model according to characteristics of the coverage path-planning problem in multi-UAV multi-region scenarios.

(2)

To tackle the challenges posed by numerous task areas, resulting in complex allocation processes and substantial demands, this paper introduces an improved fuzzy c-means clustering algorithm. This algorithm focuses on the relative distance between task areas and UAVs to efficiently search for cluster centers and boundaries. As a result, it facilitates a clear and logical partitioning of task areas.

(3)

To address the coverage path-planning challenges in multi-UAV scenarios, this paper proposes a heuristic algorithm based on the overall shortest path of formation flight to determine the UAVs’ flight paths.

The remaining part of this paper proceeds as follows. Section 2 models and formulates the coverage path-planning problem. Section 3 introduces the improved fuzzy c-means clustering-based approach. Section 4 is concerned with the pigeon-inspired optimization-based path-planning method. Section 5 analyzes the results of simulation. Finally, Section 6 summarizes this work and introduces the future work.

2. System Model and Exact Formulation

2.1. System Models

Pick $n$ UAVs $U=\{U_1,U_2,\dots ,U_n\}$ flying to $m$ mission regions $R=\{R_1,R_2,\dots ,R_m\}$ to execute a full reconnaissance mission. $U_i=<x_i,y_i,v_i>$ denotes the state of each UAV, with $x_i$ representing the initial horizontal coordinate, $y_i$ denoting the initial vertical coordinate, and $v_i$ indicating the maximum flight speed of the UAV. Typically, the maximum flight speed is influenced by various factors such as the flying environment, battery capacity, payload, etc. Nevertheless, these factors are disregarded in this work, as the research exclusively concentrates on the coverage path-planning problem, assuming that all information is known. The distance between two regions is symbolized by an $m\times m$ matrix of $D=\left\{d_{j,k}\right\}$, in which $d_{j,k}$ represents the flight length from $R_j$ to $R_k$. If $R_j$ and $R_k$ are identical, the $d_{j,j}=0$. Conversely, the length can be calculated by their coordinates.

2.2. Task Area Models

This paper focuses on UAVs equipped with visual reconnaissance sensors for ground target surveillance. The assumption is made that the UAV’s flight attitude and the line of the detection device sight are mutually independent and do not influence each other. In the absence of obstacle considerations, the detection range theoretically aligns with the UAV’s visual range, determined by the intersection of the visual cone with the ground.

In scenarios where the position of the observed target, detection device orientation, detection potential field parameters, and surface feature parameters are known, the line-of-sight propagation method is employed to determine the UAV’s visual range for the task area.

Building upon this concept, the present work develops a polygonal model based on the surface features of the task area. Initially, the center of the task area is designated as the sphere’s center, encompassing surface features in one hemisphere known as the visual hemisphere (depicted in Figure 1a). Subsequently, the relative position relationship between the detection device and the target is analyzed using the line-of-sight propagation method. By considering obstruction conditions imposed by surface features, obstructed portions in the view are removed, resulting in the detectable range of the task area. This is visualized by the intersection plane of the UAV’s flight height profile and the detection device’s visual hemisphere, as illustrated in Figure 1b.

Figure 1. Task area models: (a) the maximum detectable area of ground targets; (b) the observable range of ground targets; (c) a set of 2D simplified models.

Ultimately, the application of this method facilitates the generation of polygonal models for all task areas, as illustrated in the abstracted polygonal model diagram in Figure 1c. Based on the previously outlined modeling approach, the reconnaissance mission is considered accomplished by the UAV when it traverses the task region, touching any point within the visual range.

2.3. Exact Formulation

Coverage path planning can be formulated as the minimization of an objective function (e.g., total distance covered by the UAVs to complete the mission) while subject to linear constraints (e.g., UAV’s energy consumption constraints). It is essential that, once all regions are fully covered, the UAV’s flight path complies with the following constraints:

• (C1) Once the UAV is selected for the reconnaissance mission, it takes off from the initial location and returns back after completing all tasks.
• (C2) To ensure that all mission regions are covered with no duplications or omissions, there is one and only one UAV in the mission region to carry out the reconnaissance.
• (C3) The number of UAVs involved in the mission is to be less than or equal to the total number of mission regions.
• (C4) The UAV has to return back to initial location before it runs out of energy.
• (C5) The flight turning radius of the UAV must meet the minimum value.

$Path=\left\{p_{i,j,k}\right|1\le i\le n,0\le j\le m,1\le k\le m\}$ is adopted to represent the flight path of UAVs, where $p_{i,j,k}$ is a Boolean variable, representing $U_i$ which flies from $R_j$ to $R_k$. If the UAV flies directly from $R_j$ to $R_k$, then $p_{i,j,k}=1$, otherwise, $p_{i,j,k}=0$.

Constraint (C1) implies that the UAV needs to take off and land from the initial position at most once. The initial location is represented by virtual region $R_0$. $p_{i,0,j}$ and $p_{i,j,0}$ denote whether $U_i$ takes off from or lands in the initial position $R_j$, respectively, Constraint (C1) could be represented as:

$$\forall i\in [1,n] {\displaystyle \sum _{j=1}^m{p}_{i,0,j}}\le 1 {\displaystyle \sum _{j=1}^m{p}_{i,j,0}}\le 1$$

(1)

Constraint (C2) indicates that there is one and only one aircraft that can fly to and leave from the mission area, and Constraint (C2) can be written as:

$$\forall j\in [1,m], {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=0}^m{p}_{i,k,j}}=1,} {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m{p}_{i,j,k}}=1}$$

(2)

Constraint (C3) shows that the number of UAVs which perform tasks is to be less than or equal to the number of mission regions, i.e.,

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{p}_{i.0,j}}}\le m$$

(3)

Constraint (C4) expresses that the UAV needs to return to $R_0$ before it runs out of energy. The on-board energy constraining its voyage is $L_{i,\max }$. Therefore, Constraint (C4) requires that the sum of the distances flown by the UAV on its mission is less than or equal to its voyage, which can be written as:

$$\forall i\in [1,n],{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^m{p}_{i,j,k}}}\cdot d_{i,j,k}\le L_{i,\max }$$

(4)

Constraint (C5) expresses the limitation of turning radius. In contrast to rotorcraft, which can hover before turning, fixed-wing UAVs necessitate a circular arc to execute this action. The minimum value for the radius is determined by the circle where the arc is situated, ensuring the drone successfully completes the turning behavior.

The minimum turning radius value limits the flight segment length. That is, when UAVs are required to enter and exit a specific flight segment via the arc, the flight segment length must be sufficient to accommodate at least two circular arcs. As shown in Figure 2, the flight segment $BC$ entry and exit arcs are located on the circle $r_1$ and $r_2$, respectively. If the length decreases, the UAV will not be able to achieve normal turning. Suppose the starting waypoint of the flight segment $l_g$ is $\left(x_g,y_g\right)$ and the ending one is $\left(x_{g+1},y_{g+1}\right)$, the constraint on the shortest segment length can be expressed as (where $l_{\min }$ is the lower bound):

$$\forall i\in [1,n],{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=1}^m{p}_{i,j,k}\cdot (\sqrt{{\left(x_{\mathrm{g}+1}-x_g\right)}^2+{\left(y_{\mathrm{g}+1}-y_g\right)}^2})\ge }}{l}_{\min }$$

(5)

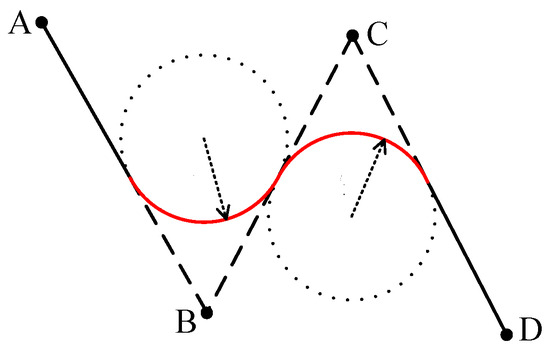
Figure 2. Schematic diagram of segment length limitation. ABCD represent four waypoints.

In addition, the minimum turning radius value also imposes restrictions on the angle between adjacent segments. If the angle is too small, the drone cannot complete the current segment before entering the next one.

Figure 3 shows that the angle between $AB$ and $BC$ needs be greater than the minimum. The constraint on the minimum arc radian can be expressed as (where ${\phi }_{\max }$ is the upper bound):

$$\forall i\in [1,n],{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^m{p}_{i,j,k}\cdot (\frac{\overline{AB}·\overline{BC}}{\left|AB\right|\left|BC\right|})\ge \cos {\phi }_{\min }}}$$

(6)

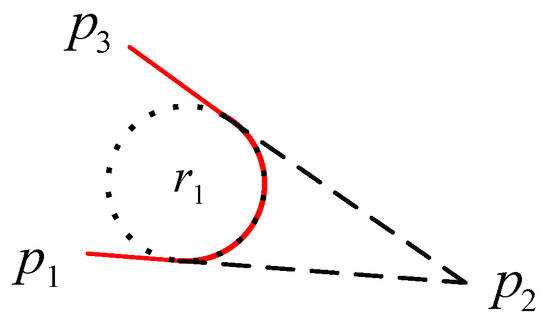
Figure 3. Schematic diagram of angle limitation.

Putting the two aspects together, Constraint (C5) can be expressed by:

$$\begin{array}{l}\forall i\in [1,n],{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=1}^m{p}_{i,j,k}\cdot (\sqrt{{\left(x_{\mathrm{g}+1}-x_g\right)}^2+{\left(y_{\mathrm{g}+1}-y_g\right)}^2})\ge }}{l}_{\min } \\ \forall i\in [1,n],{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^m{p}_{i,j,k}\cdot (\frac{\overline{AB}·\overline{BC}}{\left|AB\right|\left|BC\right|})\ge \cos {\phi }_{\min }}}\end{array}$$

(7)

Next, calculate the flight distance by the multi-UAV formation to perform regional reconnaissance tasks, i.e., the longest distance cost to characterize the performance of coverage task execution. $D(U_i)$ and $D(U,R)$ represent the flight distance of a given UAV and the UAV formation, respectively. Then, $D(U_i)$ and $D(U,R)$ can be calculated via:

$$\begin{array}{l}D(U_i)={\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^m{p}_{i,j,k}\cdot d_{i,j,k}}}\\ D(U,R)=\underset{1\le i\le n}{\max }D(U_i)\end{array}$$

(8)

In summary, the coverage path-planning problem studied in this paper can be abstracted as finding the optimal flight path sequence $Path$ for a multi-UAV formation such that the total flight distance of the coverage tasks is shortest. The objective function is $D(U,F)$, the linear constraint is from (C1) to (C5), and the exact model can be stated as:

$$\begin{array}{l}\min D(U,R)\\ s.t.(1),(2),(3),(4),(5)\end{array}$$

(9)

As evident from the abstracted formula, it is a linear model. While this model offers a solution to the coverage path-planning problem discussed in this article, it requires exploring the entire solution space, leading to a substantial time investment. As the number of UAVs and regions increases, the solution time becomes impractical, rendering the efficiency of this method unacceptable. To address this limitation, the study initially employs an enhanced fuzzy c-means algorithm for task area clustering. Subsequently, it is integrated with the PIO algorithm to allocate and plan the path more efficiently. Further details are elaborated on in the subsequent sections.

3. Region Clustering Based on Improved Fuzzy C-Means Algorithm

The focal point of this section is the development of an evaluation function rooted in the relative distance between the UAV and the area. This function aims to facilitate the identification of cluster centers and boundaries, ultimately enabling the clustering of task areas.

In the fuzzy c-means clustering algorithm, there are predefined task areas awaiting clustering. These regions are to be categorized into $n$ classes, corresponding to $n$ UAVs, with each class center denoted as $C_i$.The model is as follows:

$$\begin{array}{l}J={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{u}_{ij}^{e}F{d}_{ij}^2}}\\ s.t.0\le u_{ij}\le 1,{\displaystyle \sum _{i=1}^n{u}_{ij}=1},0\le {\displaystyle \sum _{i=1}^n{u}_{ij}<m}\end{array}$$

(10)

where $u_{ij}$ represents the membership degree of $R_j$ belonging to $C_i$. $F{d}_{ij}$ indicates the distance from $R_j$ to the center of $C_i$. $e$ is the fuzzy coefficient.

The process consists of two primary phases: the cluster centroid selection phase and the cluster boundary determination phase. In the first phase, the relative distance to each region is calculated, and the optimal clustering centroids are selected based on the initial locations of the UAVs. Moving to the second phase, the cluster boundary is established by analyzing the rate of change in relative distance, with the regions within this boundary aggregated to form a cluster.

3.1. Subsection

The cluster centers are identified as regions with the shortest distance to their neighbors. To achieve the optimal cluster center, this section introduces two matrixes: the distance radius matrix $DR$ and the distance radius accumulation matrix $ADR$. The distance radius matrix $DR$ of $R_j$ is defined as follows:

$$DR=\left(\begin{array}{c}d{r}_1\\ d{r}_2\\ ⋮\\ d{r}_m\end{array}\right)=\left(\begin{array}{cccc}d{r}_{11}& d{r}_{12}& \dots & d{r}_{1(m-1)}\\ d{r}_{21}& d{r}_{22}& \dots & d{r}_{2(m-1)}\\ ⋮& ⋮& \ddots & ⋮\\ d{r}_{m1}& d{r}_{m2}& \dots & d{r}_{m(m-1)}\end{array}\right)$$

(11)

The matrix elements represent the Euclidean distances from $R_j$ to the remaining $m-1$ mission regions, which are then sorted in ascending order according to the value to form the distance radius matrix. The corresponding region code forms the code matrix $G$:

$$G=\left(\begin{array}{c}{g}_1\\ g_2\\ ⋮\\ g_m\end{array}\right)=\left(\begin{array}{cccc}{g}_{11}& g_{12}& \dots & g_{1(m-1)}\\ g_{21}& g_{22}& \dots & g_{2(m-1)}\\ ⋮& ⋮& \ddots & ⋮\\ g_{m1}& g_{m2}& \dots & g_{m(m-1)}\end{array}\right)$$

(12)

$ADR$ is formed by accumulating the row vectors of the $DR$ to the left. The matrix enables characterization of the distance between each task region and the surrounding task region:

$$AD{R}_{j,l}={\displaystyle \sum _{k=1}^{l}D{R}_{jk}}$$

(13)

Since $DR$ is the distance from the region to the remaining regions, $ADR$ also can be written as:

$${\displaystyle \sum DR}={(AD{R}_{jl})}_{m(m-1)}$$

(14)

The cluster centroid selection steps are as follows:

(Input): region number $m$, clusters(UAVs) number $n$, region point coordinates, neighbor threshold $\epsilon$.

(S1): Compute the $DR$ according to Equation (14). Compute the $ADR$ according to Equation (16). Determine the initial search point.

(S2): Taking Figure 4 as an example, the intra-neighbor search is carried out with center and radius, and the task region is searched as $\left\{1,2,3,5,6,7,9\right\}$.

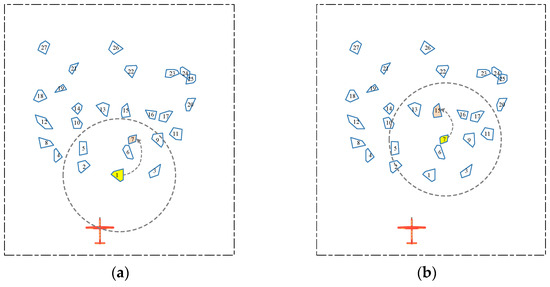
Figure 4. Schematic diagram of cluster center search: (a) Initial search; (b) Search process.

(S3): Compare the corresponding values of the mission regions in the neighbor in $DR$ and $ADR$ to find the smallest of them. In Figure 4, find the smallest values $d{r}_{7,j}$ and $AD{R}_{7,j}$ of task region $g_7$. Then, update $g_7$ as the new search center.

(S4): Take $g_7$ as the search center, $\epsilon$ as the radius, remove the task area that has been compared to obtain a new task region $\left\{10,11,13,15,16,17\right\}$. Then, repeat step (S3) to find the task region with the smallest value and update the class center.

(S5): Repeat the above steps to find the cluster center region $g_{15}$.

(Output): Cluster center region code.

3.2. Cluster Boundary Determination Phase

After determining the cluster center, the next step is to determine the boundaries. To this end, a row partial derivative matrix is designed to represent the matrix of distance change rate in order to identify the boundary points. As shown in Formula (15):

$$D{R}^{\prime }={(\frac{\partial AD{R}_{j,l}}{{\partial }_j})}_{m(m-2)}={(\frac{d{r}_{j,l+1}-d{r}_{j,l-1}}{2})}_{m(m-2)}$$

(15)

where $j$ represents the $jth$ task area, which is also the $jth$ column in the matrix. When $R_j$ is a cluster centroid, there may be a point in row $lth$ whose distance radius increases dramatically as the number of columns increases (the position of the off-center point). It is said to be the cluster boundary point.

Cluster boundary search is started based on the first-order row deflection matrix and the search steps are as follows:

(Input): Cluster center region code.

(S1): The clustering center is used as a base point to start expanding the search radius.

(S2): Compare the $\left\{dr\left(15,j\right)\right\}$ and $\left\{dr\prime \left(15,j\right)\right\}$ for each task area with the neighbor.

(S3): Taking Figure 5 as an example, find the jump point $g_{27}$, which is the clustering boundary point. The task area within the clustering boundary point belongs to this clustering, and the rest belongs to other clusters.

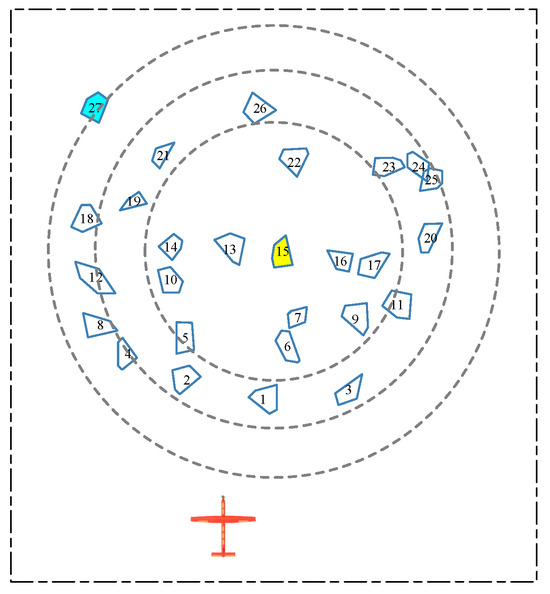
Figure 5. Schematic diagram of cluster boundary search.

(output): Search radius.

4. Path Planning Based on Pigeon-Inspired Optimization Algorithm

In this section, the pigeon-inspired optimization algorithm (PIO) [28] is employed to establish the access order within the clustering area, ultimately deriving an approximate optimal flight path. Inspired by the long-distance homing behavior of pigeons, the pigeon-inspired optimization algorithm primarily comprises two stages: the first phase influenced by the map and compass operator (MCO), and the second phase influenced by the landmark operator (LO).

4.1. First Phase

In this phase, pigeons are initialized. $N$ pigeons are in w-dimensional search space, and the position and speed of the pigeons are updated as the number of iterations increases. The position and speed of pigeon $i$ are recorded as $X_i=\left[\begin{array}{cccc}{x}_{i1}& x_{i2}& \dots & x_{iw}\end{array}\right]$ and $V_i=\left[\begin{array}{cccc}{v}_{i1}& v_{i2}& \dots & v_{iw}\end{array}\right]$, respectively, where $i=1,2,3\dots N$. After each iteration, they are updated as:

$$V_i^{N_c}=V_i^{N_c-1}{e}^{-R\times N_c}+rand(X_{best}-X_i^{N_c-1})$$

(16)

$$X_i^{N_c}=X_i^{N_c-1}+V_i^{N_c}$$

(17)

where $R$ is the factor of MCO, and its range is $0~1$. $rand$ represents a random number from 0 to 1. $N_c$ is the current iteration. $X_{best}$ indicates the global optimal position of pigeons before $N_c$ iterations.

4.2. Second Phase

Stop the work of the first phase immediately and enter the second phase when $N_c$ reaches the maximum iteration $N_{c1\max }$. In this phase, set the center of the remaining pigeons $X_{center}$ as the landmark after each iteration. Update $N^{N_c}$ and $X_i$ according to Equations (19) and (20).

$$X_{center}^{N_c-1}=\frac{{\displaystyle \sum _{i=1}^{N^{N_c-1}}{X}_i^{N_c-1}fitness(X_i^{N_c-1})}}{N^{N_c-1}{\displaystyle \sum _{i=1}^{N^{N_c-1}}fitness(X_i^{N_c-1})}}$$

(18)

$$N^{N_c}=\frac{N^{N_c-1}}{2}$$

(19)

$$X_i=X_i^{N_c-1}+rand(X_{center}^{N_c-1}-X_i^{N_c-1})$$

(20)

The fitness function is a crucial indicator used to evaluate whether an individual has reached the optimal level. In the fuzzy C-means algorithm, the minimum objective function value represents the best result. Therefore, the fitness function is designed as follows:

$$fitness(X_i^{N_c-1})=\frac{J+1}{X_i^{N_c-1}}$$

(21)

From the formula, it is evident that the fitness function value is directly proportional to the fuzzy clustering objective function value. In simpler terms, a smaller objective function corresponds to a smaller fitness value, indicating proximity to the optimal solution.

Similarly, the landmark operator stops working, and the search of the PIO ends when the $N_c$ reaches the maximum iteration $N_{c2\max }$ in the second phase.

5. Simulation Results

5.1. Task Region Clustering

A detectable area of 20 km × 20 km is randomly generated, as shown in Figure 6a. Four UAVs (depicted as triangles) are selected to execute the mission, and the base coordinate information is provided in Table 1:

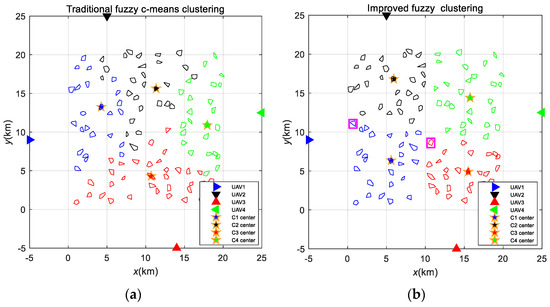
Figure 6. Fuzzy clustering results: (a) Traditional method; (b) Improved method.

Table 1. Initial position of UAVs.

UAVi	xi	yi
$UA{V}_1$	−5 km	9 km
$UA{V}_2$	5 km	25 km
$UA{V}_3$	14 km	−5 km
$UA{V}_4$	25 km	12.5 km

The improved FCM algorithm and the traditional FCM algorithm were simulated and compared. The results are depicted in Figure 6. In both approaches, the areas within the environment were clustered based on the number of UAVs, resulting in four categories (C1 to C4), with the pentagram symbolizing the cluster center. As observed, Figure 6a displays significant irrationality, featuring unclear boundaries between clusters and instances of crossings. In contrast, Figure 6b presents more reasonable results; the randomly generated mission region is distinctly divided into four clusters, and the jump points (within the magenta box) on the cluster boundary also provide the best classification.

Furthermore, the traditional FCM allocates task area quantities to four UAVs as 24, 27, 33, and 24, displaying considerable deviations. In contrast, the improved FCM assigns quantities as 26, 27, 27, and 28, achieving a more uniform distribution. The more balanced the distribution of tasks among UAVs, the shorter the planned maximum flight path within the formation, resulting in a reduced overall time for the formation to complete the tasks. Consequently, the enhanced clustering algorithm demonstrates superior effects on task area clustering, providing an advantage for formation path planning.

On the basis of the cluster results, the data of the $DR$, $ADR$, and $DR\prime$ are calculated and compared, as shown in Figure 7, Figure 8, and Figure 9, respectively.

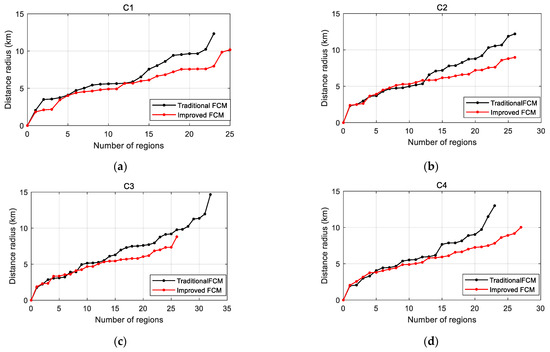
Figure 7. Distance radius comparison: (a) Cluster 1; (b) Cluster 2; (c) Cluster 3; (d) Cluster 4.

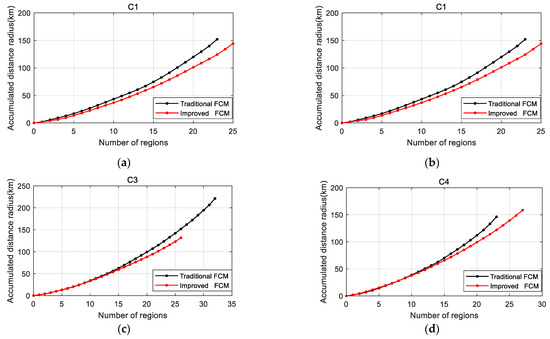
Figure 8. Accumulated distance radius: (a) Cluster 1; (b) Cluster 2; (c) Cluster 3; (d) Cluster 4.

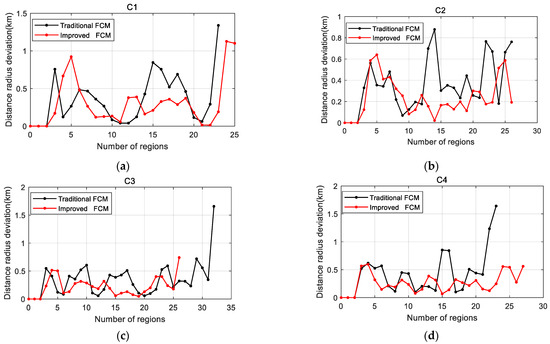
Figure 9. Distance radius deviation: (a) Cluster 1; (b) Cluster 2; (c) Cluster 3; (d) Cluster 4.

From the curves in the figures above, it is evident that the values of $DR$ and $ADR$ obtained through the improved FCM method are smaller than those from the traditional method. This difference is particularly noticeable when dealing with a large number of mission regions, suggesting that the new method aims to identify the most densely populated and highly aggregated individual task regions.

The curve for $DR\prime$ in Figure 9 reveals that the growth rate of the improved FCM tends to stabilize as the search radius increases, especially when the number of neighboring regions exceeds five. In contrast, $DR\prime$ undergoes a dramatic jump when the number of regions is at its highest, signifying the boundary point of this cluster. On the other hand, the $DR\prime$ curve for the traditional FCM exhibits erratic fluctuations, indicating poor aggregation of individual task points and unclear boundaries. This observation emphasizes that the improved FCM can obtain more suitable cluster centers with clear boundaries, resulting in superior clustering outcomes.

5.2. Path Planning

Comparative experiments between the algorithm proposed in this article and the conventional pigeon-inspired optimization algorithm were conducted to assess its performance. Figure 10a illustrates the path outcomes generated by the traditional PIO algorithm, revealing a certain level of irrationality. The planned paths fall short of reaching all task areas and exhibit a notable repetition rate of up to 2.8%. In contrast, the results obtained by the proposed algorithm in Figure 10b showcase an enhanced coverage rate of task areas, and there is an absence of repetition in task area execution.

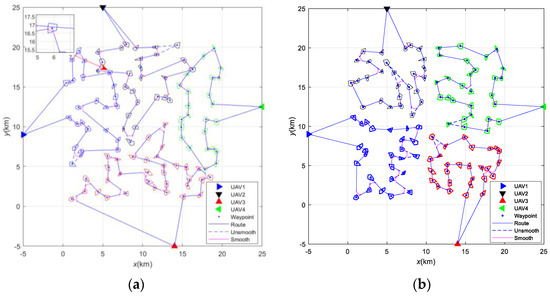
Figure 10. Path-planning results: (a) Traditional method; (b) LP-FCMPIO method.

To mitigate the impact of initialization, the experiment is conducted 20 times. Table 2 compares relevant parameters of the planned paths between the two methods. The results in Table 2 indicate that, concerning total distance and maximum path distance, those of the LP-FCMPIO are significantly smaller than those of PIO. This implies that, when the UAV speed is the same, the path generated by the former can effectively reduce the overall flight time of the formation. Regarding the number of turns, the LP-FCMPIO exhibits a considerable reduction compared to the PIO, with a 27.5% decrease in the number of large maneuvers (turn angles less than 90°), indicating a substantial reduction in UAV turns and large maneuvers. This suggests that the path planned by the former is more rational. In terms of task area coverage, the LP-FCMPIO demonstrates a higher coverage rate than the PIO, signifying that the former can attend to a larger number of task areas.

Table 2. Coverage performance of Different Methods.

Algorithm	Total Voyage	Max. Distance	Coverage Rate	Number of Turns	Number of Major Maneuvers, Turning
PIO	246.72 km	81.10 km	77.12%	91	40
LP-FCMPIO	229.43 km	62.11 km	81.53%	82	29

Figure 11 illustrates the results of coverage path planning for task areas with varying numbers of UAVs (three and five) The outcomes suggest that the algorithm proposed in this paper can effectively cluster target areas based on the number of UAVs and generate suitable flight paths.

Figure 11. Path-planning results: (a) three UAVs; (b) five UAVs.

5.3. Execution Time Evaluation

The performance of the three methods is assessed in terms of execution time, and Table 3 demonstrates the average execution time of these methods in multiple regions, with a logarithmic scale applied. As seen in Table 3, the execution time gradually increases with a growing number of regions. In scenarios with a small number of mission regions, linear programming exhibits excellent solving performance. However, as the number of regions increases, the consumed time experiences explosive growth. The PIO algorithm maintains a relatively stable computation time, albeit higher than that of LP-FCMPIO. Overall, LP-FCMPIO exhibits better ability in solving coverage path-planning problems for large-scale task areas.

Table 3. Execution time statistic of the three methods.

Number	LP	PIO	LP-FCMPIO
5	0.23 s	30.76 s	20.67 s
10	32.36 s	34.13 s	22.79 s
15	96.13 s	37.15 s	25.96 s
20	174.47 s	40.13 s	29.46 s
30	322.46 s	48.62 s	37.14 s
40	439.12 s	57.42 s	46.93 s
50	540.62 s	68.07 s	54.52 s
60	627.83 s	80.29 s	61.37 s
70	700.29 s	104.14 s	77.29 s
80	763.32 s	122.13 s	86.79 s
90	802.62 s	146.26 s	109.27 s
100	733.79 s	165.49 s	137.62 s

6. Conclusions

This study aims to investigate coverage path planning for multiple fixed-wing UAVs with the goal of identifying an approximately optimal operational path that visits all areas of interest. Firstly, considering the constraint of the turning radius of fixed-wing UAVs, a linear model for coverage path planning is established. Secondly, enhancements are introduced to the search methods for class centroids and boundaries in the fuzzy clustering algorithm to improve the clustering effect on task areas. Thirdly, the PIO algorithm is utilized to plan the flight paths within the classes. Finally, simulation experiments are conducted to assess the planned paths’ performance parameters, providing validation for the effectiveness of the LP-FCMPIO algorithm.

This work focuses on achieving the shortest flight distance for a fleet of UAVs to complete all tasks. Some idealized assumptions are made about the scenarios in which UAVs perform tasks, such as considering the task as completed when the UAV reaches the task area. However, in practical situations, issues like task area omission and incomplete tasks may arise when considering a single execution. This necessitates exploration into the effective execution of task areas, adding redundancy to task execution, making the planning approach closer to real-world scenarios, and enhancing the robustness of planning strategies. Therefore, future work needs to delve deeper into this aspect for a more comprehensive study.