Ulam-Type Stability Results for Variable Order Ψ-Tempered Caputo Fractional Differential Equations

Abstract

An initial value problem for nonlinear fractional differential equations with a tempered Caputo fractional derivative of variable order with respect to another function is studied. The absence of semigroup properties of the considered variable order fractional derivative leads to difficulties in the study of the existence of corresponding differential equations. In this paper, we introduce approximate piecewise constant approximation of the variable order of the considered fractional derivative and approximate solutions of the given initial value problem. Then, we investigate the existence and the Ulam-type stability of the approximate solution of the variable order $\mathsf{\Psi }$-tempered Caputo fractional differential equation. As a partial case of our results, we obtain results for Ulam-type stability for differential equations with a piecewise constant order of the $\mathsf{\Psi }$-tempered Caputo fractional derivative.

1. Introduction

Fractional derivatives and integrals of variable order are widely studied in the literature, and a comprehensive review and a good mathematical framework of fractional calculus of variable order, based on Scarpi’s approach, is provided in [1]. Surveys of the types of derivatives/integrals of variable order with some physical discussions are given in [2,3]. There are several types of definitions of variable order fractional derivatives/integrals (see, for example, [4,5,6]). These definitions keep the basic property of fractional derivatives—the nonlocality. This property unfortunately does not have the semigroup property when variable order is applied (see, for example, [5,7]). This does not allow us directly to convert the differential equation with variable order fractional derivative to an equivalent fractional integral equation as is possible for fractionals of constant order (see, for example, [8,9,10,11,12,13]). In [14], the author defines a derivative in a new way, again called a fractional derivative. This derivative keeps the locality property of ordinary derivatives and it enables one to apply directly a variable order with a semigroup property.

One of the main problems, existence, is studied by many authors. For the Riemann–Liouville fractional derivative of variable order for differential equations, existence is studied in [7], and the concept of approximate solution of the given problem is introduced. This concept is based on the application of piecewise constant orders of fractional integrals and derivatives used for various problems in [15,16].

To be more general, we consider a tempered Caputo fractional derivative with respect to another function and variable order. This type of derivative has an exponential kernel, and it generalizes the classical Caputo fractional derivative. Furthermore, this derivative is called the variable order $\psi$-tempered Caputo fractional derivative. In this paper, we study the initial value problem of a nonlinear differential equation with the abovementioned fractional derivative. Based on the tempered Caputo fractional derivative, its application to differential equations, and some known results for this type of derivative, we introduce approximate solutions of the given problem and study existence and Ulam-type stability. Several examples are provided to illustrate the main results. Furthermore, as a partial case, we obtain existence and Ulam-type stability results for differential equations with a piecewise constant order $\psi$-tempered Caputo fractional derivative.

2. $\mathsf{\Psi }$-Tempered Fractional Calculus of Variable Order

There are several definitions for fractional integrals and derivatives of variable order depending on the time variable (see, for example, [5]).

In this paper, we combine the ideas of variable order fractional integrals and derivatives (see [5]) with $\mathsf{\Psi }$-tempered fractional derivatives/integrals to generalize fractional calculus in variable order.

Let $0<T<\infty$ be a fixed number; $\psi :[0,T]\to (0,\infty )$ be a smooth increasing function with ${\psi }^{\prime }\left(t\right)>0$ almost everywhere in $[0,T];$ $\lambda >0$ be a given constant; the function $\delta :[0,T]\to (0,1)$ be locally integrable; and $\upsilon \in A{C}_{\psi }([0,T],\mathbb{R})$ where

$$A{C}_{\psi }([0,T],\mathbb{R})=\{h:[0,T]\to \mathbb{R}:\frac{h^{\prime }\left(t\right)}{{\psi }^{\prime }\left(t\right)}\in AC([0,T],\mathbb{R})\}.$$

Definition 1.

The tempered Riemann–Liouville fractional integral of variable order with respect to the function ψ (TFIVO) is defined by (here $t\in (0,T]$)

$${}_0{\mathcal{I}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\upsilon \left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\delta \right(t\left)\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\delta \left(t\right)-1}{\psi }^{\prime }\left(s\right)\upsilon \left(s\right)ds.$$

We will also generalize the Caputo-type fractional derivative of variable order combining the ideas of [17] and the type III Caputo fractional derivative of variable order (see Definition 2 [5]).

Definition 2.

The tempered Caputo fractional derivative of variable order with respect to the function $\psi \left(t\right)$ (GFDVO) is defined by

$$\begin{array}{cc}& {}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\upsilon \left(t\right)={}_0{\mathcal{I}}_{\psi \left(t\right)}^{1-\delta \left(t\right),\lambda }\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}+\lambda \right)\upsilon \left(t\right)\hfill \\ & =\frac{1}{\mathsf{\Gamma }(1-\delta (t\left)\right)}({\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-\delta \left(t\right)}{\nu }^{\prime }\left(s\right)ds\hfill \\ & +\lambda {\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-\delta \left(t\right)}{\psi }^{\prime }\left(s\right)\nu \left(s\right)ds),t\in (0,T].\hfill \end{array}$$

Remark 1.

The tempered derivatives/integrals with respect to another function, given in Definitions 1 and 2, are called Ψ-tempered derivatives/integrals.

Remark 2.

TFIVO and GFDVO are generalizations of the well-known and studied fractional integrals and derivatives (see, for example, [17,18,19]).

2.1. Some Results on Caputo-Type Fractional Derivatives of Constant Order

In our paper, we will use some known results for tempered Caputo fractional derivative with reference to another function and a constant order.

Lemma 1

(Theorem 5.2 [18]). Let $\alpha \in (0,1)$ be a given constant, $\lambda \in \mathbb{R}$, the function $\psi :[0,b]\to (0,\infty ),b<\infty$ be a smooth increasing function with ${\psi }^{\prime }\left(t\right)>0$ almost everywhere in $[0,b],$ and $f\in C\left(\right[0,b]\times \mathbb{R},\mathbb{R})$. Then, the IVP for the fractional differential equation with the ψ-tempered Caputo fractional derivative of constant order

$${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\alpha ,\lambda }y\left(t\right)=f(t,y\left(t\right)),t\in (0,b],y\left(0\right)=y_0,$$

(1)

is equivalent to the fractional integral equation

$$\begin{array}{cc}\hfill y\left(t\right)& =e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}{y}_0\hfill \\ & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\alpha -1}{\psi }^{\prime }\left(s\right)f(s,y\left(s\right))ds,t\in [0,b],\hfill \end{array}$$

both to be solved for functions $y\in A{C}_{\psi }([0,T],\mathbb{R}).$

Lemma 2

(Lemma 5.4 [18]). Let $\alpha \in (0,1),\lambda \in \mathbb{R}$, ψ be a smooth monotonic function on [0, b] with ${\psi }^{\prime }>0$ almost everywhere, the function $f\in C\left(\right[0,b]\times \mathbb{R},\mathbb{R})$ with $0<b<\infty$ and

$$\left|f\right(t,u)-f(t,v\left)\right|\le L|u-v|,u,v\in \mathbb{R},t\in [0,b].$$

Then, the IVP (1) has an unique solution $y\in A{C}_{\psi }([0,b],\mathbb{R})$, provided that $L<\mathsf{\Gamma }(\alpha +1){(\psi \left(b\right)-\psi \left(0\right))}^{-\alpha }{e}^{\lambda \left(\psi \right(b)-\psi (0\left)\right)}.$

Lemma 3

(Corollary 2 [20]). Let $\alpha >0$, $b\in (0,\infty )$, $\psi :[0,T]\to (0,\infty ))$ be a smooth increasing function with ${\psi }^{\prime }\left(t\right)>0$ almost everywhere in $[0,T],$ $C,K>0$, $u\in C\left(\right[0,b],[0,\infty \left)\right)$. If

$$u\left(t\right)\le C+K{\int }_0^t{(\psi \left(t\right)-\psi \left(s\right))}^{\alpha -1}{\psi }^{\prime }\left(s\right)u\left(s\right)ds,t\in (0,b],$$

then we have

$$u\left(t\right)\le C{E}_{\alpha }\left(K\mathsf{\Gamma }\left(\alpha \right){(\psi \left(t\right)-\psi \left(0\right))}^{\alpha }\right),t\in (0,b].$$

We will use the following result for the Caputo fractional derivative with respect to another function (a special case of GFDVO with $\lambda =0$ and $\delta \left(t\right)\equiv \alpha \in (0,1)$ being a constant).

Lemma 4

(Lemma 2 [21]). Let $\mu \in \mathbb{R}$, $\alpha \in (0,1)$ and $\psi :[0,T]\to (0,\infty )$ be a smooth increasing function with ${\psi }^{\prime }\left(t\right)>0$ almost everywhere in $[0,T]$. Then, the function $E_{\alpha }\left(\mu {(\psi \left(t\right)-\psi \left(0\right))}^{\alpha }\right)$ is a solution of the equation ${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\alpha }y\left(t\right)=\mu y\left(t\right)$ where ${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\alpha }$ is the Caputo fractional derivative with reference to another function given in Definition 2 with $\lambda =0$ and $\delta \left(t\right)\equiv \alpha$.

Lemma 5

(Lemma 1 [21]). Given $\beta >1$, we have

$${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\alpha }{(\psi \left(t\right)-\psi \left(0\right))}^{\beta -1}=\frac{\mathsf{\Gamma }\left(\beta \right)}{\mathsf{\Gamma }(\beta -\alpha )}{(\psi \left(t\right)-\psi \left(0\right))}^{\beta -\alpha -1}.$$

2.2. Some Results for Variable Order of Fractional Derivatives

For a general function $\delta \left(t\right)$, the $\psi$-tempered Riemann–Liouville variable order fractional integral does not have the semigroup property.

Example 1.

Let $T=2$, $\gamma \left(t\right)=0.75t+0.15$, $\delta \left(t\right)=0.25(t+1)$, $\lambda =0$, $\psi \left(t\right)=t$ and $\upsilon \left(t\right)\equiv 1$.

We will compare ${}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right),\lambda }\left({}_0{\mathcal{I}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\right){\upsilon \left(t\right)|}_{t=1}$ and ${}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right)+\delta \left(t\right),\lambda }{\upsilon \left(t\right)|}_{t=1}$ applied in Definition 1. From Definition 1 we have

$$\begin{array}{cc}& {}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right)+\delta \left(t\right),\lambda }\upsilon \left(t\right)\hfill \\ & =\frac{1}{\mathsf{\Gamma }\left(\gamma \right(t)+\delta (t\left)\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\gamma \left(t\right)+\delta \left(t\right)-1}{\psi }^{\prime }\left(s\right)\upsilon \left(s\right)ds\hfill \\ & =\frac{1}{\mathsf{\Gamma }\left(\gamma \right(t)+\delta (t\left)\right)}{\int }_0^t{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\gamma \left(t\right)+\delta \left(t\right)-1}{\psi }^{\prime }\left(s\right)ds\hfill \end{array}$$

(2)

and

$$\begin{array}{cc}& {}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right),\lambda }\left({}_0{\mathcal{I}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\right)\upsilon \left(t\right)\hfill \\ & =\frac{1}{\mathsf{\Gamma }\left(\gamma \right(t\left)\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\gamma \left(t\right)-1}{\psi }^{\prime }\left(s\right)\left({}_0{\mathcal{I}}_{\psi \left(s\right)}^{\delta \left(s\right),\lambda }\right)\upsilon \left(s\right)ds\hfill \\ & =\frac{1}{\mathsf{\Gamma }\left(\gamma \right(t\left)\right)}{\int }_0^t\frac{1}{\mathsf{\Gamma }\left(\delta \right(s\left)\right)}{\left(t-s\right)}^{\gamma \left(t\right)-1}{\int }_0^s{\left(t-s\right)}^{\delta \left(s\right)-1}d\sigma ds\hfill \\ & =\frac{1}{\mathsf{\Gamma }\left(\gamma \right(t\left)\right)}{\int }_0^t\frac{\mathsf{\Gamma }(0.25+0.25s)}{\mathsf{\Gamma }(1.25+0.25s)\mathsf{\Gamma }(0.25s+0.25)}{\left(t-s\right)}^{\gamma \left(t\right)-1}{s}^{0.25s+0.25}ds.\hfill \end{array}$$

(3)

Note

$${}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right)+\delta \left(t\right),\lambda }\upsilon \left(t\right){|}_{t=1}\approx 0.805043,$$

$${}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right),\lambda }\left({}_0{\mathcal{I}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\right)\upsilon \left(t\right){|}_{t=1}\approx \frac{1.16595}{\mathsf{\Gamma }\left(0.9\right)}=1.09107.$$

Thus, ${}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right),\lambda }\left({}_0{\mathcal{I}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\right)\upsilon \left(t\right){|}_{t=1}\ne {}_0{\mathcal{I}}_{\psi \left(t\right)}^{\gamma \left(t\right)+\delta \left(t\right),\lambda }\upsilon \left(t\right){|}_{t=1}$.

Remark 3.

Without the semigroup property of the ψ-tempered Riemann–Liouville variable order fractional integral (see Example 1), the integral presentation of Lemma 1 is not true for the case when the order is variable (see, for example, Equation (7) [22]).

In our study, we will use the ideas of Lemma 6 [7], which will be slightly modified:

Lemma 6.

Let $\delta \in C\left(\right[0,T],(0,1\left)\right).$ Then, for any $ϵ>0$ there exist a natural number $m=m\left(ϵ\right)$ and points $T_k=T_k\left(ϵ\right):0=T_0<T_1<T_2<\dots <T_{m-1}<T_m=T$ such that

$$\left|\delta \right(t)-\alpha (t\left)\right|\le ϵ,t\in [0,T],$$

where $\alpha \left(t\right)={\sum }_{k=1}^m\delta \left(T_{k-1}\right)I_k\left(t\right)$ for $t\in [0,T],$ and $I_k\left(t\right)$ is the indicator of the interval $[T_{k-1},T_k]$, $k=1,2,\dots ,m$, i.e.,

$$I_k\left(t\right)=\left\{\begin{array}{c}1,ift\in (T_{k-1},T_k],\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

Proof. 

Let $ϵ>0$ be a given fixed number. Note that $\delta$ is uniformly continuous on $[0,T]$, so there exists a $\theta >0$ with $\left|\delta \right(t)-\delta (s\left)\right|\le ϵ$ for $t,s\in [0,T]$ and $|t-s|\le \theta$.

Take $p_1=\delta \left(0\right)$. If $|\delta \left(t\right)-p_1|\le ϵ$ for $t\in (0,T]$, then we choose $m=1$ and $T_1=T$ and stop the process. Otherwise, there exists a number $T_1\in (0,T]$ (note $T_1\ge \theta$) such that $|\delta \left(t\right)-p_1|\le ϵ,t\in [0,T_1].$ Take $p_2=\delta \left(T_1\right)$. If $|\delta \left(t\right)-p_1|\le ϵ$ for $t\in (T_1,T]$, then we choose $m=2$, $T_2=T$ and stop the process. Otherwise, there exists a number $T_2\in (T_1,T]$ (note $T_2-T_1\ge \theta$) such that $|\delta \left(t\right)-p_2|\le ϵ,t\in (T_1,T_2].$ Take $p_3=\delta \left(T_2\right)$ and continue this process (the process will stop after a finite number since there exists a positive integer l with $l\theta \ge T$). Thus, we have constructed (for some m) the function

$$\alpha \left(t\right)=\sum _{k=1}^m{p}_k{I}_k\left(t\right)=\left\{\begin{array}{c}\delta \left(T_0\right),ift\in [T_0,T_1],\hfill \\ \delta \left(T_1\right),ift\in (T_1,T_2],\hfill \\ ⋮\hfill \\ \delta \left(T_m\right),ift\in (T_{m-1},T_m].\hfill \end{array}\right.$$

(4)

□

Definition 3.

The piecewise constant function α defined by (4) will be called an ϵ-approximation of the variable order $\delta \left(t\right)$.

Remark 4.

Note that the partition as well as the piecewise function α, defined by (4), depend on the number ϵ.

Example 2.

Let $T=2$, $\delta \left(t\right)=0.5sin\left(t\right)+0.4\in (0,1)$.

Let $ϵ=0.2$. We will construct an $0.2$-approximation of the fractional order $\delta \left(t\right)$. Since $\left|\delta \right(t)-\delta (0\left)\right|=|0.5sin(t\left)\right|\le 0.2$ for $t\in (0,{sin}^{-1}\left(\frac{0.2}{0.5}\right)={sin}^{-1}\left(0.4\right)]$ we take $T_1={sin}^{-1}\left(0.4\right)\in (0,2)$. Then, from $|\delta \left(t\right)-\delta \left(T_1\right)|=|0.5sin\left(t\right)-0.5\left(0.4\right)|\le 0.2$ for $t\in (T_1,T_2)$ with $T_2={sin}^{-1}\left(0.8\right)\in (T_1,2)$. Furthermore, $|\delta \left(t\right)-\delta \left(T_2\right)|=|0.5sin\left(t\right)-0.5\left(0.8\right)|\le 0.2$ for $t\in [T_2,2]$.

Therefore, the partition is $0<si{n}^{-1}\left(0.4\right)<{sin}^{-1}\left(0.8\right)<2$, and the $0.2$-approximation of $\delta \left(t\right)$ is

$$\begin{array}{c}\hfill \alpha \left(t\right)=\left\{\begin{array}{c}0.4,ift\in [0,si{n}^{-1}\left(0.4\right)],\hfill \\ 0.6,ift\in (si{n}^{-1}\left(0.4\right),si{n}^{-1}\left(0.8\right)],\hfill \\ 0.8,ift\in (si{n}^{-1}\left(0.8\right),2].\hfill \end{array}\right.\end{array}$$

(5)

Let $ϵ=0.1$. Since $\left|\delta \right(t)-\delta (0\left)\right|=|0.5sin(t\left)\right|\le 0.1$ for $t\in (0,{sin}^{-1}\left(\frac{0.1}{0.5}\right)={sin}^{-1}\left(0.2\right)]$ we take $T_1={sin}^{-1}\left(0.2\right)\in (0,3)$. Then, from $|\delta \left(t\right)-\delta \left(T_1\right)|=|0.5sin\left(t\right)-0.5\left(0.2\right)|\le 0.1$ for $t\in (T_1,T_2)$ with $T_2={sin}^{-1}\left(\frac{0.2}{0.5}\right)={sin}^{-1}\left(0.4\right)\in (T_1,2)$. Furthermore, $|\delta \left(t\right)-\delta \left(T_2\right)|=|0.5sin\left(t\right)-0.5\left(0.4\right)|\le 0.1$ for $t\in [T_2,T_3]$ with $T_3={sin}^{-1}\frac{0.3}{0.5}={sin}^{-1}\left(0.6\right)$. Furthermore, $|\delta \left(t\right)-\delta \left(T_3\right)|=|0.5sin\left(t\right)-0.5\left(0.6\right)|\le 0.1$ for $t\in [T_3,T_4]$ with $T_4=si{n}^{-1}\frac{0.4}{0.5}={sin}^{-1}0.8$.

Therefore, the partition is $0<{sin}^{-1}\left(0.2\right)<{sin}^{-1}\left(0.4\right)<{sin}^{-1}\left(0.6\right)<{sin}^{-1}\left(0.8\right)<2$ and the $0.1$-approximation of $\delta \left(t\right)$ is

$$\begin{array}{c}\hfill \alpha \left(t\right)=\left\{\begin{array}{c}0.4,ift\in [0,si{n}^{-1}\left(0.2\right)],\hfill \\ 0.5,ift\in (si{n}^{-1}\left(0.2\right),si{n}^{-1}\left(0.4\right)],\hfill \\ 0.6,ift\in (si{n}^{-1}\left(0.4\right),si{n}^{-1}\left(0.6\right)],\hfill \\ 0.7,ift\in (si{n}^{-1}\left(0.6\right),si{n}^{-1}\left(0.8\right)],\hfill \\ 0.8,ift\in (si{n}^{-1}\left(0.8\right),2].\hfill \end{array}\right.\end{array}$$

(6)

The example illustrates the ϵ-approximation of the fractional order depends on ϵ.

Note that the claim of Lemma 6 could be proved on a half real line.

Lemma 7.

Let $\delta \in C\left(\right[0,\infty ),(0,1\left)\right)$ be such that ${lim}_{t\to \infty }\delta \left(t\right)=\xi \in (0,1)$. Then, for any $ϵ>0$, there exist a natural number $m=m\left(ϵ\right)$ and points $T_k=T_k\left(ϵ\right):0<T_1<T_2<\dots <T_{m+1}<\infty$ such that

$$\left|\delta \right(t)-\alpha (t\left)\right|<ϵ,t\in [0,\infty ),$$

where $\alpha \left(t\right)={\sum }_{k=1}^{m+1}\delta \left(T_{k-1}\right)I_k\left(t\right)+\xi I_T\left(t\right)$ for $t\in [0,T],$ $I_k\left(t\right)$ is the indicator of the interval $[T_{k-1},T_k]$, $k=1,2,\dots ,m+1$, and $I_T\left(t\right)$ is the indicator of the interval $(T_{m+1},\infty )$ (here $T_0=0$).

Proof. 

Let $ϵ>0$ be a given fixed number. From ${lim}_{t\to \infty }\delta \left(t\right)=\xi \in (0,1)$ it follows that there exists a number $T>0$ such that

$$\left|\delta \right(t)-\xi |<ϵ,t>T.$$

Consider the finite interval $[0,T]$ and apply Lemma 6 to it. Then, the piecewise constant function

$$\alpha \left(t\right)=\sum _{k=1}^m{p}_k{I}_k\left(t\right)=\left\{\begin{array}{c}\delta \left(T_0\right),ift\in [T_0,T_1],\hfill \\ \delta \left(T_1\right),ift\in (T_1,T_2],\hfill \\ ⋮\hfill \\ \delta \left(T_m\right),ift\in (T_m,T_{m+1}],\hfill \\ \xi ,ift>T_{m+1},\hfill \end{array}\right.$$

(7)

is the function needed. □

3. Differential Equations with Variable Order of the Fractional Derivative

Consider the initial value problem (IVP) for the nonlinear scalar differential equation with the $\psi$-tempered Caputo fractional derivative of variable order

$$\begin{array}{cc}& {}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\varrho }\omega \left(t\right)=F\left(t,\omega \left(t\right)\right),t\in (0,T],\hfill \\ & \omega \left(0\right)=V_0,\hfill \end{array}$$

(8)

where $V_0\in \mathbb{R}$, $\varrho >0,0<T<\infty ,\delta (.):[0,T]\to (0,1)$, ${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\varrho }$ denotes the $\psi$-tempered Caputo fractional derivatives with variable order $\delta (·)$, and $F:[0,T]\times \mathbb{R}\to \mathbb{R}$ is a given function.

Definition of Approximate Solutions of the Initial Value Problem (8)

We will assume $ϵ>0$ is a fixed number and $\delta \in C\left(\right[0,T],(0,1\left)\right)$.

According to Lemma 6 for the given fixed number $ϵ$, there exists a partition $P=\{(T_{k-1},T_k],k=1,2,\dots ,m\}$ of the given interval $[0,T]$ and an $ϵ$-approximation of $\delta$, defined by (4) with $\left|\delta \right(t)-\alpha (t\left)\right|\le ϵ,t\in [0,T].$ Note that for the given number $ϵ$, the partition P is not unique. In this section, we will consider a fixed partition P, i.e., fixed points $0=T_0<T_1<T_2\dots <T_{m-1}<T_m=T$.

Let $t\in (T_{k-1},T_k],$ where k is an arbitrary integer $1\le k\le m$. Then, $\alpha \left(t\right)=p_k$ with $p_k=\delta \left(T_{k-1}\right)$, and the fractional derivative can be written

$$\begin{array}{cc}& {}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{\alpha \left(t\right),\lambda }\omega \left(t\right)\hfill \\ & =\frac{1}{\mathsf{\Gamma }(1-\alpha (t\left)\right)}({\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{-\alpha \left(t\right)}{\omega }^{\prime }\left(s\right)ds\hfill \\ & +\lambda {\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{-\alpha \left(t\right)}{\psi }^{\prime }\left(s\right)\omega \left(s\right)ds)\hfill \\ & =\frac{1}{\mathsf{\Gamma }(1-p_k)}{\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{-p_k}\left(\frac{1}{{\psi }^{\prime }\left(s\right)}\frac{d}{dt}+\lambda \right)\omega \left(s\right)ds\hfill \\ & ={}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{p_k,\lambda }\omega \left(t\right).\hfill \end{array}$$

(9)

Applying (9), we could define for any integer $k:1\le k\le m,$ the following IVP for the differential equation with tempered Caputo fractional derivative of a constant order $p_k$, which is deeply connected to the studied IVP (8) and the $ϵ$-approximation of the variable order $\delta \left(t\right)$:

$$\begin{array}{cc}& {}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{p_k,\lambda }\nu \left(t\right)=F\left(t,\nu \left(t\right)\right)fort\in (0,T_k],\hfill \\ & \nu \left(0\right)=V_0.\hfill \end{array}$$

(10)

With the help of the IVP (10), we will define an approximate solution of (8).

Definition 4.

For a given $ϵ>0$ the function

$$\omega \left(t\right)=\left\{\begin{array}{c}{\nu }_1\left(t\right),ift\in [T_0,T_1],\hfill \\ {\nu }_2\left(t\right),ift\in (T_1,T_2],\hfill \\ ⋮\hfill \\ {\nu }_m\left(t\right),ift\in (T_m,T_{m+1}],\hfill \end{array}\right.$$

(11)

is called an ϵ-approximate solution of IVP (8), where ${\nu }_k\left(t\right)\in C([0,T_k],\mathbb{R})$ is a solution of IVP (10), $k=1,2,\dots ,m$.

Example 3.

Consider the following linear IVP:

$$\begin{array}{cc}& {}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right)}\omega \left(t\right)=-0.2\omega \left(t\right),t\in [0,2],\hfill \\ & \omega \left(0\right)=V_0,\hfill \end{array}$$

(12)

where $\delta \left(t\right)=0.5sin\left(t\right)+0.4$ and ${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right)}$ is the variable order Caputo fractional derivative with reference to another function given in Definition 2 with $\lambda =0$.

Let $ϵ=0.2$. Then, according to Example 2, the $0.2$-partition of the fractional order $\delta \left(t\right)$ is given by (5), and the $0.2$-approximate solution of (12) according to Lemma 4 and Definition 4 is

$$\begin{array}{c}\hfill {\omega }_{0.2}\left(t\right)=\left\{\begin{array}{c}{V}_0{E}_{0.4}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.4}),ift\in [0,{sin}^{-1}\left(0.4\right)],\hfill \\ V_0{E}_{0.6}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.6}),ift\in ({sin}^{-1}\left(0.4\right),{sin}^{-1}\left(0.8\right)],\hfill \\ V_0{E}_{0.8}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.8}),ift\in ({sin}^{-1}\left(0.8\right),2].\hfill \end{array}\right.\end{array}$$

(13)

Let $ϵ=0.1$. Then, according to Example 2 the $0.1$-partition of the fractional order $\delta \left(t\right)$ is given by (6) and the $0.1$-approximate solution of (12) according to Lemma 4 and Definition 4 is

$$\begin{array}{c}\hfill {\omega }_{0.1}\left(t\right)=\left\{\begin{array}{c}{V}_0{E}_{0.4}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.4}),ift\in [0,{sin}^{-1}\left(0.2\right)],\hfill \\ V_0{E}_{0.5}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.5}),ift\in ({sin}^{-1}\left(0.2\right),{sin}^{-1}\left(0.4\right)],\hfill \\ V_0{E}_{0.6}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.6}),ift\in ({sin}^{-1}\left(0.4\right),{sin}^{-1}\left(0.6\right)],\hfill \\ V_0{E}_{0.7}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.7}),ift\in ({sin}^{-1}\left(0.6\right),{sin}^{-1}\left(0.8\right)],\hfill \\ V_0{E}_{0.8}(-0.2{(\psi \left(t\right)-\psi \left(0\right))}^{0.8}),ift\in ({sin}^{-1}\left(0.8\right),2].\hfill \end{array}\right.\end{array}$$

(14)

Remark 5.

If the piecewise constant function $\alpha \left(t\right)$ is an ϵ-approximation of the variable order $\delta \left(t\right)$; ${\nu }_k\left(t\right)\in C([0,T_k],\mathbb{R}),k=1,2,\dots ,m$ are solutions of the initial value problems; (10) and $\omega \left(t\right)$ is an ϵ-approximate solution of (8), then, according to (9), we have ${}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{\alpha \left(t\right),\lambda }\omega \left(t\right)={}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{p_k,\lambda }{\nu }_k\left(t\right)=F(t,{\nu }_k\left(t\right))=F(t,\omega \left(t\right))$ for any $t\in (T_{k-1},T_k]$ with $p_k=\delta \left(T_{k-1}\right),k=1,2,\dots ,m$.

We now introduce condition (H):

Hypothesis 1

(H1). The function $\psi :[0,T]\to (0,\infty )$ is a smooth increasing function with ${\psi }^{\prime }\left(t\right)>0$ almost everywhere in $[0,T],$ $\lambda >0$, and the function $\delta \in C\left(\right[0,T],(0,1\left)\right)$.

Hypothesis 2

(H2). The function $F\in C\left(\right[0,T]\times \mathbb{R},\mathbb{R})$, and it is globally Lipschitz with a constant L such that

$$L{e}^{\lambda \left(\psi \right(T)-\psi (0\left)\right)}max\left\{1,{(\psi \left(T\right)-\psi \left(0\right))}^p\right\}<A,$$

where $p={max}_{t\in [0,T]}\delta \left(t\right)\in (0,1)$, $A={min}_{p\in [0,1]}\mathsf{\Gamma }(1+p)>0$.

Theorem 1.

Let $ϵ>0$ be a given number, condition (H1) be satisfied; $P=\{(T_{k-1},T_k],k=1,\dots ,m\}$ be the the partition of the interval $[0,T]$, defined in Lemma 6 for ϵ; the function $F\in C\left(\right[0,T]\times \mathbb{R},\mathbb{R})$; and there exist constants $L_k>0,k=1,2,\dots ,m,$ such that

$$|F(t,y)-F(t,z)|\le L_k|y-z|,t\in [0,T_k],y,z\in \mathbb{R}$$

with

$$L_k<\mathsf{\Gamma }(1+p_k){(\psi \left(T_k\right)-\psi \left(0\right))}^{-p_k}{e}^{-\lambda (\psi \left(T_k\right)-\psi \left(0\right)))},k=1,2,\dots ,m.$$

Then, IVP (8) has an ϵ-approximate solution.

Proof. 

According to Lemma 2 with $L=L_k$, $b=T_k$, $f=F$, the initial value problem with the fractional derivative of constant order (10) has a solution ${\nu }_k\in A{C}_{\psi }([0,T_k],\mathbb{R})$ for all $k=1,2,\dots ,m$. Then, the function $\omega \left(t\right)$ defined by (11) is an $ϵ$-approximate solution of the IVP (8). □

We now define an approximate solution of (8).

Definition 5.

The initial value problem (8) has an approximate solution if for any $ϵ>0$ it has an ϵ-approximate solution.

Remark 6.

The approximate solution of (8) depends on the initial value.

Theorem 2.

Let condition (H) be satisfied. Then, IVP (8) has an approximate solution.

Proof. 

Let $ϵ$ be an arbitrary given number. According to Lemma 6 for the given number $ϵ$, there exist a partition P of the interval $[0,T]$ and a piecewise constant function $\alpha \left(t\right)$ defined by (4) which is an $ϵ$-approximation of the variable order $\delta \left(t\right)$.

Then, for any $k=1,2,\dots ,m$ the inequalities

$$\frac{L{(\psi \left(T_k\right)-\psi \left(0\right))}^{p_k}}{\mathsf{\Gamma }(1+p_k)}\le \frac{L{(\psi \left(T\right)-\psi \left(0\right))}^{p_k}}{A}$$

hold.

Furthermore,

-

for $\psi \left(T\right)-\psi \left(0\right)>1$ we have ${(\psi \left(T\right)-\psi \left(0\right))}^{p_k}<{(\psi \left(T\right)-\psi \left(0\right))}^p$;

-

for $\psi \left(T\right)-\psi \left(0\right)\le 1$ we have ${(\psi \left(T\right)-\psi \left(0\right))}^{p_k}\le 1.$

Thus, $e^{\lambda (\psi \left(T_k\right)-\psi \left(0\right))}{(\psi \left(T\right)-\psi \left(0\right))}^{p_k}\le e^{\lambda \left(\psi \right(T)-\psi (0\left)\right)}max\left\{1,{(\psi \left(T\right)-\psi \left(0\right))}^p\right\}$. Therefore, $\frac{L{(\psi \left(T_k\right)-\psi \left(0\right))}^{p_k}}{\mathsf{\Gamma }(1+p_k)}{e}^{\lambda (\psi \left(T_k\right)-\psi \left(0\right))}<1$, and, according to Theorem 1, the IVP (8) has an $ϵ$-approximate solution (the function ${\omega }_{ϵ}\left(t\right)$ defined by (11)). Since $ϵ$ is an arbitrary number, we are finished. □

4. Ulam-Type Stability of Approximate Solutions

Note that the Ulam-type stability for differential equations with the Caputo-tempered fractional derivative with respect to another function is studied in [5] for the case of constant order. In the case of constant order, the fractional differential equation is equivalent to a fractional integral Equation (see Lemma 1), but it is not true for the variable order. We will now study the stability of approximate solutions of (8). In this case, we change the definitions for Ulam-type stability given in [5] (Definition 5.1).

Definition 6.

Let condition (H1) be satisfied, and $F\in C\left(\right[0,T]\times \mathbb{R},\mathbb{R})$. Now, (8) is said to be approximately Hyers–Ulam-stable if there exists a constant $C_0>0$ such that for any $ϵ>0$, an ϵ-approximation $\alpha \left(t\right)$ of the fractional order $\delta \left(t\right)$ (defined by (4)) with a partition $P=\{(T_{k-1},T_k],k=1,\dots ,m\}$ and for any function ${\eta }_k\in A{C}_{\psi }([0,T_k],\mathbb{R})$ satisfying the inequality

$$|{}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{p_k,\lambda }{\eta }_k\left(t\right)-F(t,{\eta }_k\left(t\right))|\le ϵ,t\in [0,T_k],k=1,2,\dots ,m,$$

(15)

with $p_k=\delta \left(T_{k-1}\right),k=1,2,\dots ,m$, there exists an ϵ-approximate solution ${\omega }_{ϵ}\left(t\right)$ of (8) with

$$|{\omega }_{ϵ}\left(t\right)-\eta \left(t\right)|\le C_0ϵ,t\in [0,T],$$

where

$$\eta \left(t\right)=\left\{\begin{array}{c}{\eta }_1\left(t\right),ift\in [T_0,T_1],\hfill \\ {\eta }_2\left(t\right),ift\in (T_1,T_2],\hfill \\ ⋮\hfill \\ {\eta }_m\left(t\right),ift\in (T_m,T_{m+1}].\hfill \end{array}\right.$$

(16)

Theorem 3

(UHS). Let condition (H) be satisfied. Then, (8) is approximately Hyers–Ulam-stable.

Proof. 

Let $\epsilon >0$ be an arbitrary number. According to Lemma 6 there exist a partition $P=\{(T_{k-1},T_k],k=1,\dots ,m\}$ and an $ϵ$-approximation $\alpha \left(t\right)$ of the fractional order $\delta \left(t\right)$, defined by (4). Let the function ${\eta }_k\in A{C}_{\psi }([0,T_k],\mathbb{R})$ be a solution of inequality (15), $k=1,2,\dots ,m$. Then, for any $k=1,2,\dots ,m$ we consider the functions $g_k\in C([0,T_k],\mathbb{R}):\left|g_k\left(t\right)\right|\le ϵ$ such that

$$\begin{array}{cc}& {}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{p_k,\lambda }{\eta }_k\left(t\right)=F(t,{\eta }_k\left(t\right))+g_k\left(t\right),t\in [0,T_k].\hfill \end{array}$$

(17)

According to Lemma 1, the integral equality

$$\begin{array}{cc}\hfill {\eta }_k\left(t\right)& =e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}{\eta }_k\left(0\right)\hfill \\ & +\frac{1}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)(F(s,{\eta }_k\left(s\right))+g_k\left(s\right))ds,\hfill \\ & =e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}{\eta }_k\left(0\right)+{}_0{\mathcal{I}}_{\psi \left(t\right)}^{p_k,\lambda }(F(s,{\eta }_k\left(s\right))+g_k\left(s\right)),t\in [0,T_k],\hfill \end{array}$$

(18)

holds.

Denote ${\eta }_0={min}_{k=1,2\dots ,m}{\eta }_k\left(0\right)$ and consider the initial value problem (8) with $V_0\in \mathbb{R}:V_0<{\eta }_0+ϵ$. According to Theorem 1 the initial value problem (8) has an $ϵ$-approximate solution ${\omega }_{ϵ}\left(t\right)$.

Let $k:1\le k\le m$ be an arbitrary fixed integer. Then, for $t\in (T_{k-1},T_k]$ the equality ${\omega }_{ϵ}\left(t\right)={\nu }_k\left(t\right)$ holds where ${\nu }_k\left(t\right),t\in [0,T_k],$ is the solution of (10) with $V_0={\eta }_0$.

Then, for any $t\in [0,T_k]$, we obtain

$$\begin{array}{cc}& |{\nu }_k\left(t\right)-{\eta }_k\left(t\right)|\le |{\eta }_k\left(t\right)-e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}{\eta }_k\left(0\right)-{}_0{\mathcal{I}}_{\psi \left(t\right)}^{p_k,\lambda }F(s,{\eta }_k\left(s\right))|\hfill \\ & +|{\nu }_k\left(t\right)-e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}{V}_0-{}_0{\mathcal{I}}_{\psi \left(t\right)}^{p_k,\lambda }F(s,{\nu }_k\left(s\right))|+e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}|V_0-{\eta }_k\left(0\right)|\hfill \\ & +\left|{}_0{\mathcal{I}}_{\psi \left(t\right)}^{p_k,\lambda }(F(s,\eta \left(s\right))-F(s,{\nu }_k\left(s\right)))\right|\hfill \\ & \le \left|{}_0{\mathcal{I}}_{\psi \left(t\right)}^{p_k,\lambda }{g}_k\left(t\right)\right|+e^{-\lambda \left(\psi \right(t)-\psi (0\left)\right)}|V_0-{\eta }_k\left(0\right)|\hfill \\ & +\frac{L}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)|{\eta }_k\left(s\right))-{\nu }_k\left(s\right)\left)\right|ds\hfill \\ & \le ϵ\frac{1}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)ds+ϵ\hfill \\ & +\frac{L}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{e}^{-\lambda \left(\psi \left(t\right)-\psi \left(s\right)\right)}{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)|{\eta }_k\left(s\right))-{\nu }_k\left(s\right)\left)\right|ds\hfill \\ & \le \frac{ϵ}{\mathsf{\Gamma }(1+p_k)}{(\psi \left(t\right)-\psi \left(0\right))}^{p_k}+ϵ\hfill \\ & +\frac{L}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)|{\eta }_k\left(s\right))-{\nu }_k\left(s\right)\left)\right|ds\hfill \\ & \le ϵ\left(1+\frac{{(\psi \left(T_k\right)-\psi \left(0\right))}^{p_k}}{\mathsf{\Gamma }(1+p_k)}\right)\hfill \\ & +\frac{L}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)|{\eta }_k\left(s\right))-{\nu }_k\left(s\right)\left)\right|ds.\hfill \end{array}$$

(19)

Denote $M=1+\frac{max\left\{1,{(\psi \left(T\right)-\psi \left(0\right))}^p\right\}}{A}.$ We have ${(\psi \left(T_k\right)-\psi \left(0\right))}^{p_k}\le max\left\{1,{(\psi \left(T\right)-\psi \left(0\right))}^p\right\}$ (see the proof of Theorem 2).

Therefore, for any $t\in [0,T_k]$ we have

$$\begin{array}{cc}& |{\nu }_k\left(t\right)-{\eta }_k\left(t\right)|\le ϵM+\frac{L}{\mathsf{\Gamma }\left(p_k\right)}{\int }_0^t{\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{p_k-1}{\psi }^{\prime }\left(s\right)|{\eta }_k\left(s\right))-{\nu }_k\left(s\right)\left)\right|ds.\hfill \end{array}$$

(20)

According to Lemma 3 with $u\left(t\right)=|{\nu }_k\left(t\right)-{\eta }_k\left(t\right)|\in C[0,T_k],[0,\infty ))$, $C=ϵM$, $K=\frac{L}{\mathsf{\Gamma }\left(p_k\right)}$, $\alpha =p_k$, $b=T_k$ and inequalities $E_{\gamma }\left(x^{\gamma }\right)<\frac{e^x}{\gamma },x>0,\gamma \in (0,1),$ and $\sqrt[p_k]{L}(\psi \left(T\right)-\psi \left(0\right))<\sqrt[p_k]{A}\le \sqrt[p]{A}$ because $A\in (0,1]$ (see, condition (H)), we obtain

$$\begin{array}{cc}\hfill |{\nu }_k\left(t\right)-{\eta }_k\left(t\right)|& \le ϵM{E}_{p_k}\left(L{(\psi \left(t\right)-\psi \left(0\right))}^{p_k}\right)\hfill \\ & \le ϵM{E}_{p_k}\left({\left(\sqrt[p_k]{L}(\psi \left(T\right)-\psi \left(0\right))\right)}^{p_k}\right)\hfill \\ & \le ϵM\frac{e^{\sqrt[p_k]{L}(\psi \left(T\right)-\psi \left(0\right))}}{\xi }\le ϵM\frac{e^{\sqrt[p]{A}}}{\xi },t\in [0,T_k],\hfill \end{array}$$

(21)

where $\xi ={min}_{t\in [0,T]}\delta \left(t\right)>0$.

From inequality (21), it follows that

$$|{\omega }_{ϵ}\left(t\right)-\eta \left(t\right)|=|{\nu }_k\left(t\right)-{\eta }_k\left(t\right)|\le C_0ϵ,t\in (T_{k-1},T_k],k=1,2,\dots ,m,$$

(22)

with $C_0=M\frac{e^{\sqrt[p]{A}}}{\xi }.$ □

We will illustrate the approximate Hyers–Ulam stability with a simple example.

Example 4.

Consider the linear fractional differential Equation (12) with variable order $\delta \left(t\right)=0.5sin\left(t\right)+0.4$, $\psi \left(t\right)=t^2$, and ${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right)}$-the variable order Caputo fractional derivative with reference to another function given in Definition 2 with $\lambda =0$.

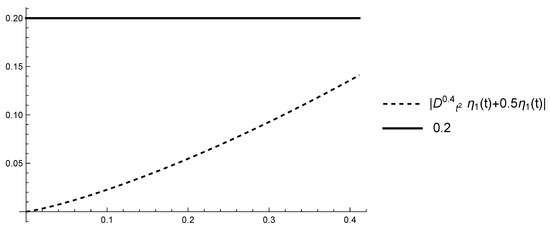
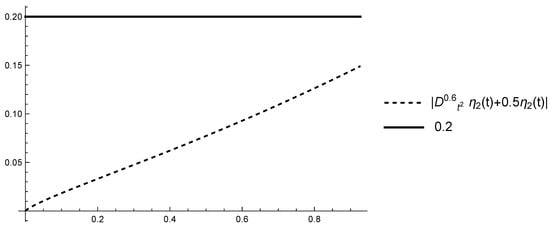
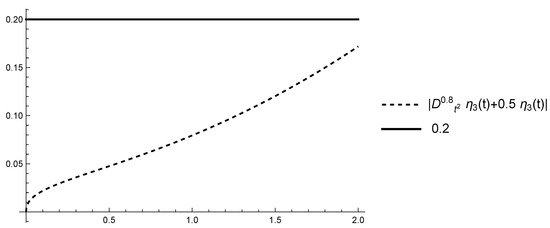
The assumptions (H1) and (H2) are satisfied with $L=0.2$ because in this case $L{e}^{\lambda \left(\psi \right(T)-\psi (0\left)\right)}max\{1,{(\psi \left(T\right)-\psi \left(0\right))}^p\}=0.2\left(4\right)=0.8<{min}_{p\in (0,1)}\mathsf{\Gamma }(1+p)=0.8872.$ According to Theorem 3 Equation (12) is approximately Hyers–Ulam-stable. We will illustrate this for a particular value of ϵ. For example, let $ϵ=0.2$.

In Example 3 several ϵ-approximate solutions of (12) are given.

Then, the inequality (15) is reduced to

$$|{}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{p_k}{\eta }_k\left(t\right)+0.2{\eta }_k\left(t\right)|\le 0.2,t\in [0,T_k],k=1,2,3,$$

(23)

with $T_1={sin}^{-1}\left(0.4\right)$, $T_2={sin}^{-1}\left(0.8\right)$, $T_3=2$ and $p_1=0.4,p_2=0.6,p_3=0.8$ (see Example 3).

Then, according to Lemma 5 with $\beta =2$, $\psi \left(t\right)=t^2$, $\alpha =0.4,0.6,0.8$, we obtain (see Figure 1, Figure 2 and Figure 3)

$$\begin{array}{cc}& {\eta }_1\left(t\right)=0.3{\left(t^2\right)}^{2-1},t\in [0,{sin}^{-1}\left(0.4\right)],\hfill \\ & {\eta }_2\left(t\right)=0.1{\left(t^2\right)}^{2-1},t\in [0,{sin}^{-1}\left(0.8\right)],\hfill \\ & {\eta }_3\left(t\right)=0.05{\left(t^2\right)}^{2-1},t\in [0,2],\hfill \end{array}$$

(24)

Figure 1. Graphs of $|{}_0^C{\mathcal{D}}_{t^2}^{0.4}{\eta }_1\left(t\right)+0.5{\eta }_1\left(t\right)|$ and $ϵ=0.2$ on $[0,{sin}^{-1}\left(0.4\right)]$.

Figure 2. Graphs of $|{}_0^C{\mathcal{D}}_{t^2}^{0.6}{\eta }_2\left(t\right)+0.5{\eta }_1\left(t\right)|$ and $ϵ=0.2$ on $[0,{sin}^{-1}\left(0.8\right)]$.

Figure 3. Graphs of $|{}_0^C{\mathcal{D}}_{t^2}^{0.8}{\eta }_3\left(t\right)+0.5{\eta }_1\left(t\right)|$ and $ϵ=0.2$ on [0,2].

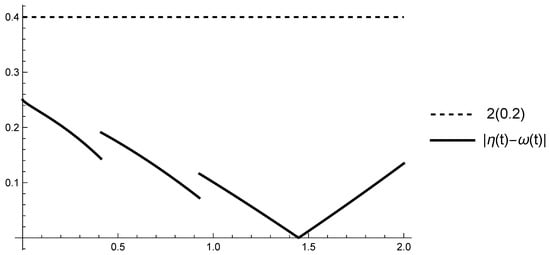
According to (13), the $0.2$-approximate solution is

$$\begin{array}{c}\hfill {\omega }_{0.2}\left(t\right)=\left\{\begin{array}{c}{V}_0{E}_{0.4}(-0.2{\left(t^2\right)}^{0.4}),ift\in [0,{sin}^{-1}\left(0.4\right)],\hfill \\ V_0{E}_{0.6}(-0.2{\left(t^2\right)}^{0.6}),ift\in ({sin}^{-1}\left(0.4\right),{sin}^{-1}\left(0.8\right)],\hfill \\ V_0{E}_{0.8}(-0.2{\left(t^2\right)}^{0.8}),ift\in ({sin}^{-1}\left(0.8\right),2],\hfill \end{array}\right.\end{array}$$

(25)

where $V_0=min(0.3,0.1,0.05)+0.2$.

Then, $|{\omega }_{0.2}\left(t\right)-\eta \left(t\right)|<C_{0}0.2$ with $C_0=2$ and $\eta \left(t\right)$ defined by (16) with $m=2$ (see Figure 4).

Figure 4. Graphs of $\left|\omega \right(t)-\eta (t\left)\right|$ and $C_0ϵ=2\left(0.2\right)$ on $[0,2]$.

5. Piecewise Constant Order of the Fractional Derivative

Consider the case when the partition $0=T_0<T_1<\dots <T_{m-1}<T_m=T$ of the interval $[0,T]$ is given initially, and the fractional order of the fractional derivative is defined by the equality

$$\delta \left(t\right)=\left\{\begin{array}{c}{p}_1,ift\in [T_0,T_1],\hfill \\ p_2,ift\in (T_1,T_2],\hfill \\ ⋮\hfill \\ p_m,ift\in (T_{m-1},T_m],\hfill \end{array}\right.$$

(26)

where the constants $p_k\in (0,1),k=1,2,\dots ,m$ are initially given.

Let $t\in (T_{k-1},T_k],$ where k is an arbitrary integer $1\le k\le m$. Then, $\delta \left(t\right)=p_k$ and from Definition 2 we have

$$\begin{array}{cc}& {}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\upsilon \left(t\right)\hfill \\ & =\frac{1}{\mathsf{\Gamma }(1-p_k)}({\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\nu }^{\prime }\left(s\right)ds\hfill \\ & +\lambda {\int }_0^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\psi }^{\prime }\left(s\right)\nu \left(s\right)ds)\hfill \\ & =\frac{1}{\mathsf{\Gamma }(1-p_k)}(\sum _{i=1}^{k-1}{\int }_{T_{i-1}}^{T_i}{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\nu }^{\prime }\left(s\right)ds\hfill \\ & {\int }_{T_{k-1}}^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\nu }^{\prime }\left(s\right)ds\hfill \\ & +\lambda \sum _{i=1}^{k-1}{\int }_{T_{i-1}}^{T_i}{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\psi }^{\prime }\left(s\right)\nu \left(s\right)ds)\hfill \\ & +\lambda {\int }_{T_{k-1}}^t{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\psi }^{\prime }\left(s\right)\nu \left(s\right)ds)\hfill \\ & ={}_{T_{k-1}}^C{\mathcal{D}}_{\psi \left(t\right)}^{p_2,\lambda }\upsilon \left(t\right)\hfill \\ & +\frac{1}{\mathsf{\Gamma }(1-p_k)}\sum _{i=1}^{k-1}({\int }_{T_{i-1}}^{T_i}{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\nu }^{\prime }\left(s\right)ds\hfill \\ & +\lambda {\int }_{T_{i-1}}^{T_i}{e}^{-\lambda \left(\psi \right(t)-\psi (s\left)\right)}{(\psi \left(t\right)-\psi \left(s\right))}^{-p_k}{\psi }^{\prime }\left(s\right)\nu \left(s\right)ds),t\in (T_{k-1},T_k].\hfill \end{array}$$

Therefore,

$${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\upsilon \left(t\right)\ne \sum _{i=1}^{k-1}{}_{T_{i-1}}^C{\mathcal{D}}_{\psi \left(t\right)}^{p_i,\lambda }{\upsilon \left(t\right)|}_{t=T_i}+{}_{T_{k-1}}^C{\mathcal{D}}_{\psi \left(t\right)}^{p_k,\lambda }\upsilon \left(t\right),t\in (T_{k-1},T_k],$$

or its equivalent

$${}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\upsilon \left(t\right)\ne \sum _{i=1}^{k-1}{}_{T_{i-1}}^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }{\upsilon \left(t\right)|}_{t=T_i}+{}_{T_{k-1}}^C{\mathcal{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\upsilon \left(t\right),t\in (T_{k-1},T_k],$$

hold and their corresponding equalities cannot be applied (see, for example, Equation (6) [23], Equation (5) [16], Equation (9) [24], Equation (3.1) [25]).

In connection with the above, we will apply our approach to study IVP (8) when the order of the fractional derivative is a piecewise constant function $\sigma \left(t\right)$. Our approach is based on (9).

We now introduce assumption (A):

Assumption 1

(A1). The function $\psi \in C^1([0,T],(0,\infty ))$ is an increasing function with ${\psi }^{\prime }\left(t\right)>0$ almost everywhere, $\lambda >0$ is a given constant, and the function $\delta :[0,T]\to (0,1)$ is defined by (26).

Assumption 2

(A2). The function $F\in C\left(\right[0,T]\times \mathbb{R},\mathbb{R})$ and there exist constants $L_k>0,k=1,2,\dots ,m,$ such that

$$|F(t,y)-F(t,z)|\le L_k|y-z|,t\in [0,T_k],y,z\in \mathbb{R},k=1,2,\dots ,m,$$

with

$$L_k{e}^{\lambda (\psi \left(T_k\right)-\psi \left(0\right))}{(\psi \left(T_k\right)-\psi \left(0\right))}^{p_k}<L(1+p_k).$$

We obtain the following existence result for the initial value problem (8) with piecewise constant order, defined by (26).

Theorem 4.

Let conditions (A1) and (A2) hold. Then, the initial value problem (8) has a solution.

Proof. 

Consider the partition $P=\{(T_{k-1},T_k],k=1,2,\dots \}$ defined by the given point $T_k,k=1,2,\dots ,m-1$. For any $k=1,2,\dots ,m$, we consider the initial value problem (10). According to Lemma 2, it has a unique solution ${\nu }_k\left(t\right),t\in (0,T_k]$ for any $k=1,2,\dots ,m$. Construct the function

$$\omega \left(t\right)=\left\{\begin{array}{c}{\nu }_1\left(t\right),ift\in [T_0,T_1],\hfill \\ {\nu }_2\left(t\right),ift\in (T_1,T_2],\hfill \\ ⋮\hfill \\ {\nu }_m\left(t\right),ift\in (T_{m-1},T_m].\hfill \end{array}\right.$$

(27)

The function $\omega \left(t\right)$ is a solution of (8) because $\omega \left(0\right)=V_0$ and for any $t\in (T_{k-1},T_k]$ we have

$${}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{\delta \left(t\right),\lambda }\omega \left(t\right)={}_0^C{\mathfrak{D}}_{\psi \left(t\right)}^{p_k,\lambda }{\nu }_k\left(t\right)=F(t,{\nu }_k\left(t\right)=F(t,\omega \left(t\right)).$$

□

Remark 7.

The solution of (8) with a fractional derivative of piecewise constant order is not continuous on the whole interval $[0,T]$.

The definition of Ulam-type stability for fractional derivatives of a piecewise constant order reduces to:

Definition 7.

Let condition (A1) hold and $F\in C\left(\right[0,T]\times \mathbb{R},\mathbb{R})$. Now, (8) is said to be Hyers–Ulam-stable if there exists a constant $C_0>0$ such that for any $ϵ>0$ and for any function ${\eta }_k\in C_{\psi }([0,T_k],\mathbb{R}),k=1,2,\dots ,m,$ satisfying the inequality

$$|{}_0^C{\mathcal{D}}_{\psi \left(t\right)}^{p_k,\lambda }\eta \left(t\right)-F(t,\eta \left(t\right))|\le ϵ,t\in [0,T_k],$$

(28)

with $p_k=\delta \left(T_{k-1}\right),k=1,2,\dots ,m$, there exists an ϵ-approximate solution ${\omega }_{ϵ}\left(t\right)$ of (8) with

$$|{\omega }_{ϵ}\left(t\right)-\eta \left(t\right)|\le C_0ϵ,t\in [0,T],$$

where the function η is defined by (16).

Theorem 5

(UHS). Let condition (A1) and (A2) hold. Then, (8) is Hyers–Ulam-stable.

The proof of Theorem 5 is similar to the one of Theorem 3 without applying $ϵ$.

6. Conclusions

In this paper, we consider differential equations with the variable order Caputo-type fractional derivative with respect to another function and we study the general case of continuous variable order of the fractional derivative. We define in appropriate way an $ϵ$-solution of the given initial value problem and an approximate solution.

Furthermore, we define and study the Hyers–Ulam stability. As a partial case, we obtain results for stability of the differential equations with fractional derivatives of piecewise constant order. In future work, we hope to appropriately define some other types of Ulam stability, such as Hyers–Ulam–Rassias stability, and obtain sufficient conditions. Furthermore, the existence on the the interval $[0,\infty )$ could be investigated. In addition, we could consider the general case of the variable order applying a local definition for fractional derivative [14] in the future.