Theoretical Analysis of a Fractional-Order LLCL Filter for Grid-Tied Inverters

Abstract

The LLCL-filter-based grid-tied inverter performs better than the LCL-type grid-tied inverter due to its outstanding switching-frequency current harmonic elimination capability, but the positive resonance peak must be suppressed by passive or active damping methods. This paper proposes a class of fractional-order LLCL (FOLLCL) filters, which provides rich features by adjusting the orders of three inductors and one capacitor of the filter. Detailed analyses are performed to reveal the frequency characteristics of the FOLLCL filter; the orders must be selected reasonably to damp the positive resonance peak while reserving the negative resonance peak to attenuate the switching-frequency harmonics. Furthermore, the control system of the grid-tied inverter based on the FOLLCL filter is studied. When the positive resonance is suppressed by the intrinsic damping effect of the FOLLCL filter, the passive or active damper can be avoided; the grid current single close-loop is adequate to control the grid-tied inverter. For low-frequency applications, proportional-resonant (PR) controller is more suitable for the FOLLCL-type grid-tied inverter compared with the proportional-integral (PI) and fractional-order PI controllers due to its overall performance. Simulation results are consistent with theoretical expectations.

1. Introduction

The grid-tied inverter is widely used in renewable energy generation; the voltage-source inverter (VSI) interfaces with the grid through a low-pass filter to limit the excessive current harmonics. A third-order LCL filter is the most popular solution over a first-order L filter due to its smaller size, lower cost, and better harmonic attenuation capability [1,2,3,4,5]. However, large inductance should be selected for an LCL filter in low-frequency applications to suppress the more abundant current harmonics. To solve this problem, a high-order LLCL filter has been proposed in [6] and further developed in [7,8,9,10,11,12,13,14,15]. Based on the LCL filter, a small inductor is inserted in series with the capacitor to form a series resonant branch. The series resonant frequency is thus designed to further attenuate the switching harmonics. The total harmonic distortion (THD) of the grid current will be much lower with LLCL-type inverters compared with LCL-type ones in low-frequency applications.

However, the LLCL filter retains the positive resonant feature of the LCL filter, which causes system instability. Passive or active dampers are used to mitigate the impact of the positive resonance, leading to power loss or control complexity. It is even worse that the capacitor current feedback, the most commonly used active damping method, may introduce a negative resistance and cause instability due to the control delay [8].

In recent years, the fractional-order modeling of power converters has been paid much attention because the inductors and capacitors, the key components of power converters, have fractional-order characteristics, or can be specially designed as fractional-order components. The research of fractional-order power converters began from the modeling of DC–DC converters. In [16], fractional calculus and the circuit-averaging technique are used to model the buck converter. This technique is also used to build the model of the fractional-order magnetic coupled boost converter [17]. The fractional-order model of the buck converter based on the Caputo–Fabrizio derivative is presented in [18]. The Riemann–Liouville derivative is also used to obtain more accurate models of the fractional-order buck converter [19] and fractional-order buck–boost converter [20]. Instead of considering the complex definitions of fractional calculus, the harmonic balance principle and equivalent small parameter method are used to describe the fractional-order DC–DC converters [21]. Different from the above studies, time domain expressions for fractional-order DC–DC converters are derived in [22]. The modeling methods for fractional-order DC–AC converters are also reported in the literature. In [23], the Caputo derivative method is used to build the model of the voltage source converter, and small-signal analysis and averaging state-space model-based analysis are developed. The fractional-order model of the three-phase voltage source PWM rectifier is constructed in [24]; the Caputo fractional calculus operator is used to describe the fractional-order characteristics of the inductor and capacitor. In addition, the influence of the orders of the inductors and the capacitor on the operating characteristics of the PWM rectifier is studied. In [25], an LCαL filter-based grid-connected inverter is modeled and a filter design example is given. However, the above literature only focuses on the modeling methods; the control strategies are not considered.

On the other hand, fractional-control theories are developed to control the power converters. The fractional-order PID control method is employed to regulate DC–DC converters [26,27]; the results show that the method achieves less overshoot and a faster recovery time compared to the integer-order PID regulator. In [28], the factional-order adaptive sliding mode control approach is proposed for fractional-order buck–boost converters, which shows stronger robustness under various disturbances. For LCL-type grid-tied inverters, an active damping method based on fractional-order proportional-derivative (PD) grid current feedback is presented in [29], which shows better performance compared to the integer-order PD damping method. In [30], a capacitive current fractional proportional-integral feedback strategy is proposed to increase the limit of the damping region of the LCL grid-tied inverter under the weak grid condition. A fractional-order LCL (FOLCL) filter-based grid-tied inverter is studied in [31]; the capacitor current feedback loop can be omitted by only changing the orders of the passive components. Especially, PI and fractional-order PI controllers especially are designed for this grid-tied inverter.

Considering the advantages of fractional-order converters, this paper proposes a fractional-order LLCL-type grid-tied inverter, which can avoid the use of an active damper. The contributions of this paper include the following points:

• The characteristics of the FOLLCL filter is analyzed, including the condition of resonance, magnitude–frequency characteristic, phase–frequency characteristic, and the impacts of inductor and capacitor orders on the characteristics.
• The control system of the FOLLCL-type grid-tied inverter is given. Active damping can be avoided, thus improving the ease of control and saving the cost of the control system.
• The performances of the FOLLCL-type grid-tied inverter based on PI, PI^λ, and PR control are analyzed through four cases. Among these three control methods, the most suitable one for the FOLLCL-type grid-tied inverter without an active damper is determined.

The remainder of the paper is organized as follows: Section 2 introduces the integer-order LLCL (IOLLCL) filter and makes a comparison between the IOLLCL filter and the IOLCL filter. Section 3 analyzes the characteristics of the FOLLCL filter, including resonant frequency, magnitude–frequency characteristic, and phase–frequency characteristic. In Section 4, the structure of the control system of the FOLLCL-type grid-tied inverter is described. Based on the expression of loop gain, the system performance is analyzed. Four cases are presented to discuss the performance of the FOLLCL-type grid-tied inverter. The simulation results are given in Section 5 to validate the theoretical analysis. Finally, Section 6 concludes this paper.

2. Integer-Order LLCL Filter

An VSI can connect the power grid through an LLCL filter to form a grid-tied inverter. The equivalent circuit of a single-phase integer-order LLCL-filter-based grid-tied inverter is shown in Figure 1, where L₁ and L₂ are the inverter-side and grid-side inductors, a small inductor L_f and a capacitor C_f composing a series resonant circuit, u_i and i₁ are the inverter output voltage and current, u_g and i_g are the grid voltage and current, and i_c is the capacitor current.

The transfer function i_g(s)/u_i(s) of the IOLLCL filter can be derived as

$$\begin{array}{c}{G}_{\mathrm{IO}}={\frac{i_g\left(s\right)}{u_i\left(s\right)}|}_{u_g\left(s\right)=0}=\frac{L_f{C}_f{s}^2+1}{\left(L_1{L}_2{C}_f+\left(L_1+L_2\right)C_f{L}_f\right)s^3+\left(L_1+L_2\right)s}\end{array}$$

(1)

Figure 2 illustrates the bode diagrams of i_g(s)/u_i(s) for both the IOLLCL filter and IOLCL filter while all the other parameters are the same except for L_f. The specific parameters of the filters are given in

Table 1. Filter Parameters.

Parameter	Symbol	Value
inverter-side inductor	L1	600 μH
grid-side inductor	L2	150 μH
series resonant circuit inductor	Lf	70.362 μH
series resonant circuit capacitor	Cf	10 μF

. Unlike the IOLCL filter, the IOLLCL filter has two resonance peaks: a negative one and a positive one; the resonance frequencies are f_rp1 (ω_rp1) and f_rp2 (ω_rp2), respectively. When the VSI operates under the condition of the dual-carrier sine-wave PWM, the uppermost harmonics of i_g are around the switching frequency 2f_s. Therefore, f_rp1 is designed to be equal to 2f_s to attenuate such harmonics. The positive resonance peak at f_rp2, as in the resonance peak at f_rp for the IOLCL filter, would lead to system instability in grid-tied inverter applications and should be damped by passive or active methods.

The negative resonant frequency of the IOLLCL filter is

$$\begin{array}{c}{\omega }_{\mathrm{rp}1}=\sqrt{\frac{1}{L_f{C}_f}}\end{array}$$

(2)

The positive resonant frequency of the IOLLCL filter is

$$\begin{array}{c}{\omega }_{\mathrm{rp}2}=\sqrt{\frac{L_1+L_2}{L_1{L}_2{C}_f+L_f{C}_f\left(L_1+L_2\right)}}\end{array}$$

(3)

It can also be seen from Figure 2 that the IOLLCL and IOLCL filters have similar low-frequency magnitude characteristics, while the IOLCL filter exhibits a better attenuation ability at a high-frequency band than the IOLLCL filter. However, overall, compared with the IOLCL filter, the grid current can obtain lower total harmonic distortion with the IOLLCL filter.

3. Fractional-Order LLCL Filter

The IOLLCL filter in the grid-tied inverter can be replaced by an FOLLCL filter to achieve better performance. The FOLLCL filter consists of four components: three inductors and a capacitor, as shown in Figure 3. In this paper, an LLCL filter can be called a fractional-order LLCL filter, with all or part of its components being fractional-order ones.

The transfer function from input (inverter output voltage u_i) to output (grid current i_g) is expressed as

$$\begin{array}{c}{G}_{\mathrm{FO}}=\frac{i_g\left(s\right)}{u_i\left(s\right)}=\frac{L_f{C}_f{s}^{{\alpha }_f+{\beta }_f}+1}{L_1{L}_2{C}_f{s}^{{\alpha }_1+{\alpha }_2+{\beta }_f}+C_f{L}_f{L}_1{s}^{{\alpha }_1+{\alpha }_f+{\beta }_f}+C_f{L}_f{L}_2{s}^{{\alpha }_2+{\alpha }_f+{\beta }_f}+L_1{s}^{{\alpha }_1}+L_2{s}^{{\alpha }_2}}\end{array}$$

(4)

where α₁, α₂, α_f, and β_f are the orders of L₁, L₂, L_f, and C_f, respectively. The magnitude–frequency and phase–frequency characteristic expressions obtained from (4) are quite complex. To simplify the analysis, set α₁ = α₂ = α; (4) is rewritten as

$$\begin{array}{c}{G}_{\mathrm{FO}}=\frac{i_g\left(s\right)}{u_i\left(s\right)}=\frac{L_f{C}_f{s}^{{\alpha }_f+{\beta }_f}+1}{L_1{L}_2{C}_f{s}^{2\alpha +{\beta }_f}+C_f{L}_f\left(L_1+L_2\right)s^{\alpha +{\alpha }_f+{\beta }_f}+\left(L_1+L_2\right)s^{\alpha }}=\frac{L_f{C}_f{s}^{{\alpha }_f+{\beta }_f}+1}{L_1{L}_2{C}_f{s}^{\alpha }\left[s^{\alpha +{\beta }_f}+B{s}^{{\alpha }_f+{\beta }_f}+A\right]}\end{array}$$

(5)

where A = (L₁ + L₂)/(L₁L₂C_f) and B = L_f (L₁ + L₂)/(L₁L₂). Substitute (jω)^α = ω^αcos(απ/2) + jω^αsin(απ/2) into (5); the mathematical model in frequency domain can be obtained as

$$G_{\mathrm{FO}}\left(j\omega \right)=\frac{L_f{C}_f{\omega }^{{\alpha }_f+{\beta }_f}\left[\cos \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}+j\sin \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right]+1}{L_1{L}_2{C}_f{\omega }^{\alpha }\left(\cos \frac{\alpha \pi }{2}+j\sin \frac{\alpha \pi }{2}\right)\left[{\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+A+j{\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+B{\omega }^{{\alpha }_f+{\beta }_f}\cos \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}+jB{\omega }^{{\alpha }_f+\beta }\sin \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right]}$$

(6)

The magnitude–frequency characteristic of G_FO is expressed as

$$\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{\sqrt{{\left[L_f{C}_f{\omega }^{{\alpha }_f+{\beta }_f}\cos \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}+1\right]}^2+{\left(\sin \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right)}^2}}{\sqrt{{\left({\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+A+B{\omega }^{{\alpha }_f+{\beta }_f}\cos \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right)}^2+{\left({\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+B{\omega }^{{\alpha }_f+\beta }\sin \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right)}^2}}$$

(7)

3.1. Resonant Frequencies

Define angular frequency ω_r1 as follows:

$$\begin{array}{c}{\omega }_{r1}={\left[-\frac{1}{L_f{C}_f\cos [\left({\alpha }_f+{\beta }_f\right)\pi /2]}\right]}^{\frac{1}{{\alpha }_f+{\beta }_f}}\end{array}$$

(8)

Then, the numerator of (7) can be expressed as

$$\begin{array}{c}\mathrm{num}\left(\left|G_{\mathrm{FO}}\right|\right)=\sqrt{{\left[-{\left(\frac{\omega }{{\omega }_{\mathrm{r}1}}\right)}^{{\alpha }_f+{\beta }_f}+1\right]}^2+{\left(\sin \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right)}^2}\end{array}$$

(9)

When ω = ω_r1, (9) can be reduced to

$$\begin{array}{c}\mathrm{num}\left(\left|G_{\mathrm{FO}}\right|\right)=\left|\sin \frac{\left({\alpha }_f+{\beta }_f\right)\pi }{2}\right|\end{array}$$

(10)

If α_f + β_f = 2n (n is an integer), sin[(α_f + β_f) nπ/2] = 0, and |G_FO(jω_r1)| as shown in (7) is zero. It means that the magnitude–frequency characteristic of the FOLLCL filter has a negative resonance (series resonance) peak at ω = ω_r1. According to the present literature, the orders of the actually realizable fractional-order inductors and capacitors are greater than 0 and less than 2, so n is set to 1 in this research. Therefore, to attenuate the switching-frequency current ripple in grid-tied inverter applications, the sum of α_f and β_f must equal 2. Substitute α_f + β_f = 2 back into (8); the negative resonant frequency can be obtained as

$$\begin{array}{c}{\omega }_{\mathrm{rp}1}=\sqrt{\frac{1}{L_f{C}_f}}\end{array}$$

(11)

It can be seen from (8) that the series resonance peak of the FOLLCL filter has the same form as the IOLLCL filter when α_f + β_f = 2. Series resonance is the most critical feature for the FOLLCL filter, so the following analysis is based on the relationship of α_f + β_f = 2.

Substitute α_f + β_f = 2 to (7); the denominator of (7) is expressed as

$$\begin{array}{c}\mathrm{den}\left(\left|G_{\mathrm{FO}}\right|\right)=L_1{L}_2{C}_f{\omega }^{\alpha }\sqrt{{\left({\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+A-B{\omega }^2\right)}^2+{\left({\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right)}^2}\end{array}$$

(12)

Define angular frequency ω_r2 as follows:

$$\begin{array}{c}{\omega }_{r2}={\left[-\frac{A-B{\omega }^2}{\cos [\left(\alpha +{\beta }_f\right)\pi /2]}\right]}^{\frac{1}{\alpha +{\beta }_f}}\end{array}$$

(13)

Therefore, (12) can be expressed as

$$\begin{array}{c}\mathrm{den}\left(\left|G_{\mathrm{FO}}\right|\right)=L_1{L}_2{C}_f{\omega }^{\alpha }\sqrt{{\left[-{\left(\frac{\omega }{{\omega }_{\mathrm{r}2}}\right)}^{\alpha +{\beta }_f}\left(A-B{\omega }^2\right)+A-B{\omega }^2\right]}^2+{\left({\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right)}^2}\end{array}$$

(14)

When ω = ω_r2, (14) can be reduced to

$$\begin{array}{c}\mathrm{den}\left(\left|G_{\mathrm{FO}}\right|\right)=L_1{L}_2{C}_f{\omega }^{\alpha }\sqrt{{\left({\omega }_{\mathrm{r}2}^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right)}^2}\end{array}$$

(15)

If α + β_f = 2, sin[(α + β_f)π/2] = 0, and |G_FO(jω_r2)| as shown in (7) is positive infinity. It means that the magnitude–frequency characteristic of the FOLLCL filter has a positive resonance peak at ω = ω_r2. Substitute α + β_f = 2 back into (13); the positive resonant frequency can be obtained as

$$\begin{array}{c}{\omega }_{\mathrm{rp}2}=\sqrt{\frac{L_1+L_2}{L_1{L}_2{C}_f+L_f{C}_f\left(L_1+L_2\right)}}\end{array}$$

(16)

It can be seen from (16) that the FOLLCL filter has the same expression of positive resonance peak as the IOLLCL filter when α_f + β_f = 2 and α + β_f = 2.

Theorem 1.

When α₁ = α₂ = α, the negative resonance (series resonance) peak of the FOLLCL filter exists only when α_f + β_f = 2; the resonant frequency is${\omega }_{\mathit{rp}\mathit{1}}=\sqrt{1/L_f{C}_f}$. The positive resonance peak of the FOLLCL filter exists only when α_f + β_f = 2 as well as α + β_f = 2; the resonant frequency is${\omega }_{\mathit{rp}\mathit{2}}=\sqrt{\left(L_1+L_2\right)/\left[L_1{L}_2{C}_f+L_f{C}_f\left(L_1+L_2\right)\right]}$. The positive resonant frequency ω_rp2 is always less than the negative resonant frequency ω_rp1.

Theorem 1 essentially reveals the resonant conditions for FOLLCL filters and provides a criterion to estimate whether an FOLLCL filter has resonance peaks. Orders α, α_f, and β_f of a conventional IOLLCL filter are all equal to 1. Both conditions α_f + β_f = 2 and α + β_f = 2 are satisfied; therefore, the IOLLCL filter is just a special case of the FOLLCL filter. Moreover, the positive resonance peak can be avoided according to Theorem 1 by choosing reasonable orders for the inverter-side inductor L₁, grid-side inductor L₂, and capacitor C_f. Passive or active damping approaches used in an IOLLCL filter can be omitted for an FOLLCL filter.

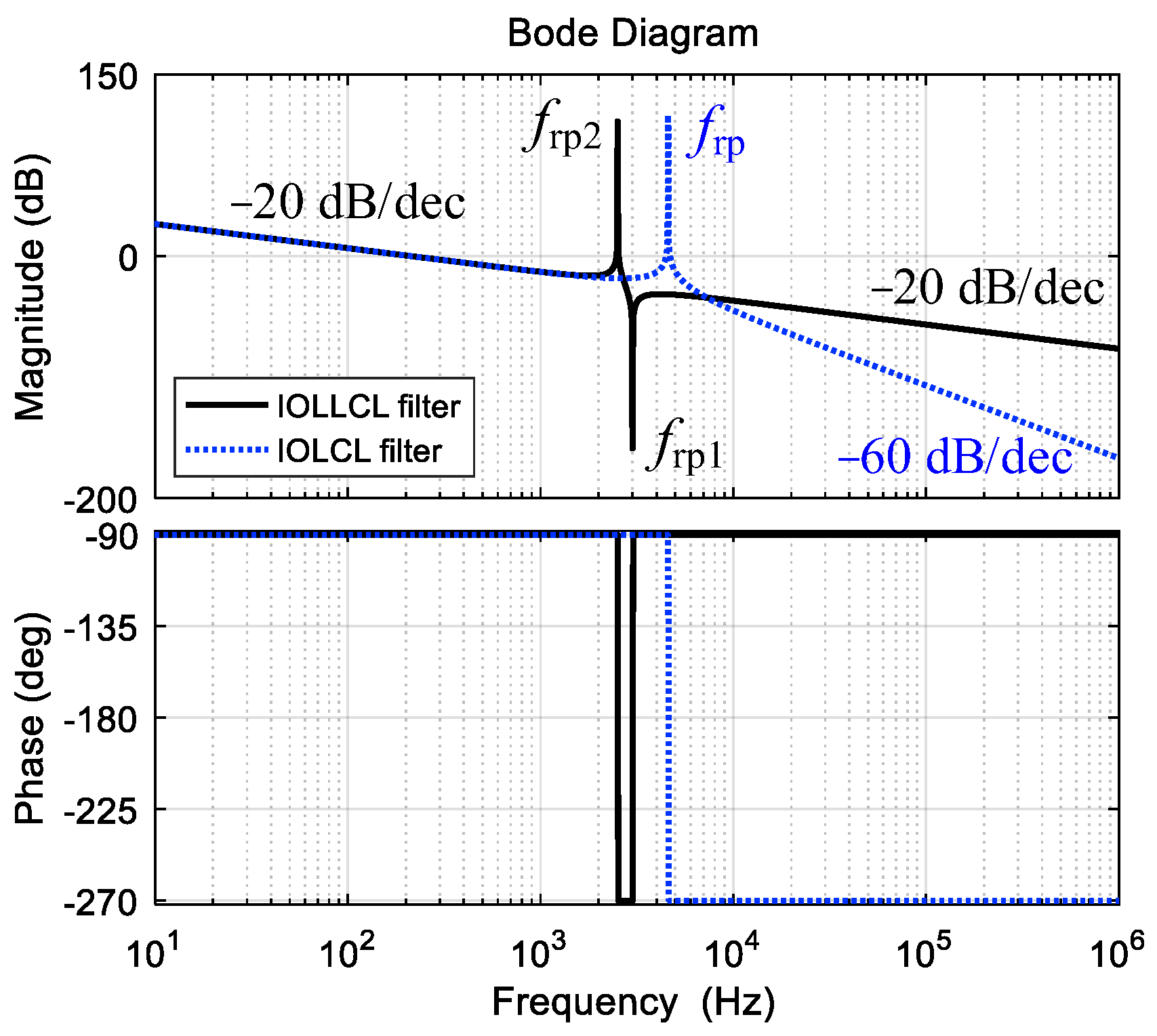
3.2. Magnitude–Frequency Characteristic

As previously mentioned, α_f + β_f = 2 must be satisfied for the FOLLCL filter, so (7) can be arranged as

$$\begin{array}{c}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{\left|-L_f{C}_f{\omega }^2+1\right|}{\sqrt{{\left({\omega }^{\alpha +{\beta }_f}+\left(A-B{\omega }^2\right)\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right)}^2+{(A-B{\omega }^2)}^2{\sin }^2\frac{\left(\alpha +{\beta }_f\right)\pi }{2}}} \end{array}$$

(17)

(1) When ω << ω_rp2, L_fC_fω² << 1, and A − Bω² ≈ A, (17) can be further expressed as

$$\begin{array}{c}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{1}{\sqrt{{\left({\omega }^{\alpha +{\beta }_f}+A\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right)}^2+A^2{\sin }^2\frac{\left(\alpha +{\beta }_f\right)\pi }{2}}}\end{array}$$

(18)

Define intermediate variables ω_t1 and ω_t2 as follows:

$$\begin{array}{c}{\omega }_{\mathrm{t}1}={\left|A\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right|}^{\frac{1}{\alpha +{\beta }_f}}\end{array}$$

(19)

$$\begin{array}{c}{\omega }_{\mathrm{t}2}={\left|A\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right|}^{\frac{1}{\alpha +{\beta }_f}}\end{array}$$

(20)

Substitute (19) and (20) into (18); the magnitude–frequency characteristic can be derived as

$$\begin{array}{c}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{1}{\sqrt{{\left({\omega }^{\alpha +{\beta }_f}+\tau {\omega }_{t1}^{\alpha +{\beta }_f}\right)}^2+{\omega }_{t2}^{2\left(\alpha +{\beta }_f\right)}}}\end{array}$$

(21)

where τ = 1 (α + β_f ∈ (0, 1] ∪ [3, 4)) or τ = −1 (α + β_f ∈ (1, 3)).

When ω << ω_t1, ${(\omega /{\omega }_{\mathrm{t}1})}^{\alpha +{\beta }_f}\approx 0$ and τ² = 1, (21) can be simplified as

$$\begin{array}{cc}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|\hfill & =\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }{\omega }_{t1}^{\alpha +{\beta }_f}}\frac{1}{\sqrt{{\left({(\omega /{\omega }_{t1})}^{\alpha +{\beta }_f}+\tau \right)}^2+{({\omega }_{t2}/{\omega }_{t1})}^{2\left(\alpha +{\beta }_f\right)}}}\hfill \\ \hfill & \approx \frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{1}{\sqrt{{\omega }_{t1}^{2\left(\alpha +{\beta }_f\right)}+{\omega }_{t2}^{2\left(\alpha +{\beta }_f\right)}}}=\frac{1}{L_1{L}_2{C}_{f}A{\omega }^{\alpha }}\hfill \end{array}$$

(22)

The log magnitude–frequency characteristic and the slope of its asymptote are expressed as (23) and (24).

$$\begin{array}{c}L\left(\omega \right)\approx -20\mathit{lg}(L_1{L}_2{C}_{f}A)-20\alpha \mathit{lg}\omega \end{array}$$

(23)

$$\begin{array}{c}\frac{dL\left(\omega \right)}{d\mathit{lg}\omega }\approx -20\alpha \mathrm{dB}/\mathrm{dec},\omega <<{\omega }_{\mathrm{t}1}\end{array}$$

(24)

(2) When ω >> ω_rp1, L_fC_fω² >> 1, and A − Bω² ≈ Bω², (17) can be expressed as

$$\begin{array}{c}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{L_f{C}_f{\omega }^2}{\sqrt{{\left({\omega }^{\alpha +{\beta }_f}+B{\omega }^2\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right)}^2+B^2{\omega }^4{\sin }^2\frac{\left(\alpha +{\beta }_f\right)\pi }{2}}}\end{array}$$

(25)

$$\begin{array}{c}{\omega }_{\mathrm{t}3}={\left|B\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right|}^{\frac{1}{\alpha +{\beta }_f}}\end{array}$$

(26)

Define intermediate variables ω_t3 and ω_t4 as follows:

$$\begin{array}{c}{\omega }_{\mathrm{t}4}={\left|B\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}\right|}^{\frac{1}{\alpha +{\beta }_f}}\end{array}$$

(27)

Substitute (26) and (27) into (25); the magnitude–frequency characteristic can be derived as

$$\begin{array}{c}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{\alpha }}\frac{L_f{C}_f{\omega }^2}{\sqrt{{\left({\omega }^{\alpha +{\beta }_f}+\tau {\omega }^2{\omega }_{t3}^{\alpha +{\beta }_f}\right)}^2+{\omega }^4{\omega }_{t4}^{2\left(\alpha +{\beta }_f\right)}}}\end{array}$$

(28)

When ω >> ω_rp1 and α + β_f ∈ [2, 4), ${\omega }^2{({\omega }_{\mathrm{t}3}/\omega )}^{\alpha +{\beta }_f}\approx 0$, and ${\omega }^2{({\omega }_{\mathrm{t}4}/\omega )}^{\alpha +{\beta }_f}\approx 0$, (17) can be expressed as

$$\begin{array}{c}\left|G_{\mathrm{FO}}\left(j\omega \right)\right|=\frac{1}{L_1{L}_2{C}_f{\omega }^{2\alpha +{\beta }_f}}\frac{L_f{C}_f{\omega }^2}{\sqrt{{\left(1+\tau {\omega }^2{({\omega }_{t3}/\omega )}^{\alpha +{\beta }_f}\right)}^2+{\omega }^4{({\omega }_{t4}/\omega )}^{2\left(\alpha +{\beta }_f\right)}}}\approx \frac{L_f}{L_1{L}_2{\omega }^{2\alpha +{\beta }_f-2}}\end{array}$$

(29)

The log magnitude–frequency characteristics and the slope of its asymptote are expressed as (30) and (31).

$$\begin{array}{c}L\left(\omega \right)\approx 20\mathit{lg}{L}_f-20\mathit{lg}(L_1{L}_2)-20\left(2\alpha +{\beta }_f-2\right)\mathit{lg}\omega \end{array}$$

(30)

$$\begin{array}{c}\frac{dL\left(\omega \right)}{d\mathit{lg}\omega }\approx -20\left(2\alpha +{\beta }_f-2\right) \mathrm{dB}/\mathrm{dec}, \omega >>{\omega }_{\mathrm{rp}1}\end{array}$$

(31)

Similarly, when ω >> ω_rp1 and α + β_f ∈ (0,2), the slope of the asymptote is −20α dB/dec.

Theorem 2.

For FOLLCL, when ω << ω_rp2, the asymptote slope of the low-frequency log magnitude–frequency characteristic is −20α dB/dec. When ω >> ω_rp1, α + β_f∈ [2, 4), the asymptote slope of the high-frequency log magnitude–frequency characteristics is −20 (2α + β_f − 2) dB/dec; if α + β_f∈ (0, 2), the asymptote slope is −20α dB/dec.

3.3. Phase–Frequency Characteristic

According to (6), when α_f + β_f = 2, the phase model can be expressed as

$$\begin{array}{c}\angle G_{\mathrm{FO}}\left(j\omega \right)=-\arctan \left(\tan \frac{\pi \alpha }{2}\right)-\arctan \frac{{\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}}{{\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+A-B{\omega }^2}\end{array}$$

(32)

(1) When ω << ω_t1, A − Bω² ≈ A and ${\omega }^{\alpha +{\beta }_f}\sin [\left(\alpha +{\beta }_f\right)\pi /2]$ << ${\omega }^{\alpha +{\beta }_f}\cos [\left(\alpha +{\beta }_f\right)\pi /2]+A$, so the low-frequency phase is expressed as

$$\begin{array}{c}\angle G_{\mathrm{FO}}\left(j\omega \right)\approx -\arctan \left(\tan \frac{\pi \alpha }{2}\right)-\arctan \frac{{\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}}{{\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}+A}\approx -\frac{\pi \alpha }{2}\end{array}$$

(33)

(2) When ω >> ω_rp1, A − Bω² ≈ −Bω² and Bω² << |${\omega }^{\alpha +{\beta }_f}\cos [\left(\alpha +{\beta }_f\right)\pi /2]$|. Moreover, when α + β_f ∈ [2, 4), $\arctan \{\tan [\left(\alpha +{\beta }_f\right)\pi /2]\}=\left(\alpha +{\beta }_f\right)\pi /2-2\pi$, so the high-frequency phase is expressed as

$$\begin{array}{c}\angle G_{\mathrm{FO}}\left(j\omega \right)\approx \pi -\arctan \left(\tan \frac{\pi \alpha }{2}\right)-\arctan \frac{{\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}}{{\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}-B{\omega }^2}\\ \approx \pi -\arctan \left(\tan \frac{\pi \alpha }{2}\right)-\arctan \frac{{\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}}{{\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}}=-\pi \left(\alpha +{\beta }_f/2\right)+\pi \end{array}$$

(34)

When α + β_f ∈ (0,2), ${\omega }^{\alpha +{\beta }_f}\sin [\left(\alpha +{\beta }_f\right)\pi /2]$ << $|{\omega }^{\alpha +{\beta }_f}\cos [\left(\alpha +{\beta }_f\right)\pi /2]-B{\omega }^2|$, so the high-frequency phase can be expressed as

$$\begin{array}{c}\angle G_{\mathrm{FO}}\left(j\omega \right)\approx -\arctan \left(\tan \frac{\pi \alpha }{2}\right)-\arctan \frac{{\omega }^{\alpha +{\beta }_f}\sin \frac{\left(\alpha +{\beta }_f\right)\pi }{2}}{{\omega }^{\alpha +{\beta }_f}\cos \frac{\left(\alpha +{\beta }_f\right)\pi }{2}-B{\omega }^2}\approx -\frac{\pi \alpha }{2}\end{array}$$

(35)

Theorem 3.

For FOLLCL, when ω << ω_rp2, the low-frequency phase is −πα/2. When ω >> ω_rp1, if α + β_f∈ [2, 4),the high-frequency phase is −π (α + β_f/2) + π; if α + β_f∈ (0, 2), the high-frequency phase is −πα/2.

It can be seen from Theorem 2 and Theorem 3 that the low-frequency characteristics only depend on the orders of L₁ and L₂, and are independent of the orders of L_f and C_f. The high-frequency characteristics are determined by the orders of L₁, L₂, and C_f when α + β_f ∈ [2, 4), and only depend on the orders of L₁ and L₂ when α + β_f ∈ (0, 2).

3.4. Simulation Analyses

The bode plots of the FOLLCL filter are shown in Figure 4. The specific parameters of the FOLLCL filter are given in Table 1. Two cases are considered, namely, α + β_f ≤ 2 and α+β_f ≥ 2. The values of the asymptote slopes and phases are marked in the plots; it can be seen that the results are consistent with the theoretical analyses. In particular, the positive resonance peak is suppressed when α + β_f ≠ 2. Furthermore, it is shown in Figure 4b that when α + β_f > 2, the phase–frequency characteristic curves do not pass through −180°, which means that the phase crossover frequency does not exist. Therefore, α + β_f must be less than or equal to 2 to guarantee the stability.

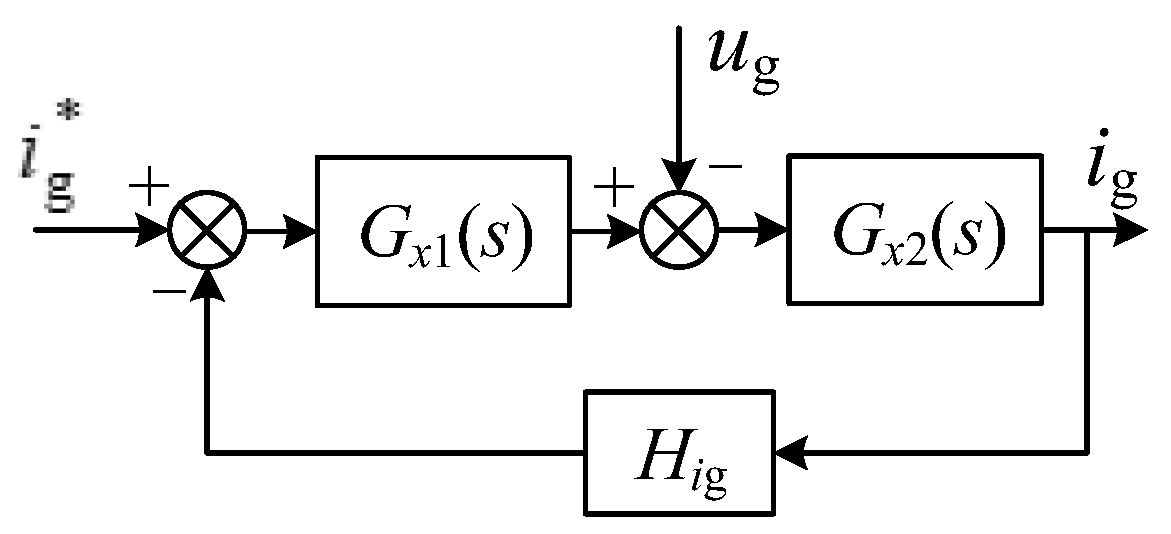
4. Grid-Tied Inverter Based on Fractional-Order LLCL Filter

An FOLLCL filter and a VSI can be combined to form a grid-tied inverter. Figure 5 shows the single-phase FOLLCL-type grid-tied inverter and its control system. The primary objective of the grid-tied inverter is to control the grid-side current i_g to be synchronized with the grid voltage, which is denoted by u_g. I* is the reference amplitude of the grid-side current, θ is the phase of grid voltage obtained by the phase-locked loop (PLL), and $i_g^{*}$ is the reference of the grid-side current. i_g is sensed with the sensor gain of H_ig and compared with $i_g^{*}$. The current error is sent to the current regulator G_i; G_i = K_p + K_i/s^λ, and K_p, K_i, and λ are the proportional coefficient, integral coefficient, and order of the integrator, respectively. For the FOLLCL filter with α + β_f equaling or very close to 2, an active damping method is used to attenuate the positive resonance. The output of G_i is sent to the PWM generator after subtracting the capacitor current i_C, which is sensed with the sensor gain of H_iC. For the FOLLCL filter with α + β_f deviating from 2, the output of G_i is sent to the PWM generator directly; the active damping can be avoided.

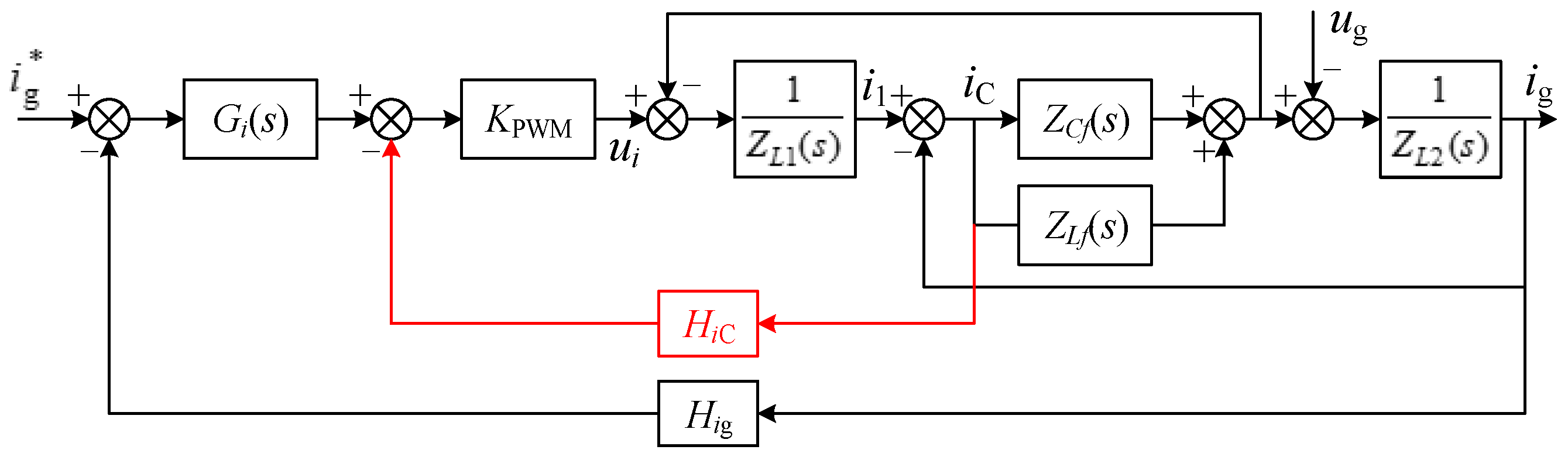
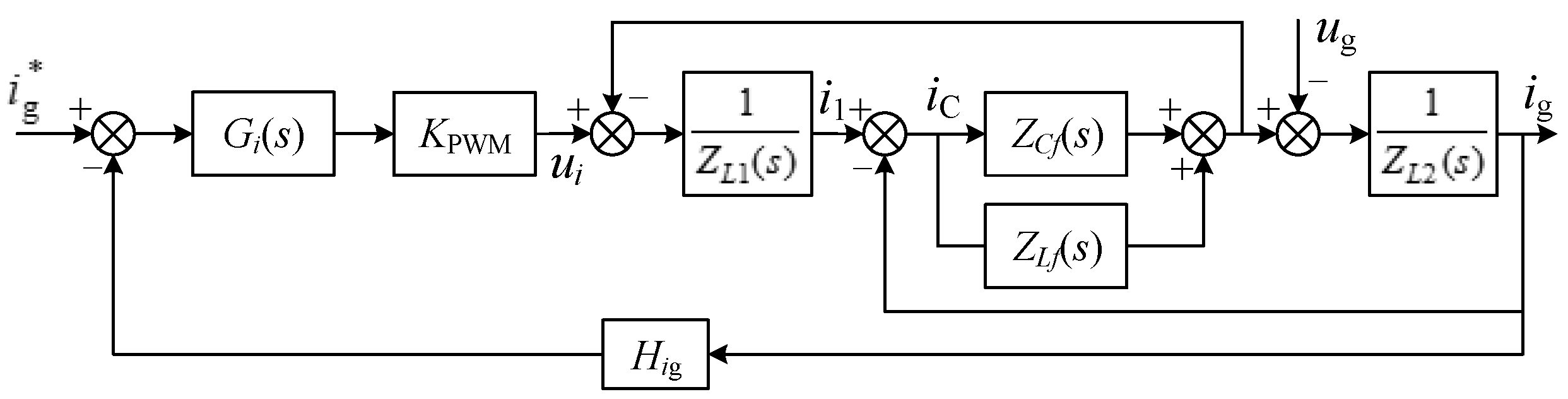
4.1. Structure of the Control System

According to Figure 5, the control block diagram of the single-phase FOLLCL-type grid-tied inverter when α + β_f equals to or is very close to 2 is shown in Figure 6, where K_PWM is the transfer function from the modulation signal to the inverter output voltage, expressed as K_PWM = u_dc/V_tri, and V_tri is the amplitude of triangular carrier. Z_L1(s), Z_L2(s), Z_Lf(s), and Z_Cf(s) are the impedance of L₁, L₂, L_f, and C_f, respectively, which are expressed as

$$\begin{array}{c}{Z}_{L1}\left(s\right)=s^{\alpha }{L}_1\begin{array}{cc},& Z_{L2}\left(s\right)=s^{\alpha }{L}_2\begin{array}{cc},& Z_{Lf}\left(s\right)=s^{{\alpha }_f}{L}_1\begin{array}{cc},& Z_{Cf}\left(s\right)=1/s^{{\beta }_f}{C}_f\end{array}\end{array}\end{array}\end{array}$$

(36)

The control block diagram of the single-phase FOLLCL-type grid-tied inverter when α+β_f deviates from 2 is shown in Figure 7. Compared with Figure 6, the capacitor current feedback loop is removed.

The control block diagrams in Figure 6 and Figure 7 can be equivalently transformed into the block diagram in Figure 8. The transfer functions G_x1 and G_x2 are expressed as (37) and (38), respectively:

$$\begin{array}{c}{G}_{x1}\left(s\right)=\frac{K_{\mathrm{PWM}}{G}_i\left(s\right)\left[Z_{Lf}\left(s\right)+Z_{Cf}\left(s\right)\right]}{Z_{L1}\left(s\right)+Z_{Lf}\left(s\right)+Z_{Cf}\left(s\right)+H_{iC}{K}_{\mathrm{PWM}}}\end{array}$$

(37)

$$\begin{array}{c}{G}_{x2}\left(s\right)=\frac{Z_{L1}\left(s\right)+Z_{Lf}\left(s\right)+Z_{Cf}\left(s\right)+H_{iC}{K}_{\mathrm{PWM}}}{Z_{L1}\left(s\right)Z_{L2}\left(s\right)+\left[Z_{L1}\left(s\right)+Z_{L2}\left(s\right)\right]\left[Z_{Lf}\left(s\right)+Z_{Cf}\left(s\right)\right]+H_{iC}{K}_{\mathrm{PWM}}{Z}_{L2}\left(s\right)}\end{array}$$

(38)

where H_iC = 0 when α + β_f ≠ 2.

According to the equivalent block diagram in Figure 8 and (36)~(38), the expression of the loop gain can be derived as

$$\begin{array}{c}{T}_A\left(s\right)=G_{x1}\left(s\right)G_{x2}\left(s\right)H_{ig}\left(s\right)=\frac{H_{ig}{K}_{\mathrm{PWM}}{G}_i\left(s\right)\left(L_f{C}_f{s}^{{\alpha }_f+{\beta }_f}+1\right)}{L_1{L}_2{C}_f{s}^{2\alpha +{\beta }_f}+\left(L_1+L_2\right)L_f{C}_f{s}^{\alpha +{\alpha }_f+{\beta }_f}+L_2{C}_f{H}_{iC}{K}_{\mathrm{PWM}}{s}^{\alpha +{\beta }_f}+\left(L_1+L_2\right)s^{\alpha }}\end{array}$$

(39)

As discussed in Part 3, α_f + β_f = 2 must be satisfied in grid-tied inverter applications, so (39) is rewritten as

$$\begin{array}{c}{T}_A\left(s\right)=\frac{H_{ig}{K}_{\mathrm{PWM}}{G}_i\left(s\right)\left(L_f{C}_f{s}^2+1\right)}{L_1{L}_2{C}_f{s}^{2\alpha +{\beta }_f}+\left(L_1+L_2\right)L_f{C}_f{s}^{\alpha +2}+L_2{C}_f{H}_{iC}{K}_{\mathrm{PWM}}{s}^{\alpha +{\beta }_f}+\left(L_1+L_2\right)s^{\alpha }}\end{array}$$

(40)

The grid current i_g can be expressed as

$$\begin{array}{c}{i}_g\left(s\right)=\frac{1}{H_{ig}}\frac{T_A\left(s\right)}{1+T_A\left(s\right)}{i}_g^{*}\left(s\right)-\frac{G_{x2}\left(s\right)}{1+T_A\left(s\right)}{u}_g\left(s\right)=i_{g1}\left(s\right)+i_{g2}\left(s\right)\end{array}$$

(41)

It can be seen from (41) that i_g(s) consists of two parts: the reference tracking component i_g1(s) and the disturbance component i_g2(s) caused by the grid voltage, which can be expressed as (42) and (43), respectively.

$$\begin{array}{c}{i}_{\mathrm{g}1}\left(s\right)=\frac{1}{H_{ig}}\frac{T_A\left(s\right)}{1+T_A\left(s\right)}{i}_g^{*}\left(s\right)\end{array}$$

(42)

$$\begin{array}{c}{i}_{\mathrm{g}2}\left(s\right)=-\frac{G_{x2}\left(s\right)}{1+T_A\left(s\right)}{u}_g\left(s\right)\end{array}$$

(43)

4.2. System Performance Analysis

The loop gain at the fundamental frequency is often much greater than one, so 1 + T_A(s) ≈ T_A(s), and (42) can be rewritten as $i_{\mathrm{g}1}\left(s\right)\approx i_g^{*}\left(s\right)/H_{ig}$. Therefore, i_g1(s) and $i_g^{*}\left(s\right)$ are almost in phase. For f ≤ f_c, the L_f − C_f branch can be considered open. According to (38) and (40), the expression of G_x2(s) and T_A(s) at the fundamental frequency can be obtained as follows:

$$\begin{array}{c}{G}_{x2}(j2\pi f_o)\approx \frac{1}{{(j2\pi f_o)}^{\alpha }\left(L_1+L_2\right)}\end{array}$$

(44)

$$\begin{array}{c}{T}_A(j2\pi f_o)\approx \frac{H_{ig}{K}_{\mathrm{PWM}}{G}_i\left(j2\pi f_o\right)}{{(j2\pi f_o)}^{\alpha }\left(L_1+L_2\right)}\end{array}$$

(45)

where f_o is the fundamental frequency. Substitute (44) and (45) into (43), and for PI regulator, G_i(j2πf_o) ≈ K_i/(j2πf_o), so we have

$$\begin{array}{c}{i}_{\mathrm{g}2}\approx -\frac{u_g}{H_{ig}{K}_{\mathrm{PWM}}{G}_i\left(j2\pi f_o\right)}\approx -\frac{j2\pi f_o{u}_g}{H_{ig}{K}_{\mathrm{PWM}}{K}_i}\end{array}$$

(46)

From (46), it can be seen that i_g2 lags behind u_g by 90°; a small i_g2 is expected to reduce the amplitude and phase tracking errors for i_g. From (45) and (46), the RMS value of i_g2 can be expressed as

$$\begin{array}{c}{I}_{\mathrm{g}2}\approx \frac{U_g}{H_{ig}{K}_{\mathrm{PWM}}\left|G_i\left(j2\pi f_o\right)\right|}\approx \frac{U_g}{{(2\pi f_o)}^{\alpha }\left(L_1+L_2\right)\left|T_A\left(j2\pi f_o\right)\right|}\end{array}$$

(47)

The magnitude of the loop gain at f_o is expressed as

$$T_{\mathrm{fo}}=20lg\left|T_A\left(j2\pi f_o\right)\right|\approx 20lg\frac{U_g}{{(2\pi f_o)}^{\alpha }\left(L_1+L_2\right)I_{g2}}$$

(48)

where the unit of T_fo is dB. Thus, the steady-state error requirement for I_g2 is converted to the requirement for T_fo. Obviously, for a given value of I_g2, a smaller-order α means bigger T_fo.

Compared to the PI regulator, the PR regulator can significantly increase T_fo, and thus decrease the steady-state error of the grid current. The expression of the PR regulator is

$$G_i\left(s\right)=K_p+\frac{2K_r{\omega }_{i}s}{s^2+2{\omega }_{i}s+{\omega }_o^2}$$

(49)

where K_p is the proportional coefficient, K_r is the resonant coefficient, ω_i is the bandwidth concerning the –3 dB cutoff frequency of the resonant compensator, and ω_o = 2πf_o is the fundamental angular frequency. The design criteria of the PR regulator have been reported in many works in the literature and will not be repeated here.

In order to demonstrate the control system design criteria of the FOLLCL-type grid-tied inverter, four cases are presented based on the system parameters listed in Table 1 and

Table 2. System Parameters.

Parameter	Symbol	Value
DC voltage	udc	360 V
grid voltage (RMS)	Ug	220 V
fundamental frequency	fo	50 Hz
switching frequency	fs	3 kHz
amplitude of the triangular carrier	Vtri	3.05 V

.

Case I (α + β_f = 2, PI control): For α + β_f = 2 (taking (α, α_f, β_f) = (1.2, 1.2, 0.8) and (α, α_f, β_f) = (1.1, 1.1, 0.9) as examples), the bode diagrams of the loop gain before compensation (G_i(s) = 1) are drawn in Figure 9 according to (40), where f_c is the cut-off frequency of the loop gain. As shown in Figure 9, the capacitor current feedback can effectively suppress the positive resonance peak of the FOLLCL filter, and the resonance damping capability becomes stronger with the increase of H_iC. As with the application in conventional IOLCL-type grid-tied inverters, this well-known active damping method only changes the magnitude–frequency characteristics around the resonant frequency f_rp2. However, the phase–frequency characteristics vary observably; they decrease from –(90α)° when f < f_rp2.

The control system parameter design principles for IOLCL-type grid-tied inverters are adopted here to control the FOLLCL-type grid-tied inverter with α + β_f = 2. The bode diagrams of the loop gain after compensation (G_i(s) = K_p + K_i/s) are shown in Figure 10. The frequency characteristics without active damping and compensation (green dotted lines) when (α, α_f, β_f) = (1.2, 1.2, 0.8) are also plotted in the same figure for comparison purpose. H_iC = 0.1, H_ig = 0.15, K_p = 0.45, and K_i = 2200 are designed in this case to yield a satisfactory overall system performance. Compared with the original system (green dotted lines), the loop gain at the fundamental frequency (T_fo) after compensation (blue solid lines) increases and the high-frequency (f > f_rp1) magnitude characteristics move down, which can guarantee the fundamental current tracking and high-frequency harmonic attenuation capabilities. It can also be seen from Figure 10 that a lower α can guarantee better performance under the condition of α + β_f = 2. When α = 1.1, the system has a sufficient gain margin (GM = 5.04 dB) and an acceptable phase margin (PM = 38.1°, while PM > 45° is required for a well-designed system), as well as a reasonable cut-off frequency (f_c = 948 Hz) and a sufficient fundamental loop gain (T_fo = 49.5 dB), while when α = 1.2, although there is a slightly higher gain margin (GM = 5.74 dB), the PM, f_c, and T_fo all decrease. The low phase margin (PM = 17.1°) especially threatens the system stability.

Case II (α + β_f ≠ 2, PI control): For α + β_f ≠ 2 (taking α = 1.1, α_f = 1.2, β_f = 0.8 as an example), the bode diagrams of the loop gain before compensation (G_i(s) = 1) are drawn in Figure 11. H_iC = 0 is set in this case to avoid active damping. The positive resonance peak is damped effectively by selecting appropriate values for orders α and β_f to make their sum unequal to 2. When H_ig = 0.15, the same value as in case I, the cut-off frequency is very close to the equivalent switching frequency 2f_s (6 kHz), which is not acceptable for a grid-tied inverter. Moreover, when H_ig = 0.1 or 0.15, the magnitude plot has three cut-off frequencies and the system behaves as a conditionally stable system. For a large H_ig, even if the system can be stable after compensation, it is not easy to obtain a sufficient gain margin. If we keep decreasing H_ig to 0.05, the magnitude plot has only one cut-off frequency. Therefore, H_ig = 0.05 is chosen for the compensated system in the next step.

The bode diagrams of the loop gain after compensation (G_i(s) = K_p + K_i/s^λ, λ = 1) are shown in Figure 12. As seen from (46), the decrease of H_ig will increase i_g2, so K_i should be increased to meet the steady-state error requirement. However, the phase margin when K_i = 2200 is only 22.7°, and after increasing K_i from 2200 to 4000, the phase margin decreases to 14.6°, and a sufficient phase margin cannot be guaranteed.

Case III (α + β_f ≠ 2, PI^λ control): In this case, (α, α_f, β_f) = (1.1, 1.2, 0.8), H_iC = 0, H_ig = 0.05, and a fractional-order PI^λ regulator is used to try to improve the phase margin. When K_p = 0.45, K_i = 2200, and λ increases from 0.8 to 1.4, the bode diagrams of the loop gain are shown in Figure 13. The phase margin increases with λ, so λ = 1.4 is selected to leave enough room for K_i adjustment.

The bode diagrams of the loop gain with varying K_i when λ = 1.4 are shown in Figure 14. With the increase of K_i, the phase margin decreases, but it is still sufficient even K_i = 6000 (PM = 49.2°). However, each curve in Figure 13 and Figure 14 has a small T_fo, so the steady-state error requirement is still not guaranteed according to (47) and (48). The contradiction between T_fo and PM cannot be balanced by a PI^λ regulator.

Case IV (α + β_f≠2, PR control): In this case, (α, α_f, β_f) = (1.1, 1.2, 0.8), H_iC = 0, H_ig = 0.05, and a PR regulator is used to control the grid current. The values of the parameters are K_p = 0.45, ω_o = 2π × 50 rad/s, and ω_i = π rad/s, and K_r increases from 100 to 300; the bode diagrams of the compensated system are shown in Figure 15. It can be seen that each curve has a large enough T_fo to eliminate the steady-state error of i_g. However, PM decreases with the increase of K_r, when K_r = 100, GM = 11.3 dB, PM is 59.3°, and the f_c also has a good value, so K_r = 100 will be selected in the simulation section.

Based on the four cases discussed previously, it can be concluded that:

(1)

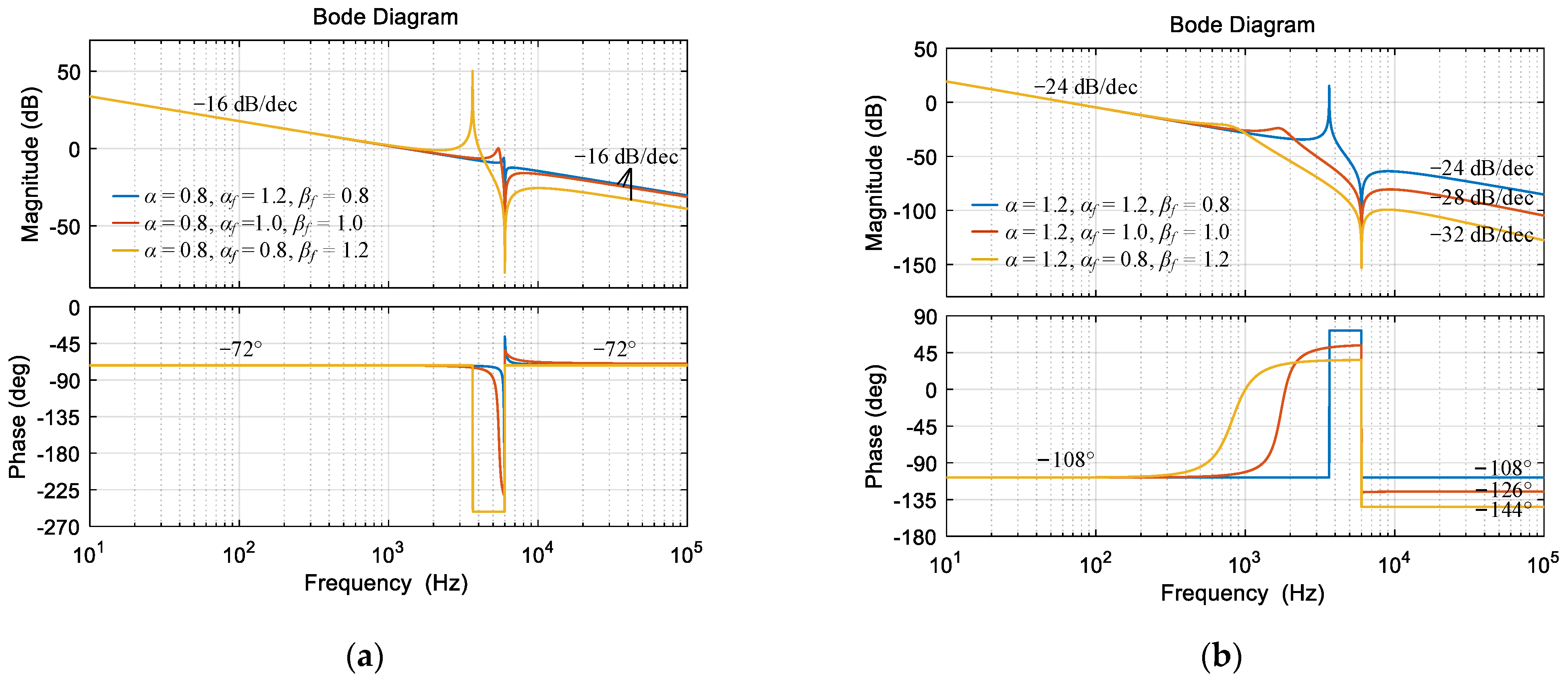
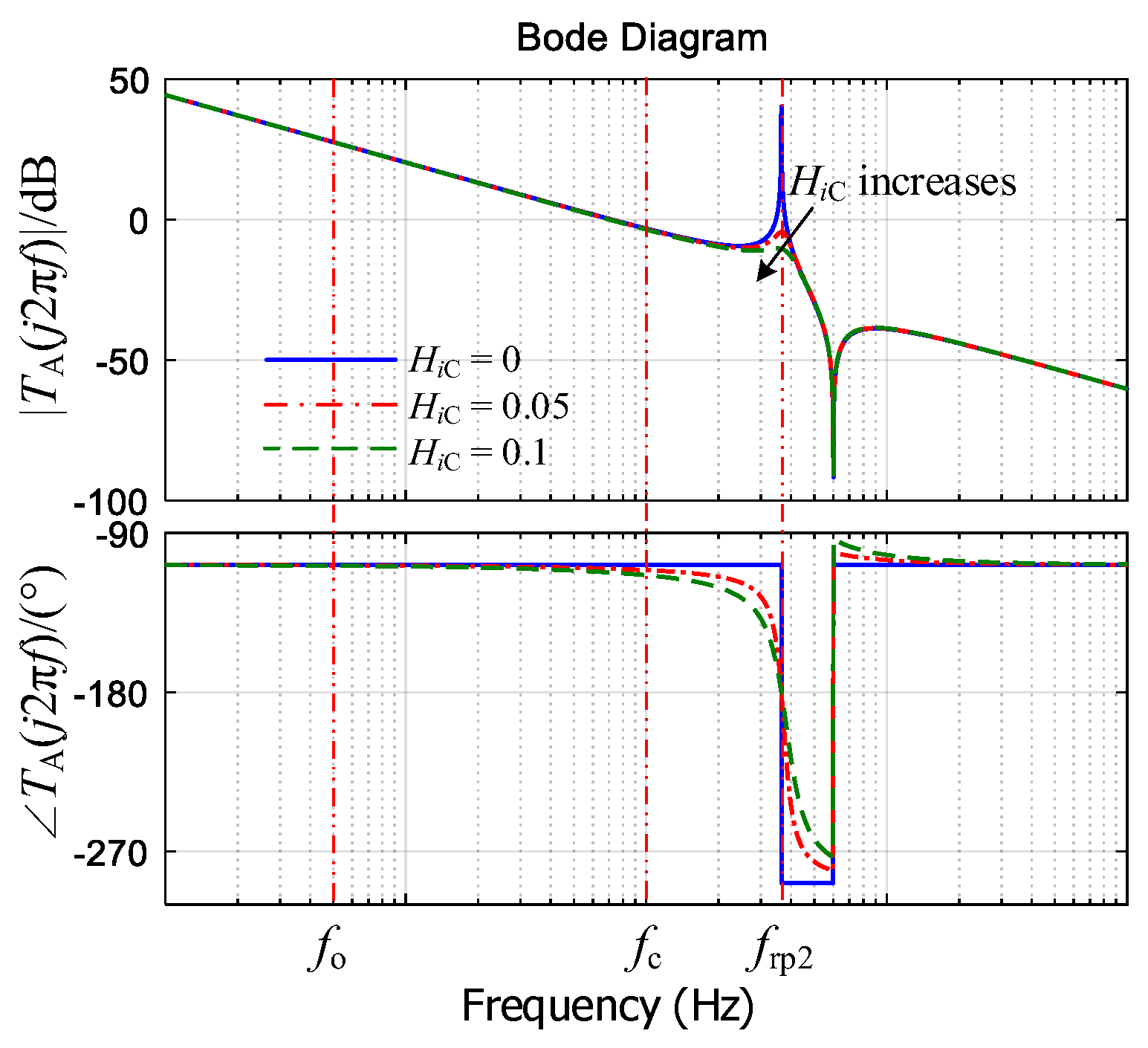
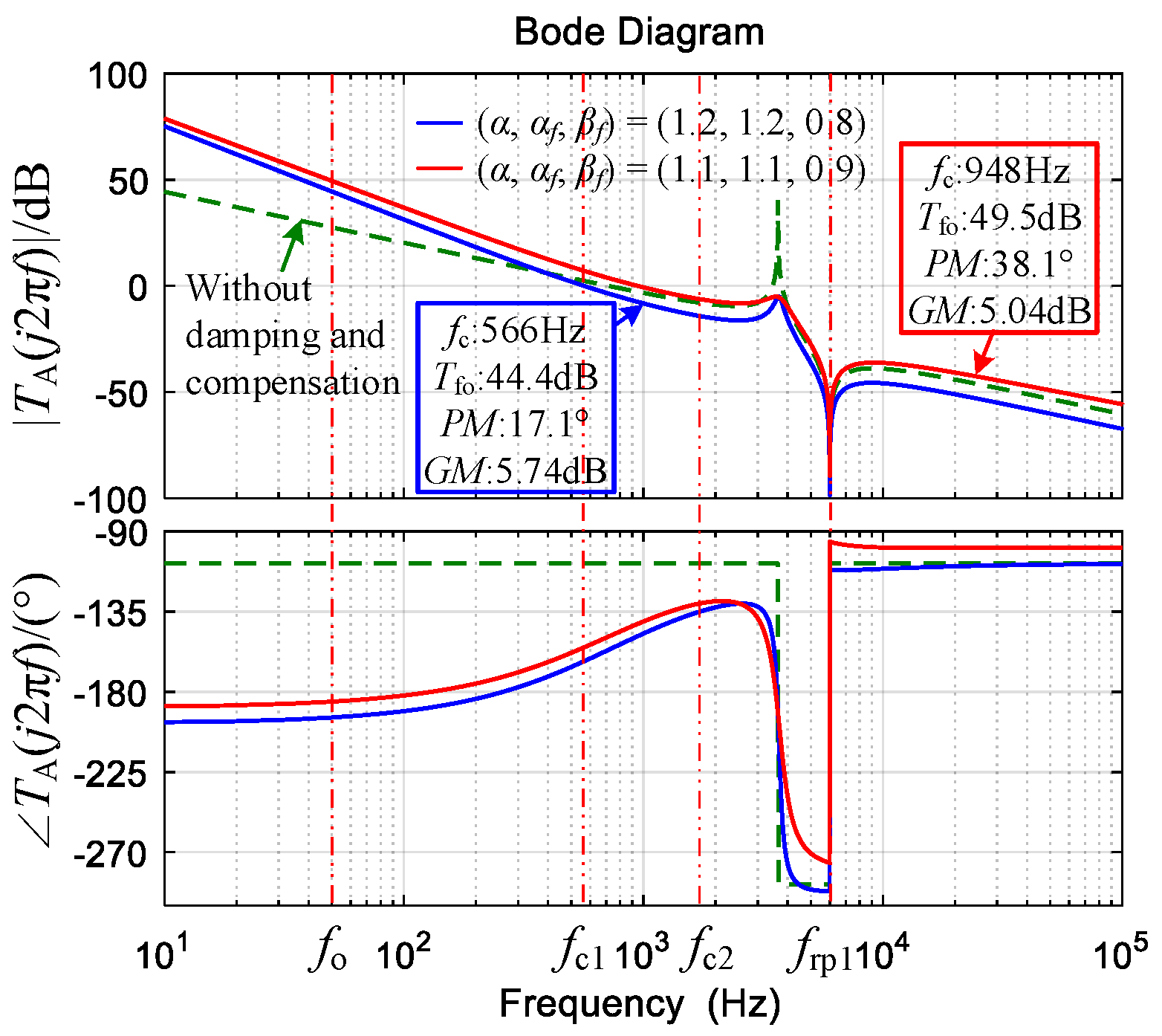
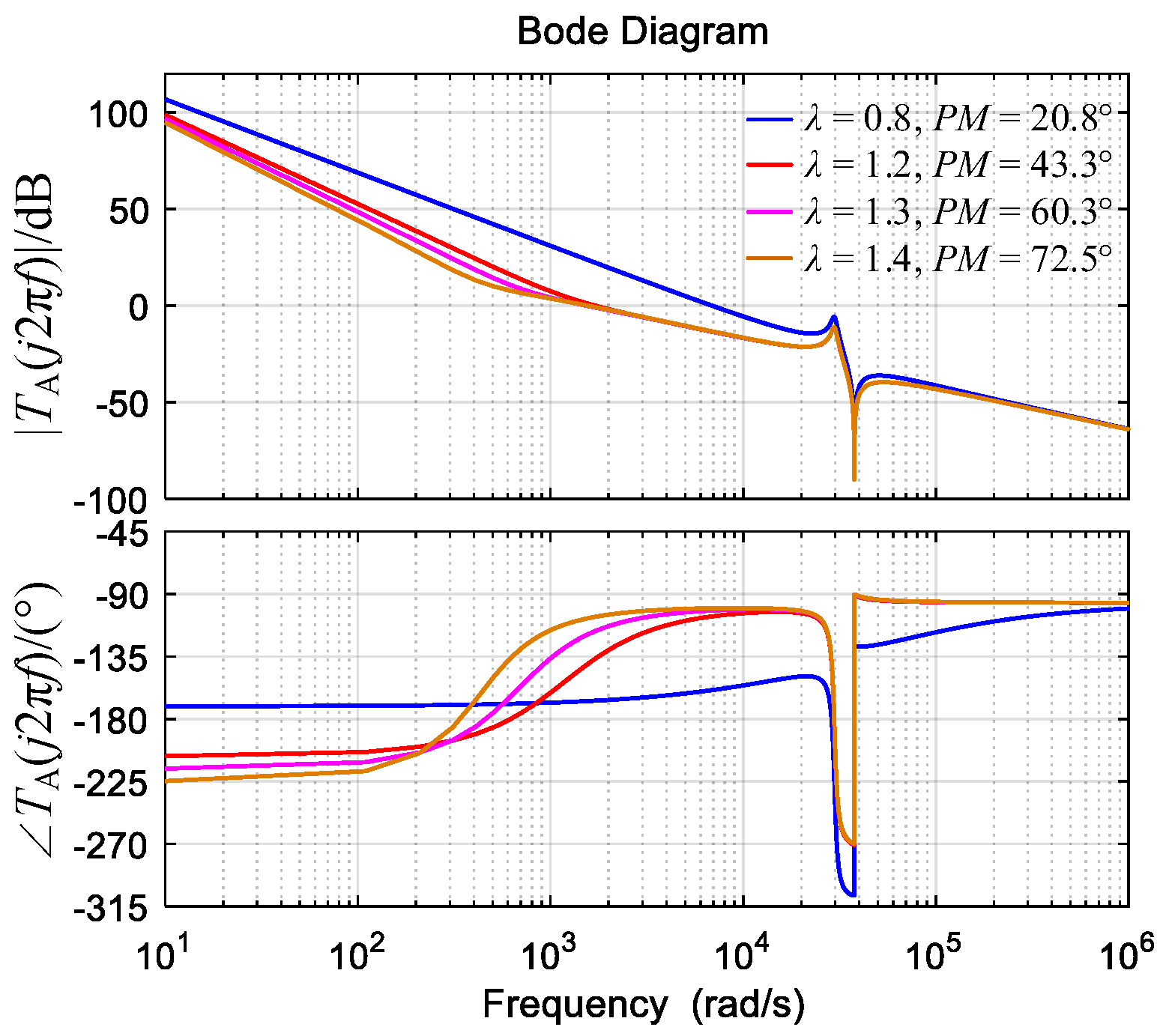
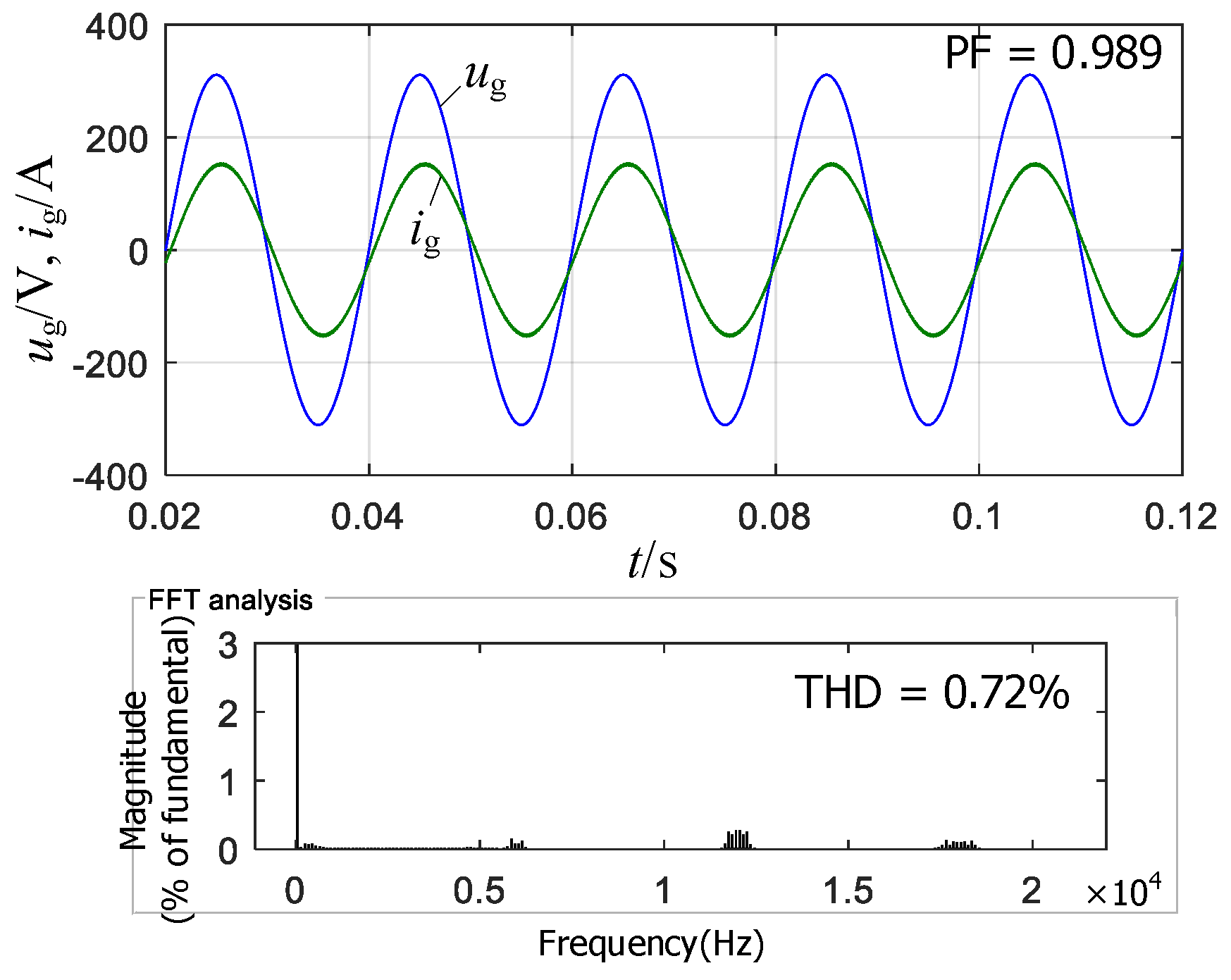
If α + β_f = 2, the FOLLCL-type grid-tied inverter can be damped by a capacitor current feedback loop. Under PI control, a lower α can achieve a larger PM but a higher f_c.

(2)

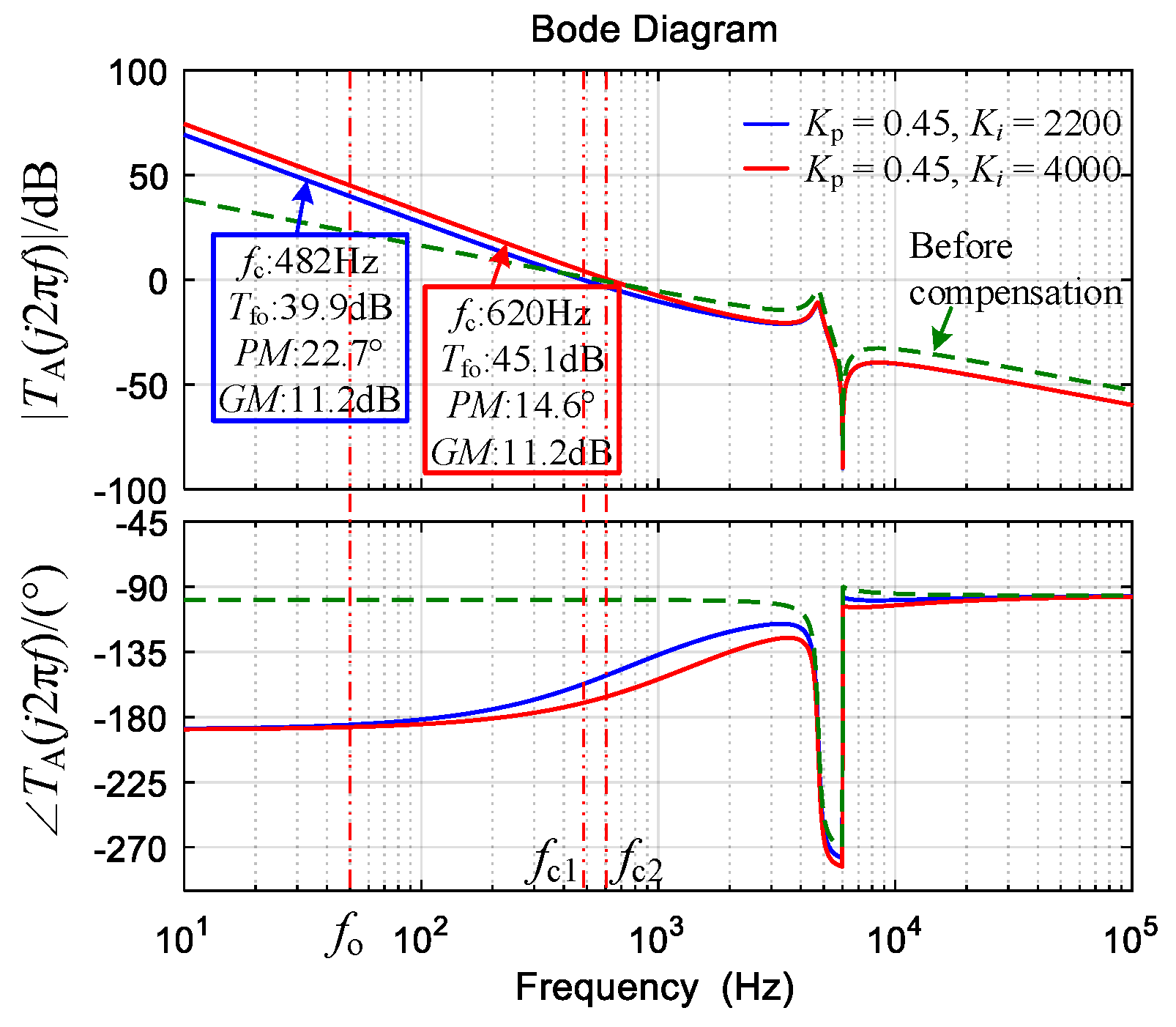
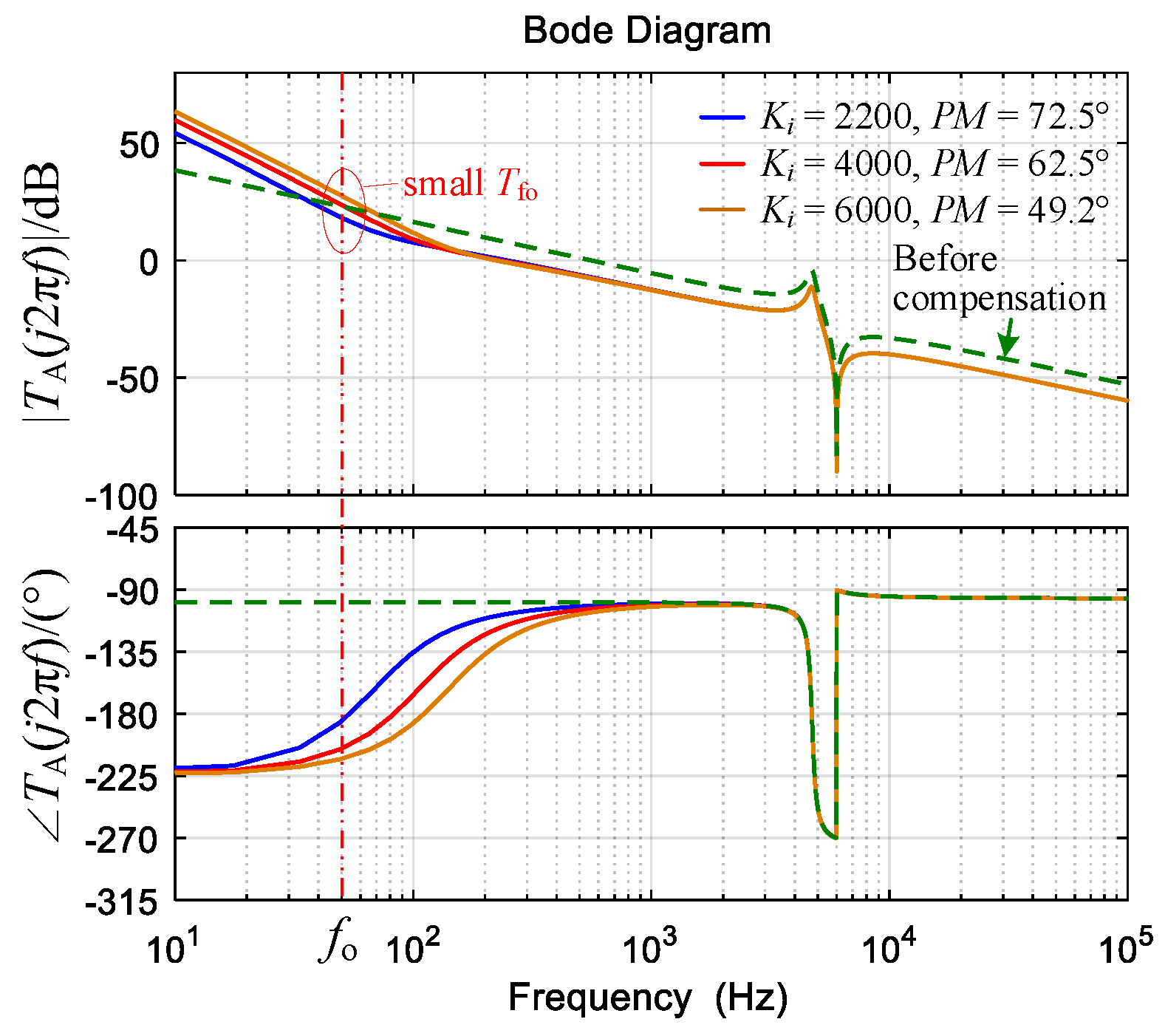
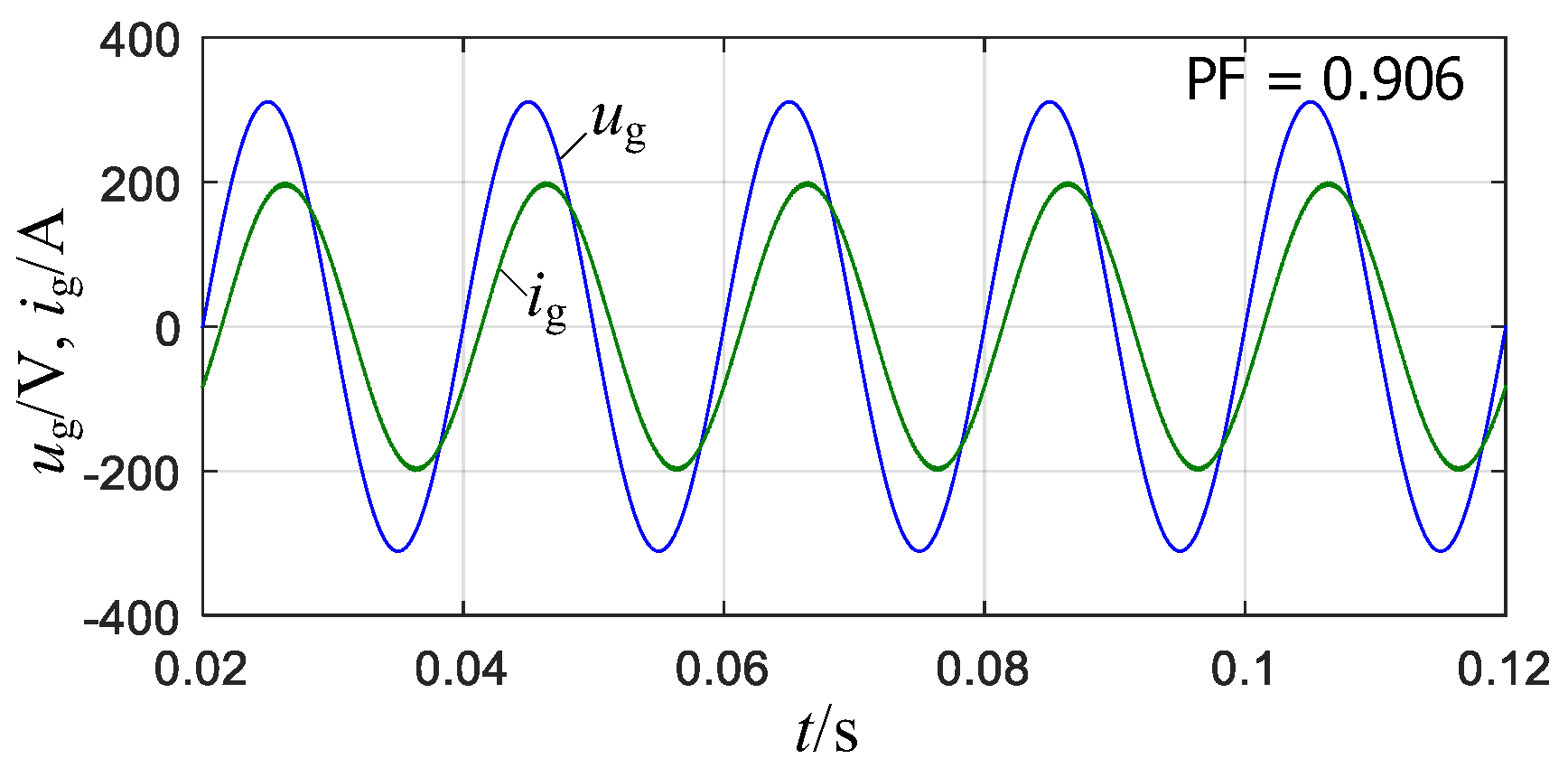
If α + β_f ≠ 2, the system is stable under the grid current feedback; the capacitor current feedback is avoided. Under PI control, a large K_i should be chosen to reduce the steady-state error of i_g, but the PM decreases significantly.

(3)

A PI^λ regulator can also make the system stable, but there is a contradiction between T_fo and PM.

(4)

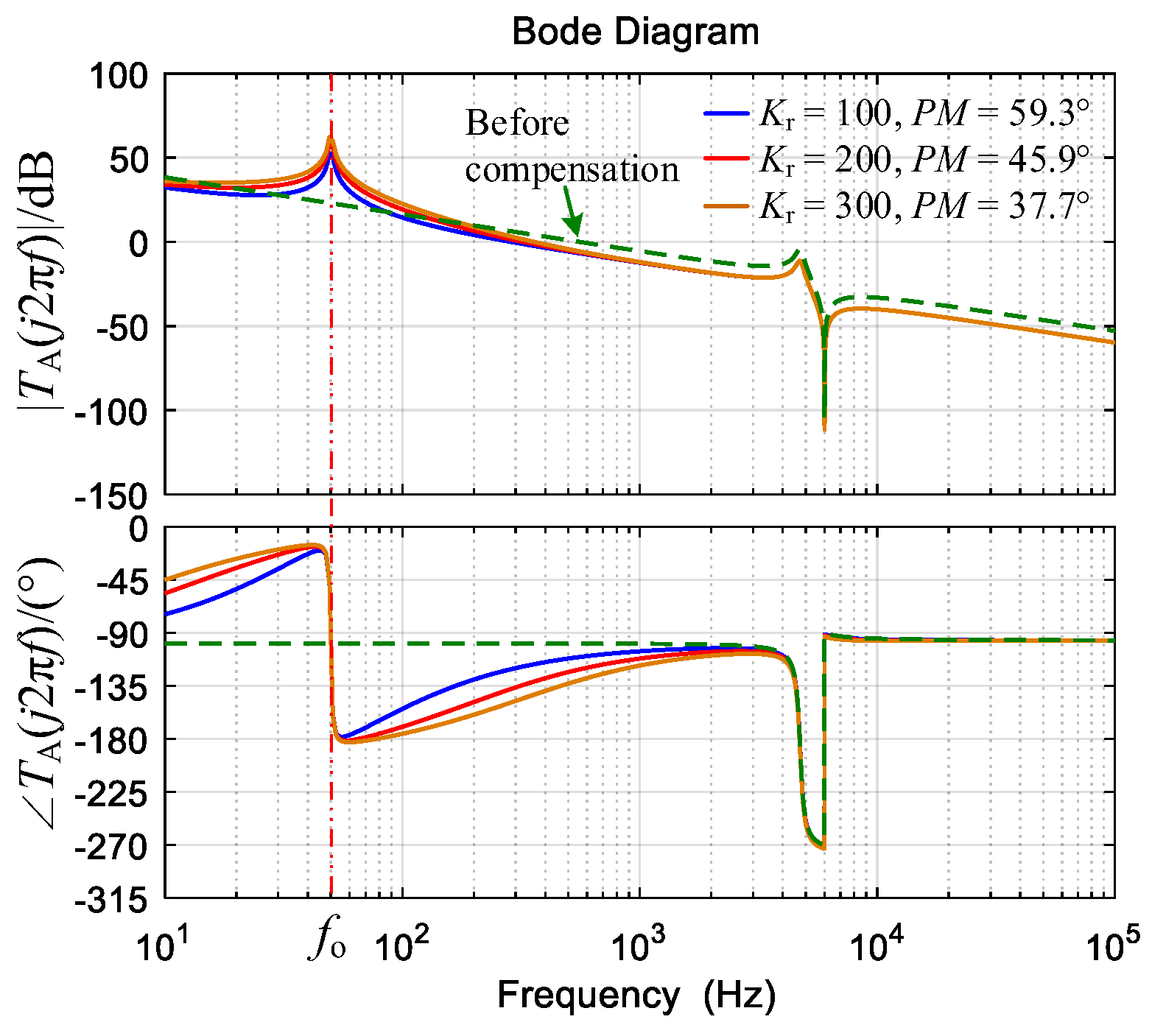
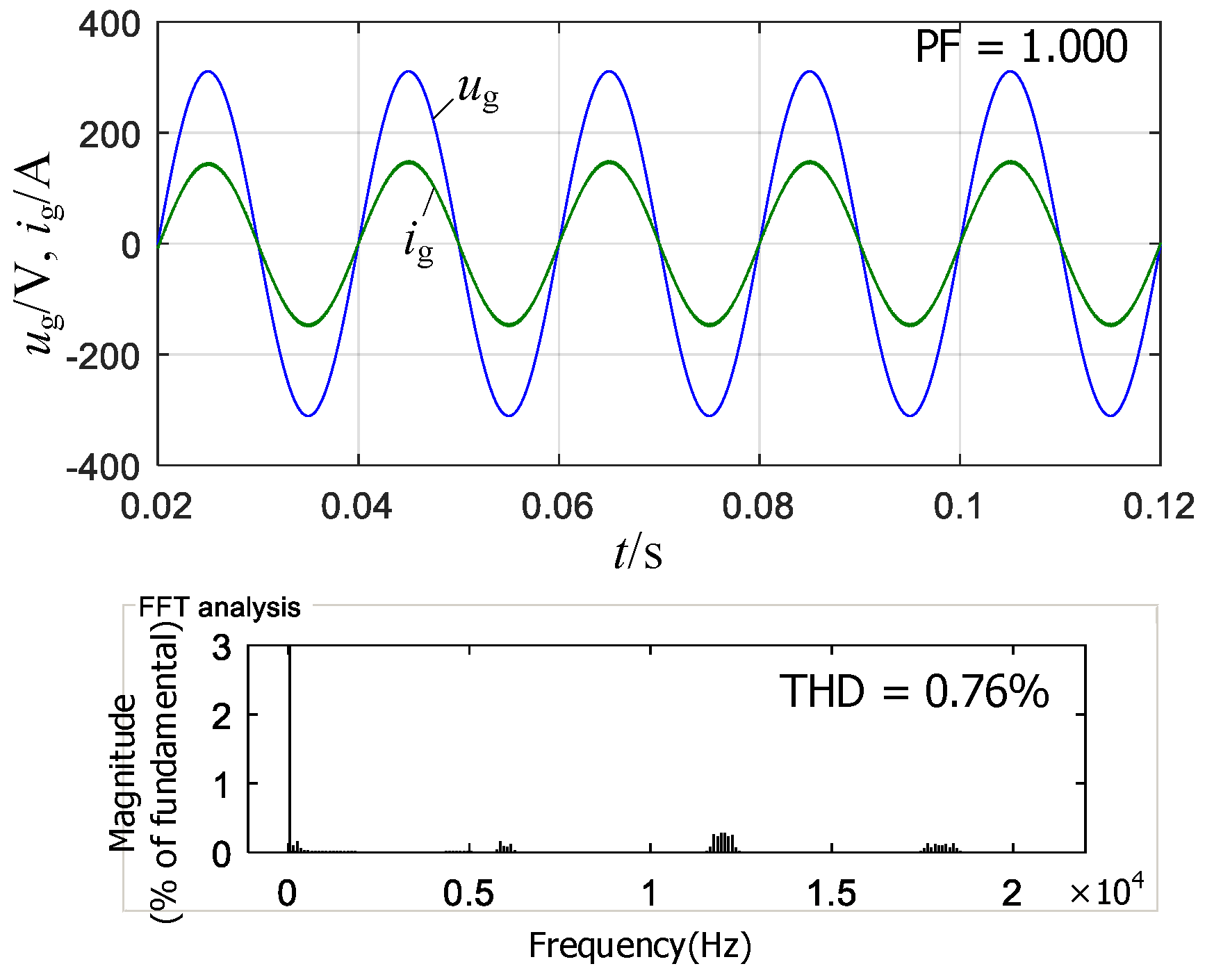
A PR regulator can simultaneously obtain good T_fo, GM, PM, and f_c, which is suitable for controlling the FOLLCL-type grid-tied inverter if α + β_f ≠ 2.

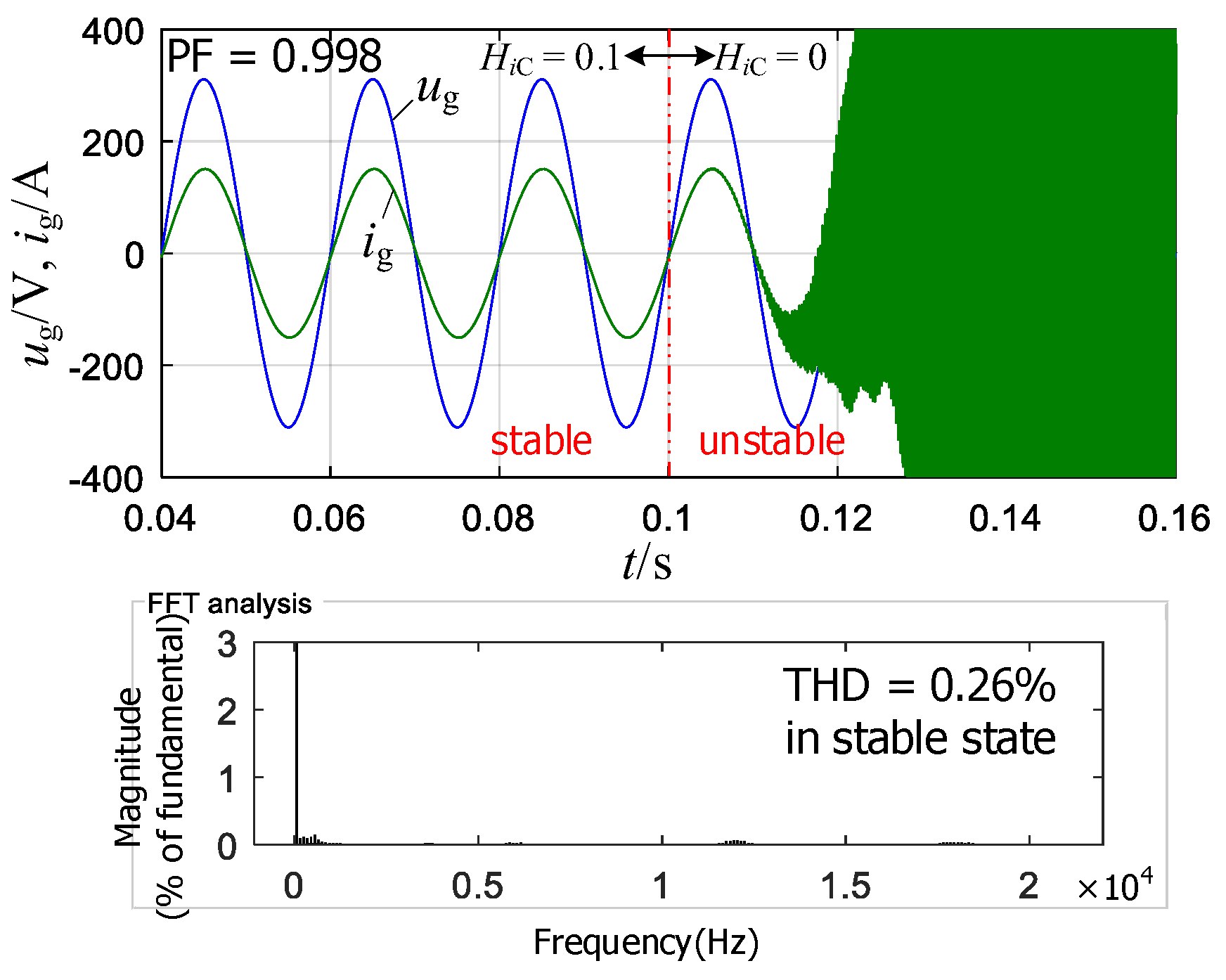
5. Simulations

To verify the characteristics of the FOLLCL-type grid-tied inverter and the effectiveness of the control methods, simulations are conducted with the parameters presented in Table 1 and Table 2. In each simulation, the reference grid current $i_g^{*}$ is set to 50sin(ωt) A; i_g is magnified three times for observation in the waveform diagram. The fractional-order inductors and capacitor are equivalent to the fractance circuit using the Oustaloup approximation method.In the first simulation, an IOLCL-type grid-tied inverter is studied. As shown in Figure 16, a large amount of harmonics, which is mainly around 2f_s (6 kHz), exists in the grid current. The THD of i_g is 14.46%, which is not acceptable in the application. The result indicates that the LCL-type grid-tied inverter has little advantage in low-frequency applications.

In the second simulation, an FOLLCL-type grid-tied inverter with α + β_f = 2 and α_f + β_f = 2 (α = 1.1, α_f = 1.1, β_f = 0.9) under PI control is investigated. As shown in Figure 17, when the capacitor current feedback loop is effective before 0.1 s, the system is stable, the grid current has a very low THD (only 0.26%), and the power factor is high (0.998). The FOLLCL-type grid-tied inverter exhibits excellent harmonic suppression ability. However, instability arises after 0.1 s due to the removal of the capacitor current feedback loop, which causes positive resonance.

Moreover, an FOLLCL-type grid-tied inverter with α + β_f ≠ 2 and α_f + β_f = 2 (α = 1.1, α = 0.2, β_f = 0.8) is studied. The inverter is regulated by a PI controller; the control parameters are K_p = 0.45 and K_i = 2200, respectively. As with the analysis in Section 4 (case II), the capacitor current feedback is eliminated and H_ig = 0.05. As shown in Figure 18, the system is stable without active damping and the grid current is close to the ideal sine, which has a THD of 0.72%. However, to obtain a sufficient phase margin, K_i cannot be too large, resulting in a certain phase error between u_g and i_g; the power factor is only 0.989.

Furthermore, in Figure 19, the simulation results of the FOLLCL-type grid-tied inverter with α + β_f ≠ 2 and α_f + β_f = 2 (α = 1.1, α_f = 1.2, β_f = 0.8) controlled by a PI^λ regulator are shown. According to the analysis in Section 4 and case III, when λ = 1.4 and K_i = 6000, although PM > 45°, the T_fo is very small, as can be seen in Figure 14. Therefore, as shown in Figure 19, both the amplitude error and phase error between $i_g^{*}$ and i_g are very large, and the power factor is only 0.906.

Finally, a PR regulator is used to control the FOLLCL-type grid-tied inverter with α + β_f ≠ 2 and α_f + β_f = 2 (α = 1.1, α_f = 1.2, β_f = 0.8). K_p = 0.45, ω_i = π, and K_r = 100 are the parameters of the regulator, and H_ig = 0.05. The results are shown in Figure 20. The grid current is in strict in-phase with the grid voltage; the power factor is 1. In addition, the amplitude error is close to 0. The results are consistent with the previous analysis in Section 4.

The above simulation results prove that the analyses in previous sections are correct and PR regulator is superior to PI and PI^λ regulators to control an FOLLCL-type grid-tied inverter with α + β_f ≠ 2.

6. Conclusions

In this paper, the fractional-order LLCL filter and the grid-tied inverter based on it are studied. By correctly selecting the orders of the components, the positive resonance can be suppressed and the negative resonance is reserved. Therefore, the passive or active damping can be avoided for the FOLLCL-type grid-tied inverter. Meanwhile, the switching-frequency harmonics in the grid current can be attenuated. For low-frequency applications, it is difficult for the PI controller and fractional-order PI controller to balance all performances simultaneously. PR controllers can guarantee good fundamental frequency loop gain, cut-off frequency, gain margin, and phase margin at the same time. The FOLLCL-type grid-tied inverter without active damping under PR control achieves excellent tracking accuracy and low grid current THD. Simulations are conducted to verify the correctness of the theoretical analyses.