The Sensitive Visualization and Generalized Fractional Solitons’ Construction for Regularized Long-Wave Governing Model
Abstract
:1. Introduction
2. Basic Preliminaries
2.1. Beta Derivative
2.2. M-Truncated Derivative
3. Application of the NAEM
Description of the NAEM
4. Fractional RLW Burgers Equation
Traveling Wave Solutions of Fractional RLW Equation
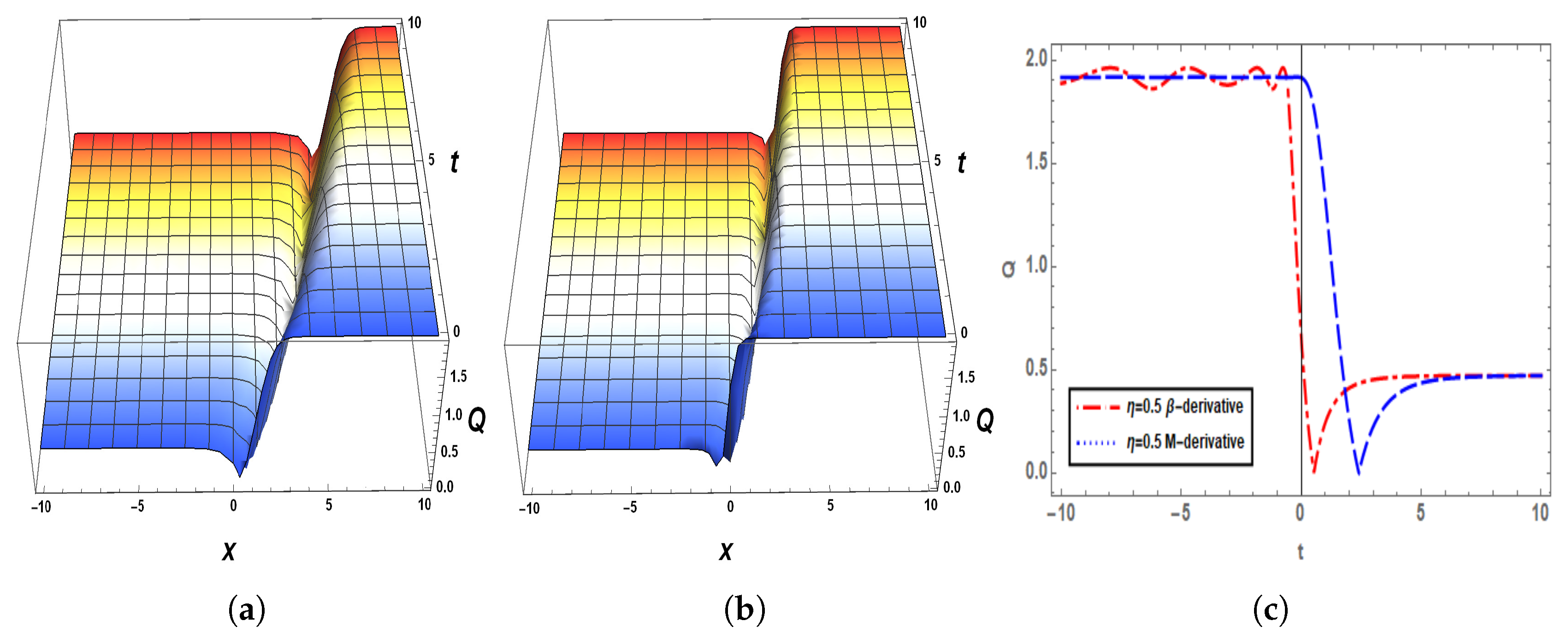
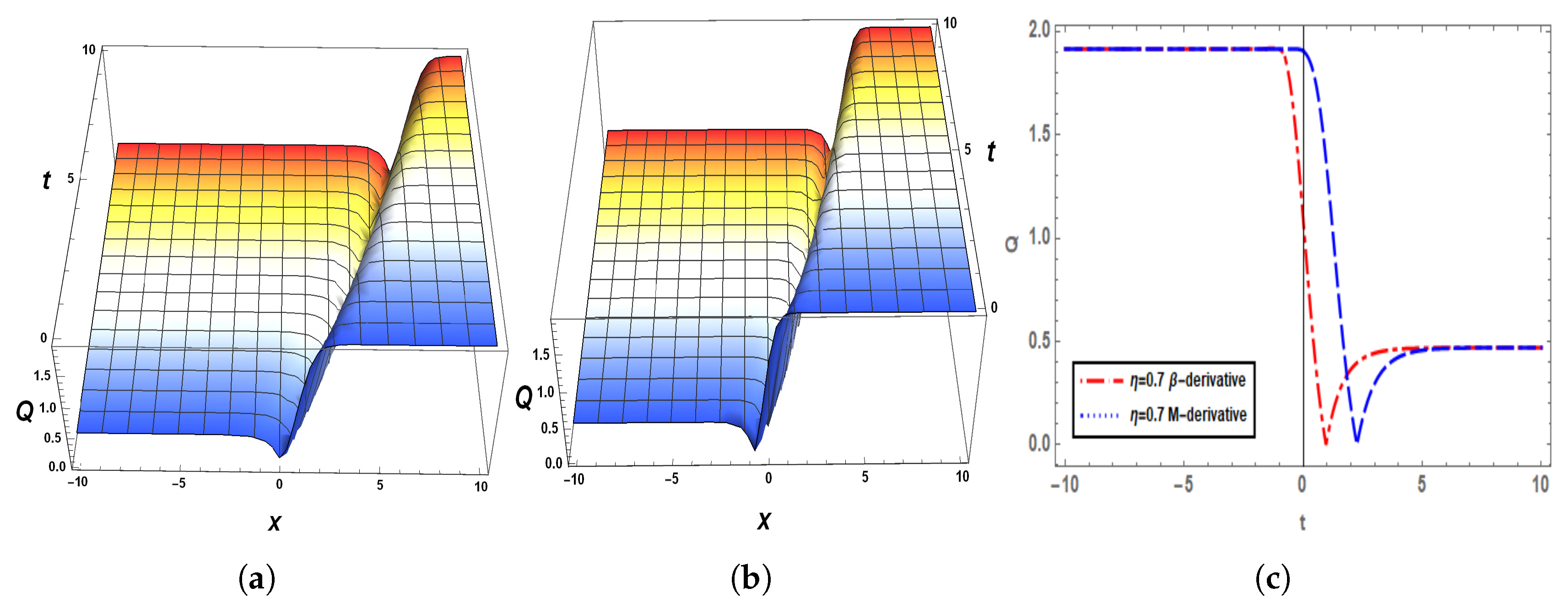
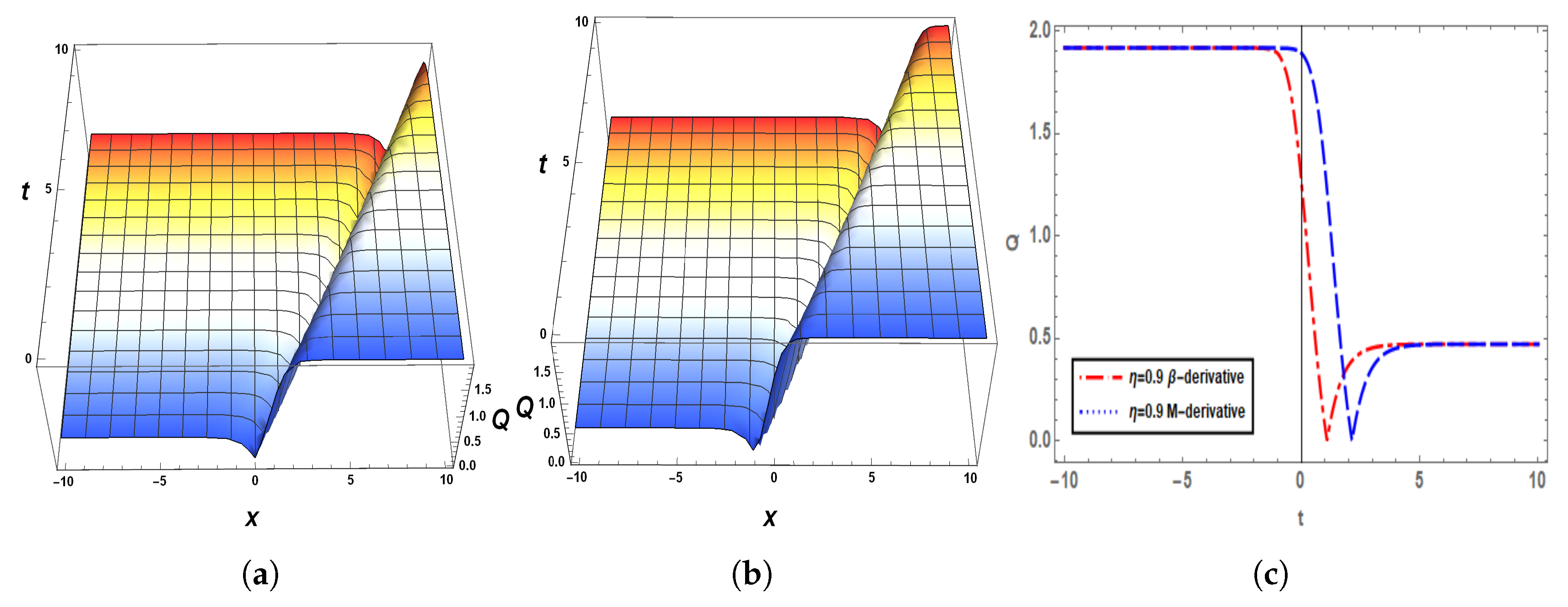
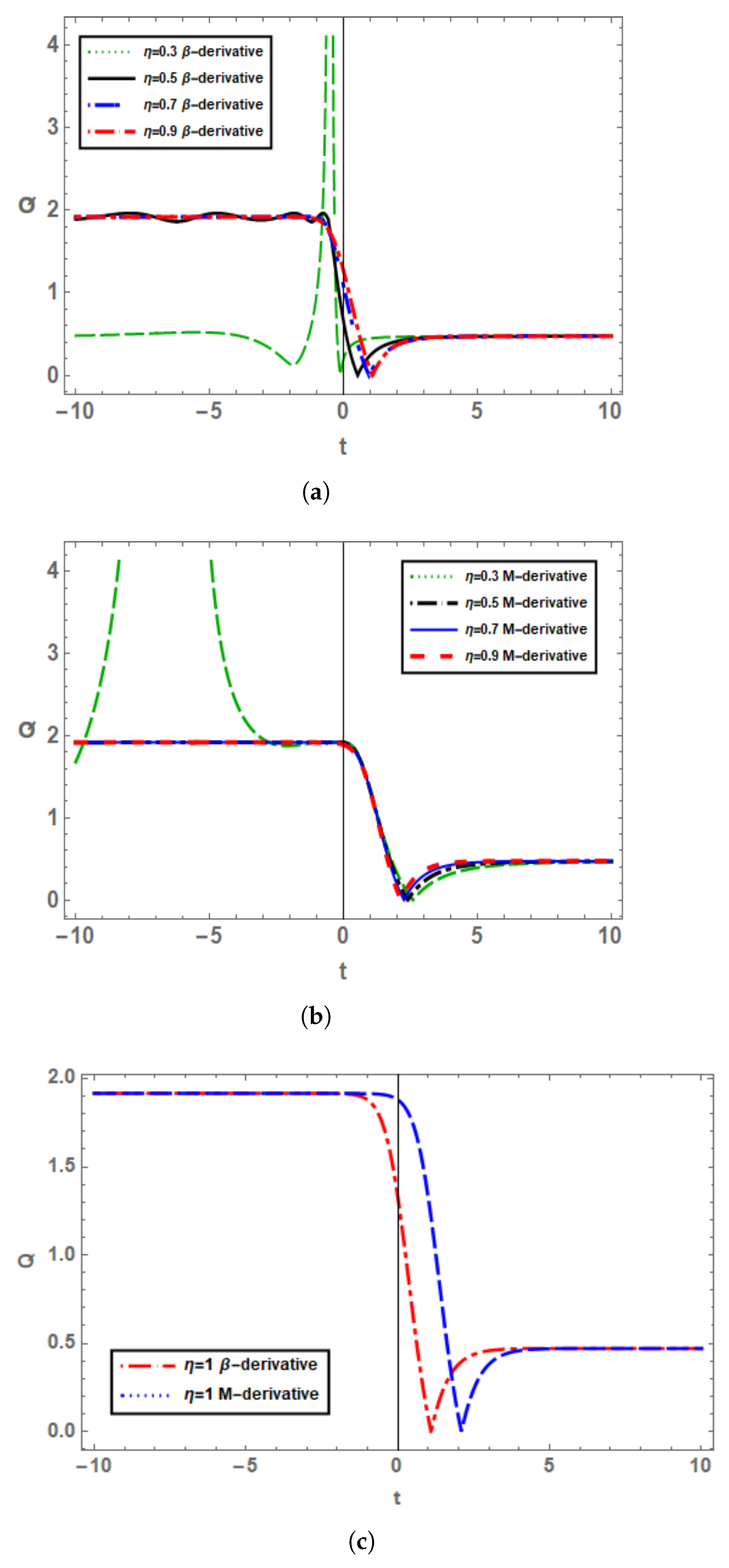
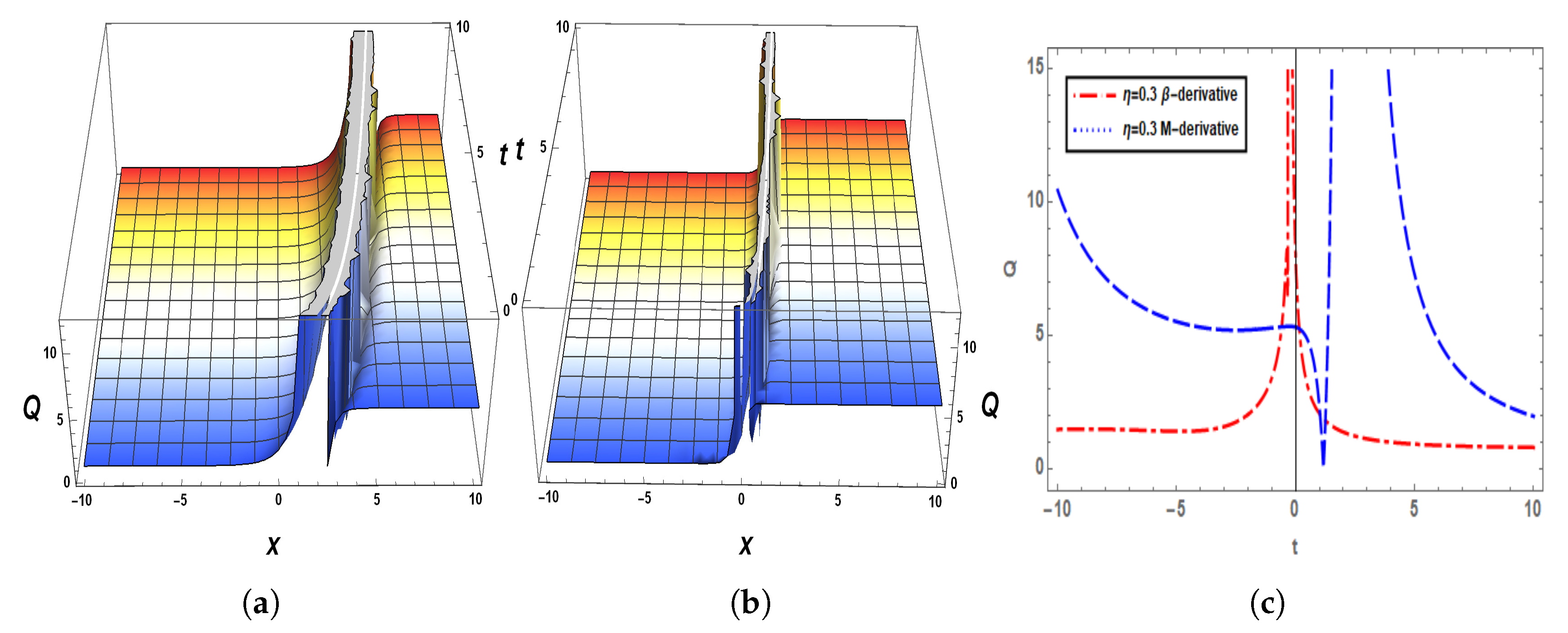
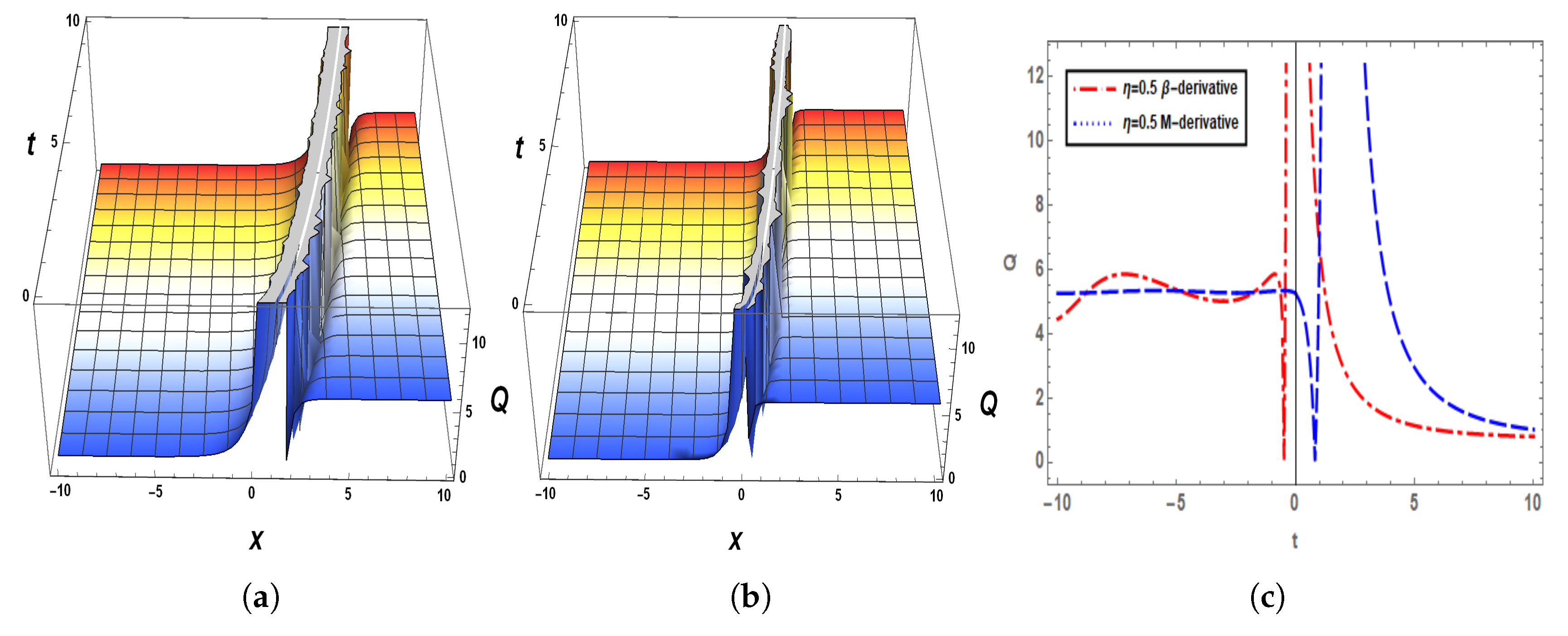
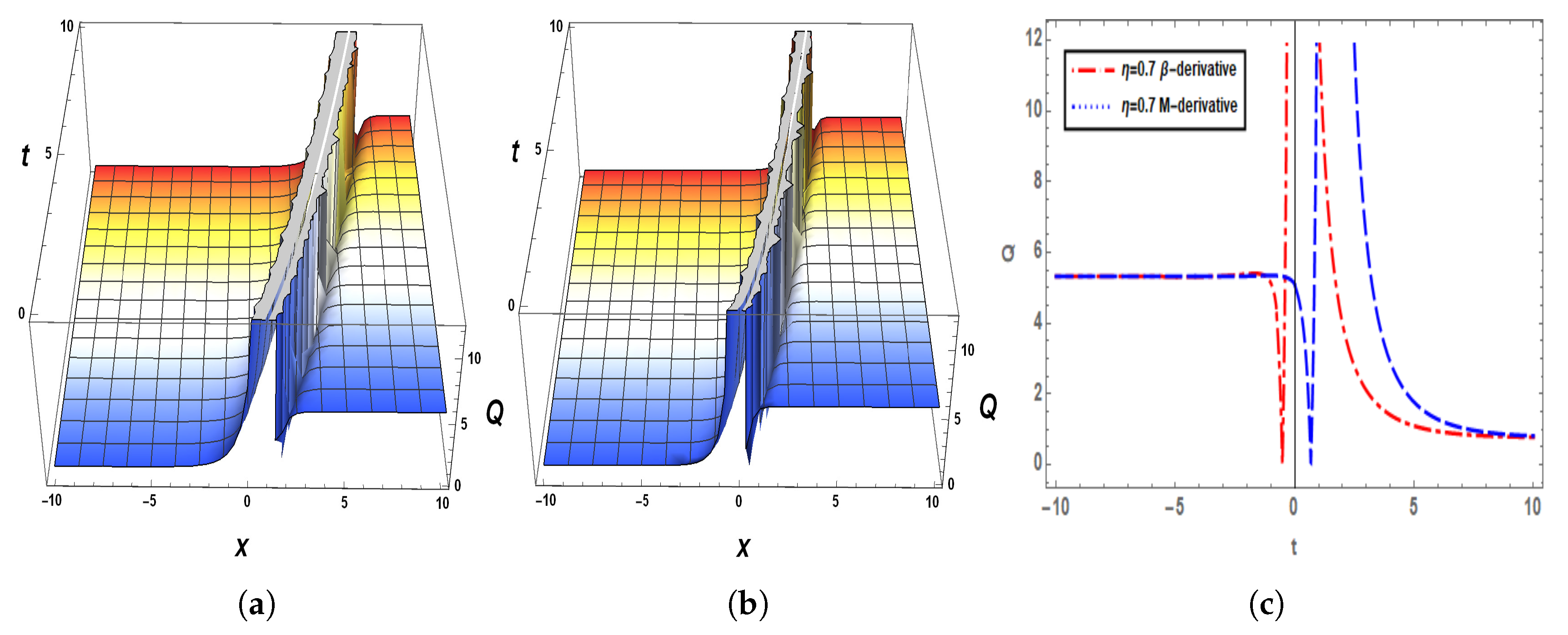
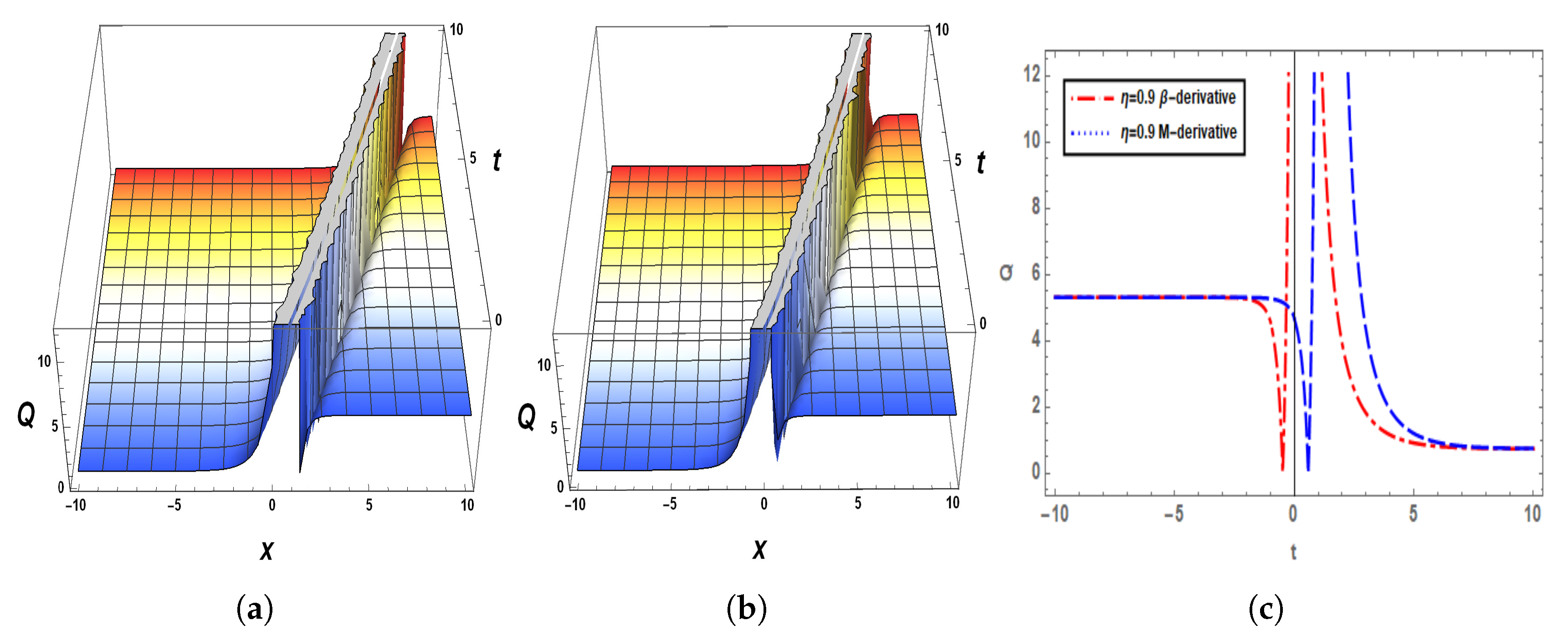
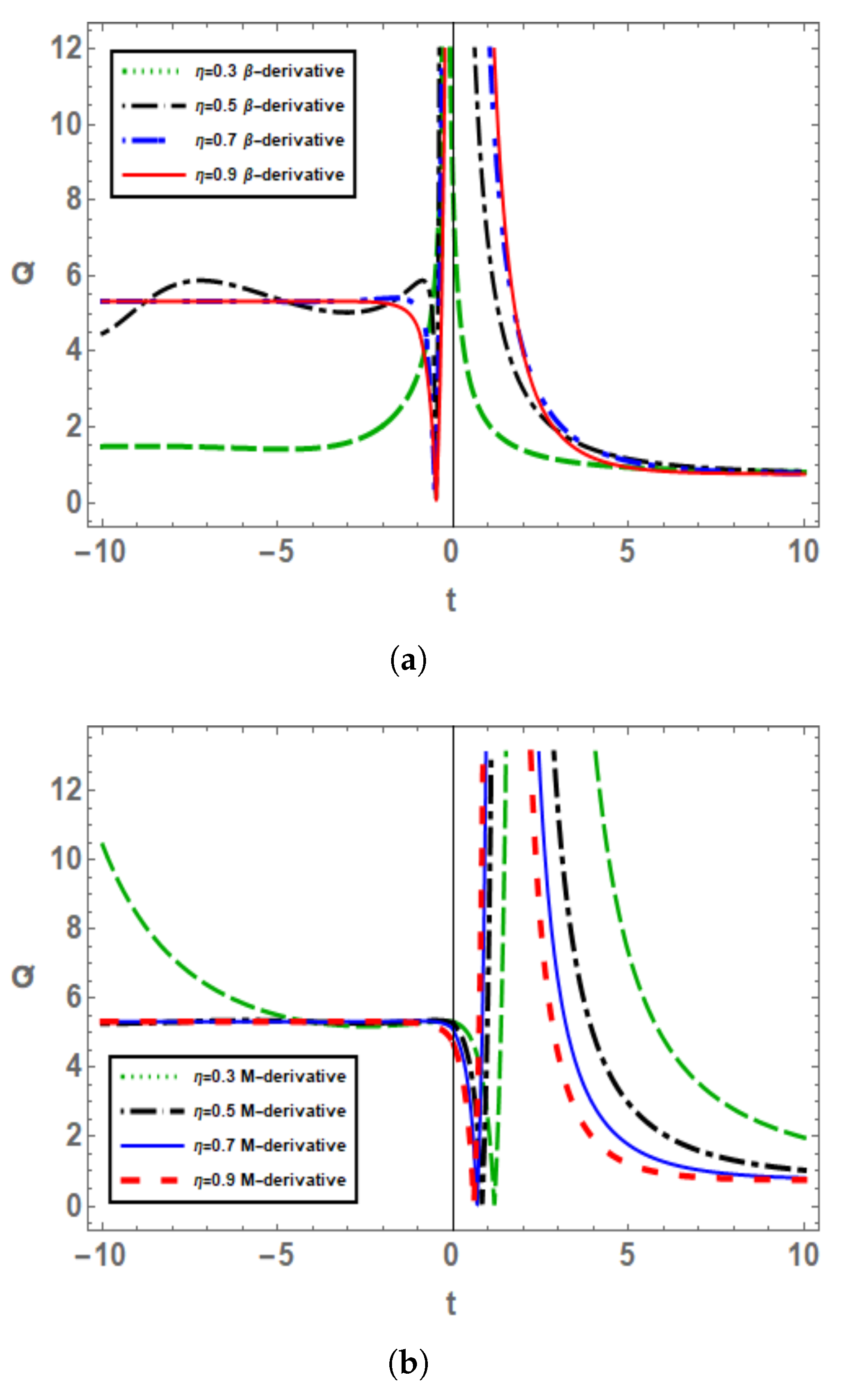
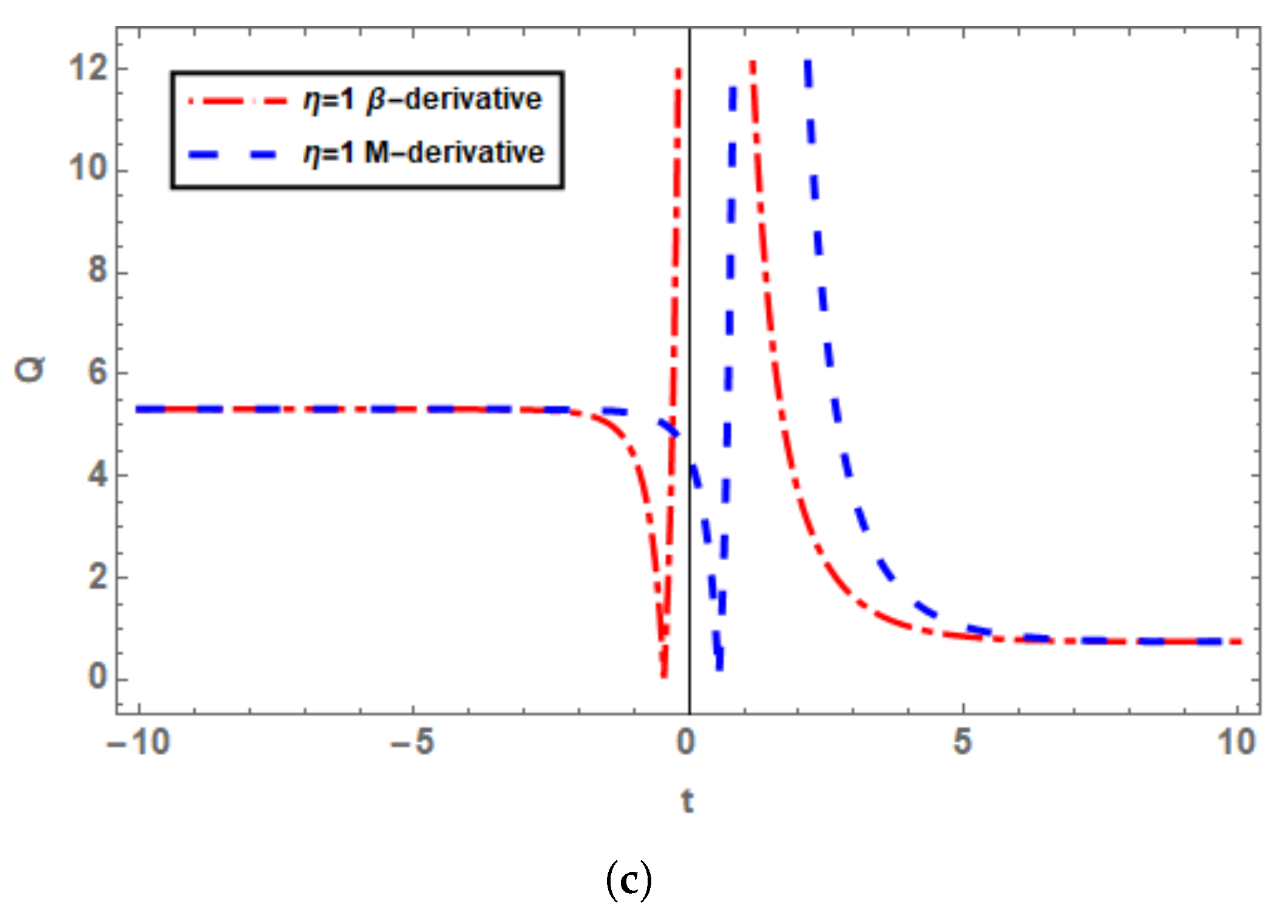
5. Graphical Analysis of the Solutions
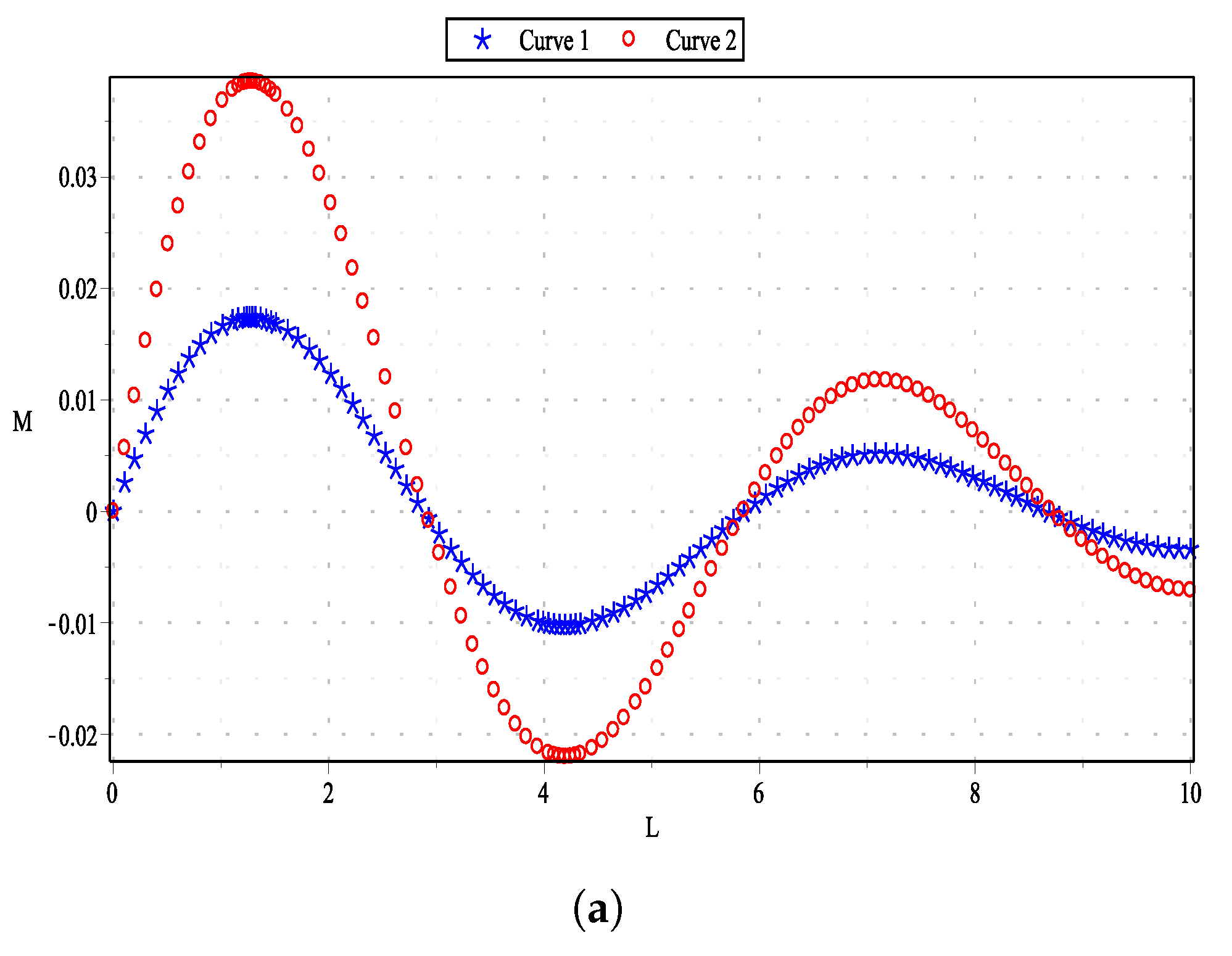
6. Sensitivity Analysis
7. Conclusions
8. Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yusuf, A.; Sulaiman, T.A.; Mirzazadeh, M.; Hosseini, K. M-truncated optical solitons to a nonlinear Schrödinger equation describing the pulse propagation through a two-mode optical fiber. Opt. Quantum Electron. 2021, 53, 1–17. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Karaca, Y.; Momani, S. New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term. Fractal Fract. 2022, 6, 724. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Peakon and solitary wave solutions for the modified Fornberg-Whitham equation using the simplest equation method. Int. J. Math. Comput. Sci. 2019, 14, 635–645. [Google Scholar]
- Sarwar, S.; Furati, K.; Arshad, M. Abundant wave solutions of conformable space-time fractional order fokas wave model arising in physical sciences. Alex. Eng. J. 2021, 60, 2687–2696. [Google Scholar] [CrossRef]
- Khodadad, F.S.; M-Alizamini, S.M.; Günay, B.; Akinyemi, L.; Rezazadeh, H.; Inc, M. Abundant optical solitons to the Sasa-Satsuma higher-order nonlinear Schrödinger equation. Opt. Quantum Electron. 2021, 53, 702. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Awrejcewicz, J.; Muhammad, T.; Baleanu, D. On soliton solutions of the fractional-order nonlinear model appears in physical sciences. AIMS Math. 2022, 7, 7421–7440. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Najafi, M.; Wazwaz, A.M. Conformable space-time fractional nonlinear (1+1)-dimensional Schrödinger-type models and their traveling wave solutions. Chaos Solitons Fractals 2021, 150, 111187. [Google Scholar] [CrossRef]
- Asghar, U.; Faridi, W.A.; Asjad, M.I.; Eldin, S.M. The Enhancement of Energy-Carrying Capacity in Liquid with Gas Bubbles, in Terms of Solitons. Symmetry 2022, 14, 2294. [Google Scholar] [CrossRef]
- Korpinar, Z.; Tchier, F.; Inç, M.; Ragoub, L.; Bayram, M. New soliton solutions of the fractional Regularized Long Wave Burgers equation by means of conformable derivative. Results Phys. 2019, 14, 102395. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Bright and dark optical solitons of the (2+1)-dimensional perturbed nonlinear Schrödinger equation in nonlinear optical fibers. Opt. Int. J. Light Electron Opt. 2021, 251, 168334. [Google Scholar] [CrossRef]
- Ding, C.C.; Gao, Y.T.; Deng, G.F.; Wang, D. Lax pair, conservation laws, Darboux transformation, breathers, and rogue waves for the coupled nonautonomous nonlinear SchrÖdinger system in an inhomogeneous plasma. Chaos Solitons Fractal 2020, 133, 109580. [Google Scholar] [CrossRef]
- Raza, N.; Jhangeer, A.; Rahman, R.U.; Butt, A.R.; Chu, Y.M. Sensitive visualization of the fractional Wazwaz-Benjamin-Bona-Mahony equation with fractional derivatives: A comparative analysis. Results Phys. 2021, 25, 104171. [Google Scholar] [CrossRef]
- Tariq, K.U.; Younis, M.; Rizvi, S.T.R.; Bulut, H. M-truncated fractional optical solitons and other periodic wave structures with Schrödinger-Hirota equation. Mod. Phys. Lett. B 2020, 34, 2050427. [Google Scholar] [CrossRef]
- Arshed, S.; Rahman, R.U.; Raza, N.; Khan, A.K.; Inc, M. A variety of fractional soliton solutions for three important coupled models arising in mathematical physics. Int. J. Mod. Phys. B 2021, 36, 2250002. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Bayram, M. On the optical soliton solutions of time-fractional Biswas–Arshed equation including the beta or M-truncated derivatives. Opt. Quantum Electron. 2023, 55, 186. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. Solitary Wave Solutions of the Fractional-Stochastic Quantum Zakharov–Kuznetsov Equation Arises in Quantum Magneto Plasma. Mathematics 2023, 11, 488. [Google Scholar] [CrossRef]
- Ismael, F.H.; Bulut, H.; Baskonus, H.M.; Gao, W. Dynamical behaviors to the coupled Schrödinger-Boussinesq system with the beta derivative. AIMS Math. 2021, 6, 7909–7928. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Ma, W.X.; Eldin, S.M.; Mehdi, K.B.; Faridi, W.A. New Explicit Propagating Solitary Waves Formation and Sensitive Visualization of the Dynamical System. Fractal Fract. 2023, 7, 71. [Google Scholar] [CrossRef]
- Ali, H.S.; Habib, M.A.; Miah, M.M.; Akbar, M.A. Solitary wave solutions to some nonlinear fractional evolution equations in mathematical physics. Heliyon 2020, 6, e03727. [Google Scholar] [CrossRef]
- Kumar, S.; Niwas, M.; Osman, M.S.; Abdou, M. Abundant different types of exact-soliton solutions to the (4+1)-dimensional Fokas and (2+1)-dimensional Breaking soliton equations. Commun. Theor. Phys. 2021, 73, 105007. [Google Scholar] [CrossRef]
- Esen, H.; Ozdemir, N.; Secer, A.; Bayram, M.; Sulaiman, T.A.; Yusuf, A. Solitary wave solutions of chiral nonlinear Schrödinger equations. Mod. Phys. Lett. B 2021, 35, 2150472. [Google Scholar] [CrossRef]
- Bekir, A.; Cevikel, A.C. New exact traveling wave solutions of nonlinear physical models. Chaos Solitons Fractals 2009, 41, 1733–1739. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Sulaiman, T.A.; Yusuf, A.; Bayram, M. Optical solitons of the (2+1)-dimensional Biswas–Milovic equation using modified extended tanh-function method. Optik 2021, 245, 167631. [Google Scholar] [CrossRef]
- Nadeem, M.; Jafari, H.; Akgül, A.; De la Sen, M. A Computational Scheme for the Numerical Results of Time-Fractional Degasperis–Procesi and Camassa–Holm Models. Symmetry 2022, 14, 2532. [Google Scholar] [CrossRef]
- Khan, A.; Ali, A.; Ahmad, S.; Saifullah, S.; Nonlaopon, K.; Akgül, A. Nonlinear Schrödinger equation under non-singular fractional operators: A computational study. Results Phys. 2022, 43, 106062. [Google Scholar] [CrossRef]
- Qureshi, Z.A.; Bilal, S.; Khan, U.; Akgül, A.; Sultana, M.; Botmart, T.; Zahran, H.Y.; Yahia, I.S. Mathematical analysis about the influence of Lorentz force and interfacial nanolayers on nanofluids flow through orthogonal porous surfaces with the injection of SWCNTs. Alex. Eng. J. 2022, 61, 12925–12941. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Pang, Y.; Akgül, A.; Baleanu, D. Dynamics of HIV-TB coinfection model using classical and Caputo piecewise operator: A dynamic approach with real data from South-East Asia, European and American regions. Chaos Solitons Fractals 2022, 165, 112879. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Alhejaili, W.; AL-Ghamdi, A.O.; El-Tantawy, S.A. Bright and dark modulated optical solitons for a (2+1)-dimensional optical Schrödinger system with third-order dispersion and nonlinearity. Optik 2023, 274, 170582. [Google Scholar] [CrossRef]
- Hussain, A.; Bano, S.; Khan, I.; Baleanu, D.; Nisar, K.S. Lie Symmetry Analysis, Explicit solutions and conservation laws of a spatially two-dimensional Burgers Huxley equation. Symmetry 2020, 12, 170. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z.; Wazwaz, A.M.; Wang, Z. A direct method for generating rogue wave solutions to the (3+1)-dimensional Korteweg-de Vries Benjamin-Bona-Mahony equation. Phys. Lett. A 2022, 449, 128355. [Google Scholar] [CrossRef]
- Akinyemi, L.; Mirzazadeh, M.; Hosseini, K. Solitons and other solutions of perturbed nonlinear Biswas–Milovic equation with Kudryashov’s law of refractive index. Nonlinear Anal. Model. Control 2022, 27, 1–7. [Google Scholar] [CrossRef]
- Wang, K.J. Variational principle and diverse wave structures of the modified Benjamin-Bona-Mahony equation arising in the optical illusions field. Axioms 2022, 11, 445. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Geng, L.L.; Yu, X.J. On fractional symmetry group scheme to the higher-dimensional space and time fractional dissipative Burgers equation. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250173–2251483. [Google Scholar] [CrossRef]
- Akbar, M.A.; Wazwaz, A.M.; Mahmud, F.; Baleanu, D.; Roy, R.; Barman, H.K.; Mahmoud, W.; Al Sharif, M.A.; Osman, M.S. Dynamical behavior of solitons of the perturbed nonlinear SchrÖdinger equation and microtubules through the generalized Kudryashov scheme. Results Phys. 2022, 43, 106079. [Google Scholar] [CrossRef]
- Siddique, I.; Jaradat, M.M.; Zafar, A.; Mehdi, K.B.; Osman, M.S. Exact traveling wave solutions for two prolific conformable M-Fractional differential equations via three diverse approaches. Results Phys. 2021, 28, 104557. [Google Scholar] [CrossRef]
- Ghayad, M.S.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Derivation of optical solitons and other solutions for nonlinear Schrödinger equation using modified extended direct algebraic method. Alex. Eng. J. 2023, 64, 801–811. [Google Scholar] [CrossRef]
- Ghanbari, B.; Baleanu, D. Applications of two novel techniques in finding optical soliton solutions of modified nonlinear Schrödinger equations. Results Phys. 2023, 44, 106171. [Google Scholar] [CrossRef]
- Sarhan, A.; Burqan, A.; Saadeh, R.; Al-Zhour, Z. Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burgers Equations Using Laplace Residual Power Series Technique. Fractal Fract. 2022, 6, 631. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Arshed, S.; Raza, N.; Butt, A.R.; Akgül, A. Exact solutions for Kraenkel-Manna-Merle model in saturated ferromagnetic materials using Beta-derivative. Phys. Scr. 2021, 96, 124018. [Google Scholar] [CrossRef]
- Riaz, M.B.; Jhangeer, A.; Awrejcewicz, J.; Baleanu, D.; Tahir, S. Fractional propagation of short light pulses in monomode optical fibers: Comparison of beta derivative and truncated M-fractional derivative. J. Comput. Nonlinear Dyn. 2022, 17, 031002. [Google Scholar] [CrossRef]
- Sousa, J.C.; Oliveira, E.C. A New Truncated M-Fractional Derivative Type Unifying Some Fractional Derivative Types with Classical Properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ur Rahman, R.; Faridi, W.A.; El-Rahman, M.A.; Taishiyeva, A.; Myrzakulov, R.; Az-Zo’bi, E.A. The Sensitive Visualization and Generalized Fractional Solitons’ Construction for Regularized Long-Wave Governing Model. Fractal Fract. 2023, 7, 136. https://doi.org/10.3390/fractalfract7020136
Ur Rahman R, Faridi WA, El-Rahman MA, Taishiyeva A, Myrzakulov R, Az-Zo’bi EA. The Sensitive Visualization and Generalized Fractional Solitons’ Construction for Regularized Long-Wave Governing Model. Fractal and Fractional. 2023; 7(2):136. https://doi.org/10.3390/fractalfract7020136
Chicago/Turabian StyleUr Rahman, Riaz, Waqas Ali Faridi, Magda Abd El-Rahman, Aigul Taishiyeva, Ratbay Myrzakulov, and Emad Ahmad Az-Zo’bi. 2023. "The Sensitive Visualization and Generalized Fractional Solitons’ Construction for Regularized Long-Wave Governing Model" Fractal and Fractional 7, no. 2: 136. https://doi.org/10.3390/fractalfract7020136
APA StyleUr Rahman, R., Faridi, W. A., El-Rahman, M. A., Taishiyeva, A., Myrzakulov, R., & Az-Zo’bi, E. A. (2023). The Sensitive Visualization and Generalized Fractional Solitons’ Construction for Regularized Long-Wave Governing Model. Fractal and Fractional, 7(2), 136. https://doi.org/10.3390/fractalfract7020136







