On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability
Abstract
1. Introduction
2. Preliminaries
3. Existence and Uniqueness
4. Stability Analysis
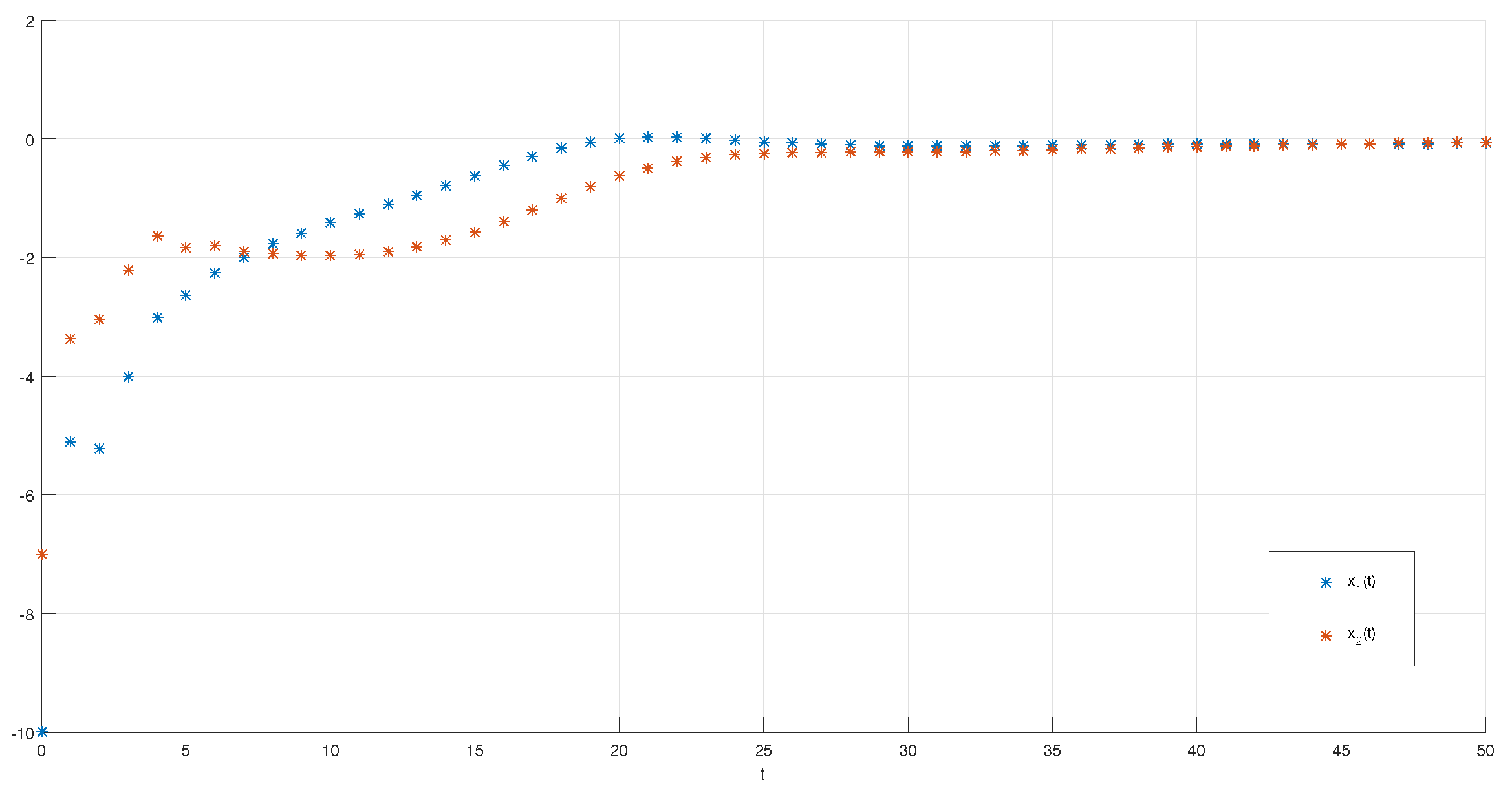
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Magin, R.L. Fractional Calculus in Bioengineering Begell House Publishers; Begell House, Inc.: Danbury, CT, USA, 2006. [Google Scholar]
- Podlubny, I. Fractional differential equations. Math. Sci. Eng. 1999, 198, 41–119. [Google Scholar]
- Magin, R.L.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. IFAC Proc. Vol. 2012, 45, 428–433. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. On fractional derivatives with exponential kernel and their discrete versions. Rep. Math. Phys. 2017, 80, 11–27. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Diaz, J.B.; Osler, T.J. Differences of fractional order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Granger, C.W.; Joyeux, R. An introduction to long-memory time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Gray, H.L.; Zhang, N.F. On a new definition of the fractional difference. Math. Comput. 1988, 50, 513–529. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Isaacs, G.L. Exponential laws for fractional differences. Math. Comput. 1980, 35, 933–936. [Google Scholar] [CrossRef]
- Khan, A.; Alshehri, H.M.; Abdeljawad, T.; Al-Mdallal, Q.M.; Khan, H. Stability analysis of fractional nabla difference COVID-19 model. Res. Phys. 2021, 22, 103888. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. A Transform method in discrete fractional calculus. Int. J. Differ. Equ. 2007, 2, 165–176. [Google Scholar]
- Atici, F.M.; Eloe, P.W. Fractional q-calculus on a time scale. J. Nonlinear Math. Phys. 2007, 14, 341–352. [Google Scholar] [CrossRef]
- Atici, F.; Eloe, P. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. Discrete fractional differences with nonsingular discrete Mittag–Leffler kernels. Adv. Differ. Equ. 2016, 2016, 1–18. [Google Scholar] [CrossRef]
- Abdeljawad, T. Fractional difference operators with discrete generalized Mittag–Leffler kernels. Chaos Solitons Fractals 2019, 126, 315–324. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 2016, 35, 69–87. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F. Constrained fractional variational problems of variable order. IEEE/CAA J. Autom. Sin. 2017, 4, 80–88. [Google Scholar] [CrossRef]
- Kaslik, E.; Rădulescu, I.R. Stability and bifurcations in fractional-order gene regulatory networks. Appl. Math. Comput. 2022, 421, 126916. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Gao, R.; Xu, C.; Shang, Y. New exploration on bifurcation in fractional-order genetic regulatory networks incorporating both type delays. Eur. Phys. J. Plus. 2022, 137, 1–31. [Google Scholar] [CrossRef]
- Liu, H.; Ma, L.; Wang, Z.; Liu, Y.; Alsaadi, F.E. An overview of stability analysis and state estimation for memristive neural networks. Neurocomputing 2020, 391, 1–12. [Google Scholar] [CrossRef]
- Mellah, M.; Ouannas, A.; Batiha, I.M. A General method for stabilizing the fractional-order discrete neural networks via linear control law. Nonlinear Stud. 2022, 29, 993–1002. [Google Scholar]
- Karoun, R.C.; Ouannas, A.; Horani, M.A.; Grassi, G. The Effect of Caputo Fractional Variable Difference Operator on a Discrete-Time Hopfield Neural Network with Non-Commensurate Order. Fractal Fract. 2022, 6, 575. [Google Scholar] [CrossRef]
- Abbes, A.; Ouannas, A.; Shawagfeh, N.; Khennaoui, A.A. Incommensurate Fractional Discrete Neural Network: Chaos and complexity. Eur. Phys. J. Plus 2022, 137, 1–15. [Google Scholar] [CrossRef]
- Gasri, A.; Ouannas, A.; Khennaoui, A.A.; Grassi, G.; Oussaeif, T.E.; Pham, V.T. Chaotic fractional discrete neural networks based on the Caputo h-difference operator: Stabilization and linear control laws for synchronization. Eur. Phys. J. Spec. Top. 2022, 231, 1–15. [Google Scholar] [CrossRef]
- Mellah, M.; Ouannas, A.; Khennaoui, A.A.; Grassi, G. Fractional Discrete Neural Networks with Different Dimensions: Coexistence of Complete Synchronization, Antiphase Synchronization and Full State Hybrid Projective Synchronization. Nonlinear Dyn. Sys. Theory 2021, 21, 410. [Google Scholar]
- Xu, Y.; Yu, J.; Li, W.; Feng, J. Global asymptotic stability of fractional-order competitive neural networks with multiple time-varying-delay links. Appl. Math. Comput. 2021, 389, 125498. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.G. New criteria for finite-time stability of fractional order memristor-based neural networks with time delays. Neurocomputing 2021, 421, 349–359. [Google Scholar] [CrossRef]
- Wu, Z. Multiple asymptotic stability of fractional-order quaternion-valued neural networks with time-varying delays. Neurocomputing 2021, 448, 301–312. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Existence and finite-time stability of discrete fractional-order complex-valued neural networks with time delays. Neural Netw. 2020, 123, 248–260. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Global Mittag–Leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw. 2020, 122, 382–394. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Huang, C.; Niezabitowski, M.; Bagdasar, O. Stability of discrete-time fractional-order time-delayed neural networks in complex field. Math. Meth. Appl. Sci. 2021, 44, 419–440. [Google Scholar] [CrossRef]
- Hioual, A.; Oussaeif, T.E.; Ouannas, A.; Grassi, G.; Batiha, I.M.; Momani, S. New results for the stability of fractional-order discrete-time neural networks. Alex. Eng. J. 2022, 61, 10359–10369. [Google Scholar] [CrossRef]
- Huang, L.L.; Park, J.H.; Wu, G.C.; Mo, Z.W. Variable-order fractional discrete-time recurrent neural networks. J. Comput. Appl. Math. 2020, 370, 112633. [Google Scholar] [CrossRef]
- Hioual, A.; Ouannas, A.; Grassi, G.; Oussaeif, T.E. Nonlinear nabla variable-order fractional discrete systems: Asymptotic stability and application to neural networks. J. Comput. Appl. Math. 2022, 423, 114939. [Google Scholar] [CrossRef]
- Hioual, A.; Ouannas, A.; Oussaeif, T.E.; Grassi, G.; Batiha, I.M.; Momani, S. On Variable-Order Fractional Discrete Neural Networks: Solvability and Stability. Fractal Fract. 2022, 6, 119. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Mert, R.; Torres, D.F. Variable order Mittag–Leffler fractional operators on isolated time scales and application to the calculus of variations. In Fractional Derivatives with Mittag–Leffler Kernel; Springer: Cham, Switzerland, 2019; pp. 35–47. [Google Scholar]
- Franco-Pérez, L.; Fernández-Anaya, G.; Quezada-Téllez, L.A. On stability of nonlinear nonautonomous discrete fractional Caputo systems. J. Math. Anal. Appl. 2020, 487, 124021. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almatroud, O.A.; Hioual, A.; Ouannas, A.; Sawalha, M.M.; Alshammari, S.; Alshammari, M. On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability. Fractal Fract. 2023, 7, 118. https://doi.org/10.3390/fractalfract7020118
Almatroud OA, Hioual A, Ouannas A, Sawalha MM, Alshammari S, Alshammari M. On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability. Fractal and Fractional. 2023; 7(2):118. https://doi.org/10.3390/fractalfract7020118
Chicago/Turabian StyleAlmatroud, Othman Abdullah, Amel Hioual, Adel Ouannas, Mohammed Mossa Sawalha, Saleh Alshammari, and Mohammad Alshammari. 2023. "On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability" Fractal and Fractional 7, no. 2: 118. https://doi.org/10.3390/fractalfract7020118
APA StyleAlmatroud, O. A., Hioual, A., Ouannas, A., Sawalha, M. M., Alshammari, S., & Alshammari, M. (2023). On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability. Fractal and Fractional, 7(2), 118. https://doi.org/10.3390/fractalfract7020118







