Stability Properties of Multi-Term Fractional-Differential Equations

Abstract

Necessary and sufficient stability and instability conditions are reviewed and extended for multi-term homogeneous linear fractional differential equations with Caputo derivatives and constant coefficients. A comprehensive review of the state of the art regarding the stability analysis of two-term and three-term fractional-order differential equations is provided, which is then extended to the case of four-term fractional-order differential equations. The stability and instability properties are characterized with respect to the coefficients of the multi-term fractional differential equations, leading to both fractional-order-dependent and fractional-order-independent characterizations. In the general case, fractional-order-independent stability and instability properties are described for fractional-order differential equations with an arbitrary number of fractional derivatives.

1. Introduction

Fractional-order differential equations have been extensively used in modelling real-world phenomena from a wide range of domains [1,2,3,4,5], considering the memory and hereditary properties that the fractional derivatives are provided with [1,5]. Two-term fractional differential equations describe the modelling of the motion of a rigid plate that is immersed in a viscous liquid, also known as the Bagley–Torvik equation [6], whereas the Basset equation [7] is also described using linear two-term fractional differential equation. Other examples worth mentioning are the equation of the inextendible pendulum [8] and the fractional harmonic oscillator [9,10], which are both described by multi-term fractional-order differential equations with three fractional derivatives of Caputo type.

The most well-known types of fractional derivatives, which are typically not equivalent, are the Grünwald–Letnikov derivative, the Riemann–Liouville derivative, and the Caputo derivative. Given that it only requires initial conditions defined in terms of integer-order derivatives, which represent well-understood characteristics of physical phenomena, the Caputo derivative seems to be more applicable to real-world problems.

The existence and uniqueness of solutions for multi-term fractional differential equations have been explored the past years [11,12,13]. Stability theory has been broadly explored as well. Two-term fractional-order differential equations have been investigated in terms of their stability properties. Refs. [14,15,16,17,18] studied the boundary-value problems for multi-term fractional-differential equations. The asymptotic behaviour of solutions of linear multi-order fractional differential systems are determined in Ref. [19], whereas Ref. [20] summarize the recent stability results of fractional differential equations, most of them in comparison to their classical integer-order counterparts.

The stability of linear systems of fractional-order differential equations is also considered in Ref. [21], where the fractional orders are proportional and transformations form the physical plane to the fractional-domain is discussed. Moreover, recent results [22] generalize the formulation, the existence of the solution, and provide stability properties for multi-term systems of fractional-order differential equations. Some stability theorems are also obtained in Ref. [23] for both systems of fractional differential equations with multi-order and for multi-term fractional differential equations.

The purpose of this paper is to investigate multi-term fractional-order equations in terms of their stability and instability properties, both with respect to the roots of the corresponding characteristic equations and with respect to the coefficients of the considered equations. Moreover, we obtain sufficient conditions for the asymptotic stability and instability of the fractional-order differential equation, independent of the choice of the considered fractional orders. Furthermore, we also determine the stability and instability conditions for multi-term fractional differential equations with four fractional-order derivatives of Caputo type, by extending the recent results obtained for multi-term fractional-order equations with three derivatives [24], considering the analogy of the corresponding characteristic equations.

The structure of this paper is as follows. The preliminaries regarding basic definitions in fractional calculus are included in Section 2. The main results obtained for fractional-order differential equations with an arbitrary number of derivatives, as well as fractional-order-independent stability and instability results, are provided in Section 3. As a particular case, we recall the main stability and instability conditions for two-term fractional differential equations described in Section 4. These are followed by an overview of the main results recently obtained in the case of three-term fractional-order differential equations, which are listed in Section 5. The next section aims to present and prove the main novel results of this work, by extending the stability and instability conditions to the case of multi-term fractional differential equations with four derivatives of Caputo type, in Section 6. Both fractional-order dependent and independent stability and instability conditions are obtained. The conclusions are drawn in Section 7.

2. Preliminaries

Definition 1. 

The Caputo fractional differential operator of order $q>0$ is defined as

$${}^c{D}^{q}x\left(t\right):=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\Gamma (n-q)}}{\int }_0^t{\displaystyle \frac{x^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{q+1-n}}}d\tau ,}\hfill & \mathrm{if}n-1<q<n\hfill \\ {\displaystyle \frac{d^{n}x\left(t\right)}{d{t}^n}},\hfill & \mathrm{if}q=n\hfill \end{array}\right.,$$

where $n\in \mathbb{N}$ and the Gamma function is ${\displaystyle \Gamma \left(z\right)={\int }_0^{\infty }{y}^{z-1}{e}^{-y}dy}$, for $\Re \left(z\right)>0$.

The Laplace transform of the Caputo derivative or an arbitrary fractional order q is given as in Ref. [12]:

Proposition 1. 

The Laplace transform for the fractional-order Caputo derivative of order $q\in (n-1,n]$, $n\in {\mathbb{N}}^{*}$, of a function x is:

$$\mathcal{L}{(}^c{D}^{q}x)\left(s\right)=s^{q}X\left(s\right)-\sum _{k=0}^{n-1}{s}^{q-k-1}{x}^{\left(k\right)}\left(0\right),$$

where $X\left(s\right)$ represents the Laplace transform of the function x.

Consider the following general linear multi-term fractional differential equation

$${}^c{D}^{q}x\left(t\right)+\sum _{i=1}^{n-1}{\alpha }_i{}^c{D}^{q_i}x\left(t\right)+\beta x\left(t\right)=0$$

(1)

where ${\alpha }_i$, $\beta$ are real coefficients, for any $i\in \{1,2,\cdots ,n-1\}$, and $q,q_1,q_2,\cdots ,q_{n-1}$ are the fractional orders of the Caputo derivatives, such that $0<q_1<q_2<...<q_{n-1}<q\le 2$.

The linear homogeneous fractional-order differential Equation (1) can be seen as the linearization at the trivial equilibrium of a nonlinear autonomous fractional-order differential equation of the following form

$${}^c{D}^{q}x\left(t\right)=f(x\left(t\right){,}^c{D}^{q_1}x\left(t\right){,}^c{D}^{q_2}x\left(t\right),\cdots {,}^c{D}^{q_{n-1}}x\left(t\right))$$

(2)

where $f:{\mathbb{R}}^n\to \mathbb{R}$ is a continuously differentiable function such that $f(0,0,\cdots ,0)=0$.

The initial condition associated to Equation (1) is either

i.

$x_i=x\left(0\right)=x_0\in \mathbb{R}$, if $q\in (0,1]$, or

ii.

$x_i=(x\left(0\right),x^{\prime }\left(0\right))=(x_0,x_1)\in {\mathbb{R}}^2$ if $q\in (1,2]$.

In what follows, $\phi (t,x_i)$ represents the unique solution of (1), which satisfies one of the initial considered above. One can prove the existence and uniqueness of the solution of the initial value problem associated to the equation (1) in a similar way to the case of fractional-order systems of differential equations [8,11]. As a matter of fact, we can express the solution of the linear constant coefficient fractional differential Equation (1) using the fractional Green’s function as presented in Ref. [12], or by employing the fractional meta-trigonometric approach in the commensurate case [25].

Henceforward, we consider a non-exponential asymptotic stability concept, named Mittag–Leffler stability [26], in particular $\mathcal{O}\left(t^{-q}\right)$-asymptotic stability, as it reflects the algebraic decay of the solution. This is justified by the fact that fractional derivatives have a memory effect and hereditary properties and therefore the asymptotic stability of the trivial solution of equation (1) is not of exponential type [15,27].

Definition 2. 

i. 

The trivial solution of (1) is called stable if for any $\epsilon >0$ there exists $\delta =\delta \left(\epsilon \right)>0$ such that for every ${\mathbf{x}}_0\in {\mathbb{R}}^n$ satisfying $\parallel {\mathbf{x}}_0\parallel <\delta$ we have $\parallel \phi (t,{\mathbf{x}}_0)\parallel \le \epsilon$ for any $t\ge 0$;

ii. 

The trivial solution of (1) is called asymptotically stable if it is stable and there exists $\rho >0$ such that $\underset{t\to \infty }{lim}\phi (t,{\mathbf{x}}_0)=0$ whenever $\parallel {\mathbf{x}}_0\parallel <\rho$;

iii. 

Let $q>0$. The trivial solution of (1) is called$\mathcal{O}\left(t^{-q}\right)$-asymptotically stable if it is stable and there exists $\rho >0$ such that for any $\parallel {\mathbf{x}}_0\parallel <\rho$ one has:

$$\parallel \phi (t,{\mathbf{x}}_0)\parallel =\mathcal{O}\left(t^{-q}\right)\mathrm{as}t\to \infty .$$

3. General Fractional-Order-Independent Stability and Instability Results

In what follows, we determine the characteristic equation associated to the multi-term fractional-order differential Equation (1), which we will analyse in order to obtain fractional-order-independent stability and instability results.

Applying the Laplace transform, Equation (1) becomes

$$\left(s^q+\sum _{i=1}^{n-1}{\alpha }_i{s}^{q_i}+\beta \right)X\left(s\right)=F\left(s\right),$$

where $X\left(s\right)$ represents the Laplace transform of the function x, $s^{q^{*}}$ represents the first branch of the complex power function [28], with $q^{*}\in \{q,q_1,q_2,\cdots ,q_{n-1}\}$ and $F\left(s\right)$ incorporates the initial conditions.

Thus, we obtain the characteristic equation

$$s^q+\sum _{i=1}^{n-1}{\alpha }_i{s}^{q_i}+\beta =0.$$

(3)

Our aim is to analyse the distribution of the roots of Equation (3). Therefore, we consider the complex valued function

$$\Delta (s;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)=s^q+\sum _{i=1}^{n-1}{\alpha }_i{s}^{q_i}+\beta .$$

The next result gives us the necessary and sufficient conditions regarding the asymptotic stability and instability of the trivial solution of Equation (1) with respect to the sign of the real parts of the roots of its associated characteristic in Equation (3). A similar result has been formulated for the case of three-term linear fractional-order differential equations [24].

Theorem 1. 

i. 

Equation (1) is $\mathcal{O}\left(t^{-q^{\prime }}\right)$-asymptotically stable if and only if all the roots of the characteristic function $\Delta (s;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)$ are in the open left half-plane ($\Re \left(s\right)<0$), where $q^{\prime }=min\{\left\{q_1\right\},\left\{q_2\right\},\cdots ,\left\{q_{n-1}\right\},\left\{q\right\}\}$, with $\left\{q^{*}\right\}=q^{*}-\lfloor q^{*}\rfloor$, $q^{*}\in \{q_1,q_2,\cdots ,q_{n-1},q\}$;

ii. 

If $\beta \ne 0$ and the characteristic function $\Delta (s;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)$ has at least one root in the open right half-plane ($\Re \left(s\right)>0$), and Equation (1) is unstable.

In what follows, let us consider the set

$$D=\{(q_1,q_2,\cdots ,q_{n-1},q)\in {\mathbb{R}}^n:0<q_1<q_2<...<q_{n-1}<q\le 2\}.$$

The following lemma provides a sufficient condition for the instability of the Equation (1) with respect to its coefficients, regardless of the fractional orders $(q_1,q_2,\cdots ,q_{n-1},q)\in D$.

Lemma 1. 

If $\beta <0$ or ${\alpha }_1+{\alpha }_2+...+{\alpha }_{n-1}+\beta +1\le 0$, the trivial solution of Equation (1) is unstable, regardless of the fractional orders $q_1$, $q_2$, ..., $q_{n-1}$ and q.

Proof. 

If ${\alpha }_1+{\alpha }_2+...+{\alpha }_{n-1}+\beta +1\le 0$ we have that

$$\Delta (1;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)=1+{\alpha }_1+{\alpha }_2+...+{\alpha }_{n-1}+\beta \le 0.$$

For $\beta <0$, it is obvious that

$$\Delta (0;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)=\beta <0.$$

On the other hand, we notice that

$$\Delta (s;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)\to \infty \mathrm{for}s\to \infty .$$

Hence, for both cases the function $s\mapsto \Delta (s;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)$ has at least one strictly positive real root. Therefore, Equation (1) is unstable, regardless of the fractional orders $q_1$, $q_2$,..., $q_{n-1}$ and q. □

In what follows, we only consider the case $\beta >0$, as we have previously seen in Lemma 1 that if $\beta <0$, the Equation (1) is unstable, regardless of the fractional orders $(q_1,q_2,\cdots ,q_{n-1},q)\in D$. Therefore, we can state the following result, which provides a sufficient condition for the asymptotic stability of the trivial solution of Equation (1), regardless of its fractional orders.

Lemma 2. 

If ${\alpha }_i>0$, $i\in \{1,2,\cdots ,n-1\}$ and $\beta >0$, the trivial solution of Equation (1) is asymptotically stable, for any fractional orders $q_1$, $q_2$, ..., $q_{n-1}$ and q.

Proof. 

Let ${\alpha }_i>0$, $i\in \{1,2,\cdots ,n-1\}$ and $\beta >0$. Assuming the contrary, that there exists $s_0\ne 0$ a root of the characteristic function $\Delta (s;{\alpha }_1,\cdots ,{\alpha }_{n-1},\beta ,q_1,\cdots ,q_{n-1},q)$ such that $\Re \left(s_0\right)\ge 0$, we have

$$s_0^q+{\alpha }_1{s}_0^{q_1}+{\alpha }_2{s}_0^{q_2}+...+{\alpha }_{n-1}{s}_0^{q_{n-1}}+\beta =0.$$

Multiplying this previous relation by $s_0^{-\frac{q}{2}}$, it follows that

$$s_0^{\frac{q}{2}}+{\alpha }_1{s}_0^{q_1-\frac{q}{2}}+{\alpha }_2{s}_0^{q_2-\frac{q}{2}}+...+{\alpha }_{n-1}{s}_0^{q_{n-1}-\frac{q}{2}}+\beta s_0^{-\frac{q}{2}}=0.$$

Since $\pm \frac{q}{2}\in [-1,1]$ and $q_1-\frac{q}{2},q_2-\frac{q}{2},\cdots ,q_{n-1}-\frac{q}{2}\in (-1,1)$, we have that the real parts of each term from the left-hand side of the equality from above are positive. Therefore,

$$\Re \left(s_0^{\frac{q}{2}}+{\alpha }_1{s}_0^{q_1-\frac{q}{2}}+{\alpha }_2{s}_0^{q_2-\frac{q}{2}}+...+{\alpha }_{n-1}{s}_0^{q_{n-1}-\frac{q}{2}}+\beta s_0^{-\frac{q}{2}}\right)>0,$$

which is a contradiction.

Thus, $\Re \left(s\right)<0$, for any s being a root of the characteristic function $\Delta$, which shows that the trivial solution of Equation (1) is asymptotically stable, regardless of the fractional orders $q_1$, $q_2$,..., $q_{n-1}$ and q. □

It is important to emphasize that Lemmas 1 and 2 generalize the recent results from Ref. [24], which strictly refer to three-term fractional differential equations. The techniques employed in the proofs presented above allow for a simple generalization to the multi-term case, leading to easily verifiable inequalities involving the constant coefficients, which guarantee the instability/stability of the trivial solution of Equation (1), for any choice of the fractional orders of the Caputo derivatives.

In the following sections, we explore fractional-order-dependent stability and instability conditions for particular cases of multi-term fractional-order differential equations. We will first review some results from the literature for the cases of two-term and three-term fractional-order differential equations, followed by an extension of the results to four-term fractional differential equations

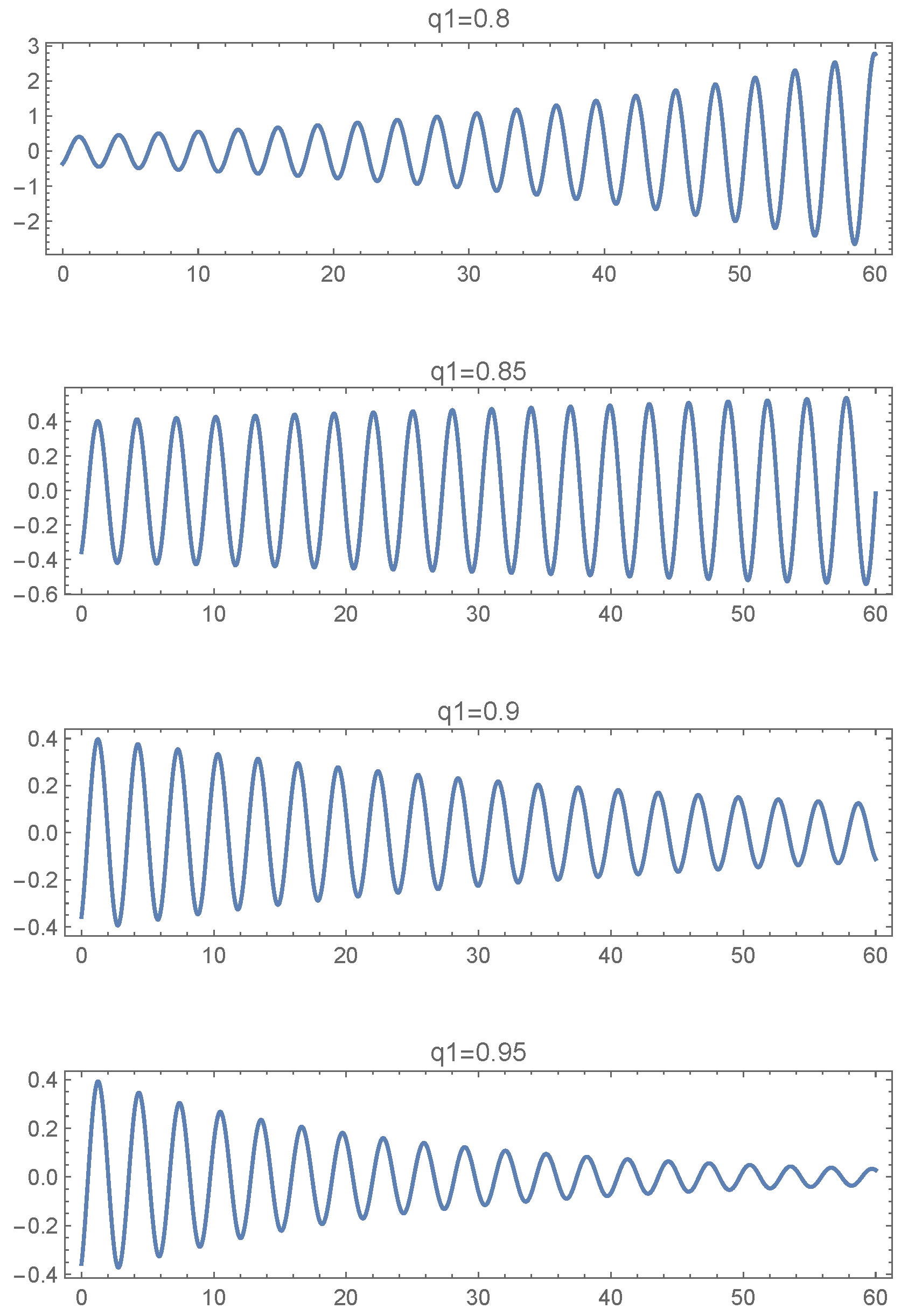
4. Two-Term Fractional-Order Differential Equations

In this section, we review some stability properties of two-term fractional differential equations similar to those obtained by Čermák and Kisela [15], as a particular case of the multi-term fractional differential Equation (1).

Consider the following two-term fractional differential equation

$${}^c{D}^{q}x\left(t\right)+{\alpha }^c{D}^{q_1}x\left(t\right)+\beta x\left(t\right)=0,$$

(4)

where the coefficients $\alpha$ and $\beta$ are the real numbers and $q_1$ and q are the fractional orders of the Caputo derivatives, with $0<q_1<q\le 2$.

The associated characteristic equation for the two-term fractional differential Equation (4) is

$$s^q+\alpha s^{q_1}+\beta =0.$$

(5)

In what follows, we give a characterisation of the stability properties of Equation (4), which may be obtained as a particular case of Theorem 2. For the proof of this theorem we refer to Ref. [24].

Proposition 2. 

Let $0<q_1<q\le 2$. For $\beta >0$, let

$${\alpha }^{*}=-{\displaystyle \frac{{\beta }^{1-\frac{q_1}{q}}sin\frac{q\pi }{2}}{{\left(sin\frac{q_1\pi }{2}\right)}^{\frac{q_1}{q}}{\left(sin\frac{(q-q_1)\pi }{2}\right)}^{1-\frac{q_1}{q}}}}.$$

Then

i. 

If $\beta <0$ or $\alpha +\beta +1\le 0$ the trivial solution of Equation (4) is unstable, regardless of the fractional orders $q_1$ and q;

ii. 

If $\beta >0$ and $\alpha >{\alpha }^{*}$, the trivial solution of Equation (4) is asymptotically stable;

iii. 

If $\beta >0$ and $\alpha <{\alpha }^{*}$, the trivial solution of Equation (4) is unstable.

Remark 1. 

The previous proposition gives us sufficient conditions of instability of the considered equation regardless of the fractional orders $q_1$ and q and sufficient conditions of both asymptotic stability and instability dependent of the fractional orders of Equation (4). We notice that the results obtained are in accordance to the conditions of stability and instability determined by Cermak and Kisela in Ref. [15], where particular rational fractional orders were considered.

In what follows, we will recall some well-known examples of two-term fractional-order differential equations, which were comprehensively described in Ref. [24].

Example 1. 

The Basset equation is described by the following linear fractional-order differential equation

$$\dot{x}\left(t\right)+{\alpha }^c{D}^{q_1}x\left(t\right)+\beta x\left(t\right)=0,0<q_1<1,$$

(6)

which originates in the study of the generalised Basset force ensuing when a spherical object is submerged in an incompressible viscous fluid [7].

It is clear that the characteristic equation associated to (6) is

$$s+\alpha s^{q_1}+\beta =0.$$

Based on the theoretical results previously mentioned we notice that:

• If $\beta <0$, the trivial solution of (6) is unstable, regardless of the fractional order $q_1$;
• If $\alpha >0$ and $\beta >0$, the trivial solution of Equation (6) is asymptotically stable, for any fractional order $q_1$;
• If $\alpha \le 0$ and $\beta >0$, the stability of the linear Equation (6) depends on the fractional order $q_1\in (0,1)$; more precisely, the trivial solution of Equation (6) is $\mathcal{O}\left(t^{-q_1}\right)$-asymptotically stable if and only if

  $$\alpha >{\alpha }^{*}(\beta ,q_1)=-{\beta }^{1-q_1}{\left(cot\frac{q_1\pi }{2}\right)}^{q_1}sec\frac{q_1\pi }{2}.$$

Example 2. 

The Bagley–Torvik equation is described by following fractional-order differential equation:

$$x^{″}\left(t\right)+{\alpha }^c{D}^{q_1}x\left(t\right)+\beta x\left(t\right)=0,0<q_1<2$$

(7)

which arises when modelling the motion of a rigid plate that immerses in a viscous liquid [6].

The characteristic equation associated to Equation (7) is

$$s^2+\alpha s^{q_1}+\beta =0.$$

The critical value for the parameter α is ${\alpha }^{*}(\beta ,q_1)=0$, for any fractional order $q_1$ and any $\beta >0$. The trivial solution of Equation (7) will then be asymptotically stable of order $\mathcal{O}\left(t^{-\left\{q_1\right\}}\right)$ if and only if $\alpha >0$ and $\beta >0$, which is in accordance to the results obtained in Ref. [29].

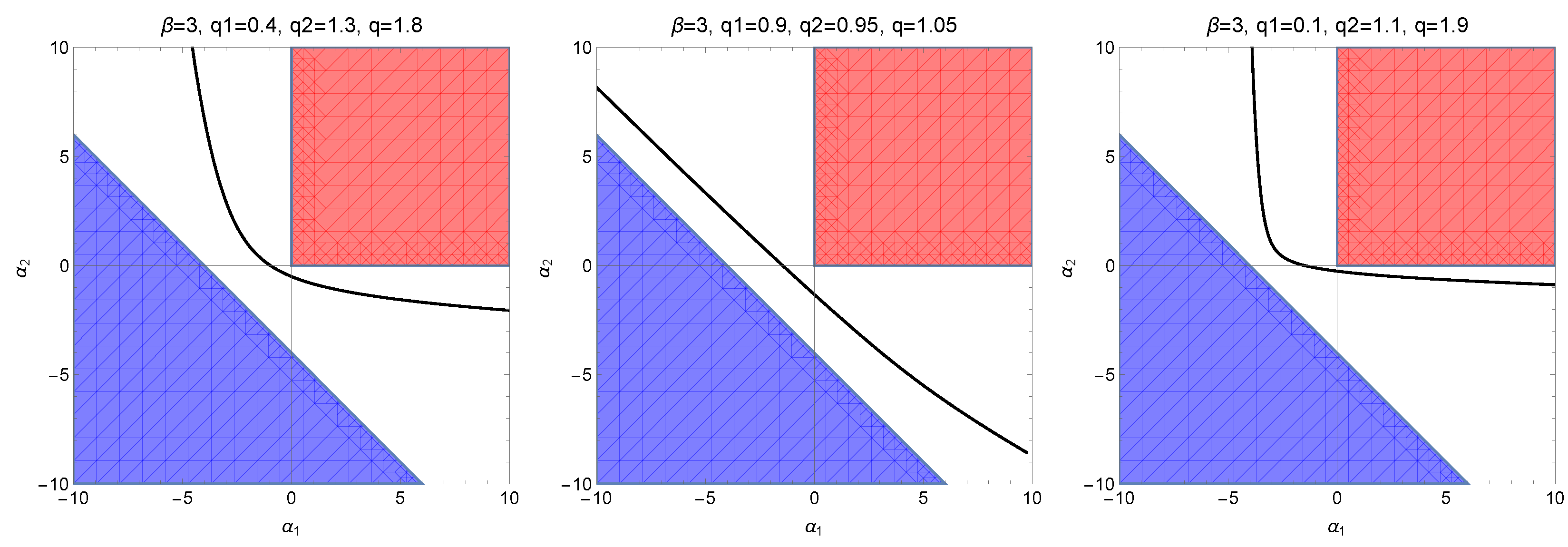
5. Three-Term Fractional-Differential Equations

The results presented in this section were rigorously investigated in Ref. [24] and will be enumerated in the following.

We consider the following multi-term fractional differential equation

$${}^c{D}^{q}x\left(t\right)+{\alpha }_1^c{D}^{q_1}x\left(t\right)+{\alpha }_2^c{D}^{q_2}x\left(t\right)+\beta x\left(t\right)=0$$

(8)

where ${\alpha }_1,{\alpha }_2,\beta$ are the real numbers and $q,q_1,q_2$ are the fractional orders of the Caputo derivatives, with $0<q_1<q_2<q\le 2$.

The characteristic equations becomes

$$\Delta (s;{\alpha }_1,{\alpha }_2,\beta ,q_1,q_2,q):=s^q+{\alpha }_1{s}^{q_1}+{\alpha }_2{s}^{q_2}+\beta =0.$$

(9)

Let $D=\{(q_1,q_2,q)\in {\mathbb{R}}^3:0<q_1<q_2<q\le 2\}$ and let $\beta >0$.

Lemma 3. 

Let $(q_1,q_2,q)\in D$ and $\beta >0$ be arbitrarily fixed. We consider the smooth parametric curve in the $({\alpha }_1,{\alpha }_2)$-plane defined by

$$\Gamma \left(\beta ,q_1,q_2,q\right):\left\{\begin{array}{c}{\alpha }_1={\beta }^{1-\frac{q_1}{q}}h\left(\omega ,q_1,q_2,q\right)\hfill \\ {\alpha }_2={\beta }^{1-\frac{q_2}{q}}h\left(\omega ,q_2,q_1,q\right)\hfill \end{array}\right.,\omega >0,$$

where $h:(0,\infty )\times D\to (0,\infty )$ is given by:

$$h\left(\omega ,q_1,q_2,q\right)={\omega }^{-\frac{q_1}{q}}\left[\omega \rho (q-q_2,q_2-q_1)-\rho (q_2,q_2-q_1)\right]$$

with the function ρ defined as $\rho (a,b)={\displaystyle \frac{sin\frac{a\pi }{2}}{sin\frac{b\pi }{2}}}$, for any $a\in [0,2],b\in [-1,0)\cup (0,1].$

The following statements hold:

i. 

The curve $\Gamma (\beta ,q_1,q_2,q)$ is the graph of a smooth, decreasing, convex bijective function ${\varphi }_{\beta ,q_1,q_2,q}:\mathbb{R}\to \mathbb{R}$ in the $({\alpha }_1,{\alpha }_2)$-plane;

ii. 

The curve $\Gamma (\beta ,q_1,q_2,q)$ lies outside the first quadrant of the $({\alpha }_1,{\alpha }_2)$-plane.

Theorem 2 

(Fractional-order-dependent results).

Let $\beta >0$, $0<q_1<q_2<q\le 2$ be arbitrarily fixed. Consider the curve $\Gamma (\beta ,q_1,q_2,q)$ and the function ${\varphi }_{\beta ,q_1,q_2,q}:\mathbb{R}\to \mathbb{R}$ previously defined.

i. 

The characteristic Equation (9) has a pair of complex conjugated roots on the imaginary axis of the complex plane if and only if $({\alpha }_1,{\alpha }_2)\in \Gamma (\beta ;q_1,q_2,q)$;

ii. 

The trivial solution of equation (8) is $\mathcal{O}\left(t^{-q^{\prime }}\right)$-asymptotically stable (where $q^{\prime }=min\{\left\{q\right\},$$\left\{q_1\right\},\left\{q_2\right\}\}$) if and only if

$${\alpha }_2>{\varphi }_{\beta ,q_1,q_2,q}\left({\alpha }_1\right).$$

iii. 

If ${\alpha }_2<{\varphi }_{\beta ,q_1,q_2,q}\left({\alpha }_1\right)$, the trivial solution of equation (8) is unstable.

Remark 2. 

If $q_1=q_2=:q^{*}$, $\Gamma (\beta ,q_1,q_2,q)$ becomes the line

$${\alpha }_1+\alpha +2=-{\displaystyle \frac{{\beta }^{1-\frac{q^{*}}{q}}sin{\displaystyle \frac{q\pi }{2}}}{{\left(sin{\displaystyle \frac{q^{*}\pi }{2}}\right)}^{\frac{q^{*}}{q}}{\left(sin{\displaystyle \frac{(q-q^{*})\pi }{2}}\right)}^{1-\frac{q^{*}}{q}}}},$$

which is in accordance with the results from Proposition 2.

Remark 3. 

We emphasize that in the particular case of multi-term fractional-order differential equations with three derivatives, the fractional-order independent asymptotic stability and instability conditions described by Lemmas 1 and 2 become necessary and sufficient conditions, compared to the general case of fractional-order differential equations of n fractional derivatives.

Remark 4. 

In Figure 1, we have plotted three parametric curves $\Gamma (\beta ,q_1,q_2,q)$ for $\beta =3$ and different values of the fractional orders $q_1,q_2,q$ such that $0<q_1<q_2<q\le 2$ in the $({\alpha }_1,{\alpha }_2)$-plane, along with the fractional-order-independent stability and instability regions, respectively (plotted with red and blue). In fact, we have proved in Ref. [24] that the reunion of all the parametric curves $\Gamma (\beta ,q_1,q_2,q)$ fill the space between the fractional-order-independent stability and instability regions and will not intersect neither of them.

Similar to the case of two-term fractional-order differential equations described in Section 3, we will next enumerate some examples of practical applications described by three-term fractional-order differential equations, which were presented in detail in [24].

Example 3. 

The equation of motion of the inextendible pendulum [8] is described by the following three term fractional-differential equation

$${\varphi }^{″}+\mu {\tau }^{q_1}{·}^c{D}^{q_1}\varphi +\nu {\tau }^{q_2}{·}^c{D}^{q_2}\varphi +{\displaystyle \frac{g}{L}}sin\varphi =0.$$

(10)

The trivial equilibrium of the equation is asymptotically stable, for any fractional orders $q_1$ and $q_2$. Moreover, Theorem 1 gives us that

$$\varphi \left(t\right)=\mathcal{O}\left(t^{-q^{\prime }}\right)\mathrm{as}t\to \infty ,\mathrm{where}{q}^{\prime }=min\{\left\{q_1\right\},\left\{q_2\right\}\}.$$

Example 4. 

The fractional harmonic oscillator is modelled by the following fractional differential equation:

$$x^{″}+{\alpha }_1^c{D}^{q_1}x+{\alpha }_2{x}^{\prime }+\beta x=0,\mathrm{with}{q}_1\in (0,1)$$

(11)

where ${\alpha }_1$ and ${\alpha }_2$ represent the friction coefficient and viscous damping coefficient [9,10], and $\beta >0$.

• If ${\alpha }_1>0$, ${\alpha }_2>0$ and $\beta >0$, then Equation (11) is asymptotically stable, regardless of the fractional order $q_1$;
• If ${\alpha }_2<0$ (negative damping), the stability properties of Equation (11) depend on the fractional order $q_1$ and on the magnitude of the parameters.

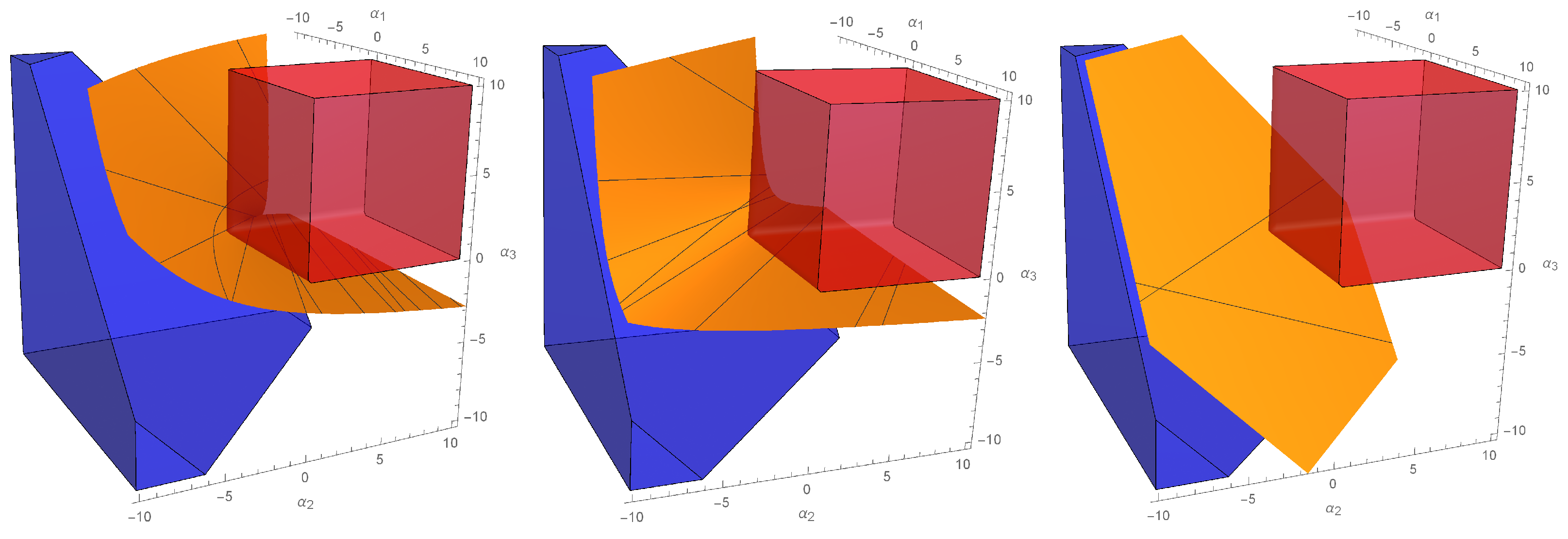
6. Four-Term Fractional-Differential Equations

In this section, our main objective is to generalize the previously presented results of Theorem 2, by considering a linear fractional differential equations with four Caputo derivatives:

$${}^c{D}^{q}x\left(t\right)+{\alpha }_1^c{D}^{q_1}x\left(t\right)+{\alpha }_2^c{D}^{q_2}x\left(t\right)+{\alpha }_3^c{D}^{q_3}x\left(t\right)+\beta x\left(t\right)=0,$$

(12)

where ${\alpha }_1,{\alpha }_2,{\alpha }_3,\beta$ are the real numbers and $q,q_1,q_2,q_3$ are the fractional orders of the Caputo derivatives, with $0<q_1<q_2<q_3<q\le 2$.

By means of the Laplace transform technique, we obtain the characteristic equation

$$\Delta (s;{\alpha }_1,{\alpha }_2,{\alpha }_3,\beta ,q_1,q_2,q_3,q)=s^q+{\alpha }_1{s}^{q_1}+{\alpha }_2{s}^{q_2}+{\alpha }_3{s}^{q_3}+\beta =0.$$

(13)

Next, we will assume that the fractional orders $q_1,q_2,q_3,q$ are arbitrarily fixed inside the domain

$$D=\{(q_1,q_2,q_3,q)\in {\mathbb{R}}^4:0<q_1<q_2<q_3<q\le 2\}.$$

Moreover, as $\beta <0$ implies that the Equation (12) is unstable (according to Lemma 1), for any choice of the fractional orders $q_1,q_2,q_3,q$, we will further assume that $\beta >0$.

Lemma 4. 

Let $(q_1,q_2,q_3,q)\in D$ and $\beta >0$ be arbitrarily fixed. Consider the parametric surface in the $({\alpha }_1,{\alpha }_2,{\alpha }_3)$-space defined by

$$S\left(\beta ,q_1,q_2,q_3,q\right):\left\{\begin{array}{c}{\alpha }_1={\beta }^{1-\frac{q_1}{q}}h\left(\omega ,\eta ,q_1,q_2,q_3,q\right)\hfill \\ {\alpha }_2={\beta }^{1-\frac{q_2}{q}}h\left(\omega ,\eta ,q_2,q_1,q_3,q\right)\hfill \\ {\alpha }_3={\beta }^{1-\frac{q_3}{q}}\eta {\omega }^{-\frac{q_3}{q}}\hfill \end{array}\right.,\omega >0,\eta \in \mathbb{R}$$

where $h:(0,\infty )\times \mathbb{R}\times D\to (0,\infty )$ is given by:

$$h\left(\omega ,\eta ,q_1,q_2,q_3,q\right)={\omega }^{-\frac{q_1}{q}}\left[\eta \rho (q_3-q_2,q_2-q_1)+\omega \rho (q-q_2,q_2-q_1)-\rho (q_2,q_2-q_1)\right]$$

with the function ρ defined as

$$\rho (a,b)=\frac{sin\frac{a\pi }{2}}{sin\frac{b\pi }{2}},\forall a\in [0,2],b\in [-1,0)\cup (0,1].$$

The surface $S\left(\beta ,q_1,q_2,q_3,q\right)$ lies outside the first octant (${\alpha }_1>0,{\alpha }_2>0,{\alpha }_3>0$) of the $({\alpha }_1,{\alpha }_2,{\alpha }_3)$-space.

Proof. 

Assuming the contrary, that there exist $\omega >0$ and $\eta \in \mathbb{R}$ such that ${\alpha }_1>0$, ${\alpha }_2>0$ and ${\alpha }_3>0$, it follows that $\eta >0$ and

$$\left\{\begin{array}{cc}& \eta \rho (q_3-q_2,q_2-q_1)+\omega \rho (q-q_2,q_2-q_1)-\rho (q_2,q_2-q_1)>0\hfill \\ & \eta \rho (q_3-q_1,q_1-q_2)+\omega \rho (q-q_1,q_1-q_2)-\rho (q_1,q_1-q_2)>0\hfill \end{array}\right.$$

which is equivalent to

$$\left\{\begin{array}{cc}& \eta ·sin(q_3-q_2)\frac{\pi }{2}+\omega ·sin(q-q_2)\frac{\pi }{2}-sin\frac{q_2\pi }{2}>0\hfill \\ & -\eta ·sin(q_3-q_1)\frac{\pi }{2}-\omega ·sin(q-q_1)\frac{\pi }{2}+sin\frac{q_1\pi }{2}>0\hfill \end{array}\right.$$

Eliminating $\omega$, it leads to the following inequality:

$$\begin{array}{cc}\hfill & \eta \left(sin(q_3-q_2)\frac{\pi }{2}sin(q-q_1)\frac{\pi }{2}-sin(q_3-q_1)\frac{\pi }{2}sin(q-q_2)\frac{\pi }{2}\right)>\hfill \\ \hfill & >sin\frac{q_2\pi }{2}sin(q-q_1)\frac{\pi }{2}-sin\frac{q_1\pi }{2}sin(q-q_2)\frac{\pi }{2}.\hfill \end{array}$$

By applying elementary trigonometric identities, the previous relation is equivalent to the inequality:

$$\eta sin(q_3-q)\frac{\pi }{2}>sin\frac{q\pi }{2},$$

which is absurd, as $\eta >0$, $sin(q_3-q)\frac{\pi }{2}<0$ and $sin\frac{q\pi }{2}>0$.

Thus, the surface $S\left(\beta ,q_1,q_2,q_3,q\right)$ does not intersect the first octant of the $({\alpha }_1,{\alpha }_2,{\alpha }_3)$-space. □

Remark 5. 

If $q_1=q_2=q_3=:q^{*}$, $S(\beta ,q_1,q_2,q_3,q)$ represents the plane

$${\alpha }_1+{\alpha }_2+{\alpha }_3=-{\displaystyle \frac{{\beta }^{1-\frac{q^{*}}{q}}sin{\displaystyle \frac{q\pi }{2}}}{{\left(sin{\displaystyle \frac{q^{*}\pi }{2}}\right)}^{\frac{q^{*}}{q}}{\left(sin{\displaystyle \frac{(q-q^{*})\pi }{2}}\right)}^{1-\frac{q^{*}}{q}}}}.$$

Lemma 5. 

Let $\beta >0$, $(q_1,q_2,q_3,q)\in D$ be arbitrarily fixed. Consider the surface $S(\beta ,q_1,q_2,q_3,q)$ defined in Lemma 4. The characteristic Equation (13) has a pair of complex conjugated roots on the imaginary axis of the complex plane if and only if $({\alpha }_1,{\alpha }_2,{\alpha }_3)\in S(\beta ,q_1,q_2,q_3,q)$.

Proof. 

The characteristic Equation (13) has a pair of pure imaginary roots if and only if there exists $\omega >0$ such that

$$\Delta (s;{\alpha }_1,{\alpha }_2,{\alpha }_3,\beta ,q_1,q_2,q_3,q)=0,\mathrm{where}s=i{\left(\beta \omega \right)}^{\frac{1}{q}},$$

which is equivalent to

$$i^q\beta \omega +{\alpha }_1{i}^{q_1}{\left(\beta \omega \right)}^{\frac{q_1}{q}}+{\alpha }_2{i}^{q_2}{\left(\beta \omega \right)}^{\frac{q_2}{q}}+{\alpha }_3{i}^{q_3}{\left(\beta \omega \right)}^{\frac{q_3}{q}}+\delta =0.$$

Dividing the previous relation by $\beta$, we have:

$$i^q\omega +{\alpha }_1{\beta }^{\frac{q_1}{q}-1}{\omega }^{\frac{q_1}{q}}{i}^{q_1}+{\alpha }_2{\beta }^{\frac{q_2}{q}-1}{\omega }^{\frac{q_2}{q}}{i}^{q_2}+{\alpha }_3{\beta }^{\frac{q_3}{q}-1}{\omega }^{\frac{q_3}{q}}{i}^{q_3}+1=0.$$

Taking the real and imaginary part from the relation from above, we obtain the following system:

$$\left\{\begin{array}{cc}& \omega cos{\displaystyle \frac{q\pi }{2}}+{\alpha }_1{\beta }^{\frac{q_1}{q}-1}{\omega }^{\frac{q_1}{q}}cos{\displaystyle \frac{q_1\pi }{2}}+{\alpha }_2{\beta }^{\frac{q_2}{q}-1}{\omega }^{\frac{q_2}{q}}cos{\displaystyle \frac{q_2\pi }{2}}+{\alpha }_3{\beta }^{\frac{q_3}{q}-1}{\omega }^{\frac{q_3}{q}}cos{\displaystyle \frac{q_3\pi }{2}}+1=0\hfill \\ \\ & \omega sin{\displaystyle \frac{q\pi }{2}}+{\alpha }_1{\beta }^{\frac{q_1}{q}-1}{\omega }^{\frac{q_1}{q}}sin{\displaystyle \frac{q_1\pi }{2}}+{\alpha }_2{\beta }^{\frac{q_2}{q}-1}{\omega }^{\frac{q_2}{q}}sin{\displaystyle \frac{q_2\pi }{2}}+{\alpha }_3{\beta }^{\frac{q_3}{q}-1}{\omega }^{\frac{q_3}{q}}sin{\displaystyle \frac{q_3\pi }{2}}=0\hfill \end{array}\right.$$

We solve the previous system for ${\alpha }_1$ and ${\alpha }_2$ and, denoting $\eta ={\alpha }_3{\omega }^{\frac{q_3}{q}}{\delta }^{\frac{q_3}{q}-1}$, it follows that the characteristic Equation (13) has a pair of complex conjugated roots on the imaginary axis if and only if the triplet $({\alpha }_1,{\alpha }_2,{\alpha }_3)$ belongs to the parametric surface $S(\beta ,q_1,q_2,q_3,q)$ defined in Lemma 4. □

Theorem 3 

(Fractional-order-dependent results).

Let $\beta >0$, $0<q_1<q_2<q_3<q\le 2$ be arbitrarily fixed. Consider the surface $S(\beta ,q_1,q_2,q_3,q)$ previously defined. The trivial solution of Equation (12) is $\mathcal{O}\left(t^{-q^{\prime }}\right)$-asymptotically stable (where $q^{\prime }=min\{\left\{q\right\},\left\{q_1\right\},\left\{q_2\right\},\left\{q_3\right\}\}$) if and only if $({\alpha }_1,{\alpha }_2,{\alpha }_3)$ belongs to the connected component of the three-dimensional space bounded by the surface $S(\beta ,q_1,q_2,q_3,q)$, which contains the positive octant.

Proof. 

If ${\alpha }_i>0$, for $i=\overline{1,3}$, it follows from Lemma 2 that the trivial solution of Equation (12) is asymptotically stable. As the parameters ${\alpha }_i$, $i=\overline{1,3}$ are varied, the qualitative behaviour may change if and only if $({\alpha }_1,{\alpha }_2,{\alpha }_3)\in S(\beta ,q_1,q_2,q_3,q)$, which follows from Lemma 5. Therefore, it is clear that if $({\alpha }_1,{\alpha }_2,{\alpha }_3)$ belongs to the open connected region, which contains the positive octant, then the trivial solution of Equation (12) is asymptotically stable.

In what follows, we verify the transversality condition.

Let $\beta >0$, $(q_1,q_2,q_3,q)\in D$ be arbitrarily fixed. Consider the surface $S(\beta ,q_1,q_2,q_3,q)$ defined in Lemma 4. For simplicity, denote $Q_j={\displaystyle \frac{q_j}{q}}$, with $j\in \{1,2,3\}$.

We first compute the cross product of the vectors $\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}\right)$ and

$\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}\right)$, which is the normal vector to the surface $S(\beta ,q_1,q_2,q_3,q)$.

$$\begin{array}{cc}\hfill & \overrightarrow{N}=\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}\right)\times \left({\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}\right)=\hfill \\ \hfill & =\left({\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}-{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}-{\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }}·{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }}-·{\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }}·{\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }}\right)\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }}& ={\beta }^{1-Q_1}{\omega }^{-Q_1-1}[-Q_1\eta \rho (q_3-q_2,q_2-q_1)-Q_1\omega \rho (q-q_2,q_2-q_1)+\hfill & \\ & +Q_1\rho (q_2,q_2-q_1)+\omega \rho (q-q_2,q_2-q_1)]\hfill & \\ \hfill {\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }}& ={\beta }^{1-Q_2}{\omega }^{-Q_2-1}[-Q_2\eta \rho (q_3-q_1,q_1-q_2)-Q_2\omega \rho (q-q_1,q_1-q_2)+\hfill & \\ & +Q_2\rho (q_1,q_1-q_2)+\omega \rho (q-q_1,q_1-q_2)]\hfill & \\ \hfill {\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}& =-Q_3\eta {\beta }^{1-Q_3}{\omega }^{-Q_3-1}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }}& ={\beta }^{1-Q_1}{\omega }^{-Q_1}\rho (q_3-q_2,q_2-q_1)\hfill & \\ \hfill {\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }}& ={\beta }^{1-Q_2}{\omega }^{-Q_2}\rho (q_3-q_1,q_1-q_2)\hfill & \\ \hfill {\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}& ={\beta }^{1-Q_3}{\omega }^{-Q_3}\hfill \end{array}$$

Let $s({\alpha }_1,{\alpha }_2,{\alpha }_3,\beta ,q_1,q_2,q_3,q)$ denote the root of the characteristic function $\Delta (s;{\alpha }_1,{\alpha }_2,{\alpha }_3,\beta ,q_1,q_2,q_3,q)$ which satisfies $s({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*},\beta ,q_1,q_2,q_3,q)=i{\left(\beta \omega \right)}^{\frac{1}{q}}$, with $({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})\in S(\beta ,q_1,q_2,q_3,q)$.

Taking the derivative with respect to ${\alpha }_1$ in the characteristic equation

$$s^q+{\alpha }_1{s}^{q_1}+{\alpha }_2{s}^{q_2}+{\alpha }_3{s}^{q_3}+\beta =0,$$

we obtain

$$q{s}^{q-1}{\displaystyle \frac{\partial s}{\partial {\alpha }_1}}+s^{q_1}+{\alpha }_1{q}_1{s}^{q_1-1}{\displaystyle \frac{\partial s}{\partial {\alpha }_1}}+{\alpha }_2{q}_2{s}^{q_2-1}{\displaystyle \frac{\partial s}{\partial {\alpha }_1}}+{\alpha }_3{q}_3{s}^{q_3-1}{\displaystyle \frac{\partial s}{\partial {\alpha }_1}}=0,$$

which is equivalent to

$${\displaystyle \frac{\partial s}{\partial {\alpha }_1}}={\displaystyle \frac{-s^{q_1}}{q{s}^{q-1}+{\alpha }_1{q}_1{s}^{q_1-1}+{\alpha }_2{q}_2{s}^{q_2-1}+{\alpha }_3{q}_3{s}^{q_3-1}}}.$$

Taking the real part of the previous relation, it follows that:

$${\displaystyle \frac{\partial \Re \left(s\right)}{\partial {\alpha }_1}}=\Re \left({\displaystyle \frac{\partial s}{\partial {\alpha }_1}}\right)=\Re \left({\displaystyle \frac{-s^{q_1}}{q{s}^{q-1}+{\alpha }_1{q}_1{s}^{q_1-1}+{\alpha }_2{q}_2{s}^{q_2-1}+{\alpha }_3{q}_3{s}^{q_3-1}}}\right).$$

We have:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial \Re \left(s\right)}{\partial {\alpha }_1}}{|}_{({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})}& =\Re \left({\displaystyle \frac{-{\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)}^{q_1}}{P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)}}\right)=-{\left(\beta \omega \right)}^{\frac{q_1}{q}}\Re \left({\displaystyle \frac{i^{q_1}\overline{P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)}}{|P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right){|}^2}}\right)=\hfill & \\ \hfill & ={\displaystyle \frac{-{\left(\beta \omega \right)}^{\frac{q_1}{q}}}{|P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right){|}^2}}\Re \left(i^{q_1}\overline{P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)}\right).\hfill \end{array}$$

Computing $\Re \left(i^{q_1}\overline{P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)}\right)$ we obtain:

$$\begin{array}{cc}\hfill & \Re \left(i^{q_1}\overline{P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)}\right)=\Re \left(\overline{i^{q_1}}P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)\right)=\hfill \\ \hfill & =\Re \left(i^{-q_1}{\left(\beta \omega \right)}^{-\frac{1}{q}}\left[q{i}^{q-1}\beta \omega +{\alpha }_1^{*}{q}_1{i}^{q_1-1}{\left(\beta \omega \right)}^{Q_1}+{\alpha }_2^{*}{q}_2{i}^{q_2-1}{\left(\beta \omega \right)}^{Q_2}+{\alpha }_3^{*}{q}_3{i}^{q_3-1}{\left(\beta \omega \right)}^{Q_3}\right]\right)\hfill \\ \hfill & =\Re \left(q{\beta }^{1-\frac{1}{q}}{\omega }^{-\frac{1}{q}}\right[i^{q-q_1-1}\omega +Q_1{i}^{-1}{\omega }^{Q_1}h(\omega ,\eta ,q_1,q_2,q_3,q)+\hfill \\ & +Q{}_2{i}^{q_2-q-1}{\omega }^{Q_2}h(\omega ,\eta ,q_2,q_1,q_3,q)+Q_3{i}^{q_3-q_1-1}\eta \left]\right)\hfill \end{array}$$

As the second term from the precious relation is purely imaginary and

$$\Re \left(i^{q-q_1-1}\right)=sin{\displaystyle \frac{(q-q_1)\pi }{2}},\Re \left(i^{q_2-q_1-1}\right)=sin{\displaystyle \frac{(q_2-q_1)\pi }{2}},\Re \left(i^{q_3-q_1-1}\right)=sin{\displaystyle \frac{(q_3-q_1)\pi }{2}},$$

it follows that

$$\begin{array}{cc}\hfill \Re \left(\overline{i^{q_1}}P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right)\right)& =q{\beta }^{1-\frac{1}{q}}{\omega }^{-\frac{1}{q}}(\omega sin(q-q_1){\displaystyle \frac{\pi }{2}}+Q_{2}sin(q_2-q_1){\displaystyle \frac{\pi }{2}}[\eta \rho (q_3-q_1,q_1-q_2)+\hfill \\ \hfill & +\omega \rho (q-q_1,q_1-q_2)-\rho (q_1,q_1-q_2)]+Q_3\eta sin(q_3-q_1){\displaystyle \frac{\pi }{2}})\hfill \end{array}$$

A simple computation leads to

$${\displaystyle \frac{\partial \Re \left(s\right)}{\partial {\alpha }_1}}{|}_{({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})}={\displaystyle \frac{q{\beta }^{Q_1+Q_2+Q_3-\frac{1}{q}-1}{\omega }^{Q_1+Q_2+Q_3-\frac{1}{q}+1}}{|P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right){|}^{2}sin(q_2-q_1)\frac{\pi }{2}}}·\left({\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}-{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}\right).$$

Following similar steps, we can deduce that

$${\displaystyle \frac{\partial \Re \left(s\right)}{\partial {\alpha }_2}}{|}_{({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})}={\displaystyle \frac{q{\beta }^{Q_1+Q_2+Q_3-\frac{1}{q}-1}{\omega }^{Q_1+Q_2+Q_3-\frac{1}{q}+1}}{|P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right){|}^{2}sin(q_2-q_1)\frac{\pi }{2}}}·\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}-{\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }}·{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}\right)$$

and

$${\displaystyle \frac{\partial \Re \left(s\right)}{\partial {\alpha }_3}}{|}_{({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})}={\displaystyle \frac{q{\beta }^{Q_1+Q_2+Q_3-\frac{1}{q}-1}{\omega }^{Q_1+Q_2+Q_3-\frac{1}{q}+1}}{|P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right){|}^{2}sin(q_2-q_1)\frac{\pi }{2}}}·\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }}·{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }}-{\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }}·{\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }}\right).$$

Therefore, we obtain that

$$\begin{array}{cc}\hfill \nabla \Re \left(s\right)& ({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})=\left(\frac{\partial \Re \left(s\right)}{\partial {\alpha }_1},\frac{\partial \Re \left(s\right)}{\partial {\alpha }_2},\frac{\partial \Re \left(s\right)}{\partial {\alpha }_3}\right){|}_{({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})}=\hfill \\ & ={\displaystyle \frac{q{\beta }^{Q_1+Q_2+Q_3-\frac{1}{q}-1}{\omega }^{Q_1+Q_2+Q_3-\frac{1}{q}+1}}{|P\left(i{\left(\beta \omega \right)}^{\frac{1}{q}}\right){|}^{2}sin(q_2-q_1)\frac{\pi }{2}}}\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \omega }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \omega }}\right)\times \left({\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}\right)\hfill \end{array}$$

Thus, the vector $\nabla \Re \left(s\right)({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})$ is a normal vector to the surface $S(\beta ,q_1,q_2,q_3,q)$. Moreover, the vector $\nabla \Re \left(s\right)({\alpha }_1^{*},{\alpha }_2^{*},{\alpha }_3^{*})$ points away from the open connected region which contains the positive octant and is bounded by the surface $S(\beta ,q_1,q_2,q_3,q)$, as it is perpendicular to the tangent vector $\left({\displaystyle \frac{\partial {\alpha }_1}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_2}{\partial \eta }},{\displaystyle \frac{\partial {\alpha }_3}{\partial \eta }}\right)$, where ${\displaystyle \frac{\partial {\alpha }_i}{\partial \eta }}>0$, $i=\overline{1,3}$. □

Remark 6. 

In Figure 2, we have plotted three parametric surfaces $S(\beta ,q_1,q_2,q_3,q)$ for $\beta =5$ and different values of the fractional orders $q_1,q_2,q_3,q$ such that $0<q_1<q_2<q_3<q\le 2$ in the $({\alpha }_1,{\alpha }_2,{\alpha }_3)$-space, along with the fractional-order-independent stability and instability regions, respectively (plotted red and blue). We theorize that the reunion of all the parametric surfaces $S(\beta ,q_1,q_2,q_3,q)$ will fill the space between the fractional-order-independent stability and instability regions and will not intersect neither of them.

Example 5. 

To exemplify the previous theoretical results, we consider a mathematical model of a damped unforced Duffing-type oscillator expressed as the following multi-term fractional differential equation:

$$m{x}^{″}+c_1{}^c{D}^{q_1}x+c_2{}^c{D}^{q_2}x+c{x}^{\prime }+k_{1}x+k_2{x}^3=0,\mathrm{with}{q}_1,q_2\in (0,1)$$

(14)

where $m>0$ is the mass, $k_1$ and $k_2$ are the linear and non-linear stiffness coefficients, respectively, while $c_1$, $c_2$ and c are linear viscous damping coefficients [30]. The linearization of this equation at the trivial equilibrium represents a particular case of Equation (12) with $q=2$ and $q_3=1$.

By Lemma 2 it follows that if $c_1>0$, $c_2>0$, $c>0$ and $k_1>0$, then the trivial equilibrium of (14) is asymptotically stable, regardless of the choice of the fractional order $q_1$. Nevertheless, if a negative damping coefficient c is chosen, the stability of the trivial solution depends on the fractional orders $q_1$ and $q_2$.

For example, if $m=1$, $c_1=1$, $c_2=0.1$, $c_3=-1$, $k_1=4$ and $k_2=1$, for $q_2=0.95$, then the corresponding critical value of the fractional order $q_1$ is found numerically by solving the parametric equations of the surface defined in Lemma 4 for ω, η and $q_1$, leading to $q_1^{🟊}=0.885052$. The trivial equilibrium of Equation (14) is asymptotically stable if and only if $q_1>q_1^{🟊}$. The numerical solutions [31,32] of Equation (14) with respect to several values of $q_1$ are plotted in Figure 3, showing that when $q_1<q_1^{🟊}$, the trivial solution of (14) becomes unstable and persistent oscillations appear.

7. Conclusions

In this paper, on the one hand, we have focused our attention on determining general fractional-order-independent stability and instability conditions for multi-term fractional-order differential equations of an arbitrary number of terms. In fact, the obtained conditions are formulated as easily verifiable inequalities involving the constant coefficients of the linear fractional differential equations.

On the other hand, we also presented a brief overview of fractional-order-dependent stability and instability conditions for two-term and three-term fractional-order differential equations, previously reported in the literature. As a generalisation, we provided an investigation of fractional-order dependent stability and instability conditions for four-term fractional-differential equations.

Employing similar techniques as in the proof of Theorem 3, these results can further be generalized to the case of fractional differential equations with multiple Caputo derivatives, leading to a characterisation of the hypersurface, which represents the boundary of the stability region in the hyperspace of coefficients. However, it becomes clear that fractional-order-dependent stability and instability conditions for multi-term fractional differential equations cannot be expressed in a simple way, and as expected, the complexity of the problem increases along with the number of Caputo derivatives included in the fractional differential equation. As a possible direction for future research, our aim is to find a way to overcome this limitation, possibly by finding a different parametrization of the hypersurface at the boundary of the stability region.

Moreover, at this stage, the results presented in this paper represent a timely review of the main contributions related to qualitatively characterizing the stability and instability properties of multi-term fractional-order differential equations with Caputo derivatives. Fractional-order dependent stability and instability properties for multi-order fractional differential equations having an arbitrary number of Caputo derivatives are still yet to be determined. Moreover, we foresee that this investigation shall become more arduous as we increase the number of fractional derivatives, or if we consider different types of fractional derivatives, such as the more general Prabhakar derivatives or derivatives with Sonine kernels.