Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach
Abstract
1. Introduction
- Presenting a framework model for price predictions of BTC, ETH, and LTC cryptocurrencies;
- Application of DL algorithms such as LSTM, Bi-LSTM, and GRU techniques;
- Evaluating the prediction performance of the proposed deep learning algorithms using metrics of RMSE and MAPE
2. Literature Review
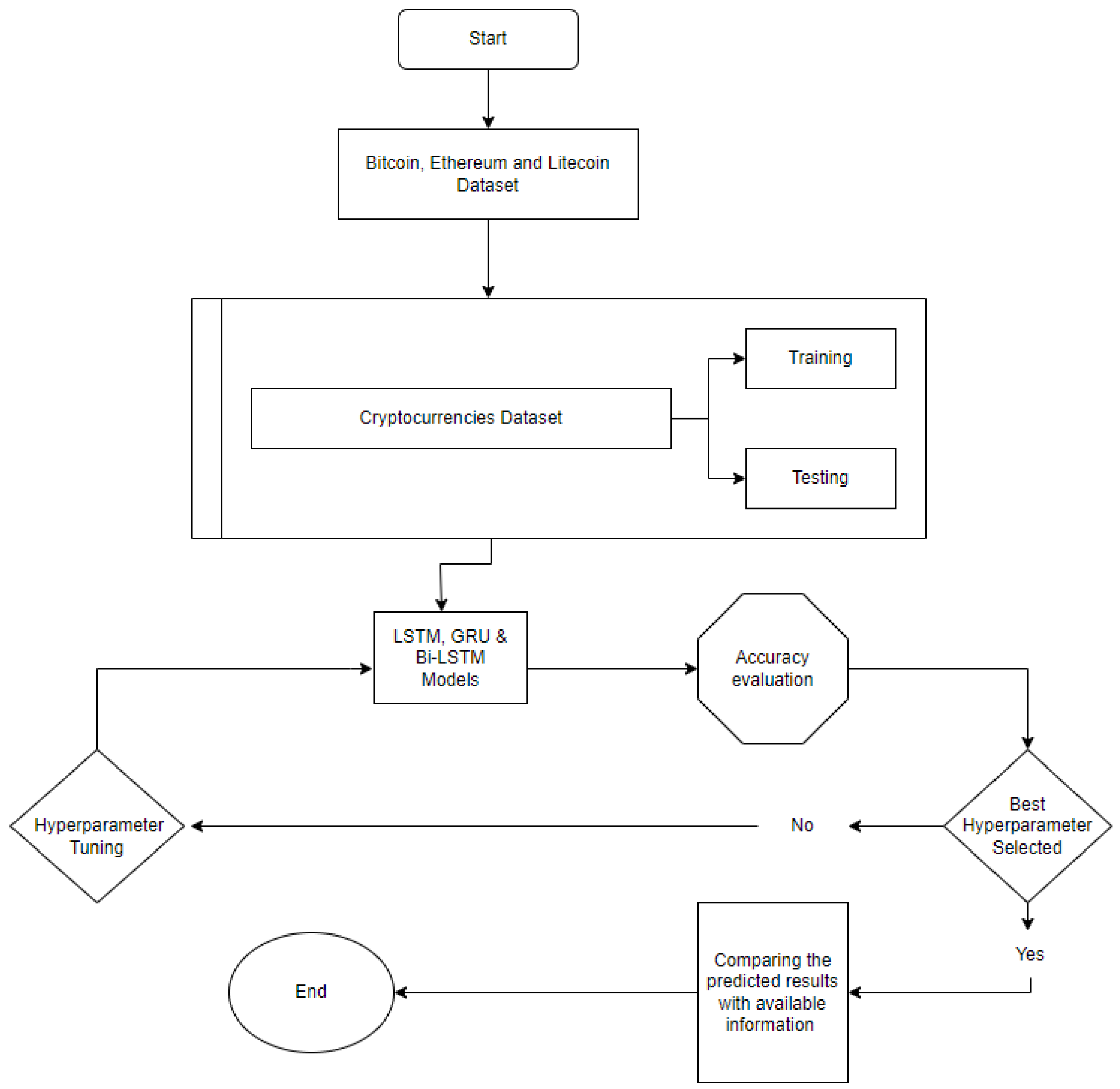
3. Materials and Methods
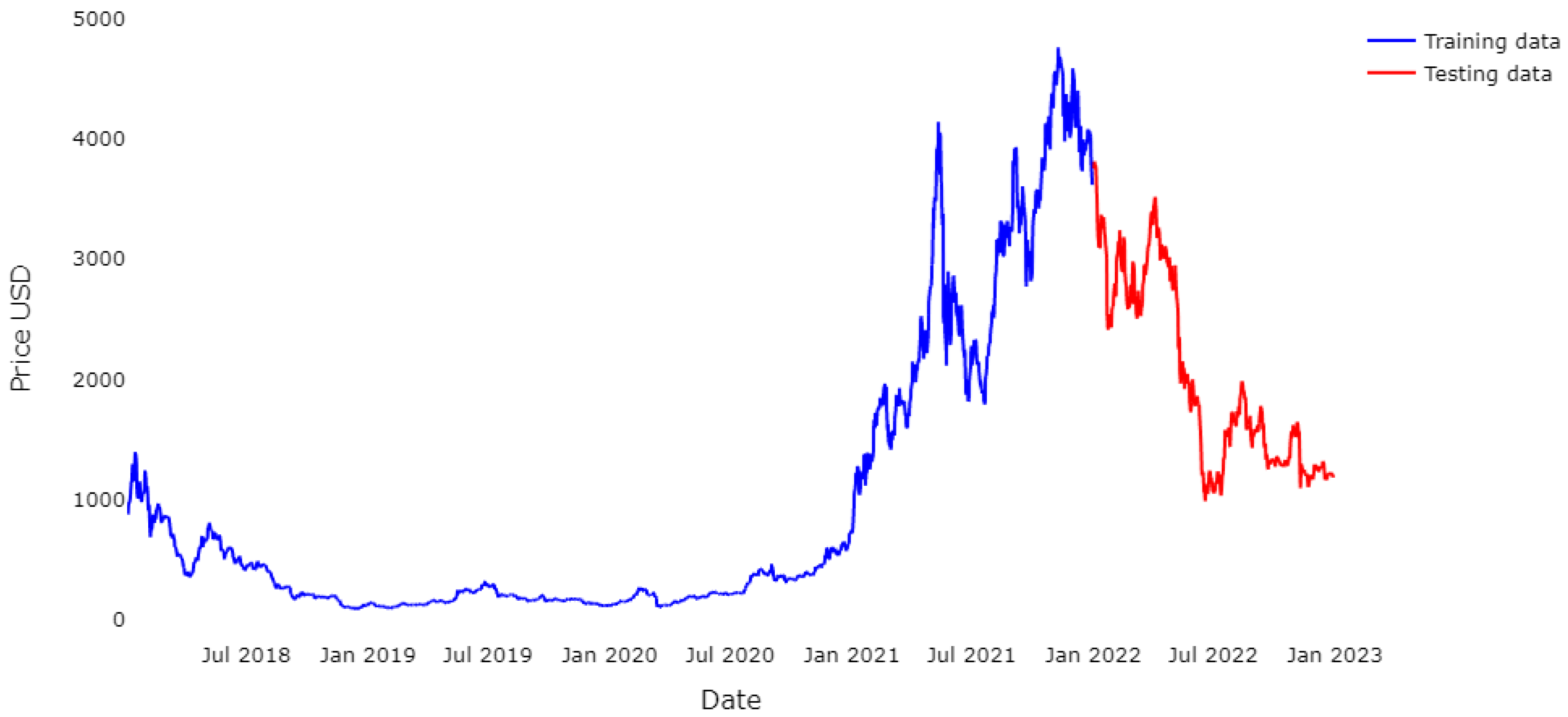
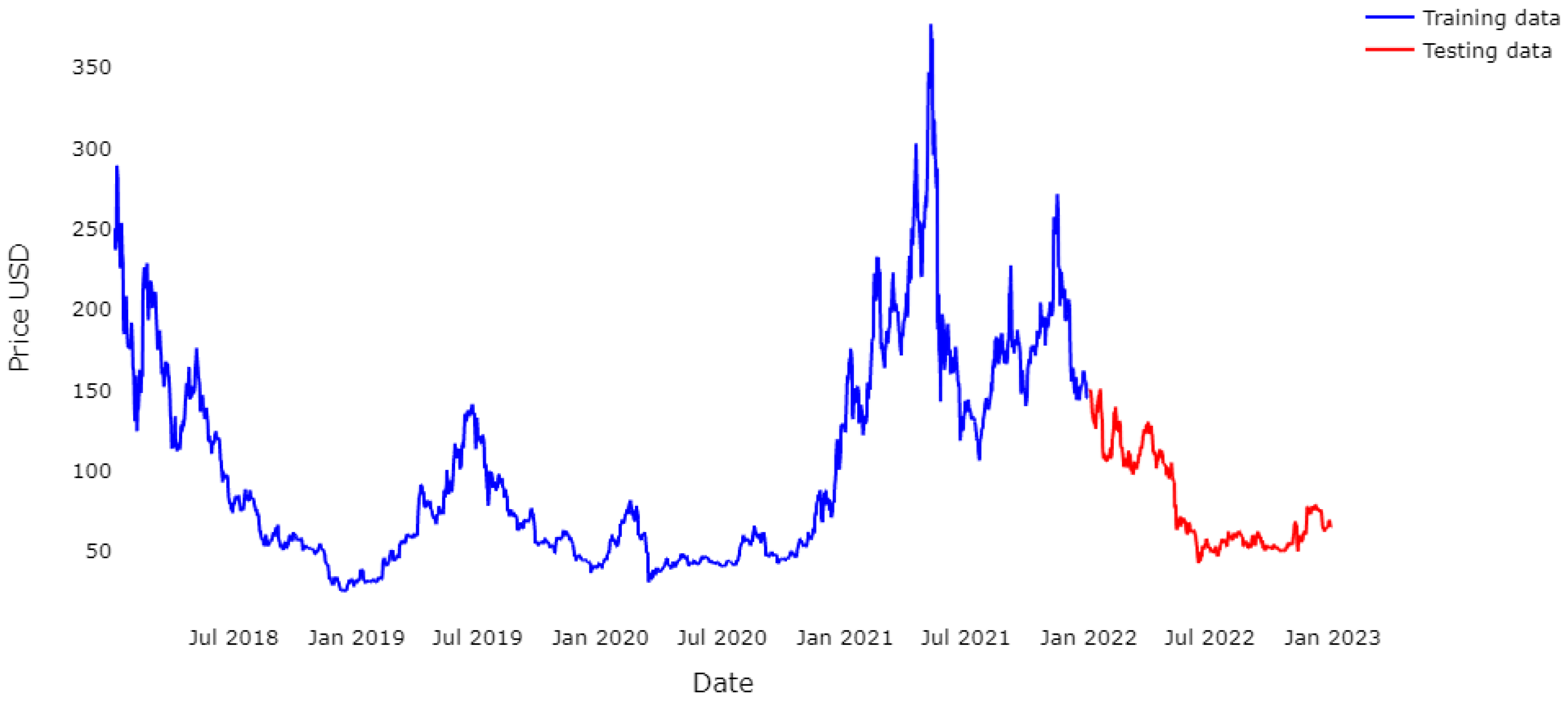
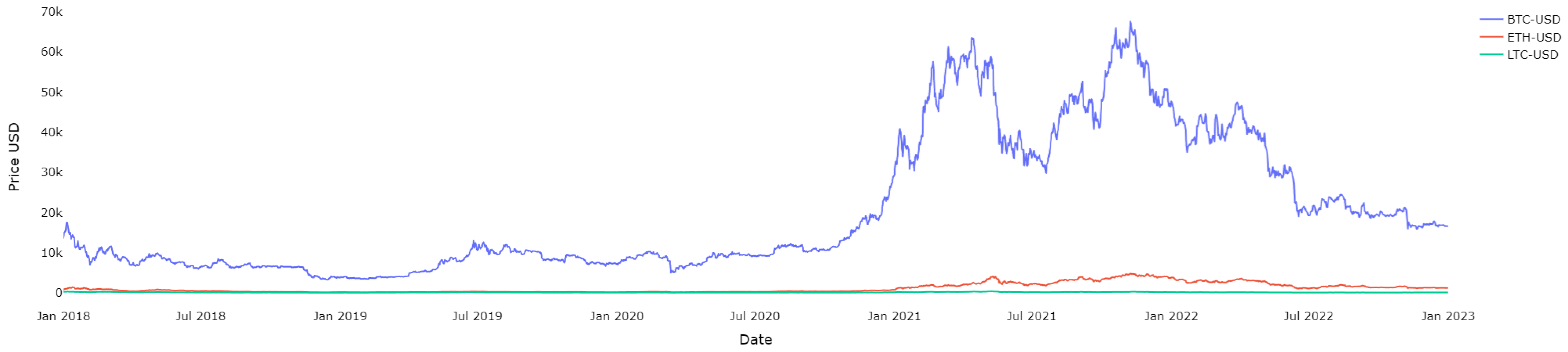
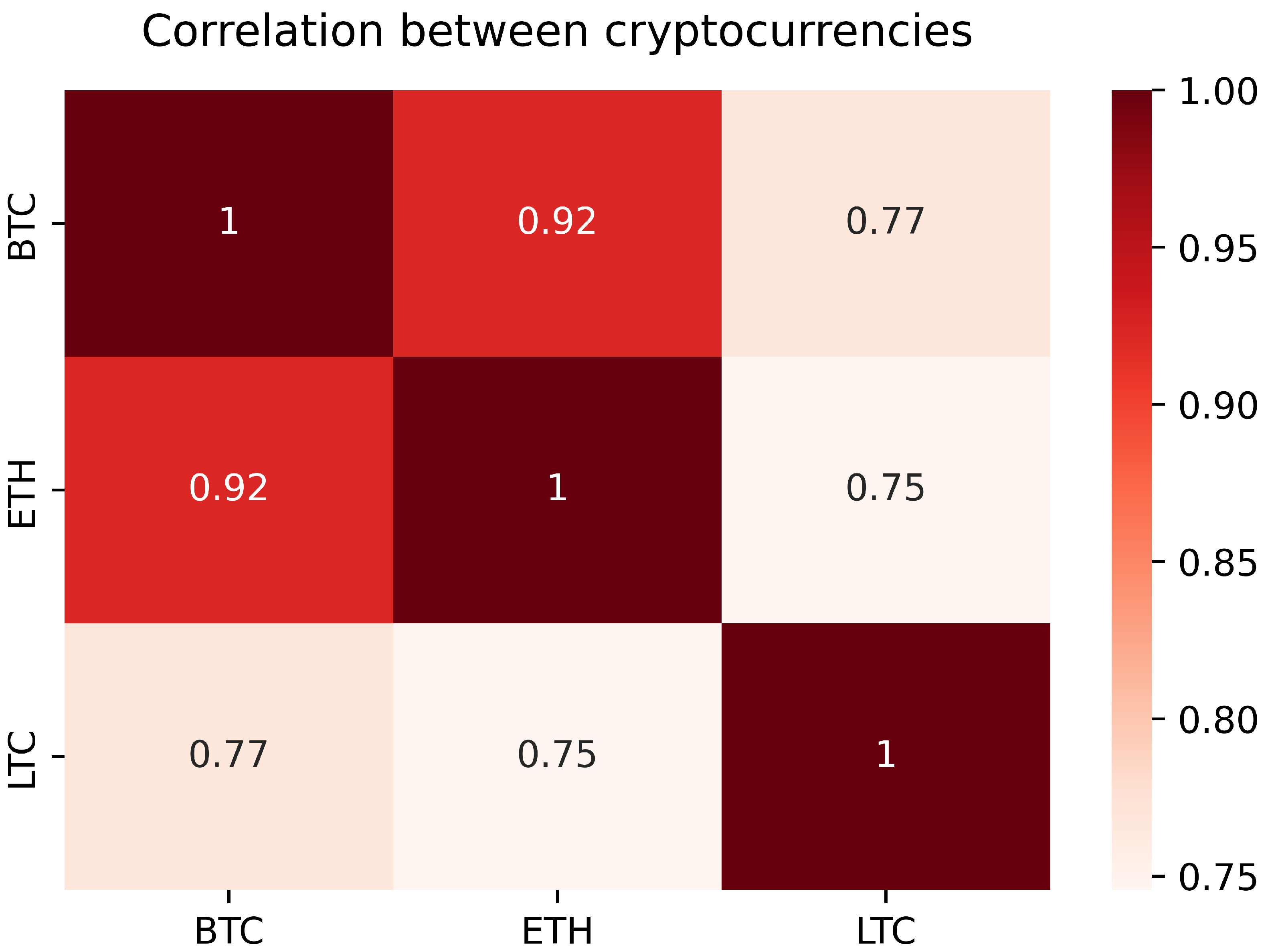
3.1. Dataset
3.2. Deep Leaning Algorithms
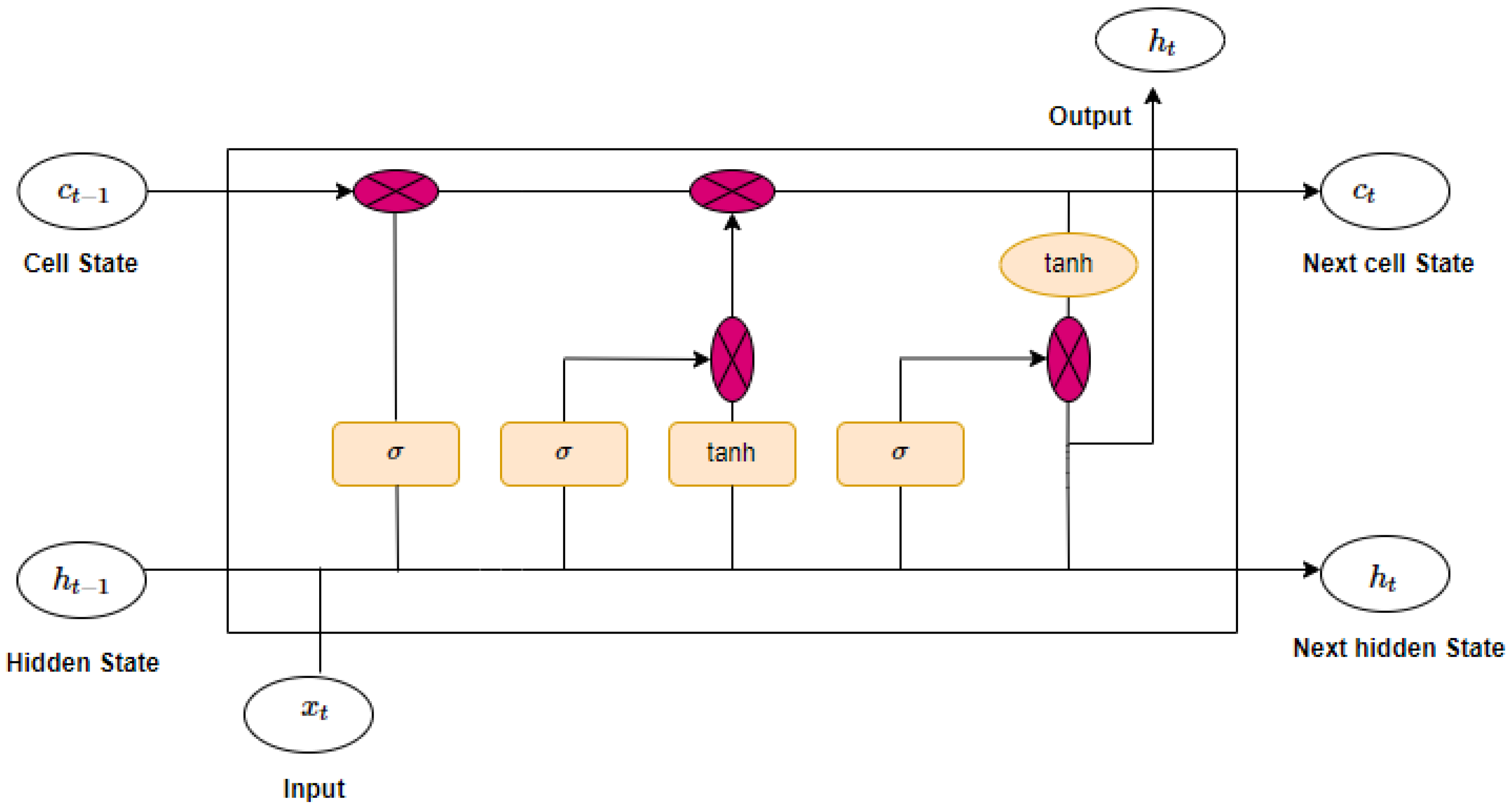
3.2.1. Long Short-Term Memory—LSTM
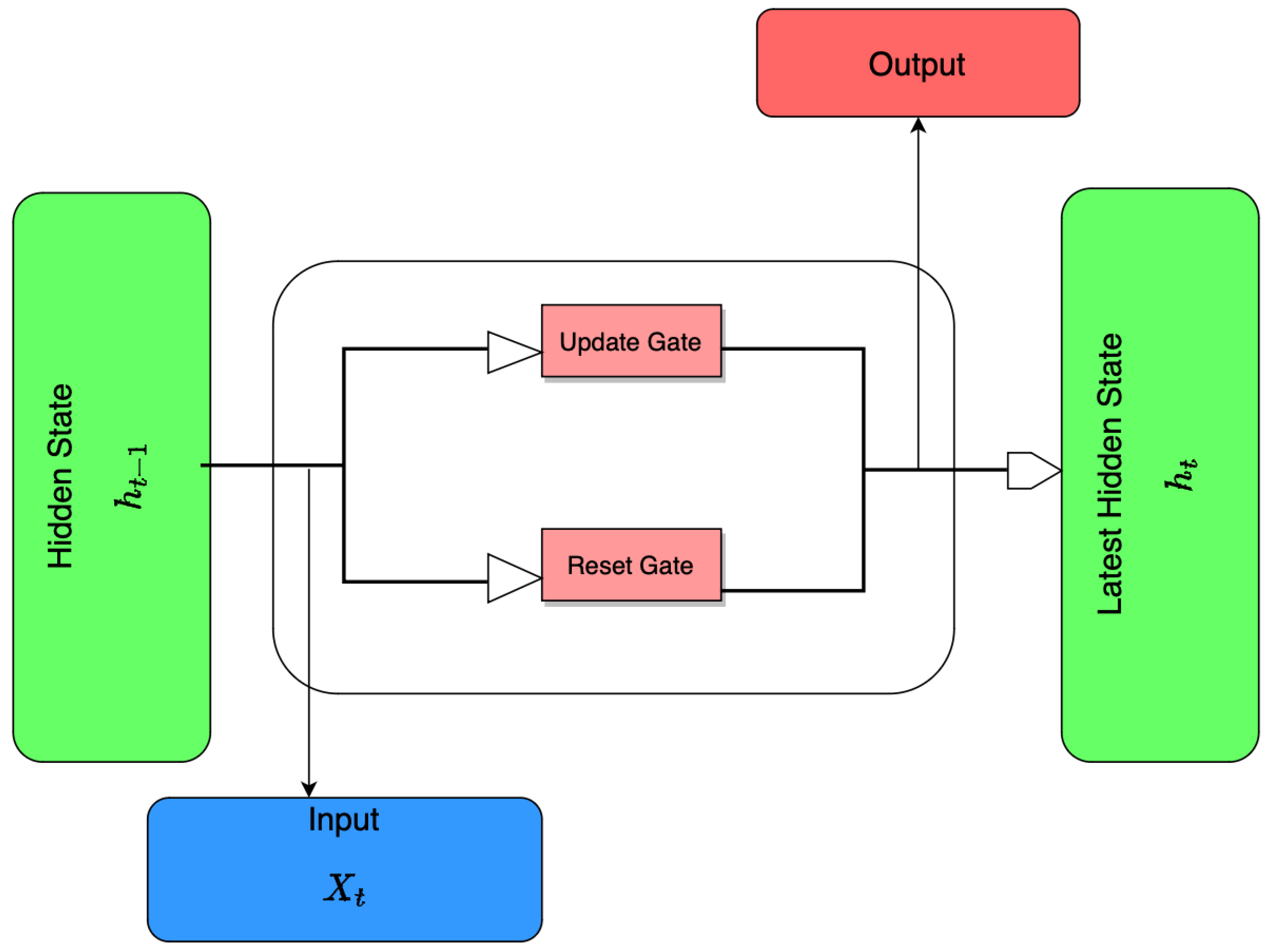
3.2.2. Gated Recurrent Unit—GRU
3.2.3. Bi-Directional LSTM
3.3. Hyperparameter Tuning
3.4. Performance Metrics
4. Results
4.1. Results for BTC
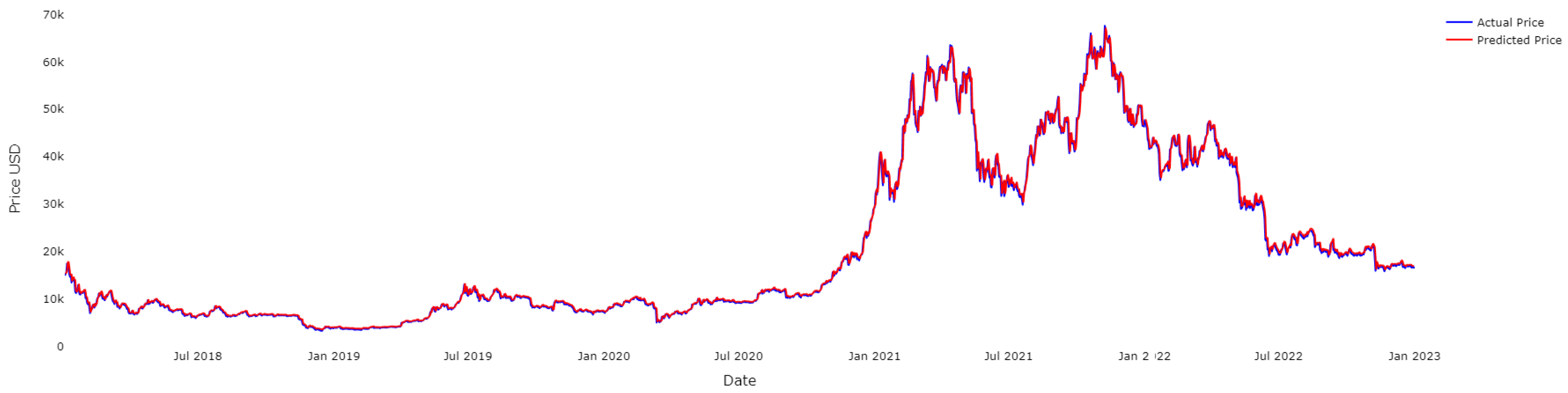
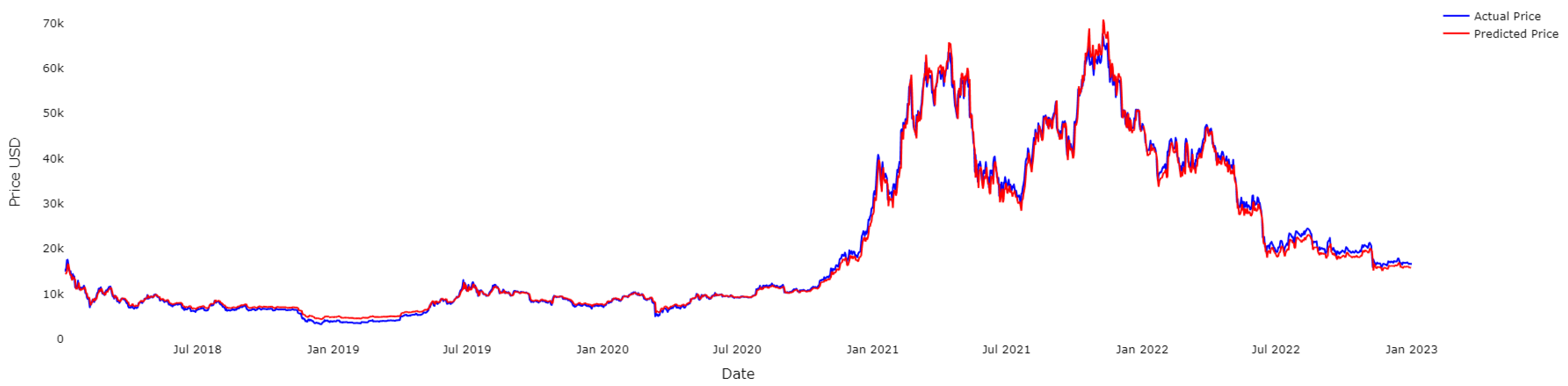
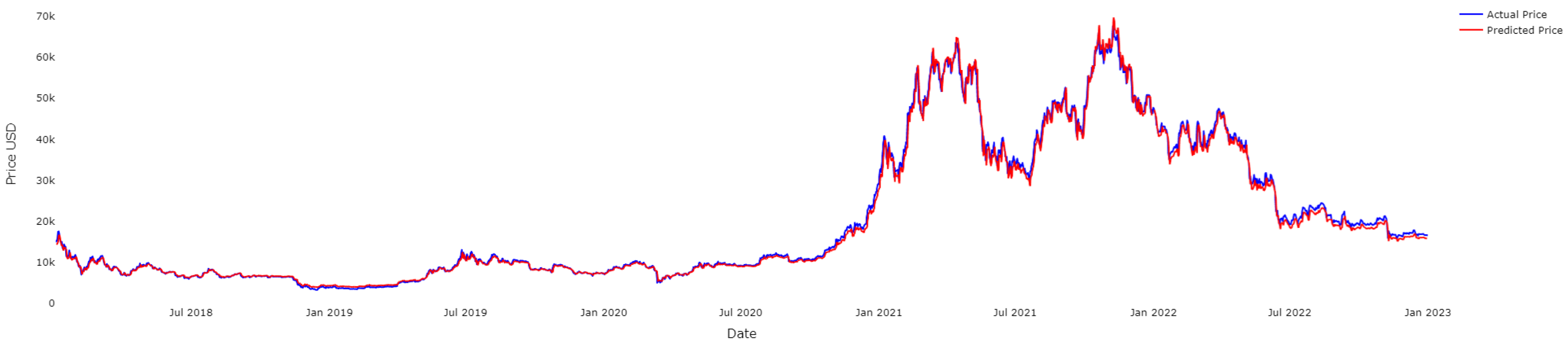
4.2. Results for ETH
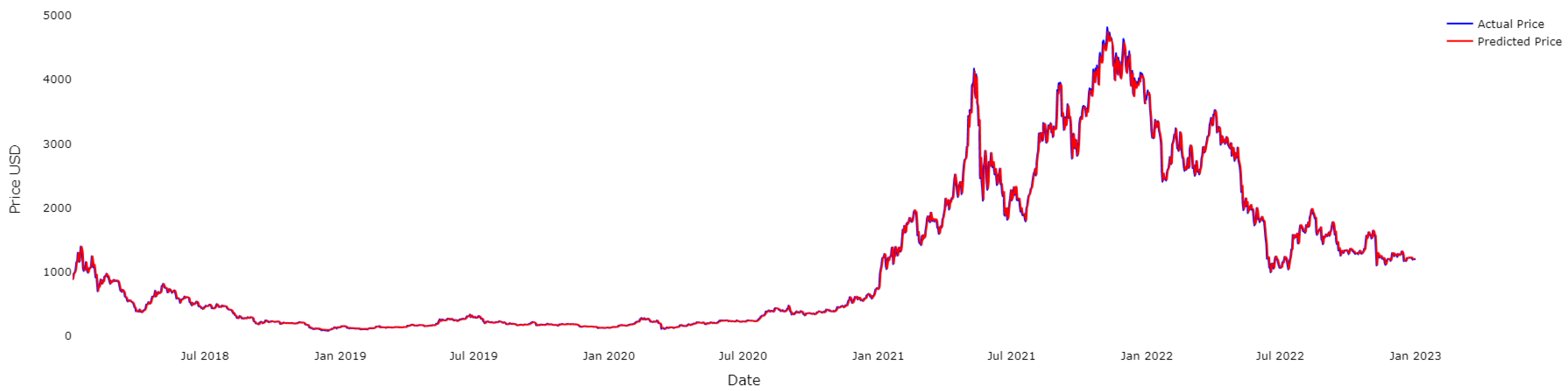
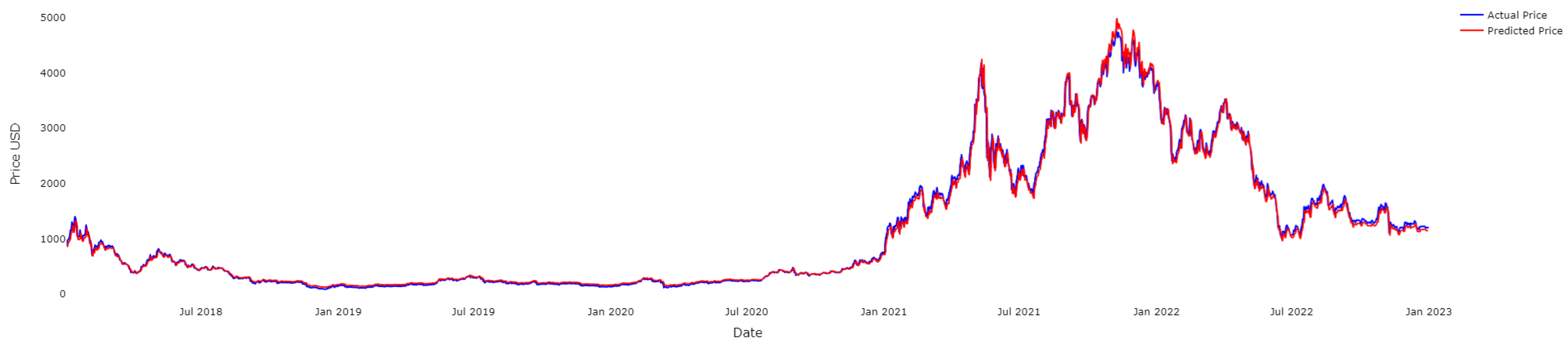
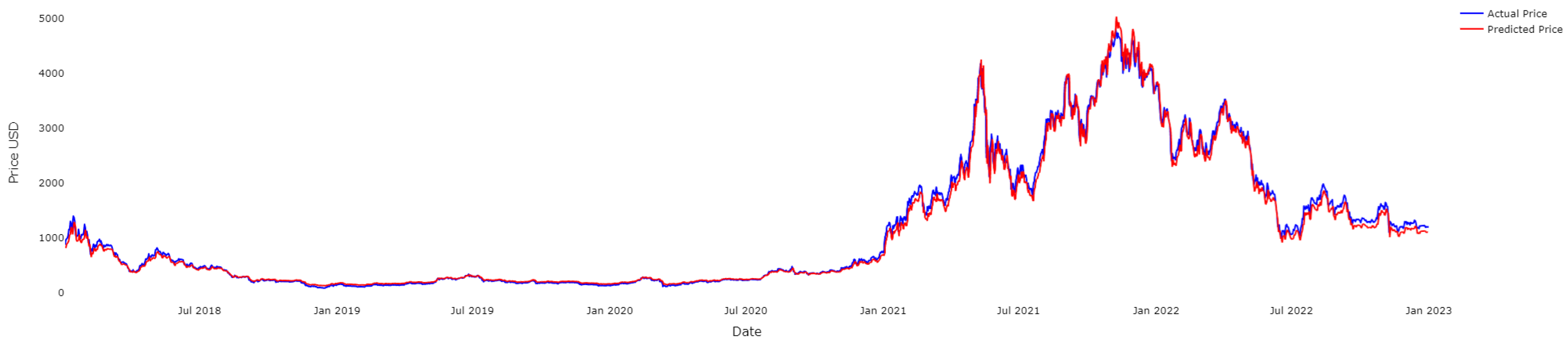
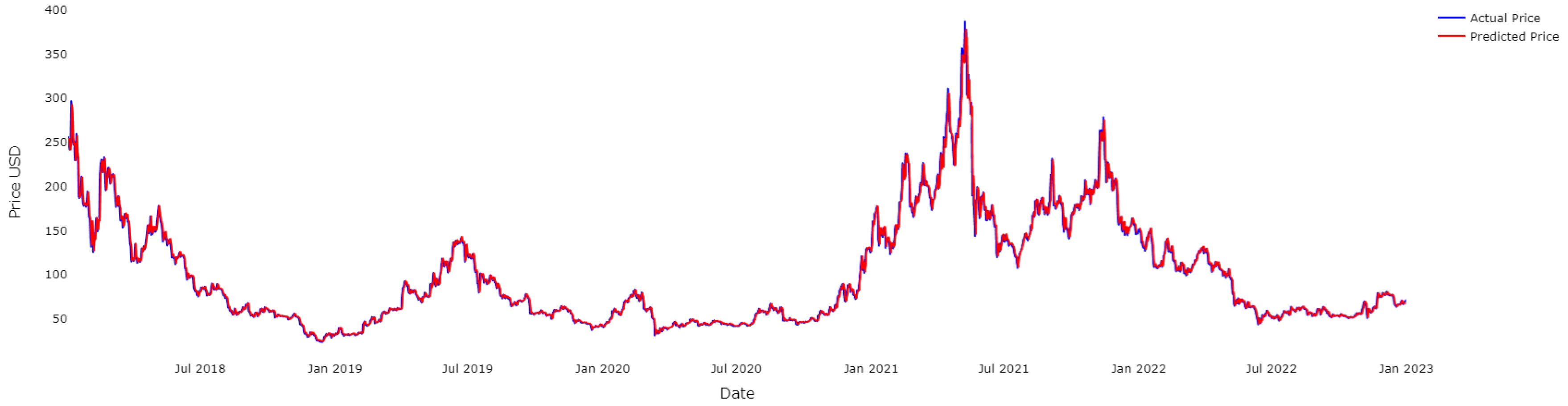
4.3. Results for LTC


5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Melitz, J. DP178 Monetary Discipline, Germany, and the European Monetary System; National Bureau of Economic Research (NBER) Working Paper No. 2319; National Bureau of Economic Research (NBER): Cambridge, MA, USA, 1987; Available online: https://ssrn.com/abstract=884539 (accessed on 24 September 2022).
- Bulíř, A. Income inequality: Does inflation matter? IMF Staff. Pap. 2001, 48, 139–159. [Google Scholar]
- Basco, S. Globalization and financial development: A model of the Dot-Com and the Housing Bubbles. J. Int. Econ. 2014, 92, 78–94. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. Decentralized Bus. Rev. 2008, 21260. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 19 October 2022).
- Sureshbhai, P.N.; Bhattacharya, P.; Tanwar, S. KaRuNa: A blockchain-based sentiment analysis framework for fraud cryptocurrency schemes. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Rose, C. The evolution of digital currencies: Bitcoin, a cryptocurrency causing a monetary revolution. Int. Bus. Econ. Res. J. (IBER) 2015, 14, 617–622. [Google Scholar] [CrossRef]
- Badea, L.; Mungiu-Pupăzan, M.C. The economic and environmental impact of bitcoin. IEEE Access 2021, 9, 48091–48104. [Google Scholar] [CrossRef]
- Vranken, H. Sustainability of bitcoin and blockchains. Curr. Opin. Environ. Sustain. 2017, 28, 1–9. [Google Scholar] [CrossRef]
- Iwamura, M.; Kitamura, Y.; Matsumoto, T. Is bitcoin the only cryptocurrency in the town? economics of cryptocurrency and friedrich a. hayek. SSRN Electron. J. 2014. [Google Scholar] [CrossRef]
- Hassani, H.; Huang, X.; Silva, E. Big-crypto: Big data, blockchain and cryptocurrency. Big Data Cogn. Comput. 2018, 2, 34. [Google Scholar] [CrossRef]
- Hwang, K.; Chen, M. Big-Data Analytics for Cloud, IoT and Cognitive Computing; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Hitam, N.A.; Ismail, A.R.; Samsudin, R.; Alkhammash, E.H. The Effect of Kernel Functions on Cryptocurrency Prediction Using Support Vector Machines. In Proceedings of the International Conference of Reliable Information and Communication Technology; Springer: Cham, Switzerland, 2022; pp. 319–332. [Google Scholar]
- Andrianto, Y.; Diputra, Y. The effect of cryptocurrency on investment portfolio effectiveness. J. Financ. Account. 2017, 5, 229–238. [Google Scholar] [CrossRef]
- Saad, M.; Choi, J.; Nyang, D.; Kim, J.; Mohaisen, A. Toward characterizing blockchain-based cryptocurrencies for highly accurate predictions. IEEE Syst. J. 2019, 14, 321–332. [Google Scholar] [CrossRef]
- Chowdhury, R.; Rahman, M.A.; Rahman, M.S.; Mahdy, M. An approach to predict and forecast the price of constituents and index of cryptocurrency using machine learning. Phys. A Stat. Mech. Its Appl. 2020, 551, 124569. [Google Scholar] [CrossRef]
- Derbentsev, V.; Babenko, V.; Khrustalev, K.; Obruch, H.; Khrustalova, S. Comparative performance of machine learning ensemble algorithms for forecasting cryptocurrency prices. Int. J. Eng. 2021, 34, 140–148. [Google Scholar]
- Chen, W.; Xu, H.; Jia, L.; Gao, Y. Machine learning model for Bitcoin exchange rate prediction using economic and technology determinants. Int. J. Forecast. 2021, 37, 28–43. [Google Scholar] [CrossRef]
- Patel, M.M.; Tanwar, S.; Gupta, R.; Kumar, N. A deep learning-based cryptocurrency price prediction scheme for financial institutions. J. Inf. Secur. Appl. 2020, 55, 102583. [Google Scholar] [CrossRef]
- Wu, C.H.; Lu, C.C.; Ma, Y.F.; Lu, R.S. A new forecasting framework for bitcoin price with LSTM. In Proceedings of the 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singapore, 17–20 November 2018; pp. 168–175. [Google Scholar]
- Livieris, I.E.; Pintelas, E.; Stavroyiannis, S.; Pintelas, P. Ensemble deep learning models for forecasting cryptocurrency time-series. Algorithms 2020, 13, 121. [Google Scholar] [CrossRef]
- Derbentsev, V.; Datsenko, N.; Babenko, V.; Pushko, O.; Pursky, O. Forecasting Cryptocurrency Prices Using Ensembles-Based Machine Learning Approach. In Proceedings of the 2020 IEEE International Conference on Problems of Infocommunications. Science and Technology (PIC S&T), Kharkiv, Ukraine, 6–9 October 2020; pp. 707–712. [Google Scholar]
- Zhang, Z.; Dai, H.N.; Zhou, J.; Mondal, S.K.; García, M.M.; Wang, H. Forecasting cryptocurrency price using convolutional neural networks with weighted and attentive memory channels. Expert Syst. Appl. 2021, 183, 115378. [Google Scholar] [CrossRef]
- Ahsan, M.M.; Mahmud, M.P.; Saha, P.K.; Gupta, K.D.; Siddique, Z. Effect of data scaling methods on machine learning algorithms and model performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ayoobi, N.; Sharifrazi, D.; Alizadehsani, R.; Shoeibi, A.; Gorriz, J.M.; Moosaei, H.; Khosravi, A.; Nahavandi, S.; Chofreh, A.G.; Goni, F.A.; et al. Time series forecasting of new cases and new deaths rate for COVID-19 using deep learning methods. Results Phys. 2021, 27, 104495. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and gru neural network performance comparison study: Taking yelp review dataset as an example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; pp. 98–101. [Google Scholar]
- Wang, X.; Jiang, W.; Luo, Z. Combination of convolutional and recurrent neural network for sentiment analysis of short texts. In Proceedings of the Proceedings of COLING 2016, the 26th International Conference on Computational Linguistics: Technical Papers, Osaka, Japan, 11–16 December 2016; pp. 2428–2437. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Lai, S.; Ye, C.; Zhou, H.J.H. Chinese stock trend prediction based on multi-feature learning and model fusion. In Proceedings of the 2021 IEEE International Conference on Smart Data Services (SMDS), Chicago, IL, USA, 5–10 September 2021; pp. 18–23. [Google Scholar]
- Singh, A.; Kumar, A.; Akhtar, Z. Bitcoin Price Prediction: A Deep Learning Approach. In Proceedings of the 2021 8th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 26–27 August 2021; pp. 1053–1058. [Google Scholar]
- Althelaya, K.A.; El-Alfy, E.S.M.; Mohammed, S. Stock market forecast using multivariate analysis with bidirectional and stacked (LSTM, GRU). In Proceedings of the 2018 21st Saudi Computer Society National Computer Conference (NCC), Riyadh, Saudi Arabia, 25–26 April 2018; pp. 1–7. [Google Scholar]
- Na, Z.; Wang, Y.; Li, X.; Xia, J.; Liu, X.; Xiong, M.; Lu, W. Subcarrier allocation based simultaneous wireless information and power transfer algorithm in 5G cooperative OFDM communication systems. Phys. Commun. 2018, 29, 164–170. [Google Scholar] [CrossRef]
- Hansun, S.; Wicaksana, A.; Khaliq, A.Q. Multivariate cryptocurrency prediction: Comparative analysis of three recurrent neural networks approaches. J. Big Data 2022, 9, 1–15. [Google Scholar] [CrossRef]
- Ozturk Birim, S. An Analysis for Cryptocurrency Price Prediction Using Lstm, Gru, and the Bi- Directional Implications. In Developments in Financial and Economic Fields at the National and Global Scale; Cömert, M., Şimşek, A.E., Eds.; Gazi Kitabevi: Ankara, Türkiye, 2022; pp. 377–392. [Google Scholar]

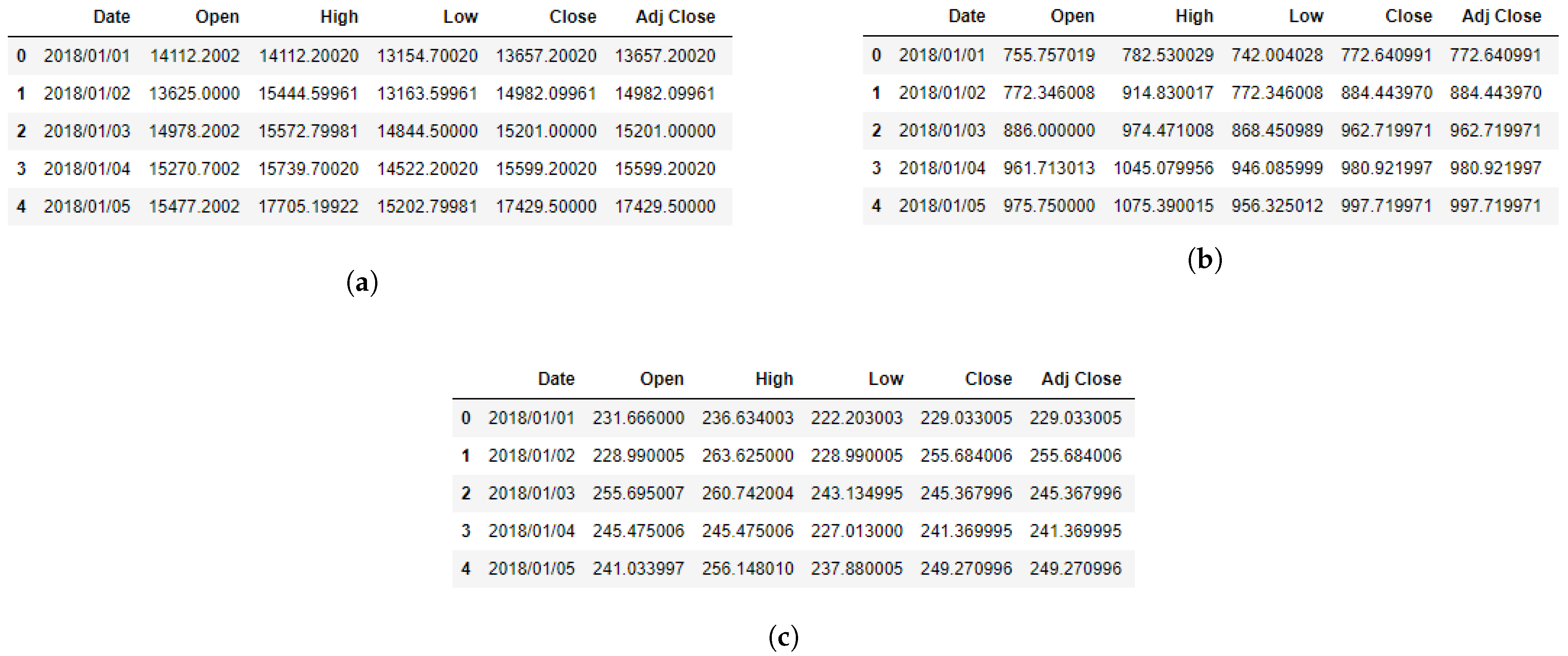

| Parameter | Description | Data Type |
|---|---|---|
| Date | Date of the observation | Date |
| Open | Daily opening price of the selected cryptocurrency | Number |
| High | Daily high price of the selected cryptocurrency | Number |
| Low | Daily low price of the selected cryptocurrency | Number |
| Close | Daily close price of the selected cryptocurrency | Number |
| Close Adj Close | Daily Adjusted close price of the selected cryptocurrency | Number |
| Currency | Model | RMSE | MAPE |
|---|---|---|---|
| BTC | LSTM | 1031.3401 | 0.0394 |
| Bi-LSTM | 1029.3617 | 0.0356 | |
| GRU | 1274.1706 | 0.0572 | |
| ETH | LSTM | 148.5215 | 0.2971 |
| Bi-LSTM | 83.9531 | 0.1243 | |
| GRU | 98.3136 | 0.1479 | |
| LTC | LSTM | 9.6680 | 0.0636 |
| Bi-LSTM | 8.0249 | 0.0411 | |
| GRU | 8.1224 | 0.0458 |
| Authors | Cryptocurrencies | Methods | MAPE | RMSE |
|---|---|---|---|---|
| [35] | BTC - USD | LSTM | 0.042 | 2518.02 |
| Bi-LSTM | 0.038 | 2222.74 | ||
| GRU | 0.035 | 1777.31 | ||
| [35] | ETH -USD | LSTM | 0.064 | 150.09 |
| Bi-LSTM | 0.060 | 147.85 | ||
| GRU | 0.057 | 151.62 | ||
| [36] | BTC - USD | LSTM | 0.040 | 2350.53 |
| Bi-LSTM | 0.033 | 1992.88 | ||
| GRU | 0.053 | 3223.01 | ||
| [36] | ETH -USD | LSTM | 0.047 | 183.84 |
| Bi-LSTM | 0.042 | 168.60 | ||
| GRU | 0.047 | 181.03 | ||
| [36] | XRP -USD | LSTM | 0.063 | 0.098 |
| Bi-LSTM | 0.048 | 0.079 | ||
| GRU | 0.072 | 0.104 | ||
| Our approach | BTC - USD | LSTM | 0.039 | 1031.340 |
| Bi-LSTM | 0.036 | 1029.362 | ||
| GRU | 0.057 | 1274.171 | ||
| Our approach | ETH -USD | LSTM | 0.297 | 148.522 |
| Bi-LSTM | 0.124 | 83.953 | ||
| GRU | 0.148 | 98.314 | ||
| Our approach | LTC-USD | LSTM | 0.064 | 9.668 |
| Bi-LSTM | 0.041 | 8.025 | ||
| GRU | 0.046 | 8.122 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seabe, P.L.; Moutsinga, C.R.B.; Pindza, E. Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach. Fractal Fract. 2023, 7, 203. https://doi.org/10.3390/fractalfract7020203
Seabe PL, Moutsinga CRB, Pindza E. Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach. Fractal and Fractional. 2023; 7(2):203. https://doi.org/10.3390/fractalfract7020203
Chicago/Turabian StyleSeabe, Phumudzo Lloyd, Claude Rodrigue Bambe Moutsinga, and Edson Pindza. 2023. "Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach" Fractal and Fractional 7, no. 2: 203. https://doi.org/10.3390/fractalfract7020203
APA StyleSeabe, P. L., Moutsinga, C. R. B., & Pindza, E. (2023). Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach. Fractal and Fractional, 7(2), 203. https://doi.org/10.3390/fractalfract7020203







