Application of Empirical Bode Analysis for Delay-Margin Evaluation of Fractional-Order PI Controller in a Renewable Distributed Hybrid System

Abstract

For an uninterrupted power supply, renewable energy promises to be a suitable alternative compared to the conventional sources. System delays or communication delays may cause significant synchronization imbalances between various components in big electrical grids. Since the properties of solar and wind generation constantly change with climatic circumstances, engineers encounter many difficulties when substituting sustainable power with conventional electricity. The computation delay margin may be leveraged to handle a time-delayed automatic generation control (AGC) system. In order to regulate a distributed hybrid renewable energy system in a three-area AGC configuration, this paper investigates the influence of the fractional integral order on the stable system’s delay parameter region. By changing the fractional order range, the delay margin can be increased, potentially broadening the time-delayed system’s stability region. The controller’s stability region has dependency on the order of fraction and the time delay. For this purpose, the asymptotic Bode diagram of the time-delayed fractional proportional-integral controller is determined. The gain and phase margins are used to calculate the delay margin for the application in discussion. The Honey Badger algorithm helps to adjust the controller parameters. It is also confirmed that the suggested controller is resilient to random load perturbations, nonlinearities, and parameter variations.

1. Introduction

For the past few decades, renewable-resource research has been creating a roadmap for green energy [1] across 143 countries in order to battle the greenhouse effect and environmental pollution and to improve energy stability. The issues posed by global warming inspire energy policymakers to continue their research in this field. Due to the rapid change in characteristics of diverse RERs such as solar [2] and wind into the current power system, some issues and constraints on the system’s stability, security, operation, and control have become major factors. With a big interconnected grid, this may result in a large synchronising imbalance between different units, considerable system latency, or communication delay. Hence, researchers devote a large span of time and effort to identifying control strategies to balance supply and demand.

Automatic generation control (AGC) ensures the overall system’s reliability and power quality in the power sector. For the past few decades, an open communication channel [3] has been allocated to exchange information between the control unit and the generating station via a remote terminal unit. To run a deregulated market using open communication [4] channels between generation companies (GENCOs) and distribution companies (DISCOs), communication delay may be acceptable during the construction and operation of vast interconnected grids. However, in a vast area of interconnected grid, various nonlinearities and communication delays have a significant impact on system stability. Open networks also expose numerous deficiencies in distributed generation system (DGS)-AGC services, such as increased communication lag, packet loss, and cyber attacks (e.g., false data injection). Hence, it is critical to figure out how communication variations in DGS-AGC affect system frequency stability in the future electric grid with severe intensity. Depending on the exact communications networks, normal time delays ranging from a few tens to hundreds of milliseconds are imposed when sending and processing remote signals. These delays are projected to increase when open communication channels and layered structures (DGS aggregators) are implemented, especially during periods of congested communication due to the massive amount of data interchange. The overall time delay also affects the AGC system’s damping performance, resulting in synchronism loss and system instability [5]. Within a wide area interconnected system, depending on the non-linearity, these delays could range upto several hundreds of milliseconds [6]. As a result, determining the margin of allowable delay (MADB) [7] is critical for understanding the consequences of delay-coupled systems.

There are numerous methods for measuring the stability delay margin of a symmetrical system with time delay. These can be classified into two categories such as (i) delay margin analysis in frequency-domain methods, and (ii) delay margin analysis using time-domain methods. In the frequency domain, the Schur–Cohn approach [8], Rekasius’s substitution [9], Kronecker multiplication [10], root locus analysis [11], and empirical bode analysis (EBA) [12] are the techniques for evaluating the delay margin. Delay evaluation in the time domain is demonstrated by the frequency sweeping test [13] and the linear matrix inequality [14] approach. All of the existing approaches outlined above aim to compute delay margin only on the basis of stability, and estimates of the delay margin values at which the load-frequency control (LFC) system will be marginally stable for a particular set of proportional-integral (PI) controller gains for various fractional orders. However, practical LFC systems cannot operate near such sites due to unacceptable frequency-response oscillation. As a result, various design specifications such as gain margin (GM) and phase margin (PM) that provide a desired dynamic performance (i.e., damping, overshoot, and settling time) must be taken into account in delay-margin calculation in addition to addressing the stability consideration.

The time-domain based direct technique fails to compute MADB when GM and PM are taken into account because it is not possible to incorporate GM and PM in the computational procedure. In contrast, the frequency-domain methods may be able to solve this issue. By maximizing an objective function, time-domain optimization algorithms look for the best controller settings. The resultant closed-loop control system can attain the best time-domain dynamic performance. However, system stability with gain and phase margins, as well as frequency-domain resilience performance, should be assured at the same time.

The application of different optimization techniques for solving AGC problems has been reported in the literature. Some traditional optimization techniques have strong convergence characteristics, but they suffer from a local optimality problem. Different heuristic strategies are efficiently adapted to various AGC problems to prevent this form of local optimality. For tuning the integral-minus tilt-derivative control with filter, Babu et al. developed the hybrid crow-search with the particle swarm optimization [15] technique. A novel adaptive distributed auction-based algorithm [16] was employed for optimal mileage basis dispatch to quickly identify a high-quality dispatch scheme in a distributed way. The gravitational search algorithm [17] was proposed for adjusting a dual PI-based load-frequency controller. Shouran et al. [18] used the bees algorithm to the proportional integral derivative (PID)/fuzzy PID filter (FPIDF)/fractional-order PID (FOPID) controller to stabilize and balance the frequency in the multi source system at the rated value. In a multi-area system, Hakimuddin et al. employed the bacteria foraging algorithm [19] for the tuning of PID controller. To optimize the weighted matrices of the linear quadratic controller, Mohanty et al. proposed [20] the modified fruit fly optimization algorithm (MFOA) to a multi source system. Goswami et al. proposed a new heuristic algorithm called the chaotic oppositional krill herd algorithm (COKHA) [21] for solving multi-source AGC problems. For the frequency control of multi-area power systems with wind power penetration, Elsisi et al. proposed a novel supervisor fuzzy nonlinear sliding mode control algorithm [22]. Biswas et al. [23] applied the grasshopper optimization algorithm (GOA) to solve AGC in a deregulated environment. Hashim et al. recently developed the honey badger algorithm (HBA) [24] for solving different types of optimization problems.

The literature survey on traditional controllers proves that their performances worsen as the nonlinearities increase and the disturbance rejection capability decreases. Furthermore, the classical controller only takes countermeasures against disturbances when the control variable deviates from the reference level. The capacity to reject disturbances can be improved by incorporating fractional order into conventional controllers. To increase the performance of typical integral (I)/PI/PID [25] controllers, fractional order I (FOI) [26], fractional-order PI (FOPI) [26], and FOPID [27] controllers are suggested. Fractional calculus theory is applied to I/PI/PID controllers, resulting in the FOI/FOPI/FOPID models, to improve their performance. FO controllers have been used to solve AGC problems in power systems during the last few years and have shown to be superior to traditional controllers. Heuristic techniques have become very effective to enhance the performance of fractional-order controllers, such as the ICA optimization [28] technique applied to the CFFOPI–FOPID controller, and the Firefly algorithm optimized FOI/FOPI/2DOF-FOPID [29] controllers to single- and two-area power systems . Nayak et al. [30] suggested a hybrid salp swarm algorithm-simulated annealing based three-degree-of-freedom FO-PID controller on a two-area hybrid system. A non-fragile PID controller [31] was also used to regulate the frequency of an interconnected multi-source (restructured environment) system.

Due to various non-linearities present in the system, the RERs-based hybrid system with continuous time delay is the subject of this paper. The main goal of this paper is to develop a relationship between delay margin (${\tau }_{dm}$) and fractional order ($\lambda$) in the $K_P$–$K_I$ parameter plane, which not only robustly stabilizes uncertain control systems with varying rate $\mu =0$ but also specifically determines the stability region for the different order ($\lambda$) of the FOPI controller. This is performed by using EBA to determine the delay margin [32] using GM and PM for various fractional orders ($\lambda$ varying from 0 to 1) of the FOPI controllers. The contributions of this research are as follows:

1.

This article proposes a method for designing delay dependent stable systems using EBA and the delay-margin calculation (MADB) of constant time-delay systems.

2.

This study also demonstrates how nonlinearities can generate delays, lowering the dynamic performance of an AGC system and, in the worst-case scenario, causing a significant stability concern. The delay margin for an FOPI controller is estimated using the proposed (EBA) [32] method, and the controller is designed using a systematic methodology.

3.

To test the efficacy of the suggested approach on a three-area renewable-based [31] hybrid system with distributed generation [33] in a deregulated environment for constant delays, ($\mu =0$) is considered.

4.

The simulation results validate the accuracy of the EBA used to calculate the delay margin of the FOPI controller for a certain fractional order range ($\lambda$ = 0 to 1). The increase in the fractional order value ($\lambda$) may enhance the delay margin (${\tau }_{dm}$) for a specific control parameter set ($K_P$ and $K_I$) and vice versa. As a result, the higher value of $\lambda$ is preferable, which is used to optimize the hybrid system’s dynamic response with a set delay margin. HBA [24] has been devised in this work for the fine-tuning of the above control parameters. The taxonomy of the publications regarding the time-delay-based AGC system is shown in Table 1.

Table 1. The following is a taxonomy of the publications regarding the time-delay-based AGC system.

References	AGC System							Area	Time Delay	Controllers					Prototype	${\mathit{\tau }}_{\mathit{d}}\mathbf{Vs}$ Controller Type			Stability Region
	Thermal	Gas	Solar	Hydro	Wind	EV	DGS *	Type		I	PI	PID	FOPI	FACTs		I	PI	FOPI	with Fractional Order
[7]	√		√		√			Two	Yes		√			√			√
[26]	√	√		√				Two	Yes				√	√	TID
[34]	√							single	Yes						MPC
[11]	√			√				Two	Yes		√						√
[14]	√							Two	Yes		√						√
[34]				√				Single	Yes	√						√
[35]				√				Single	Yes	√						√
[36]	√		√					Two	Yes			√			PIDN
[37]	√							Two	Yes						MPC
[4]	√					√		Two	Yes			√			FPID
[38]	√							Two	Yes			√			DMPID
Present work	√		√		√		√	Three	Yes				√					√	√

* Distributed generation system (DGS).

5.

In the AGC system, FOPI [26,27] and other combinations[29] are still employed directly for frequency regulation. In contrast, the author of this paper attempts to develop the relationship between the FOPI controller’s fractional order ($\lambda$) and the delay margin for MADB evaluation in a time-delayed agc system.

2. Description of the Proposed System

A two-area thermal [20] system has been considered as the primary test system (Test system-1) in this paper. Initially, test system-1 was used to test the efficacy of the HBA against other evolutionary algorithms such as BFA [19], MFOA [20], COKHA [21], and and GOA [23]. Then, the research is extended to a three-area hybrid system with distributed generation in a deregulated environment (test system 2) [23] that includes non-conventional resources such as solar and wind power plants with distributed generation [33]. For test system-1, the total power rating of the power system is 600 MW, with each area consisting of 300 MW units. Total output power for test system 2 has been set at 1600 MW, with 750 MW, 50 MW, 600 MW, and 200 MW being allocated to thermal, wind, solar, and distributed generation, respectively, as illustrated in Figure 1. The details of the DGS are discussed below.

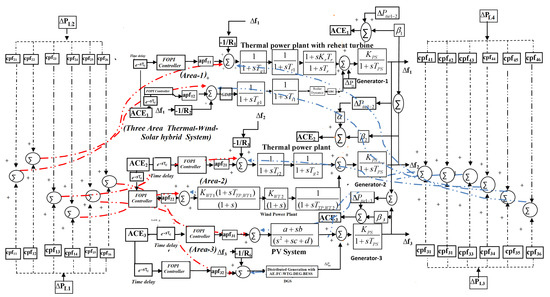
Figure 1. Linearized model of three−area renewable−based (Solar−PV) system with distributed generation.

2.1. Wind-Turbine Generator (WTG)

Wind power, also known as wind energy, is the use of air movement through wind turbines that fluctuates with time and is connected to previous wind speeds. The auto regressive and moving average time-series models can be used to represent the changer of wind speed over time. Mathematically, the wind speed may be expressed as per (1)

$$y\left(t\right)=\sum _{i=1}^n{\Phi }_i{y}_{t-i}+{\alpha }_t-\sum _{j=1}^m{\theta }_j{\alpha }_{t-j},$$

(1)

where ${\Phi }_i,{\alpha }_t$ and ${\theta }_j$ are the auto regressive parameter, moving average parameter, and a normal white noise process with zero mean in order. Calculation for the speed of wind may be carried out according to (2).

$${\omega }_{WT}={\eta }_{WT}+{\sigma }_{WT}x\left(t\right),$$

(2)

where the mean and standard deviation of wind speed are ${\eta }_{W}T$ and ${\sigma }_{W}T$, respectively. The output power of wind power generation is calculated using (3), which is shown in Figure 2.

$$\begin{array}{c}{P}_{WTG}=0\mathrm{if}{\omega }_{WT}<W_{in},{\omega }_{WT}>W_{out};\hfill \\ P_{WTG}=\lambda \left(WS-W_{in}\right)\mathrm{if}{W}_{in}<{\omega }_{WT}<W_{rs};\hfill \\ P_{WTG}=1\mathrm{if}{W}_{rs}<{\omega }_{WT}<W_{out}.\hfill \end{array}$$

(3)

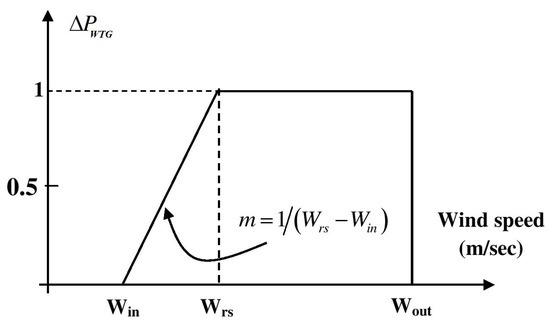
Figure 2. Characteristic of the wind turbine.

Equation (3) represents cut-in, rated, and cut-out wind speed, respectively, where the straight line passes through the points of cut-in and rated wind speed. The linear approximated model of wind-turbine generator for LFC analysis is given by the first-order transfer function, as defined by (4).

$$\begin{array}{c}{G}_{WTG}\left(s\right)=\frac{K_{WTG}}{(1+s{T}_{WTG})},\hfill \end{array}$$

(4)

where $\Delta P_{WTG}$ represents change in power output in wind power generator.

2.2. Aqua Electrolyzer and Fuel Cell

Hydrogen cell is the alternative resource for electric power generation. Aqua electrolyzer (AE) takes a portion of $(1-\gamma )$ WTG to disintegrate water molecules into hydrogen gas, that can then be utilized to generate electricity via the fuel cell (FC). AE and FC play an important role in producing the electrical power in the DGS. The transfer functions of AE and FC are defined as per (5).

$$\begin{array}{c}{G}_{AE}=\frac{K_{AE}}{1+s{T}_{AE}},\hfill \\ G_{FC}=\frac{K_{FC}}{1+s{T}_{FC}},\hfill \end{array}$$

(5)

where the gain of AE and FC systems are given by $K_{AE}$&$K_{FC}$; $T_{AE}$&$T_{FC}$ are the time constants of AE & FC, respectively.

2.3. Diesel Unit

Usually a diesel power station (also known as stand-by power station) uses a diesel engine as a prime mover for the generation of electrical energy. This power station may work as an auxiliary power generating unit. This kind of power station can be used to produce limited amount of electrical energy that may serve as an emergency supply station. The transfer function of the diesel power plant is stated in (6).

$$G_{DEG}\left(s\right)=\frac{K_{DEG}}{1+s{T}_{DEG}},$$

(6)

where $\Delta P_{DEG}$ is incremental change of output power from diesel power plant; $K_{DEG}$ and $T_{DEG}$ are the gain and time constant, respectively, of the diesel unit plant.

2.4. Battery-Energy-Storage System (BESS)

Storage renewable energy resources are used to maintain the constant power flow through tie-line during intermittent load demand, especially in the peak-demand period. The role of BESS (such as the Tesla power wall battery, the redox-flow battery, and the super-magnetic energy storage devices) in the grid is elucidated below:

1.

Maintain proper coordination between different generating units.

2.

Optimize the operating cost.

3.

The BESS consists of power coverter with bank of DC batteries. The power converter is helpful for bi-directional power conversion (DC to AC and vice-versa) as per the grid requirement.

4.

It is also used to neutralize the system harmonics and control the system voltage.

5.

The transfer function of the BESS is modeled as per (7).

$$G_{BESS}\left(s\right)=\frac{K_{BESS}}{1+s{T}_{BESS}},$$

(7)

where $K_{BESS}$ and $T_{BESS}$ are the gain value and time constant, respectively, of the BESS.

The linearized model of a DGS is illustrated in Figure 3a. As shown in Figure 3b–d, some non-linearities are included to the thermal unit, such as the governor dead-band (GDB), boiler dynamics (BD), and governor rate constraints (GRC), to test the effectiveness of HBA in a realistic environment. In the literature, GRC has been calculated to be 3% every minute. Backlash non-linearity of 2% for the thermal system and 0.05% for the hydro system are usually considered. In a deregulated environment, this research studies a delay-dependent stability. Before the controller, a single delay is taken into account, which is caused by nonlinearities and a lack of synchronism between solar, wind, and thermal power plants. It is expressed by an exponential term, $e^{-s{\tau }_d}$ [34,39] where ${\tau }_d$ indicates the total time delay in the system. The use of a three-area hybrid system (thermal, wind, and solar) with DGS is being studied [23] under the deregulated environment.

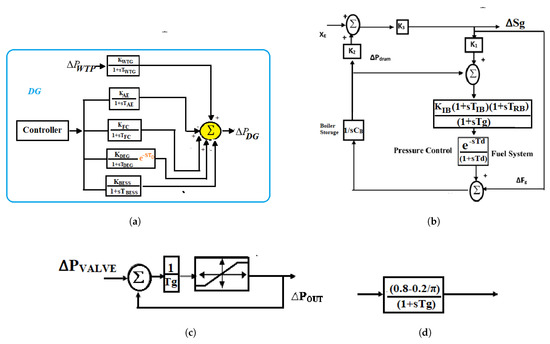
Figure 3. (a) Linearized model of DGS. (b) Schematic block diagram of boiler dynamics in test system 2. (c) Schematic Block diagram of GRC in test system 2. (d) Schematic diagram of governor dead−band in test system 2.

As previously stated, the total study was conducted in a deregulated environment, with the power contracts between various DISCOs and GENCOS being reflected in the distribution participation matrix (DPM) for the various scenarios (unilateral, bi-lateral, and contract-violation).

Hence, DPM can be defined as per ().

$$\mathrm{DPM}=\left[\begin{array}{cccc}{cpf}_{11}& {cpf}_{12}& {cpf}_{13}& {cpf}_{14}\\ {cpf}_{21}& {cpf}_{22}& {cpf}_{23}& {cpf}_{24}\\ {cpf}_{31}& {cpf}_{32}& {cpf}_{33}& {cpf}_{34}\\ {cpf}_{41}& {cpf}_{42}& {cpf}_{43}& {cpf}_{44}\\ {cpf}_{51}& {cpf}_{52}& {cpf}_{53}& {cpf}_{54}\\ {cpf}_{61}& {cpf}_{62}& {cpf}_{63}& {cpf}_{64}\end{array}\right]$$

(8)

The sum of all entities (`$cpf$’ or coefficient of participation factor) in a DPM matrix placed in a column should be equal to one as represented in (9).

$$\sum _{\mathrm{i}=1}^{\mathrm{NGENCO}}\mathrm{C}{\mathrm{P}}_{\mathrm{ij}}=1;\mathrm{for}\mathrm{j}=1,2,\dots NDISCO,$$

(9)

where $NDISCO$ is chosen as four for four different load ends.

3. Generalized Form of Transfer Function of a Fractional-Order Time Delayed System

The transfer function of a FO system is given by (10).

$$G_{FO}\left(s^{\gamma }\right)=\frac{a_n{s}^{{\gamma }_n}+a_{n-1}{s}^{{\gamma }_{n-1}}+\dots +a_0{s}^{{\gamma }_0}}{C_m{s}^{{\gamma }_m}+C_{m-1}{s}^{{\gamma }_{m-1}}+\dots +C_0{s}^{{\gamma }_0}}=\frac{{\Delta }_N\left(s^{\gamma }\right)}{{\Delta }_D\left(s^{\gamma }\right)}$$

(10)

In the transfer function, there exists a common division factor $Q\in S$ such that ${\gamma }_i=p{f}_i(i=0,1,\dots ,m),{\alpha }_k=p{f}_k(k=0,1,2,\dots ,n);e_i,$ where P is called the commensurate order, which can be rational or irrational. Therefore, the transfer function can be represented as per (11).

$$\tau \left(s\right)=\frac{y\left(s\right)}{u\left(s\right)}=\frac{M\left(s^P\right)}{N\left(s^P\right)}=\frac{M\left(q\right)}{N\left(q\right)},$$

(11)

where $q=s^{\gamma }$ in the polynomial equation. The generalized form of fractional order system is given by (12).

$$G_{FO}\left(q\right)=\frac{{\prod }_{k=0}^{n_1}(q+d_k){\prod }_{i=0}^{n_2}(c_i{q}^2+e_i^q+f_i)}{{\prod }_{j=0}^{n_3}(q+g_j){\prod }_{m=0}^{n_4}(h_m{q}^2+o_{m}q+z_m)},$$

(12)

where $d_k(k=0,1,2,\dots ,n_1),c_i,e_i,f_i(i=0,1,\dots ,n_2),g_j(j=0,1,2,\dots ,n_3),h_m,o_m,z_m$, where ($m=$ 0,1,…,$n_4)$ are positive integers. Now substituting $q=s^p$, (12) can be rewritten as per (13).

$$G_{FO}\left(s^{\gamma }\right)=\frac{{\prod }_{k=0}^{n_1}(s^p+d_k){\prod }_{i=0}^{n_2}(c_i{q}^2+e_i^q+f_i)}{{\prod }_{j=0}^{n_3}(s^p+g_j){\prod }_{m=0}^{n_4}(h_m{q}^2+o_{m}q+z_m)}=\frac{{\Delta }_N\left(s^{\gamma }\right)}{{\Delta }_D\left(s^{\gamma }\right)}$$

(13)

This method is also applicable for analyzing the FO non-linear time delayed system.

Let us consider transfer function of a FO linear time delayed system as defined by (14).

$$G_{FO}\left(s^{\lambda }\right)=\frac{{\Delta }_{N0}\left(s^{\lambda }\right)+\sum _{j=1}^{p_1}{\Delta }_{Nj}\left(s^{\lambda }\right)e^{-{\tau }_{i}s}}{{\Delta }_{D0}\left(s^{\lambda }\right)+\sum _{i=1}^{p_2}{\Delta }_{Di}\left(s^{\lambda }\right)e^{-{\tau }_{i}s}}=\frac{{\Delta }_N\left(s^{\lambda }\right)}{{\Delta }_D\left(s^{\lambda }\right)},$$

(14)

where ${\tau }_d$ is the delay time, and the real coefficients of FO polynomial are given by (15).

$$\begin{array}{c}{\Delta }_{Di}\left(s^{\lambda }\right)=\sum _{k=1}^m{q}_{ik}{s}^{{\lambda }_{DK}};i\in 0,1,2,\dots ,p_1\hfill \\ {\Delta }_{Nj}\left(s^{\lambda }\right)=\sum _{k=1}^n{z}_{jk}{s}^{{\lambda }_{NK}};j=0,1,2,\dots ,p_2\hfill \end{array}$$

(15)

where ${\lambda }_{DK}$&${\lambda }_{NK}$ are the non-real native numbers.

The transfer function of the FO system is the commensurate order if and only if ${\lambda }_{DK}$ and ${\lambda }_{DK}\in k\lambda (k=0,1,\dots ,n)\mathrm{and}{\lambda }_{NK}\in k\alpha (k=0,1,\dots ,n)$; otherwise, it is in the range of non-commensurate order. Now, the characteristic equation of a commensurate fractional order system is given by (16).

$$\Delta D\left(s^{\lambda }\right)={\Delta }_D\left(s^{\lambda }\right)+\sum _{i=1}^{y_1}{\Delta }_{Di}\left(s^{\lambda }\right)e^{-{\tau }_{i}s}$$

(16)

Evaluation of Delay Margin Using Empirical Bode Analysis (EBA) of Time-Delayed Fractional Controller

A study of the fractional order system proves that the equation carries a fractional pole and zeros in form of double term. Hence, it is helpful to construct asymptotic bode plots $G\left(s\right)$ by adding or subtracting the FO system, which is similar to that of the $P{I}^{\lambda }$ controller transfer function.

In this article, the authors have used the gain plot and the phase plot to analyze the stability of a time-delayed fractional-order controller, which can be defined as per (17).

$$G_{FOC}\left(s^{\lambda }\right)=G_c\left(s^{\lambda }\right)=\frac{{\Delta }_{Nc}\left(s^{\lambda }\right)}{{\Delta }_{Dc}\left(s^{\lambda }\right)}=\frac{{\Delta }_{Nc}\left(s^{\lambda }\right){\Delta }_{Dc}^{*}\left(s^{\lambda }\right)}{{\Delta }_{Dc}^{*}\left(s^{\lambda }\right){\Delta }_{Dc}\left(s^{\lambda }\right)}=\frac{{\Delta }_{Nc}\left(s^{\lambda }\right){\Delta }_{Dc}^{*}\left(s^{\lambda }\right)}{{\left|{\Delta }_{Dc}{\left(s\right)}^{\lambda }\right|}^2}$$

(17)

Now, equating the imaginary part of the numerator to zero, the value of phase crossover frequency (PCF) is obtained according to (18).

$$Im\left[{\Delta }_{NC}{\left(j{\omega }_{pc}\right)}^{\lambda }{\Delta }_{DC}^{*}\left(j{\omega }_{pc}\right)\right]=0;\{puttings=j\omega =j{\omega }_{pc}\}$$

(18)

The GM is obtained using the PCF $\left({\omega }_{pc}\right)$, as defined by (19).

$$GM=-1/G_c{\left(j{\omega }_{pc}\right)}^{\lambda }$$

(19)

The value of gain crossover frequency (GCF), as denoted by ${\omega }_{gc}$, may be yielded using (20).

$${\left|G_c{\left(j{\omega }_{gc}\right)}^{\lambda }\right|}^2=1={\left|{\Delta }_N{\left(j{\omega }_{gc}\right)}^{\lambda }\right|}^2={\left|{\Delta }_D{\left(j{\omega }_{gc}\right)}^{\lambda }\right|}^2$$

(20)

The PM obtained using the GCF is given by (21).

$$PM={180}^{\circ }+\angle G(j{\omega }_{gc}{)}^{\lambda }$$

(21)

Now, consider the time delay effect in the fractional-order controller transfer function, as defined by (22).

$$G_{FOC}\left(s^{\lambda }\right)=G_C{e}^{-s{\tau }_d}$$

(22)

where ${\tau }_d$ is the time delay.

The condition for the fractional controller on the verge of stability is given by (23).

$$G_c\left(s^{\lambda }\right)e^{-j{\omega }_{gc}{\tau }_{dm}}=-1$$

(23)

where ${\tau }_{dm}$ is the delay margin.

Now, satisfying (23) for stability, the modified equation can be rewritten as per (24).

$$\angle G_c{\left(j{\omega }_{gc}\right)}^{\lambda }-({\omega }_{gc}{)}^{\lambda }{\tau }_{dm}\times \frac{{180}^{\circ }}{\pi }=-{180}^{\circ }$$

(24)

Thus, using (24), the delay margin may be given by (25).

$${\tau }_{dm}=\frac{PM}{{\left({\omega }_{gc}\right)}^{\lambda }}\times \frac{\pi }{{180}^{\circ }}=\frac{{180}^{\circ }+\angle G{\left(j{\omega }_{gc}\right)}^{\lambda }}{{\left({\omega }_{gc}\right)}^{\lambda }}\times \frac{\pi }{{180}^{\circ }}$$

(25)

4. Mathematical Formulation of the Proposed System

The delay margin is calculated in this research to achieve the generation-load balance at their schedule level, in order to analyze the suggested hybrid system’s delay-dependent stability. The choice of objective function has a significant impact on the dynamic response of the system.

4.1. Objective Function

The performance index is determined by using a defined objective function to obtain optimum controller gain. The control error is responsible for delivering control signals for the FOPI controller for different fractional orders ($\lambda$) for the constant ($\mu =0.0$) time-delay system. The objective function (J) is defined as the linear combination of frequency deviation and tie-line power. The integral squared error (ISE) technique is commonly used in controller design. The construction of an optimization-based controller necessitates the selection of acceptable weighted values of frequency deviation for both areas in the performance indices (J) based on the intended requirements and constraints. Large control signals were generated by weighting solely frequency and tie-line power deviations in the performance index, which quickly forces frequency and tie-line deviations to zero. The objective function treated as performance index is given by (26).

$$J=\underset{0}{\overset{t_{min}}{\int }}(\Delta P_{tie1-2}^2+\alpha \Delta f_1^2+\delta \Delta f_2^2)dt$$

(26)

The values of $\alpha$ and $\delta$ are assumed to be equal in this situation, i.e., 0.056. The weighted values for the frequency deviation in both locations, $\alpha$ and $\delta$, are used to assign equal importance to tie-line power and frequency responses. Aside from that, a new Honey Badger technique is presented to improve the FOPI controller’s $K_P$ and $K_I$ values. Section 5.2.1 outlines the steps for optimizing the gain value of an FOPI controller with various values of $\lambda$.

4.2. System Constraints

The suggested AGC system can be thought of as a restricted optimization problem with the following constraints given by (27):

$$\begin{array}{c}{K}_{P1,min}\le K_{P1}\le K_{P1,max};K_{I1,min}\le K_{I1}\le K_{I1,max};\hfill \\ K_{P2,min}\le K_{P2}\le K_{P2,max};K_{I2,min}\le K_{I2}\le K_{I2,max};\hfill \\ K_{P3,min}\le K_{P3}\le K_{P3,max};K_{I3,min}\le K_{}\le K_{I3,max};\hfill \\ {\lambda }_{min}\le {\lambda }_{}\le {\lambda }_{max};\hfill \end{array}$$

(27)

where the control parameters for case-1 ($K_P$, $K_I$&$K_D$) are in the range of 0 to 10. Only the performance of the FOPI controller with fractional order ($\lambda$) has been examined for different ranges of delay in case-2 to estimate the delay margin (using EBA). The value of fractional order ($\lambda$) of FOPI controllers gain is set between 0.1 and 0.8.

4.3. Mathematical Explanation of $MADB$ Calculation for Time-Delayed FOPI Controller

Optimal design of FOPI controller is determined using the transfer function expressed in (28).

$$T_{FO-PI}=G_c\left(s\right)=\left(K_P+\frac{K_I}{s^{\lambda }}\right)=K_P+K_I{\omega }^{\lambda }cos(\pi \lambda /2)-j{k}_I{\omega }^{-\lambda }sin(\pi \lambda /2)$$

(28)

The stability margin of time delay is established by evaluating the delay margin of the FOPI controller. For this purpose, we substitute $s=j\omega$ in the time-delayed FOPI controller to evaluate the characteristic equation

$$T_{FO-PI}=G_c\left(j\omega \right)=\left(K_P+\frac{K_I}{j{\omega }^{\lambda }}\right)e^{-j\omega {\tau }_d}=K_P+K_i{\omega }^{\lambda }cos(\pi \lambda /2)-j{k}_i{\omega }^{-\lambda }sin(\pi \lambda /2))e^{{}^{-j(arctan(\pi \lambda /2)}}$$

(29)

The necessary and sufficient conditions to meet the controller’s robustness requirement are stated as follows:

(i)

PM at GCF:

$$\angle G\left(j{\omega }_{gc}\right)=PM-\pi$$

(30)

(ii)

Gain of the system at GCF:

$$\left|G\left(j{\omega }_{gc}\right)\right|=1$$

(31)

(iii)

PM at PCF:

$$\angle G\left(j{\omega }_{pc}\right)=-\pi$$

(32)

(iv)

Gain of the system at PCF:

$$\left|G\left(j{\omega }_{pc}\right)\right|={10}^{GM/20}$$

(33)

Applying (30) and (31) in (29), the gain value and phase value of FOPI controller can be obtained using (34) and (35), respectively,

$$\left|C\left(j\omega \right)\right|=\sqrt{K_P+K_I{\omega }^{\lambda }cos{(\pi \lambda /2)}^2+(-K_I{\omega }^{-\lambda }sin{(\pi \lambda /2)}^2}=1$$

(34)

and

$$\angle C\left(j\omega \right)=arctan\left[\frac{-K_{I}sin(\pi \lambda /2)}{K_P+K_I{\omega }^{-\lambda }cos(\pi \lambda /2)}\right]=PM-\pi$$

(35)

Equations (36) and (37) may be used to find an FOPI controller that ensures the attainment of the desired GCF.

$$K_P=\pm \frac{{10}^{GM/20}cot(\pi \lambda /2)tan\left({\varphi }_2\right)}{\sqrt{1+{(tan{\varphi }_2)}^2}}$$

(36)

and

$$K_I=\pm \frac{{10}^{GM/20}cos(\pi \lambda /2)tan\left({\varphi }_2\right)}{\sqrt{1+{(tan{\varphi }_2)}^2}}$$

(37)

where ${\varphi }_2=-\pi arctan\left(\tau {\omega }_{pc}\right)$.

The values of $K_P$ and $K_I$ have been utilized to define the basic fractional controller and simulate the individual asymptotic magnitude of the bode plot. Moreover, the stability condition is judged through the evaluation of the delay margin (${\tau }_{dm}$) for different FO controllers ($\lambda =0.1$ to $0.8$). The value of the delay margin (${\tau }_{dm}$) is evaluated using (36) and (37).

Algorithm Steps for Computation of MADB

The proposed approach for MADB computation using GM and PM includes the following steps:

1.

Without a controller, create a linearized model of a hybrid system (solar-wind-thermal with DGS).

2.

The state space equation of the AGC system with the P-I controller is established. Then, the linearized hybrid system with time-varying delay is used to design the controller.

3.

Based on the linearized model obtained in Step 2, the delay margin is calculated. After evaluating GM and PM, the value $K_P$ and $K_I$ using the HBA is obtained, and system stability is analyzed by satisfying (24) and (25).

4.

The search interval for calculating the delay margin starts with ${\tau }_i$ and concludes with ${\tau }_f$. Furthermore, the following steps are used to determine a specified time delay ${\tau }_d$ for a collection of $K_P$ and $K_I$: [leftmargin=15mm,labelsep=4.9mm,itemsep=0pt]

Step 1:

Obtain the transfer function of the FOPI controller for different time delay ${\tau }_i$ and ends with ${\tau }_f$.

Step 2:

Evaluate GM and PM for different time-delayed FOPI-controllers.

Step 3:

Calculate delay margin using (24) and (25).

Step 4:

Continue the searching process ${\tau }_{\mathrm{int}}=\left|{\tau }_i-{\tau }_f\right|$ with ${\tau }_d$, and if ${\tau }_{\mathrm{int}}\ge {\tau }_d$, go to step 1 for further tuning. The output is treated as delay margin of ${\tau }_d$.

5.

The stability of the abovementioned hybrid system is then verified using a simulation approach with a particular time delay ${\tau }_d$ for ${\tau }_d\le {\tau }_{set}$.

5. Proposed Honey Badger Algorithm (HBA)

5.1. Honey Badger Algorithm

HBA is based on the behavior of a mammal found in the rain forest of Asia-Pacific and the Indian sub-continent and it is well known for its fearless nature. Throughout the world sixty different species of fearless forager preys exist, out of which 12 are recognized as honey badger subspecies in Asia Pacific region. HBA was designed using the foraging behavior of the honey badger. Searching for the food source, the honey badger either digs and smells or follows the honey-bird. It completes its tasks in two different modes such as digging mode and honey mode. In the first step, the honey badger uses its smelling ability to select the appropriate location for digging. In the second phase, the badger accepts the help of the honey guide bird to directly locate a beehive.

5.2. Mathematical Model

As discussed in the previous section, the search process of HBA is classified into two different phases. They are (i) the digging phase and (ii) the honey phase.

The exploration and exploitation capability of the algorithm helps it to obtain the optimal solution of a global optimization problem. At the initial phase, a population consisting of N number of solutions with D-dimensions is represented according to (38).

$$\left[\begin{array}{ccccccc}{\phi }_{11}& {\phi }_{12}& {\phi }_{13}& .& .& .& {\phi }_{1D}\\ {\phi }_{21}& {\phi }_{22}& {\phi }_{23}& .& .& .& {\phi }_{2D}\\ {\phi }_{31}& {\phi }_{32}& {\phi }_{33}& .& .& .& {\phi }_{3D}\\ .& .& .& .& .& .& .\\ .& .& .& .& .& .& .\\ {\phi }_{N1}& {\phi }_{N2}& {\phi }_{N3}& .& .& .& {\phi }_{ND}\end{array}\right]$$

(38)

where the set of badgers up to the $i^{th}$ position is given by ${\phi }_i=\left[{\phi }_i^1,{\phi }_i^2,{\phi }_i^3......{\phi }_i^N\right]$.

Steps of Proposed Optimization Technique

The proposed design steps employing the HBA technique are outlined as follows:

• Step 1: Initialization

  Initialize the number of honey badgers with population size N, as per (39).

  $${\phi }_k=l{b}_k\times r{b}_k(u{b}_k-l{b}_k).$$

  (39)

  where $r_{bk}$ lies between 0 and 1; ${\phi }_K$ is the honey badger at the $k^{th}$ position; and $u{b}_k$ and $l{b}_k$ are the lower bound and upper bound in the search domain.

• Step 2: Defining Intensity

  The $I_i$ intensity of the prey is inversely proportional to the honey badger, as given by (40).

  $$I_i=r_2\times \frac{s}{4\pi d_i^2}$$

  (40)

  where $r_2$ is a random variable lying between 0 to 1; $s={({\phi }_i-{\phi }_{i+1})}^2$ &$d_i={\varphi }_{prey}-{\varphi }_i$.

• Step 3: Density Factor

  The density factor ($\beta$) is a continuous time-varying randomization used for constant transformation from exploration to exploitation. The expression for $\beta$ is given by (41).

  $$\beta =C\times exp\left(\frac{-\tau }{{\tau }_{max}}\right)$$

  (41)

  where $C\ge 1$; ${\tau }_{max}$ is the maximum iteration time.

• Step 4: Escaping Local Optima

  This step, along with the next one, is used to overcome the local optima in HBA. In this context, the proposed approach employs a flag F that changes the search direction, allowing agents to thoroughly investigate the search space.
• Updating the Agent Position
  As previously stated, the HBA position update process (${\phi }_{new}$) is split into two phases, namely, the digging phase and the honey phase.

1.

Digging Phase

In the digging phase, a honey badger performs an action similar to the cardioid shape, as given by (42).

$${\phi }_{new}={\phi }_{prey}+F\times \gamma \times I\times {\phi }_{prey}+F\times r_3\times \beta \times d_i\times \left|cos\left(2\pi r_4\right)\times [1-cos\left(2\pi r_5\right)]\right|$$

(42)

where ${\phi }_{prey}$ is position of the prey, which is the best position found so far; $r_3$, $r_4$, and $r_5$ are the three different random numbers lying between 0 and 1; and F works as a flag that alters the search direction based on (43).

$$F=\left\{\begin{array}{c}1,if{r}_6\le 5,r_{6}istherandomnumber.\hfill \\ -1,else\hfill \end{array}\right.$$

(43)

2.

Honey Phase

In this case, where a honey badger follows a honey guide bird to find the food source, the modeling expression is defined by (44).

$${\phi }_{new}={\phi }_{prey}+F\times r_1\times \beta \times d_1$$

(44)

where $r_1$ lies in between 0 to 1, and ${\phi }_{new}$ is the new position of the honey badger.

The pseudo-code of HBA for solving the time delayed hybrid system problem is illustrated in Algorithm 1.

Algorithm 1:Pseudo-code for implementing HBA for a time-delayed hybrid system

5.2.1. Application of HBA in Time-Delayed AGC Problem

1.

Using (39), initialize the control variables $K_{P1}$, $K_{I1}$, $K_{P2}$, $K_{I2}$, $K_{P3}$, $K_{I3}$&$\lambda$. Calculate the appropriate control variables’ fitness value at the $m^{th}$ position.

2.

The maximum and minimum operating limits are used to standardize the value of the control parameters.

3.

Depending on the population size, several sets of control variables are formed to generate matrix pools.

4.

Equation (44) is used to update the control variables.

5.

For each new updated control variable position, calculate the objective function until an optimal solution is achieved.

6. Simulation Results

The HBA, MFOA, BFA, COKHA, and GOA algorithms are coded in MATLAB, and the AGC system is designed using MATLAB/SIMULINK tools. The total number of iterations for HBA, MFOA, COKHA, and GOA approaches for tuning control parameters are considered as 150 in both cases. Furthermore, EBA is utilized to examine the delay margin of stability for various delay ranges. To control the mutation in the perturbation process, the controllers are set to a range of 0.1 to 0.8 for test system 2, and the simulation is run in MATLAB (R2014a) on an Intel Core I3 CPU running at 2.20 GHz. To assess the success of the suggested approach, a variety of simulation combinations are used to fine-tune the HBA adjusted control parameters.

6.1. Case Study with Two-Area Thermal System

At first, the efficacy of the suggested HBA method is evaluated through the dynamic responses of the two-area thermal system [20]. Appendix A lists the values of the system parameters for a two-area thermal unit. Table 2 shows how to maximize the gain value of the PID controller and the objective function with a 20% step load disturbance at area 1 using various strategies. When the proposed method is compared with the published methods, the objective function `J’ and other response characteristics such as overshoot, undershoot, and steady-state error are found to be smaller with the HBA methodology. The second-best value of the objective function comes from a GOA-tuned [23] PID. Figure 4a–c shows that the HBA [24] -optimized PID controller gives better outcomes than other heuristic techniques such as COKHA, BFA, and MFOA in terms of dynamic responses. The dynamic responses of $\Delta f_1$, $\Delta f_2$, and $\Delta P_{tie1-2}$ are improved with the suggested HBA optimized PID controllers, as shown in Table 2. When the suggested HBA optimized PID is compared with GOA, COKHA [21], and BFA [19] optimized PID, objective function (ISE) is improved by 18.3%, 49.15%, 63.42%, and 74.79%, respectively. HBA-optimized controllers improve the dynamic response of `$\Delta f_1$’, i.e., overshoot by 43.84%, 48.29%, 99.95%, and 99.55%, respectively, as compared to reported COKHA-, BFA-, and GA-tuned PID controllers .

Table 2. Gain values of PID controllers for the two-area system.

PID Controller	${\mathit{K}}_{\mathit{p}1}$	${\mathit{K}}_{\mathit{i}1}$	${\mathit{K}}_{\mathit{d}1}$	${\mathit{K}}_{\mathit{p}2}$	${\mathit{K}}_{\mathit{i}2}$	${\mathit{K}}_{\mathit{d}2}$	($\mathbf{OBJ}\times {10}^{-5}$)
MFOA [20]	4.2993	4.6376	4.1970	0.0260	1.0959	0.6929	1.0271
BFA [19]	6.623	5.2453	5.9213	1.4410	0.8187	0.1730	0.6119
COKHA [21]	8.623	6.2493	4.923	3.746	1.425	0.687	0.474
GOA [23]	9.121	8.423	5.9213	3.7462	2.425	0.379	0.0293
HBA	9.82	9.679	6.231	3.782	2.494	0.172	0.00241
PID	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$
Controller	$\mathbf{OS}\times {\mathbf{10}}^{-\mathbf{6}}$	$\mathbf{US}\times {\mathbf{10}}^{-\mathbf{4}}$	SS	$\mathbf{OS}\times {\mathbf{10}}^{-\mathbf{6}}$	$\mathbf{US}\times {\mathbf{10}}^{-\mathbf{4}}$	SS
MFOA [20]	2.498	−4.27	9.02	8.94	−1.082	7.67
BFA [19]	3.55	−3.37	20.77	0.09503	−0.646	8.25
COKHA [21]	0.00234	−2.65	8.4	0.00763	−0.4963	7.10
GOA[23]	0.002141	−1.99	6.31	0.005063	−0.4289	7.79
HBA	0.00121	−1.76	6.74	0.00	−0.3609	10.4

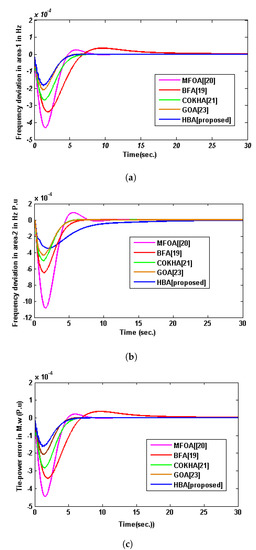
Figure 4. (a) Frequency deviation in area 1 in Hz $p.u$. (b) Frequency deviation in area 2 in Hz $p.u$. (c) Tie−power error in MW in $p.u$. (BFA [19], MFOA [20], COKHA [21], and GOA [23].)

6.2. Case Study with Time Delays Using the FOPI Controller

6.2.1. A Deregulated Environment with a Renewable Multi-Source System

An experiment using a time-delayed AGC model of a three-area renewable-based hybrid system with distributed generation is conducted in this research. Appendix B depicts the hybrid system’s parameter values. The GM and PM [32] for the provided AGC system outlined in Section 3 are used to calculate the MADB. For the constant time delay with the varying rate $\mu =0.0$, the delay margins of ${\tau }_d$ for different values of $K_P$&$K_I$ for the different fractional order ($\lambda$) are obtained, which can aid in the design of FOPI controllers for a wide range of stable operations of the proposed three-area hybrid system.

Here, a renewable hybrid system with an FOPI controller is studied in a deregulated context. Table 3, Table 4 and Table 5 show the delay margin of ${\tau }_d$ determined using EBA for the different values of $\lambda$ in the $K_P$&$K_I$ plane. The delay margin is evaluated for different sets of fractional orders through the proposed technique to identify the stability region of the proposed time delayed system under a deregulated scenario. The delay margin results for the constant time delay ($\mu =0$) for different fractional orders ($\lambda =0.1$ to $0.4$, 0.6, and 0.8) have been summarized.

Table 3. Delay margin for FOPI controller for $\lambda =0.1$ and 0.2.

$\mathit{\mu }=0$ (For Constant Time Delay) [40,41] Fractional Order $\mathit{\lambda }=0.1$
${\mathbf{K}}_{\mathbf{P}}$	Unilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)						Bilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)
	For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{3}.\mathbf{521}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$						For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{2}.\mathbf{245}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$
0.1	18.69	16.55	12.05	5.624	3.921	1.625	3.854	4.201	4.869	2.935	2.899	3.675
0.2	11.95	10.02	7.965	3.875	3.118	1.496	3.447	4.268	3.512	2.754	1.985	2.489
0.3	10.16	8.056	7.112	3.886	3.112	2.076	3.021	3.954	2.887	2.335	1.357	4.367
0.4	6.562	4.021	3.521	3.021	2.567	1.456	3.124	2.964	2.245	2.004	1.33	3.925
0.5	4.865	4.345	3.662	2.632	2.016	1.425	1.665	1.565	1.242	1.056	0.995	1.589
0.6	3.596	3.945	2.867	3.112	2.079	1.895	1.112	1.668	2.019	1.662	2.435	3.167
0.7	2.567	2.231	1.892	1.652	1.106	0.765	1.557	1.356	1.662	2.009	1.361	2.461
0.8	1.210	2.142	1.667	1.251	1.324	0.462	0.541	1.092	1.117	0.625	1.092	1.312
0.9	0.657	1.351	1.452	1.001	0.967	0.456	0.974	1.221	1.621	0.462	1.012	1.217
1.0	0.524	0.746	0.532	0.447	0.608	0.346	0.445	0.562	0.947	0.436	1.025	1.401
1.1	0.376	0.228	0.314	0.537	0.258	0.462	1.021	0.312	1.006	0.537	0.628	1.229
$\mathbf{\mu }=\mathbf{0}.\mathbf{0}$(Varying Rate of Time Delay) [40,41] Fractional Order $\mathbf{\lambda }=\mathbf{0}.\mathbf{2}$
${\mathbf{K}}_{\mathbf{P}}$	Unilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)						Bilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)
	For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{4}.\mathbf{032}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$						For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{2}.\mathbf{776}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$
	0.2	0.4	0.6	0.8	1.0	1.2	0.2	0.4	0.6	0.8	1.0	1.2
0.1	15.03	11.43	9.64	6.321	2.035	0.325	9.821	7.69	5.035	3.254	2.132	1.117
0.2	13.24	10.25	8.115	6.796	2.115	1.254	10.12	8.254	6.785	3.285	2.875	1.085
0.3	12.98	8.641	7.125	6.549	3.102	0.956	7.625	6.166	4.225	2.789	2.995	4.675
0.4	8.652	6.385	4.032	3.685	2.295	0.792	3.654	4.325	2.776	1.602	2.469	3.679
0.5	8.110	7.110	6.542	4.825	1.259	0.992	3.356	2.976	3.214	3.679	2.224	3.025
0.6	7.665	6.532	3.102	2.516	1.296	0.561	3.691	3.998	2.976	1.965	2.291	1.765
0.7	7.869	3.271	1.652	2.109	0.567	0.329	0.1576	1.254	2.302	3.021	2.163	1.219
0.9	6.894	3.102	1.851	0.867	0.325	0.112	0.916	1.096	2.954	2.110	1.657	2.957
1.0	5.789	1.129	0.649	0.320	0.109	0.096	1.127	2.254	1.897	2.214	1.627	2.961
1.1	1.425	0.697	0.527	0.339	0.246	0.194	0.762	1.165	1.562	1.602	1.658	2.118
1.2	0.557	0.395	0.302	0.114	0.259	0.112	1.112	2.621	2.102	1.579	1.221	2.187

Table 4. Delay margin for proposed FOPI controller for $\lambda =0.3$ and 0.4

$\mathit{\mu }=0$ (For Constant Time Delay) [40,41] Fractional Order $\mathit{\lambda }=0.3$
${\mathbf{K}}_{\mathbf{P}}$	Unilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)						Bilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)
	For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{6}.\mathbf{328}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$						For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{3}.\mathbf{014}\mathrm{s}.\mathbf{0}.\mathbf{05}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{3}\&\mathbf{0}.\mathbf{1}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{2}$
0.1	20.55	18.33	7.651	5.951	3.891	2.321	4.412	5.042	3.379	2.402	1.875	2.024
0.2	11.03	12.54	6.689	4.328	2.887	1.957	3.135	2.781	1.878	1.562	1.251	2.012
0.3	8.861	6.669	5.032	3.102	2.451	1.210	2.965	3.701	2.425	1.861	1.560	2.865
0.4	7.765	6.562	6.328	4.321	1.746	1.152	2.954	3.613	3.014	1.814	1.583	3.189
0.5	4.576	5.176	3.954	2.021	2.689	1.290	0.989	1.476	1.435	1.902	1.117	2.452
0.6	3.897	4.108	2.759	2.591	2.113	1.995	1.195	1.005	2.294	1.501	0.752	0.531
0.7	2.292	2.012	1.765	1.425	1.140	0.762	1.421	1.097	1.712	2.439	1.392	3.057
0.8	1.337	2.154	1.619	1.379	1.134	0.731	0.632	1.193	1.575	0.925	1.349	1.125
0.9	0.701	1.693	1.228	0.924	1.135	1.477	0.7254	1.098	1.299	0.719	1.125	1.369
1.0	0.577	0.919	0.717	0.795	0.601	0.389	0.652	1.025	1.569	1.229	0.987	1.125
1.1	0.695	0.762	0.479	0.964	0.351	0.7161	1.596	1.125	0.993	0.412	0.817	1.227
$\mathbf{\mu }=\mathbf{0}.\mathbf{0}$[40,41] Fractional Order $\mathbf{\lambda }=\mathbf{0}.\mathbf{4}$
${\mathbf{K}}_{\mathbf{P}}$	Unilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)						Bilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)
	For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{7}.\mathbf{102}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$						For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{4}.\mathbf{325}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$
	0.2	0.4	0.6	0.8	1.0	1.2	0.2	0.4	0.6	0.8	1	1.2
0.1	20.21	13.51	7.214	6.541	3.0285	0.785	9.842	7.698	5.785	3.894	3.185	2.441
0.2	19.54	14.25	9.584	7.895	2.854	1.334	9.798	8.195	5.445	3.025	2.051	3.195
0.3	20.54	10.29	8.065	7.968	1.462	0.115	7.956	5.036	3.016	3.025	2.112	2.956
0.4	20.65	8.325	7.102	4.912	1.952	0.234	5.165	4.225	4.325	2.521	2.028	3.235
0.5	21.03	8.432	6.102	3.895	1.229	0.109	3.295	4.069	3.194	3.526	2.445	3.012
0.6	20.02	6.105	3.025	2.052	1.102	0.292	2.002	3.896	3.399	3.112	2.092	2.145
0.7	17.89	3.563	2.353	1.869	0.659	0.259	2.405	2.559	3.755	4.119	1.895	3.757
0.8	10.02	2.672	1.652	0.812	0.702	0.235	1.775	1.572	2.095	2.685	1.775	3.025
0.9	5.726	1.115	0.8325	0.720	0.514	0.232	1.362	2.012	2.105	2.899	1.852	2.954
1.1	1.586	0.772	0.835	0.312	0.739	0.445	0.742	2.332	3.025	2.425	1.667	2.547
1.1	0.778	0.5471	0.5124	0.6951	0.3591	0.2421	1.227	2.521	2.901	2.039	1.001	2.135

Table 5. Delay margin for FOPI controller for $\lambda =0.6$ and 0.8.

$\mathit{\mu }=0$ (For Constant Time Delay) [40,41] Fractional Order $\mathit{\lambda }=0.6$
${\mathbf{K}}_{\mathbf{P}}$	Unilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)						Bilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)
	For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{7}.\mathbf{234}\mathrm{s}\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$						For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{4}.\mathbf{112}\mathrm{s}\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$
0.1	30.225	21.025	17.85	12.24	7.845	6.621	4.425	4.105	3.102	2.785	2.102	2.522
0.2	15.03	13.02	11.054	7.895	6.425	3.775	2.471	1.987	3.657	1.442	1.014	2.957
0.3	12.34	8.964	9.163	4.752	3.254	1.476	3.95	4.302	4.112	2.103	1.897	3.147
0.4	6.725	7.258	7.234	4.067	1.897	1.251	3.478	2.897	3.255	1.987	1.425	3.752
0.5	5.761	4.325	3.965	2.462	2.229	1.658	1.289	0.896	1.987	1.625	1.235	2.785
0.6	4.789	3.987	3.125	2.995	2.257	1.992	1.025	0.954	2.654	1.972	1.065	0.765
0.7	2.189	1.892	1.567	1.665	1.140	0.967	1.314	1.005	1.254	2.957	1.659	3.992
0.8	2.567	2.068	1.954	1.462	1.203	0.941	0.786	1.335	1.776	1.292	1.465	1.214
0.9	0.981	1.975	1.524	1.321	1.213	1.577	0.925	1.945	1.542	0.967	1.456	1.251
1.0	0.964	0.867	0.627	0.430	0.612	0.967	0.183	1.235	1.569	1.798	0.887	1.035
1.1	0.767	0.625	0.514	0.320	0.102	0.9614	1.897	1.234	0.975	0.532	0.977	1.876
$\mathbf{\mu }=\mathbf{0}.\mathbf{0}$ (For Constant Time Delay) [40,41] Fractional Order $\mathbf{\lambda }=\mathbf{0}.\mathbf{8}$
${\mathbf{K}}_{\mathbf{P}}$	Unilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)						Bilateral Contract (${\mathbf{K}}_{\mathbf{I}}$)
	For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{8}.\mathbf{265}\mathrm{s}\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$						For${\mathbf{\tau }}_{\mathbf{d}}=\mathbf{4}.\mathbf{025}\mathrm{s}.\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{P}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$
	0.2	0.4	0.6	0.8	1.0	1.2	0.2	0.4	0.6	0.8	1.0	1.2
1.0	30.02	26.62	14.45	12.24	6.85	3.525	14.64	12.24	8.785	6.954	5.784	4.321
0.2	22.65	18.75	12.90	9.451	8.354	3.452	11.147	10.075	7.652	5.847	3.995	2.652
0.3	21.54	17.58	11.71	10.375	8.475	3.654	6.487	4.321	2.801	2.224	1.841	2.024
0.4	10.04	9.524	8.265	6.147	4.320	1.221	0.992	3.954	4.025	2.721	1.942	2.864
0.5	21.99	14.25	10.02	8.765	6.754	0.541	2.574	2.728	2.002	1.954	3.957	7.015
0.6	19.75	9.754	7.871	4.574	3.024	1.279	2.995	3.976	4.652	3.214	1.954	2.745
0.7	18.92	9.471	6.974	5.471	3.114	1.287	2.975	3.102	3.897	4.775	1.947	3.257
0.8	12.25	7.651	3.14	1.847	0.702	0.235	1.258	1.957	2.147	2.775	1.525	3.147
0.9	6.021	2.154	0.987	0.564	0.314	0.127	1.678	2.758	2.564	3.287	1.957	3.002
1.0	1.425	0.772	0.9325	0.757	0.8725	0.652	0.512	3.214	3.324	2.214	1.857	2.957
1.1	0.978	0.625	0.312	0.725	0.478	0.342	1.574	2.521	3.775	2.432	1.467	2.025

6.2.2. Poolco-Based Transaction

Poolco-based operations, in which DISCOs have a contract with other GENCOs in the same area, involve all GENCOs equally. A load disturbance of 0.1 $p.u$ (MW) occurred in area 1. In this example study, time delays ${\tau }_d$ = 6.102 s to 6.238 s were employed constant time delay ($\mu =0$) before controller for area 1, area 2 and area 3 respectively. Consider the following scenario, where $DISC{O}_1$, $DISC{O}_2$ have a power contract with $GENC{O}_1$, $GENC{O}_2$, and $GENC{O}_3$, which are represented by a DPM matrix [23], as given in (45).

$$\mathrm{DPM}=\left[\begin{array}{cccc}0.5& 0.5& 0& 0\\ 0.25& 0.25& 0& 0\\ 0.25& 0.25& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

(45)

Total generation must match the load demand in steady-state conditions, which is given by (46).

$$\left[\begin{array}{c}\Delta P_{g1ss}\\ \Delta P_{g2ss}\\ \Delta P_{g3ss}\\ \begin{array}{c}\Delta P_{g4ss}\hfill \\ \Delta P_{g5ss}\hfill \\ \Delta P_{g6ss}\hfill \end{array}\end{array}\right]=\left[\begin{array}{cccc}0.5& 0.5& 0& 0\\ 0.25& 0.25& 0& 0\\ 0.25& 0.25& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}0.1\\ 0.1\\ 0.0\\ 0.0\end{array}\right]$$

(46)

Simulations are conducted primarily for constant time delay using an FOPI controller with $\lambda$) ranging from 0 to 1. The EBA approach is used to calculate the delay margin, as shown in Table 3, Table 4 and Table 5. In the case of constant time delay ($\mu =0.0$), the delay margin of ${\tau }_{dm}$ grows (from 3.521 s to 6.102 s) with rising value of fractional order ($\lambda$ = 0.1 to 0.8) for a set of $K_P$ and $K_I$ values within a particular range ($0.1<K_p<0.5$&$0.2<K_I<0.6$). The stability range for an FOPI controller with $\lambda =0.6$ for ${\tau }_d=6.102$ s is the same as the time-varying delay ${\tau }_d=8.265$ s with $\lambda =0.8$. For $K_P>0.4$ or $K_I>0.6$, the system moves into an unstable zone for the time-varying delay ${\tau }_d=8.265$ s with $\lambda =0.8$ and ${\tau }_d=6.102$ s with $\lambda =0.4$ of the FOPI controller. The system stability for the HBA-tuned P-I controller $(K_{I1}=0.5624;K_{P1}=0.3132;K_{I2}=0.5624;K_{P2}=0.2304;K_{I3}=0.5566;K_{P3}=0.2395)$ with $\lambda =0.8$ approaches a stable area, as shown in Figure 5a,b and as shown in Table 6.

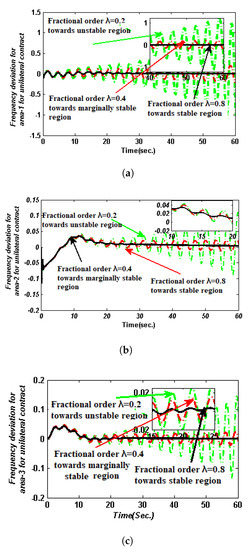
Figure 5. (a) Area 1 frequency deviation for unilateral condition with 10% SLP type of load disturbance with time−varying delay ${\tau }_d=6.102s.$ at a rate of $\mu =0.0$. (b) Area 2 frequency deviation for unilateral scenario with 10 % SLP type of load with time−varying delay ${\tau }_d=6.102s.$ at a rate $\mu =0.0$. (c) Area 3 frequency deviation for for unilateral scenario with 10 % SLP type of load with constant time delay ${\tau }_d$ = 6.328 s. at a rate $\mu =0.0$.

Table 6. Gain values of FOPI controllers for thermal-solar-wind system (test system 2) with DGS under deregulated environment in unilateral condition with time delays.

Fractional	$0.1\le {\mathit{K}}_{\mathit{p}}\le 0.5\&0.2\le {\mathit{K}}_{\mathit{I}}\le 0.6$ (Table 3, Table 4 and Table 5)
Order		${\mathbf{K}}_{\mathbf{P}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{3}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{3}}$	$\mathbf{OBJ}\times {\mathbf{10}}^{-\mathbf{2}}$
$\lambda =0.2$	${\tau }_d=6.{102}^{\prime }with\mu =0.0$	0.3142	0.1496	0.2258	0.5914	0.4695	0.4453	1.964
$\lambda =0.4$	${\tau }_d=6.{102}^{\prime }with\mu =0.0$	0.3542	0.4965	0.1167	0.321	0.196	0.3345	0.7916
$\lambda =0.6$	${\tau }_d=6.{102}^{\prime }with\mu =0.0$	0.3954	0.2349	0.4748	0.3951	0.2286	0.5672	0.3542
$\lambda =0.8$	${\tau }_d=6.{102}^{\prime }with\mu =0.0$	0.3132	0.5624	0.2304	0.5954	0.2395	0.5566	0.0251
	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$			$\Delta {\mathbf{f}}_{\mathbf{3}}$
	OS	US	SS	OS	US	SS	OS	US	SS
$\lambda =0.2$	HBA-tuned FOPI controller with fractional order $\lambda =0.2$ go towards unstable system
$\lambda =0.4$	HBA-tuned FOPI controller with fractional order $\lambda =0.4$ go towards marginally stable system
$\lambda =0.6$	0.213	−0.09654	16.21	0.32324	−0.005954	10.11	0.00263	−0.07892	18.99
$\lambda =0.8$	0.00157	−0.07978	21.37	0.06183	−0.05963	25.83	0.04107	−0.0007595	13.53
Fractional	$\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{p}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$ (Table 3, Table 4 and Table 5)
Order		${\mathbf{K}}_{\mathbf{P}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{3}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{3}}$	$\mathbf{OBJ}\times {\mathbf{10}}^{-\mathbf{2}}$
$\lambda =0.2$	${\tau }_d=6.{328}^{\prime }with\mu =0.0$	0.321	0.573	0.3965	0.576	0.3061	0.5647	0.965
$\lambda =0.4$	${\tau }_d=6.{328}^{\prime }with\mu =0.0$	0.3357	0.5802	0.321	0.574	0.4621	0.4765	0.2471
$\lambda =0.6$	${\tau }_d=6.{328}^{\prime }with\mu =0.0$	0.324	0.5874	0.3789	0.5624	0.3054	0.684	0.0457
$\lambda =0.8$	${\tau }_d=6.{328}^{\prime }with\mu =0.0$	0.375	0.594	0.3127	0.601	0.3571	0.5974	0.00754
	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$			$\Delta {\mathbf{f}}_{\mathbf{3}}$
	OS	US	SS	OS	US	SS	OS	US	SS
$\lambda =0.2$	HBA-tuned FOPI controller with fractional order $\lambda =0.2$ go towards unstable system
$\lambda =0.4$	HBA-tuned FOPI controller with fractional order $\lambda =0.4$ go towards marginally stable system
$\lambda =0.6$	0.4512	−0.0165	5.97	0.674	−0.00447	8.63	0.00446	−0.0128	7.124
$\lambda =0.8$	0.2239	−0.00912	11.24	0.01294	−0.001967	5.78	0.0000158	−0.00135	6.532

For the steady-state operation range of $K_P$&$K_I$ are $0.3\le K_P\le 0.4$ and $0.4\le K_I\le 0.6$, where the value of fractional order of the FOPI controller should greater than 0.4 ($\lambda \ge 0.4$) for constant time delay ($\mu =0$) at ${\tau }_d=7.234$ s. As a result, the system lost its stability approach towards the oscillation mode for $K_P>0.4$ or $K_I>0.6$ at ${\tau }_d=7.234s.$ On the other hand, as the fractional order decreases, the system becomes unstable ($\lambda =0.4$ to 0.2), even if the range of $K_P$ and $K_I$ (i.e., $0.4\le K_I\le 0.6$&$0.3\le K_I\le 0.4$) is maintained. A simulation-based delay margin further demonstrates that the suggested HBA-tuned FOPI controller is capable of achieving system stability with a specific range of fractional orders ($0.4\le \lambda \le 0.8$). The dynamic responses for frequency deviation in area 1 and area 2 in the context of constant time delay are presented in Figure 5c. The simulation results clearly show that as the value of $\lambda$ decreases, the oscillations become more unstable, whereas as the fractional order ($\lambda$) increases, the oscillations slowly die out. For the time delay (${\tau }_d=8.265$ s), the dynamic response for HBA-tuned FOPI with $\lambda =0.8$ steady state (ST/ 10.25 s /$\Delta f_1$) is considerably faster than $\lambda =0.4$ (ST/17.12 s/$\Delta f_1$). From the standpoint of stability, HBA-based FOPI with $\lambda =0.8$ yields the lowest values of the ITSE, OS, US, and ST.

The simulation results serve to verify the accuracy of the EBA used to calculate the delay margin, the comparative analysis of which is mentioned in Table 7 & shown in Figure 6a–c. The FOPI controller lies in the stable region for the time-varying delay as well as the constant time delay with the specific fractional order $\lambda$ during the design of the LFC scheme under the unilateral condition, which has been verified through the dynamic responses of the time delayed hybrid system.

Table 7. Stability analysis for $0.3\le K_P\le 0.4\&0.4\le K_I\le 0.6$ using gain margin (GM) and phase margin (PM) from Bode plots for specified time delay (${\tau }_d$).

Gain of ${\mathit{K}}_{\mathit{P}}$&${\mathit{K}}_{\mathit{I}}$	GM ($\mathit{\mu }=0.0$)	PM ($\mathit{\mu }=0.0$)	Delay	Stability
with Fractional Order ($\mathit{\lambda }$)	at ${}^{\prime }{\mathit{\tau }}_{\mathit{d}}=7.102\mathbf{s}.$’	at ${}^{\prime }{\mathit{\tau }}_{\mathit{d}}=7.102\mathbf{s}.$’	Margin (${\mathit{\tau }}_{\mathbf{dm}})$
$\lambda =0.2$, $K_P$ = 0.3021:0.3789:0.3112, $K_I$ = 0.4603:0.5914:0.5861	4.786 dB	$-1.{086}^{\circ }$	6.542 s.	No
$\lambda =0.4$, $K_P$ = 0.3692:0.3021:0.3214, $K_I$ = 0.4786:0.6012:0.5314	7.56 dB	$0^{\circ }$	7.102 s	Marginally stable
$\lambda =0.6$, $K_P$ = 0.3066:0.4166:0.3101, $K_I$ = 0.5541:0.3106:0.5041	1.925 dB	∞	s	Yes
Gain of ${\mathbf{K}}_{\mathbf{P}}$&${\mathbf{K}}_{\mathbf{I}}$	GM ($\mathbf{\mu }=\mathbf{0}.\mathbf{0}$)	PM ($\mathbf{\mu }=\mathbf{0}.\mathbf{0}$)	Delay	Stability
with Fractional Order ($\mathbf{\lambda }$)	at ${}^{\prime }{\mathbf{\tau }}_{\mathbf{d}}=\mathbf{6}.\mathbf{328}\mathrm{s}$’	at ${}^{\prime }{\mathbf{\tau }}_{\mathbf{d}}=\mathbf{6}.\mathbf{328}\mathrm{s}$’	Margin (${\mathbf{\tau }}_{\mathbf{dm}})$
$\lambda =0.1$, $K_P$ = 0.321:0.396:0.3061, $K_I$ = 0.573:0.516:0.5647	1.184 dB	$-1.{025}^{\circ }$	3.521 s	No
$\lambda =0.3$, $K_P$ = 0.3357:0.321:0.4021, $K_I$ = 0.5502:0.574:0.5106	11.03 dB	$5.{625}^{\circ }$	6.328 s	Marginally stable
$\lambda =0.8$, $K_P$ = 0.375:0.3127:0.3571, $K_I$ = 0.544:0.601:0.5974	1.0856 dB	∞	8.265 s	Yes

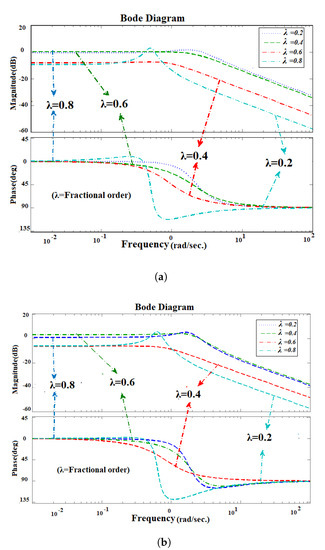
Figure 6. (a) Bode diagram when $\mu =0$ for constant time delay at ${\tau }_d$ = 7.102 s in unilateral case. (b) Bode diagram when ($\mu =0$) for time delay at ${\tau }_d$ = 7.234 s in the unilateral case.

6.2.3. Bilateral Transaction

In the bilateral case, the constant time delay ${\tau }_d=3.014$ s and ${\tau }_d=3.194$ s for $\lambda$ are considered. For the bilateral contract, power is transferred from the GENCO to the own DISCO as well as other area DISCOs. A change in the DPM matrix in this scenario can be stated as per (47).

$$\mathrm{DPM}=\left[\begin{array}{cccc}0.1& 0.2& 0.5& 0.3\\ 0.2& 0.1& 0& 0.1\\ 0.0& 0.1& 0.3& 0.2\\ 0.3& 0.2& 0.1& 0.1\\ 0.2& 0.3& 0.0& 0.1\\ 0.2& 0.1& 0.1& 0.2\end{array}\right]$$

(47)

The following values, as given by (48), are created to meet demand and maintain the system’s steady-state:

$$\left.\begin{array}{c}\Delta P_{g1ss}=0.11p.u.\left(MW\right);\hfill \\ \Delta P_{g2ss}=0.03p.u.\left(MW\right);\hfill \\ \Delta P_{g3ss}=0.06p.u.\left(MW\right);\hfill \\ \Delta P_{g4ss}=0.07p.u.\left(MW\right);\hfill \\ \Delta P_{g5ss}=0.06p.u.\left(MW\right);\hfill \\ \Delta P_{g6ss}=0.06p.u.\left(MW\right);\hfill \end{array}\right\}$$

(48)

The dynamic response depicts that for $\lambda =0.4$, the system evolves towards an unstable area when $K_P>0.5$ and $K_I>0.6$ for ${\tau }_d=3.194$ s. When the time delay ${\tau }_d$ is shorter than the delay margin (${\tau }_{dm}<{\tau }_d$), the oscillations fade away and the system’s response approaches a stable area, which can be achieved using the HBA technique. As demonstrated in Table 8, the gain value of an FOPI controller based on HBA is within the delay margin. As described before, the delay margin is primarily estimated using EBA. The simulation results are first used to investigate the delay margin for a constant time delay ($\mu =0.0$) with a delay of ${\tau }_d=3.194$ s. Figure 7a depicts the system’s response. The stability limit of the FOPI controller for the time-varying delay (${\tau }_d=3.194$ s) is $0.1\le K_P\le 0.5$ & $0.2\le K_I\le 0.6$ ($K_P$ & $K_I$) for fractional order range ($0.2\le \lambda \le 0.8$).

Table 8. Gain values of FOPI controllers for thermal−solar−wind system (test system 2) with DGS under deregulated environment in bilateral condition with time delays.

Fractional	$0.1\le {\mathit{K}}_{\mathit{p}}\le 0.5\&0.2\le {\mathit{K}}_{\mathit{I}}\le 0.6$ (Table 3, Table 4 and Table 5)
Order		${\mathbf{K}}_{\mathbf{P}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{3}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{3}}$	$\mathbf{OBJ}\times {\mathbf{10}}^{-\mathbf{2}}$
$\lambda =0.2$	${\tau }_d=3.{194}^{\prime }with\mu =0.0$	0.1212	0.3591	0.4214	0.2514	0.1148	0.1067	1.997
$\lambda =0.4$	${\tau }_d=3.{194}^{\prime }with\mu =0.0$	0.1559	0.5016	0.3621	0.1054	0.6214	0.5745	0.198
$\lambda =0.6$	${\tau }_d=3.{194}^{\prime }with\mu =0.0$	0.3398	0.598	0.3547	0.5617	0.3097	0.4758	0.1421
$\lambda =0.8$	${\tau }_d=3.{194}^{\prime }with\mu =0.0$	0.375	0.594	0.3127	0.601	0.3571	0.5974	0.00754
	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$			$\Delta {\mathbf{f}}_{\mathbf{3}}$
	OS	US	SS	OS	US	SS	OS	US	SS
$\lambda =0.2$	HBA-tuned FOPI controller with fractional order $\lambda =0.2$ go towards unstable system
$\lambda =0.4$	HBA-tuned FOPI controller with fractional order $\lambda =0.4$ go towards marginally stable system
$\lambda =0.6$	0.2794	−0.1952	6.57	0.1192	−0.8132	7.12	0.3174	−0.574	14.34
$\lambda =0.8$	0.00157	−0.07978	21.37	0.06183	−0.05963	25.83	0.04107	−0.0007595	13.53
Fractional	$\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{p}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$(Table 3, Table 4 and Table 5)
Order		${\mathbf{K}}_{\mathbf{P}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{3}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{3}}$	$\mathbf{OBJ}\times {\mathbf{10}}^{-\mathbf{2}}$
$\lambda =0.1$	${\tau }_d=3.{014}^{\prime }with\mu =0.0$	0.3010	0.5914	0.374	0.3947	0.313	0.5531	1.008
$\lambda =0.4$	${\tau }_d=3.{014}^{\prime }with\mu =0.0$	0.3972	0.5701	0.3071	0.4348	0.3901	0.5147	0.7014
$\lambda =0.6$	${\tau }_d=3.{014}^{\prime }with\mu =0.0$	0.33952	0.4021	0.3965	0.4965	0.3925	0.3414	0.04312
$\lambda =0.8$	${\tau }_d=3.{014}^{\prime }with\mu =0.0$	0.375	0.594	0.3127	0.601	0.3571	0.5974	0.00754
	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$			$\Delta {\mathbf{f}}_{\mathbf{3}}$
	OS	US	SS	OS	US	SS	OS	US	SS
$\lambda =0.2$	HBA-tuned FOPI controller with fractional order $\lambda =0.2$ go towards unstable system
$\lambda =0.4$	HBA-tuned FOPI controller with fractional order $\lambda =0.4$ go towards marginally stable system
$\lambda =0.6$	0.4512	−0.0165	5.97	0.674	−0.00447	8.63	0.00446	−0.0128	7.124
$\lambda =0.8$	0.002239	−0.001054	9.87	0.00364	−0.01287	11.47	0.0000158	−0.00226	8.324

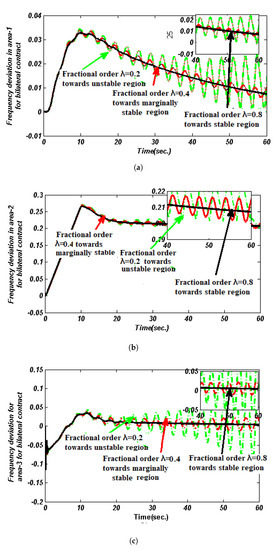
Figure 7. (a) Area 1 frequency deviation for Bilateral condition with a 10 % SLP type of load with time-varying delay ${\tau }_d$ = 4.325 s. at a rate $\mu =0.0$. (b) Area 2 frequency deviation for bilateral scenario 10% SLP type of load with constant time delay ${\tau }_d$ = 3.014 s at a rate of $\mu =0$. (c) Area 3 frequency deviation for 10 % SLP type of load with constant time delay ${\tau }_d=3.014$ s at rate of $\mu =0$.

The time delay is evaluated as ${\tau }_d=3.194$ s for time delays ($\mu =0$). The time delay attack decreases the system’s performance and pushes it towards an unstable zone, as seen in Figure 7a–c. Similar conclusions may be drawn from those findings, which show that an HBA-based FOPI controller with $\lambda =0.3$ is capable of achieving system stability within a delay margin. Lowering $\lambda$ from 0.8 to 0.6 slows down the system and takes a long time to achieve steady state (ST/29.14 s/$\Delta f_1$). However, increasing $\lambda$ from 0.3 to 0.8 at constant time delay ($\mu =0$) can improve it efficiently (ST/9.87 s/$\Delta f_1$). As a result, the proposed coordinated HBA-tuned FOPI controller with $\lambda =0.8$ has a better dynamic response and provides better overshoot, undershoot, and settling time, which can produce a sufficient increase in stability and quickly restore the frequency and tie-line power to their steady-state values, as shown in Table 8. The HBA-tuned FOPI with a greater order of fraction delivers the best dynamic response and has better overshoot (OS), undershoot (US), and settling time (ST) (as seen in the dynamic responses).

6.2.4. Contract Violation

The results are checked in case of contract violation to authenticate the effectiveness of the proposed HBA technique in case of constant time delay of ${\tau }_d=5.231$ s and the constant time delay of ${\tau }_d=3.021$ s. Table 9 shows the optimum gain values of the $K_P$ and $K_I$ of FOPI controllers achieved by the suggested HBA for various fractional ($\lambda =0.1\mathrm{to}0.4$, 0.6, and 0.8) orders. The FOPI controller gain values are also given with a delay margin $(0.05\le K_P\le 0.4\&0.1\le K_I\le 0.6)$, which is derived using EBA.

Table 9. Gain values of FOPI controllers for thermal−solar−wind system (test system 2) with DGS system under deregulated environment in contract violation condition with time delays.

Fractional	$0.1\le {\mathit{K}}_{\mathit{p}}\le 0.5\&0.2\le {\mathit{K}}_{\mathit{I}}\le 0.6$ (Table 3, Table 4 and Table 5)
Order		${\mathbf{K}}_{\mathbf{P}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{3}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{3}}$	$\mathbf{OBJ}\times {\mathbf{10}}^{-\mathbf{2}}$
$\lambda =0.2$	${\tau }_d=5.{231}^{\prime }with\mu =0.5$	0.3671	0.4342	0.3012	0.5647	0.3301	0.5647	1.547
$\lambda =0.4$	${\tau }_d=5.{231}^{\prime }with\mu =0.5$	0.3649	0.5012	0.3352	0.5741	0.3901	0.5019	0.8914
$\lambda =0.6$	${\tau }_d=5.{231}^{\prime }with\mu =0.5$	0.3961	0.4108	0.3374	0.5814	0.3397	0.5712	0.0941
$\lambda =0.8$	${\tau }_d=5.{231}^{\prime }with\mu =0.5$	0.2167	0.3241	0.287	0.1247	0.4214	0.1147	0.002387
	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$			$\Delta {\mathbf{f}}_{\mathbf{3}}$
	OS	US	SS	OS	US	SS	OS	US	SS
$\lambda =0.2$	HBA-tuned FOPI controller with fractional order $\lambda =0.2$ go towards unstable system
$\lambda =0.4$	HBA-tuned FOPI controller with fractional order $\lambda =0.4$ go towards marginally stable system
$\lambda =0.6$	0.00894	−0.002604	33.65	0.012945	−0.01014	12.24	0.00921	−0.00685	9.12
$\lambda =0.8$	0.00157	−0.07978	21.37	0.06183	−0.05963	25.83	0.04107	−0.0007595	13.53
Fractional	$\mathbf{0}.\mathbf{3}\le {\mathbf{K}}_{\mathbf{p}}\le \mathbf{0}.\mathbf{4}\&\mathbf{0}.\mathbf{4}\le {\mathbf{K}}_{\mathbf{I}}\le \mathbf{0}.\mathbf{6}$ (Table 3, Table 4 and Table 5)
Order		${\mathbf{K}}_{\mathbf{P}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{1}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{2}}$	${\mathbf{K}}_{\mathbf{P}\mathbf{3}}$	${\mathbf{K}}_{\mathbf{I}\mathbf{3}}$		$\mathbf{OBJ}\times {\mathbf{10}}^{-\mathbf{2}}$
$\lambda =0.1$	${\tau }_d=3.{021}^{\prime }with\mu =0.0$	0.3094	0.5391	0.3602	0.5422	0.3658	0.5712	1.847
$\lambda =0.3$	${\tau }_d=3.{021}^{\prime }with\mu =0.0$	0.3127	0.5464	0.3901	0.5667	0.3201	0.4967	0.0567
$\lambda =0.6$	${\tau }_d=3.{021}^{\prime }with\mu =0.0$	0.396	0.5654	0.3142	0.5254	0.3647	0.5247	0.00147
$\lambda =0.8$	${\tau }_d=3.{021}^{\prime }with\mu =0.0$	0.3891	0.5022	0.3451	0.5714	0.3522	0.5214	0.001191
	$\Delta {\mathbf{f}}_{\mathbf{1}}$			$\Delta {\mathbf{f}}_{\mathbf{2}}$			$\Delta {\mathbf{f}}_{\mathbf{3}}$
	OS	US	SS	OS	US	SS	OS	US	SS
$\lambda =0.2$	HBA-tuned FOPI controller with fractional order $\lambda =0.2$ go towards unstable system
$\lambda =0.4$	HBA-tuned FOPI controller with fractional order $\lambda =0.4$ go towards marginally stable system
$\lambda =0.6$	0.001147	−0.0014	9.54	0.1942	−0.003267	14.22	0.09211	0	10.22
$\lambda =0.8$	0.00214	−0.000142	6.24	0.1046	−0.000921	5.64	0.009164	0	4.67

In a contract violation case, DISCO breaks the contract by demanding more electricity from GENCO than is specified in the contract. An extra amount of power 0.1 $p.u$ (MW) is demanded by DISCO, so that $\Delta {\mathrm{P}}_{uc1}=0.1$$p.u$ (MW), $\Delta {\mathrm{P}}_{uc2}=0.0$; $\Delta {\mathrm{P}}_{uc3}=0.0$; $\Delta {\mathrm{P}}_{uc4}=0.0$. The rest of the scenarios are the same as they were in the bilateral transaction. Therefore, $\Delta {\mathrm{P}}_{uc1}$ + $\Delta {\mathrm{P}}_{uc1}$ = $\Delta {\mathrm{P}}_{uc1,loc1}$ = 0.1 + 0.0 = 0.1 $p.u$ (MW), and $\Delta {\mathrm{P}}_{uc1,loc2}$ = $\Delta {\mathrm{P}}_{uc3}$ + $\Delta {\mathrm{P}}_{uc4}$ = 0.0 $p.u$ (MW). In the event of a contract violation scenario, the area control error (ACE) participation factor (apf) plays a critical part in violating the contract between GENCOs and DISCOs. The following equation is created to meet demand and maintain the system’s steady-state:

$$\begin{array}{c}\left[\begin{array}{c}\Delta {\mathrm{P}}_{\mathrm{g}1\mathrm{ss}}\\ \Delta {\mathrm{P}}_{\mathrm{g}2\mathrm{ss}}\\ \Delta {\mathrm{P}}_{\mathrm{g}3\mathrm{ss}}\\ \Delta {\mathrm{P}}_{\mathrm{g}4\mathrm{ss}}\end{array}\right]=\left[\begin{array}{cccc}\mathrm{cp}{\mathrm{f}}_{11}& \mathrm{cp}{\mathrm{f}}_{12}& \mathrm{cp}{\mathrm{f}}_{13}& \mathrm{cp}{\mathrm{f}}_{14}\\ \mathrm{cp}{\mathrm{f}}_{21}& \mathrm{cp}{\mathrm{f}}_{22}& \mathrm{cp}{\mathrm{f}}_{23}& \mathrm{cp}{\mathrm{f}}_{24}\\ \mathrm{cp}{\mathrm{f}}_{31}& \mathrm{cp}{\mathrm{f}}_{32}& \mathrm{cp}{\mathrm{f}}_{33}& \mathrm{cp}{\mathrm{f}}_{34}\\ \mathrm{cp}{\mathrm{f}}_{41}& \mathrm{cp}{\mathrm{f}}_{42}& \mathrm{cp}{\mathrm{f}}_{43}& \mathrm{cp}{\mathrm{f}}_{44}\end{array}\right]\left[\begin{array}{c}\Delta {\mathrm{P}}_{\mathrm{L}1}\\ \Delta {\mathrm{P}}_{\mathrm{L}2}\\ \Delta {\mathrm{P}}_{\mathrm{L}3}\\ \Delta {\mathrm{P}}_{\mathrm{L}4}\end{array}\right]+\hfill \\ \hfill \left[\begin{array}{cccc}\Delta {\mathrm{P}}_{\mathrm{uc},\mathrm{Loc}1}& 0& 0& 0\\ 0& \Delta {\mathrm{P}}_{\mathrm{uc},\mathrm{Loc}2}& 0& 0\\ 0& 0& \Delta {\mathrm{P}}_{\mathrm{uc},\mathrm{Loc}3}& 0\\ 0& 0& 0& \Delta {\mathrm{P}}_{\mathrm{uc},\mathrm{Loc}4}\end{array}\right]\left[\begin{array}{c}\mathrm{ap}{\mathrm{f}}_{11}\\ \mathrm{ap}{\mathrm{f}}_{12}\\ \mathrm{ap}{\mathrm{f}}_{13}\\ \mathrm{ap}{\mathrm{f}}_{14}\end{array}\right]\end{array}$$

(49)

As a result, area 1 demands surplus un-contract power, which is automatically compensated by $GENC{O}_2$ and $GENC{O}_3$ of area 2 and area 3. Therefore,

$$\left.\begin{array}{c}\Delta P{g}_{1ss}=0.18p.u.\left(MW\right);\hfill \\ \Delta P{g}_{2ss}=0.1155p.u.\left(MW\right);\hfill \\ \Delta P{g}_{3ss}=0.085p.u.\left(MW\right);\hfill \\ \Delta P{g}_{4ss}=0.16p.u.\left(MW\right);\hfill \\ \Delta P{g}_{5ss}=0.16p.u.\left(MW\right);\hfill \\ \Delta P{g}_{6ss}=0.16p.u.\left(MW\right);\hfill \end{array}\right\}$$

(50)

Table 9 and Figure 8 compare the performance of the FOPI controller with various fractional orders ($\lambda =0.10.4$, 0.6, and 0.8) by recording the dynamic responses of the multi-source hybrid system in the form of OS, US, and ST, as well as the objective function. The results show that the suggested HBA-based FOPI with fractional order $\lambda =0.8$ is responsible for the best solution quality for $K_P$, $K_I$ ($0.3\le K_P\le 0.4$&$0.4\le K_I\le 0.6$) for time delays ${\tau }_d=5.231s$ and ${\tau }_d=3.021s$ for the proposed AGC system.

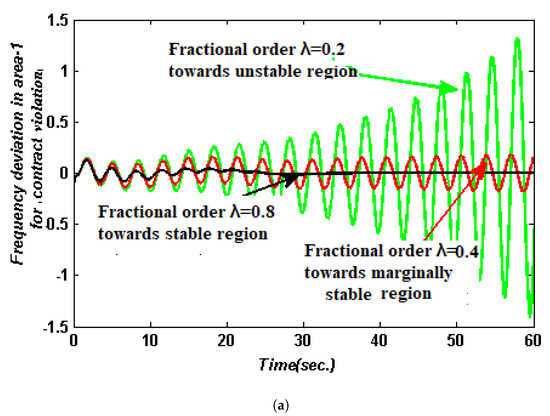
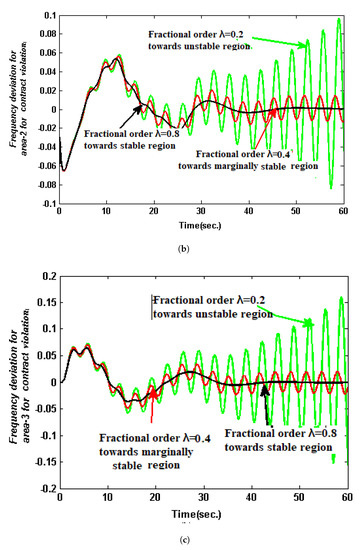
Figure 8. (a) Area 1 frequency deviation for contract violation with SLP type load and 10% load disturbance with time−varying delay ${\tau }_d=5.231$ s at a rate $\mu =0$. (b) Area 2 frequency deviation for contract violation case with SLP type of load and 10% load disturbance with constant time delay ${\tau }_d$ = 3.021 s at a rate of $\mu =0$. (c) Frequency deviation of Area 3 with constant time delay ${\tau }_d$ = 3.021 s. at a rate $\mu =0$ at 10% load disturbance.

7. Robustness Analysis of the Proposed Method

To test the robustness of the FOPI controller, a random load perturbation (RLP) is applied to area 1 of the supplied solar-wind-thermal system using the proposed HBA with different values of $\lambda$. The RLP load type value varies by $\pm 0.02$$p.u$ (MW).

A random step load change is applied in area 1 with a time delay ${\tau }_d=7.365$ s to judge the robustness of the proposed HBA-based FOPI controller under specified time delays. Figure 9a depicts the RLP (random type of load) pattern applied to the suggested hybrid system. Under the deregulated scenario, the gain value of the different parameters of the FOPI controller (within the delay margin) is optimized simultaneously in three separate cases. The comparison results are shown in Table 10. As demonstrated in Figure 9b–d, the peak magnitude of the frequency and the tie-power oscillations with HBA-based FOPI with the fractional order ($\lambda =0.8$) is quickly attenuated under the RLP type of load, proving the robustness of the HBA-based proposed controller.

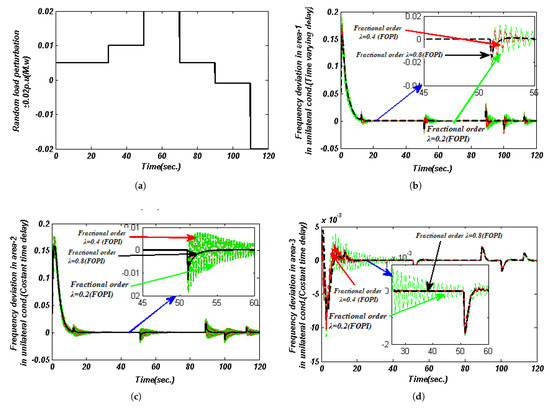
Figure 9. (a) Using a load of ±0.02 $p.u$., random load perturbation was performed (MW). (b) For a ±0.02 ($p.u$) RLP type of load, frequency variation in area 1 in Hz for unilateral condition with time−varying (${\tau }_d=7.365s$) ($\mu =0$) delay. (c) For a ±0.02 ($p.u$) RLP type of load, frequency variation in area 2 in Hz for unilateral condition with time−varying (${\tau }_d=7.365s$) ($\mu =0$) delay. (d) For a ±0.02 ($p.u$) RLP type of load, frequency variation in area 3 in Hz for unilateral condition with constant time (${\tau }_d=5.127s$) ($\mu =0$) delay.

Table 10. Gain values of FOPI controller to (test system 2) hybrid thermal−wind−solar system with DGS constant time delays ${\tau }_d$ = 7.365 s and RLP type of load for ±0.02 MW ($p.u$).

$0.3\le {\mathit{K}}_{\mathit{P}}\le 4.0\&0.4\le {\mathit{K}}_{\mathit{I}}\le 0.6$	Optimized Parameter	Unilateral Contract
		FOPI ($\lambda =0.2$)	FOPI ($\lambda =0.4$)	FOPI ($\lambda =0.8$)
	$K_{P1}$	0.3036	0.354	0.3364
	$K_{I1}$	0.571	0.5014	0.5892
P-I Controller with	$K_{P2}$	0.3296	0.3964	0.3345
Fractional order	$K_{I2}$	0.5012	0.5361	0.5714
0.2, 0.4 & 0.8	$K_{P3}$	0.3120	0.3941	0.3241
	$K_{I3}$	0.5941	0.5601	0.5901
OBJ		1.231	0.621	0.1754
		Bilateral Contract
		FOPI ($\lambda =0.2$)	FOPI ($\lambda =0.4$)	FOPI ($\lambda =0.8$)
	$K_{P1}$	0.3017	0.3924	0.3195
	$K_{I1}$	0.5952	0.5010	0.5431
	$K_{P2}$	0.3016	0.3891	0.3457
	$K_{I2}$	0.5013	0.5512	0.5014
	$K_{P3}$	0.3901	0.3410	0.3324
	$K_{I3}$	0.5001	0.5447	0.5131
OBJ		0.0674	0.0221	0.00754
		Contract violation
		FOPI ($\lambda =0.2$)	FOPI ($\lambda =0.4$)	FOPI ($\lambda =0.8$)
	$K_{P1}$	0.3001	0.3109	0.3794
	$K_{I1}$	0.5974	0.5197	0.5661
	$K_{P2}$	0.3914	0.3107	0.3761
	$K_{I2}$	0.5013	0.5512	0.5014
	$K_{P3}$	0.3741	0.3011	0.3951
	$K_{I3}$	0.5201	0.5901	0.5461
OBJ		0.002513	0.000954	0.000124

8. Conclusions

This article focuses on optimal delay tuning to overcome the communication delay problem during the synchronization of non-conventional (wind-solar) power plants with conventional energy plants in order to reduce dependency on traditional resources and bring renewable energy resources into the mainstream of the power generating sector (thermal plants). To assess the performance of the proposed HBA, initially, a two-area thermal system is studied, and a comparison is performed between HBA, COKHA, GOA, BFA, and MFOA. The proposed HBA technique excels the other algorithms in terms of dynamic response. Furthermore, by considering time delays with a specified range of `$\lambda$’ in the LFC control loop, a delay dependent stability criterion is proposed to find the delay margin for the FOPI controller. It has been analyzed how the delay margin considerably fluctuates with different values of `$\lambda$’ of the FOPI controller for a certain range of delay. The results revealed that as the value of `$\lambda$’ rises, the delay margin (${\tau }_{dm}$) increases in a renewable-based three-area hybrid system with distributed generation in a deregulated environment. Finally, it can be seen that a hybridized DGS system performs better since it can meet specific power requirements and minimize the system oscillation totally.

The major findings of this paper are summarized below:

• The delay margin of the FOPI controller is determined using empirical bode analysis (EBA), which may be used in designing the controller for the aforesaid linearized time delayed system and verifying it using their dynamic performance in three different instances.
• Using the HBA method, all of the parameters of the FOPI controller in area 1, area 2, and area 3 are stable within the permissible delay margin. An experiment is run with a range of fractional order ($\lambda$ from 0.1 to 0.8) for an FOPI controller with a set of $K_P$ and $K_I$ values maintained within a given delay margin. The investigation shows that the frequency response and tie-line power fluctuations are strongly affected by the controller for a given time delay. Within a specified control parameter set ($K_P$&$K_I$), the fractional order ($\lambda$) may enhance the delay margin (${\tau }_{dm}$).
• Use the RLP type of load to test the FOPI controller’s resilience performance for the provided system.
• The findings show how the proposed controlling technique can make the hybrid system optimally stable over a wide range of delays.

The technique proposed in this paper may be extended to consider the following research initiatives in the future:

• The AGC time-delay systems with multiple areas (more than three).
• In the case of random nature time delay in a multi-area system, structured singular value and Schur–Cohn (hemetic matrix creation) may determine the MADB and provide a thorough stability study.
• Test the stability of a time-delay system with advanced controllers (such as tilt-integral-derivative (TID), two-degrees-of-freedom (2DOF)-PID, 3DOF-PID, fractional-order PID, and cascade PI–PID, TID, and cascade-TID, which are designed to handle both constant and time-varying delays.