Evaluation of Residual Stress Relaxation in a Rolled Joint by Neutron Diffraction
Abstract
1. Introduction
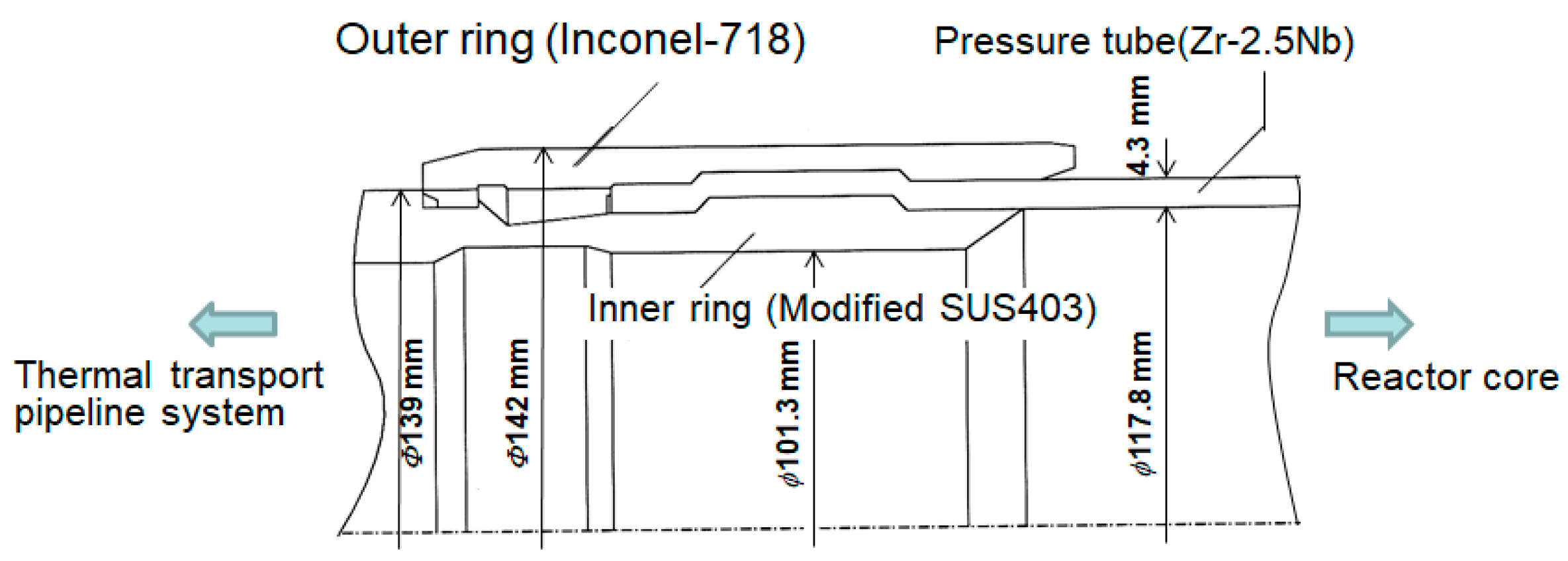
2. Experimental Procedures
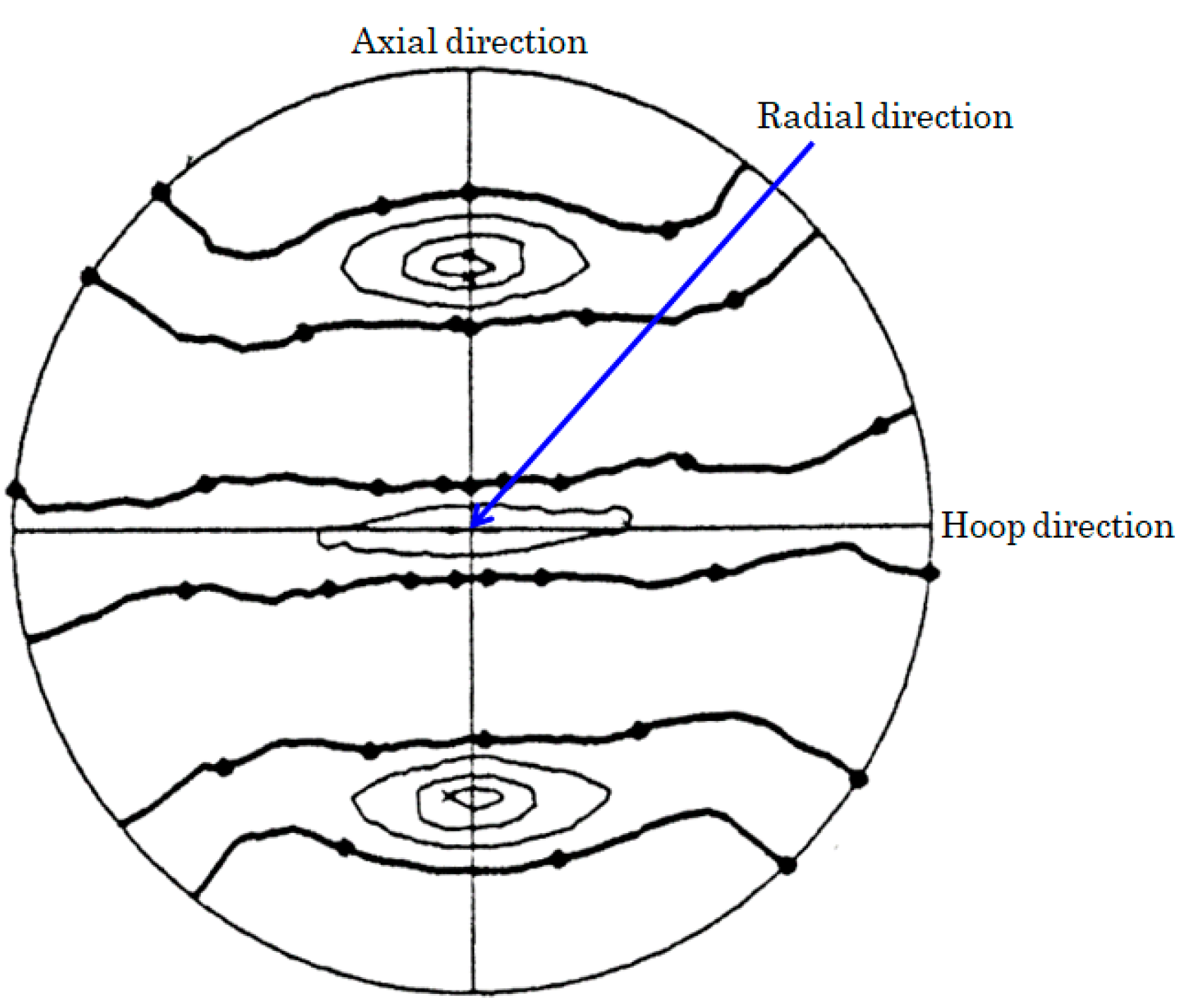
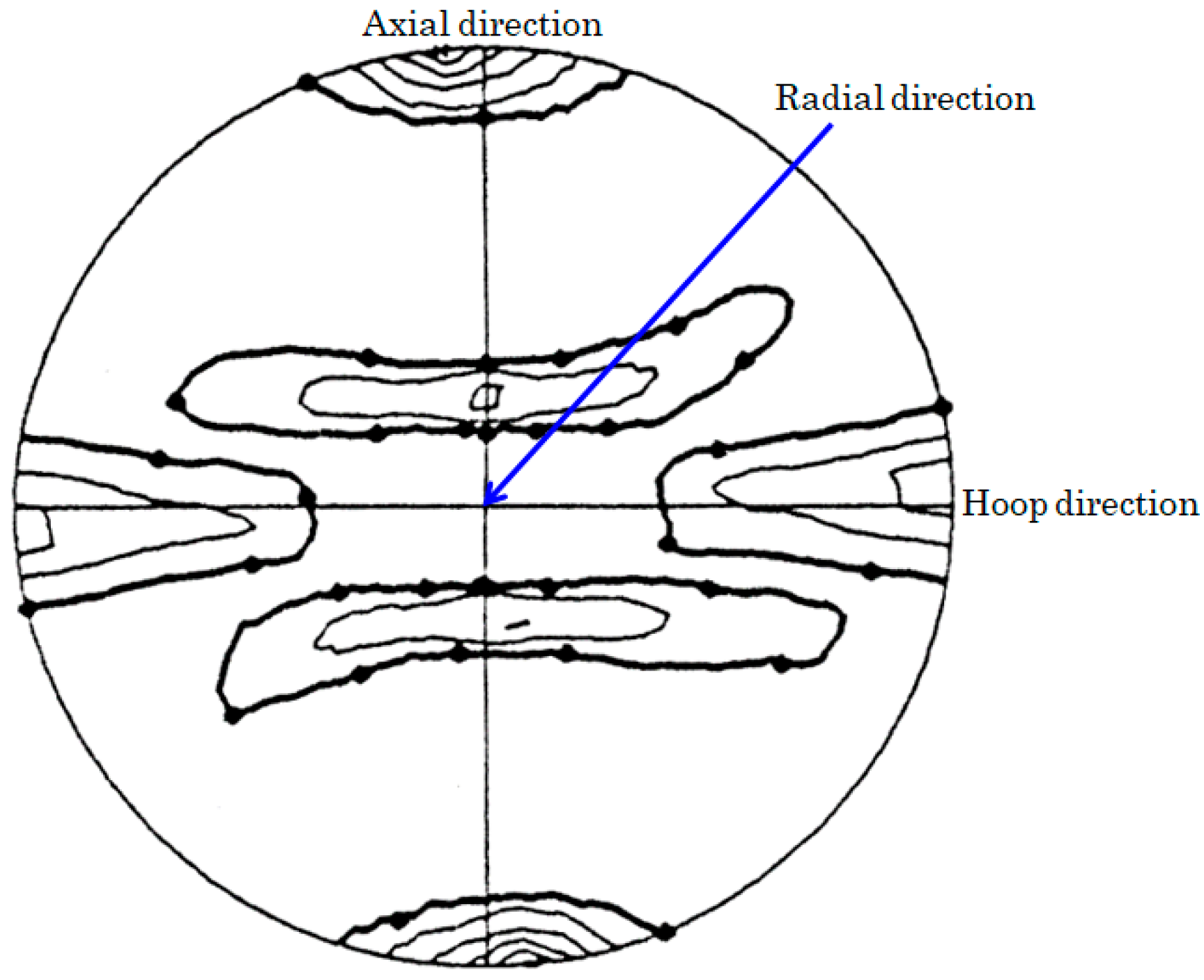
2.1. Texture Measurements
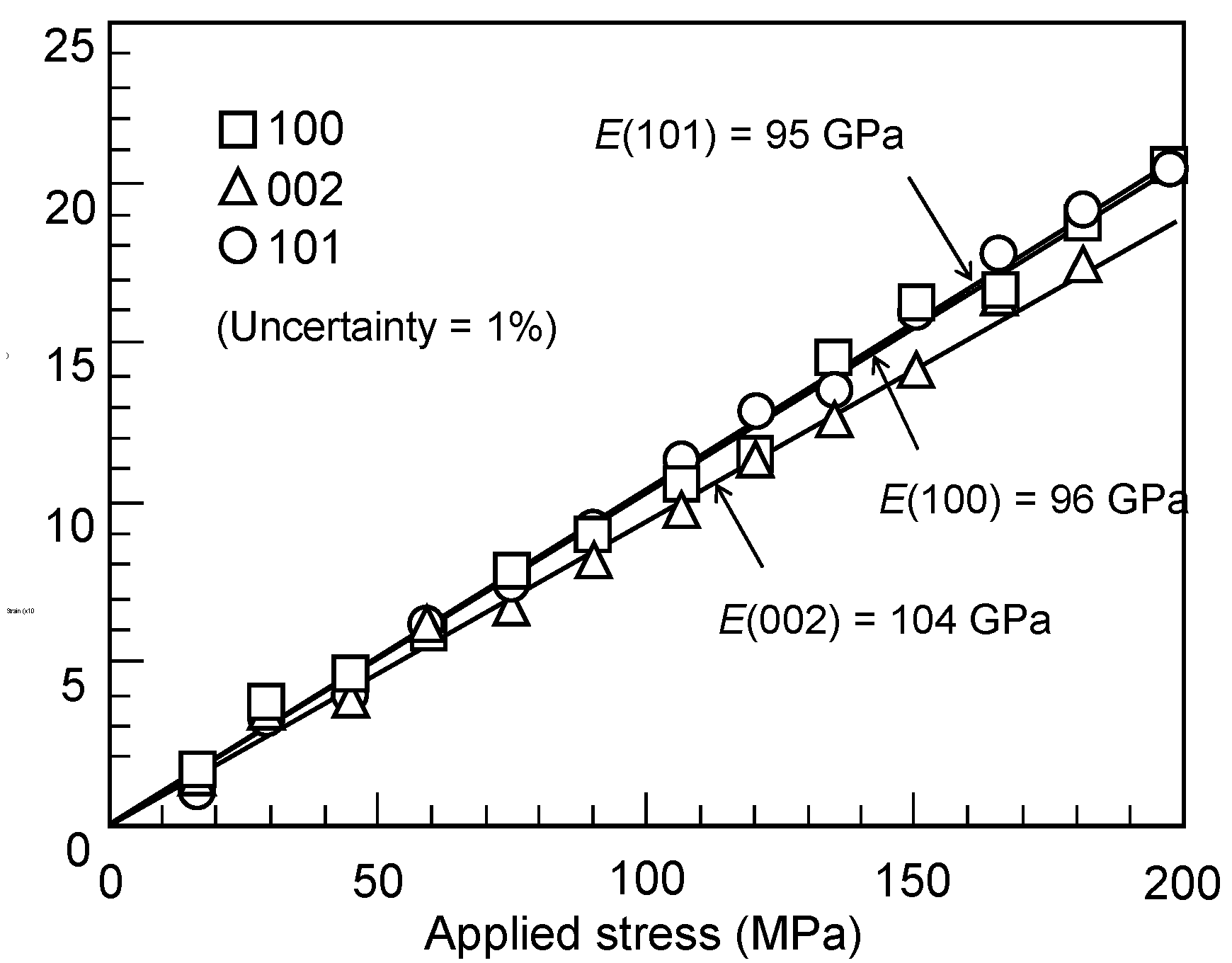
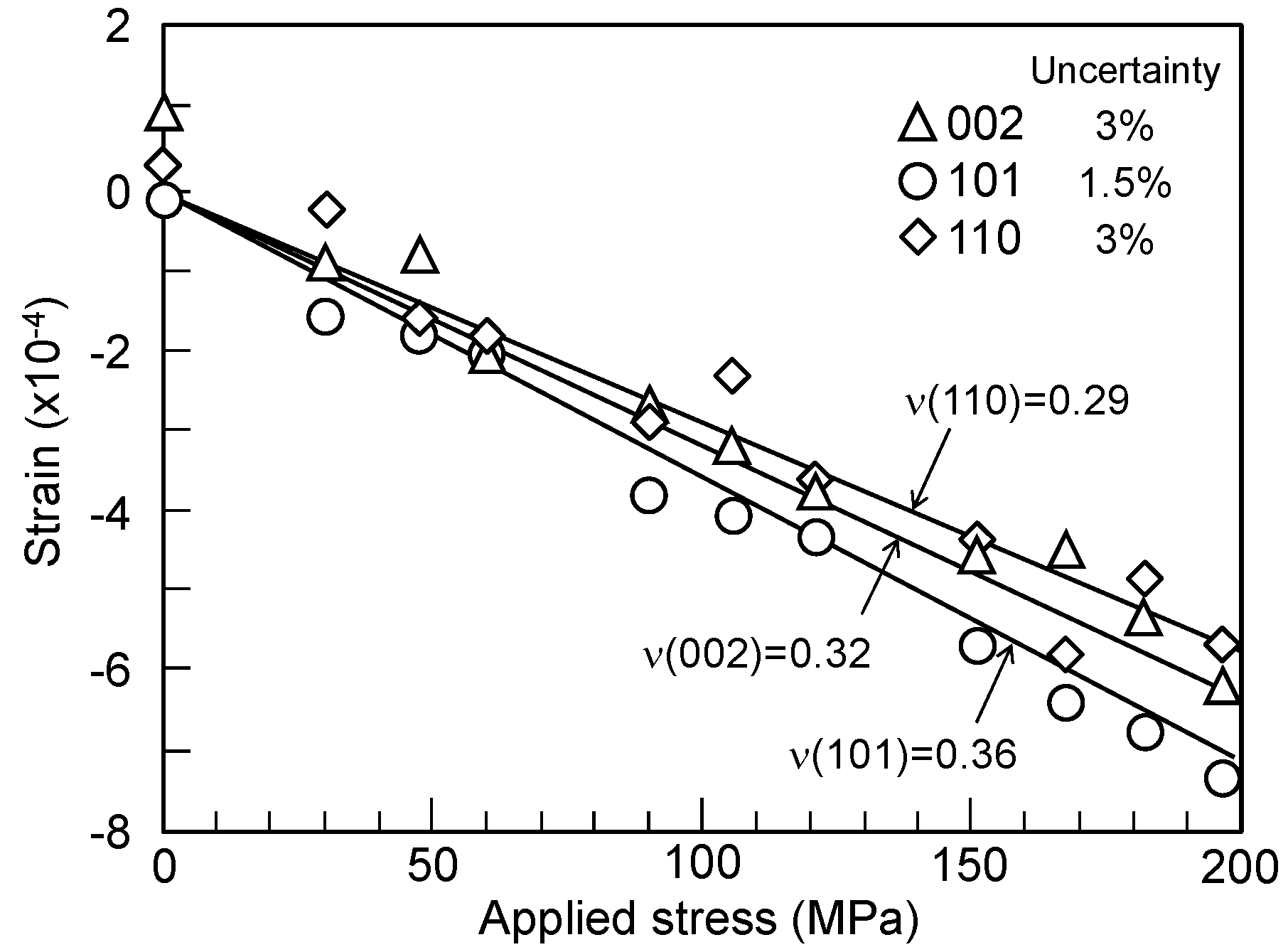
2.2. Elastic Constants
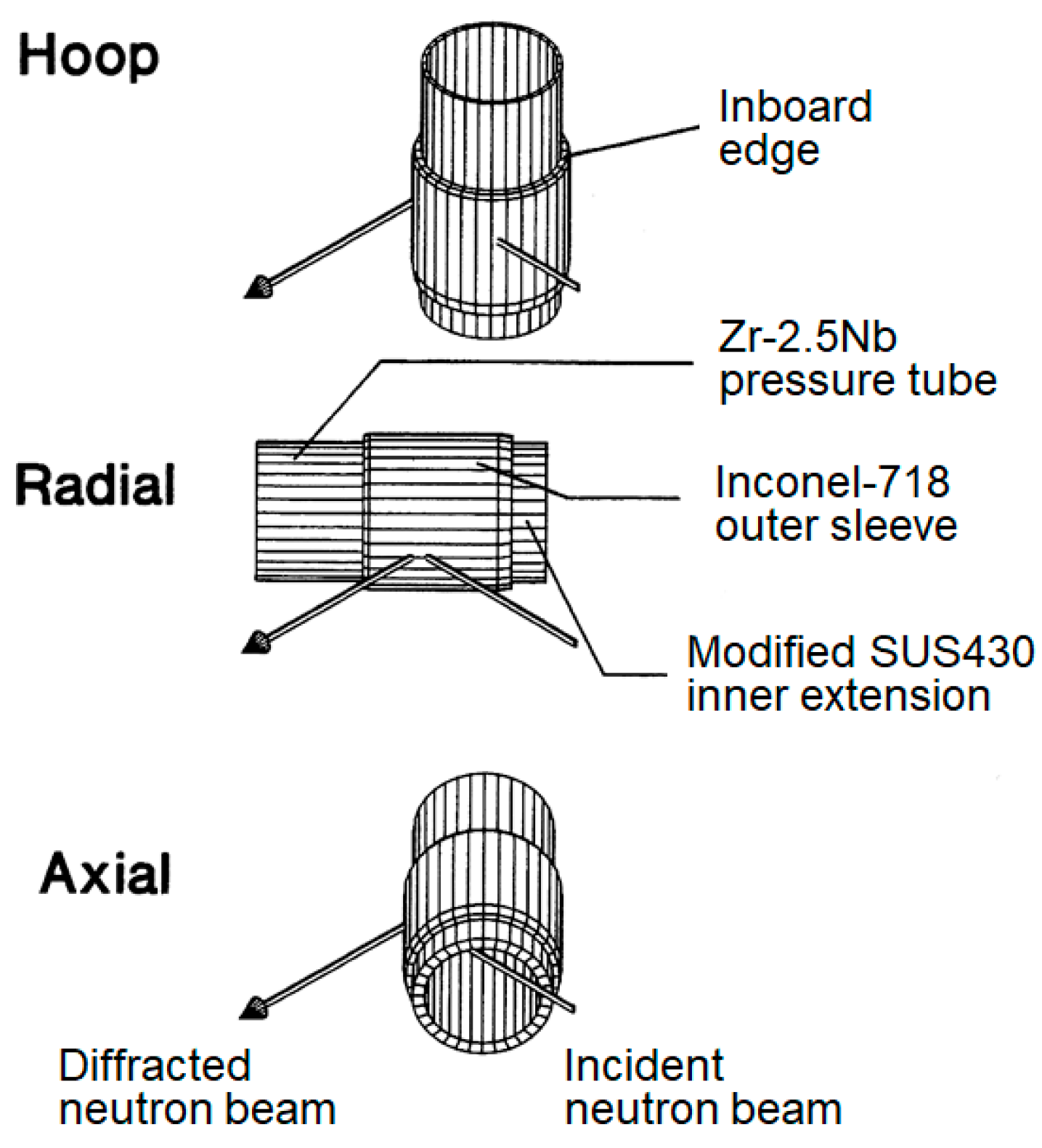
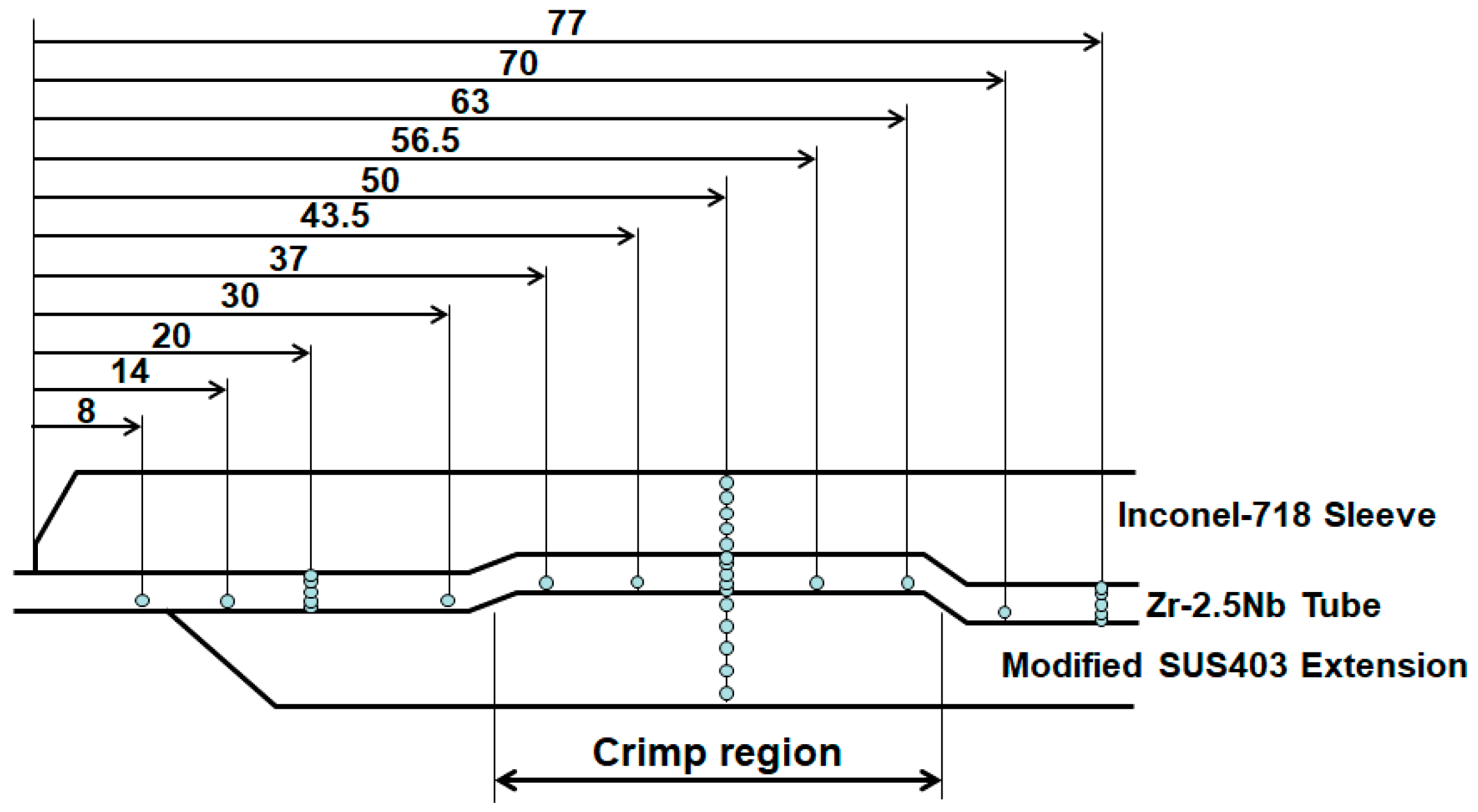
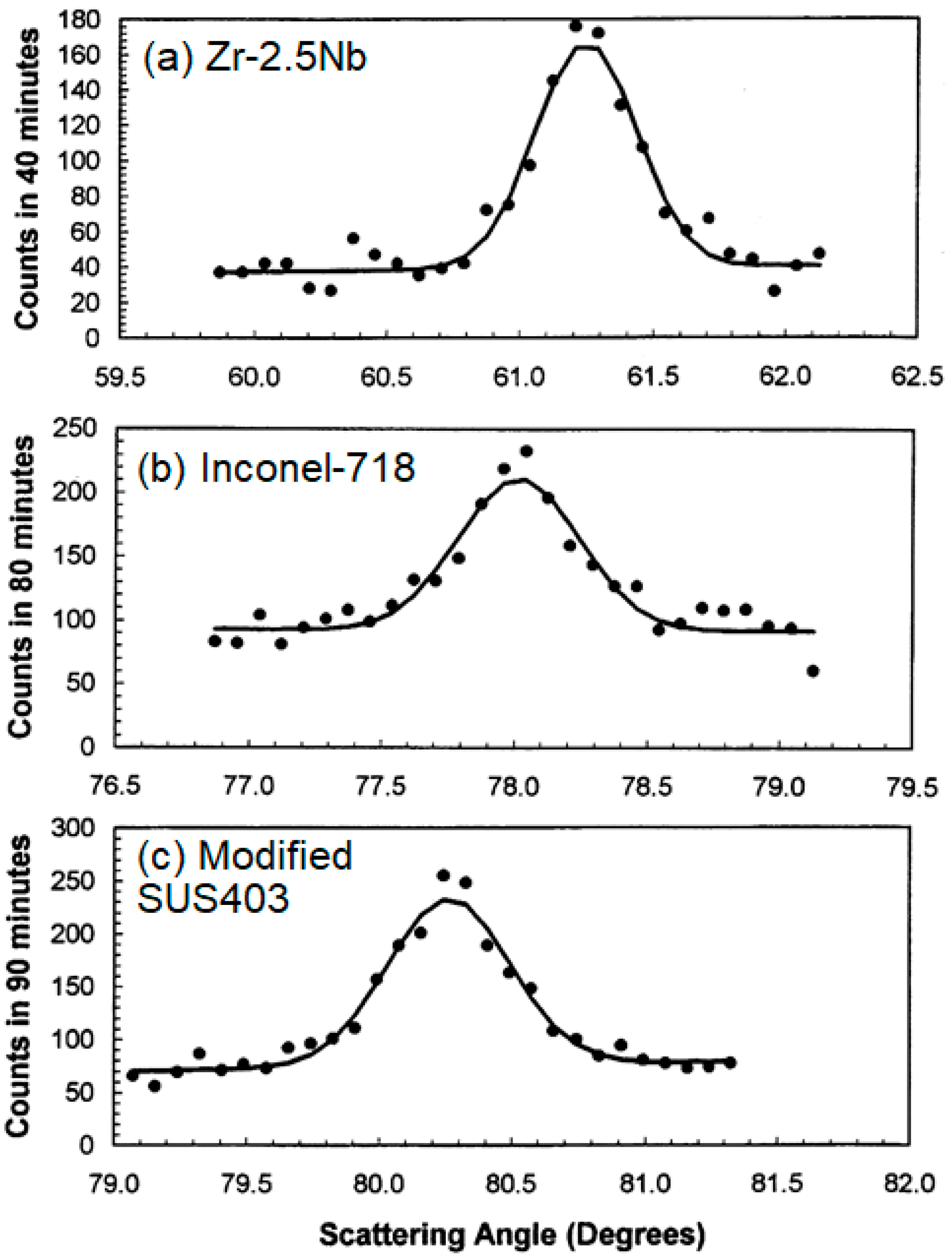
2.3. Residual Stress Measurements
2.4. Heat Treatments
3. Results and Discussion
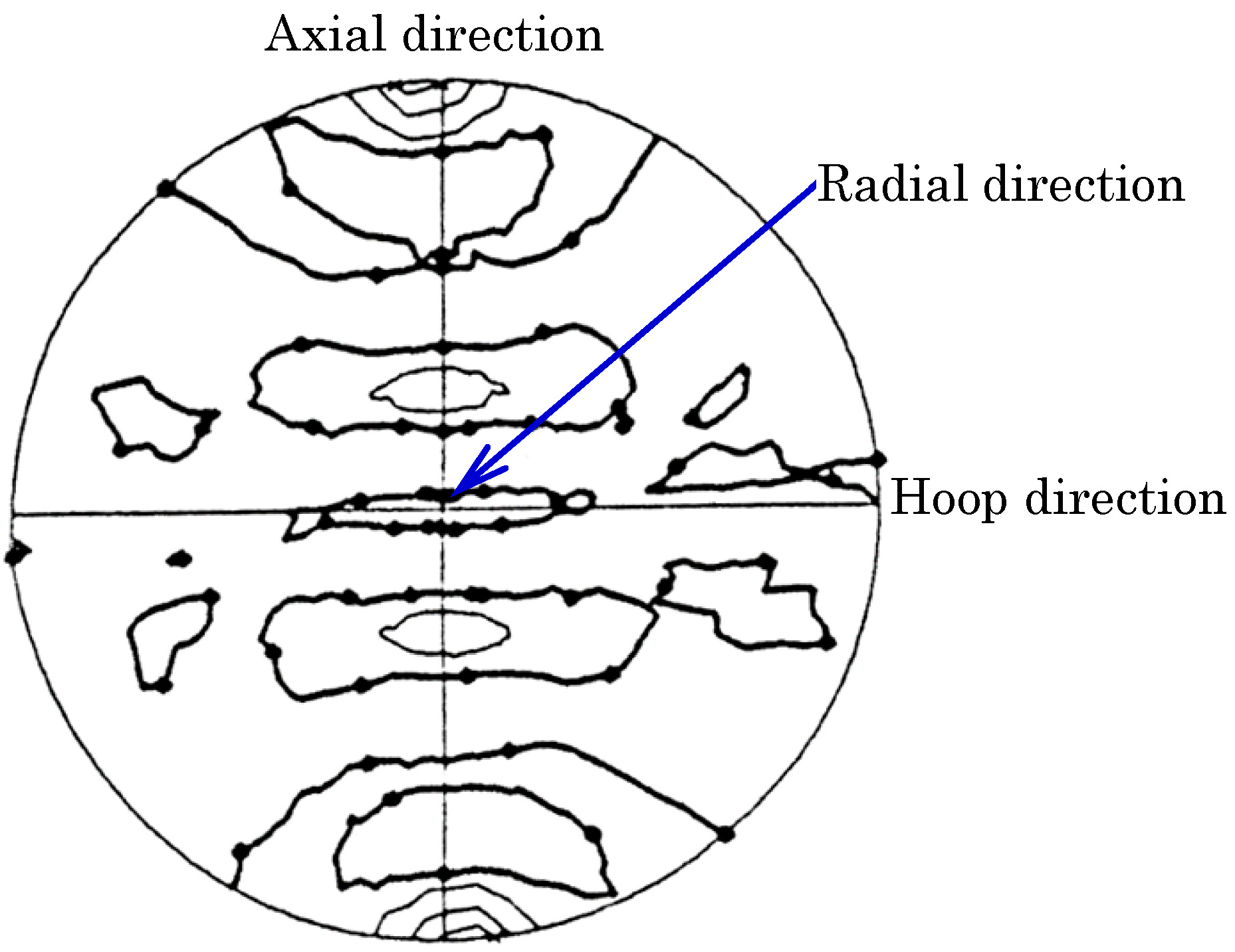
3.1. Texture Measurements
3.2. Elastic Constants
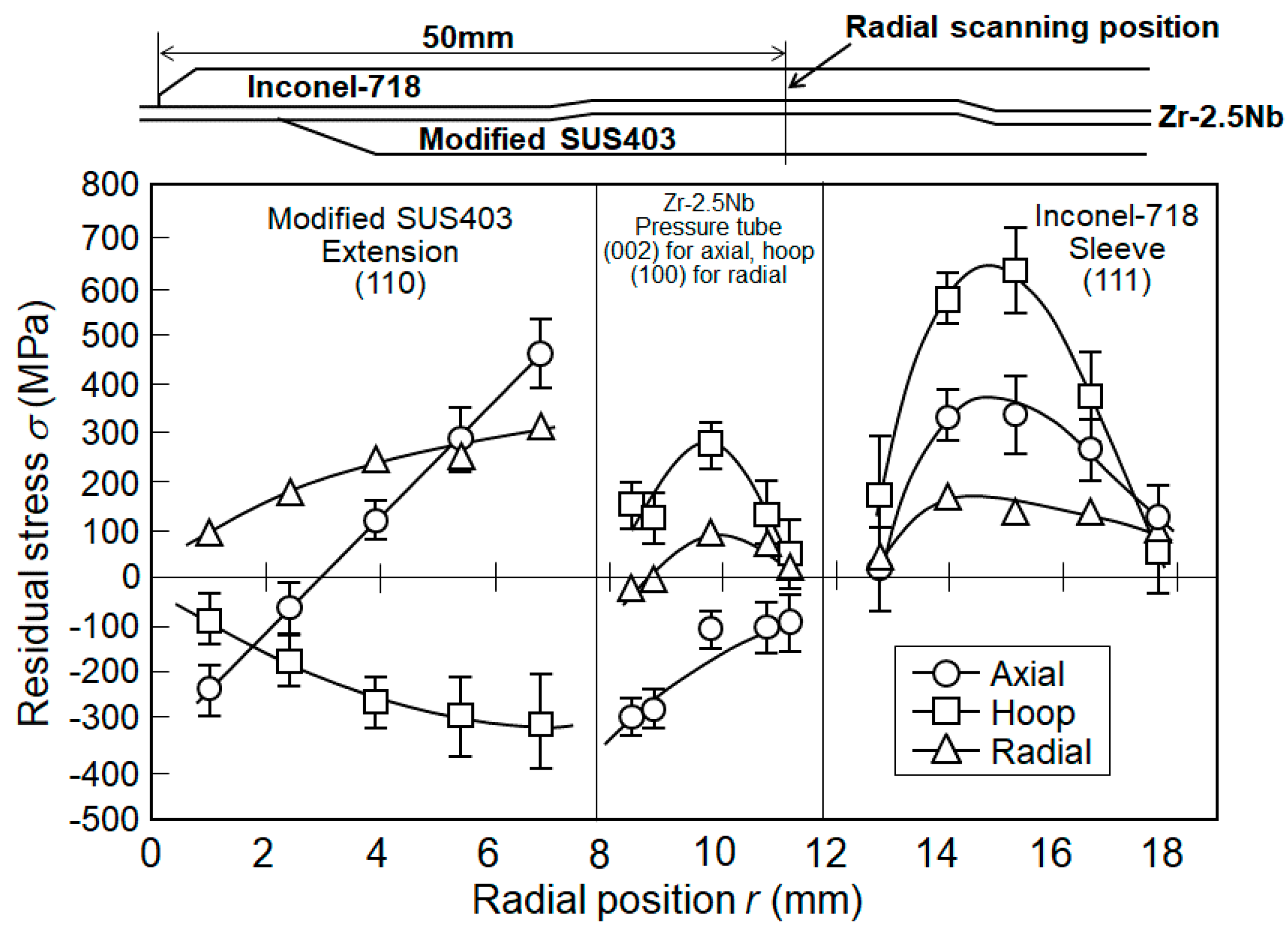
3.3. Residual Stresses
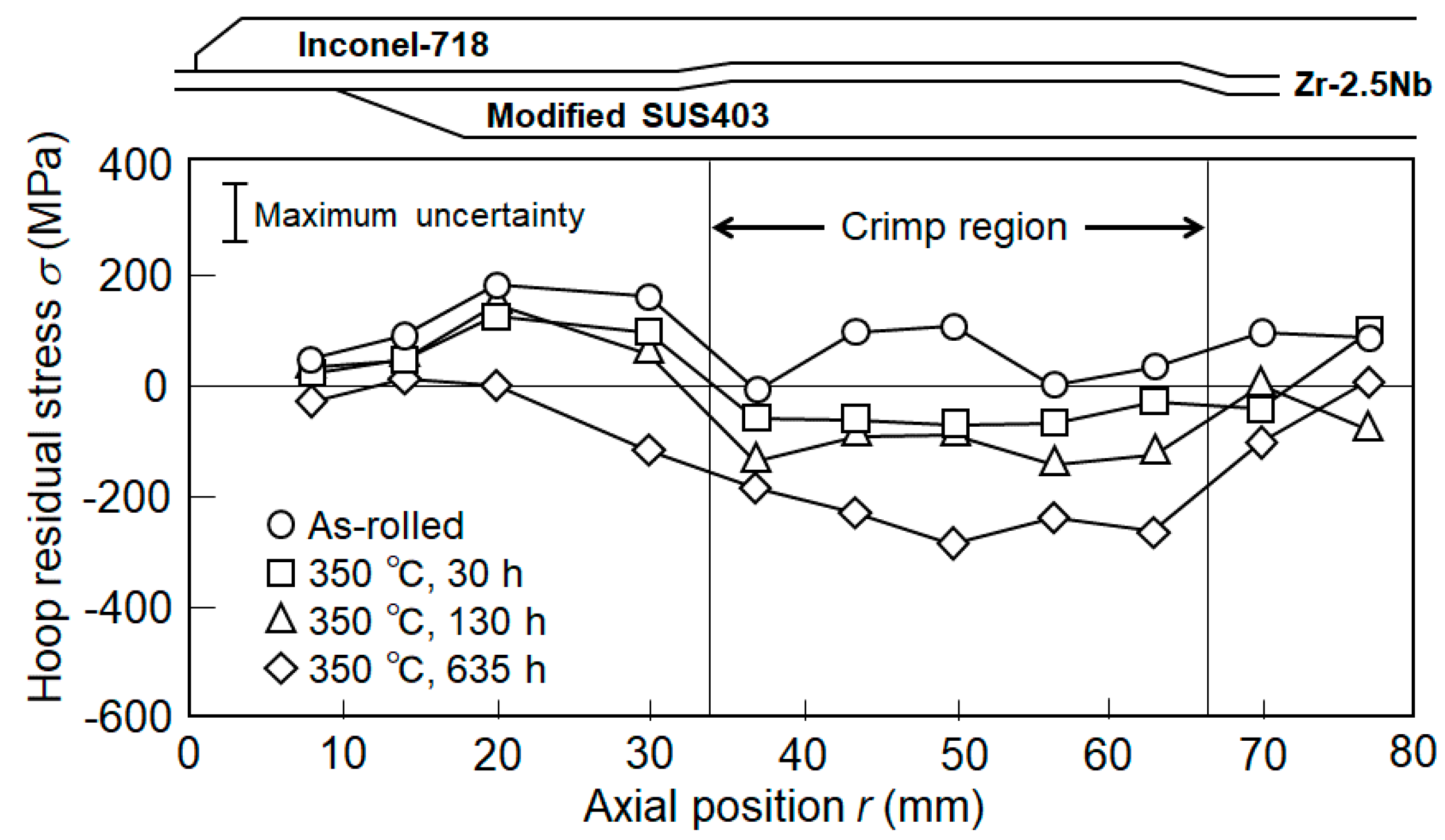
3.4. Residual Stress Relaxation in a Zr–2.5Nb Pressure Tube
4. Summary and Prospects
Author Contributions
Conflicts of Interest
References
- Mita, S.; Akebi, M.; Sawamura, O.; Kondo, T. Development of the Advanced Thermal Reactor in Japan. Nuclear Eng. Des. 1993, 144, 283–292. [Google Scholar] [CrossRef]
- Uematsu, S.; Mitsugi, T.; Kikuchi, K.; Kobayashi, T.; Yokoya, J. Irradiation Experiment of MOX Fuel Assembly for Advanced Thermal Reactor. J. Nucl. Sci. Technol. 1997, 39, 870–880. [Google Scholar]
- Allen, A.J.; Hutching, M.T.; Windsor, C.G.; Andreani, C. Neutron diffraction methods for the study of residual stress fields. Adv. Phys. 1985, 34, 445–473. [Google Scholar] [CrossRef]
- Bourke, M.A.M.; MacGillivray, H.J.; Webster, G.A.; Low, K.S.; Webster, P.J. Improving the resolution of neutron diffraction residual stress measurements in engineering components. In Proceedings of the IITT International Conference on Fatigue and Stress, Paris, France, 10 July 1987. [Google Scholar]
- Bourke, M.A.M.; Smith, D.J.; Webster, G.A.; Webster, P.J. Neutron diffraction measurements of residual stresses in plastically deformed cracked beams. In Proceedings of the 9th Conference on Experimental Mechanics, Copenhagen, Denmark, 20–24 August 1990; pp. 1198–1206. [Google Scholar]
- Webster, G.A. Role of neutron diffraction in engineering stress analysis. In Measurement of Residual and Applied Stress Using Neutron Diffraction; Hutching, M.T., Krawits, A.D., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 21–35. [Google Scholar]
- Buttle, D.J.; Hutching, M.T. Residual stress measurement at NNDTC. Br. J. Nondestruc. Test. 1992, 34, 175–182. [Google Scholar]
- Hayashi, M.; Ishiwata, M.; Minakawa, N.; Funahashi, S.; Root, J.H. Diffraction Plane Dependence of Elastic Constants in Ferritic Steel in Neutron Diffraction Stress Measurement. ZAIRYO-J. Soc. Mater. Sci. Jpn. 1995, 44, 1115–1120. (In Japanese) [Google Scholar] [CrossRef]
- Kröner, E. Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls. Z. Physik. 1958, 151, 504–518. [Google Scholar] [CrossRef]
- Hayashi, M.; Ishiwata, M.; Minakawa, N.; Funahashi, S. Residual Stress Measurement in Socket Welded Joints by Neutron Diffraction. ZAIRYO-J. Soc. Mater. Sci. Jpn. 1995, 44, 1464–1469. (In Japanese) [Google Scholar] [CrossRef]
- Hayashi, M.; Ishiwata, M.; Morii, S.; Minakawa, N. Residual Stress Distribution in Carbon Steel Pipe Welded Joints Measured by Neutron Diffraction. ZAIRYO-J. Soc. Mater. Sci. Jpn. 1996, 45, 772–778. (In Japanese) [Google Scholar] [CrossRef]
- Mochizuki, M.; Hayashi, M.; Hattori, T. Numerical Analysis of Welding Residual Stress and Its Verification Using Neutron Diffraction Measurement. Trans. ASME 2000, 122, 98–103. [Google Scholar] [CrossRef]
- Holden, T.M.; Hosbons, R.R.; Root, J.H.; Ibrahim, E.F. Neutron Diffraction Measurements of Strain and Texture in Welded Zr–2.5Nb Tube. MRS Proc. 1988, 142, 59–64. [Google Scholar] [CrossRef]
- Root, J.H.; Colemen, C.E.; Bowden, J.W.; Hayashi, M. Residual Stresses in Steel and Zirconium Weldments. J. Press. Vess. Technol. 1997, 119, 137–141. [Google Scholar] [CrossRef]
- MacEwen, S.R.; Christodoulou, N.; Salinas-Rodríguez, A. Residual grain-interaction stresses in zirconium alloys. Meter. Trans. A 1990, 21, 1083–1095. [Google Scholar] [CrossRef]
- Hayashi, M.; Kimoto, H.; Michishita, H.; Root, J.H. Measurement of Texture and Elastic Constants of Zr–2.5%Nb Alloy by Neutron Diffratcion. ZAIRYO-J. Soc. Mater. Sci. Jpn. 1997, 46, 743–749. (In Japanese) [Google Scholar] [CrossRef]
- Hayashi, M.; Ohkido, S.; Morii, Y.; Minakawa, N. Measurement of Residual Stress in Structural Components by Neutron Diffraction; Technical Report; The Society of Material Science: Kyoto, Japan, 2001; pp. 418–423. [Google Scholar]
- Hayashi, M.; Ohkico, S.; Morii, Y.; Minakawa, N.; Root, J.H. Measurement of Residual Stress in Structural Components by Neutron Diffraction and Proposal of Measurement Standard. Mater. Sci. Forum 2003, 426–432, 3969–3974. [Google Scholar] [CrossRef]
- Roe, R.J. Description of Crystallite Orientation in Polycrystalline Materials. 3. General Solution to Pole Figure Inversion. J. Appl. Phys. 1965, 36, 2024–2031. [Google Scholar] [CrossRef]
- Hayashi, M.; Root, J.H. Effect of miss-alignment on residual stress in carbon steel socket welded joint. Zairyo-J. Soc. Mater. Sci. Jpn. 2014, 63, 602–607. [Google Scholar] [CrossRef]
- Benken, H.; Hauk, V. Berechnung der röntgenographischen Elastizitätkonstanten (REK) des Vielkristalls aus Einkristalldaten für beliebige Kristalsymmetrie. Z. Metallkde. 1986, 77, 620–626. [Google Scholar]
- Smithells, C.J.; Brandes, E.A.; Fulmer Research Institute. Smithells Metals Reference Book, 6th ed.; Brandes, E.A., Ed.; Fulmer Research Institute Ltd., Butterworth Scientific: London, UK, 1983. [Google Scholar]
- Suzuki, H.; Holden, T.M. Neutron diffraction measurements of stress in an austenitic butt weld. J. Strain Anal. Eng. Des. 2006, 41, 575–582. [Google Scholar] [CrossRef]
- Xu, P.G.; Tomota, Y.; Suzuki, H.; Suzuki, T.; Machiya, S.; Yin, F.X. Bulk Texture Measurement of Interstitial-Free Annealed Steel Using Gaussian Integrated Intensities of Neutron Diffraction Spectra. Mater. Trans. 2008, 49, 2033–2039. [Google Scholar] [CrossRef]
- Suzuki, H.; Kanematsu, M.; Kusunoki, K. Neutron diffraction studies on strain evaluation of rebar in reinforced concrete. Powder Diffr. 2009, 24, S68–S72. [Google Scholar] [CrossRef]
- Tsuchiya, Y.; Suzuki, H.; Umeno, T.; Machiya, S.; Osamura, K. Development of a cryogenic load frame for a neutron diffractometer. Meas. Sci. Technol. 2010, 21, 025904. [Google Scholar] [CrossRef]
- Xu, P.G.; Akita, K.; Suzuki, H.; Metoki, N.; Moriai, A. Establishment and Optimization of Angle Dispersive Neutron Diffraction Bulk Texture Measurement Environments. Mater. Trans. 2012, 53, 1831–1836. [Google Scholar] [CrossRef]
- Suzuki, H.; Harjo, S.; Abe, J.; Xu, P.G.; Aizawa, K.; Akita, K. Effects of gauge volume on pseudo-strain induced in strain measurement using time-of-flight neutron diffraction. Nucl. Instrum. Methods Phys. Res. Sect. A 2013, 715, 28–38. [Google Scholar] [CrossRef]
- Onuki, Y.; Hoshikawa, A.; Sato, S.; Xu, P.G.; Ishigaki, T.; Saito, Y.; Todoroki, H.; Hayashi, M. Rapid measurement scheme for texture in cubic metallic materials using time-of-flight neutron diffraction at iMATERIA. J. Appl. Cryst. 2016, 49, 1579–1584. [Google Scholar] [CrossRef]
- Xu, P.G.; Harjo, S.; Ojima, M.; Suzuki, H.; Ito, T.; Gong, W.; Vogel, S.C.; Inoue, J.; Tomata, Y.; Aizawa, K.; et al. High stereographic resolution texture and residual stress evaluation using time-of-flight neutron diffraction. J. Appl. Cryst. 2018, 51, 746–760. [Google Scholar] [CrossRef] [PubMed]
- Ojima, M.; Inoue, J.; Nambu, S.; Xu, P.G.; Akita, K.; Suzuki, H.; Koseki, T. Stress Partitioning Behavior of Multilayered Steels during Tensile Deformation Measured by in situ Neutron Diffraction. Scr. Mater. 2012, 66, 139–142. [Google Scholar] [CrossRef]
- Suzuki, T.; Yamanaka, K.; Ishino, M.; Nagai, K.; Tsuru, E.; Shinohara, Y.; Xu, P.G. Neutron Diffraction Study on Anisotropy of Strain Age Hardening in Ferritic steel. Tetsu-to-Hagane 2012, 98, 262–266. (In Japanese) [Google Scholar] [CrossRef]
- Mo, F.; Sun, G.; Li, J.; Zhang, C.; Wang, H.; Chen, Y.; Liu, Z.; Yang, Z.; Li, H.; Yang, Z.; et al. Recent Progress of Residual Stress Distribution and Structural Evolution in Materials and Components by Neutron Diffraction Measurement at RSND. Quantum Beam Sci. 2018, 2, 15. [Google Scholar] [CrossRef]





| Material | hkl | E (GPa) | v |
|---|---|---|---|
| Inconel-718 | 111 | 259 | 0.27 |
| Modified SUS403 | 110 | 224 | 0.28 |
| Kröner Elastic Constants | ||||
| Bulk Average | (100) | (002) | (101) | |
| Young’s Module | 97 | 98 | 110 | 95 |
| Poisson’s ratio | 0.33 | 0.33 | 0.32 | 0.34 |
| Measured elastic constants | ||||
| Extensometer | (100) | (002) | (101) | |
| Young’s Module | 97 | 96 | 104 | 95 |
| Poisson’s ratio | 0.34 | 0.34 | 0.32 | 0.36 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayashi, M.; Root, J.H.; Rogge, R.B.; Xu, P. Evaluation of Residual Stress Relaxation in a Rolled Joint by Neutron Diffraction. Quantum Beam Sci. 2018, 2, 21. https://doi.org/10.3390/qubs2040021
Hayashi M, Root JH, Rogge RB, Xu P. Evaluation of Residual Stress Relaxation in a Rolled Joint by Neutron Diffraction. Quantum Beam Science. 2018; 2(4):21. https://doi.org/10.3390/qubs2040021
Chicago/Turabian StyleHayashi, Makoto, John H. Root, Ronald B. Rogge, and Pingguang Xu. 2018. "Evaluation of Residual Stress Relaxation in a Rolled Joint by Neutron Diffraction" Quantum Beam Science 2, no. 4: 21. https://doi.org/10.3390/qubs2040021
APA StyleHayashi, M., Root, J. H., Rogge, R. B., & Xu, P. (2018). Evaluation of Residual Stress Relaxation in a Rolled Joint by Neutron Diffraction. Quantum Beam Science, 2(4), 21. https://doi.org/10.3390/qubs2040021






