Abstract
In strongly disordered matter, such as liquids and glasses, atomic and magnetic excitations are heavily damped and partially localized by disorder. Thus, the conventional descriptions in terms of phonons and magnons are inadequate, and we have to consider spatially correlated atomic and spin dynamics in real-space and time. Experimentally this means that the usual representation of dynamics in terms of the dynamic structure factor, S(Q, E), where Q and E are the momentum and energy exchanges in scattering, is insufficient. We propose a real-space description in terms of the dynamic pair-density function (DyPDF) and the Van Hove function (VHF) as an alternative, and discuss recent results on superfluid 4He by inelastic neutron scattering and water by inelastic X-ray scattering. Today much of the objects of research in condensed-matter physics and materials science are highly complex materials. To characterize the dynamics of such complex materials, the real-space approach is likely to become the mainstream method of research.
1. Introduction
Modern theories of condensed-matter physics are mostly formulated with the assumption of a periodic structure as found in crystals. However, most of real materials are not crystalline and are often not even a solid. About 70% of the surface of the earth is covered by water, and our body is mostly made of liquid and amorphous soft matters. Consequently, much of the condensed-matter theories and concepts are useless in describing the properties and dynamics of such dynamic aperiodic matter (DAM). This presents a very serious challenge, because periodicity so wonderfully simplifies the description of the structure and dynamics of matter through Bragg’s law, Bloch theorem, group theory and other symmetry-related theoretical tools, and without them we have to face the many-body problem squarely.
An important gift of periodicity is that the structure and dynamics can be described in the momentum (Q) space. Thus, the atomic dynamics is usually described by the dynamic structure factor [1],
where Q and E are the momentum and energy exchanges in scattering, ri(t) is the position of the atom i at time t, and E = ħω. Collective excitations, such as phonons, appear with well-defined dispersions in S(Q, E), which can be determined by inelastic neutron scattering (INS) or inelastic X-ray scattering (IXS). However, in liquids not only the structure is disordered but it is dynamic. As a consequence for liquids the purely elastic scattering, S(Q, 0), is zero, and S(Q, E) is dominated by quasi-elastic scattering intensity.
At present atomic dynamics is described well only in two extreme cases, phonons in a periodic solid, or random diffusion in solid or gas. However, the atomic dynamics in liquids is in-between the two. Phonons are strongly damped, with the energy width exceeding the frequency, so that the phonon dispersion is far from sufficient in describing the dynamics. Also, the Brownian picture of dense gas where atoms are randomly colliding each other does not apply to liquids, because liquids are condensed matter with the density close to those of crystals and atomic motions are locally highly correlated, but not fully collective either. These correlated dynamics of dynamic aperiodic matter has been rarely uncovered by direct experimental observation. So far most quasi-elastic neutron scattering (QENS) experiments focused on incoherent scattering which tracks the self-part (i = j) of S(Q, E) and describes self-diffusion of atoms. It has been most frequently applied to hydrogen, because it has a very large incoherent neutron scattering cross-section. On the other hand the distinct-part (i ≠ j) of S(Q, E) measured by coherent scattering has only been beginning to attract attention recently [2,3]. Even though simulations are suggesting highly correlated dynamics in liquids [4,5,6], there has been scant experimental proof of such correlated dynamics.
2. Dynamic Pair-Density Function and Van Hove Function
To break the logjam, we propose to adopt two novel approaches to describe the local dynamics, i.e., the dynamic pair-density function (DyPDF) and the Van Hove function (VHF), both of which can be experimentally determined using the modern scattering methods. First, we assume that the system is isotropic. The extension to the anisotropic case is straightforward using the spherical harmonics expansion [7]. Then the isotropic dynamic structure factor is
where and Ω is the solid angle in Q space. The DyPDF is defined by,
where ρ0 is the atomic number density of the system. This is a frequency (energy) resolved PDF. The usual same-time (snapshot) PDF is obtained by
The VHF [8] is given by
The VHF is a time-delayed PDF, given by
Thus,
The VHF describes how g(r) decays with time. On the other hand the energy Fourier-transform of S(Q, E),
is known as the intermediate scattering function [1], and has been widely used in the analysis of soft matter dynamics [9,10,11]. This function is directly determined by the neutron spin-echo experiment [12]. The VHF is a Fourier-transform (Q → r) of F(Q, t).
The VHF has been known for a long time, but was never really used, except for one feasibility demonstration with approximation [13]. This is because in order to obtain the VHF, S(Q, E) has to be known for wide Q-E space to reduce the termination error, whereas the inelastic scattering measurement has been very time-consuming and the measurement of S(Q, E) over wide Q-E space was impractical until recently. However, the advent of the pulsed neutron sources with large two-dimensional detector arrays [14] and notable advances in synchrotron sources and instrumentation for the inelastic X-ray scattering [15], have made it fully feasible. Now S(Q, E) can be determined over sufficiently wide Q-E space typically in 12 h for IXS and 4 hrs. for INS. Often energy resolution and energy range are coupled. Thus to obtain an optimal result, measurements have to be made with a several initial (incident) energies, and the results have to be combined with the maximum use of the high-resolution data. Even in such a case a set of measurements can be finished within a day. The software to produce DyPDF is now available for the public [16].
A related approach with the Green’s function using IXS was applied to the study of local fast dynamic response by water [17]. The S(Q, E) is directly related to the imaginary part of the Green’s function, but the real part has to be obtained by the Kramers-Kronig analysis which makes this approach less accurate. Because of the low resolution (0.3 eV) the time-scale was of the order of 0.1 fs. A study with better resolution (1.7 meV) was later carried out to examine the evolution of hydration dynamics around salt ions at the time-scale of 100 fs [18]. The idea of DyPDF goes back to Carpenter and Pelizzari [19], and was used in a different form, after division by the energy-resolved Debye-Waller factor to remove vibrational dynamics, for the analysis of local dynamics in amorphous and crystalline solids [20,21].
One may argue that the DyPDF and VHF are merely the Fourier-transforms of S(Q, E), and thus offer no new information. This argument is seriously flawed because,
- In order to determine the DyPDF and VHF with accuracy S(Q, E) has to be measured over wide Q-E space to reduce termination errors, and thus new information is garnered from high-Q data which would not be obtained otherwise.
- Local dynamics gives rise to diffuse inelastic scattering intensities in S(Q, E) which is often difficult to recognize. They look like a part of the background and are usually discarded. However, upon Fourier-transformation they become visible. We will demonstrate this in the two examples to follow.
- To determine the dispersion of excitation we only need to know the peak position of S(Q, E) in Q-E space. However, to obtain the DyPDF and VHF we have to know the correct normalized intensity of S(Q, E). For this purpose S(Q, E) has to be determined with much higher statistical accuracy and proper normalization.
The situation is a complete parallel of what we encountered in the drive to use the PDF method for the study of disordered crystalline materials decades ago [7]. The conventional method of crystal structure analysis requires the knowledge of the precise positions of several Bragg peaks and relative peak intensity, whereas to determine the PDF we need a well-normalized S(Q) over a wide Q space with good statistics, including diffuse scattering as well. Consequently, much richer information is collected by the PDF study compared to the conventional crystallographic study.
3. Dynamic Pair-Density Function of Superfluid 4He
Superfluidity of 4He was discovered by Kapitza in 1938 [22]. Soon afterwards London proposed to explain it in terms of Bose-Einstein condensation (BEC) [23]. However, BEC occurs in ideal gas, whereas helium liquid is not a gas but is a condensed correlated liquid with significant van der Waals interaction. In fact, in proposing the celebrated roton model of superfluidity, Landau never mentioned BEC [24]. Since then reconciling these two conflicting views has been a major subject of research [25,26]. It is now known that only 7% of He atoms condense into the Bose-Einstein ground state because of the van der Waals force [27]. Even though the collective dynamics of helium was carefully studied, particularly by inelastic neutron scattering [28], the real-space atomic correlation was never directly observed. Our study using inelastic neutron scattering and DyPDF [29] is the first to report such observation.
The INS measurements were carried out at the CNCS beamline of the Spallation Neutron Source (SNS) of Oak Ridge National Laboratory. To cover a wide Q-E range we have to choose a high incident energy, but it results in poor energy resolution. Thus, balancing the range and resolution is a key to the success of this kind of experiment. Three incident energies, (Ei = 3.5, 15 and 50 meV) were chosen, and the composite S(Q, E) was created by joining the data sets, by using the high-resolution (low Ei) data as much as possible. The sample was liquid 4He in the standard volume-pressure (SVP) condition, and the measurement was made at five temperature points above and below the critical temperature, Tc = 2.17 K. Figure 1 [29] shows S(Q, E) at T = 1.83 K (superfluid state) and the difference in S(Q, E) between T = 1.83 K and 2.85 K (normal state). In the difference figure (Figure 1b) sharpening of the roton excitation at 0.7 meV and 2 Å−1 and opening of the energy gap below the roton are clearly seen.
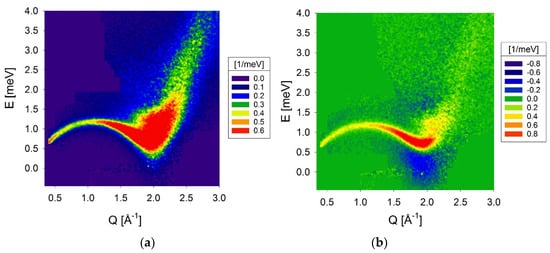
Figure 1.
(a) Dynamics structure factor, S(Q, E), of 4He liquid at T = 1.83 K (superfluid state) and (b) the difference in S(Q, E) between T = 1.83 K and 2.85 K (normal state) [29].
The DyPDF at T = 1.83 K is shown in Figure 2. Here the red stripe around r = 0 is due to self-correlation, and the intensity peak at 4 Å and 0.7 meV is due to the nearest neighbor correlation at this energy. Because 0.7 meV is the roton energy, this peak must represent the atomic correlation in BEC. The difference DyPDF between T = 1.83 K and 2.85 K is shown in Figure 3a. The intensity peak at 0.7 meV and 4 Å is even more pronounced, and its intensity follows the known temperature dependence of the superfluid order parameter as shown in Figure 4. Therefore, the peak at 4 Å and 0.7 meV is unquestionably due to BEC atoms. The results are in excellent agreement with the DyPDF calculated from the dynamic structure factor obtained by the path-integral quantum Monte-Carlo simulation [30], shown in Figure 3b, including the BEC peak at 4 Å and 0.7 meV. The BEC nearest neighbor distance, 4 Å, is longer than the known neighbor distance in the normal 4He fluid, 3.6 Å [31], by a margin well above the experimental error. This result demonstrates that the BEC atoms have different atomic correlations than the normal atoms, a conclusion not expected by the current theory.
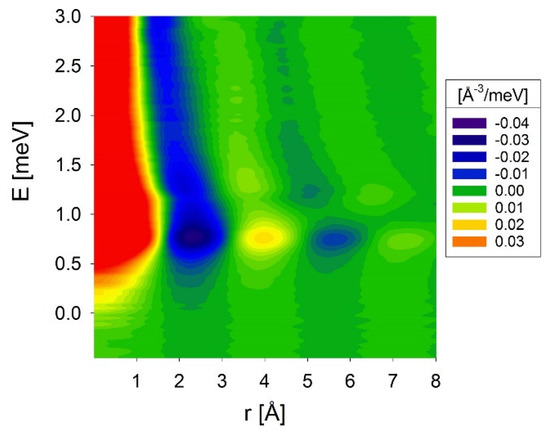
Figure 2.
Dynamic pair-density function (DyPDF) of 4He liquid at T = 1.83 K [29].
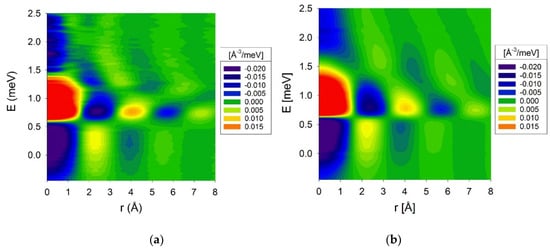
Figure 3.
Difference in DyPDF between T = 1.83 K and 2.85 K, (a) by inelastic neutron scattering (INS) and (b) by quantum Monte-Carlo simulation [29].
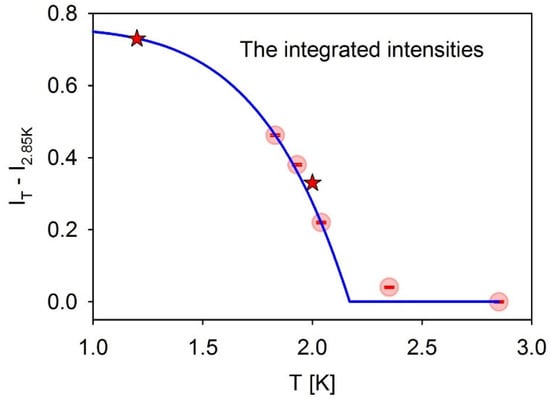
Figure 4.
Temperature dependence of the DyPDF intensity at 0.7 meV and 4 Å, by INS (circles) and by quantum Monte-Carlo simulation (stars) [29]. The solid line describes that of the superfluid order parameter [27].
Now the snapshot PDF, obtained by integrating the DyPDF by Equation (4), shown in Figure 5, shows a peak at 3.55 Å [29] in agreement with the earlier results. However, in the earlier neutron diffraction work [31] which is highly cited, the authors used a two-axis neutron spectrometer, thus carrying out the energy integration by not using the energy analyzer. This does not present a problem for X-ray scattering for which the beam energy (10 s of keV) is much higher than the excitation energies in liquid. However, for neutron scattering the neutron energy (27 meV for Ref. [31]) is not high enough to eliminate the dependence of the momentum transfer on energy. Thus, the energy integration is not done at a constant Q. This effect was corrected for the kinetic energy in Ref. [31], but the effect of significant changes in the roton dispersion was not included. On the other hand, in our case the energy integration is done numerically at a constant Q, resulting in the true snapshot PDF. The result shown in Figure 5 indicates that the PDF peak height does not show the decrease below Tc as suggested by the earlier work [31], raising suspicion that the reported temperature dependence may be an artifact of incorrect energy integration.
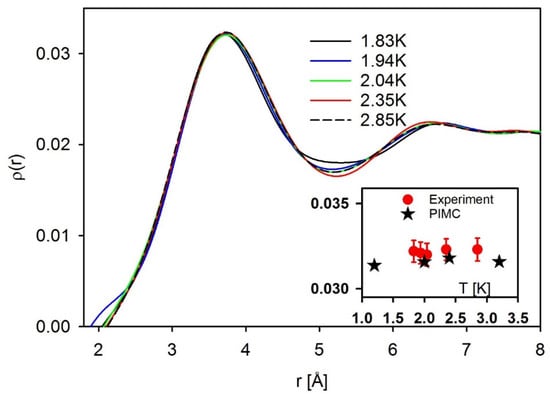
Figure 5.
Snapshot PDF, ρ0g(r), obtained by integration of DyPDF over energy by Equation (4) at various temperatures [29]. The inset shows the variation of the first peak height with temperature, by experiment (circles) and path-integral Monte-Carlo (PIMC) simulation (stars).
In addition, a new peak was found at 0.4 meV and 2.3 Å, both in experiment and simulation (Figure 3). We interpret this peak to originate from coherent atomic tunneling, which provides the atomistic mechanism of superflow. Because helium atom is so light tunneling is easy and occurs even in the normal state. But in the normal state it is a random walk process with the distance of tunneling distributed as the three-dimensional Gaussian function. On the other hand, in the BEC all atoms are equivalent because they are degenerated in the single BEC ground state. Thus, they move coherently in the same fashion, giving rise to a well-defined peak in the DyPDF. Landau explained the mechanism of superfluidity in terms of the loss of energy dissipation channels because of the roton energy gap. However, no discussions have been made on the real-space mechanism of superflow. This observation provides a strong evidence that the coherent tunneling is the atomistic mechanism of superflow. Even though the superfluidity in helium has been studied for a long time, these results suggest there are still more to learn from the real space correlated dynamics in the superfluid.
4. Local Dynamics of Water
Water is arguably the most important liquid for life, and is most abundant on the surface of the earth. Yet we do not fully understand its anomalous properties, such as the high freezing/melting points and the maximum in density at 4 °C. These anomalous behaviors are considered to originate from the hydrogen bond, but its highly quantum-mechanical nature makes it very difficult to explain these behaviors quantitatively. To understand the water dynamics at the molecular level in real space and to relate it to viscosity we carried out inelastic X-ray scattering measurements [32] with Ei = 21.747 keV and determined the dynamic structure factor, S(Q, E), over a wide Q-E space (1.3 Å−1 ≤ Q ≤ 9.5 Å−1 and −10 meV ≤ E ≤ 100 meV) as shown in Figure 6, and obtained the Van Hove function through the double Fourier-transformation. Earlier studies of water dynamics by IXS [33,34] focused on the phonons at low Q. However, in water the phonons are overdamped and spread in the Q-E space. In Figure 6 phonons are present but they are too weak to be seen. Instead the majority of spectral intensity is in the quasi-elastic scattering (QES) around E = 0. The QES has been used widely to determine diffusivity in liquids at low Q, but its Q-dependence has rarely been explored. Figure 6 clearly shows significant Q-dependence, but it is difficult to figure out what this means. The best way to interpret this result is to transform it into the Van Hove function, G(r, t).
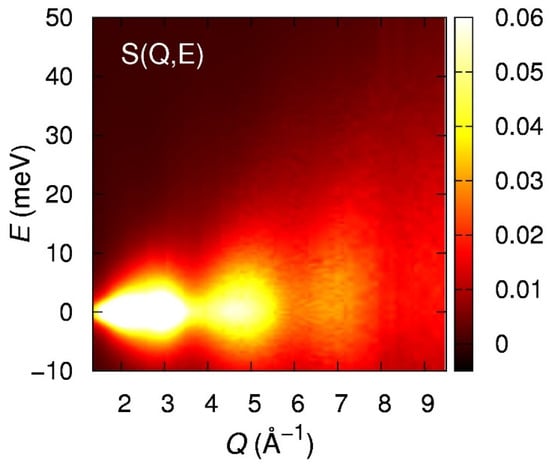
Figure 6.
Dynamic structure factor, S(Q, E), for water at room temperature determined by inelastic X-ray scattering [32].
Figure 7 shows G(r, t) − 1 of water, H2O, determined by IXS, compared to the results of MD simulation [32]. Because X-rays are scattered mainly by oxygen atoms, the results mostly describe the O-O correlation. The features near r = 0 describes self-correlation, the motion of one atom due to ballistic motion and diffusion, whereas the features at larger r describe the correlation between distinct atoms. At t = 0 the Van Hove function is equal to the snapshot PDF; G(r, 0) = g(r). The peak at r = 2.8 Å describes the first neighbor O-O distances whereas the second peak at 4.5 Å corresponds to the second O-O distances. As time increases these two peaks move closer to each other, and appear to merge. Clearly the dynamics of the first and second neighbors are correlated, and molecules are not making random walk. As soon as a nearest neighbor goes away a second neighbor moves in to take its place, in order to maintain the coordination around the molecule. Such correlations are absent in metallic liquids [32]. Metallic atoms are bound by isotropic metallic bonds, and have coordination numbers (the number of nearest neighbors) as high as 12 or more [35]. Thus, the leaving and joining of a nearest neighbor are not correlated [36]. In contrast the hydrogen bond keeps the local coordination of water constant, creating the dynamic correlation between the nearest and next-nearest neighbors. The Van Hove function captures such dynamic correlation convincingly.
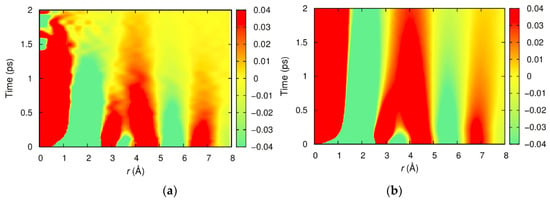
Figure 7.
The Van Hove function, G(r, t) − 1, for water at room temperature (a) determined by inelastic X-ray scattering, (b) by molecular dynamics simulation [32].
As time increases the PDF peaks decay, indicating that correlations become weaker. The decay function has two components, the fast one due to ballistic motion of atoms, and the slow one because of the rearrangement of molecular connectivity due to cutting of bonds [37]. With the help of MD simulation it is possible to relate the second relaxation time to the time to lose one neighbor, τLC. As shown in Figure 8 τLC is nearly equal to the Maxwell relaxation time, τM = η/G∞, where τM is η is viscosity and G∞ is the high-frequency shear modulus. The mechanical response of a liquid is time-dependent, and τM is the time-scale to separate the solid-like response (τ < τM) from the liquid-like response (τM < τ). This equality, τLC = τM, was predicted by simulation for metallic liquids [38]. Note that this equality connects a macroscopic time-scale, τM, to a microscopic time-scale, τLC, and explains the atomistic origin of viscosity. The reason behind this remarkable relationship can be explained in terms of the atomic-level stress [39]. As is well-known the Maxwell relaxation time is given by the Green-Kubo equation of the fluctuation-dissipation theorem [40],
where σxy(t) is the shear stress at time t. Thus, τM is the time-scale of the shear stress correlation. Now we can express the macroscopic stress, σxy(t), in terms of the atomic-level stress;
where V is the macroscopic volume, and Ωi and σxy(i) are the local atomic volume and the atomic-level shear stress of the i-th atom [39]. This equates τM to the correlation time of the atomic-level shear stress [41]. Now the atomic-level stress depends on the local configuration of the neighbor atoms [42], and changes when the neighbor configuration is changed. This is the reason why losing one neighbor kills the temporal correlation of the atomic-level stress, equating τLC to τM. The result in Figure 8 proves this equality for water. The fact that it was predicted for metallic liquids and proven for water suggests that this equality is a general property of a liquid. Indeed, this relationship holds even for organic molecular liquid [43].
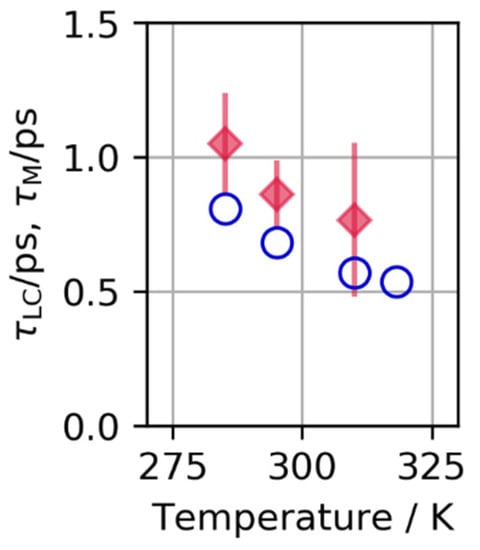
Figure 8.
Temperature dependence of the Maxwell relaxation time (circle) and τLC determined from the Van Hove function (diamond) for water, in pico-second [37].
It is interesting to note that the decay of the Van Hove function with time is not uniform in r. For instance, the decay times of the first and second peaks are vastly different. A recent simulation shows that the decay time increases linearly with distance for uncorrelated high-temperature liquid, as shown in Figure 9 [44]. This r-dependence is a purely geometrical effect, and does not suggest collective atomic motions. In Ref. [44] the power law of r-dependence is shown to be equal to (d − 1)/2, where d is dimensionality. Therefore the widely known de Gennes narrowing, the narrowing of QES at the peak of S(Q), is not necessarily indicative of collective excitation as is often claimed, but more often than not it is a mere consequence of this geometrical statistical effect. For the same reason, the α-relaxation time, defined at the maximum of S(Q), is not a real structural relaxation time. It is just the Maxwell relaxation time enhanced by a geometrical factor. For this reason it is not possible to differentiate the collective effect from the geometrical effect just by studying F(Q, t) or the relaxation time τ(Q) at several Q values as is often done. Only through the r-dependence of the VHF collective effect can be separated from the pure geometrical effect.
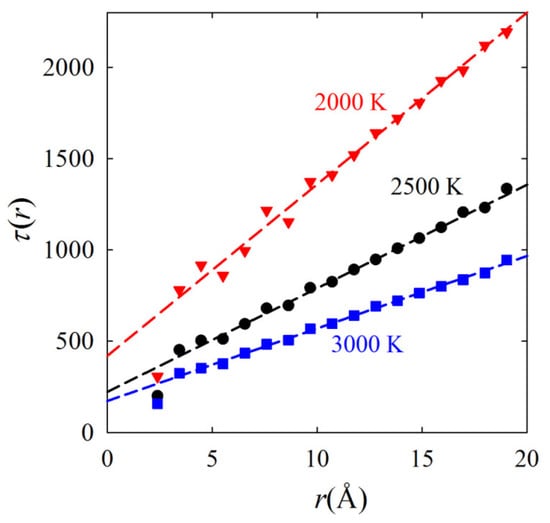
Figure 9.
Distance dependence of the decay time of the Van Hove function at various temperatures, simulated for liquid Fe in the unit of femto-second [44].
5. Limitations of the Method
In the INS and IXS measurements the maximum of the timescale is set by the energy resolution, and the minimum by the incident energy (4 meV = 1 THz). The energy resolution in INS is typically a few percent of the incident energy. For IXS the backscattering analyzer crystal sets a hard limit of about 1.6 meV, thus limiting the timescale only up to 3 ps. The Q-range is determined by the incident energy and the spectrometer set-up in both cases. For our IXS measurement Ei was 21.747 keV, with 2θ up to 60°, which limited the Q-range up to 9.5 Å−1. With INS we can achieve better energy resolution, but then the Q-range becomes limited. In the case of the experiment shown in Figure 1 Ei = 3.5 meV results in ∆E = 0.2 meV, but the Q-range is limited to 2.5 Å−1. By combining with the data with Ei = 15 meV the Q-range up to 5 Å−1 was attained, and extended to 9 Å−1 with Ei = 50 meV.
The limited Q-range results in spurious oscillations upon Fourier-transformation, known as termination errors [7]. Unlike in crystals in liquids S(Q, E) do not have sharp features and attenuate relatively fast with Q. Thus the limitation of the Q-range up to 10 Å−1 does not pose serious threat to the integrity of the results. Simulations in Ref. [27] indicate that only the portion of the Van Hove function below 100 fs is compromised, and beyond 100 fs the termination effects are minimal. Thus at present the time range of the VHF by IXS is 0.1–3 ps, that by INS is 0.1–20 ps.
It is possible to extend this range up to 100 ps using backscattering INS [45], but the Q-range of backscattering INS is limited to about 2 Å−1, appropriate only for some soft matter. The neutron spin-echo technique (NSE) [12] stretches this rage even further to 1 ns. However, NSE measurements are time-consuming, and it is difficult to cover wide Q-range necessary for obtaining the VHF. A major future possibility is to use an X-ray free-electron laser (XFEL) with X-ray photon correlation spectroscopy (XPCS) [46]. With the expected upgrade of LCLS-II [47] with 1 MHz repetition rate the prospect of determining F(Q, t) over a very wide Q-t range is becoming realistic.
6. Study of Local Dynamics: Major Change in Near Future
Majority of materials studied in the 20th Century in condensed-matter-physics, materials science and related disciplines were crystalline, even though actual materials used were both crystalline and non-crystalline. This is already changing in the 21st Century, as more complex materials are being studied and used, and life sciences move closer to the center of scientific research activities. Therefore, the traditional approach to atomic dynamics in terms of phonons and diffusion has to evolve, shifting the focus more on local correlated dynamics. The Van Hove function and the dynamic PDF are the right languages to discuss such local dynamics. Now that their feasibility has been proven, they will be more widely used by many researchers. Indeed, the VHF was recently measured for liquid Bi [48]. I predict in ten years up to 1/3 of the results of inelastic neutron scattering experiments may be presented in real-space, just as that much of neutron powder diffraction results are now presented as the PDF in real space following our advocacy [7]. Indeed, DyPDF was recently used in the study of local dynamics in lead-free relaxor ferroelectrics [49], and more measurements to determine DyPDFs for various complex matters are scheduled. Concomitantly the scattering facilities need to be developed to accommodate this demand. We need wider Q range, low background, high intensity and high energy resolution to achieve better results in real-space. These needs are in conflict with each other. In the design of a new instrument good compromises have to be struck to produce the optimal result.
7. Conclusions
The science of dynamic aperiodic matter, such as liquid, gel and colloid, has been less developed compared to that of crystalline solids, because most of the theories and experimental approaches in condensed-matter-physics assume periodicity and thus are powerless for aperiodic matter. We propose a real-space approach to dynamics as an alternative to the traditional approach in the momentum space. Recent advances in radiation sources and instrumentation made it possible to determine the dynamic pair-density function (DyPDF) and the Van Hove function by inelastic scattering experiments. We have shown that they bring in new information hitherto impossible to garner, by the demonstrations on superfluid 4He and water. We predict that these real-space methods will be used widely in the study of dynamics in complex materials in near future.
Funding
This research was funded by the Department of Energy, Office of Science, Basic Energy Sciences, Materials and Science and Engineering Division.
Acknowledgments
The author acknowledges the extraordinary effort to bring this new approach to reality by his team members, Wojciech Dmowski, Takuya Iwashita and Yuya Shinohara in particular.
Conflicts of Interest
The author declares no conflict of interest.
References
- Lovesey, S.W. Theory of Neutron Scattering from Condensed Matter; Oxford University Press: Oxford, UK, 1984; Volume 1. [Google Scholar]
- Arbe, A.; Colmenero, J.; Farago, B.; Monkenbusch, M.; Buchenau, U.; Richter, D. Intermediate length scale dynamics in glass forming polymers: Coherent and incoherent quasielastic neutron scattering results on polyisobutylene. Chem. Phys. 2003, 292, 295–309. [Google Scholar] [CrossRef]
- Novikov, V.N.; Schweizer, K.S.; Sokolov, A.P. Coherent neutron scattering and collective dynamics on mesoscale. J. Chem. Phys. 2013, 138, 164508. [Google Scholar] [CrossRef] [PubMed]
- Donati, C.; Douglas, J.F.; Kob, W.; Plimpton, S.J.; Poole, P.H.; Glotzer, S.C. Stringlike cooperative motion in a supercooled liquid. Phys. Rev. Lett. 1998, 80, 2338–2341. [Google Scholar] [CrossRef]
- Glotzer, S.C.; Novikov, V.N.; Schröder, T.B. Time-dependent, four-point density correlation function description of dynamic heterogeneity and decoupling in supercooled liquids. J. Chem. Phys. 2000, 112, 509–512. [Google Scholar] [CrossRef]
- Widmer-Cooper, A.; Harrowell, P. Predicting the long-time dynamic heterogeneity in a supercooled liquid on the basis of short-time heterogeneities. Phys. Rev. Lett. 2006, 96, 185701. [Google Scholar] [CrossRef] [PubMed]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials, 2nd ed.; Pergamon Materials Series Vol. 16; Pergamon Press, Elsevier Ltd.: Oxford, UK, 2012. [Google Scholar]
- Van Hove, L. Correlation in space and time and Born approximation scattering in systems of interacting particles. Phys. Rev. 1954, 95, 249–262. [Google Scholar] [CrossRef]
- Mezei, F.; Knaak, W.; Farago, B. Neutron spin-echo study of dynamic correlations near liquid-glass transition. Phys. Scr. 1987, T19B, 363–368. [Google Scholar] [CrossRef]
- Richter, D.; Monkenbusch, M.; Arbe, A.; Colmenero, J. Neutron spin echo in polymer systems. Adv. Polym. Sci. 2005, 174, 1–221. [Google Scholar]
- Ruta, B.; Baldi, G.; Chuskin, Y.; Ruffle, B.; Cristoflini, L.; Fonatan, A.; Zanatta, M.; Nazzani, F. Revealing the fast atomic motion of network glasses. Nat. Commun. 2014, 5, 3939. [Google Scholar] [CrossRef] [PubMed]
- Mezei, F. The Principles of Neutron Spin Echo; Neutron Spin Echo. Lecture Notes in, Physics; Mezei, F., Ed.; Springer: Berlin/Heidelberg, Germany, 1980; Volume 128. [Google Scholar]
- Dahlborg, U.; Gudowski, W.; Davidovic, M. Van Hove correlation functions from coherent neutron inelastic scattering. J. Phys. Cond. Matter 1989, 1, 6173–6179. [Google Scholar] [CrossRef]
- Mason, T.E.; Abernathy, D.; Anderson, I.; Ankner, J.; Egami, T.; Ehlers, G.; Ekkebus, A.; Granroth, G.; Hagen, M.; Herwig, K.; et al. The Spallation Neutron Source in Oak Ridge: A Powerful Tool for Materials Research. Phys. B 2006, 385, 955–960. [Google Scholar] [CrossRef]
- Baron, A.Q.R. High-resolution inelastic X-ray scattering I: Context, spectrometers, samples, and superconductors. In Synchrotron Light Sources and Free-Electron Lasers; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Arnold, O.; Bilheux, J.C.; Borreguero, J.M.; Buts, A.; Campbell, S.I.; Chapon, L.; Doucet, M.; Draper, N.; Leal, R.F.; Gigg, M.A.; et al. Mantid—Data analysis and visualization package for neutron scattering and image μ SR experiments. Nucl. Instrum. Methods Phys. Res. Sect. A 2014, 764, 156–166. [Google Scholar] [CrossRef]
- Abbamonte, P.; Finkelstein, K.D.; Collins, M.D.; Gruner, S.M. Imaging density disturbances in water with a 41.3-attosecond time resolution. Phys. Rev. Lett. 2004, 92, 237401. [Google Scholar] [CrossRef] [PubMed]
- Coridan, R.H.; Schmidt, N.W.; Lai, G.H.; Godawat, R.; Krisch, M.; Garde, S.; Abbamonte, P.; Wong, G.C.L. Hydration dynamics at femtosecond time scales and angstrom length scales from inelastic X-ray scattering. Phys. Rev. Lett. 2009, 103, 237402. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, J.M.; Pelizzari, C.A. Inelastic neutron scattering from amorphous solids. II. Interpretation of measurements. Phys. Rev. B 1975, 12, 2397–2401. [Google Scholar] [CrossRef]
- Hannon, A.C.; Arai, M.; Sinclair, R.N.; Wright, A.C. A dynamic correlation function for amorphous solids. J. Non-Cryst. Solids 1992, 150, 239–244. [Google Scholar] [CrossRef]
- Arai, M.; Hannon, A.C.; Otomo, T.; Hiramatsu, A.; Nishijima, T. Dynamic correlation function studies of the medium-range order in materials. J. Non-Cryst. Solids 1995, 192, 230–237. [Google Scholar] [CrossRef]
- Kapitza, P. Viscosity of liquid helium below the λ-point. Nature 1938, 141, 74. [Google Scholar] [CrossRef]
- London, F. The λ-phenomenon of liquid helium and the Bose-Einstein condensation. Nature 1938, 141, 643–644. [Google Scholar] [CrossRef]
- Landau, L.D. Theory of the superfluidity in helium II. Phys. Rev. 1941, 60, 356–358. [Google Scholar] [CrossRef]
- Feynman, R.P. Atomic theory of liquid helium near absolute zero. Phys. Rev. 1953, 91, 1301–1308. [Google Scholar] [CrossRef]
- Griffin, A. Excitations in a Bose-Condensed Liquid; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Glyde, H.R.; Azuah, R.T.; Stirling, W.G. Condensate, momentum distribution, and final-state effects in liquid 4He. Phys. Rev. B 2000, 62, 14337–14349. [Google Scholar] [CrossRef]
- Glyde, H.R. Excitations in Liquid and Solid Helium; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Dmowski, W.; Diallo, S.O.; Lokshin, K.; Ehlers, G.; Ferré, G.; Boronat, J.; Egami, T. Observation of dynamic atom-atom correlation in liquid helium in real space. Nat. Commun. 2017, 8, 15294. [Google Scholar] [CrossRef] [PubMed]
- Ferré, G.; Boronat, J. Dynamic structure factor of liquid 4He across the normal-superfluid transition. Phys. Rev. B 2016, 93, 104510. [Google Scholar] [CrossRef]
- Svensson, E.C.; Sears, V.F.; Woods, A.D.B.; Martel, P. Neutron-diffraction study of the static structure factor and pair correlations in liquid 4He. Phys. Rev. B 1980, 21, 3538–3651. [Google Scholar] [CrossRef]
- Iwashita, T.; Wu, B.; Chen, W.; Tsutsui, S.; Baron, A.Q.R.; Egami, T. Seeing real-space dynamics of liquid water through inelastic X-ray scattering. Sci. Adv. 2017, 3, e1603079. [Google Scholar] [CrossRef] [PubMed]
- Sette, F.; Ruocco, G.; Krisch, M.; Masciovecchio, C.; Verbeni, R.; Bergmann, U. Transition from normal to fast sound in liquid water. Phys. Rev. Lett. 1996, 77, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Scopigno, T.; Balucani, U.; Ruocco, G.; Sette, F. Inelastic X-ray scattering and the high-frequency dynamics of disordered systems. Phys. B 2002, 318, 341–349. [Google Scholar] [CrossRef]
- Bernal, J.D. A geometrical approach to the structure of liquids. Nature 1959, 183, 141–147. [Google Scholar] [CrossRef]
- Iwashita, T.; Egami, T. Local energy landscape in simple liquids. Phys. Rev. E 2014, 90, 052307. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, Y.; Dmowski, W.; Iwashita, T.; Wu, B.; Ishikawa, D.; Baron, A.Q.R.; Egami, T. Viscosity and real space molecular motion of water: Observation with inelastic X-ray scattering. Phys. Rev. E 2018, 98, 022604. [Google Scholar] [CrossRef] [PubMed]
- Iwashita, T.; Nicholson, D.M.; Egami, T. Elementary excitations and crossover phenomenon in liquids. Phys. Rev. Lett. 2013, 110, 205504. [Google Scholar] [CrossRef] [PubMed]
- Egami, T.; Maeda, K.; Vitek, V. Structural defects in amorphous solids: A computer simulation study. Philos. Mag. A 1980, 41, 883–901. [Google Scholar] [CrossRef]
- Hansen, J.; McDonald, I.R. Theory of Simple Liquids; Academic Press: New York, NY, USA, 2006. [Google Scholar]
- Levashov, V.A.; Morris, J.R.; Egami, T. The origin of viscosity as seen through atomic level stress correlation function. J. Chem. Phys. 2013, 138, 044507. [Google Scholar] [CrossRef] [PubMed]
- Egami, T.; Srolovitz, D. Local structural fluctuations in amorphous and liquid metals: A simple theory of glass transition. J. Phys. F 1982, 12, 2141–2163. [Google Scholar] [CrossRef]
- Perticaroli, S.; Mostofian, B.; Ehlers, G.; Neuefeind, J.C.; Diallo, S.O.; Stanley, C.B.; Daemen, L.; Katsaras, J.; Egami, T.; Cheng, X.; et al. Structural relaxation, viscosity, and network connectivity in a hydrogen bonding liquid. Phys. Chem. Chem. Phys. 2017, 19, 25859–25869. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Iwashita, T.; Egami, T. Atomic dynamics in simple liquid: De Gennes narrowing revisited. Phys. Rev. Lett. 2018, 120, 135502. [Google Scholar] [CrossRef] [PubMed]
- Mamontov, E.; Herwig, K.W. A time-of-flight backscattering spectrometer at the Spallation Neutron Source, BASIS. Rev. Sci. Instr. 2011, 82, 085109. [Google Scholar] [CrossRef] [PubMed]
- Marinelli, A.; Ratner, D.; Lutman, A.A.; Turner, J.; Welch, J.; Decker, F.; Loss, H.; Behrens, C.; Gilevich, S.; Miahnahri, A.A.; et al. High-intensity double-pulse X-ray free-electron laser. Nat. Commun. 2015, 6, 6369. [Google Scholar] [CrossRef] [PubMed]
- Linac Coherent Light Source. Available online: https://lcls.slac.stanford.edu/lcls-ii (accessed on 25 October 2018).
- Kawakita, Y.; Kikuchi, T.; Inamura, Y.; Tahara, S.; Maruyama, K.; Hanashima, T.; Nakamura, M.; Kiyanagi, R.; Yamauchi, Y.; Chiba, K.; et al. Anomaly of structural relaxation in complex liquid metal of bismuth—Dynamic correlation function of coherent quasi-elastic neutron scattering. Phys. B Cond. Matter 2018, in press. [Google Scholar] [CrossRef]
- Pramanick, A.; Dmowski, W.; Egami, T.; Budisuharto, A.S.; Weyland, F.; Novak, N.; Christianson, A.D.; Borreguero, J.M.; Abernathy, D.L.; Jørgensen, M.R.V. Stabilization of polar nano regions in Pb-free ferroelectrics. Phys. Rev. Lett. 2018, 120, 207603. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).