Abstract
Reduction-oxidation (redox) reactions that transfer conduction electrons from the anode to the cathode are the fundamental processes responsible for generating power in Li-ion batteries. Electronic and microstructural features of the cathode material are controlled by the nature of the redox orbitals and how they respond to Li intercalation. Thus, redox orbitals play a key role in performance of the battery and its degradation with cycling. We unravel spectroscopic descriptors that can be used to gain an atomic-scale handle on the redox mechanisms underlying Li-ion batteries. Our focus is on X-ray Compton Scattering and Positron Annihilation spectroscopies and the related computational approaches for the purpose of identifying orbitals involved in electrochemical transformations in the cathode. This review provides insight into the workings of lithium-ion batteries and opens a pathway for rational design of next-generation battery materials.
1. Introduction
Lithium-ion batteries (LIBs), which have also been referred to as rocking-chair LIBs, are the result of a long process of research and development [1,2,3,4]. They were proposed by Michel Armand in the 1970s [5] and are based on the concept of a reversible flow of Li ions between an anode and a cathode. In 2019, the Nobel Prize in Chemistry was awarded to John B. Goodenough, M. Stanley Whittingham, and Akira Yoshino for their contributions to LIBs [6]—a key technology underlying wireless electronics, smart phones, and laptops in the transformation of the automotive sector [7]. In the past, the field of electrochemistry involved in battery materials was not well connected with condensed matter physics community, despite its exploration of oxide materials for superconductivity and magnetism. However, the functional oxides have also turned out to be promising materials for LIB cathodes [8,9,10], and advanced spectroscopies and computational techniques, which are part of the standard condensed matter physics toolbox, are now beginning to contribute to LIB development cycles. It is therefore becoming possible to accelerate the development of new battery materials and understand at a fundamental atomistic level how a battery functions and ages [4,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].
LIBs possess a high degree of hierarchical complexity that ranges from the atomic to the macroscopic scale [27,28]. Some properties can be studied using impedance spectroscopy [29,30], which probes the behaviour of the battery as a whole. X-ray Compton scattering, in contrast, can probe LIBs, not only at the quantum-mechanical atomic scale [31,32,33,34,35,36] but also at the macroscopic scale by mapping the lithium distribution [35,37,38,39,40].
The Compton scattering technique is based on probing the momentum density of the material, much like the positron annihilation spectroscopies that couple with the electron-positron momentum density [41,42,43,44]. Thus, positron annihilation spectroscopies can complement and validate results obtained through Compton scattering experiments, both processes represented by the same Feynman diagram [45]. Positron annihilation studies have been especially useful for probing surfaces of nano-particles [46,47], making them promising for battery studies as well [48]. Compton scattering and positron annihilation studies of high-temperature cuprate superconductors have been reviewed in Reference [49].
An outline of this article is as follows. Following the introductory section, Section 2 discusses X-ray Compton scattering experiments. Electron momentum density is explained in Section 3, and the models based on first principles computations are introduced in Section 4. Section 5 is devoted to discussing positron annihilation studies of interfaces and defects in batteries. Finally, Section 6 presents conclusions and outlook. This review provides a link between the quantum-level spectroscopic characterizations of batteries and their macroscopic level performance.
2. Hard X-ray Compton Scattering Spectroscopy
2.1. X-ray Studies
High-energy X-rays in the 100 keV range have proven especially useful in advanced characterization of batteries because they can easily penetrate the metal containers of electrochemical cells and allow high spatial resolution due to their wavelengths of a few picometers. The most widely used technique to analyze the atomic scale composition and structure of LIBs is high-energy X-ray diffraction [50,51]. At lower energies, X-ray absorption spectroscopy (XAS) and X-ray emission spectroscopy (XES) have been used to access densities of states [52,53]. However, XAS and XES cannot measure the momentum of the electrons in materials. In this regard, Compton scattering [54] offers unique opportunities for investigating materials through its ability to probe electronic momentum densities.
Figure 1a illustrates the Compton scattering process. When the photon is scattered with an electron, part of its momentum is transferred to the electron, like in billiard balls collisions. Thus, the photon changes its wavelength and the direction of its wave vector. The relationship between the wavelength shift and the scattering angle is given by [55]. This formula assumes that the electron is initially at rest. In reality, the electron also possesses momentum due to its orbital motion around the atomic nucleus. As shown in Figure 1b, this motion leads to a broadened wavelength distribution rather than a delta function in the scattered spectrum. The corresponding line-shape as a function of energy is known as the Compton profile, which is the basic deliverable coming from a Compton scattering experiment. The shape of the Compton profile depends on the atomic elements and the orbitals involved in the scattering process. This shape can be described in terms of an S-parameter (or shape parameter) [37]. The S-parameter increases if the profile narrows and it has been shown to be proportional to the lithium concentration in LIB materials [37].
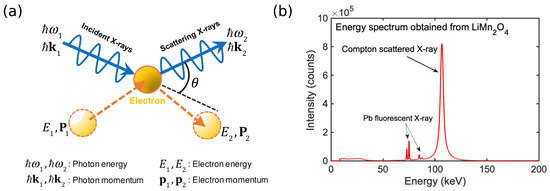
Figure 1.
(a) Schematic of a Compton scattering event. (b) Example of an experimental Compton profile. (LiMnO, data taken from Reference [31]). The scattering angle is 90°, see also Figure 2a. The broadened Compton peak around 110 keV and the secondary fluorescent peaks over effects 70–90 keV are marked.
2.2. Experiments at the SPring-8 Synchrotron Facility
Figure 2a illustrates a typical setup of a Compton scattering experiment. High-energy Compton scattering experiments are usually carried out at large synchrotron facilities with advanced detector systems [54]. The BL08W beamline at the SPring-8 synchrotron facility (Japan) [56,57,58] is one of the leading facilities in the field. BL08W employs linearly and elliptically polarized X-rays in the 100–300 keV range. It has been designed specifically for Compton scattering spectroscopy studies, including magnetic Compton scattering experiments [34,36] (Section 3.2), where measurements are performed at low temperatures with an external magnetic field of few teslas. The schematic of the BL08W beamline is shown in Figure 2b, see Refs. [59,60] for details. All high-energy Compton scattering studies reviewed here have been conducted at the BL08W beamline.
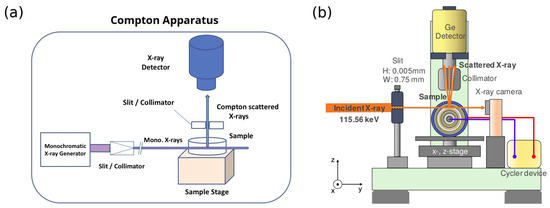
Figure 2.
Schematic of (a) a Compton setup and (b) the SPring-8 BL08W beamline. Panel 2(b) is adapted from Reference [40].
2.3. Case Study 1: Lithium Distribution in Commercial LIBs
An important objective in battery engineering is to understand and control electrochemical reactions throughout the battery. Migration of lithium ions in a LIB involves complex pathways and inhomogeneous lithium distributions connected with the battery’s state of charge, state of health, discharge speed, and temperature [28]. Suzuki et al. [37] have imaged the behaviour of Li ions inside the commercial battery CR2032 using the S-parameter of the Compton profile, as shown in Figure 3. As noted already, the S-parameter increases linearly with increasing Li concentration in the LiMnO cathode. The spatio-temporal images of the S-parameter capture the migration of lithium ions and reveal the internal structural changes resulting from volume expansion of the anode and the shrinkage of the cathode. The present method thus provides an in operando visualization of Li concentration in a closed cell and enables identification of the mechanism of cell degradation. This approach has been used for several commercial batteries [37,38,39,40,61].
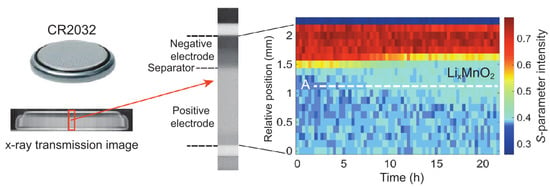
Figure 3.
Compton scattering intensity as a function of time during the discharge of the CR2032 commercial battery. Red and blue regions correspond to the negative electrode and the LiMnO in the positive electrode, respectively. The olefin separator is marked with yellow. The battery was discharged under a constant current of 5.5 mA for 15.75 h. Adapted from Ref. [37].
3. Electron Momentum Density
Note that the electronic charge density and momentum density , which describe the probability distribution of electrons in the positions and momentum space, respectively reflect effects of Heisenberg’s uncertainty principle [62,63,64]. When an electron localizes in an atomic orbital, the uncertainty in its momentum must increase. Therefore, atomic orbitals bounds tightly to the nuclei, which appear at small distances in the charge density mapped at high momenta in the momentum-density [55]. This provides a conceptual basis for imaging orbitals via the electron momentum density spectrum [65].
3.1. Spectral Function and Redox Orbitals
The electron momentum density can also be described in terms of the spectral density or spectral function [66]:
where is the electron chemical potential or Fermi energy. The spectral function captures the many-body electronic states in the solids [66,67,68] and can be calculated via the Dyson equation [69]. Near the Fermi level, the spectral function can be obtained as an energy derivative of and thus visualized by taking differences of electron momentum distributions for different values of the chemical potential [70].
The redox process involves transfer of electrons between the two electrodes. In a lithium-ion battery, the current is generated when conduction electrons from the lithium anode are transferred to the redox orbitals of the cathode material. The key underlying electronic process is the change in the formal valence of the involved ions. Here, the concept of the redox orbitals is useful for describing the electronic state of the cathode during lithium insertion and extraction processes. The relevant lithium orbitals in the cathode often posessess a strong 2-p character, and these orbitals can be visualized by considering momentum densities of the cathode material at different states of charging via Compton scattering experiments [31,35].
For example, Hafiz et al. [33] extracted the redox orbitals of lithium iron phosphate during lithiation/delithiation by monitoring the changes in Compton profiles [33]. The contribution of corresponding to Li insertion can be reconstructed (Figure 4) and used to gain insight into voltage shifts in the LIB and how these shifts are connected with the modification of the bond between the transition metal and oxygen atoms. The redox orbital concept is also related to the Fukui function [71,72], which has been used to visualize orbitals related to electron transfer processes in electrode materials [72].
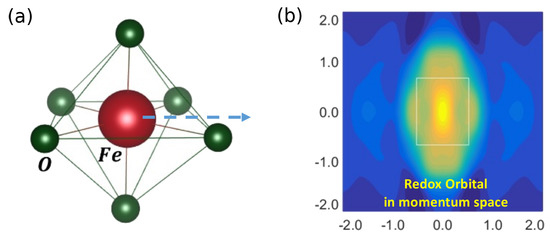
Figure 4.
(a) The FeO octahedron in LiFePO (the dashed blue arrow represents the redox Fe/Fe reaction) and (b) the redox orbital on Fe atom displayed in momentum space. The momentum density is averaged along the c axis. Blue represents lower and yellow higher momentum density. Rectangle marks the Brillouin zone. Momentum is given in atomic units. Adapted from Reference [33].
3.2. Impulse Approximation to Calculate the Compton Profile
Assuming that the Compton scattering process is so fast that the many-body electron system has no time to rearrange itself, the excited electron can be considered as a free electron. Within this approximation, which is known as the impulse approximation, the Compton profile is given as a function of the electron momentum by [66]
where is the momentum value along the scattering vector (see Figure 1a) and and are perpendicular- components. Integration over and reflects the fact that in a typical Compton experiment, the kinematics of the recoil electron are not measured, so that the information perpendicular to is effectively lost. In magnetic materials, the momentum density is spin-polarized, and one obtains the magnetic Compton profile [54]:
where and are the momentum densities of the majority and minority spins, respectively.
3.3. Case Study 2: Phase Diagram of LiCoO
The phase diagram of the layered cobalt oxide cathode material LiCoO is highly complex [73], including charge density waves and stripe-like behavior, where the itinerant cobalt electrons can localize [74]. In this connection, Barbiellini et al. [32] have analyzed the Compton spectra taken from polycrystalline LiCoO samples for different lithium concentrations x and found that the spectral functions related to the Compton profile differences are dominated by contributions of O- electrons, see Figure 5. One can also identify the distinct signature of electron delocalization in Figure 5 (green curves). This contribution is stronger for to , where the material is known to be a good conductor, which connects this feature to the conductivity of the material and provides a descriptor based on Compton spectra for monitoring the domain of x with improved conductivity and kinetics for safe electrochemical operations.
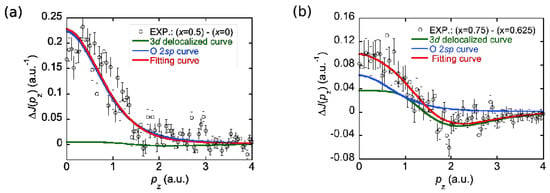
Figure 5.
The Compton profile difference between Li concentrations of (a): and and (b): and . Adapted from Reference [32].
This study is limited to spherically averaged Compton profiles because the cathode materials are normally available in powder form.
Directional Compton profiles from single crystals, which entail much greater experimental effort, will allow full reconstruction of ; see, for example, the work of Sakurai et al. on high- superconductors [58] and other studies [75,76,77,78]. Such reconstructions of the momentum density can also yield the Fermi surface, which lies at the heart of the metallic state [74].
4. Computational Models of Compton Scattering
4.1. Density-Functional Theory
Development of modern computing facilities and first-principle methodologies has triggered an exponential growth of the field of computational material design. The theory and modeling of Compton scattering spectra of ordered and disordered materials has taken advantage of these advances [70,79,80,81,82] and accelerated the pace of discovery Density-functional theory (DFT) [83,84,85,86,87] has enabled obtaining chemical information at the quantum-mechanical level, and a variety of DFT codes are available [88], including the Vienna ab initio simulation package (VASP) [89] and Quantum Espresso [90]. These codes use the projector augmented wave method [91] and the plane wave basis set, which is particularly suitable for treating crystalline solids. DFT has been used in describing many LIB materials [13,92,93,94,95]. Implementations of DFT requires approximations to the exchange-correlation energy that contains the many-body interactions, including Coulomb correlation effects for localized electronic states.
Common approximations for the exchange-correlation energy include the local spin density approximation (LSDA) and the generalized gradient approximation (GGA) [96]. However, materials that are strongly correlated cannot be described well within the LSDA and GGA. Systematic improvement have been demonstrated in treating many classes of correlated materials, including the high- superconductors, using the strongly constrained and appropriately normed (SCAN) approximation [87,97,98,99,100].
For computational purposes, the electron momentum density can be expressed in terms of the natural spin orbitals , (the eigenvectors of the density operator) [101]:
where is the occupation number of the ith natural spin orbital [102,103]. The natural spin orbitals can be approximated in terms of the Kohn-Sham orbitals obtained from the DFT calculations [103].
4.2. Case Study 3: Verwey Transition in the LiMnO Spinel Battery
The Li-Mn-O spinel battery has attracted interest because of the low cost of its components. However, close to room temperature, the LiMnO stoichiometric compound undergoes a structural Verwey transition [104,105]. This mechanism was introduced by Verwey in 1941 [106] to explain the low temperature transition in magnetite FeO at the B-sites of the spinel structure. In LiMnO spinel material, the Verwey transition also drives the onset of long-range antiferromagnetic ordering, triggers changes in the Mn valence states, and produces Jahn-Teller distortions that lead to cathode degradation [107]. Hafiz et al. [34] have studied whether a magnetic field can alleviate these distortions in LiMnO. They used magnetic Compton scattering with an external magnetic field, which favours a ferrimagnetic phase in LiMnO and prevents the Verwey transition in the competing antiferromagnetic phase and allowed the identification of the magnetic orbital residing on the manganese atoms of the ferrimagnetic phases. Figure 6a shows the momentum-space map of this orbital that is obtained by subtracting the spin down momentum density from the spin-up contribution.
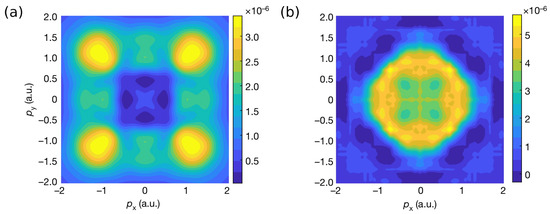
Figure 6.
(a) Magnetic momentum density of LiMnO, corresponding to the magnetic Mn orbitals. (b) Momentum density of the O redox orbitals involved in the O/O anionic process in LiTiMnO. The image has been obtained by subtracting the momentum density corresponding to from that of . Adapted from Reference [35].
4.3. Case Study 4: Lithium-Rich Battery Material LiTiMnO
Li-rich layered oxides present a promising class of cathode materials for developing batteries with high capacities of 300 mAh/g [9,108,109,110,111,112,113]. The atomic level origin of the high capacity remains unclear. If the redox process involves only the molecular orbitals of the octahedron formed by the transition metal atom, the capacity would be expected to be lower than the observed values. There is a growing consensus that high observed capacities imply that at play is a reversible redox reaction of the O anions, through which extra electrons are contributed by the non-bonding O- orbitals [112]. This anionic mechanism has been investigated using spectroscopy techniques capable of probing oxygen activity, including X-ray photoemission spectroscopy (XPS) [114] XAS [115] and X-ray resonant inelastic scattering (RIXS) [116]. However, in these techniques, the surface effects can dominate over the signal from the anionic reaction in the bulk. Additionally, it has proven difficult to detect oxygen activity [117] using X-ray Raman spectroscopy, even though the technique is more bulk-sensitive. Using X-ray Compton scattering in LiTiMnO, Hafiz et al. [35] have confirmed the microscopic mechanism involving O- orbitals [112]. A similar conclusion was reached through magnetic X-ray Compton scattering study of Suzuki et al. [36]. These studies, which involve a combination of X-ray Compton scattering experiments and parallel first principles modeling, have shown how electrons from Li atoms unleash electrical energy at the atomic level while occupying the redox orbitals at the active oxygen sites and how the electronic structure responds to Li intercalation. In this way, different behaviors of the redox processes of the transition metal and oxygen atoms are revealed. An image of the redox orbital in the momentum space associated with the anionic reaction is shown in Figure 6b.
5. Defect Evolution in Lithium-Ion Cathodes Studied by Positron Annihilation Spectroscopy
Positron annihilation spectroscopy (PAS) is a powerful technique for studies of the electronic and structural properties of solids, providing, among others, useful information about the size, type, and number density of various defects and surfaces [41,43,44]. Combined theoretical and experimental PAS studies show that PAS provides a unique and efficient approach for investigating vacancy-like defects and the microstructural properties of LIB electrode materials [48]. PAS is highly defect-sensitive and non-destructive. When combined with other techniques, such as X-ray diffraction, as applied to LiNiMnCoO in Reference [118], PAS can help monitor phase transitions and structural evolution of the cathode materials. Other PAS studies of cathode materials include those by Parz et al. [119], Zhang et al. [120], and Pagot et al. [121]. Figure 7 depicts the principles of PAS spectroscopy. It is common to employ Na isotopes as the positron source in PAS experiments. Positrons typically thermalize within a few picoseconds after implantation in a solid. They then diffuse ∼100 nm in a defect-free and between a few and tens of nanometers in a defective cathode before annihilation with a characteristic lifetime of 100–300 ps [43,121]. After thermalization, the position can be either in a free bulk state or trapped in a defect [43,122]. Two -quanta with a center-of-mass energy of 511 keV [43] are emitted in the annihilation event. Microstructural properties and the chemical environment at the annihilation site can be captured by analyzing the PAS spectra. The complementary features of PAS and X-ray techniques can be used effectively to highlight the structural evolution of the cathodes and the degradation mechanisms of lithium-ion batteries with repeated charge/discharge cycles.
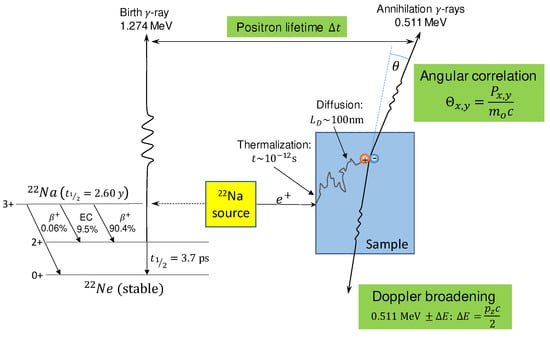
Figure 7.
Schematic illustrating principles of PAS. Na decay and the positron annihilation processes are shown. In its main decay channel (90.4%), the Na nucleus decays by emitting a positron with a maximum energy of 0.546 MeV to the excited state of Ne, which nearly simultaneously ( ps) de-excites to its ground state and emits a 1.274 MeV -quantum. The positron implanted into the sample annihilates with an electron after thermalization and diffusion and emits two 0.511 MeV -rays, which are detected in a Doppler broadening and an angular correlation experiment. Positrons typically thermalize in the sample within about 10 ps.
Prior to its annihilation, the positron can be trapped in open volume defects, such as atomic vacancies, pores, and cavities. The trapping probability depends on the charge state of the defects. The charge state can become attractive for the positron if the defect is neutral carries or negative charge because positive ions repel the positron. Positron trapping is not possible with positively charged defects that exist, for example, in silicon [123] and metal oxide semiconductors [124]). The trapped positrons have a longer lifetime than positrons in a defect-free crystal due to reduced local electron density [43]. The type and size of the vacancies can be characterized by measuring the lifetime of the positron, which is the time difference between the detection of the Na de-excitation photon and the annihilation -rays, see Figure 7. This technique is referred to as the positron annihilation lifetime spectroscopy (PALS). Moreover, the concentration of various defect types can be extracted from the associated relative spectral intensities.
Momentum of the annihilating electron-positron pair induces a Doppler shift of up to several keV, with respect to the 511 keV-line and an angular deviation from collinearity, see Figure 7. In Doppler broadening measurements, the spectra are characterized by parameters like in Compton Scattering spectroscopy, and it is common to consider the shape parameter S and the wing parameter W, where the latter describes the tail of the spectrum [41]. The S and W parameters contain information about the electronic orbital characters, as well as the electron momentum distribution. They can be used to extract information on defects in the sample. For example, an increase of the S-parameter indicates an increase in the size and/or the number density of open-volume vacancies, if the positron localizes in these regions [43].
5.1. State of Charge-Dependent Structural Features of LiCoO
LiCoO (LCO) is one of the most widely used cathode materials in LIBs. Its lithiation/delithiation processes in terms of Li-ion content, State-of-charge (SoC) dependent structural features, and defect formation caused by charging/discharging have been studied extensively via PAS [48,119,121]. Computational models based on first principles are well developed for predicting and validating experimental PAS results [43,122]. Electron-positron DFT [125] is an efficient way of treating positron states in materials. The electron-positron correlation effects in this generalization of DFT have been treated within the framework of the GGA [126,127,128]. This approximation has been made parameter-free by Barbiellini and Kuriplach [129] and it has been used to study the positron properties of the LCO cathode [48].
The positron annihilation rate , which is the inverse of the lifetime , is given by the integral of the electron-positron pair momentum distribution [80,103,122]. By using mathematical identities given by Kaiser et al. [130], one can derive the formula
where is the classical radius of the electron, c is the speed of light, is the electron density, is the electron-positron contact term given by GGA [129], is the ground state positron wave function, and V is the volume of the unit cell. The positron density distribution (PDD) in LiCoO at different SoCs ( and ) is visualized in Reference [48]. The positron lifetimes in the discharged and partially charged LCO (i.e., LiCoO and LiCoO) have been computed with GGA to be 131 and 179.2 ps, respectively. A recent study was carried out by Pagot et al. [121] using PALS and Doppler broadening measurements to investigate the effect of SoC on the structural and morphological features of graphite-incorporated LCO samples. A typical experimental PALS setup is shown in Figure 8.
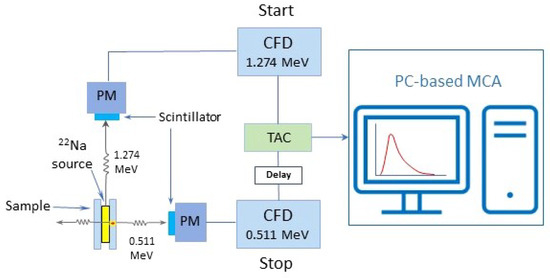
Figure 8.
Schematic of a typical experimental PALS setup. 1.274 MeV -quanta emitted by source in the sandwich configuration are detected as the start signal by the scintillation counter; the 0.511 MeV -quanta emitted at the annihilation site are then detected as the stop signal by another detector. Both signals are delivered to the corresponding CFD (Constant Fraction Discriminator) set with energy windows of 1.274 and 0.511 MeV, respectively. Electric signals collected within the correct energy window of each CFD are converted to logic signals that subsequently feed the TAC (Time-to-Amplitude Converter) to generate an output analog signal with an amplitude proportional to the time interval between the start and stop signals (i.e., positron lifetime). The signal is then processed by the MCA (Multi-Channel Analyzer) for analysis.
For the partially charged cathode (LiCoO), the positron lifetime was measured to be 180 ps, in excellent agreement with the value calculated in Reference [48]. This implies that the bulk-like state assumed by the theoretical model becomes very similar to the actual positron state. In the case of an LCO cathode with higher Li content (), due to the more rapid positron spillover from the LCO nanoparticles, the measured lifetime of the bulklike state is about 30 ps higher than the calculated value. An interesting finding of Pagot et al. [121] is that, compared to the initial thickness of the discharged LCO cathode, the thickness of the sample increased by 14% after charging to LiCoO. They also observe in their Doppler broadening measurements that the S-parameter of discharged LiCoO generally tends to be higher compared to that of the partially discharged LiCoO sample, see Figure 9, which is in agreement with X-ray Compton scattering results [32]. The study of Parz et al. [119] reports an average positron lifetime of about 207 ps for the charged LiCoO sample (), which is in reasonable agreement with the value of 215 ps obtained by Pagot et al. [121].
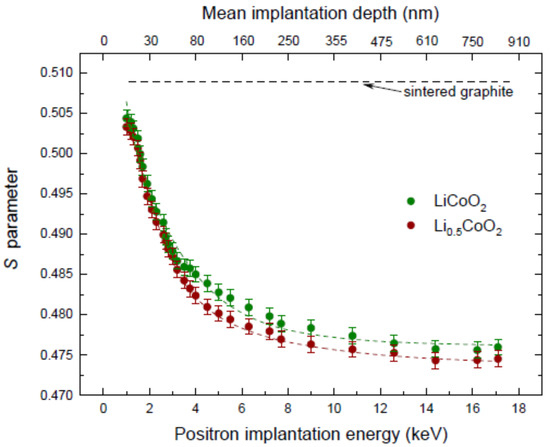
Figure 9.
Evolution of the S parameter as a function of the positron implantation energy in LiCoO (green dots), LiCoO (brown dots), and a graphite reference sample (black dashed line), taken from [121]. Positron diffusion lengths in the LiCoO and LiCoO samples were estimated to be 60 and 55 nm, respectively.
5.2. Charging-Induced Defect Formation in LCO Cathodes
The limit of reversible charging of the LCO cathode is well established at about . Further Li extraction from the Li sublattice is expected to result in irreversible structural evolution and battery degradation in terms of loss of capacity and cyclability [119,131]. A systematic investigation of the vacancy-type defect formation in the LCO cathode caused induced via charging was performed using PAS over a the range of Li concentration from down to and reported by Parz et al. [119]. The measured positron annihilation parameters (S and ) show highly sensitive responses to free volume defect formations at various Li contents, see Figure 10. The results of Parz et al. [119] and first-principle simulations [132] provide explicit evidence that transition of the two-dimensional randomly distributed Li vacancies into one-dimensional vacancy chains occurs at around . Upon further Li extraction beyond the limit, a drastic increase of both S and annihilation characteristics was observed, indicating that strong distortion of the LCO lattice structure results in cathode degradation.
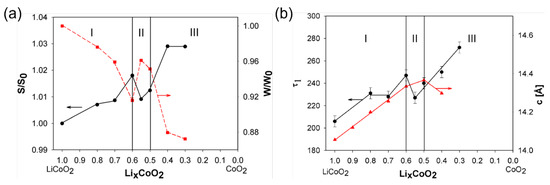
Figure 10.
PAS results from a LCO cathode at various Li-ion concentrations, adapted from [119]. (a): Doppler broadening S and W parameters with respect to and of the fully Li-loaded state. (b): Positron lifetime component and lattice parameter c of the hexagonal phase.
5.3. In Operando Characterization
PAS techniques have been also successfully applied to in operando characterization of battery materials during charging and discharging processes [131]. In operando studies have an advantage over ex situ measurements owing to their greatly enhanced sensitivity via continuous signal monitoring, while the Li content on a single electrode is varied. In order to achieve the improved cathode performance, composite cathodes offering advantageous redox potential, energy density, and structural stability have been developed, e.g., LiNiMnCoO [25,26]. The process of charging-induced defect formation in this material while charging the cathode from down to was studied by Klinser et al. [131] through in operando PALS characterization. Figure 11 displays the change in positron lifetime with respect to that of the fully discharged state as a function of Li-content [131], together with the electrode potential behaviour for the first charging cycle of LiNiMnCoO.
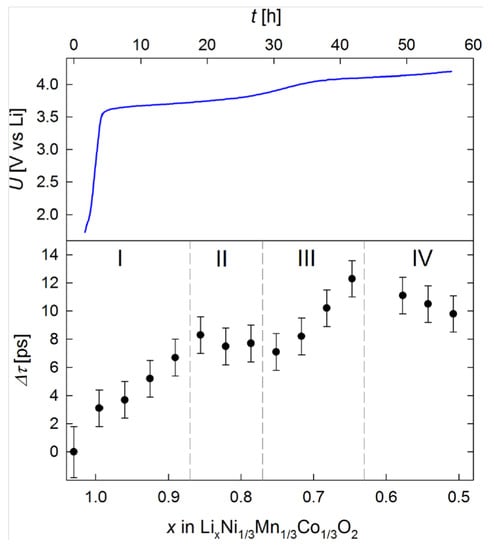
Figure 11.
Behaviour of electrode potential U as a function of charging time t and change in positron lifetime as a function of Li-content x measured on the LiNiMnCoO cathode, taken from [131]. In charging stage I (), a constant increase in the positron lifetime was observed. Following this, in charging stage II (), a slight decrease instead of increase in was discerned. increased again for of (charging stage III), followed by a decrease when .
As discussed above, continuous monitoring of lifetime evolution facilitates sensitive probing of charging-induced defect formation and phase transition with changes in Li concentration.
5.4. Opportunities for PAS
Intrinsic and lithiation-induced defects exhibit strong affinity towards positively charged Li-ions, so that the trapped Li ions at defects become more difficult to extract, causing capacity loss and degradation of battery performance [26]. Approaches that have been developed to improve Li-ion diffusion between the layered electrodes and enhance their electrochemical properties and structural/cyclic stability include doping, surface coating, and strain engineering [6,133]. Advanced characterizations of structural and electronic aspects of energy storage materials via PAS and other spectroscopies will facilitate the development of new strategies for optimizing electrode materials for sustainable energy storage and utilization technologies.
6. Conclusions and Outlook
Replacing fossil fuels with renewable energy sources is one of the most pressing challenges facing humankind. This transition includes electric vehicles that are expected to reach 200 million by 2030 [134], where the main bottleneck is the availability of long-lasting, sustainable batteries [135]. This will require new battery design strategies based on a deeper, atomic level understanding of the working of the batteries. Li-ion batteries involve a variety of interacting processes over time and space scales that span many orders of magnitude. At the smallest scale lie the redox orbitals that drive the charging/discharging reactions at the cathode and could be viewed as the “genes” of the battery because they code the key electronic properties of the cathode material. Redox orbitals are also involved intimately in determining the capacity and lifetime of the battery and in the processes that control efficient flow of Li ions between the electrodes.
This review discusses recent work towards developing spectroscopic approaches that enable an atomic level understanding of the battery materials and the visualization of the redox orbitals through charge/discharge reactions in real time, i.e., in operando. The focus is on X-ray Compton scattering, which is mostly aimed at probing bulk electronic properties and PAS, which serves to complement Compton scattering studies by monitoring open-volume defects, such vacancies, vacancy clusters, dislocations, surfaces, and interfaces. Parallel first principles modeling is key for extracting material-specific electronic and structural information from the experimental Compton scattering and PAS spectra. This combination of theory and experiment has been specially successful in interpreting Compton scattering results. However, theoretical modeling in the case of PAS has been more challenging due to difficulties of treating electron-positron interaction.
The combination of Compton scattering and PAS has been invoked traditionally for investigating Fermi surfaces and other delicate features of electronic momentum distributions in materials [136,137]. Although this has not been the case so far in connection with cathode materials, such complementary studies will be valuable, as shown, for example, by the work of Laverock et al. [138] on sodium cobalt oxides.
Author Contributions
J.N., B.B., J.K., H.H., K.P., F.K., V.K. and A.B. have worked on the theory part. K.S. and H.S. have taken care of the experimental part of X-ray Compton scattering. S.E., R.F., and X.L. have covered the PAS part. All the authors have participated in the writing of this review. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Education and Culture (Finland). J.N. is supported by the INERCOM platform at LUT university and Osk. Huttunen Foundation. The work at Northeastern University was supported by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences grant number DE-FG02-07ER46352 and benefited from Northeastern University’s Advanced Scientific Computation Center (ASCC) and the NERSC supercomputing center through DOE grant number DE-AC02-05CH11231.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to acknowledge the CSC-IT Center for Science, Finland, for computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Density Functional Theory |
| GGA | Generalized Gradient Approximation |
| LIB | Li-Ion Battery |
| LSDA | Local Spin Density Approximation |
| PAS | Positron Annihilation Spectroscopy |
| PALS | Positron Annihilation Lifetime Spectroscopy |
| RIXS | Resonant Inelastic X-ray Scattering |
| SCAN | Strongly constrained and appropriately normed |
| SoC | State of Charge |
| XAS | X-ray Absorption Spectroscopy |
| XES | X-ray Emission Spectroscopy |
| XPS | X-ray photo-emission spectroscopy |
References
- Scrosati, B. History of lithium batteries. J. Solid State Electrochem. 2011, 15, 1623–1630. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Park, K.S. The Li-ion rechargeable battery: A perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Goodenough, J.B. How we made the Li-ion rechargeable battery. Nat. Electron. 2018, 1, 204. [Google Scholar] [CrossRef]
- Pellegrini, V.; Bodoardo, S.; Brandell, D.; Edström, K. Challenges and perspectives for new material solutions in batteries. Solid State Commun. 2019, 303, 113733. [Google Scholar] [CrossRef]
- Mauger, A.; Julien, C.M.; Goodenough, J.B.; Zaghib, K. Tribute to Michel Armand: From Rocking Chair–Li-ion to Solid-State Lithium Batteries. J. Electrochem. Soc. 2019, 167, 070507. [Google Scholar] [CrossRef]
- Ramström, O. Scientific Background on the Nobel Prize in Chemistry 2019: “Lithium-Ion Batteries”. 2019. Available online: https://www.nobelprize.org/uploads/2019/10/advanced-chemistryprize2019.pdf (accessed on 24 July 2022).
- Scott, A. Electric aspirations. C&EN 2020, 98, 30–35. [Google Scholar] [CrossRef]
- Littlewood, P. An X-ray oxygen regulator. Nat. Mater. 2011, 10, 726–727. [Google Scholar] [CrossRef] [PubMed]
- Assat, G.; Tarascon, J.M. Fundamental understanding and practical challenges of anionic redox activity in Li-ion batteries. Nat. Energy 2018, 3, 373–386. [Google Scholar] [CrossRef]
- Harris, M. Interview of Peter Littlewood: “Virtual Lab, Real-World Challenges”. 2018. Available online: https://physicsworld.com/a/virtual-lab-real-world-challenges (accessed on 24 July 2022).
- Liu, X.; Liu, J.; Qiao, R.; Yu, Y.; Li, H.; Suo, L.; Hu, Y.s.; Chuang, Y.D.; Shu, G.; Chou, F.; et al. Phase Transformation and Lithiation Effect on Electronic Structure of LixFePO4: An In-Depth Study by Soft X-ray and Simulations. J. Am. Chem. Soc. 2012, 134, 13708–13715. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, Y.J.; Barbiellini, B.; Hafiz, H.; Basak, S.; Liu, J.; Richardson, T.; Shu, G.; Chou, F.; Weng, T.C.; et al. Why LiFePO4 is a safe battery electrode: Coulomb repulsion induced electron-state reshuffling upon lithiation. Phys. Chem. Chem. Phys. 2015, 17, 26369–26377. [Google Scholar] [CrossRef]
- Urban, A.; Seo, D.H.; Ceder, G. Computational understanding of Li-ion batteries. Npj Comput. Mater. 2016, 2, 1–13. [Google Scholar] [CrossRef]
- Franco, A.A. Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: Concepts, methods and challenges. RSC Adv. 2013, 3, 13027–13058. [Google Scholar] [CrossRef]
- Islam, M.S.; Fisher, C.A. Lithium and sodium battery cathode materials: Computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 2014, 43, 185–204. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, M.D.; O’Dwyer, C. Recent progress in theoretical and computational investigations of Li-ion battery materials and electrolytes. Phys. Chem. Chem. Phys. 2015, 17, 4799–4844. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Marcelli, A.; Xia, D. Application of Synchrotron Radiation Technologies to Electrode Materials for Li-and Na-Ion Batteries. Adv. Energy Mater. 2017, 7, 1700460. [Google Scholar] [CrossRef]
- Canepa, P.; Sai Gautam, G.; Hannah, D.C.; Malik, R.; Liu, M.; Gallagher, K.G.; Persson, K.A.; Ceder, G. Odyssey of multivalent cathode materials: Open questions and future challenges. Chem. Rev. 2017, 117, 4287–4341. [Google Scholar] [CrossRef] [PubMed]
- Yoon, G.; Kim, D.H.; Park, I.; Chang, D.; Kim, B.; Lee, B.; Oh, K.; Kang, K. Using First-Principles Calculations for the Advancement of Materials for Rechargeable Batteries. Adv. Funct. Mater. 2017, 27, 1702887. [Google Scholar] [CrossRef]
- Hoang, K.; Johannes, M. Defect physics in complex energy materials. J. Phys. Condens. Matter 2018, 30, 293001. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Devereaux, T.P. Anionic and cationic redox and interfaces in batteries: Advances from soft X-ray absorption spectroscopy to resonant inelastic scattering. J. Power Sources 2018, 389, 188–197. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; Chen, Z.; Amine, K. 30 years of lithium-ion batteries. Adv. Mater. 2018, 30, 1800561. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kunnikuruvan, S.; Kumar, S.; Markovsky, B.; Aurbach, D.; Dixit, M.; Major, D.T. Layered Cathode Materials for Lithium-Ion Batteries: Review of Computational Studies on LiNi1−x−yCoxMnyO2 and LiNi1−x−yCoxAlyO2. Chem. Mater. 2020, 32, 915–952. [Google Scholar] [CrossRef]
- Cheng, Z.; Liu, M.; Ganapathy, S.; Li, C.; Li, Z.; Zhang, X.; He, P.; Zhou, H.; Wagemaker, M. Revealing the Impact of Space-Charge Layers on the Li-Ion Transport in All-Solid-State Batteries. Joule 2020, 4, 1311–1323. [Google Scholar] [CrossRef]
- Mohamed, N.; Allam, N.K. Recent advances in the design of cathode materials for Li-ion batteries. RSC Adv. 2020, 10, 21662–21685. [Google Scholar] [CrossRef] [PubMed]
- Pender, J.P.; Jha, G.; Youn, D.H.; Ziegler, J.M.; Andoni, I.; Choi, E.J.; Heller, A.; Dunn, B.S.; Weiss, P.S.; Penner, R.M.; et al. Electrode Degradation in Lithium-Ion Batteries. ACS Nano 2020, 14, 1243–1295. [Google Scholar] [CrossRef] [PubMed]
- Morgan, L.M.; Islam, M.M.; Yang, H.; O’Regan, K.; Patel, A.N.; Ghosh, A.; Kendrick, E.; Marinescu, M.; Offer, G.J.; Morgan, B.J.; et al. From Atoms to Cells: Multiscale Modeling of LiNixMnyCozO2 Cathodes for Li-Ion Batteries. ACS Energy Lett. 2021, 7, 108–122. [Google Scholar] [CrossRef]
- Krewer, U.; Röder, F.; Harinath, E.; Braatz, R.D.; Bedürftig, B.; Findeisen, R. Review—Dynamic Models of Li-Ion Batteries for Diagnosis and Operation: A Review and Perspective. J. Electrochem. Soc. 2018, 165, A3656–A3673. [Google Scholar] [CrossRef]
- Osaka, T.; Nara, H.; Mukoyama, D.; Yokoshima, T. New analysis of electrochemical impedance spectroscopy for lithium-ion batteries. J. Electrochem. Sci. Technol. 2013, 4, 157–162. [Google Scholar] [CrossRef]
- Brivio, C.; Musolino, V.; Merlo, M.; Ballif, C. A Physically-Based Electrical Model for Lithium-Ion Cells. IEEE Trans. Energy Convers. 2019, 34, 594–603. [Google Scholar] [CrossRef]
- Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Go, N.; Sakurai, H.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Uchimoto, Y.; Wang, Y.J.; et al. Extracting the Redox Orbitals in Li Battery Materials with High-Resolution X-ray Compton Scattering Spectroscopy. Phys. Rev. Lett. 2015, 114, 087401. [Google Scholar] [CrossRef]
- Barbiellini, B.; Suzuki, K.; Orikasa, Y.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Wang, Y.J.; Hafiz, H.; Yamada, R.; Uchimoto, Y.; et al. Identifying a descriptor for d-orbital delocalization in cathodes of Li batteries based on X-ray Compton scattering. Appl. Phys. Lett. 2016, 109, 073102. [Google Scholar] [CrossRef]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Callewaert, V.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Yamada, R.; Uchimoto, Y.; et al. Visualizing redox orbitals and their potentials in advanced lithium-ion battery materials using high-resolution X-ray Compton scattering. Sci. Adv. 2017, 3, e1700971. [Google Scholar] [CrossRef] [PubMed]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Kaprzyk, S.; Tsuji, N.; Yamamoto, K.; Terasaka, A.; Hoshi, K.; Uchimoto, Y.; et al. Identification of ferrimagnetic orbitals preventing spinel degradation by charge ordering in LixMn2O4. Phys. Rev. B 2019, 100, 205104. [Google Scholar] [CrossRef]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Tsuji, N.; Yabuuchi, N.; Yamamoto, K.; Orikasa, Y.; Uchimoto, Y.; Sakurai, Y.; Sakurai, H.; et al. Tomographic reconstruction of oxygen orbitals in lithium-rich battery materials. Nature 2021, 594, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Otsuka, Y.; Hoshi, K.; Sakurai, H.; Tsuji, N.; Yamamoto, K.; Yabuuchi, N.; Hafiz, H.; Orikasa, Y.; Uchimoto, Y.; et al. Magnetic Compton Scattering Study of Li-Rich Battery Materials. Condens. Matter 2022, 7, 4. [Google Scholar] [CrossRef]
- Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Wang, Y.J.; Hafiz, H.; Uchimoto, Y.; Bansil, A.; et al. Non-destructive measurement of in-operando lithium concentration in batteries via X-ray Compton scattering. J. Appl. Phys. 2016, 119, 025103. [Google Scholar] [CrossRef]
- Suzuki, K.; Suzuki, A.; Ishikawa, T.; Itou, M.; Yamashige, H.; Orikasa, Y.; Uchimoto, Y.; Sakurai, Y.; Sakurai, H. In operando quantitation of Li concentration for a commercial Li-ion rechargeable battery using high-energy X-ray Compton scattering. J. Synchrotron Radiat. 2017, 24, 1006–1011. [Google Scholar] [CrossRef]
- Suzuki, K.; Kanai, R.; Tsuji, N.; Yamashige, H.; Orikasa, Y.; Uchimoto, Y.; Sakurai, Y.; Sakurai, H. Dependency of the Charge—Discharge Rate on Lithium Reaction Distributions for a Commercial Lithium Coin Cell Visualized by Compton Scattering Imaging. Condens. Matter 2018, 3, 27. [Google Scholar] [CrossRef]
- Suzuki, K.; Honkanen, A.P.; Tsuji, N.; Jalkanen, K.; Koskinen, J.; Morimoto, H.; Hiramoto, D.; Terasaka, A.; Hafiz, H.; Sakurai, Y.; et al. High-Energy X-Ray Compton Scattering Imaging of 18650-Type Lithium-Ion Battery Cell. Condens. Matter 2019, 4, 66. [Google Scholar] [CrossRef]
- Leipner, R.; Krause-Rehberg, R.; Leipner, H. Positron Annihilation in Semiconductors: Defect Studies; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Saniz, R.; Barbiellini, B.; Denison, A. Compton scattering, positron annihilation, and the electronic properties of quantum dots. Phys. Rev. B 2002, 65, 245310. [Google Scholar] [CrossRef]
- Tuomisto, F.; Makkonen, I. Defect identification in semiconductors with positron annihilation: Experiment and theory. Rev. Mod. Phys. 2013, 85, 1583–1631. [Google Scholar] [CrossRef]
- Čížek, J. Characterization of lattice defects in metallic materials by positron annihilation spectroscopy: A review. J. Mater. Sci. Technol. 2018, 34, 577–598. [Google Scholar] [CrossRef]
- Barbiellini, B. Positron states in materials: DFT and QMC studies. In New Directions in Antimatter Chemistry and Physics; Springer: Berlin/Heidelberg, Germany, 2001; pp. 127–150. [Google Scholar] [CrossRef]
- Eijt, S.W.H.; van Veen, A.; Schut, H.; Mijnarends, P.E.; Denison, A.B.; Barbiellini, B.; Bansil, A. Study of colloidal quantum-dot surfaces using an innovative thin-film positron 2D-ACAR method. Nat. Mater. 2006, 5, 23–26. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Callewaert, V.; Barbiellini, B.; Saniz, R.; Butterling, M.; Egger, W.; Dickmann, M.; Hugenschmidt, C.; Shakeri, B.; Meulenberg, R.W.; et al. Nature of the Positron State in CdSe Quantum Dots. Phys. Rev. Lett. 2018, 121, 057401. [Google Scholar] [CrossRef]
- Barbiellini, B.; Kuriplach, J. Advanced characterization of lithium battery materials with positrons. J. Phys. Conf. Ser. 2017, 791, 012016. [Google Scholar] [CrossRef]
- Barbiellini, B. High-Temperature Cuprate Superconductors Studied by X-ray Compton Scattering and Positron Annihilation Spectroscopies; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2013; Volume 443, p. 012009. [Google Scholar] [CrossRef]
- Llewellyn, A.V.; Matruglio, A.; Brett, D.J.L.; Jervis, R.; Shearing, P.R. Using In-Situ Laboratory and Synchrotron-Based X-ray Diffraction for Lithium-Ion Batteries Characterization: A Review on Recent Developments. Condens. Matter 2020, 5, 75. [Google Scholar] [CrossRef]
- Pussi, K.; Gallo, J.; Ohara, K.; Carbo-Argibay, E.; Kolen’ko, Y.V.; Barbiellini, B.; Bansil, A.; Kamali, S. Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions. Condens. Matter 2020, 5, 19. [Google Scholar] [CrossRef]
- Aquilanti, G.; Giorgetti, M.; Dominko, R.; Stievano, L.; Arčon, I.; Novello, N.; Olivi, L. Operando characterization of batteries using X-ray absorption spectroscopy: Advances at the beamline XAFS at synchrotron Elettra. J. Phys. D Appl. Phys. 2017, 50, 074001. [Google Scholar] [CrossRef]
- Zimmermann, P.; Peredkov, S.; Abdala, P.M.; DeBeer, S.; Tromp, M.; Müller, C.; van Bokhoven, J.A. Modern X-ray spectroscopy: XAS and XES in the laboratory. Coord. Chem. Rev. 2020, 423, 213466. [Google Scholar] [CrossRef]
- Cooper, M.; Mijnarends, P.; Shiotani, N.; Sakai, N.; Bansil, A. X-ray Compton Scattering; OUP: Oxford, UK, 2004; Volume 5. [Google Scholar] [CrossRef]
- Mijnarends, P.E.; Bansil, A. Scattering techniques, Compton. In Encyclopedia of Condensed Matter Physics; Elsevier: Amsterdam, The Netherlands, 2005; pp. 182–193. [Google Scholar] [CrossRef]
- Hiraoka, N.; Itou, M.; Ohata, T.; Mizumaki, M.; Sakurai, Y.; Sakai, N. A new X-ray spectrometer for high-resolution Compton profile measurements at SPring-8. J. Synchrotron Radiat. 2001, 8, 26–32. [Google Scholar] [CrossRef]
- Itou, M.; Hiraoka, N.; Ohata, T.; Mizumaki, M.; Deb, A.; Sakurai, Y.; Sakai, N. Present status of the Cauchois-type compton scattering spectrometer at SPring-8. Nucl. Instrum. Methods Phys. Res. A 2001, 467–468, 1109–1112. [Google Scholar] [CrossRef]
- Sakurai, Y.; Itou, M. A Cauchois-type X-ray spectrometer for momentum density studies on heavy-element materials. J. Phys. Chem. Solids 2004, 65, 2061–2064. [Google Scholar] [CrossRef]
- Sakurai, Y. High-energy inelastic-scattering beamline for electron momentum density study. J. Synchrotron Radiat. 1998, 5, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Kakutani, Y.; Kubo, Y.; Koizumi, A.; Sakai, N.; Ahuja, B.L.; Sharma, B.K. Magnetic Compton profiles of Fcc-Ni, Fcc-Fe50Ni50 and Hcp-Co. J. Phys. Soc. Jpn. 2003, 72, 599–606. [Google Scholar] [CrossRef]
- Suzuki, K.; Suzuki, S.; Otsuka, Y.; Tsuji, N.; Jalkanen, K.; Koskinen, J.; Hoshi, K.; Honkanen, A.P.; Hafiz, H.; Sakurai, Y.; et al. Redox oscillations in 18650-type lithium-ion cell revealed by in operando Compton scattering imaging. Appl. Phys. Lett. 2021, 118, 161902. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 478–504. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Gatti, C.; Macchi, P. A Guided Tour Through Modern Charge Density Analysis. In Modern Charge-Density Analysis; Springer: Berlin, Germany, 2011; pp. 1–78. [Google Scholar] [CrossRef]
- Sakurai, Y.; Itou, M.; Barbiellini, B.; Mijnarends, P.E.; Markiewicz, R.S.; Kaprzyk, S.; Gillet, J.M.; Wakimoto, S.; Fujita, M.; Basak, S.; et al. Imaging Doped Holes in a Cuprate Superconductor with High-Resolution Compton Scattering. Science 2011, 332, 698–702. [Google Scholar] [CrossRef]
- Kaplan, I.G.; Barbiellini, B.; Bansil, A. Compton scattering beyond the impulse approximation. Phys. Rev. B 2003, 68, 235104. [Google Scholar] [CrossRef]
- Weigold, E.; McCarthy, I. Electron Momentum Spectroscopy; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Schwarz, W.E. Measuring orbitals: Provocation or reality? Angew. Chem. Int. Ed. 2006, 45, 1508–1517. [Google Scholar] [CrossRef]
- Barbiellini, B.; Bansil, A. Dyson orbitals, quasi-particle effects and Compton scattering. J. Phys. Chem. Solids 2004, 65, 2031–2034. [Google Scholar] [CrossRef]
- Wang, Y.J.; Barbiellini, B.; Lin, H.; Das, T.; Basak, S.; Mijnarends, P.E.; Kaprzyk, S.; Markiewicz, R.S.; Bansil, A. Lindhard and RPA susceptibility computations in extended momentum space in electron-doped cuprates. Phys. Rev. B 2012, 85, 224529. [Google Scholar] [CrossRef]
- Fukui, K. Role of Frontier Orbitals in Chemical Reactions. Science 1982, 218, 747–754. [Google Scholar] [CrossRef] [PubMed]
- Keshavarz, F.; Kadek, M.; Barbiellini, B.; Bansil, A. Electrochemical Potential of the Metal Organic Framework MIL-101 (Fe) as Cathode Material in Li-Ion Batteries. Condens. Matter 2021, 6, 22. [Google Scholar] [CrossRef]
- Antolini, E. LiCoO2: Formation, structure, lithium and oxygen nonstoichiometry, electrochemical behaviour and transport properties. Solid State Ion. 2004, 170, 159–171. [Google Scholar] [CrossRef]
- Motohashi, T.; Ono, T.; Sugimoto, Y.; Masubuchi, Y.; Kikkawa, S.; Kanno, R.; Karppinen, M.; Yamauchi, H. Electronic phase diagram of the layered cobalt oxide system LixCoO2 (0.0 ≤ x ≤ 1.0). Phys. Rev. B 2009, 80, 165114. [Google Scholar] [CrossRef]
- Tanaka, Y.; Sakurai, Y.; Stewart, A.T.; Shiotani, N.; Mijnarends, P.E.; Kaprzyk, S.; Bansil, A. Reconstructed three-dimensional electron momentum density in lithium: A Compton scattering study. Phys. Rev. B 2001, 63, 045120. [Google Scholar] [CrossRef]
- Hamalainen, K.; Manninen, S.; Kao, C.C.; Caliebe, W.; Hastings, J.B.; Bansil, A.; Kaprzyk, S.; Platzman, P.M. High resolution Compton scattering study of Be. Phys. Rev. B 1996, 54, 5453–5459. [Google Scholar] [CrossRef]
- Stutz, G.; Wohlert, F.; Kaprolat, A.; Schülke, W.; Sakurai, Y.; Tanaka, Y.; Ito, M.; Kawata, H.; Shiotani, N.; Kaprzyk, S.; et al. Electron momentum-space densities and Fermi surface of Li100−xMgx (0 <∼ x <∼ 40) alloys: Compton scattering experiment versus theory. Phys. Rev. B 1999, 60, 7099–7112. [Google Scholar] [CrossRef]
- Bansil, A.; Pankaluoto, R.; Rao, R.S.; Mijnarends, P.E.; Długosz, W.; Prasad, R.; Smedskjaer, L.C. Fermi Surface, Ground-State Electronic Structure, and Positron Experiments in YBa2Cu3O7. Phys. Rev. Lett. 1988, 61, 2480–2483. [Google Scholar] [CrossRef]
- Barbiellini, B.; Dugdale, S.; Jarlborg, T. The EPMD-LMTO program for electron–positron momentum density calculations in solids. Comput. Mater. Sci. 2003, 28, 287–301. [Google Scholar] [CrossRef]
- Makkonen, I.; Hakala, M.; Puska, M. Calculation of valence electron momentum densities using the projector augmented-wave method. J. Phys. Chem. Solids 2005, 66, 1128–1135. [Google Scholar] [CrossRef]
- Mijnarends, P.E.; Bansil, A. Momentum density for Compton scattering from random alloys. Phys. Rev. B 1976, 13, 2381–2390. [Google Scholar] [CrossRef]
- Bansil, A.; Rao, R.S.; Mijnarends, P.E.; Schwartz, L. Electron momentum densities in disordered muffin-tin alloys. Phys. Rev. B 1981, 23, 3608–3616. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Jones, R.O.; Gunnarsson, O. The density functional formalism, its applications and prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Jones, R.O. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 2015, 87, 897–923. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Corso, A.D.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Ceder, G.; Chiang, Y.M.; Sadoway, D.; Aydinol, M.; Jang, Y.I.; Huang, B. Identification of cathode materials for lithium batteries guided by first-principles calculations. Nature 1998, 392, 694–696. [Google Scholar] [CrossRef]
- Meng, Y.S.; Arroyo-de Dompablo, M.E. Recent Advances in First Principles Computational Research of Cathode Materials for Lithium-Ion Batteries. Acc. Chem. Res. 2013, 46, 1171–1180. [Google Scholar] [CrossRef] [PubMed]
- Di Valentin, C.; Botti, S.; Cococcioni, M. First Principles Approaches to Spectroscopic Properties of Complex Materials; Springer: Berlin/Heidelberg, Germany, 2014; Volume 347. [Google Scholar] [CrossRef]
- Wu, X.; Kang, F.; Duan, W.; Li, J. Density functional theory calculations: A powerful tool to simulate and design high-performance energy storage and conversion materials. Prog. Nat. Sci. Mater. Int. 2019, 29, 247–255. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Furness, J.W.; Zhang, Y.; Lane, C.; Buda, I.G.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. An accurate first-principles treatment of doping-dependent electronic structure of high-temperature cuprate superconductors. Commun. Phys. 2018, 1, 11. [Google Scholar] [CrossRef]
- Lane, C.; Furness, J.W.; Buda, I.G.; Zhang, Y.; Markiewicz, R.S.; Barbiellini, B.; Sun, J.; Bansil, A. Antiferromagnetic ground state of La2CuO4: A parameter-free ab initio description. Phys. Rev. B 2018, 98, 125140. [Google Scholar] [CrossRef]
- Zhang, Y.; Lane, C.; Furness, J.W.; Barbiellini, B.; Perdew, J.P.; Markiewicz, R.S.; Bansil, A.; Sun, J. Competing stripe and magnetic phases in the cuprates from first principles. Proc. Natl. Acad. Sci. USA 2020, 117, 68–72. [Google Scholar] [CrossRef]
- Nokelainen, J.; Lane, C.; Markiewicz, R.S.; Barbiellini, B.; Pulkkinen, A.; Singh, B.; Sun, J.; Pussi, K.; Bansil, A. Ab initio description of the Bi2Sr2CaCu2O8+δ electronic structure. Phys. Rev. B 2020, 101, 214523. [Google Scholar] [CrossRef]
- Barbiellini, B. Natural orbital functional theory and pairing correlation effects in electron momentum density. Low Temp. Phys. 2014, 40, 318–322. [Google Scholar] [CrossRef]
- Barbiellini, B. A natural orbital method for the electron momentum distribution in matter. J. Phys. Chem. Solids 2000, 61, 341–344. [Google Scholar] [CrossRef]
- Barbiellini, B.; Bansil, A. Treatment of correlation effects in electron momentum density: Density functional theory and beyond. J. Phys. Chem. Solids 2001, 62, 2181–2189. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J.; Rousse, G.; Masquelier, C.; Hervieu, M. Electronic Crystallization in a Lithium Battery Material: Columnar Ordering of Electrons and Holes in the Spinel LiMn2O4. Phys. Rev. Lett. 1998, 81, 4660–4663. [Google Scholar] [CrossRef]
- Fang, T.; Chung, H. Reassessment of the Electronic-Conduction Behavior above the Verwey-Like Transition of Ni2+- and Al3+-Doped LiMn2O4. J. Am. Ceram. Soc. 2007, 91, 342–345. [Google Scholar] [CrossRef]
- Verwey, E.; Haayman, P. Electronic conductivity and transition point of magnetite (“Fe3O4”). Physica 1941, 8, 979–987. [Google Scholar] [CrossRef]
- Wills, A.S.; Raju, N.P.; Greedan, J.E. Low-Temperature Structure and Magnetic Properties of the Spinel LiMn2O4: A Frustrated Antiferromagnet and Cathode Material. Chem. Mater. 1999, 11, 1510–1518. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Takeuchi, M.; Nakayama, M.; Shiiba, H.; Ogawa, M.; Nakayama, K.; Ohta, T.; Endo, D.; Ozaki, T.; Inamasu, T.; et al. High-capacity electrode materials for rechargeable lithium batteries: Li3NbO4-based system with cation-disordered rocksalt structure. Proc. Natl. Acad. Sci. USA 2015, 112, 7650–7655. [Google Scholar] [CrossRef]
- Seo, D.H.; Lee, J.; Urban, A.; Malik, R.; Kang, S.; Ceder, G. The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials. Nat. Chem. 2016, 8, 692–697. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Nakayama, M.; Takeuchi, M.; Komaba, S.; Hashimoto, Y.; Mukai, T.; Shiiba, H.; Sato, K.; Kobayashi, Y.; Nakao, A.; et al. Origin of stabilization and destabilization in solid-state redox reaction of oxide ions for lithium-ion batteries. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Li, B.; Xia, D. Anionic redox in rechargeable lithium batteries. Adv. Mater. 2017, 29, 1701054. [Google Scholar] [CrossRef] [PubMed]
- Okubo, M.; Yamada, A. Molecular orbital principles of oxygen-redox battery electrodes. ACS Appl. Mater. Interfaces 2017, 9, 36463–36472. [Google Scholar] [CrossRef] [PubMed]
- Clément, R.; Lun, Z.; Ceder, G. Cation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium-ion cathodes. Energy Environ. Sci. 2020, 13, 345–373. [Google Scholar] [CrossRef]
- Naylor, A.J.; Makkos, E.; Maibach, J.; Guerrini, N.; Sobkowiak, A.; Björklund, E.; Lozano, J.G.; Menon, A.S.; Younesi, R.; Roberts, M.R.; et al. Depth-dependent oxygen redox activity in lithium-rich layered oxide cathodes. J. Mater. Chem. A 2019, 7, 25355–25368. [Google Scholar] [CrossRef]
- Li, M.; Liu, T.; Bi, X.; Chen, Z.; Amine, K.; Zhong, C.; Lu, J. Cationic and anionic redox in lithium-ion based batteries. Chem. Soc. Rev. 2020, 49, 1688–1705. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Sun, M.; Qiao, R.; Renfrew, S.E.; Ma, L.; Wu, T.; Hwang, S.; Nordlund, D.; Su, D.; Amine, K.; et al. Elucidating anionic oxygen activity in lithium-rich layered oxides. Nat. Commun. 2018, 9, 947. [Google Scholar] [CrossRef]
- Mukai, K.; Nonaka, T.; Uyama, T.; Nishimura, Y.F. In situ X-ray Raman spectroscopy and magnetic susceptibility study on Li[Li0.15Mn1.85]O4 oxygen anion redox reaction. Chem. Commun. 2020, 56, 1701–1704. [Google Scholar] [CrossRef]
- Seidlmayer, S.; Buchberger, I.; Reiner, M.; Gigl, T.; Gilles, R.; Gasteiger, H.A.; Hugenschmidt, C. First-cycle defect evolution of Li1−xNi1/3Mn1/3Co1/3O2 lithium ion battery electrodes investigated by positron annihilation spectroscopy. J. Power Sources 2016, 336, 224–230. [Google Scholar] [CrossRef]
- Parz, P.; Fuchsbichler, B.; Koller, S.; Bitschnau, B.; Mautner, F.A.; Puff, W.; Würschum, R. Charging-induced defect formation in LixCoO2 battery cathodes studied by positron annihilation spectroscopy. Appl. Phys. Lett. 2013, 102, 151901. [Google Scholar] [CrossRef]
- Zhang, L.L.; Duan, S.; Yang, X.L.; Liang, G.; Huang, Y.H.; Cao, X.Z.; Yang, J.; Ni, S.B.; Li, M. Systematic investigation on cadmium-incorporation in Li2FeSiO4/C cathode material for lithium-ion batteries. Sci. Rep. 2014, 4, 5064. [Google Scholar] [CrossRef] [PubMed]
- Pagot, G.; Toso, V.; Barbiellini, B.; Ferragut, R.; Di Noto, V. Positron Annihilation Spectroscopy as a Diagnostic Tool for the Study of LiCoO2 Cathode of Lithium-Ion Batteries. Condens. Matter 2021, 6, 28. [Google Scholar] [CrossRef]
- Puska, M.J.; Nieminen, R.M. Theory of positrons in solids and on solid surfaces. Rev. Mod. Phys. 1994, 66, 841–897. [Google Scholar] [CrossRef]
- Watkins, G.D. EPR and ENDOR studies of defects in semiconductors. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 1998; Volume 51, pp. 1–43. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Z.; Fang, Z.; Qiu, M.; Ling, L.; Long, J.; Chen, L.; Tong, Y.; Su, W.; Zhang, Y.; et al. Defect engineering of metal–oxide interface for proximity of photooxidation and photoreduction. Proc. Natl. Acad. Sci. USA 2019, 116, 10232–10237. [Google Scholar] [CrossRef] [PubMed]
- Boroński, E.; Nieminen, R.M. Electron-positron density-functional theory. Phys. Rev. B 1986, 34, 3820–3831. [Google Scholar] [CrossRef] [PubMed]
- Barbiellini, B.; Puska, M.J.; Torsti, T.; Nieminen, R.M. Gradient correction for positron states in solids. Phys. Rev. B 1995, 51, 7341–7344. [Google Scholar] [CrossRef] [PubMed]
- Barbiellini, B.; Puska, M.J.; Korhonen, T.; Harju, A.; Torsti, T.; Nieminen, R.M. Calculation of positron states and annihilation in solids: A density-gradient-correction scheme. Phys. Rev. B 1996, 53, 16201–16213. [Google Scholar] [CrossRef]
- Kuriplach, J.; Barbiellini, B. Improved generalized gradient approximation for positron states in solids. Phys. Rev. B 2014, 89, 155111. [Google Scholar] [CrossRef]
- Barbiellini, B.; Kuriplach, J. Proposed Parameter-Free Model for Interpreting the Measured Positron Annihilation Spectra of Materials Using a Generalized Gradient Approximation. Phys. Rev. Lett. 2015, 114, 147401. [Google Scholar] [CrossRef]
- Kaiser, J.H.; West, R.N.; Shiotani, N. Electronic structure studies with positrons: A new approach to wavefunction effects. J. Phys. F Met. Phys. 1986, 16, 1307–1318. [Google Scholar] [CrossRef]
- Klinser, G.; Kren, H.; Koller, S.; Würschum, R. Operando monitoring of charging-induced defect formation in battery electrodes by positrons. Appl. Phys. Lett. 2019, 114, 013905. [Google Scholar] [CrossRef]
- Van der Ven, A.; Aydinol, M.K.; Ceder, G.; Kresse, G.; Hafner, J. First-principles investigation of phase stability in LixCoO2. Phys. Rev. B 1998, 58, 2975–2987. [Google Scholar] [CrossRef]
- Li, J.J.; Dai, Y.; Zheng, J.C. Strain engineering of ion migration in LiCoO2. Front. Phys. 2022, 17, 13503. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook. 2022. Available online: https://www.iea.org/reports/global-ev-outlook-2022 (accessed on 24 July 2022).
- Quinteros-Condoretty, A.R.; Golroudbary, S.R.; Albareda, L.; Barbiellini, B.; Soyer, A. Impact of circular design of lithium-ion batteries on supply of lithium for electric cars towards a sustainable mobility and energy transition. Procedia CIRP 2021, 100, 73–78. [Google Scholar] [CrossRef]
- Ketels, J.; Billington, D.; Dugdale, S.B.; Leitner, M.; Hugenschmidt, C.P. Momentum density spectroscopy of Pd: Comparison of 2D-ACAR and Compton scattering using a 1D-to-2D reconstruction method. Phys. Rev. B 2021, 104, 075160. [Google Scholar] [CrossRef]
- Al-Sawai, W.; Barbiellini, B.; Sakurai, Y.; Itou, M.; Mijnarends, P.E.; Markiewicz, R.S.; Kaprzyk, S.; Wakimoto, S.; Fujita, M.; Basak, S.; et al. Bulk Fermi surface and momentum density in heavily doped La2−xSrxCuO4 using high-resolution Compton scattering and positron annihilation spectroscopies. Phys. Rev. B 2012, 85, 115109. [Google Scholar] [CrossRef]
- Laverock, J.; Dugdale, S.B.; Duffy, J.A.; Wooldridge, J.; Balakrishnan, G.; Lees, M.R.; Zheng, G.q.; Chen, D.; Lin, C.T.; Andrejczuk, A.; et al. Elliptical hole pockets in the Fermi surfaces of unhydrated and hydrated sodium cobalt oxides. Phys. Rev. B 2007, 76, 052509. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).