Abstract
The study of ions in the gas phase has a long history and has involved both chemists and physicists. The interplay of their competences with the use of very sophisticated commercial and/or homemade instrumentations and theoretical models has improved the knowledge of thermodynamics and kinetics of many chemical reactions, even if still many stages of these processes need to be fully understood. The new technologies and the novel free-electron laser facilities based on plasma acceleration open new opportunities to investigate the chemical reactions in some unrevealed fundamental aspects. The synchrotron light source can be put beside the FELs, and by mass spectrometric techniques and spectroscopies coupled with versatile ion sources it is possible to really change the state of the art of the ion chemistry in different areas such as atmospheric and astro chemistry, plasma chemistry, biophysics, and interstellar medium (ISM). In this manuscript we review the works performed by a joint combination of the experimental studies of ion–molecule reactions with synchrotron radiation and theoretical models adapted and developed to the experimental evidence. The review concludes with the perspectives of ion–molecule reactions by using FEL instrumentations as well as pump probe measurements and the initial attempt in the development of more realistic theoretical models for the prospective improvement of our predictive capability.
1. Introduction
The study of gas phase ionic chemistry finds its fundamental relevance in different areas of physical chemistry such as atmospheric and astro chemistry [1], plasma chemistry [2], biophysics [3], interstellar medium (ISM) [4], and the activation and/or functionalization of simple starting materials [5].
The atmosphere is composed of a mixture of gases, the main components are N2 and O2 but also trace gases such as carbon dioxide, carbon monoxide, methane, water, nitrous oxide, ozone, argon, sulfur dioxide, and haloalkanes are important. These gases are present in very little amounts but cannot be undervalued; they are emitted in the atmosphere by natural or anthropogenic phenomena and could have a key role in some fundamental reactions that change the budget of some important species and consequently alter the composition of the atmosphere with a social healthy impact. Chlorofluorocarbon molecules are a classic and well-known example. They interact with sun light and produce chlorine radicals that catalytically destroy the ozone molecules. These species can also interact with high energetic cosmic rays with the production of reactive, neutral, and charged species. Chemical networks that explain the formation of species in the atmosphere involve mainly neutral species. Despite the fundamental role of neutrals in many processes, the formation of neutral species from ion–molecule reactions is also important because these reactions may represent more efficient paths to neutrals than neutral–neutral reactions, either destroying or producing neutral molecules by faster reactions. The study of ionic processes is fundamental to understand how they alter the neutral chemistry and identify the link between the ion and neutral chemistry in many processes occurring in different environments. Moreover, greenhouse gases (GHGs) such as carbon dioxide and depleting substances (ODSs) such as haloalkanes are considered responsible for climate change due to global warming [6]. One of the strategies to contrast global warming is solar geoengineering [7], which considers cooling the planet by introducing small reflective particles, such as sulfur dioxide, into the upper atmosphere to reflect some sunlight before it reaches the surface of the Earth. The idea is to mimic the effects of the natural emission of sulfur dioxide by volcanic eruptions. However, there are many criticisms. Some scientists say that the potential risks of such technologies are still far from being fully understood. Indeed, accurate models do not exist, and current models give controversial answers. Hence, the study of possible effects that an emission of SO2 into stratosphere where stratosphere ionizing radiations are also not negligible, is strongly required.
The universe is also an environment where chemicals are synthesized and destroyed through complicated chemical networks that researchers are exploring. The radiation present in space ionizes and dissociates simple molecules [8,9], producing radicals and ions, which can start fast, barrierless, and exothermic ion–molecule reactions resulting in the intricate chemical synthesis of molecules. For instance, methanol, first observed in 1970 [10], is one of the most abundant astrochemical organic molecules. The planets’ atmospheres are also composed of different gases and in the interstellar medium have been identified several species both neutral and ionic [11].
Recently, plasma technology has received attention for the activation of stable molecules, such as CO2. Plasma is an ionized gas where atoms, molecules, radicals, and excited species are present and react. Although several setups have been realized for the plasma-based molecules conversion, the mechanistic insights of their transformations are still not clear.
In this framework, the study of gas phase chemistry through different experimental equipment and methodologies, as well as theoretical calculations and modeling, became fundamental and can give a relevant contribution going beyond the state of art. This field of chemistry investigates the photofragmentation of ions and charged clusters and the dynamics of the formation of charged species, molecules, and radicals through chemical reactions. Laboratory studies have an important role in the characterization of the nature of the relevant processes down to the molecular level and give information that can be used to assess how these processes guide environmental phenomena such as climate change, human health, and stratospheric ozone depletion: “laboratory studies are an essential bridge between field measurements and models” [12]. Hence, deep insights in the kinetic, thermochemical, and mechanistic features of these reactions are of paramount multidisciplinary significance, both under thermal and no-thermal conditions as well as at a low, room, and high temperature.
The review is divided in five sections. Section 1 introduction. Section 2 methodology: typical experimental conditions used to study ion–molecule reactions and photo fragmentations at the synchrotron ELETTRA (Trieste, Italy), and computational methodology. Section 3 atom/ion transfer reactions: SO2•+ reactivity with water, methane, hydrogen, and carbon monoxide, and methanol reactivity. Section 4 photofragmentation studies of halomethanes. Section 5 perspectives: planning experiments at the FEL facilities and the improvement in modeling the ion–molecule reactions.
2. Methodology
2.1. Experiments at Elettra Synchrotron
The apparatus (Figure 1) for ion–molecule reaction studies is accessible at the circular polarization (CiPo) beamline of ELETTRA and is fully described in different papers [13,14]. The use of synchrotron radiation is mandatory because the experiments require high photon fluxes and tunability of the photon energy. The beamline has a normal incidence monochromator and it is provided with an electromagnetic elliptical undulator/wiggler. Two gratings can be used for the experiments: (i) an aluminum-coated holographic spherical grating with 1200 grooves per mm (Al-NIM) that provides radiation in the range 5–17 eV with an energy resolution of approximately 20 meV; (ii) gold holographic spherical grating with 2400 grooves mm−1 (Au-NIM) used to cover the 16–35 eV energy range.
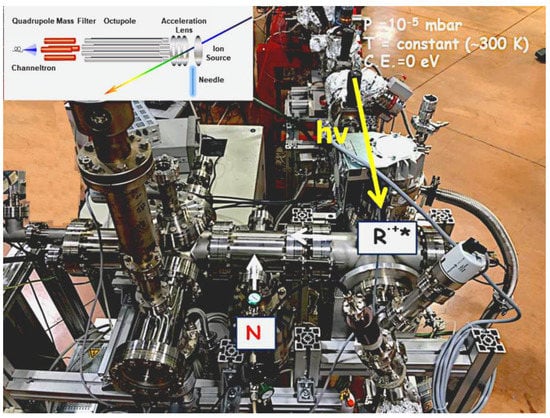
Figure 1.
Experimental apparatus used to study ion–molecule and photofragmentation reactions. R.+* is the radical cation and N is the molecule.
The ion source is equipped with ion optics (one planar repeller and three extractor lenses) set in front of the octupolar RF-driven ion guide. The effusive beam of the neutral precursor introduced at a constant pressure of approximately 10−6 mbar via a needle, arrives at the center of the ionization region crossed at 90° by the photon beam. In the ion–molecule reactions experiments, ions produced by photoionization are guided into the octupole by the extraction optics, set perpendicularly to the propagation axis of the photon beam. The neutral reagents are introduced in the octupole (reaction cell) via a needle valve that finely regulates the pressure in the range 10−7–10−4 mbar. All ions are then transferred in the quadrupole mass spectrometer equipped with a channeltron multiplier detector. The nominal collision energy (CE) is generally kept at 0 eV and it is obtained by measuring the reagent ion yields as a function of the retarding field. The energy spread of the ion packet is between 100 and 200 meV. In a typical experiment, the yields of ionic reagent and product were recorded scanning the photon energy from the ionization energy of the reagent molecule to approximately 14–15 eV at different fixed pressures and CE (0, 0.5, or 1.0 eV).
The photoionization efficiency curves (PIECs) to determine the appearance energy (AE) of the fragment ions in the photo fragmentation studies are obtained by reporting the yield of the fragment versus photon energy and scanning the undulator/monochromator in order to have the maximum flux at a given energy. The PIECs were normalized to the photon intensity, which is measured simultaneously by a photodiode located at the end of the beamline. The photon energy is also calibrated against the autoionization features observed in the Ar total photoionization efficiency spectra between the 3p spin orbit components. The contribution of the second order radiation is evaluated by comparing the Ar+ ion yield measured as a function of the photon energy to its ionization cross section [15]. A lithium fluoride (LiF) filter was used to remove the higher order radiation contribution when the energy was below 11.7 eV.
2.2. Computational Methodology
In the studies of ion–molecule reactions presented in this review, theoretical calculations have been carried out by combining the density functional theory formalism (DFT) [16] with variational transition state theory (VTST) [17]. DFT was used to explore the minimum energy path (MEP) of the reactions, while VTST, specifically suited for barrierless reactions, has been used to search for the “bottleneck” of the reaction, namely the variational transition state (VTS) configuration at which the reaction slows down, to compute the reaction-rate coefficients.
In the theoretical photofragmentation studies of halomethanes presented in Section 4, all calculations were performed at the MP2 level using 6-311++G** basis set for C and H atoms. For the iodine atom small-core (28 electrons), scalar-relativistic effective potential (ECP-28) in conjunction with the aug-cc-pVTZ-PP basis set have been chosen [18,19]. CCSD(T) [20] has been employed to obtain accurate total energies and both MP2 and CCSD(T) were used within the frozen-core approximation by using the 4s4p4d frozen-core orbitals for the I atom. Time-dependent density functional theory (TD-DFT) [21] with the Tamm–Dancoff approximation has been also used. More details can be found in the original papers.
The charge and spin population are based on the Mulliken analysis, and it has been computed to study, in a qualitative way, the electron rearrangement occurring during the reactions. The reaction region of the potential energy surface (PES) is studied by full optimizations during the scanning of the chosen coordinates, which generally are the formed and broken bonds in the reaction.
The evaluation of the rate constant is based on the calculation of the molecular partition functions of both reagents in their minimum-energy geometries and of the complex variational transition-state geometry, which is defined as the phase-space point where the molecular partition function of the complex itself has a minimum value. The canonical rate constant is Equation (1):
The minimization of the molecular partition function of the complex along the relevant MEPs is carried out at each temperature. The vibrational partition function is computed by using the vibrational frequencies from normal mode analysis within the harmonic approximation. The σ term in Equation (1) is a symmetry factor that considers the different equivalent, indistinguishable ways in which the reaction can occur. However, when the VTS geometry of the complex is in the region of the products and, hence, the reaction is fast and efficient, the rate constant is obtained by using capture theory based on variational transition state theory/classical trajectory study of thermal energy ion–polar molecule collisions: Equation (2) [22]
where kL is the Langevin rate coefficient, and α and μD are the polarizability and the dipole moment of the neutral, respectively. The VTST approach is generally used when the reaction follows a statistic energy redistribution (local equilibrium) [23,24] but it could fail when a high-frequency vibration does not couple efficiently to others in the reaction complex and when reagents are not in thermal equilibrium with the surrounding and within the complex. In these cases, nonthermal rate coefficients must be calculated by modeling the system with the introduction of effective temperature and by correlating the temperature with the internal energy of the ion generated by synchrotron radiation, as in the case of the reaction of SO2•+ with H2 molecules (see Section 3.2) and in a recent published work where the reaction of CO2•+ with H2 has been studied [25].
The theoretical modeling of the competitive fragmentation of excited ions has been based on the calculation of the microcanonical rate coefficient:
where, N≠(E − E0) is the sum of the vibrational states from 0 to E − E0 in the TS, which is localized on the top of the barrier or by variational minimization of N≠ along the coordinate of reaction for barrierless processes, σ is the reaction symmetry factor, ρ(E)ion is the density of vibrational states of parent ion, Qrotion and Qrot≠ are rotational partition functions of parent ion and transition state respectively. The microcanonical rate coefficients have been computed under the assumptions that the translational and rotational modes were not coupled with the vibrational modes, and that their energy distribution follows the Boltzmann law, so that Qrot could be used.
3. Atom/Ion Transfer Reactions
3.1. SO2-CH4/H2O
Sulfur dioxide is one of the main sulfur-containing molecules present on Earth, interstellar space, molecular clouds, and in the extraterrestrial atmospheres [26]. It is the main constituent of the atmosphere of Jupiter’s satellite, Io. As neutral (SO2) and cationic radical species, SO2•+ (where • is sometime omitted for the sake of clarity) reacts with compounds R–H via a proton transfer (PT) reaction from R–H0/+ to SO2 and/or hydrogen atom transfer (HAT) from R–H to SO2•+, both leading to the same ionic HSO2+ compound (Figure 2). Ions H3O+ (m/z = 19) are also detected in the case of water due to the consecutive reaction of HSO2+ with another H2O molecule.

Figure 2.
Mass spectra (m/z in amu) recorded at the photon energy of 14.0 eV, nominal CE = 0 eV, and P H2O/CH4 = 1.0 × 10−5 mbar for the reactions of SO2•+ with (a) CH4, and (b) H2O. Reproduced with permission from [26]; Copyright (2017) John Wiley & Sons.
In the specific case of the reaction of SO2•+ with CH4 and H2O, the two stable molecules are activated by two different mechanisms: HAT in the first case and PT in the second case.
The reactivity of O–H and C–H bonds with comparable bond dissociation energy BDE 497.1 and 439.3 kJ/mol, respectively, depends on the dynamical processes occurring along the reaction paths on the potential energy surfaces of the ionic ground state explored by theoretical calculations (Figure 3, left panel).

Figure 3.
Left Panel: optimized energy geometries of the reactants and products and the minimum energy path (MEP) along the reactive coordinate of the reactions between SO2•+ and: (a) methane and (b) water. The red rhombus and the green circle represent the VTS (T = 298 K) and the minimum structure (MIN), respectively. Right panel: partial charge and spin distribution at the B3LYP/6–31++G** level of the theory for the relevant species H (black), CH3 (cyan), OH (green), and SO2 (red) involved in both the reactions of SO2•+ with methane (c,d) and water (e,f) as a function of the reaction coordinate H–CH3 and H–OH, respectively. Reproduced with permission from [26]; Copyright (2017) John Wiley & Sons.
The MEPs show that the reactions are barrierless. Moreover, by exploring the charge and spin evolution along the reaction path (Figure 3, right panel) it is possible to assert that in the case of water, a rapid proton-coupled electron transfer (PCET) mechanism is operative while a slower HAT occurs with methane. Indeed, in the reaction of SO2•+ with H2O, the doublet spin and the charge belong to an intact water molecule before the H+ proton transfer from H2O•+ to SO2 occurs (Figure 3, right panel (e) and (f)).
Moreover, the variational transition state theory allows us to obtain the canonical rate constants of the two reactions whose trend with temperature was compared with the experimental results obtained with tunable synchrotron radiation by plotting the ratio of the yields of both HSO2+ and SO2•+ as a function of photon energy (Figure 4). This joint experimental and theoretical study provides new kinetic and mechanistic insights on the reactivity of the sulfur dioxide ions relevant for astro chemistry as well as for the chemistry of activation and the functionalization of simple model molecules.

Figure 4.
(Left panel) HSO2+/SO2•+ ratio versus photon energy in the reaction of SO2•+ with water (blue) and methane (red), at the fixed pressure of 1.0 × 10−5 mbar and nominal CE = 0 eV. (Right panel) calculated rate constants vs. temperature (in K and eV) for the hydrogen transfer reactions of SO2•+ with water (blue line) and methane (red line). Reproduced with permission from [26]; Copyright (2017) John Wiley & Sons.
3.2. SO2/H2
The radical cation SO2•+ that can be formed by ionizing radiation in the upper atmosphere, could produce species that should be taken into account in the models when this molecule is present [27]. Moreover, the non-thermal effects should be also considered, especially when SO2•+, excited in ro-vibrational levels of the ionic ground state after photon excitation with synchrotron radiation, reacts with a rigid molecule such as H2:
SO2•+ + H2 → HSO2+ + H•
In the stratosphere, atomic hydrogen is produced by the reaction of O(1D) (formed by the sunlight photodissociation of ozone) and H2, and H• reacts with ozone with a rate coefficient of 2.89 × 10−11 cm3∙molecule−1∙s−1, leading to molecular oxygen and a hydroxyl radical:
H• + O3 → O2 + OH•
The reaction of SO2•+ with molecular hydrogen leads always to H•, also when sunlight is absent, and, hence, reaction (4) can be considered a nighttime alternative pathway to the sunlight formation of OH• as well as the reaction of SO2•+ with H2O (see Section 3.1).
The dynamics of reaction (4), explored by DFT and VTST, gives a thermal VTS rate k calculated at 300 K of 2.9 × 10−11 cm3∙molecule−1∙s−1, close to that obtained experimentally by Anicich [28]. The calculation for the reaction with D2 gives a rate coefficient of 1.20 × 10−11 cm3∙molecule−1∙s−1, with an isotopic effect of 2.42 at 300 K. The thermal computed k for reaction with H2 is shown in Figure 5 and it increases monotonically with the temperature (blue dashed line).
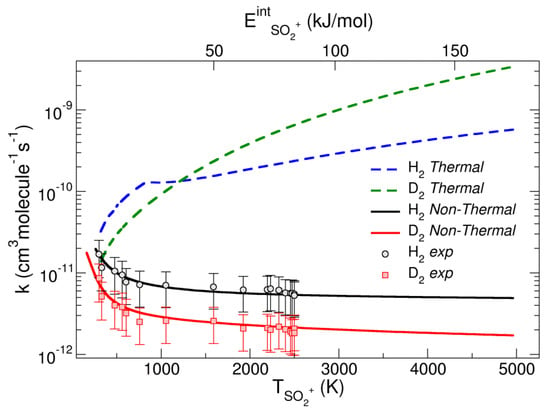
Figure 5.
k for the reactions of SO2•+ with D2 and H2 computed with the non-thermal model and with thermal equilibrium conditions. Reproduced with permission from [27]. Copyright (2020) John Wiley & Sons.
A similar behavior is observed for the D2 reaction (green dashed line in Figure 5). The temperature of the excited ion (TSO2•+) is shown on the bottom axis of abscissas, while the internal energy of the ion (ESO2•+) is reported in the top axis of abscissas. A decrease in the experimental rate coefficients (black and red circles) is observed with the increase in TSO2•+, a behavior not in agreement with canonical thermal rates (green and blue lines of Figure 5). Hence, a new model to compute the rate coefficients has been formulated, taking into account the conditions of the experiments. The Q (T = 300 K) of H2 has been separated in two factors: a translational factor that depends on the room temperature QtrVTS (300 K), and a ro-vibrational part Qro-vibVTS (Teff) depending on an effective temperature Teff. This latter depends on the internal temperature of SO2•+ (TSO2•+) and takes into account that during the reaction there is a transfer of the ro-vibrational energy towards the H–H coordinate. All these assumptions allow us to write the non-thermal rate coefficient kNT as:
The plot of the non-thermal rate coefficient vs. T (black line of Figure 5) shows the very different behavior with respect to the thermal rate coefficient for H2 (blue line). The non-thermal rate is in agreement with the experimental rates (black circles in Figure 5) where there is a decrease with T, whereas the thermal rate showed an opposite thermal trend. Similar data are obtained for the reaction with D2. The work highlights the importance of non-thermal effects in the redistribution of the internal energy of the encounter complex generated in synchrotron experiments.
3.3. SO2/CO
In chemistry, an important topic is the oxidation of CO into CO2, together with the oxidation of simple species such as alcohols or methane [29,30]. The small dipole moment of CO (μD = 0.112 D), in which there is a partial negative charge on the carbon atom, together with its polarizability (1.953 Å3) and bond length (1.13 Å) [31], characterize this molecule, which is one of the most common environmental pollutants due to human activities.
The oxidation can be seen as an oxygen transfer to the carbon monoxide molecule, hence all the species, either neutral or ionic, which favor the O-transfer, should be considered since the formation enthalpy of CO2 (ΔHf = −94.05 kcal mol−1) is lower than of CO (ΔHf = −26.42 kcal mol−1). O2 is the most important and used oxidant at high temperatures and with catalysts, but other species could be considered for the transformation of CO into CO2, also at room temperature and without catalysts. Hence, the development of a green-friendly, more efficient and metal-free oxidation of carbon monoxide is required, and the study of the dynamical aspects of these processes is of great interest [32].
Besides the evident environmental aspects inherent to the study of the carbon monoxide oxidation, these types of reactions are relevant also for reaction studies in the chemistry of interstellar medium, of Earth’s atmosphere, and also of extra-terrestrial atmospheres. The reactivity in the troposphere is particularly interesting, where CO, SO2, H2O, NOx, CO2, and O3 are present in a fraction of ppm (whose actual values depend on the geographical position and environmental conditions) [33], and which can be either neutral or ionized because of corona-discharged events [34]. In the reaction of SO2•+ with H2O and CH4, the H+ and H transfer from neutral to ions is observed. However, SO2•+ can be also a source of oxygen atoms in reactions with other molecules, especially when the oxidized form is more stable, as is in the case of the carbon monoxide (reaction 7). These processes can be discussed in terms of quite similar values of the formation enthalpy of SO2•+ and SO•+: 213.0 and 239.2 kcal mol−1, respectively [35].
SO2•+ + CO → SO•+ + CO2
At T = 300 K, this reaction is known to have a rate coefficient [36] of 3.00 × 10−10 ± 20% cm3 s−1 molecule−1 but no other experimental or computational studies were available at that time. This reaction is exothermic [35] by 41.4 kcal mol−1 and its dynamics have been studied with the help of theoretical tools: DFT, VTST, and capture theory [37]. This allowed us to determine the minimum energy path (MEP) of the reaction and to compute the reaction coefficient vs. T. The charge and spin of the reactive complex [SO2–CO]•+ have been analyzed along the path of the reaction to obtain kinetic details of the oxidation process. By using kcoll the collision rate [38] and the experimental rate constant k, the reaction efficiency (ϕ = k/kcoll) has been obtained. SO2•+ is produced in its vibrational excited levels of the ionic ground state by using tunable VUV radiation. Theoretical calculations and experimental data have been compared by analyzing the role of the photon energy on the reaction. This study provided relevant kinetic details on this reaction, and this can be important in future possible applications of removal of anthropogenic CO from the lower atmosphere of the Earth. In environmental studies, this is an interesting research area because the CO reacts slowly with the O2, and the reaction with OH, even if it seems the main tropospheric path to carbon monoxide removal, is not the only active mechanism [39]. In this work, the SO•+ (at m/z = 48) cation has been observed as the only product of the reaction, and, hence, the CO2 is the neutral other product. At different fixed pressures of CO, the ion yields of SO•+ and SO2•+ vs. the photon energy have been recorded, and in Figure 6 the relative data are reported. These findings indicate that the reaction is favored when the internal energy of the SO2•+ is decreased, and this is in agreement with the presence of a weakly bound complex that leads to a very fast reaction. A full theoretical analysis has been conducted to explore the kinetic aspects of this apparently simple reaction: the MEP has a barrier that connects two different minima, which correspond to a first reactive complex [SO2–CO]•+ 1, and a second complex [OS–OCO]•+ 2, which is more stable and resembles the products (Figure 7). The above energy barrier is below the reagents’ energy so that the reaction is overall barrierless. The labels of the O are shown in Figure 7: the Oa is the oxygen bound to the sulfur atom and it is not active, the Ob is the oxygen atom transferred to the carbon atom from the sulfur atom, the Oc is the third atom that is not active, and it is bound to the C atom.
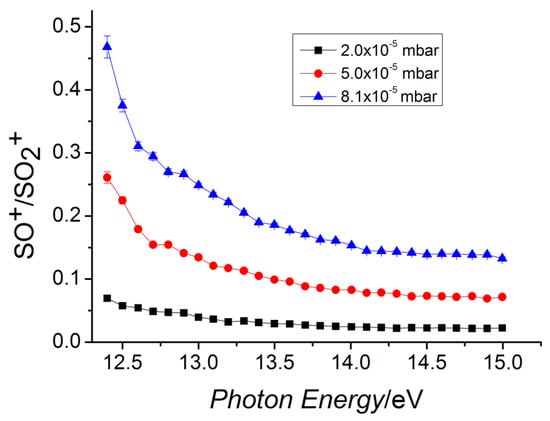
Figure 6.
Ratio of the SO•+/SO2•+ as a function of the photon energy in the reaction of SO2•+ with carbon monoxide. The nominal collision energy is 0 eV. Different pressures of carbon monoxide: 8.1 × 10−5 mbar (blue line), 5.0 × 10−5 mbar (red line), and 2.0 × 10−5 mbar (black line). Reprinted with permission from [29]. Copyright (2019), Frontiers.
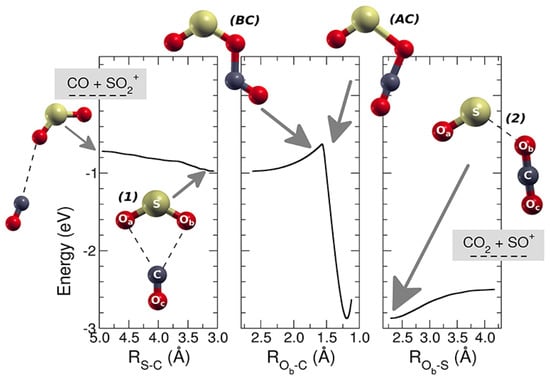
Figure 7.
MEP for the reaction SO2•+ with carbon monoxide leading to SO•+ and carbon dioxide. On the left there is the approaching region where the reactants are shown (leftmost structure), together with the geometry of the first complex [SO2–CO]•+ (1). In the central panel, it is shown the barrier (intersystem crossing) and the geometry of the molecular complex just before (BC) and after the crossing (AC). On the right, the region of the products is shown together with the geometry of the most stable complex (2) [OS–OCO]•+. Reprinted with permission from [29]. Copyright (2019), Frontiers.
The rate coefficient k at different temperatures has been calculated with the capture theory. The value of 2.95 × 10−10 cm3 s−1 molecule−1 is obtained at 300 K in very good agreement with the literature experimental value of 3.00 × 10−10 cm3 s−1 molecule−1 ± 20% and the reaction efficiency (ϕ = k/kcoll) results to be 1.
3.4. CH3OH+-CH3OH
The chemistry occurring in different gas-phase environments, such as interstellar medium or the atmosphere of planets has a relevant interest for what concerns reactive dynamics. In particular, the outer space can be considered as a chemical laboratory in which complex chemical networks are at play, and which involves the synthesis and degradation of several classes of molecules [40,41].
One of the organic molecules that is most abundant as astrochemical species is methanol, whose first observation dates back to 1970. Its radical cation [CH3OH]•+ has a high probability of formation, but up to now it has not been observed, probably because of its high reactivity. This cation can have a fundamental role in the formation of more complex organic molecules in the interstellar medium [42]. The most stable isomer of [CH3OH]•+ is the distonic •CH2O(H)H+ methyleneoxonium radical cation, and it is lower in energy of approximately 29.3–46.0 kJmol−1 with respect to [CH3OH]•+ [43]. In any case, this isomerization is forbidden because the activation barrier [44] for this process is 104.6 kJ mol−1, and, hence, the [1,2] H-shift is strongly improbable even if the very low temperatures of the interstellar medium can activate the hydrogen tunneling [45]. The most abundant and low-energy fragments are CH2OH+ and H, which appear at 11.649 ± 0.003 eV [46], only approximately 1 eV over the ionization energy of methanol, which has been determined at 10.84 ± 0.01 eV [31]. In hydrocarbon synthesis, the methanol cation and its fragment CH2OH+ play a fundamental role in reacting with neutral CH3OH, whose neutral products are CH3O•, CH2O, •CH2OH, and ionic CH3OH2+. These species can be involved in the process of molecular growth, which happens via the coupling with C-C or C-O, in particular temperature and pressure conditions, as observed in extraterrestrial ices where CH3OH is activated and ionized by radiation [47].
The methanol can be a source of H atoms either from the O-H bond (437.6 ± 2.9 kJ mol−1) or from the C-H bond (402.1 ± 0.8 kJ mol−1) [48]. The isotopic species CD3OH has been used to understand the source of hydrogen in reactions involving the methanol cation. The branching ratio (BR) and the rate coefficient of the reaction between methanol with its cation form have been the object of studies in the past years, and in Scheme 1 they are reported. These reactions have been studied with a tunable VUV synchrotron to form methanol radical cations in an energy range between the ionization energy threshold and 14.0 eV and by computational chemistry in order to analyze the (a) and (b) paths of Scheme 1. The main purpose of these studies was to assess the role of the internal energy distribution of the ions on the branching ratio of paths (a) and (b), whereas for path (c) we were interested in analyzing the kinetics in the energy range above the AE (11.739 ± 0.003 eV) [49] of the fragment CD2OH+. The masses at m/z = 36 and 37, corresponding to the ions CD3O(H)H+ and CD3O(H)D+, have been observed, and their intensities have been recorded as a function of photon energy from 10.6 to 11.7 eV (Figure 8a).

Scheme 1.
Reactions of CD3OH with CD3OH•+ and CD2OH+. The experimental rate coefficients (k1 and k2) are expressed in units of 10−9 molecule−1 s−1 cm3. The branching ratios are taken from ref. [50]. Reprinted with permission from [40]. Copyright (2021), Elsevier.

Figure 8.
Intensity of the ion CD3OH•+ and of the product ions CD3O(H)H+ and CD3O(H)D+ (a) and branching ratio (b) vs. hv in the energy range of 10.6–11.7 eV (a) and 10.9–11.7 eV (b), respectively, at p = 3.0 × 10−5 mbar in the reaction cell. Reprinted with permission from [40]. Copyright (2021), Elsevier.
The BR have been determined at the reaction cell pressure of 3.0 × 10−5 mbar, and relative data are shown in Figure 8b.
From experimental data, the formation of CD3O(H)D+ and CD3O(H)H+ ions are observed, whereas the isomerization of CD3O• into a •CD2OD radical should also be considered when the energy gain obtained in the formation of the reactive complex is enough to overcome the barrier that leads to the formation of •CD2OD. The interaction of CH3OH (CD3OH) with CH3OH•+ (CD3OH•+) has been also studied with computational chemistry models, so that a full comprehension of the dynamical aspects of these reactions can be obtained at hν < 11.7 eV [51]. In Figure 9, the geometries and the relative energies of the molecules active in reaction (a) and (b) of the Scheme 1 are reported.
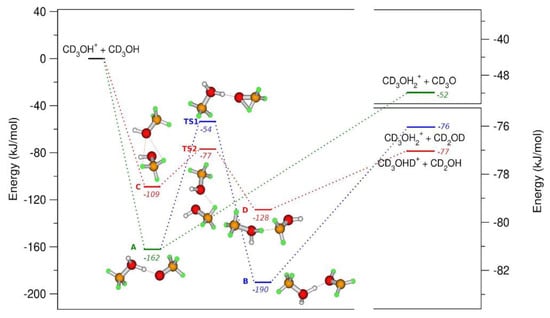
Figure 9.
B2PLYP/6-31++G** calculation of the energies relative to the reagents in kJ/mol with zeropoint correction (left axis). On the right axis it is reported the energies of the products. Different colors identify different reaction paths. The geometry of the molecules follows the color code: white and green for the H and D, and orange and red for carbon and oxygen atoms. Reprinted with permission from [40]. Copyright (2021), Elsevier.
From the experimental point of view, these ion–molecule reactions have been analyzed also at energies higher (hν > 11.7 eV) when the fragment CD2OH+ (m/z = 33) can be formed, and whose appearance energy has been determined at 11.739 ± 0.003 eV [49].
The mass spectrum of CD3OH+, without reaction with neutral methanol, is reported in Figure 10a at hν = 12.5 eV. The loss of the D atom from CD3OH•+ produces the peak at m/z = 33, which is related to the CD2OH+ ion, whereas the very small peak at m/z = 34 can be related to the CD2OD+ due to the scrambling of the hydrogen atom. We have excluded the formation of the CD3O+ species since its appearance energy is determined to be higher than 15.0 eV [49].
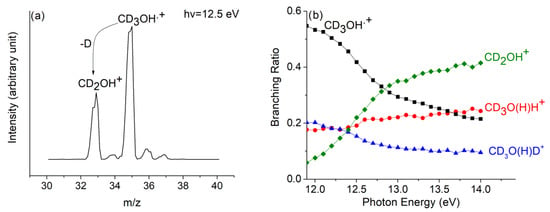
Figure 10.
(a) Mass spectrum of CD3OH at hv = 12.5 eV, in the ion source PCD3OH = 1.7 × 10−5 mbar and in the reaction cell there is no gas; (b) branching ratio of CD2OH+ (green diamond), and CD3OH•+ (black square), as well as of ions, CD3O(H)D+ (blue triangles), and CD3O(H)H+ (red dots), are shown as a function of hv at PCH3OH = 5.1 × 10−5 mbar. Reprinted with permission from [40]. Copyright (2021), Elsevier.
The branching ratio of all the products and reagent ions of the (a–c) reactions of Scheme 1 have been reported in Figure 10b at p = 5.1 × 10−5 mbar, and for hv in the range of 11.9–14.0 eV.
It has to be noted that the relative intensity of CD3O(H)H+ (m/z = 36), with respect to the intensity of CD3O(H)D+ (m/z = 37), has a positive increase with the increase in hv. This is due to the fact that here, the production of CD2OH+ is increased, and it protonates by H+ transfer from the O-H bond as seen in path (c) of Scheme 1. Both protonated methanol and CD2O (CH2O) are formed, which are also possible precursors of prebiotic compounds.
4. Photofragmentations of Halomethanes
Many halomethanes have relevant roles in atmospheric chemistry, for instance, CH2Cl2, which is used as a solvent and a propellant in industry, has an air emission that can modify the budget of ozone due to the production of the Cl radical [52]. On the other hand, CH2F2 (HFC-32, Freon 32) is a greenhouse gas, playing a fundamental role in the terrestrial atmosphere with no depletion potential. It is used as etching gas replacing also chlorofluorcarbons in the refrigerant industry. As regards the presence of iodine and bromine organic compounds, they are predominantly natural, and mostly of oceanic source by macroalgae and phytoplankton [53]. In particular, CH2I2, which is one of the most photolabile iodocarbons emitted in the atmosphere from marine algae [54], is a source of reactive iodine atoms by the photoreaction with VUV light, playing an important role in ozone depletion and in affecting the oxidative ability of the atmosphere. Furthermore, iodine participates to the ultrafine marine aerosol particles affecting the Earth’s radiation budget and, thus, drives climate change [55]. In addition, bromine-containing compounds, coming primarily from oceans and called “very short-lived substances” (VSLSs), bromocarbons, such as CH2Br2 and CHBr3, have been largely studied in the past few years [56]. These compounds are very interesting because together with mainly anthropogenic, long-lived gases such as chlorofluorocarbons (CFC), bromofluorocarbons and methyl bromide are thought to contribute significantly to the production of reactive inorganic bromine (Br, BrO, HOBr, and HBr) after their degradation. Actually, they are rapidly destroyed in the troposphere (atmospheric lifetime shorter than six months) via a reaction with hydroxyl radicals and photolysis. Eventually, these reactive species can enter the stratosphere and participate in the catalytic destruction of molecules.
Up to now, much effort has been devoted to the understanding of the chemical physics of halomethanes in order to manipulate and control their use and to explain their behavior in different processes. In particular, many studies have been devoted to investigating the halomethanes fragmentation leading to different radicals and/or cations, which can play a role in several fields, from atmospheric chemistry to etching- and plasma-assisted industrial processes as well as organic synthesis. Several works have been dedicated to the study of the photodissociation of CH2I2 and CH2Cl2 molecules by proton impact or VUV absorption [57,58,59]. Several studies have been carried out to obtain thermochemical data with different radiation sources [60]. Quite exhaustive is the paper where there is a discussion of the VUV photofragmentation of the series of halomethane compounds where either the halogen atom (dihalomethane, CH2X2 with X = F, Cl, Br, I) or the number of halogen atoms (chloromethane, CHnCCl4-n with n = 0–3) are changed [61].
This work has three main goals: (a) the study in the VUV range of the two competitive channels, X-loss (X = F, Cl, Br, I) and H-loss, observed in the fragmentation of the dihalomethanes even though other channels have also been considered; (b) the study of the effect of the particular halogen atom in the photofragmentation, comparing CH2X2 molecules; and (c) the investigation of the effect of the number of halogen atoms in the photofragmentation, going from chloromethanes containing one (CH3Cl) to four (CCl4) chlorine atoms. The results show that the CH2F2 compound is the only dihalomethane that opens the H-loss channel yielding a CHF2+ ion and H atom. This finding has an implication in atmospheric chemistry since these species can produce HF. The loss of the halogen atom is evident in all the mass spectra of halomethanes. Moreover, the CCl4+ molecular ion is not observed due to the instability of this ion towards the exothermic loss of the chlorine atom. CH2I2 is the only dihalomethane that produces I2+ ions. This fragmentation pathway is generally a high-energy process, which might be relevant in the upper atmosphere. In Figure 11, the photoionization curves for the I2+, CH2+, and I+ species are presented.
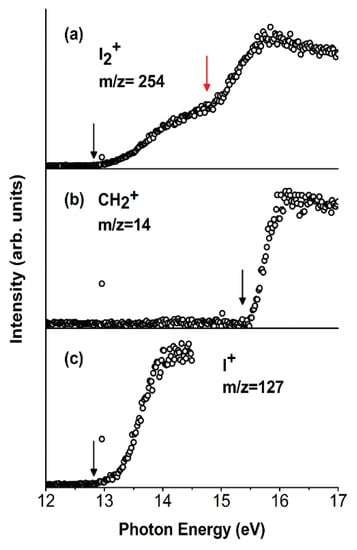
Figure 11.
Photoionization efficiency curves (PIECs) of the three fragment ions I2+ (a), CH2+ (b), and I+ (c) from the [CH2I2]+ parent ion. The AEexp values are indicated by black arrows. The red arrow in (a) indicates a clear change of slope in the I2+ PIEC at the photon energy around 14.90 ± 0.05 eV. Reprinted with permission from [62]. Copyright (2015), AIP Publishing.
The results show that the appearance energy of I2+ (AEexp) is 12.76 ± 0.03 eV. Moreover, the PEPICO measurements (Figure 12) demonstrate that the I2+ loss involves electronic states with B.E. >12.0 eV as well as the channel that produces CH2+ (AEexp = 15.34 ± 0.05 eV). In the latter case, theoretical calculations demonstrate that the formation of CH2+ ions produce two iodine atoms and not the I2 molecule. As clearly seen in Figure 12, the parent ion (m/z = 268) is present until BE~11 eV [62].
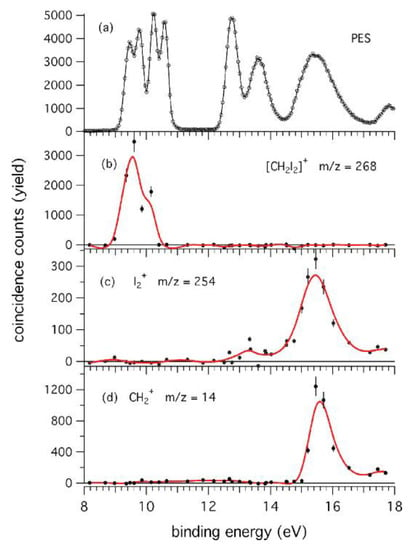
Figure 12.
The top panel (a), reports the PES of CH2I2 recorded at hν = 39 eV in the experimental conditions used in the PEPICO experiments. For several binding energies, the ion yield for the parent ion CH2I2+ (b) and fragment ions I2+ (c) and CH2+ (d) are illustrated. The red lines represent a spline representation of the data to guide the eye. Reprinted with permission from [62]. Copyright (2015), AIP Publishing.
In Figure 13, the PEPICO spectra acquired in the BE region between 9 and 11 eV are shown to investigate the fragment ions generated from the lower ionic states. At the BE = 9.7 eV (Figure 13a), only the peak at m/z = 268 due to the molecular ion [CH2I2]•+ is observed, while at the BE = 10.9 eV (Figure 13b) the fragment ion at m/z = 141 (CH2I+) is also observed. This result clearly demonstrates that at an energy lower than 11 eV, the only pathway accessible by the electronic states of [CH2I2]•+ is the I-loss channel, whereas the other fragments observed in the mass spectrum at hν = 40 eV are formed from higher excited states of [CH2I2]•+.
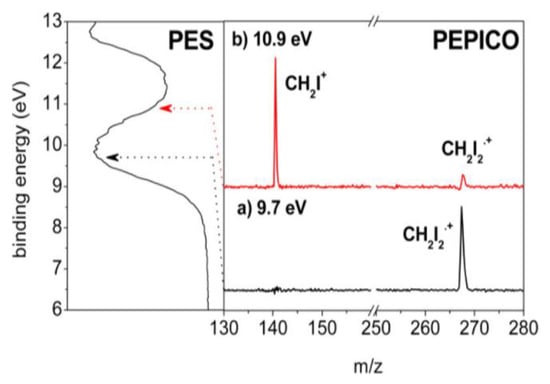
Figure 13.
PEPICO measurements at the BE of 9.7 (a) and 10.9 eV (b) of the PES spectrum (panel on the left). Reprinted with permission from [63]. Copyright (2015), American Chemical Society.
A computational study has been carried out to investigate the mechanism of the I-loss channel from [CH2I2]•+ [63]. In Figure 14, the optimized geometries of the minima (1, 2, and 3) found on the [CH2I2]•+ potential energy surface, the transition states TS1 and TS2 connecting 1–2 and 2–3, respectively, and the optimized structure of the CH2I+ fragment, are reported.
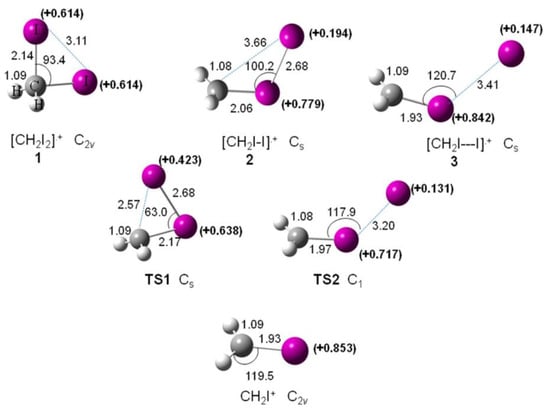
Figure 14.
Optimized geometries (distances in Å and angles in degree) calculated at the MP2 level and the NBO atomic charge, e (in bold) on the iodine atoms of the species involved in the I-loss channel from [CH2I2]•+. Reprinted with permission from [63]. Copyright (2015), American Chemical Society.
The results show that the isomerization of geminal [CH2I2]•+ into iso-diiodomethane is a relevant process in the CH2I2 radical cation as well as in the CH2I2 molecule and it can have a role in the photochemical reactions. Moreover, this isomerization is not a key process for molecular I2-loss at the lower electronic states of the cation. Recently, the transient [CH2-I-I]+ isomeric ion 2 in the dissociation of the [CH2I2]•+ molecular has been proven experimentally with the XUV FEL at Hamburg [64].
5. Perspectives
5.1. Planning Experiments at the FEL Facilities
The development of new radiation sources has undergone a notable increase in the last ten years starting from attosecond high-harmonic radiation source [65] to phase-stabilized few-cycle optical laser pulses [66], femtosecond electron beams [67], and lastly free-electron lasers (FELs) [68,69,70].
Unlike the conventional femtochemistry, which uses IR and UV laser pulses to trigger and interrogate molecular processes, FELs extend the pump–probe scheme into the regime of XUV and X-ray radiation.
By combining ultra-short pulse durations and never-before-seen pulse intensities, FELs offer the possibility to study completely new and largely unexplored very basic and fundamental molecular behavior.
The experiments at the FEL facilities aim to study the peculiarities of electronic dynamics, known to be active on attosecond time scales, and the formation/breaking of bonds that occur in the femtosecond regime. Particular attention is paid to the study of the electronic and nuclear motion in photoexcited molecules, the redistribution of the energy stored by the molecule as a result of photo-absorption, and the nuclear dynamics of chemical reactions involving highly excited states in cold molecular ions, in order to mimic the XUV photochemistry of higher planetary atmospheres and interstellar clouds [71].
For these purposes, FELs combine the key features of optical lasers, such as a short pulse duration at a high intensity, with those of synchrotron radiation sources delivering XUV and X-ray radiation.
The first laser operating in the XUV regime was FLASH in Hamburg in 2005 [72] followed by LCLS in Stanford in 2009 [73], which reached for the first time the hard X-ray range. To date, two other facilities are operating in the XUV regime, which are FERMI [74] in Italy and SCSS [75] in Japan, while SACLA [76] in Japan falls within the hard X-ray FELs. In the very near future, more FEL facilities will become online such as EUPRAXIA in Italy, where the ultrashort X-ray pulses, made available by the plasma accelerator-driven FEL, will open up to new possibilities of measuring ultrafast processes in nature that can be analyzed at the electronic level without perturbation.
In this section, the recent achievements in the field of molecular dynamics and gas-phase chemistry and possible future prospects in the field of gas phase ion–molecules reaction with FELs will be presented.
5.1.1. Ultrafast Reaction Dynamics
The main questions that generally arise in the ultrafast photodynamics of molecular systems concern the time scale and the mechanism of the reaction, how many steps it implies, whether it is possible to “photograph” some intermediate species, and whether it is possible to manipulate and control the system by varying some instrumental and temporal parameters.
The ability to observe the temporal evolution of a chemical reaction has often been called “molecular film making”, implying the need to capture consecutive images of bond breaking and formation with a temporal resolution ranging from femtoseconds to picoseconds and possibly electronic and/or geometric structural resolution for all species involved. With the new FEL sources, this possibility is gradually becoming a reality, although it must be emphasized that until recently, many FELs showed a jitter in photon energy generally too large to provide sufficiently resolved spectra without an accurate post-processing of the data and an average over different time delays, while HHG (high-harmonic generation) laser sources lose resolution due to the simultaneous presence of several harmonics. In the latter case, even with the application of suitable filters that generate single pulses, the resulting intensity is very low, and this limits the plethora of possible experiments to be performed and requiring a high density of molecules.
Unfortunately, there is still no suitable FEL source with a negligible photonic energy jitter and very short pulses (down to the attosecond) whose construction is mandatory if you want to reach another planned goal, i.e., the study of the electronic motion preceding bond breaking/formation on its “natural” timescale.
Attosecond laser technology has already proven to trace the electronic dynamics in small atoms and molecules, while for large molecules such as those involved in biological processes (photosynthesis, radiation damage, etc.) [77,78,79,80,81,82], the study is still in its infancy. Usually, attosecond pump–probe spectroscopy is used to study electron dynamics with a temporal resolution of a few femtoseconds and sub-femtoseconds [83,84,85,86]. It consists in the use of an extreme attosecond generally ultraviolet (XUV) pulse to excite/ionize the target molecule, followed by a delayed probe pulse ranging from the near infrared (NIR) to the X-ray domain capable of tracing the dynamics generated by the first pulse. In this way, the target molecule is ionized by an attosecond pulse, creating a delocalized electron hole that moves across the molecule on a time scale of sub-femtoseconds. The evolution of the hole depends on the interaction between electronic and nuclear motions, which can lead to a final localization of the charge on a specific molecular site or on a specific molecular fragment. So, depending on the initially created hole, fragmentation will occur leading to different chemical species, hence to a distinct reactivity. Full controllability would allow attosecond chemistry to synthesize any stoichiometrically allowed molecular structure or even a macroscopic object from a bunch of atoms in the ultimate realization of a molecular 3D printer [87]. The experimental approach generally used to trace charge migration is based on measuring the yield of photofragmentation as a function of the probe delay with respect to the pump. Reliable theoretical tools are required for the interpretation of attosecond spectroscopy experiments, but unfortunately, currently, a full dimensional quantum mechanical treatment of molecular ionization dynamics, which considers all electronic and nuclear degrees of freedom, is still difficult to obtain. One of the most tempting challenges of attosecond science is to induce ultra-fast electronic dynamics in molecules in order to selectively break and form chemical bonds, thus leading to new chemical reactions. In an ambitious vision, this approach could be applied to study and eventually control the chemical ion–molecule dynamics that occur in high atmosphere by inducing chemical reactions to counteract environmental pollution. The near-future technological frontier in attosecond science is the attosecond pump–attosecond probe measurement of electron motion that would allow us to specifically address and temporally resolve time-dependent processes in complex systems on the electronic time scale [88].
5.1.2. Study the Intermediate State of a Reaction: A Challenge Still Open
In the XUV/hard X-ray regime active in FELs, the dominant mechanism in the molecule radiation interaction is the absorption of photons with subsequent emission of photoelectrons. This process generates a molecular ion that remains in an energetically and vibrationally excited state, which can relax through different reaction pathways, sometimes passing through intermediate stages. The study of the lifetimes of reaction intermediates is still in its infancy. For this purpose, dedicated spectroscopic methods are needed that are able to isolate or label the population of the intermediate states, to follow their evolution as a function of time and to determine their essential characteristics. One way to do this is by leveraging pump–probe technology. The intermediate electronic state is populated by the ionization of a molecule through the pump pulse launching a nuclear wave packet due to the coherent population of several vibrational levels. During its motion along the internuclear axis, a second time-delayed probe pulse may further ionize the system promoting the molecule onto a repulsive Coulomb curve. As a result, the molecule may break up into two ions. In these conditions the Coulomb explosion imaging [89] can reconstruct the molecular geometry and the internuclear distances by analyzing the kinetic energies and emission directions of the repelling ionic constituents. Moreover, the momenta of electrons and the remaining ion can be measured in coincidence by Reaction Microscope/COLTRIMS [90]. In COLTRIMS experiments the emission directions of the ionic fragments coincide with the spatial orientation of molecular bonds at the instant of photoabsorption. One of the main challenges is to extend the acquisition of coincident electrons and ions to the time domain, which seems to be possible thanks to the advent of higher repetition rate lasers and FEL, but some technical challenges still persist. Up to now, only a few true ion-electron coincidence imaging experiments performed at a FEL have been reported [91]. Nevertheless, COLTRIMS coincidence experiments provide the most detailed and complete account of photon driven dynamics in the gas phase. They are the eyes that scan the many-body quantum world, providing images of otherwise invisible details.
5.1.3. Time-Resolved Ion-Molecule Reactions in Gas Phase
Looking at the recent experiments performed at FEL regarding molecular physics and photochemistry, we can report examples of photon-induced fragmentation dynamics of cold molecular ions with relevance of the XUV photochemistry in atmospheric clouds [92], time resolved measurements of van der Waals-bonded molecules called interatomic Coulombic decay (ICD) [93,94,95], real-time observations of electron migration and charge transfer in small dissociating molecules [96,97], temporal tracing of the isomerization dynamics in acetylene cations [98], and X-ray diffractive imaging of spatially aligned small- and medium-sized molecules in the gas phase [99]. The chemistry of upper planetary atmospheres and interstellar clouds is dominated by the dynamics of small and medium-sized molecular ions, and some of them are presumed to play a crucial role in the emergence of life. We found few examples of time-resolved bimolecular reactions such as Scherer et al. [100], who studied the collision dynamics between HI and CO2 and Hu et al. [101], who studied the energy-rich intermediate collision complex K2Rb2* in the reaction KRb + KRb → K2Rb2* → K2 + Rb2. In the first example, Scherer et al. used the first pulse to liberate the H atom from HI with a known translational energy and a second pulse to probe the nascent OH products. The experiments established that the intermediate HOCO lives for a time of 1 ps, and for this reason, the OH bond making and the CO bond breaking happen in a non-concerted pathway. If the lifetime was found to be 10–100 fs, the picture would have been entirely different; bond making and breaking would occur as a result of the electron redistribution with the nuclei essentially “frozen” in configuration. This consideration is important, because it means that depending on the time duration of the pulse available, one can investigate different phenomena and distinguish in this context, reactions that occur in a concerted and non-concerted pathway.
In Hu et al. [101], they tuned the wavelength of the laser well below the lowest dissociative ionization channel of the intermediate complex K2Rb2* and recorded the mass spectrum where a visible K2Rb2+ signal was evident. It is important to note that in this case, the dynamics of the intermediate complex after photoionization is not followed. A possible step forward in this direction would be using the pump–probe approach.
In all gas phase experimental studies that have been addressed in Section 3, only information about the mass/charge ratio of the products and reactants involved in the reaction were obtained, but nothing about their reaction dynamics as well as the reactive intermediate. Hence, in our opinion, a step forward in this direction would be necessary. Gas phase studies have two main goals with respect to the condensed phase: (i) the investigation of the intrinsic nature of isolated species free from the effect of solvent and intermolecular forces, and (ii) models for processes occurring in planets’ atmospheres and the interstellar medium relevant in astrochemistry and becoming a benchmark for the development of new computational/theoretical models capable of explaining such reactions. The limit of the present studies could be overcome through an interdisciplinary approach by homemade instrumentations and advanced technologies that allow a more accurate and complete analysis of the processes. The fabrication of a versatile ion source that can interface with the FEL beamline to perform pump–probe experiments would be the case (Figure 15). The instrumentation should be able to accommodate several ion sources from electron impact ionization to an electrospray ionization source depending on the nature of the species to ionize. Then, the ion of interest should be selected with a mass filter, accumulated in an ion trap, and then analyzed with an intense ultrafast pump–probe spectroscopy better if interfaced with a reaction microscope/COLTRIMS.
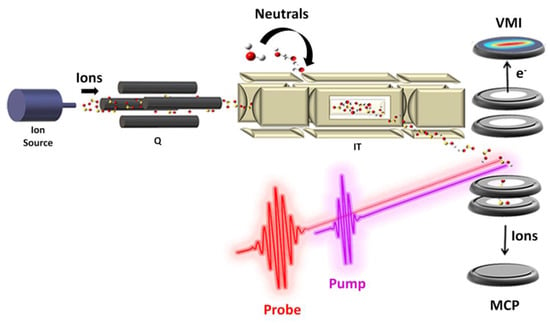
Figure 15.
Sketch of a hypothetical instrumentation for pump–probe analysis of ion–molecule reaction. The apparatus could consist of: (i) ion source (e.g., electron impact, electrospray ionization (ESI), VUV radiation etc.) coupled to a: (ii) quadrupole mass filter (Q) to select the ion of interest; (iii) a temperature controlled ion trap (IT) where the ions can be accumulated and eventually allowed to react with a neutral and subsequently analyzed with: (iv) an intense ultrafast pump–probe laser field interfaced with an ions/electrons coincidence spectroscope.
Three different scenarios of possible studies open up: (i) studying the dynamic of the parent ion I1+ produced in the ion source (path (a) in Figure 16); (ii) inserting the neutral molecule into the ion trap and studying the dynamic of the product ion I2+ formed by the ion–molecule interaction (path (b) in Figure 16), and most important of all; (iii) applying the ultra-low temperature regime at the trap in order to greatly extend the lifetime of the reaction–intermediate complex [I1N1]+ that can be selected and studied by pump–probe spectroscopy (path (c) in Figure 16).
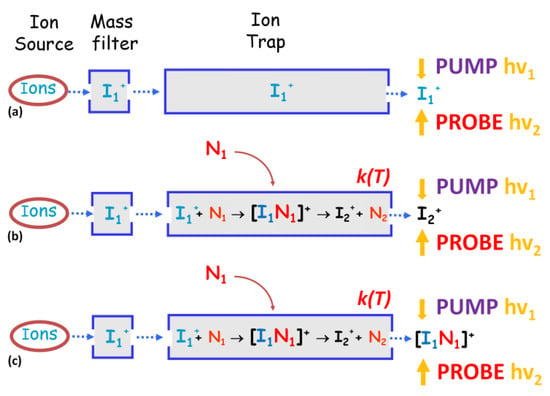
Figure 16.
Possible experiments: paths (a), (b) and (c) to be performed with a hypothetical instrumentation shown in Figure 15. For more details see the manuscript.
To follow the kinetics of the process inside the ion trap, it should be better to use a trap with a temperature control, to obtain the rate coefficients as a function of the temperature for the improvements of the theoretical models and the study of the ionic product dynamics and the energetics.
Obviously, the choice of the ion source, the pump–probe pulses, and the spectroscopy will depend on the species under investigations. This review aims to stress about the fundamental role of ions. Molecular ions were decisive in the cooling of the early universe, are ubiquitous in aqueous solutions, play an important role in the chemistry of upper planetary atmospheres, in interstellar space, and they seem to have been crucial for the beginning of life. The photochemistry of ions is not easy to study in the laboratories since it requires high-intensity VUV and X-ray sources and most of the time the ion density is too low, but with the improvement of technologies we can improve our knowledge. The goal would be to obtain relaxation lifetimes for ionic reagents, products, and intermediate states with high accuracy in order to gain reliable chemical networks for more realistic complex modelling. In this way, we could improve our predictive capability.
5.2. Improvement in Modeling the Ion–Molecule Reactions
A fundamental aspect, still poorly studied, is the role of cosmic rays (CRs) in increasing the reaction rate and modifying the type of chemical reactions by producing ions. Indeed, the reaction rate between an ion and a molecule can be up to 10 orders of magnitude higher than that with only neutrals. Moreover, the spatial distribution of the ions is extremely inhomogeneous, since it increases in particular in the neighbourhood of the passage area of the ionising radiation. Ions are leading actors in several atmospheric processes such as ion-induced nucleation, precipitation, and aerosol formation. However, the connection of CRs with ions and the climate parameters is a challenging topic. The amount and state of ionisation, as well as the spatial distribution of ions in the atmosphere, is one of the open questions for the atmosphere models that are fundamental to investigate also in the very low-energy range. To compute cosmic rays-induced ionisation (CRII), models of the new generation consider the atmospheric cascade initiated by cosmic rays to its full extent using a Monte Carlo numerical simulation by means of a toolkit such as FLUKA [102], CORSIKA [103], and Geant4 [104,105,106]. Over the years, several numerical models were created and validated via a comparison with direct observations and measurements of the cosmic rays-induced ionization, e.g., the Sofia model [107,108], the Bern model, also called ATMOCOSMIC/PLANETOCOSMIC [109], and the Oulu model, also called CRAC:CRII [110]. All these numerical CRII models allow us to simulate the 3D time-dependent ionisation rate in the atmosphere, down to the lower stratosphere (below∼20 km), providing a reliable tool to study ionisation effects due to cosmic rays. The ion pair production rates (ions·cm−3·s−1) are the fundamental information to be considered in the atmospheric chemistry models, and they are calculated by taking into account the mean energy required to produce an ion–electron couple. Recently, a newly developed GEANT4-based code, atmospheric radiation interaction simulator AtRIS [111], has been developed, tailored specifically to enable parametric studies of radiation propagation through various planetary atmospheres.
However, the average approach used by current models cannot provide the exact interaction of low-energy secondary radiation with molecules, nor the exact concentration of the ions produced, their spatial distribution, and ionization state. Together with the ions produced in the initial ionisation, the low-energy secondary particles produce a large number of ions and excited atoms and molecules. In addition, the distribution of reactive chemical species, although present in very small amounts, cannot be underestimated as they trigger fast reactions that can alter the balance of important molecules and have a key role in fundamental reactions.
To precisely estimate these quantities, it is necessary to simulate particle–molecule interactions, following a step-by-step tracking down to very low energies. Interaction models that enable these simulations require interaction probabilities over a broad energy range and for all possible energetically allowed scattering processes.
Our work to find such models for each molecule relevant to climatology has just begun, and in the following we focus on electron impact interactions with N2 and O2 molecules, being the most abundant atmospheric chemical species. For these two molecules, we reviewed the state-of-the-art models needed to describe the interactions relevant to our purpose, namely ionization, elastic scattering, and electronic excitation cross sections.
In the next sections, we present some reliable theoretical models for differential (DCS) and integral (ICS) cross sections in the low-energy range up to few MeV, looking for a good compromise between accuracy and computational time. Models that provide an analytical expression for the cross section as a function of energy will be preferred, as they are ideally suited for future modeling applications and Monte Carlo simulations.
5.2.1. Ionisation
Many standard theoretical methods for ionisation cross sections work well at high-incident energies, but few are reliable at low-incident energies, particularly near the ionization threshold. Furthermore, theories requiring continuum wave functions are difficult to compute for molecules especially polyatomic ones. To date, major sources of ionization cross sections for molecules come from experimental data and theories, often semiempirical, that worked well only on limited types of targets and limited ranges of incident energies [112].
To treat electron impact ionisation for the case object of this review, we selected the binary encounter Bethe (BEB) model developed by Kim and Rudd [113]. It combines a modified form of the Mott cross section [114,115] with the high-energy behavior of the Bethe cross section [113,116,117]. The BEB model has been successfully used to calculate electron impact differential and total ionisation cross sections for a large number of atmospheric molecules [118,119,120,121,122]. The agreement with experimental data is excellent for small size molecules in the energy range from the ionization threshold up to hundreds of electron volts [123].
An extension of the BEB model to relativistic incident electrons (few MeV) is the relativistic BEB (RBEB) model, by Kim and Santos [124].
In the BEB and RBEB models, the scattering angle of the primary electron and the ejected angle of the secondary electron are considered to be isotropic. This approximation can be reduced by introducing a sampling of both angles determined by the kinematics of binary collisions [125].
Figure 17 shows the BEB cross sections for N2 and O2 calculated using orbital parameters provided by the NIST database [112] compared with the experimental data of Rapp and Englander-Golden [126], the data of Schram et al. [127,128], the data of Krishnakumar and Srivastava [129], and the more recent experimental data of Straub et al. [130]. As the plots show, the BEB cross sections for both molecules agree very well with the experiments, even near threshold. We expect the behavior at high energies of the RBEB model will be even more accurate than that obtained with the BEB model.

Figure 17.
(Left) the electron impact ionization cross sections for O2 from threshold to 2 keV calculated using the BEB model, compared with the experimental data from ref. [127,128,129]. (Right) same cross sections model but calculated for N2 molecule, compared with the experimental data from ref. [127,128,129,130]. Plots taken from ref. [112].
However, it can be noticed that BEB underestimates the cross section for O2 near the peak compared with the experimental measurement of Rapp and Englander-Golden [126]. In this case, the theoretical binding energy values used for the outer valence orbitals do not agree well with the known experimental values, which can be interpreted as an indication of the need for a better wave function in the calculations.
5.2.2. Elastic Scattering
Elastic scattering, although it does not practically lead to energy loss, strongly influences the accuracy of the spatial distribution of energy deposition. The process is typically calculated with the additivity rule (AR), which is a simple sum of atomic cross sections, or with the single-scattering independent atom model (IAM), which is a coherent sum of atomic scattering amplitudes that takes into account relative atomic positions [131,132]. In the IAM model, the interaction of the projectile with each atom of a molecule is assumed to be given by the spherically complex symmetric potential due to a free atom, which is the sum of the electrostatic, exchange, correlation–polarization potentials, and absorption potential. This approximation prepares the ground for the application of partial-wave analysis of scattering.
Atomic scattering amplitudes can be calculated with the ELSEPA (ELastic Scattering of Electrons and Positrons by neutral Atoms) code, developed by Salvat et al. [133]. This code is based on Dirac partial-wave calculations for elastic scattering of electrons by an atom, with energies ranging from a few eV up to 100 MeV in a variety of materials. Another advantage of ELSEPA is the ability to easily modify the computational parameters and interaction potential models to optimize the results and get better agreement with experimental data. Details on these potentials are available in ref. [133].
It should be noted that the concept of independent scattering centers becomes invalid at relatively low energies (<100 eV) or for large molecules, since this approximation ignores the interactions of the incident electron with more than one atom at a time. Another reason for the low-energy failure of this model is its ignorance of the mutual overlapping of nearby atomic cross-sections, which leads to an overestimation of cross sections calculated with the IAM model. To make up for this lack, Blanco and García [134,135] proposed the screening corrected additivity rule method, derived from a semiclassical analysis of atomic geometrical overlapping. This method has been proved to be a powerful tool for calculating electron scattering cross sections down to about 30 eV for a wide variety of nonpolar molecules [136,137,138]. A more sophisticated model, which falls under the same optical potential formalism as the IAM model, is the modified independent atom model (MIAM). MIAM divides the elastic interaction into a short-range potential that describes multiple electrons scattering by individual atoms, and a long-range potential that can account for non-spherical effects such as polarization. This multicenter process is described within the Born approximation, with higher-order terms representing successive scattering events from different atoms within the molecule and does not make use of empirical correction factors.
For the N2 and O2 molecules under study, several results in the literature are in very good agreement with experimental data using the IAM method down to energies of 50 eV [139,140]. For this reason, and because of its simplicity, we consider it the best option for our application. The IAM approach has also proven to be successful for other polyatomic molecules down to energies of tens of eV [141,142,143]. For energies below 50 eV, the theoretical model can be supplemented with the large amount of experimental data in the literature for these two molecules [144,145,146,147,148].
5.2.3. Electronic Excitation
The electronic excitation process plays an important role in determining the internal energy and state distribution of the gaseous particles in the atmosphere.
The Born approximation is the most commonly used method for the calculation of electron impact excitation cross sections for optically allowed states at high collision energies. However, it does not account for electron exchange, polarization of the target electrons by the free electron, and distortion of the free electron by the target at lower energies, which are described by higher-order terms in the perturbation series. In order to approximately incorporate these effects, Kim extended the BEB method to electronic excitation by developing the new simple BEf-scaling theory described in detail by Kim [149]. This method aims to scale the first-order plane-wave Born cross sections for electron impact excitation of neutral atoms [149] and molecules [150], provided that the scaling is applicable only to integral cross sections for electric dipole-allowed transitions.
The scaling process has the effect of replacing the wave function used to calculate the Born cross section with an accurate one and correcting the well-known deficiency of the Born approximation at low energies, without losing its validity at high energies.
The use of the BEf method requires two initial ingredients: the Born integral cross sections and reliable optical oscillator strengths.
Once these quantities have been obtained theoretically or experimentally, a fairly reasonable cross section can be produced at any incident energy with the BEf-scaling approach. Indeed, the BEf-scaled method has been found to provide good agreement for the cross section in the energy range from threshold to about 10 keV for a large number of molecules, including N2 and O2 [151,152]. Full details on the method can be found in ref. [153].
Finally, it is important to point out that only advanced ab initio electron–molecule collision theories, such as complex Kohn [154], Schwinger multi-channel [155], and the R-matrix [156,157], although computationally demanding, are able to reproduce the existence of resonances, and accurately address the low-energy (<30 eV) scattering problem. All three methods are based on the variation principle, and the results obtained using each method with the same target and scattering models often exhibit good agreement.
The fixed-nuclei approximation R-matrix theory is by far the most widely used method. It is already implemented in the UK molecular R-matrix (UKRMol) codes [158] and executable through the Quantemol-N expert system [159], which uses the MOLPRO quantum chemistry code to provide the target molecular orbitals. This code has proven to be the most versatile tool for calculating both elastic and electronic cross sections from threshold up to about 100 eV in molecules dominated by resonances. Indeed, it has been successfully used to study a large number of molecules, including N2 and O2 [160,161,162,163].
The UKRmol code can be used, in conjunction with experimental data, to compensate for those energies or excited states not included in the previous BEf model.
In conclusion, the ionisation state and spatial distribution of ions produced by cosmic rays can significantly change chemical reaction rates by orders of magnitude. In this section, we reviewed models that could be used to simulate electron interactions with the most abundant species in the atmosphere, i.e., N2 and O2. Using these models, it would be possible to accurately simulate the interaction of electrons produced by primary and secondary cosmic rays in the atmosphere, thus allowing the calculations of the concentration of the ions produced, their spatial distribution, and their ionisation state. We are working on implementing, or interfacing, these models with Geant4-DNA [164,165,166,167], to perform such a simulation. Geant4-DNA is an extension of Geant4, the most widely used toolkit for performing Monte Carlo simulations of radiation–matter interactions. Geant4-DNA makes it possible to explicitly simulate every single electromagnetic particle interaction down to eV, as well as diffusion and chemical reactions, on some specific materials of interest in radiobiology. We are working to extend Geant4-DNA to simulate radiation transport in the atmosphere.
Our ultimate goal will be to obtain the ionisation effect in the Earth’s troposphere and stratosphere based on cosmic ray spectra, and subsequent Monte Carlo simulations of the cosmic ray-induced atmospheric cascade. The interaction of protons, photons, kaons, and muons with matter will be simulated using the Geant4 toolkit, while our cross-section models will be used to simulate the electron impact processes on N2 and O2 in small volumes at different altitudes in the atmosphere.
The development of the physics for each molecule of climatological interest may open the way to a better description of the physicochemical processes used in atmospheric prediction models, but also to new space-related studies regarding chemistry and exobiology.
Author Contributions
Conceptualization, M.S. and A.C.; writing—original draft preparation, M.S., M.C.C., F.N., A.R.C. and A.C.; writing—review and editing, M.S., M.C.C., F.N. and A.C.; review and editing, A.R.C., C.M.T.; supervision, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This review received no external funding.
Acknowledgments
We acknowledge ELETTRA Sincrotrone Trieste for providing access to its synchrotron radiation facilities. Francesca Nicolanti thanks Programma Operativo Nazionale (PON) “Ricerca e Innovazione” 2014-2020 (D.M. 1061/2021) Azione IV.5 “Dottorati su tematiche Green”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Larsson, M.; Geppert, W.D.; Nyman, G. Ion chemistry in space. Rep. Prog. Phys. 2012, 75, 066901. [Google Scholar] [CrossRef] [PubMed]
- Mollah, M.Y.A.; Schennach, R.; Patscheider, J.; Promreuk, S.; Cocke, D.L. Plasma Chemistry as a Tool for Green Chemistry, Environmental Analysis and Waste Management. J. Hazard. Mater. 2000, 79, 301–320. [Google Scholar] [CrossRef]
- Castrovilli, M.C.; Markush, P.; Bolognesi, P.; Rousseau, P.; Maclot, S.; Cartoni, A.; Delaunay, R.; Domaracka, A.; Kočišek, J.; Huber, B.A.; et al. Fragmentation of pure and hydrated clusters of 5Br-uracil by low energy carbon ions: Observation of hydrated fragments. Phys. Chem. Chem. Phys. 2017, 19, 19807–19814. [Google Scholar] [CrossRef] [PubMed]
- Geppert, W.D.; Larsson, M. Experimental Investigations into Astrophysically Relevant Ionic Reactions. Chem. Rev. 2013, 113, 8872–8905. [Google Scholar] [CrossRef]
- de Petris, G.; Cartoni, A.; Troiani, A.; Angelini, G.; Ursini, O. Water activation by SO2+ ions: An effective source of OH radicals. Phys. Chem. Chem. Phys. 2009, 11, 9976. [Google Scholar] [CrossRef]
- Ravishankara, A.R.; Randall, D.A.; Hurrell, J.W. Complex and yet predictable: The message of the 2021 Nobel Prize in Physics. Proc. Natl. Acad. Sci. USA 2022, 119, e2120669119. [Google Scholar] [CrossRef]
- Board, O.S. ; National Research Council. Climate Intervention: Reflecting Sunlight to Cool Earth; National Academies Press: Washington, DC, USA, 2015. [Google Scholar]
- Satta, M.; Casavola, A.R.; Cartoni, A.; Castrovilli, M.C.; Catone, D.; Chiarinelli, J.; Borocci, S.; Avaldi, L.; Bolognesi, P. “Ionization of 2- and 4(5)-Nitroimidazoles Radiosensitizers: A “Kinetic Competition” Between NO2 and NO Losses” Chem. Phys. Chem. 2021, 22, 2387–2391. [Google Scholar] [CrossRef]
- Casavola, A.R.; Cartoni, A.; Castrovilli, M.C.; Borocci, S.; Bolognesi, P.; Chiarinelli, J.; Catone, D.; Avaldi, L. VUV Photofragmentation of Chloroiodomethane: The Iso-CH2I-Cl and Iso-CH2Cl-I Radical Cation Formation. J. Phys. Chem. A 2020, 124, 7491–7499. [Google Scholar] [CrossRef]
- Ball, J.A.; Gottlieb, C.A.; Lilley, A.E.; Radford, H.E. Detection of Methyl Alcohol in Sagittarius. Astrophys. J. 1970, 162, L203. [Google Scholar] [CrossRef]
- Available online: http://astrochymist.org (accessed on 5 May 2022).
- Burkholder, J.B.; Abbatt, J.P.D.; Barnes, I.; Roberts, J.M.; Melamed, M.L.; Ammann, M.; Bertram, A.K.; Cappa, C.D.; Carlton, A.G.; Carpenter, L.J.; et al. The Essential Role for Laboratory Studies in Atmospheric Chemistry. Environ. Sci. Technol. 2017, 51, 2519–2528. [Google Scholar] [CrossRef] [Green Version]
- Derossi, A.; Lama, F.; Piacentini, M.; Prosperi, T.; Zema, N. High flux and High Resolution Beamline for Elliptically Polarized Radiation in the Vacuum Ultraviolet and Soft X-ray Regions. Rev. Sei. Instrum. 1995, 66, 1718–1720. [Google Scholar] [CrossRef]
- Cartoni, A.; Casavola, A.R.; Bolognesi, P.; Castrovilli, M.C.; Catone, D.; Chiarinelli, J.; Richter, R.; Avaldi, L. Insights into 2- and 4(5)-Nitroimidazole Decomposition into Relevant Ions and Molecules Induced by VUV Ionization. J. Phys. Chem. A 2018, 122, 4031–4041. [Google Scholar] [CrossRef] [PubMed]
- Marr, G.V.; West, J.B. Absolute Photoionization Cross-Section Tables for Helium, Neon, Argon, and Krypton in the VUV Spectral Regions. At. Data Nucl. Data Tables 1976, 18, 497–508. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecule; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Bao, J.L.; Truhlar, D.G. Variational Transition State Theory: Theoretical Framework and Recent Developments. Chem. Soc. Rev. 2017, 46, 7548–7596. [Google Scholar] [CrossRef]
- Peterson, K.A.; Shepler, B.C.; Figgen, D.; Stoll, H. On the spectroscopic and thermochemical properties of ClO, BrO, IO, and their anions. J. Phys. Chem. A 2006, 110, 13877. [Google Scholar] [CrossRef]
- Available online: http://www.uni-stuttgart.de/ (accessed on 19 June 2022).
- Raghavachary, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Häser, M.; Treutler, O.; Ahlrichs, R. Calculation of excitation energies within time-dependent density functional theory using auxiliary basis set expansions. Chem. Phys. Lett. 1997, 264, 573. [Google Scholar] [CrossRef]
- Su, T.; Chesnavich, W.J. Parametrization of the ion–polar molecule collision rate constant by trajectory calculations. J. Chem. Phys. 1982, 76, 5183–5185. [Google Scholar] [CrossRef]
- Viggiano, A.A.; Morris, R.A.; Paschkewitz, J.S.; Paulson, J.F. Kinetics of the gas-phase reactions of chloride anion, Cl-with CH3Br and CD3Br: Experimental evidence for nonstatistical behavior? J. Am. Chem. Soc. 1992, 114, 10477–10482. [Google Scholar] [CrossRef]
- Liu, A.J.; Anderson, S.L. Dynamical control of ‘statistical’ ion–molecule reactions. Int. J. Mass Spectrom. 2005, 241, 173–184. [Google Scholar] [CrossRef]
- Satta, M.; Catone, D.; Castrovilli, M.C.; Bolognesi, P.; Avaldi, L.; Zema, N.; Cartoni, A. Ion Chemistry of Carbon Dioxide in Nonthermal Reaction with Molecular Hydrogen. J. Phys. Chem. A 2022, 126, 3463–3471. [Google Scholar] [CrossRef] [PubMed]
- Cartoni, A.; Catone, D.; Bolognesi, P.; Satta, M.; Markus, P.; Avaldi, L. HSO2+ Formation from Ion-Molecule Reactions of SO2⋅+ with Water and Methane: Two Fast Reactions with Reverse Temperature-Dependent Kinetic Trend. Chem. Eur. J. 2017, 23, 6772–6780. [Google Scholar] [CrossRef] [PubMed]
- Satta, M.; Cartoni, A.; Catone, D.; Castrovilli, M.C.; Bolognesi, P.; Zema, N.; Avaldi, L. The Reaction of Sulfur Dioxide Radical Cation with Hydrogen and its Relevance in Solar Geoengineering Models. Chem. Phys. Chem. 2020, 21, 1146–1156. [Google Scholar] [CrossRef]
- Anicich, V.G. An Index of the Literature for Bimolecular Gas Phase Cation-Molecule Reaction Kinetics; JPL Publication 03-19: Pasadena, CA, USA, 2003. [Google Scholar]
- Catone, D.; Satta, M.; Cartoni, A.; Castrovilli, M.C.; Bolognesi, P.; Turchini, S.; Avaldi, L. Gas Phase Oxidation of Carbon Monoxide by Sulfur Dioxide Radical Cation: Reaction Dynamics and Kinetic Trend with the Temperature. Front. Chem. 2019, 7, 140. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, H.; Shaik, S.; Li, J. Electronic effects on room temperature, gas-phase C–H bond activations by cluster oxides and metal carbides: The methane challenge. J. Am. Chem. Soc. 2017, 139, 17201–17212. [Google Scholar] [CrossRef] [PubMed]
- Linstrom, P.J.; Mallard, W.G. NIST Chemistry WebBook, NIST Standard Reference Database. Gaithersburg, MD: National Institute of Standards and Technology, 20899. 2005. Available online: http://webbook.nist.gov (accessed on 19 June 2022).
- Crabtree, R.H. C–H bond activation: A radical non-metal solution. Nat. Chem. 2009, 1, 348–349. [Google Scholar] [CrossRef] [PubMed]
- Speidel, M.; Nau, R.; Arnold, F.; Schlager, H.; Stohl, A. Sulfur dioxide measurements in the lower, middle and upper troposphere: Deployment of an aircraft-based chemical ionization mass spectrometer with permanent in-flight calibration. Atmos. Environ. 2007, 41, 2427–2437. [Google Scholar] [CrossRef] [Green Version]
- Cacace, F.; de Petris, G. Mass spectrometric study of simple main group molecules and ions important in atmospheric processes. Int. J. Mass Spectrom. 2000, 194, 1–10. [Google Scholar] [CrossRef]
- Lias, S.G.; Bartmess, J.E.; Liebman, J.F.; Holmes, J.L.; Levin, R.D.; Mallard, W.G. Gas-Phase Ion and Neutral Thermochemistry. J. Phys. Chem. Ref. Data 1988, 17, 872. [Google Scholar]
- Fehsenfeld, F.C.; Ferguson, E.E. Atmospheric atomic sulfur ion reactions. J. Geophys. Res. 1973, 78, 1699–1701. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C. Variational transition state theory. Annu. Rev. Phys. Chem. 1984, 35, 159–189.1146. [Google Scholar] [CrossRef]
- Bowers, M.T. Gas Phase Ion Chemistry; Accademic Press: New York, NY, USA, 1979; Volume 1. [Google Scholar]
- Carpenter, L.J.; Nightingale, P.D. Chemistry and release of gases from the surface ocean. Chem. Rev. 2015, 115, 4015–4034. [Google Scholar] [CrossRef] [PubMed]
- Catone, D.; Satta, M.; Castrovilli, M.C.; Bolognesi, P.; Avaldi, L.; Cartoni, A. Photoionization of Methanol: A Molecular Source for The Prebiotic Chemistry. Chem. Phys. Lett. 2021, 771, 138467. [Google Scholar] [CrossRef]
- Sandford, A.; Nuevo, M.; Bera, P.P.; Lee, T.J. Prebiotic Astrochemistry and the Formation of Molecules of Astrobiological Interest in Interstellar Clouds and Protostellar Disks. Chem. Rev. 2020, 120, 4616–4659. [Google Scholar] [CrossRef] [PubMed]
- Herbst, E. The Synthesis of Large Interstellar Molecules. Int, Rev. Phys. Chem. 2017, 36, 287–331. [Google Scholar] [CrossRef]
- Bouma, W.J.; Nobes, R.H.; Radom, L. Methylenoxonium Radical Cation CH2OH2 +: A Surprisingly Stable Isomer of the Methanol Radical Cation. J. Am. Chem. Soc. 1982, 104, 2929–2930. [Google Scholar] [CrossRef]
- Ma, N.L.; Smith, B.J.; Pople, J.A.; Radom, L. Rearrangement and Dissociative Reactions of the Methanol Radical Cation (CH3OH.+): A Comparison of Theory and Experiment. J. Am. Chem. Soc. 1991, 113, 7903–7912. [Google Scholar] [CrossRef]
- Wagner, J.P.; Bartlett, M.A.; Allen, W.D.; Duncan, M.A. Tunneling Isomerizations on the Potential Energy Surfaces of Formaldehyde and, Methanol Radical Cations. ACS Earth Space Chem. 2017, 1, 361–367. [Google Scholar] [CrossRef]
- Ruscic, B.; Berkowitz, J. Heat of formation of hydroxymethyl and methanol D0(H CH2OH). J. Phys. Chem. 1993, 97, 11451–11455. [Google Scholar] [CrossRef]
- Olah, G.A.; Mathew, T.; Prakash, G.K.S.; Rasul, G. Chemical Aspects of Astrophysically Observed Extraterrestrial Methanol, Hydrocarbon Derivatives, and Ions. J. Am. Chem. Soc. 2016, 138, 1717–1722. [Google Scholar] [CrossRef]
- Blanksby, S.J.; Ellison, G.B. Dissociation Energies of Organic Molecules. Acc. Chem. Res. 2003, 36, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Borkar, S.; Sztaraya, B.; Bodi, A. Bond Dissociative photoionization mechanism of methanol isotopologues (CH3OH, CD3OH, CH3OD and CD3OD) by iPEPICO: Energetics, statistical and non-statistical kinetics and isotope effects. Phys. Chem. Chem. Phys. 2011, 13, 13009–13020. [Google Scholar] [CrossRef] [PubMed]
- Okada, S.; Matsumoto, A.; Dohmaru, T.; Taniguchi, S.; Hayakawa, T. Ion-molecule reactions in acetaldehyde and methanol. Mass Spectrom. 1972, 20, 311–319. [Google Scholar] [CrossRef]
- Herbst, E. Journal Proceedings of the NASA LAW 2006. In Proceedings of the 2006 NASA Workshop on Laboratory Astrophysics, Las Vegas, NV, USA, 14–16 February 2006. [Google Scholar]
- Rowland, F.S.; Molina, M.J. Chlorofluoromethanes in the environment. Rev. Geophys. 1975, 13, 1–35. [Google Scholar] [CrossRef]
- Mössinger, J.C.; Shallcross, D.E.; Cox, R.A. UV–VIS absorption cross-sections and atmospheric lifetimes of CH2Br2, CH2I2 and CH2BrI. J. Chem. Soc., Faraday Trans. 1998, 94, 1391–1396. [Google Scholar] [CrossRef]
- O’ Dowd, C.D.; Jimenez, J.L.; Bahreini, R.; Flagan, R.C.; Seinfeld, J.H.; Hämeri, K.; Pirjola, L.; Kulmala, M.; Jennings, S.G.; Hoffmann, T. Marine aerosol formation from biogenic iodine emissions. Nature 2002, 417, 632. [Google Scholar] [CrossRef]
- Saiz-Lopez, A.; Plane, J.M.C.; Baker, A.R.; Carpenter, L.J.; von Glasow, R.; Gómez Martín, J.C.; McFiggans, G.; Saunders, R.W. Atmospheric chemistry of iodine. Chem. Rev. 2012, 112, 1773. [Google Scholar] [CrossRef]
- Tegtmeier, S.; Krüger, K.; Quack, B.; Atlas, E.L.; Pisso, I.; Stohl, A.; Yang, X. Emission and transport of bromocarbons: From the West Pacific ocean into the stratosphere. Atmos. Chem. Phys. 2012, 12, 10633. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.H.; Wang, Y.Q.; Ma, J.J.; Wang, L.; He, G.Z. Concerted elimination of CH2I2 and CH2ICl under intense femtosecond laser excitation. Chem. Phys. Lett. 2004, 383, 198. [Google Scholar] [CrossRef]
- Alcantara, K.F.; Wolff, W.; Gomes, A.H.A.; Sigaud, L.; Soriano, S.; Oliveira, V.; Rocha, A.B.; Santos, A.C.F. Fragmentation of the CH2Cl2 molecule by proton impact and VUV photons. J. Phys. B At., Mol. Opt. Phys. 2011, 44, 165205. [Google Scholar] [CrossRef]
- Lago, A.F.; Kercher, J.P.; Bödi, A.; Sztáray, B.; Miller, B.; Wurzelmann, D.; Baer, T. Dissociative Photoionization and Thermochemistry of Dihalomethane Compounds Studied by Threshold Photoelectron Photoion Coincidence Spectroscopy. J. Phys. Chem. A 2005, 109, 1802. [Google Scholar] [CrossRef] [PubMed]
- Harvey, J.; Tuckett, R.P.; Bodi, A. A halomethane thermochemical network from iPEPICO experiments and quantum chemical calculations. J. Phys. Chem. A 2012, 116, 9696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cartoni, A.; Bolognesi, P.; Fainelli, E.; Avaldi, L. Photofragmentation Spectra of Halogenated Methanes in The VUV Photon Energy Range, J. Chem. Phys. 2014, 140, 184307. [Google Scholar] [CrossRef] [PubMed]
- Satta, M.; Bolognesi, P.; Cartoni, A.; Casavola, A.R.; Catone, D.; Markus, P.; Avaldi, L. A joint theoretical an experimental study on diiodomethane: Ions and neutrals in the gas phase J. Chem. Phys. 2015, 143, 244312. [Google Scholar] [CrossRef] [PubMed]
- Cartoni, A.; Casavola, A.R.; Bolognesi, P.; Borocci, S.; Avaldi, L. VUV Photofragmentation of CH2I2: The [CH2I-I].+ Iso-diiodomethane Intermediate in the I-loss Channel from [CH2I2].+. J. Phys. Chem. A. 2015, 119, 3704. [Google Scholar] [CrossRef]
- Rebholz, M.; Thomas, D.; Despré, V.; Aufleger, L.; Hartmann, M.; Meyer, K.; Stooß, V.; Magunia, A.; Wachs, D.; Birk, P.; et al. All-XUV Pump-Probe Transient Absorption Spectroscopy of the Structural Molecular Dynamics of Di-iodomethane. Phys. Rev. X 2021, 11, 031001. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef] [Green Version]
- Gallmann, L.; Cirelli, C.; Keller, U. Attosecond dynamics. Ann. Rev. Phys. Chem. 2012, 63, 447–469. [Google Scholar] [CrossRef] [Green Version]
- Miller, R.J.D. Femtosecond crystallography with ultrabright electrons and X-rays: Capturing chemistry in action. Science 2014, 343, 1108–1116. [Google Scholar] [CrossRef]
- Fang, L.; Osipov, T.; Murphy, B.F.; Rudenko, A.; Rolles, D.; Petrovic, V.S.; Bostedt, C.; Bozek, J.D.; Bucksbaum, P.H.; Berrah, N. Probing ultrafast electronic and molecular dynamics with free-electron lasers. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 124006. [Google Scholar] [CrossRef] [Green Version]
- Barty, A.; Küpper, J.; Chapman, H.N. Molecular imaging using X-ray free-electron lasers. Annu. Rev. Phys. Chem. 2013, 64, 415–435. [Google Scholar] [CrossRef] [PubMed]
- Feldhaus, J.; Krikunova, M.; Meyer, M.; Möller, T.; Moshammer, R.; Rudenko, A.; Tschentscher, T.; Ullrich, J. AMO science at the FLASH and European XFEL free-electron laser facilities. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 164002. [Google Scholar] [CrossRef]
- Wolf, A.; Pedersen, H.B.; Lammich, L.; Jordon-Thaden, B.; Altevogt, S.; Domesle, C.; Hergenhahn, U.; Förstel, M.; Heber, O. Soft-x-ray fragmentation studies of molecular ions. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 194007. [Google Scholar] [CrossRef]
- Feldhaus, J. FLASH—the first soft x-ray free electron laser (FEL) user facility. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 194002. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an angstrom-wavelength free electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Yabashi, M.; Tanaka, H.; Tanaka, T.; Tomizawa, H.; Togashi, T.; Nagasono, M.; Ishikawa, T.; Harries, J.R.; Hikosaka, Y.; Hishikawa, A.; et al. Compact XFEL and AMO sciences: SACLA and SCSS. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 164001. [Google Scholar] [CrossRef]
- Grguraš, I.; Maier, A.R.; Behrens, C.; Mazza, T.; Kelly, T.J.; Radcliffe, P.; Düsterer, S.; Kazansky, A.K.; Kabachnik, N.M.; Tschentscher, T.; et al. Ultrafast X-ray pulse characterization at free-electron lasers. Nat. Photonics 2012, 6, 852–857. [Google Scholar] [CrossRef]
- Bolognesi, P.; Castrovilli, M.C.; O’Keeffe, P.; Casavola, A.R.; Catone, D.; Turchini, S.; Avaldi, L. Photofragmentation of organic molecules of biological interest: The pyrimidine and 2Br-pyrimidine cases. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2012, 279, 118–123. [Google Scholar] [CrossRef]
- Bolognesi, P.; Carravetta, V.; Sementa, L.; Barcaro, G.; Monti, S.; Mishra, P.M.; Cartoni, A.; Castrovilli, M.C.; Chiarinelli, J.; Tosic, S.; et al. Core shell investigation of 2-nitroimidazole. Front. Chem. 2019, 7, 151. [Google Scholar]
- Castrovilli, M.C.; Bolognesi, P.; Casavola, A.; Cartoni, A.; Catone, D.; O’Keeffe, P.; Avaldi, L. Insights into 2-Chloropyrimidine fragmentation through a thermochemical analysis of the ionic fragments. Eur. Phys. J. D 2014, 68, 253. [Google Scholar] [CrossRef]
- Chiarinelli, J.; Casavola, A.R.; Castrovilli, M.C.; Bolognesi, P.; Cartoni, A.; Wang, F.; Richter, R.; Catone, D.; Tosic, S.; Bratislav, P.; et al. Radiation Damage Mechanisms of Chemotherapeutically Active Nitroimidazole Derived Compounds. Front. Chem. 2019, 7, 329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zettergren, H.; Domaracka, A.; Schlathölter, T.; Bolognesi, P.; Diaz-Tendero, S.; Labuda, M.; Tosic, S.; Maclot, S.; Johnsson, P.; Steber, A.; et al. Roadmap on dynamics of molecules and clusters in the gas phase. Eur. Phys. J. D 2021, 75, 152. [Google Scholar] [CrossRef]
- Chiarinelli, J.; Bolognesi, P.; Domaracka, A.; Rousseau, P.; Castrovilli, M.C.; Richter, R.; Chatterjee, S.; Wang, F.; Avaldi, L. Insights into the dissociative ionization of glycine by PEPICO experiments. Phys. Chem. Chem. Phys 2018, 20, 22841–22848. [Google Scholar] [CrossRef] [PubMed]
- Månsson, E.P.; De Camillis, S.; Castrovilli, M.C.; Galli, M.; Nisoli, M.; Calegari, F.; Greenwood, J.B. Ultrafast dynamics in the DNA building blocks thymidine and thymine initiated by ionizing radiation. Phys.Chem.Chem.Phys. 2017, 19, 19815. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Seiffert, L.; Trabattoni, A.; Castrovilli, M.C.; Galli, M.; Rupp, P.; Frassetto, F.; Poletto, L.; Nisoli, M.; Rühl, E.; et al. Attosecond streaking metrology with isolated nanotargets. J. Opt. 2018, 20, 024002. [Google Scholar] [CrossRef] [Green Version]
- Castrovilli, M.C.; Trabattoni, A.; Bolognesi, P.; O’Keeffe, P.; Avaldi, L.; Nisoli, M.; Calegari, F.; Cireasa, R. Ultrafast Hydrogen Migration in Photoionized Glycine. J. Phys. Chem. Lett. 2018, 9, 6012–6016. [Google Scholar] [CrossRef] [Green Version]
- Månsson, E.P.; Latini, S.; Covito, F.; Wanie, V.; Galli, M.; Perfetto, E.; Stefanucci, G.; Hübener, H.; De Giovannini, U.; Castrovilli, M.C.; et al. Real-time observation of a correlation-driven sub 3 fs charge migration in ionised adenine. Commun. Chem. 2021, 4, 73. [Google Scholar] [CrossRef]
- Ueda, K.; Sokell, E.; Schippers, S.; Aumayr, F.; Sadeghpour, H.; Burgdörfer, J.; Lemell, C.; Tong, X.-M.; Pfeifer, T.; Calegari, F.; et al. Roadmap on photonic, electronic and atomic collision physics: I. Light–matter interaction. J. Phys. B: At. Mol. Opt. Phys. 2019, 52, 171001. [Google Scholar] [CrossRef]
- Leone, S.R.; McCurdy, C.W.; Burgdörfer, J.; Cederbaum, L.S.; Chang, Z.; Dudovich, N.; Feist, J.; Greene, C.H.; Ivanov, M.; Kienberger, R.; et al. What will it take to observe processes in ‘real time’? Nat. Photon. 2014, 8, 162. [Google Scholar] [CrossRef]
- Vager, Z.; Naaman, R.; Kanter, E.P. Coulomb explosion imaging of small molecules. Science 1989, 244, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Ullrich, J.; Moshammer, R.; Dorn, A.; Dörner, R.; Schmidt, L.P.H.; Schmidt-Böcking, H. Recoil-ion and electron momentum spectroscopy: Reaction-microscopes. Rep. Prog. Phys. 2003, 66, 1463–1545. [Google Scholar] [CrossRef]
- Kurka, M.; Rudenko, A.; Foucar, L.; Kuhnel, K.U.; Jiang, Y.H.; Ergler, T.; Havermeier, T.; Smolarski, M.; Schossler, S.; Cole, K.; et al. Two-photon double ionization of Ne by free-electron laser radiation: A kinematically complete experiment. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 141002. [Google Scholar] [CrossRef]
- Domesle, C.; Dziarzhytski, S.; Guerassimova, N.; Harbo, L.S.; Heber, O.; Lammich, L.; Jordon-Thaden, B.; Treusch, R.; Wolf, A.; Pedersen, H.B. Photoionization and fragmentation of H3O+ under XUV irradiation. Phys. Rev. A 2013, 88, 043405. [Google Scholar] [CrossRef] [Green Version]
- Takanashi, T.; Golubev, N.V.; Callegari, C.; Fukuzawa, H.; Motomura, K.; Iablonskyi, D.; Kumagai, Y.; Mondal, S.; Tachibana, T.; Nagaya, K.; et al. Time-resolved measurement of interatomic Coulombic decay induced by two-photon double excitation of Ne2. Phys. Rev. Lett. 2017, 118, 033202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iablonskyi, D.; Nagaya, K.; Fukuzawa, H.; Motomura, K.; Kumagai, Y.; Mondal, S.; Tachibana, T.; Takanashi, T.; Nishiyama, T.; Matsunami, K.; et al. Slow Interatomic Coulombic Decay of Multiply Excited Ne Clusters. Phys. Rev. Lett. 2016, 117, 276806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnorr, K.; Senftleben, A.; Kurka, M.; Rudenko, A.; Foucar, L.; Schmid, G.; Broska, A.; Pfeifer, T.; Meyer, K.; Anielski, D.; et al. Time-resolved measurement of interatomic coulombic decay in Ne2. Phys. Rev. Lett. 2013, 111, 093402. [Google Scholar] [CrossRef] [Green Version]
- Schnorr, K.; Senftleben, A.; Kurka, M.; Rudenko, A.; Schmid, G.; Pfeifer, T.; Meyer, K.; Kübel, M.; Kling, M.F.; Jiang, Y.H.; et al. Electron rearrangement dynamics in dissociating I2n+ molecules accessed by extreme ultraviolet pump-probe experiments. Phys. Rev. Lett. 2014, 113, 073001. [Google Scholar] [CrossRef] [Green Version]
- Erk, B.; Boll, R.; Trippel, S.; Anielski, D.; Foucar, L.; Rudek, B.; Epp, S.W.; Coffee, R.; Carron, S.; Schorb, S.; et al. Imaging charge transfer in iodomethane upon x-ray photoabsorption. Science 2014, 345, 288–291. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Rudenko, A.; Herrwerth, O.; Foucar, L.; Kurka, M.; Kühnel, K.U.; Lezius, M.; Kling, M.F.; van Tilborg, J.; Belkacem, A.; et al. Ultrafast extreme ultraviolet induced isomerization of acetylene cations. Phys. Rev. Lett. 2010, 105, 263002. [Google Scholar] [CrossRef]
- Küpper, J.; Stern, S.; Holmegaard, L.; Filsinger, F.; Rouzée, A.; Rudenko, A.; Johnsson, P.; Martin, A.V.; Adolph, M.; Aquila, A.; et al. X-ray diffraction from isolated and strongly aligned gas-phase molecules with a free-electron laser. Phys. Rev. Lett. 2014, 112, 083002. [Google Scholar] [CrossRef] [Green Version]
- Scherer, N.F.; Khundkar, L.R.; Bernstein, R.B.; Zewail, A.H. Real-time picosecond clocking of the collision complex in a bimolecular reaction: The birth of OH from H+CO2. J. Chem. Phys. 1987, 87, 1451. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.G.; Liu, Y.; Grimes, D.D.; Lin, Y.W.; Gheorghe, A.H.; Vexiau, R.; Bouloufa-Maafa, N.; Dulieu, O.; Rosenband, T.; Ni, K.K. Direct observation of bimolecular reactions of ultracold KRb molecules. Science 2019, 366, 1111–1115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferrari, A.; Sala, P.R.; Fasso, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code (Program Version 2005); CERN: Geneva, Switzerland, 2005. [Google Scholar]
- Engel, R.; Heck, D.; Huege, T.; Pierog, T.; Reininghaus, M.; Riehn, F.; Ulrich, R.; Unger, M.; Veberič, D. Towards A Next Generation of CORSIKA: A Framework for the Simulation of Particle Cascades in Astroparticle Physics. Comput. Softw. Big Sci. 2019, 3, 2. [Google Scholar] [CrossRef] [Green Version]
- Agostinelli, S.; Allison, J.; Allison, J.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4 -a simulation toolkit. Nucl. Instrum. Methods Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef] [Green Version]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef] [Green Version]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Velinov, P.; Buchvarova, M.; Mateev, L.; Ruder, H. Determination of electron production rates caused by cosmic ray particles in ionospheres of terrestrial planets. Adv. Space Res. 2001, 27, 1901–1908. [Google Scholar] [CrossRef]
- Velinov, P.; Mishev, A. Cosmic ray induced ionization in the atmosphere estimated with CORSIKA code simulations, C. R. Acad. Bulg. Sci. 2007, 60, 493–500. [Google Scholar]
- Desorgher, L.; Fluckiger, E.O.; Gurtner, M.; Moser, M.R.; Butikofer, R. Atmocosmics: A GEANT 4 code for computing the intercation of cosmic rays with the Earth’s atmopshere. Int. J. Mod. Phys. A 2005, 20, 6802–6804. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Kovaltsov, G.A. Cosmic ray induced ionization in the atmosphere: Full modeling and practical applications. J. Geophys. Res. 2006, 111, D21206. [Google Scholar] [CrossRef] [Green Version]
- Banjac, S.; Heber, B.; Herbst, K.; Berger, L.; Burmeister, S. On-the-Fly Calculation of Absorbed and Equivalent Atmospheric Radiation Dose in A Water Phantom with the Atmospheric Radiation Interaction Simulator (AtRIS). J. Geophys. Res. Space Phys. 2019, 124, 9774–9790. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-K.; Irikura, K.K.; Rudd, M.E.; Ali, M.A.; Stone, P.M.; Chang, J.; Coursey, J.S.; Dragoset, R.A.; Kishore, A.R.; Olsen, K.J.; et al. Electron-Impact Ionization Cross Section for Ionization and Excitation Database (Version 3.0). Available online: http://physics.nist.gov/ionxsec (accessed on 14 June 2022).
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. 1994, A50, 3954–3967. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mott, N.F. The collision between two electrons Proc. R. Soc. London. 1930, A126, 259–267. [Google Scholar]
- Vriens, L.; Mac-Daniel, E.W. Case Studies in Atomic Collision Physics; Mac-Daniel, E.W., McDowell, M.R.C., Eds.; North Holland Publishing Co.: Amsterdam, The Netherlands, 1974; Volume 1, p. 335. [Google Scholar]
- Bethe, H. Zur theorie des durchgangs schneller korpuskularstrahlen durch materie Ann. Phys. 1930, 397, 325–400. [Google Scholar]
- Kim, Y.K.; Irikura, K.K. Electron-impact ionization cross sections for polyatomic molecules, radicals, and ions AIP. Conf. Proc. 2000, 543, 220–241. [Google Scholar]
- Hwang, W.; Kim, Y.K.; Rudd, M.E. New model for electron-impact ionization cross sections of molecules. J. Chem. Phys. 1996, 104, 2956–2966. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.K.; Irikura, K.K.; Rudd, M.E.; Ali, M.A.; Stone, P.M.; Chang, J.; Coursey, J.S.; Dragoset, R.A.; Kishore, A.R.; Olsen, K.J.; et al. Electron-impact cross Sections for Ionization and Excitation Database NIST Physical Measurement Laboratory. 1997. Available online: https://www.nist.gov/pml/electron-impact-cross-sections-ionization-and-excitation-database (accessed on 19 May 2022).
- Kim, Y.K.; Hwang, W. Electron-impact ionization cross sections of atmospheric molecules J. Chem. Phys. 1997, 106, 1026–1033. [Google Scholar] [CrossRef] [Green Version]
- Bull, J.N.; Harland, P.W.; Vallance, C. Absolute Total Electron Impact Ionization Cross-Sections for Many-Atom Organic and Halocarbon Species. J. Phys. Chem. 2012, A116, 767–777. [Google Scholar] [CrossRef]
- Bull, J.N.; Lee, J.W.L.; Vallance, C. Absolute electron total ionization cross-sections: Molecular analogues of DNA and RNA nucleobase and sugar constituents. Phys. Chem. Chem. Phys. 2014, 16, 10743. [Google Scholar] [CrossRef]
- Bordage, M.C.; Bordes, J.; Edel, S.; Terrissol, M.; Franceries, X.; Bardies, M.; Lampe, N.; Incerti, S. Implementation of new physics models for low energy electrons in liquid water in Geant4-DNA. Physica Med. 2016, 32, 1833–1840. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Santos, J.; Parente, F. Extension of the Binary-Encounter-Dipole Model to Relativistic Incident Electrons. Phys. Rev. 2000, A62, 052710. [Google Scholar] [CrossRef] [Green Version]
- Edel, S. Modelisation du Transport des Photons et de s’Electrons Dans l’ADN Plasmide. PhD Thesis, Universite Toulouse III-Paul Sabatier, Toulouse, France, 2006. [Google Scholar]
- Rapp, D.; Englander Golden, P. Total Cross Sections for Ionization and Attachment in Gases by Electron Impact. I. Positive Ionization. J. Chem. Phys. 1965, 43, 1464. [Google Scholar] [CrossRef]
- Schram, B.I.; De Heer, F.J.; Van Der Wiel, M.J.; Kistemaker, J. Ionization cross sections for electrons (0.6-20 keV) in noble and diatomic gases. Physica 1965, 31, 94–112. [Google Scholar] [CrossRef]
- Schram, B.I.; Moustafa, H.R.; Schutten, J.; De Heer, F.J. Ionization cross sections for electrons (100-600eV) in noble and diatomic gases. Physica 1966, 32, 734–740. [Google Scholar] [CrossRef]
- Krishnakumar, E.; Srivastava, S.K. Cross sections for the production of N+2, N++ N2+2 and N2+ by electron impact on N2. J. Phys. B At. Mol. Opt. Phys. 1990, 23, 1893. [Google Scholar] [CrossRef]
- Straub, H.C.; Renault, P.; Lindsay, B.G.; Smith, K.A.; Stebbings, R.F. Absolute partial cross sections for electron-impact ionization of H2, N2, and O2 from threshold to 1000 eV. Phys. Rev. A 1996, 54, 2146–2153. [Google Scholar] [CrossRef]
- Raj, D. A note on the use of the additivity rule for electron-molecule elastic scattering. Phys. Lett. A 1991, 160, 571–574. [Google Scholar] [CrossRef]
- Mott, N.F.; Massey, H.S.W. The Theory of Atomic Collisions; Clarendon Press: Oxford, UK, 1965. [Google Scholar]
- Salvat, F.; Jablonski, A.; Powell, C.J. ELSEPA—Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules. Comput. Phys. Commun. 2005, 165, 157–190. [Google Scholar] [CrossRef]
- Blanco, F.; García, G. A screening-corrected additivity rule for the calculation of electron scattering from macro-molecules. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 145203. [Google Scholar] [CrossRef]
- Blanco, F.; García, G. Screening corrections for calculation of electron scattering differential cross sections from polyatomic molecules. Phys. Lett. A 2004, 330, 230–237. [Google Scholar] [CrossRef]
- Limao-Vieira, P.; Blanco, F.; Oller, J.C.; Munoz, A.; Pèrez, J.M.; Vinodkumar, M.; Garcìa, G.; Mason, N. Electron scattering cross sections for SF6 and SF5CF3 at intermediate and high energies 100–10,000 eV. J. Phys. Rev. A 2005, 71, 032720. [Google Scholar] [CrossRef] [Green Version]
- Limao-Vieira, P.; Horie, M.H.; Kato Hoshino, M.; Blanco, F.; Garcìa, G.; Buckman, S.J.; Tanaka, H. Differential elastic electron scattering cross sections for CCl4 by 1.5–100 eV energy electron impact. J. Chem. Phys. 2011, 135, 234309. [Google Scholar] [CrossRef] [Green Version]
- Kato, H.; Suga, A.; Hoshino, M.; Blanco, F.; Garcìa, G.; Limao-Vieira, P.; Brunger, M.J.; Tanaka, H. Elastic cross sections for electron scattering from GeF4: Predominance of atomic-F in the high-energy collision dynamics. J. Chem. Phys. 2012, 136, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khandker, M.H.; Arony, N.T.; Haque, A.K.F.; Maaza, M.; Billah, M.M.; Uddin, M.A. Scattering of e± from N2 in the energy range 1eV–10keV. Mol. Phys. 2019, 118, 1699183. [Google Scholar] [CrossRef]
- Raj, D.; Kumar, A. Elastic scattering of electrons by molecular oxygen. Phys. Lett. A 2001, 282, 284–287. [Google Scholar] [CrossRef]
- Shyn, T.W.; Sharp, W.E. Angular distribution of electrons elastic scattered from O2: 2.0-200 eV impact energy. Phys. Rev. A 1982, 26, 3. [Google Scholar] [CrossRef]
- Vukalović, J.; Maljković, J.B.; Tökési, K.; Predojević, B.; Marinković, B.P. Elastic Electron Scattering from Methane Molecule in the Energy Range from 50–300 eV. Int. J. Mol. Sci. 2021, 22, 647. [Google Scholar] [CrossRef]
- Billah, M.M.; Billah, M.M.; Khatun, M.M.; Haque, M.M.; Ali, M.Y.; Khandker, M.H.; Haque, A.K.F.; Watabe, H.; Uddin, M.A. A Theoretical Study of Scattering of Electrons and Positrons by CO2 Molecule. Atoms 2022, 10, 31. [Google Scholar] [CrossRef]
- Gote, M.; Ehrhardt, H. Rotational excitation of diatomic molecules at intermediate energy: Absolute differential state-to-state transition cross sections for electron scattering from N2, Cl2, CO and HCl. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 3957. [Google Scholar] [CrossRef]
- Shyn, T.W.; Carignan, G.R. Angular Nstribution of electrons elastically scattered from gases: 1.5-400 eV on N2. II. Phy. Rev. A 1980, 22, 923–929. [Google Scholar] [CrossRef]
- Nickel, J.C.; Mott, C.; Kanik, I.; McCollum, D.C. Absolute elastic differential electron scattering cross sections for carbon monoxide and molecular nitrogen in the intermediate energy region. J. Phys. B At. Mol. and Opt. Phys. 1988, 21, 1867–1877. [Google Scholar] [CrossRef]
- Srivastava, S.K. Absolute elastic differential electron scattering cross sections in the intermediate energy region. J. Chem. Phys. 1976, 64, 1340. [Google Scholar] [CrossRef]
- Jansen, R.H.J.; De Heer, F.J.; Luyken, H.J.; Van Wingerden, B.; Blaauw, H.J. Absolute differential cross sections for elastic scattering of electrons by helium, neon, argon and molecular nitrogen. J. Phys. B: Atom. Mol. Phys. 1976, 9, 185. [Google Scholar] [CrossRef]
- Kim, Y.-K. Scaling of plane-wave Born cross sections for electron-impact excitation of neutral atoms. Phys. Rev. A 2001, 64, 032713. [Google Scholar] [CrossRef]
- Kim, Y.-K. Scaled Born cross sections for excitations of H2 by electron impact. J. Chem. Phys. 2007, 126, 064305. [Google Scholar] [CrossRef]
- Suzuki, D.; Kato, H.; Ohkawa, M.; Anzai, K.; Tanaka, H.; Limão-Vieira, P.; Brunger, M.J.J. Electron excitation of the Schumann–Runge continuum, longest band, and second band electronic states in O2. Chem. Phys. 2011, 134, 064311. [Google Scholar] [CrossRef]
- Tanaka, H.; Brunger, M.J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A.R.P. Scaled plane-wave Born cross sections for atoms and molecules. Rev. Mod. Phys. 2016, 88, 025004. [Google Scholar] [CrossRef]
- Bartschat, K.; Tennyson, J.; Zatsarinny, O. Quantum-Mechanical Calculations of Cross Sections for Electron Collisions with Atoms and Molecules. Plasma Processes. Polym. 2016, 14, 1600093. [Google Scholar] [CrossRef] [Green Version]
- Isaacs, W.A.; McCurdy, C.W.; Rescigno, T.N. Theoretical support for a Ramsauer-Townsend minimum in electron-CF4 scattering. Phys. Rev. A 1998, 58, 309. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V.; Sun, Q. Low-energy elastic electron scattering by tetrafluoromethane (CF4). J. Chem. Phys. 1993, 98, 1105–1109. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J. Electron–molecule collision calculations using the -matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Burke, P.G.; Noble, C.J.; Scott, P. R-matrix theory of electron scattering at intermediate energies. A. Math. Phys. Sci. 1987, 410, 289–310. [Google Scholar]
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. A suite for modeling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2019, 249, 107092. [Google Scholar] [CrossRef] [Green Version]
- Carr, J.M.; Galiatsatos, P.; Gorfinkiel, J.; Harvey, A.; Lysaght, M.; Madden, D.; Masın, Z.; Plummer, M.; Tennyson, J.; Varambhia, H. UKRmol: A low-energy electron- and positron-molecule scattering suite. Eur. Phys. J. D 2012, 66, 58–69. [Google Scholar] [CrossRef]
- Tashiro, M.; Morokuma, K.; Tennyson, J. R-matrix calculation of differential cross sections for low-energy electron collisions with ground-state and electronically excited-state O2 molecules. Phy. Rev. A: At. Mol. Opt. Phys. 2006, 74, 022706. [Google Scholar] [CrossRef] [Green Version]
- Tashiro, M.; Morokuma, K.; Tennyson, J. R-matrix calculation of electron collisions with electronically excited O2 molecules. Phy. Rev. A At. Mol. Opt. Phys. 2006, 73, 052707. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Cheng, X.; Zhang, H.; Tennyson, J. Electron collisions with molecular nitrogen in its ground and electronically excited states using the R-matrix method. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 115203. [Google Scholar] [CrossRef]
- Meltzer, T.; Tennyson, J.; Mašín, Z.; Zammit, M.C.; Scarlett, L.H.; Fursa, D.V.; Bray, I. Benchmark calculations of electron impact electronic excitation of the hydrogen molecule. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 145204. [Google Scholar] [CrossRef] [Green Version]
- Incerti, S.; Kyriakou, I.; Bernal, M.A.; Bordage, M.C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. BrownGeant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739. [Google Scholar] [CrossRef] [Green Version]
- Bernal, M.A.; Bordage, M.C.; Brown, J.M.C.; Davídková, M.; Delage, E.; El Bitar, Z.; Enger, S.A.; Francis, Z.; Guatelli, S.; Ivanchenko, V.N.; et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys. Med. 2015, 31, 861–874. [Google Scholar] [CrossRef] [PubMed]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guatelli, S.; Guèye, P.; Mantero, A.; Mascialino, B.; et al. The Geant4-DNA project. Int. J. Model. Simul. Sci. Comput. 2010, 1, 157–178. [Google Scholar] [CrossRef]
- Incerti, S.; Ivanchenko, A.; Karamitros, M.; Mantero, A.; Moretto, P.; Tran, H.N.; Mascialino, B.; Champion, C.; Ivanchenko, V.N.; Bernal, M.A.; et al. Comparison of Geant4 very low energy cross section models with experimental data in water. Med. Phys. 2010, 37, 4692–4708. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).