Abstract
We discuss optical properties of layered Lithium Nickel oxide (LiNiO), which is an attractive cathode material for realizing cobalt-free lithium-ion batteries, within the first-principles density functional theory (DFT) framework. Exchange correlation effects are treated using the generalized gradient approximation (GGA) and the strongly-constrained-and-appropriately-normed (SCAN) meta-GGA schemes. A Hubbard parameter (U) is used to model Coulomb correlation effects on Ni 3d electrons. The GGA+U is shown to correctly predict an indirect (system wide) band gap of 0.46 eV in LiNiO, while the GGA yields a bandgap of only 0.08 eV. The calculated refractive index and its energy dependence is found to be in good agreement with the corresponding experimental results. Finally, our computed optical energy loss function yields insight into the results of recent RIXS experiments on LiNiO.
1. Introduction
With the current focus on clean energy, demand for more efficient batteries with greater capacity and lighter weight is increasing rapidly. In this connection, lithium-ion batteries (LIBs) are promising due to their higher power and energy densities, even though the LIBs are less cost-effective than the conventional Pb-based batteries [1]. In fact, the LIBs have been the key players for several decades for powering portable electronics and the transportation sector [2,3].
The positive electrodes in LIBs often consist of layered transition-metal (TM) oxides such as LiCoO (LCO), LiNiO (LNO) and LiMnO (LMO) [4]. Compared to other cathode materials, LCO is attractive due to its high energy density and specific capacity [5], and it is still the material of choice for commercial applications. These advantages of LCO, however, come with relatively high manufacturing cost, low thermal stability, and the limited supply of the material. Therefore, interest has been growing in LNO as environmentally more friendly cathode material, which offers higher discharge capacity and lower cost compared to LCO [6]. Ni-rich cathode materials have been shown specific capacity close to 300 mAh/g [7], although LNO suffers stability problems at high potential [8].
In view of its stability concerns, it is important to understand the interplay between the structural, electronic, and optical properties of LNO. For example, LNO in its ground state is a small band gap insulator, whose band gap is driven by the presence of Jahn Teller distortions [9]. Here, we examine the LNO ground state in-depth by using density functional theory (DFT) based first-principles simulations. We compare results obtained with the generalized gradient approximation (GGA) and strongly-constrained-and-appropriately-normed (SCAN) exchange-correlation functionals, along with computations using the DFT+U scheme [9,10], in order to gain a handle on the importance of correlation effects in LNO. Optical properties of LNO are computed, including the dielectric function, refractive index, and the absorption coefficient. Our theoretical predictions are compared with the corresponding experimental results [11]. We also compute the energy loss function, which is related to the resonant inelastic X-ray scattering (RIXS) cross Section [12,13]. RIXS can provide a useful window on redox reactions in LNO cathodes as recently shown by Li et al. [14].
2. Computational Methods
Calculations were performed using the Vienna Ab initio Simulation Package (VASP) [15,16] and the Projector-Augmented-Wave (PAW) method [17]. The GGA computations employed the Perdew, Burke, and Ernzerhof (PBE) scheme [18]. To account for effects of d electron localization on the Ni atoms, GGA+U calculations with U = 4 eV [19,20,21] were also carried out. Some calculations were repeated with the SCAN functional [22] using a reduced value of U = 2 eV. Note that SCAN is generally expected to be more accurate for handling correlation effects than the GGA [23]. To sample the Brillouin zone of the primitive unit cell, a 4 × 10 × 4 Monkhorst-Pack [24] k-point grid was employed. For geometry optimizations, total energies were converged within a tolerance of 1 × 10 eV. Gaussian smearing width was set at 0.05 eV in density of states computations.
The dielectric function was computed by using the method by Gajdoš et al. [25] which is based on the random phase approximation (RPA) without local fields. Dielectric function calculations employed the “LOPTICS =.True” input tag, which mandates a reasonable number of empty conduction band states: to fulfill this requirement, NBANDS was taken to be 150. The PAW pseudopotentials were generated with the following atomic configurations: Li(12), Ni(334), and O(22). The plane-wave basis set used in the calculations was determined by 520 eV kinetic energy cuttoff. Various optical properties can be derived from real () and imaginary () parts of the dielectric function. In particular, the refractive index , the absorption coefficient and the loss function of LNO were calculated using the formulae [26]:
We will see below that the GGA+U scheme yields optical results in good agreement with the corresponding experimental findings [11]. It also respects the F-sum rule [27].
3. Results and Discussions
We now discuss the equilibrium atomic positions, electronic structure, and optical properties of LNO. SCAN-based results are also considered because SCAN is known to yield an improved description of materials. Therefore, it is of interest to understand the extent to which SCAN reduces the need for including a Hubbard correction given by U. Devi et al. [10] have recently reported an analysis of FeN along similar lines.
3.1. Structural Properties
LNO assumes a variety of crystalline structures, including the rhombohedral (Rm), orthorhombic (oP8) and monoclinic (mC8 and P2/c) structures at low temperatures [19]. Previous studies have mostly focused on the rhombohedral (Rm) phase where both GGA+U and SCAN give reasonable results [28,29,30,31]. Our focus, however, is on the monoclinic mC8 structure of LiNiO because it is energetically the most stable phase according to GGA+U calculations [19]. The mC8 crystal structure, which is a distortion of the hexagonal cell, is illustrated in Figure 1. In the interest of brevity, we refer the reader to Figure 7 in the review of Bianchini et al. [8], which gives further details of the monoclinic unit cell. The atomic coordinates are obtained from the Materials Project database [32]. Our equilibrium lattice parameters after full relaxation and the volume per atom are given in Table 1. The X-ray diffraction (XRD) pattern of the mC8 phase is presented in Figure 2. Here, two XRD peaks with the highest spectral intensity have Miller indices of (003) and (104). Their intensity ratio can be used to characterize the electroactivity of the samples investigated. In particular, the samples with the highest integrated intensity ratios of I(003)/I(104) show the highest discharge capacity as shown by Valikangas et al. [33].
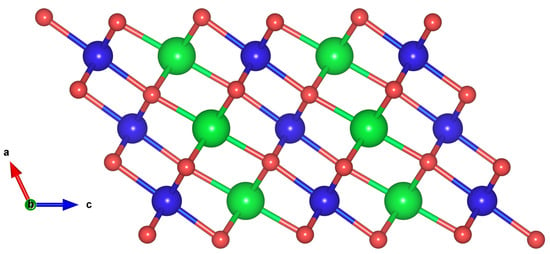
Figure 1.
Crystallographic monoclinic (mC8) structure of LiNiO [ Li (green), Ni (blue), and Oxygen (red)]. The image was obtained from DFT structure relaxation.

Table 1.
Lattice parameters and the volume per atom after full relaxation with GGA, GGA+U with U = 4 eV, SCAN, and SCAN+U with U = 2 eV. Experimental values are given [8].
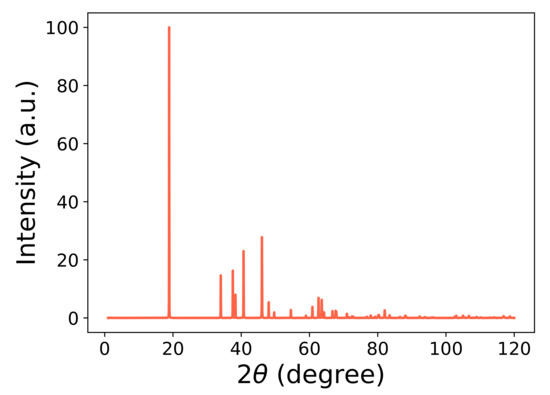
Figure 2.
X-ray diffraction pattern (Cu-K radiation) of the monoclinic (mC8) structure of LiNiO using the VESTA software.
It should be noted that some discrepancies between the theoretical and experimental lattice parameters as well as the angle can be seen in Table 1. However, geometry optimization in LNO remains a challenging task due to the presence of dynamical Jahn-Teller distortions in the system [34]. Among the various approximations considered, the GGA gives the best agreement with the experimental volume per atom.
3.2. Electronic Structures
Figure 3 presents the partial density of states (pDOSs) associated with the Li-s, Ni-d, and O-p states based on GGA (left column) and GGA+U (right column). 2p-O and 3d-Ni states show strong hybridization in all cases in Figure 3. Results for the mC8, op8 and P2/C crystal structures are compared in Figure 3. We focus on the results for the mC8 since this is the lowest energy structure of the LNO. The GGA here predicts too small a bandgap. GGA+U with U of 4 eV, however, cures this problem and yields a (system wide) bandgap of 0.46 eV for the mC8 structure, which is in agreement with the corresponding experimental value of about 0.4 eV [9]. Interestingly, the SCAN+U functional also opens a similar gap, but with a reduced Hubbard U parameter of 2 eV. Since the two approaches give similar results, we will focus on GGA+U which is computationally less demanding than SCAN+U.
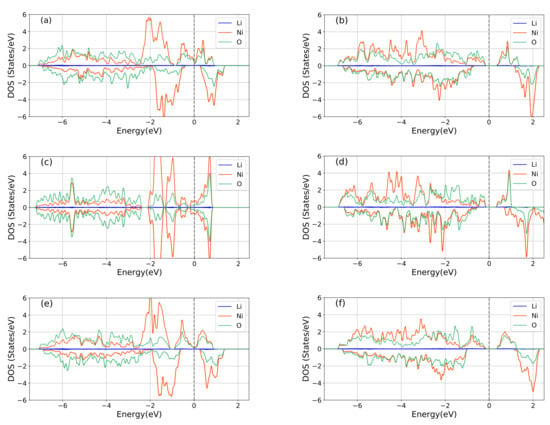
Figure 3.
Partial densities of states (PDOSs) associated with the Li-s, Ni-d, and O-p states in various LNO crystal structures based on GGA (left column) and GGA+U (right column). GGA based results: (a) mC8, (c) op8, and (e) P2/C. GGA+U based results: (b) mC8, (d) op8, and (f) P2/C. The dashed vertical line marks the Fermi level.
We find that the LNO mC8 phase becomes ferromagnetic [8] with a total magnetic moment of 1.00 per Ni atom. Since we have neglected spin–orbit coupling effects, the integer value of the magnetic moment is a direct consequence of the opening of the energy gap in the band structure of LNO. Note that opening of a band gap throughout the BZ at the Fermi level will yield integral numbers of majority and minority spin electrons, and hence an integral net magnetic moment.
The GGA+U based band structure along the high-symmetry directions of the BZ is shown in Figure 4. For details of the BZ and the related symmetry points of the monoclinic structure, we refer the reader to Ref. [35] in the interest of brevity. The energy difference between the valence band maximum and the conduction band minimum, which lie between the Y and symmetry points, is 0.62 eV. However, if one considers all the k-points in the BZ, the indirect (system wide) gap value is 0.46 eV as seen in the DOS: this value is consistent with experimental results [9]. Notably, the smallest direct bandgap in Figure 4 is seen to be located around the middle of the line joining and points.
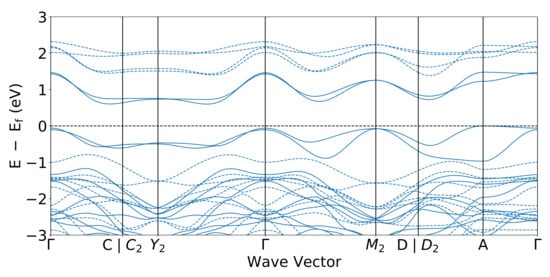
Figure 4.
Band structure of LiNiO. Solid and dashed lines denote the spin-up and spin-down band structure, respectively.
3.3. Optical Properties
Optical spectroscopies [36] can probe particle-hole excitations that are involved in battery charging and discharging processes [37]. To understand how the dielectric function is connected with the potential-capacity characteristics of batteries, we consider a number of representative plots to visualize the optical response.
Figure 5 illustrates the real () and imaginary () parts of the dielectric function, which are connected by the dispersion relations [25]. These functions are given in units of the dielectric constant in vacuum (). The photon energy range is limited to 0–7 eV. The static value of is 8.43, and it reaches a maximum value of 12.15 at 2.27 eV. With increasing photon energy, it drastically decreases to a minimum negative value of −0.70 around 4.0 eV, although at higher photon energies it again starts to go above zero. Our analysis indicates that the distinctive features (peaks) of are due to optical transitions involving hybrid O-2p and transition-metal 3d orbital as is the case in LiCoO [38]. Interestingly in LNO, the band transitions are observed without excitonic effects.
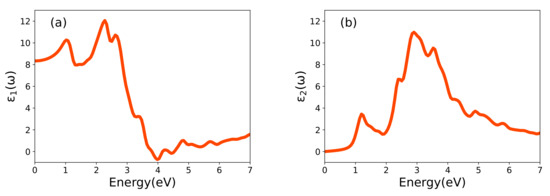
Figure 5.
(a) The computed real part, , and (b) the imaginary part, , of the dielectric function as a function of energy in LNO.
Many other optical properties can be obtained from and . The refractive index computed using Equation (1) is shown in Figure 6. The maximum refractive index value of 3.56 occurs at 2.28 eV, and as expected, decreases gradually beyond the optical energies. We also consider the refractive index as a function of the wavelength to allow for more direct comparison- with the experimental results. Interestingly, our calculations reproduce the dispersion of the refractive index between the visible and infrared range observed by El-Bana et al. [11]. Using the absorption coefficient , one can characterize the optical bandgap [11]. Figure 7 shows the quantity = plotted against photon energy, where A is a constant. The extrapolation given by these so-called Tauc plot provides an estimated value of the optical bandgap of 1.69 eV. The energy loss function shown in Figure 7 gives the energy loss resulting from dispersion or scattering [39,40].
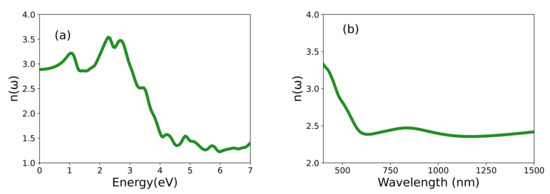
Figure 6.
The computed refractive index of LNO as a function of (a) energy and (b) wavelength.
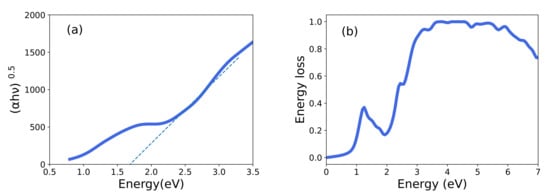
Figure 7.
(a) The computed Tauc plot of in units of and (b) the energy-loss spectrum of LNO.
The loss function (Figure 7b) displays peaks at different energies. The first peak corresponds to the bandgap. The plateau around 4 eV, can explain the redox potential of LNO–it is consistent with RIXS experiment [14]. Craco and Leoni [37] have predicted dramatic changes in the optical response when the LiFePO cathode is charged by removing lithium. In particular, they observed that the peak corresponding to the redox potential shifts to higher energies when the battery is charged. We expect a similar effect here. These results indicate that optical and RIXS experiments can provide a window on lithiation/delithiation processes [41]. The redox orbitals associated with the redox potential could be extracted by considering the electromagnetic response beyond the optical limit at zero momentum transfer () [12,42]. In fact, one can obtain the momentum dependent spectral function of a redox orbital in terms of the difference between two X-ray Compton profiles measured for two lithium concentrations via tomographic techniques [43]. In this connection, we are investigating nonstoichiometric LiNiO samples that we have obtained by co-precipitation [33] for Compton scattering experiments at the SPring-8 synchrotron facility in Japan. Some preliminary Compton scattering results from LNO have been obtained by Chabaud et al. [44] at the ESRF synchrotron facility in France.
4. Conclusions
We discuss the structural, electronic, and optical properties (complex dielectric function , absorption coefficient , and the energy loss spectrum of LNO cathode material using first-principles calculations. The theoretical energy bandgap results are compared with the available experimental data, and the GGA+U functional is shown to yield excellent agreement with experiment. The bandgap is found to be indirect with a GGA+U based (system wide) value of 0.46 eV. The computed refractive index is 3.56. The computed energy loss function is consistent with RIXS experiments and displays a maximum related to the electronic states responsible for the redox potential of the LiNiO cathode. Compton [43] and magnetic Compton [45] X-ray scattering studies will be valuable in providing an atomic level reconstruction of the redox orbitals of LNO.
Author Contributions
V.N.K., A.A.S.D., J.N., M.A., B.B. and A.B. have formulated the theoretical part and have performed DFT calculations. T.H., U.L., K.S. and H.S. have conceptualized links between theory and experiments. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Education and Culture (Finland). J.N. is supported by the INERCOM platform at LUT university and Osk. Huttunen Foundation. The work at Northeastern University was supported by the Air Force Office of Scientific Research under award number FA9550-20-1-0322, and benefited from the computational resources of Northeastern University’s Advanced Scientific Computation Center (ASCC) and the Discovery Cluster.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We are grateful to Mariarosaria Tuccillo for sending us data. The authors acknowledge the CSC—IT Center for Science, Finland for computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BZ | Brillouin Zone |
| DFT | Density Functional Theory |
| DOS | Density of states |
| GGA | Generalized Gradient approximation |
| LIB | Lithium-Ion Battery |
| LNO | Lithium Nickel Oxide |
| PAW | Projector-Augmented-Wave |
| PBE | Perdew–Burke–Ernzerhof |
| PDOS | Partial density of states |
| RIXS | Resonant Inelastic X-ray Scattering (RIXS) |
| SCAN | Strongly constrained and appropriately normed |
| XRD | X-ray diffraction |
References
- Larcher, D.; Tarascon, J. Towards greener and more sustainable batteries for electrical energy storage. Nat. Chem. 2015, 7, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Arumugam, M.; James, C.; Seung-Taek, M.; Seung-Min, O.; Yang-Kook, S. Nickel-Rich and Lithium-Rich Layered Oxide Cathodes: Progress and Perspectives. Adv. Energy Mater. 2016, 6, 1501010. [Google Scholar] [CrossRef]
- Arumugam, M. A reflection on lithium-ion battery cathode chemistry. Nature 2020, 11, 1550. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C.; Eshetu, G.; Laruelle, S.; Grugeon, S.; Zaghib, K.; Julien, C.; Mauger, A.; Guyomard, D.; Rojo, T.; et al. From Solid-Solution Electrodes and the Rocking-Chair Concept to Today’s Batteries. Angew. Chem. Int. Ed. 2020, 59, 534–538. [Google Scholar] [CrossRef] [PubMed]
- Du Pasquier, A.; Plitz, I.; Menocal, S.; Amatucci, G. A comparative study of Li-ion battery, supercapacitor and nonaqueous asymmetric hybrid devices for automotive applications. J. Power Sources 2003, 115, 171–178. [Google Scholar] [CrossRef]
- Kim, Y.; Seong, W.M.; Manthiram, A. Cobalt-free, high-nickel layered oxide cathodes for lithium-ion batteries: Progress, challenges, and perspectives. Energy Storage Mater. 2021, 34, 250–259. [Google Scholar] [CrossRef]
- Schipper, F.; Erickson, E.M.; Erk, C.; Shin, J.; Francois, F.C.; Aurbach, D. Review—Recent Advances and Remaining Challenges for Lithium Ion Battery Cathodes. J. Electrochem. Soc. 2016, 164, A6220–A6228. [Google Scholar] [CrossRef]
- Bianchini, M.; Roca-Ayats, M.; Hartmann, P.; Brezesinski, T.; Janek, J. There and Back Again—The Journey of LiNiO2 as a Cathode Active Material. Angew. Chem. Int. Ed. 2019, 58, 10434–10458. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Devi, A.A.S.; Nokelainen, J.; Barbiellini, B.; Devaraj, M.; Alatalo, M.; Bansil, A. Re-examining the giant magnetization density in α -Fe16N2 with the SCAN+U method. Phys. Chem. Chem. Phys. 2022, 24, 17879–17884. [Google Scholar] [CrossRef]
- El-Bana, M.; El Radaf, I.; Fouad, S.; Sakr, G. Structural and optoelectrical properties of nanostructured LiNiO2 thin films grown by spray pyrolysis technique. J. Alloys Compd. 2017, 705, 333–339. [Google Scholar] [CrossRef]
- Wang, Y.J.; Barbiellini, B.; Lin, H.; Das, T.; Basak, S.; Mijnarends, P.E.; Kaprzyk, S.; Markiewicz, R.S.; Bansil, A. Lindhard and RPA susceptibility computations in extended momentum space in electron-doped cuprates. Phys. Rev. B 2012, 85, 224529. [Google Scholar] [CrossRef]
- Barbiellini, B.; Hancock, J.N.; Monney, C.; Joly, Y.; Ghiringhelli, G.; Braicovich, L.; Schmitt, T. Inelastic x-ray scattering from valence electrons near absorption edges of FeTe and TiSe2. Phys. Rev. B 2014, 89, 235138. [Google Scholar] [CrossRef]
- Li, N.; Sallis, S.; Papp, J.K.; Wei, J.; McCloskey, B.D.; Yang, W.; Tong, W. Unraveling the cationic and anionic redox reactions in a conventional layered oxide cathode. ACS Energy Lett. 2019, 4, 2836–2842. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Tuccillo, M.; Palumbo, O.; Pavone, M.; Muñoz-García, A.; Paolone, A.; Brutti, S. Analysis of the Phase Stability of LiMO2 Layered Oxides (M = Co, Mn, Ni). Crystals 2000, 10, 526. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Analysis of the Phase Stability of LiMO2 Layered Oxides (M = Co, Mn, Ni). Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Ping Ong, S.; Moore, C.; Fischer, C.; Persson, K.; Ceder, G. Formation enthalpies by mixing GGA and GGA + U calculations. Phys. Rev. B 2011, 84, 045115. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef]
- Liu, Y.; Lian, J.; Sun, Z.; Zhao, M.; Shi, Y.; Song, H. The first-principles study for the novel optical properties of LiTi2O4, Li4Ti5O12, Li2Ti2O4 and Li7Ti5O12. Chem. Phys. Lett. 2017, 677, 114–119. [Google Scholar] [CrossRef]
- Altarelli, M.; Dexter, D.L.; Nussenzveig, H.M.; Smith, D.Y. Superconvergence and Sum Rules for the Optical Constants. Phys. Rev. B 1972, 6, 4502–4509. [Google Scholar] [CrossRef]
- Laubach, S.; Laubach, S.; Schmidt, P.C.; Ensling, D.; Schmid, S.; Jaegermann, W.; Thißen, A.; Nikolowski, K.; Ehrenberg, H. Changes in the crystal and electronic structure of LiCoO2 and LiNiO2 upon Li intercalation and de-intercalation. Phys. Chem. Chem. Phys. 2009, 11, 3278–3289. [Google Scholar] [CrossRef]
- Hoang, K.; Johannes, M.D. Defect chemistry in layered transition-metal oxides from screened hybrid density functional calculations. J. Mater. Chem. A 2014, 2, 5224–5235. [Google Scholar] [CrossRef]
- Hoang, K.; Johannes, M.D. Defect physics in complex energy materials. J. Phys. Condens. Matter 2018, 30, 293001. [Google Scholar] [CrossRef]
- Chakraborty, A.; Dixit, M.; Aurbach, D.; Major, D.T. Predicting accurate cathode properties of layered oxide materials using the SCAN meta-GGA density functional. NPJ Comput. Mater. 2018, 4, 1–9. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Välikangas, J.; Laine, P.; Hietaniemi, M.; Hu, T.; Tynjälä, P.; Lassi, U. Precipitation and Calcination of High-Capacity LiNiO2 Cathode Material for Lithium-Ion Batteries. Appl. Sci. 2020, 10, 8988. [Google Scholar] [CrossRef]
- Sicolo, S.; Mock, M.; Bianchini, M.; Albe, K. Furthermore, Yet It Moves: LiNiO2, a Dynamic Jahn–Teller System. Chem. Mater. 2020, 32, 10096–10103. [Google Scholar] [CrossRef]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Fox, M. Optical Properties of Solids, 2nd ed.; Oxford Master Series in Condensed Matter Physics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Craco, L.; Leoni, S. Electrodynamics and quantum capacity of LixFePO4 battery material. Appl. Phys. Lett. 2011, 99, 192103. [Google Scholar] [CrossRef]
- Radha, S.K.; Lambrecht, W.R.L.; Cunningham, B.; Grüning, M.; Pashov, D.; van Schilfgaarde, M. Optical response and band structure of LiCoO2 including electron-hole interaction effects. Phys. Rev. B 2021, 104, 115120. [Google Scholar] [CrossRef]
- Scafetta, M.D.; Cordi, A.M.; Rondinelli, J.M.; May, S.J. Band structure and optical transitions in LaFeO3: Theory and experiment. J. Phys. Condens. Matter 2014, 26, 505502. [Google Scholar] [CrossRef]
- Tan, G.; DeNoyer, L.; French, R.; Guittet, M.; Gautier-Soyer, M. Kramers–Kronig transform for the surface energy loss function. J. Electron Spectrosc. Relat. Phenom. 2005, 142, 97–103. [Google Scholar] [CrossRef]
- Jia, Y.; Ye, Y.; Liu, J.; Zheng, S.; Lin, W.; Wang, Z.; Li, S.; Pan, F.; Zheng, J. Breaking the energy density limit of LiNiO2: Li2NiO3 or Li2NiO2? Sci. China Mater. 2022, 65, 913–919. [Google Scholar] [CrossRef]
- Prange, M.P.; Rehr, J.J.; Rivas, G.; Kas, J.J.; Lawson, J.W. Real space calculation of optical constants from optical to x-ray frequencies. Phys. Rev. B 2009, 80, 155110. [Google Scholar] [CrossRef]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Tsuji, N.; Yabuuchi, N.; Yamamoto, K.; Orikasa, Y.; Uchimoto, Y.; Sakurai, Y.; Sakurai, H.; et al. Tomographic reconstruction of oxygen orbitals in lithium-rich battery materials. Nature 2021, 564, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Chabaud, S.; Bellin, C.; Mauri, F.; Loupias, G.; Rabii, S.; Croguennec, L.; Pouillerie, C.; Delmas, C.; Buslaps, T. Electronic density distorsion of NiO2 due to intercalation by Li. J. Phys. Chem. Solids 2004, 65, 241–243. [Google Scholar] [CrossRef]
- Suzuki, K.; Otsuka, Y.; Hoshi, K.; Sakurai, H.; Tsuji, N.; Yamamoto, K.; Yabuuchi, N.; Hafiz, H.; Orikasa, Y.; Uchimoto, Y.; et al. Magnetic Compton Scattering Study of Li-Rich Battery Materials. Condens. Matter 2022, 7, 4. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).