Stability Analysis of Buoyancy Magneto Flow of Hybrid Nanofluid through a Stretchable/Shrinkable Vertical Sheet Induced by a Micropolar Fluid Subject to Nonlinear Heat Sink/Source
Abstract
1. Introduction
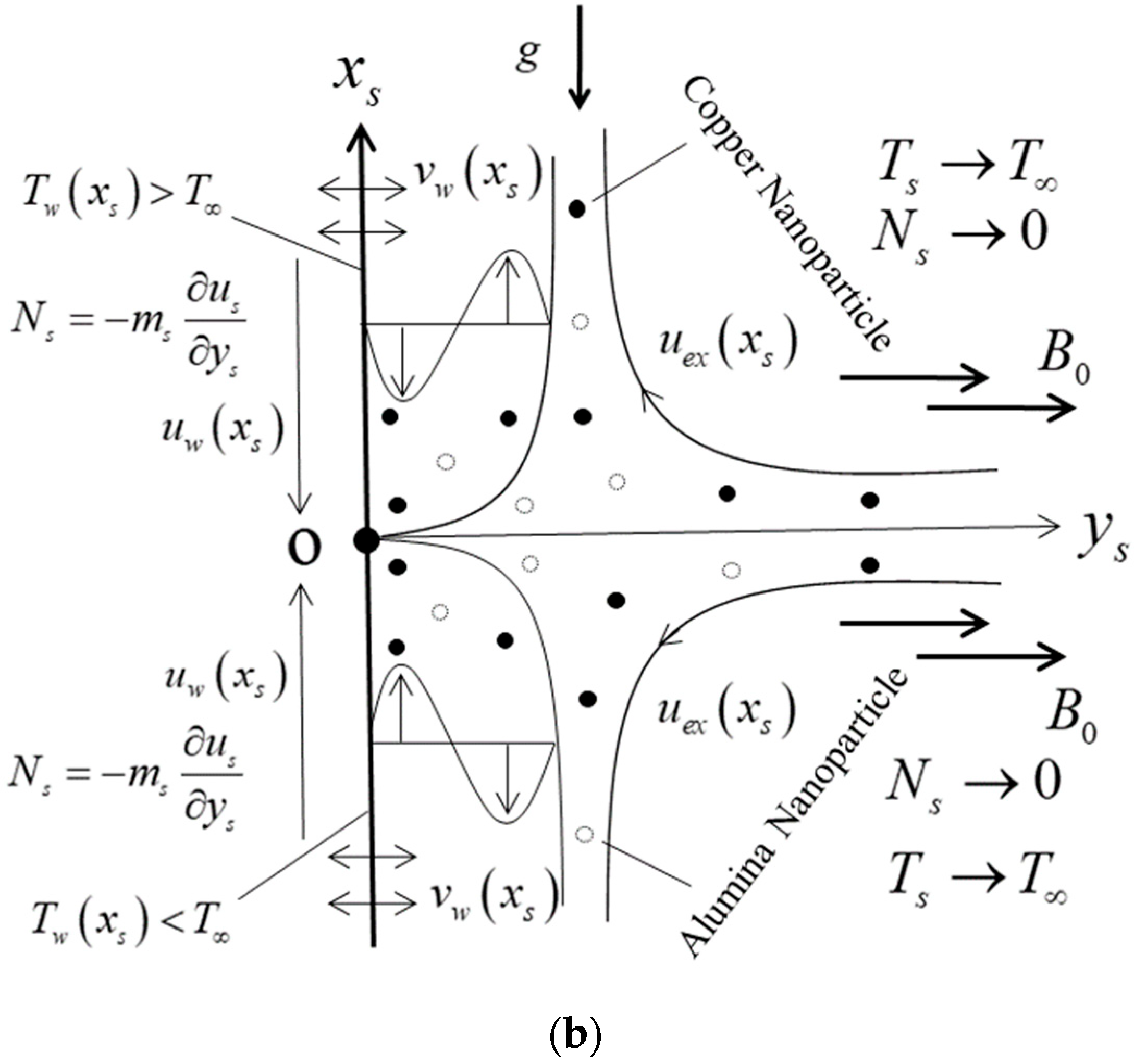
2. Description and Background of the Model
2.1. The Engineering Quantities of Interest
2.1.1. The Shear Stress Coefficient (SSC)
2.1.2. The Couple-Stress Coefficient (CSC)
2.1.3. The Heat Transfer Rate (HTR)
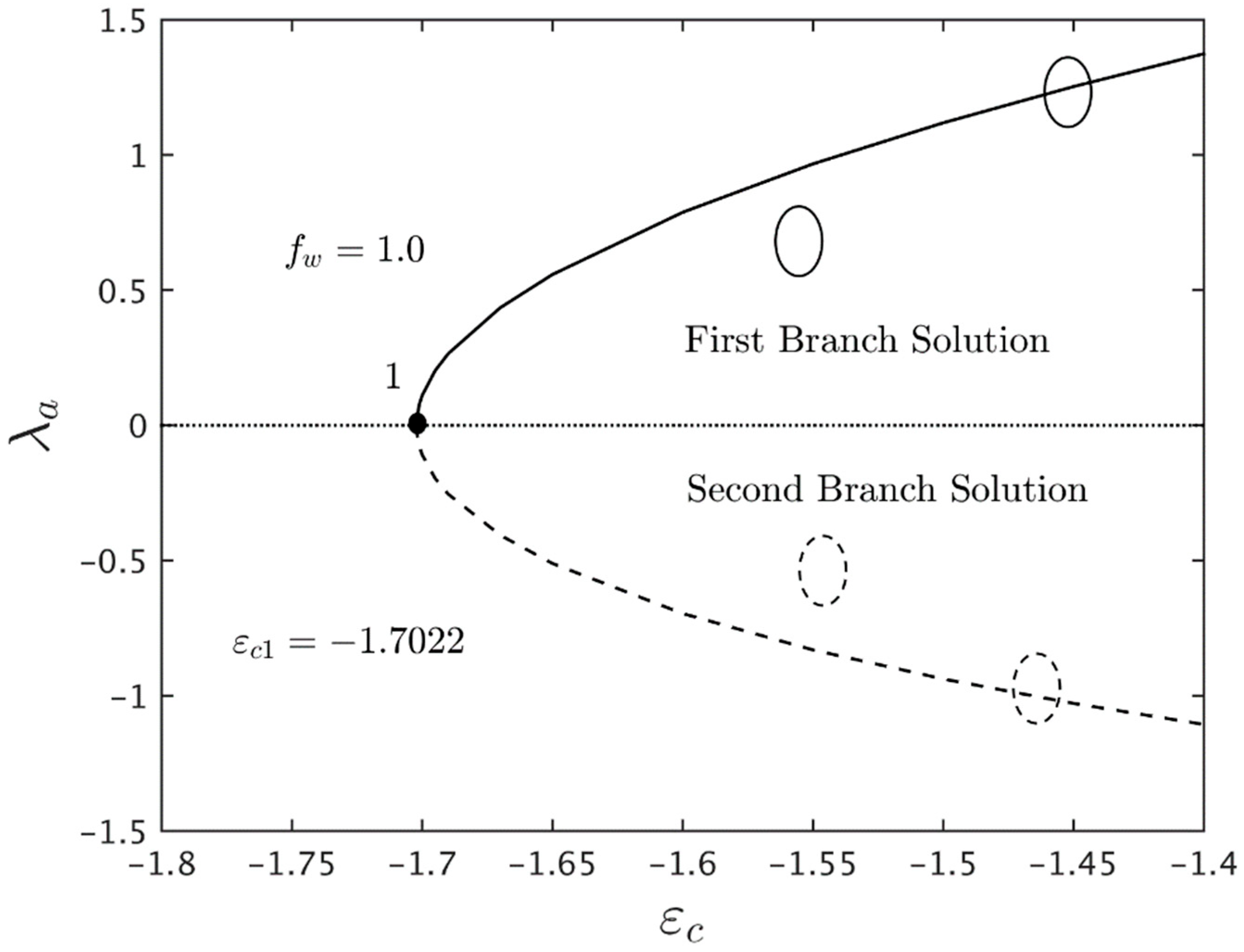
3. Stability Analysis
4. Multiple Solution Methodology and Authentication of the Code
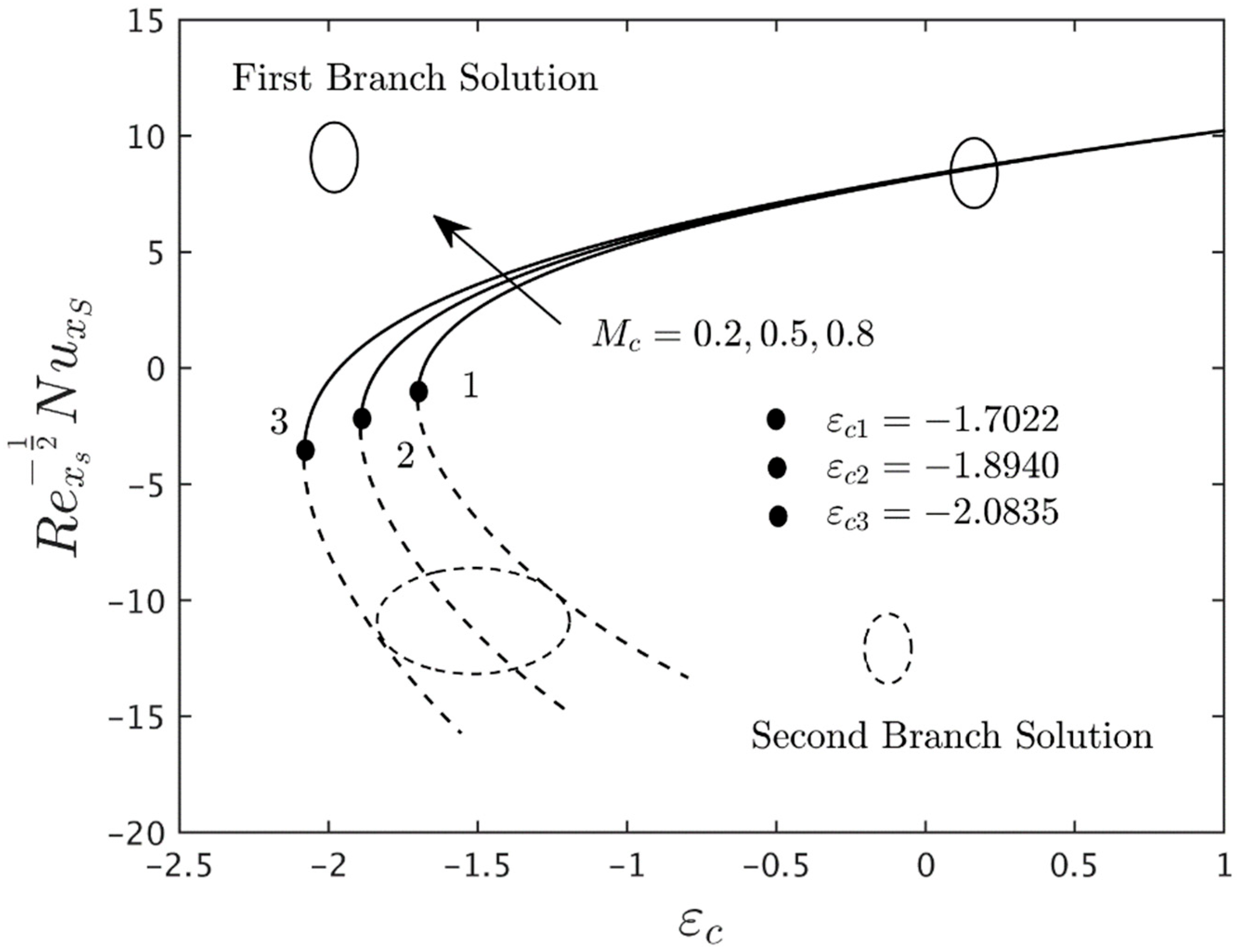
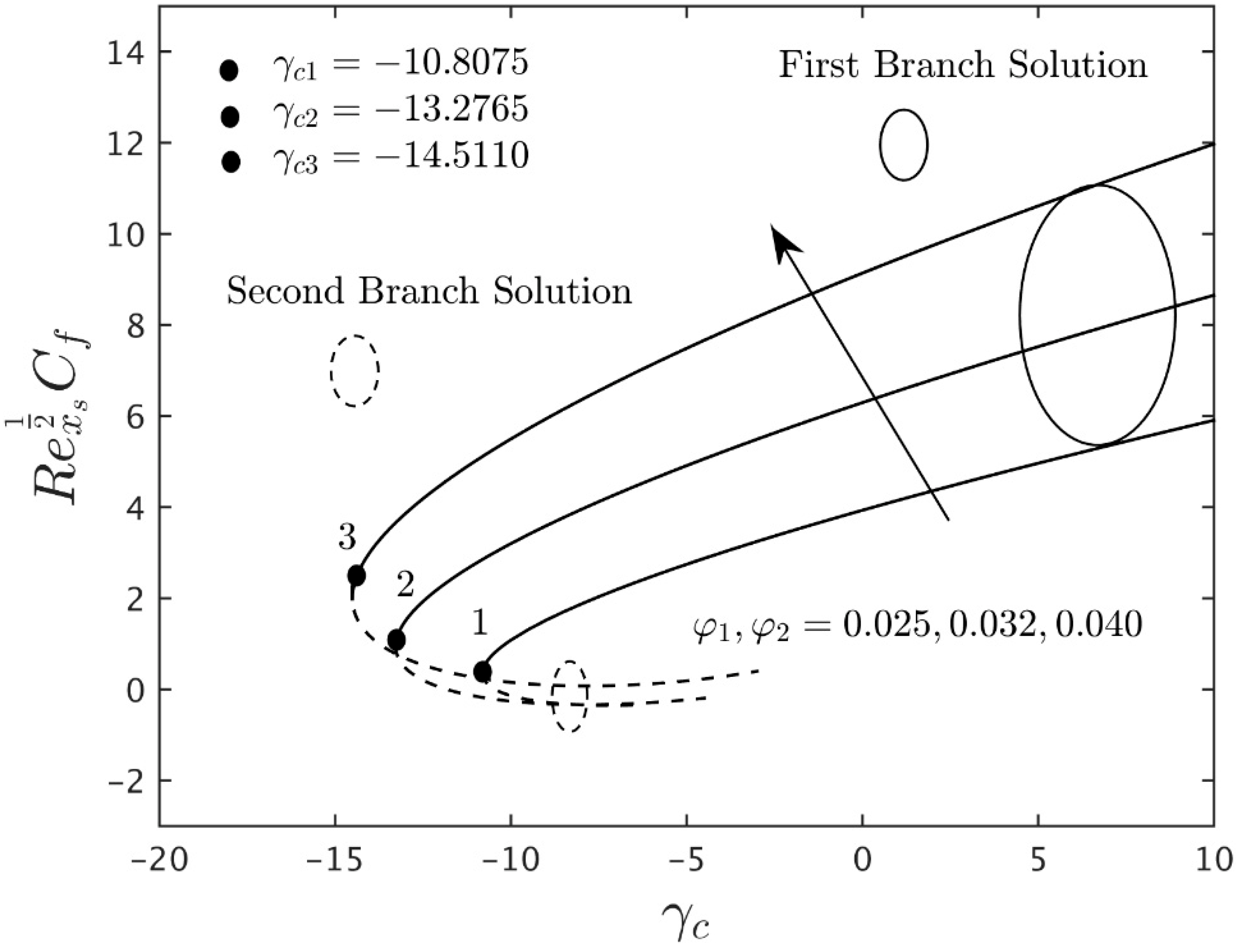
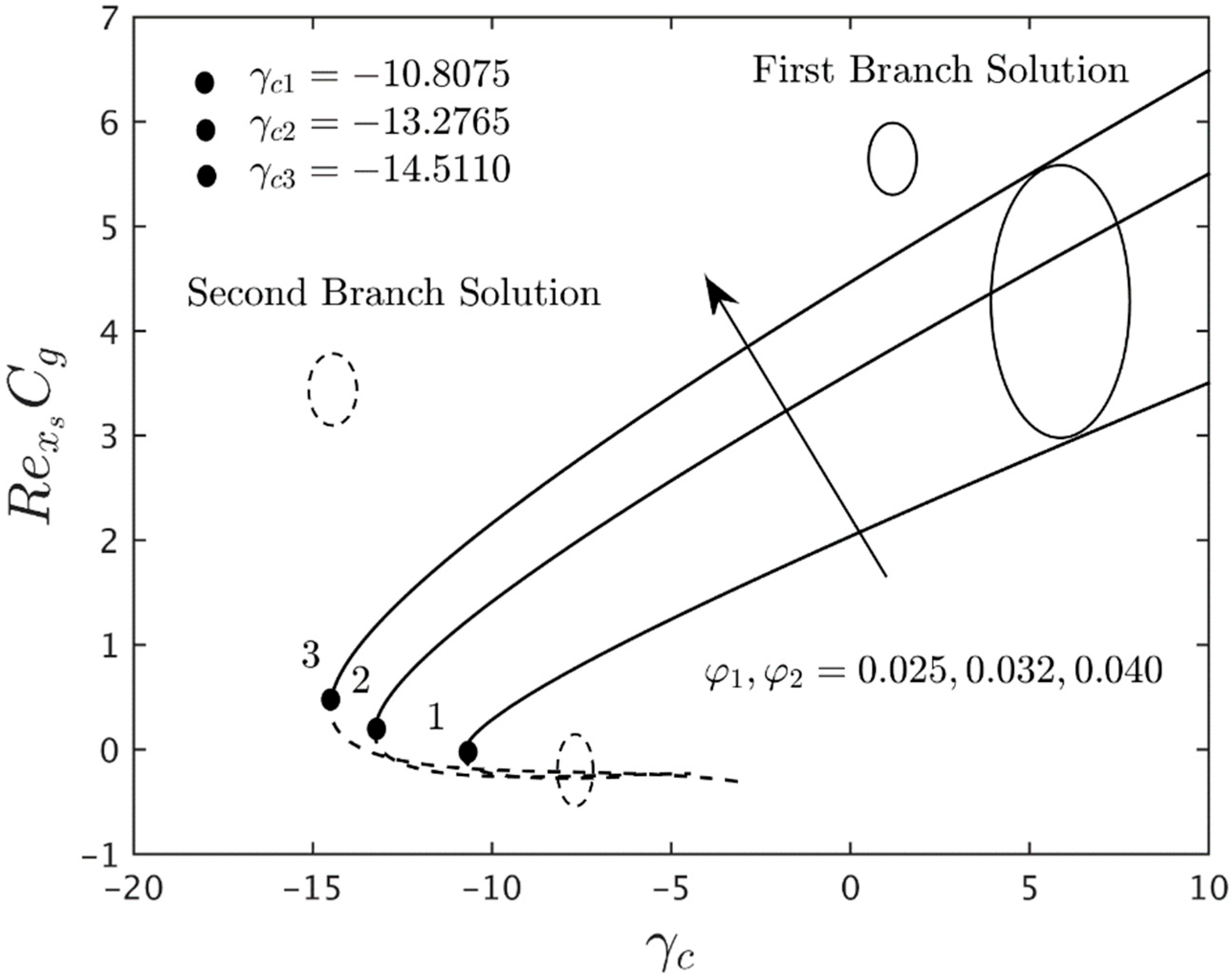
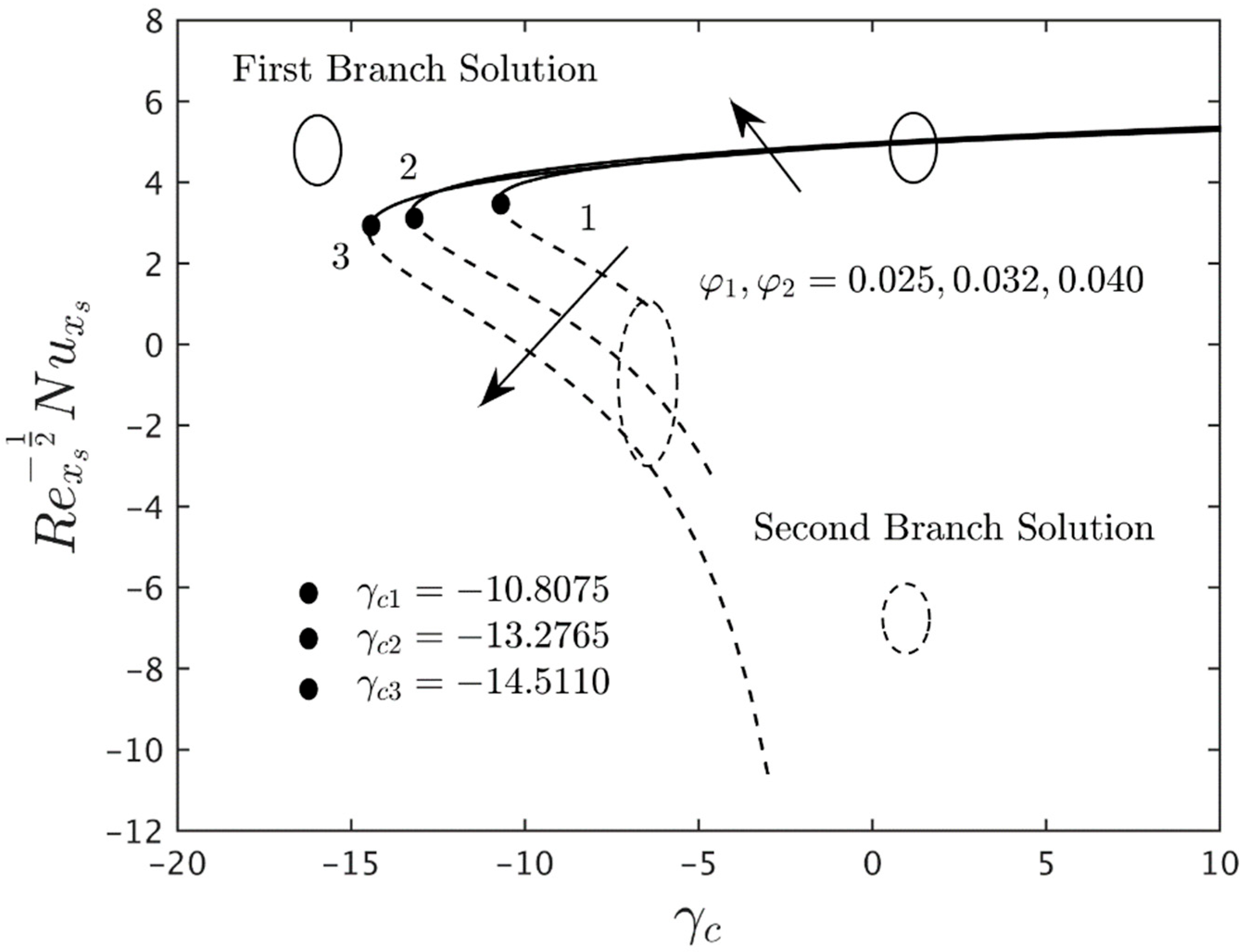
5. Analysis of Results
6. Conclusions
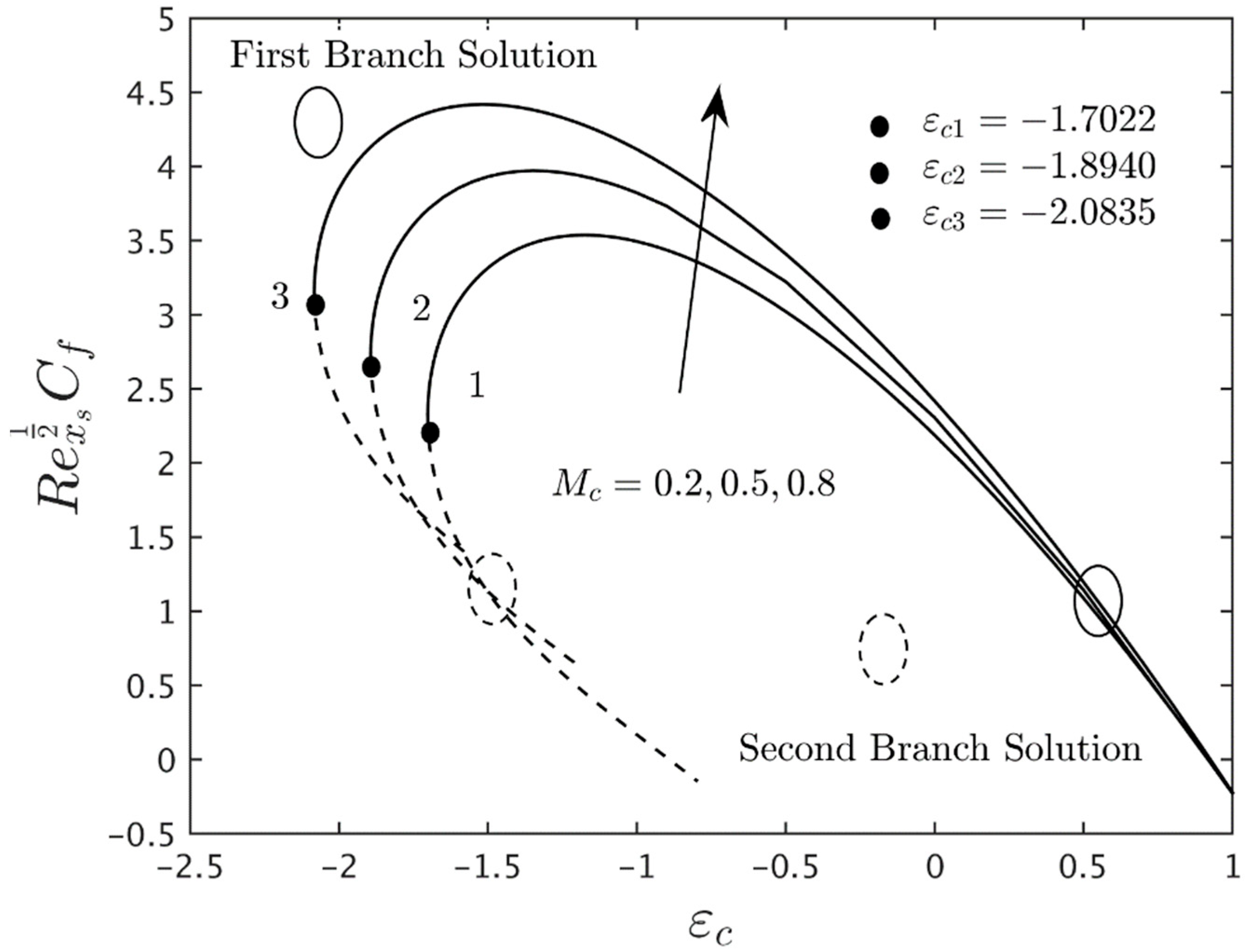
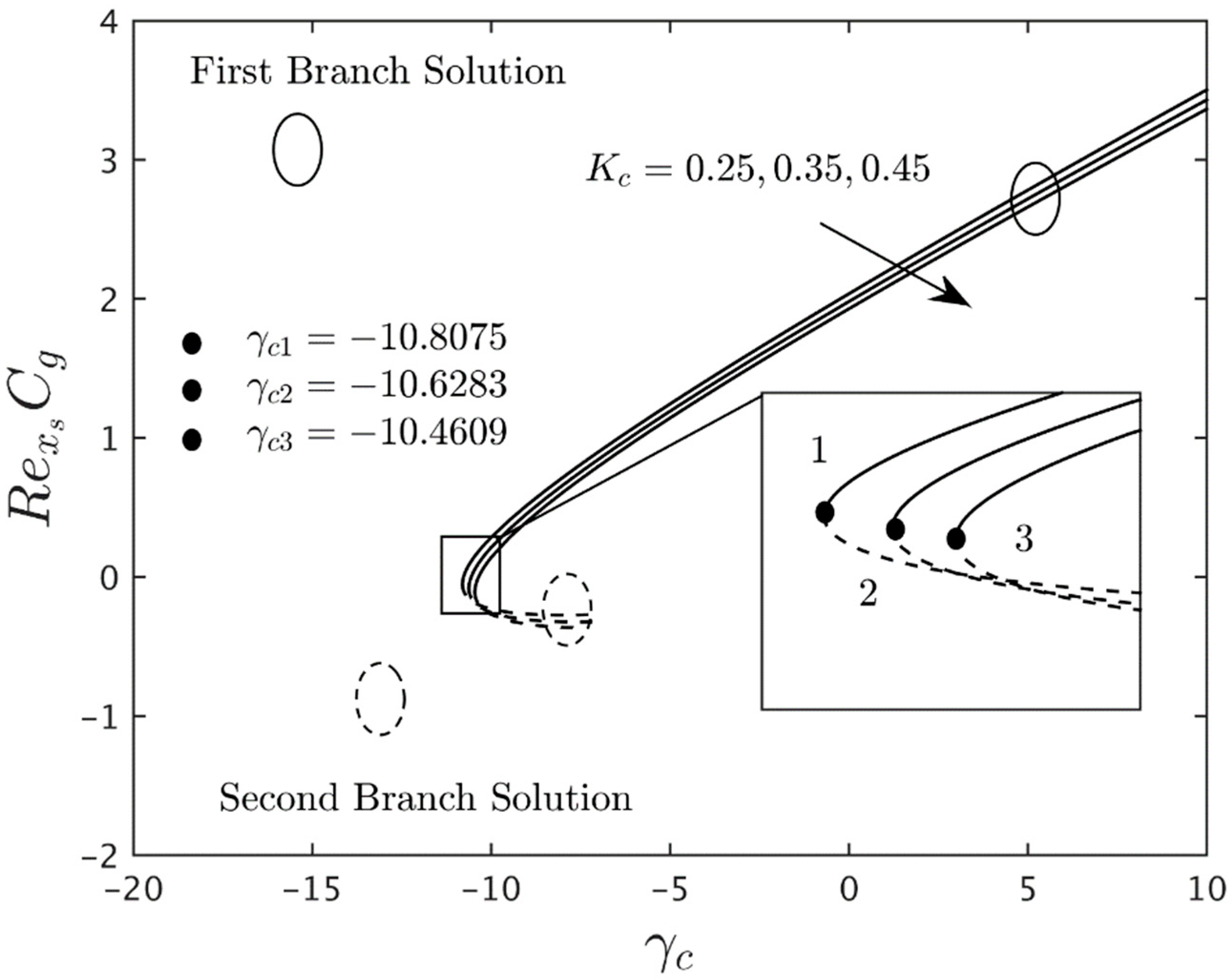
- The mass suction parameter and the magnetic parameter contributes to enhancing the SSC and the CSC, as well as the heat transfer performance of the HN.
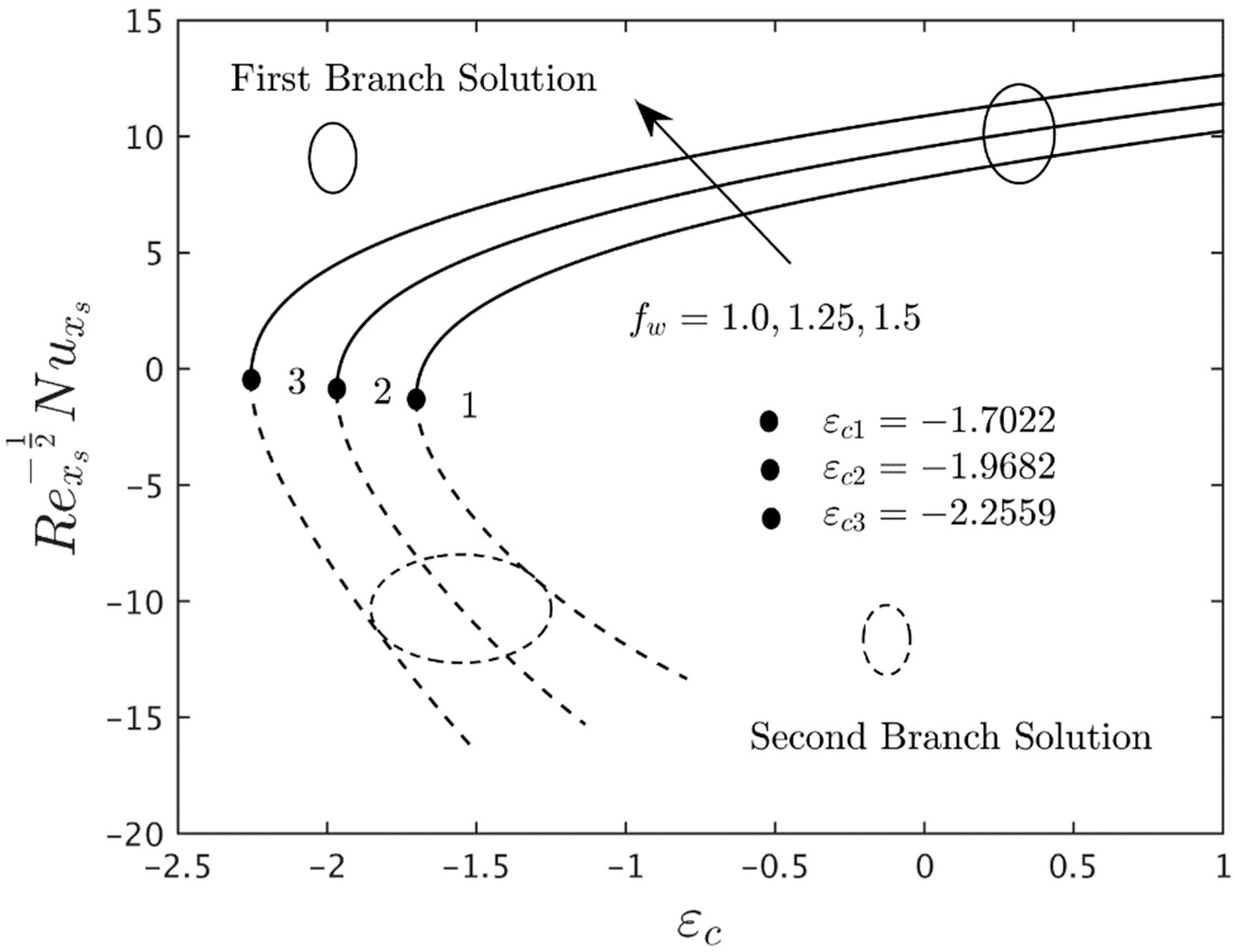
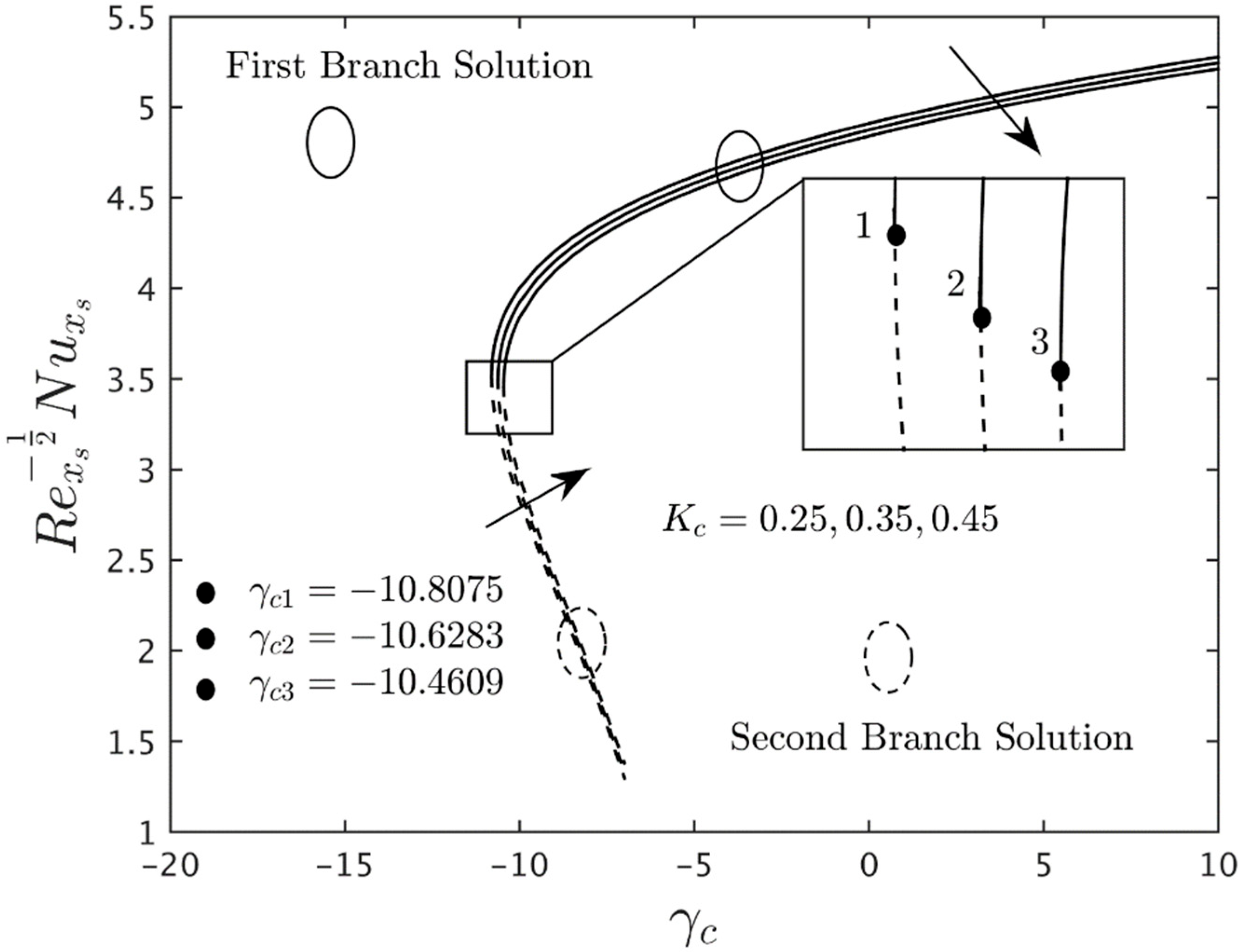
- Besides enhancing the skin friction and the couple stress coefficients, the added nanoparticles volume fraction and also improves the Nusselt number. This behavior is expected since the nanoparticles improve the thermal conductivity of the base fluid due to their synergic effect.
- Moreover, the material parameter lowers the couple stress coefficient and heat transfer performance of the hybrid nanofluid, but the SSC is slightly increased with this parameter.
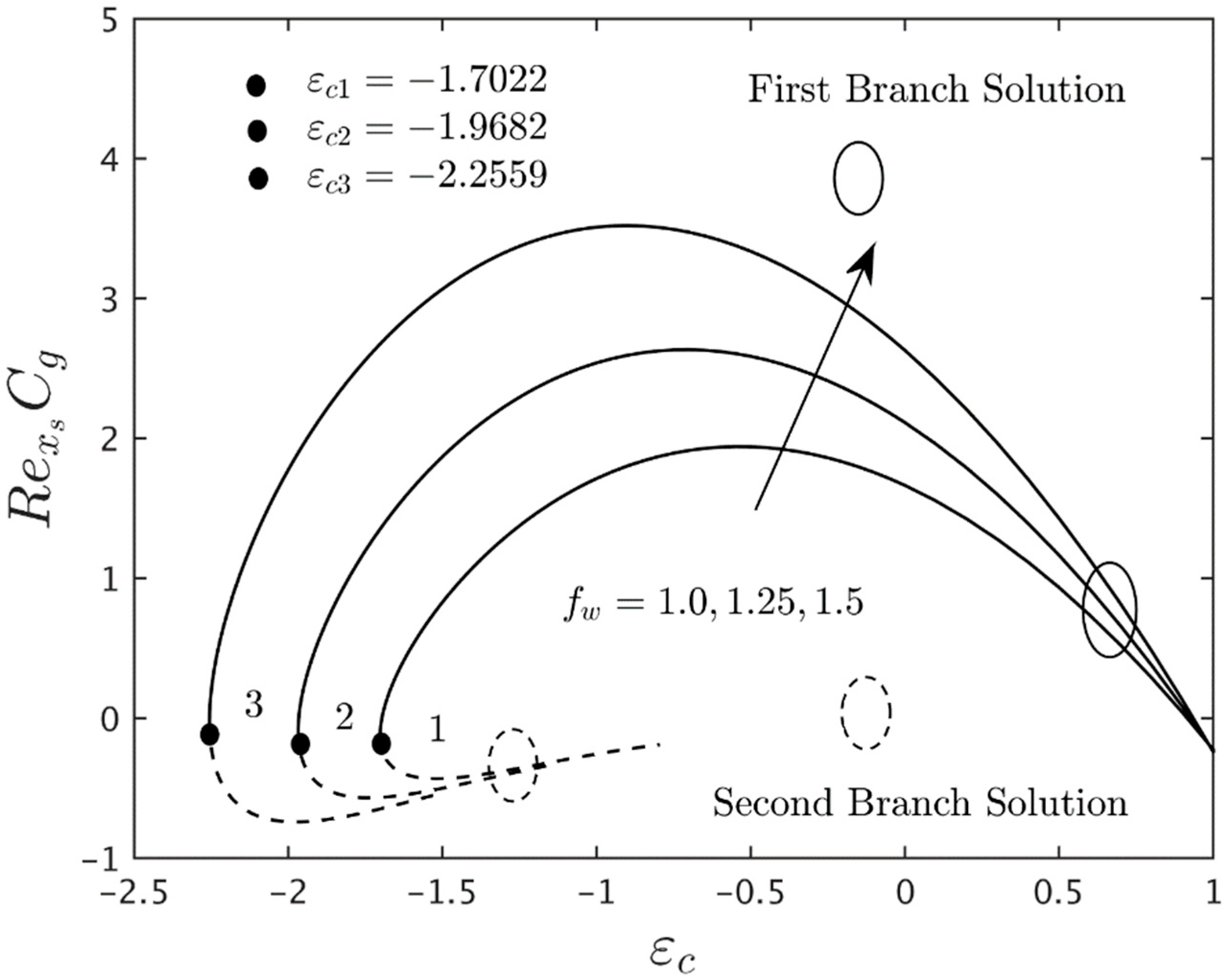
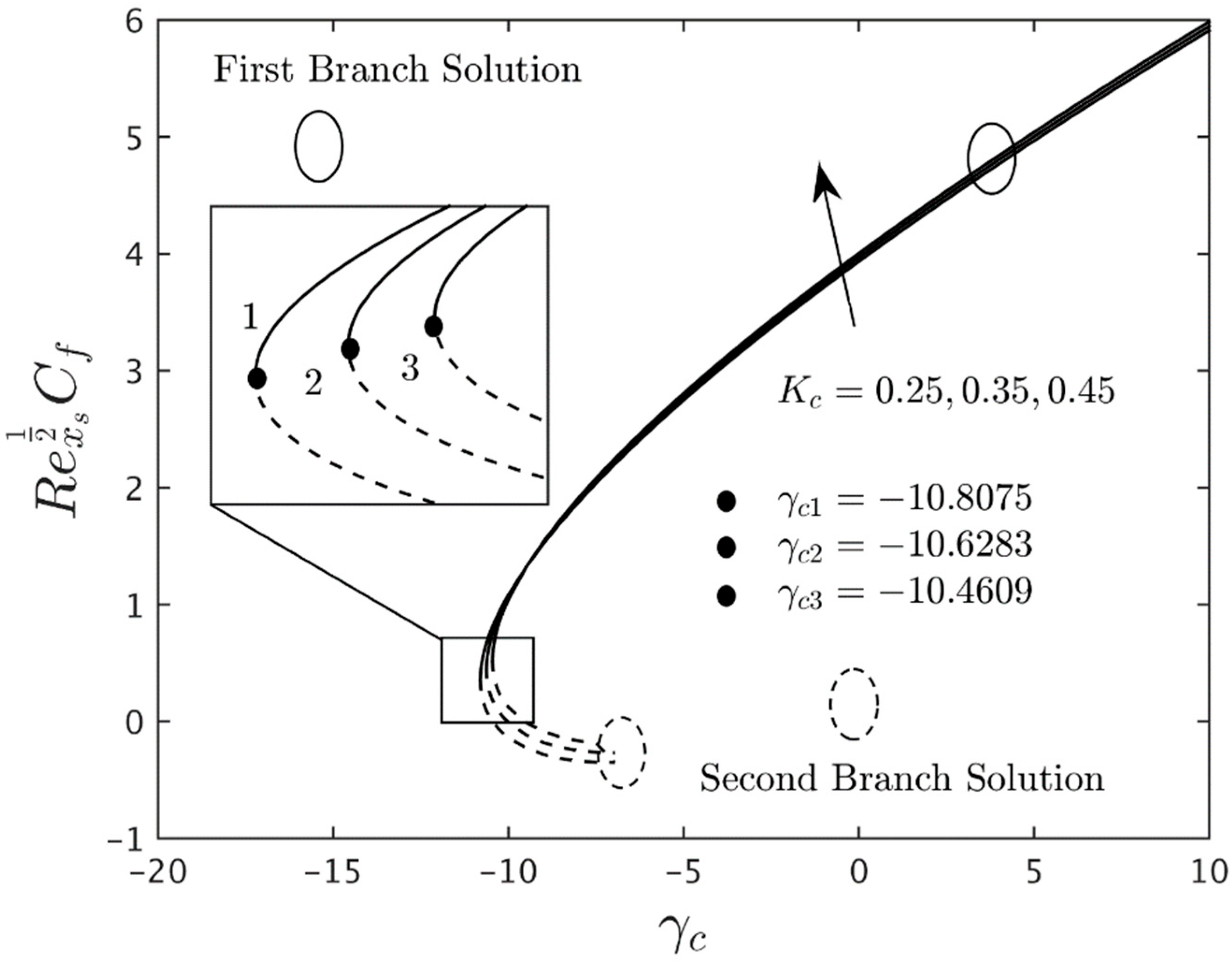
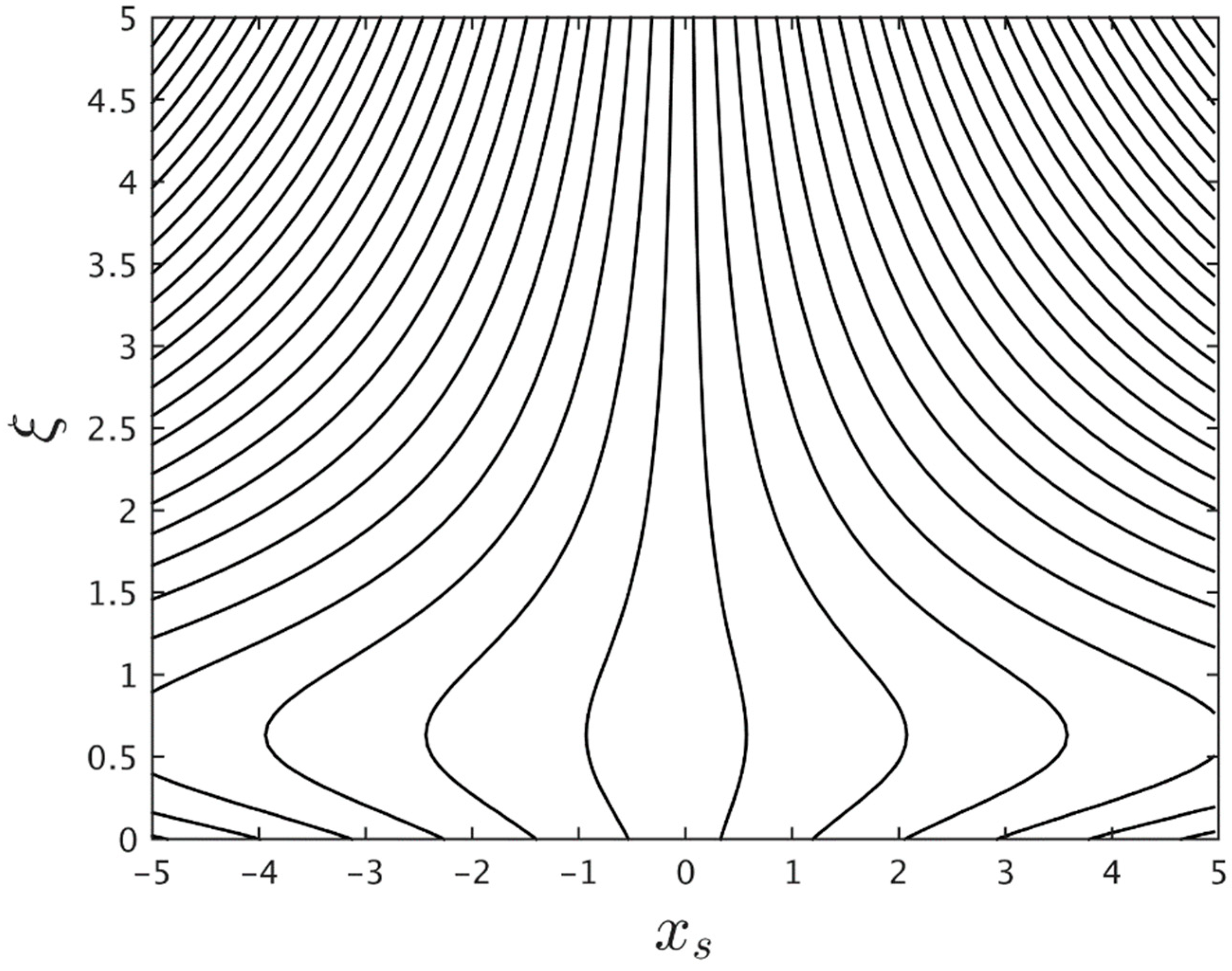
- The domain of the stretching/shrinking parameter is expanded for the larger mass suction parameter and the magnetic parameter . These behaviors are proven by looking at the critical points of the parameter where they are moving on the left side of the shrinking regions. Similar behavior is observed for the buoyancy parameter for some values of the material parameter .
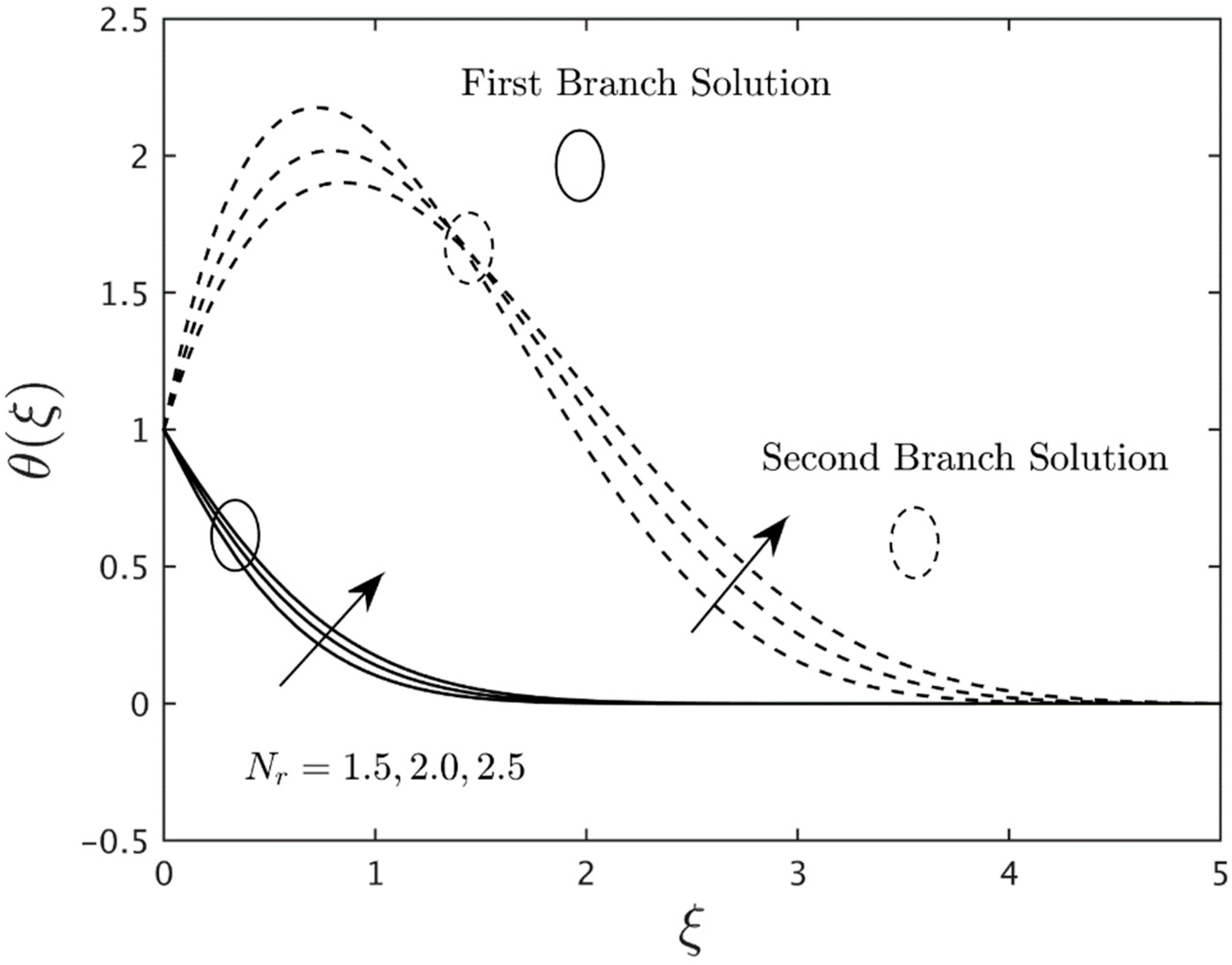
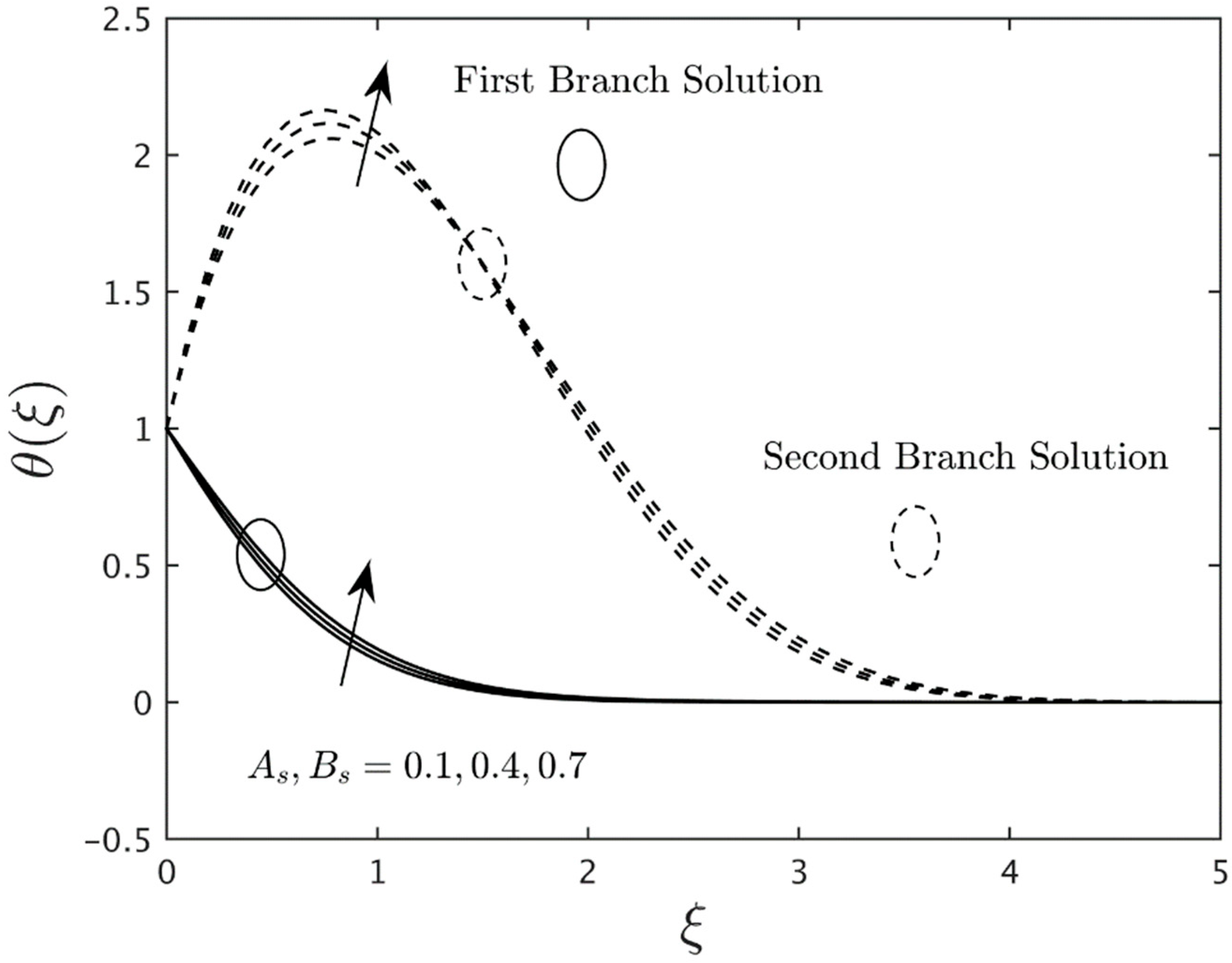
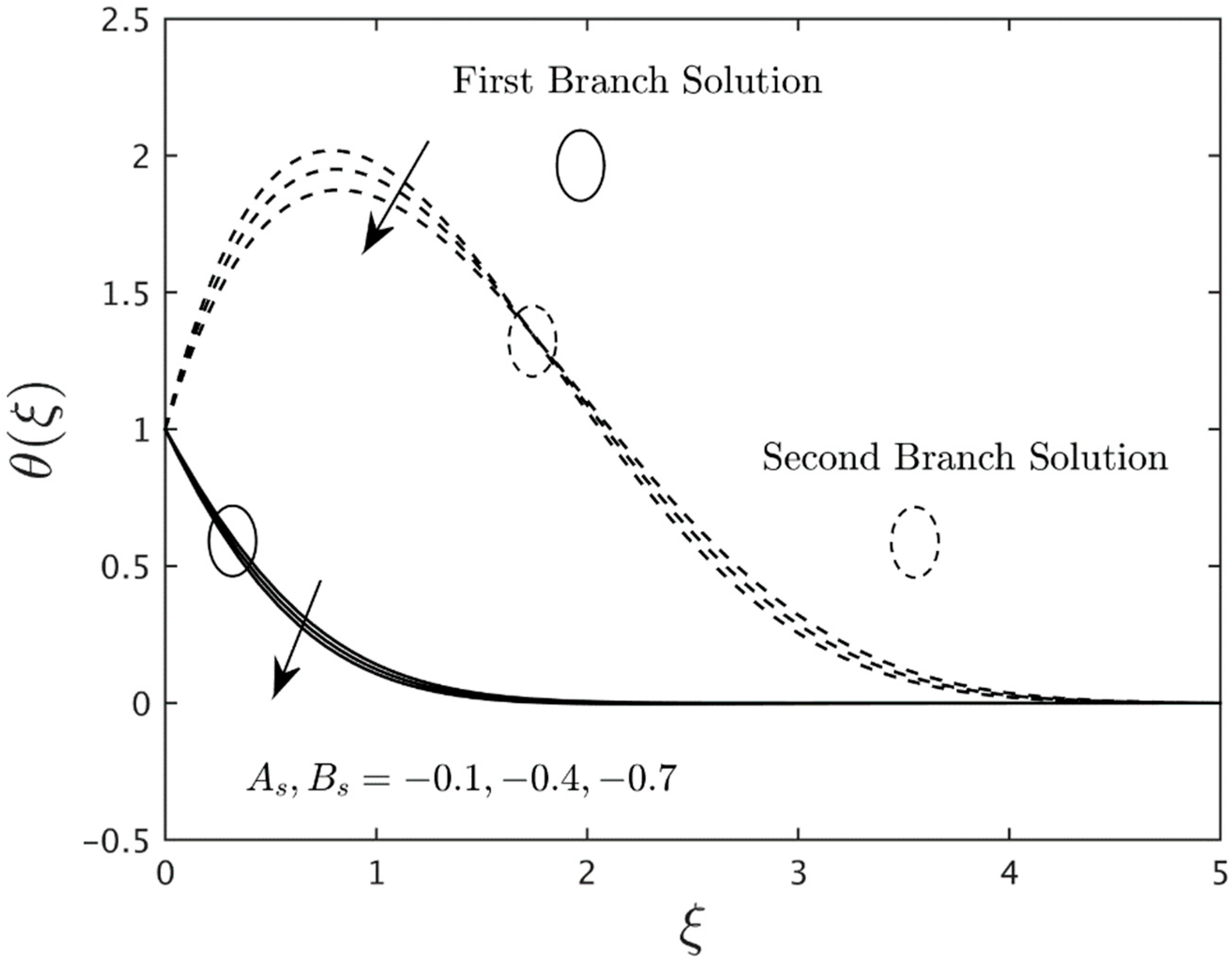
- The heat source parameter boosts the temperature profiles, and the opposite behavior is shown by the heat sink parameter for both the first and second solutions.
- According to the stability analysis, the eigenvalue obtained for the first solution is in positive values, while the negative values of the eigenvalues are shown in the second solution. These behaviors prove that the FBS is stable in the long run and vice versa.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows, FED; Siginer, D.A., Wang, H.P., Eds.; ASME: New York, NY, USA, 1995; Volume 231/MD-66, pp. 99–105. [Google Scholar]
- Lin, Y.; Zheng, L. Marangoni boundary layer flow and heat transferof copper-water nanofluid over a porous medium disk. AIP Adv. 2015, 5, 107225. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ganji, D.D. Thermal radiation effect on the Nanofluid buoyancy flow and heat transfer over a stretching sheet considering Brownian motion. J. Mol. Liq. 2016, 223, 521–527. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Entropy generation as a practical tool of optimisation for non-Newtonian nanofluid flow througha permeable stretching surface using SLM. J. Comput. Des. Eng. 2017, 4, 21–28. [Google Scholar]
- Sheremet, M.A.; Cimpean, D.S.; Pop, I. Free convection in a partially heated wavy porous cavity filled with a nanofluid under the effects of Brownian diffusion and thermophoresis. Appl. Therm. Eng. 2017, 113, 413–418. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Chamkha, A.J.; Seyyedi, S.M.; Ganji, D.D. Radiative nanofluid flow and heat transfer between parallel disks with penetrable and stretchable walls considering Cattaneo-Christov heat flux model. Heat Transf. Asian Res. 2018, 47, 735–753. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A. Magnetic field effect on Sisko fluid flow containing gold nanoparticles through a porous curved surface in the presence of radiation and partial slip. Mathematics 2021, 9, 921. [Google Scholar] [CrossRef]
- Gasmi, H.; Khan, U.; Zaib, A.; Ishak, A.; Eldin, S.M.; Raizah, Z. Analysis of mixed convection on two-phase nanofluid flow past a vertical plate in Brinkman-Extended Darcy porous medium with Nield conditions. Mathematics 2022, 10, 3918. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D.D. Investigation on thermophysical properties ofTiO2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid nanofluids preparation, thermal properties, heat transfer andfriction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. MHD mixed convection stagnation-point flow of Cu-Al2O3/water hybrid nanofluid over a permeable stretching/shrinking surface with heat source/sink. Eur. J. Mech. B Fluids 2020, 84, 71–80. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed convective stagnation point flow towards a vertical Riga plate in hybrid Cu-Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer of a hybrid nanofluid past a permeable moving surface. Chin. J. Phys. 2020, 66, 606–619. [Google Scholar] [CrossRef]
- Abu Bakar, S.; Md Arifin, N.; Khashi’ie, N.S.; Bachok, N. Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts. Mathematics 2021, 9, 878. [Google Scholar] [CrossRef]
- Salawu, S.O.; Obalalu, A.M.; Shamshuddin, M.D. Nonlinear solar thermal radiation efficiency and energy optimization for magnetized hybrid Prandtl–Eyring nanoliquid in aircraft. Arabian J. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Eringen, A. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Ishak, A.; Lok, Y.Y.; Pop, I. Stagnation-point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Commun. 2010, 197, 1417–1427. [Google Scholar] [CrossRef]
- Yacob, N.A.; Ishak, A. Stagnation point flow towards a stretching/shrinking sheet in a micropolar fluid with a convective surface boundary condition. Can. J. Chem. Eng. 2012, 90, 621–626. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. MHD stagnation-point flow over a stretching/shrinking sheet in a micropolar fluid with a slipboundary. Sains Malays. 2018, 47, 2907–2916. [Google Scholar] [CrossRef]
- El-Aziz, M.A. Viscous dissipation effect on mixed convection flow of a micropolar fluid over an exponentially stretching sheet. Can. J. Phys. 2009, 87, 359–368. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated/cooled deformable plate: Exact solutions. Int. J. Heat Mass Transf. 2017, 106, 127–134. [Google Scholar] [CrossRef]
- Ramadevi, B.; Anantha Kumar, K.; Sugunamma, V.; Ramana Reddy, J.V.; Sandeep, N. Magnetohydrodynamic mixed convective flow of micropolar fluid past a stretching surface using modified fourier’s heat flux model. J. Therm. Anal. Calorim. 2020, 139, 1379–1393. [Google Scholar] [CrossRef]
- Rafique, K.; Alotaibi, H.; Nofal, T.A.; Anwar, M.I.; Misiran, M.; Khan, I. Numerical solutions of micropolar nanofluid over an inclined surface using Keller box analysis. J. Math. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Sajid, T.; Jamshed, W.; Shahzad, F.; Eid, M.R.; Alshehri, H.M.; Goodarzi, M.; Akgül, E.K.; Nisar, K.S. Micropolar fluid past a convectively heated surface embedded with nth order chemical reaction and heat source/sink. Phys. Scr. 2021, 96, 104010. [Google Scholar] [CrossRef]
- Kausar, M.S.; Hussanan, A.; Waqas, M.; Mamat, M. Boundary layer flow of micropolar nanofluid towards a permeable stretching sheet in the presence of porous medium with thermal radiation and viscous dissipation. Chin. J. Phys. 2022, 78, 435–452. [Google Scholar] [CrossRef]
- Attia, H.A. Stagnation point flow and heat transfer of a micropolar fluid with uniform suction or blowing. J. Braz. Soc. Mech. Sci. Eng. 2008, 30, 51–55. [Google Scholar] [CrossRef]
- Awaludin, I.S.; Weidman, P.D.; Ishak, A. Stability analysis of stagnation-point flow over a stretching/shrinking sheet. AIP Adv. 2016, 6, 045308. [Google Scholar] [CrossRef]
- Sadiq, M.A. MHD stagnation point flow of nanofluid on a plate with anisotropic slip. Symmetry 2019, 11, 132. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady stagnation point flow of hybrid nanofluid past a convectively heated stretching/shrinking sheet with velocity slip. Mathematics 2020, 8, 1649. [Google Scholar] [CrossRef]
- Mahmood, Z.; Ahamm, N.A.; Alhazmi, S.E.; Khan, U.; Bani-Fwaz, M.Z. Ternary hybrid nanofluid near a stretching/shrinking sheet with heat generation/absorption and velocity slip on unsteady stagnation point flow. Int. J. Modern Phys. B 2022, 36, 2250209. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 2017, 126, 308–318. [Google Scholar] [CrossRef]
- Sharma, K.; Gupta, S. Viscous dissipation and thermal radiation effects in MHD flow of Jeffrey nanofluid through impermeable surface with heat generation/absorption. Nonlinear Eng. 2017, 6, 153–166. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow ofa nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Eldin, S.M.; Alotaibi, A.M.; Raizah, Z.; Waini, I.; Elattar, S.; Abed, A.M. Features of hybridized AA7072 and AA7075 alloys nanomaterials with melting heat transfer past a movable cylinder with Thompson and Troian slip effect. Arab. J. Chem. 2022, 104503. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Elattar, S.; Eldin, S.M.; Raizah, Z.; Waini, I.; Waqas, M. Impact of irregular heat sink/source on the wall Jet flow and heat transfer in a porous medium induced by a nanofluid with slip and buoyancy effects. Symmetry 2022, 14, 1312. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Bachok, N. Effect of thermal dispersion on transient natural convection in a wavy-walled porous cavity filled with a nanofluid: Tiwari and Das’ nanofluid model. Int. J. Heat Mass Transf. 2016, 92, 1053–1060. [Google Scholar] [CrossRef]
- Pang, C.; Jung, J.Y.; Kang, Y.T. Aggregation based model for heat conduction mechanism in nanofluids. Int. J. Heat Mass Transf. 2014, 72, 392–399. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Rikhtegar, F.; Sabaghan, A.; Roohi, E. Heat transfer and entropy generation in a microchannel with longitudinal vortex generators using nanofluids. Energy 2016, 101, 190–201. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. The Schneider problem for a micropolar fluid. Fluid Dyn. Res. 2006, 38, 489. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Mixed convection stagnation point flow of a micropolar fluid towards a stretching sheet. Meccanica 2008, 43, 411–418. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Khan, I.; Seikh, A.H.; Sherif, E.S.M. Entropy generation and dual solutions in mixed convection stagnation point flow of micropolar Ti6Al4V nanoparticle along a Riga surface. Processes 2019, 8, 14. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; El-Sayed Sherif, M.; Waini, I.; Chu, Y.-M.; Pop, I. Radiative mixed convective flow induced by hybrid nanofluid over a porous vertical cylinder in a porous media with irregular heat sink/source. Case Stud. Therm. Eng. 2022, 30, 101711. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation points on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor. Notes 2000, 2000, 1–27. [Google Scholar]
- Shampine, L.F.; Gladwell, I. Thompson. S. Solving ODEs with Matlab; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Shah, S.H.A.M.; Suleman, M.; Khan, U. Dual solution of MHD mixed convection flow and heat transfer over a shrinking sheet subject to thermal radiation. Partial. Differ. Equ. Appl. Math. 2022, 6, 100412. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Amin, N.; Campean, D.; Pop, I. Steady mixed convection flow of a micropolar fluid near the stagnation point on a vertical surface. Int. J. Numer. Methods Heat Fluid Flow 2005, 15, 654–670. [Google Scholar] [CrossRef]



| Properties | Pr | |||||
|---|---|---|---|---|---|---|
| Water | 997.1 | 4179 | 21 | 0.613 | 6.2 | |
| Alumina | 3970 | 765 | 0.85 | 40 | ||
| Copper | 8933 | 385 | 1.67 | 400 | --- |
| Lok et al. [50] | Present Solution | ||||
|---|---|---|---|---|---|
| FBS | SBS | FBS | SBS | ||
| −1.1 | 0.0 | 0.631500 | −0.350112 | 0.631412 | −0.350102 |
| −1.4 | - | 0.440161 | −0.494103 | 0.440116 | −0.494124 |
| −1.7 | - | 0.225110 | −0.574153 | 0.225075 | −0.574135 |
| −2.0 | - | −0.039513 | −0.578523 | −0.039541 | −0.578493 |
| −1.1 | 3.0 | 0.338030 | - | 0.337967 | - |
| −1.4 | - | 0.272370 | −0.232634 | 0.272212 | −0.232728 |
| −1.7 | - | 0.202475 | −0.273943 | 0.202345 | −0.273934 |
| −2.0 | - | 0.126644 | −0.030171 | 0.126452 | −0.030198 |
| Lok et al. [50] | Present Solution | ||||
|---|---|---|---|---|---|
| FBS | SBS | FBS | SBS | ||
| −1.1 | 0.0 | 0.623635 | −0.174194 | 0.623650 | −0.174172 |
| −1.4 | - | 0.590886 | −0.044680 | 0.590846 | −0.044371 |
| −1.7 | - | 0.549045 | 0.073812 | 0.590150 | 0.073804 |
| −2.0 | - | 0.486596 | 0.198590 | 0.486586 | 0.198590 |
| −1.1 | 3.0 | 0.541705 | - | 0.541039 | - |
| −1.4 | - | 0.523084 | −0.149594 | 0.523015 | −0.149688 |
| −1.7 | - | 0.502440 | −0.059305 | 0.502333 | −0.059348 |
| −2.0 | - | 0.477867 | 0.020600 | 0.477732 | 0.020533 |
| FBS | SBS | ||||
|---|---|---|---|---|---|
| 0.025 | 0.25 | 0.20 | 1.0 | 3.2811 | 1.2167 |
| 0.030 | - | - | - | 3.4592 | 1.2056 |
| 0.035 | - | - | - | 3.6352 | 1.1979 |
| 0.025 | 0.25 | 0.20 | 1.0 | 3.2811 | 1.2167 |
| - | 0.30 | - | - | 3.2775 | 1.2558 |
| - | 0.35 | - | - | 3.2733 | 1.2952 |
| 0.025 | 0.25 | 0.20 | 1.0 | 3.2811 | 1.2167 |
| - | - | 0.25 | - | 3.4014 | 1.1981 |
| - | - | 0.30 | - | 3.5140 | 1.1882 |
| 0.025 | 0.25 | 0.20 | 0.90 | 2.8005 | 1.4393 |
| - | - | - | 0.95 | 3.0547 | 1.3151 |
| - | - | - | 1.0 | 3.2811 | 1.2167 |
| FBS | SBS | |||
|---|---|---|---|---|
| 0.025 | 0.25 | 0.5 | 0.8057 | −0.3938 |
| 0.030 | - | - | 0.8956 | −0.4363 |
| 0.035 | - | - | 0.9843 | −0.4786 |
| 0.025 | 0.25 | 0.5 | 0.8057 | −0.3938 |
| - | 0.30 | - | 0.7696 | −0.3929 |
| - | 0.35 | - | 0.7344 | −0.3909 |
| 0.025 | 0.25 | 0.1 | 0.8144 | −0.3519 |
| - | - | 0.3 | 0.8099 | −0.3745 |
| - | - | 0.5 | 0.8057 | −0.3938 |
| FBS | SBS | |||
|---|---|---|---|---|
| 0.025 | 2.0 | 0.1 | 2.1035 | −6.8374 |
| 0.030 | - | - | 2.2358 | −7.3791 |
| 0.035 | - | - | 2.3492 | −7.9004 |
| 0.025 | 1.5 | 0.1 | 2.0141 | −7.1554 |
| - | 2.0 | - | 2.1035 | −6.8374 |
| - | 2.5 | - | 2.2270 | −6.5757 |
| 0.025 | 2.0 | 0.1 | 2.1035 | −6.8374 |
| - | - | 0.2 | 1.8660 | −6.9680 |
| - | - | 0.3 | 1.6205 | −7.0865 |
| - | −0.1 | 2.5575 | −6.5426 | |
| - | −0.2 | 2.7750 | −6.3797 | |
| - | −0.3 | 2.9868 | −6.2073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, U.; Zaib, A.; Ishak, A.; Alotaibi, A.M.; Eldin, S.M.; Akkurt, N.; Waini, I.; Madhukesh, J.K. Stability Analysis of Buoyancy Magneto Flow of Hybrid Nanofluid through a Stretchable/Shrinkable Vertical Sheet Induced by a Micropolar Fluid Subject to Nonlinear Heat Sink/Source. Magnetochemistry 2022, 8, 188. https://doi.org/10.3390/magnetochemistry8120188
Khan U, Zaib A, Ishak A, Alotaibi AM, Eldin SM, Akkurt N, Waini I, Madhukesh JK. Stability Analysis of Buoyancy Magneto Flow of Hybrid Nanofluid through a Stretchable/Shrinkable Vertical Sheet Induced by a Micropolar Fluid Subject to Nonlinear Heat Sink/Source. Magnetochemistry. 2022; 8(12):188. https://doi.org/10.3390/magnetochemistry8120188
Chicago/Turabian StyleKhan, Umair, Aurang Zaib, Anuar Ishak, Abeer M. Alotaibi, Sayed M. Eldin, Nevzat Akkurt, Iskandar Waini, and Javali Kotresh Madhukesh. 2022. "Stability Analysis of Buoyancy Magneto Flow of Hybrid Nanofluid through a Stretchable/Shrinkable Vertical Sheet Induced by a Micropolar Fluid Subject to Nonlinear Heat Sink/Source" Magnetochemistry 8, no. 12: 188. https://doi.org/10.3390/magnetochemistry8120188
APA StyleKhan, U., Zaib, A., Ishak, A., Alotaibi, A. M., Eldin, S. M., Akkurt, N., Waini, I., & Madhukesh, J. K. (2022). Stability Analysis of Buoyancy Magneto Flow of Hybrid Nanofluid through a Stretchable/Shrinkable Vertical Sheet Induced by a Micropolar Fluid Subject to Nonlinear Heat Sink/Source. Magnetochemistry, 8(12), 188. https://doi.org/10.3390/magnetochemistry8120188








