MHD Nanofluid Convection and Phase Change Dynamics in a Multi-Port Vented Cavity Equipped with a Sinusoidal PCM-Packed Bed System
Abstract
1. Introduction
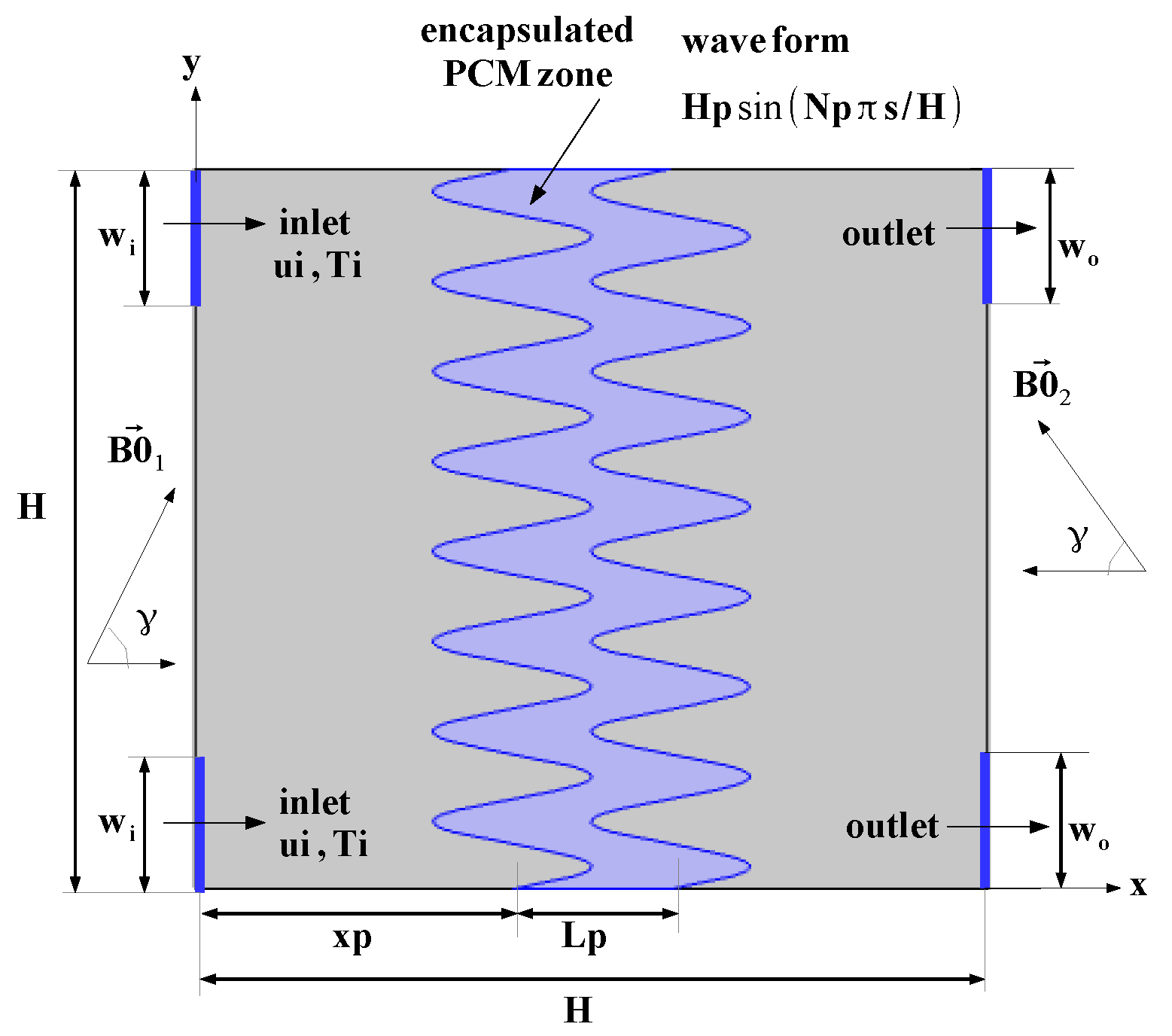
2. Computational Model of PCM-PB Installed System
3. Results and Discussion
4. Conclusions
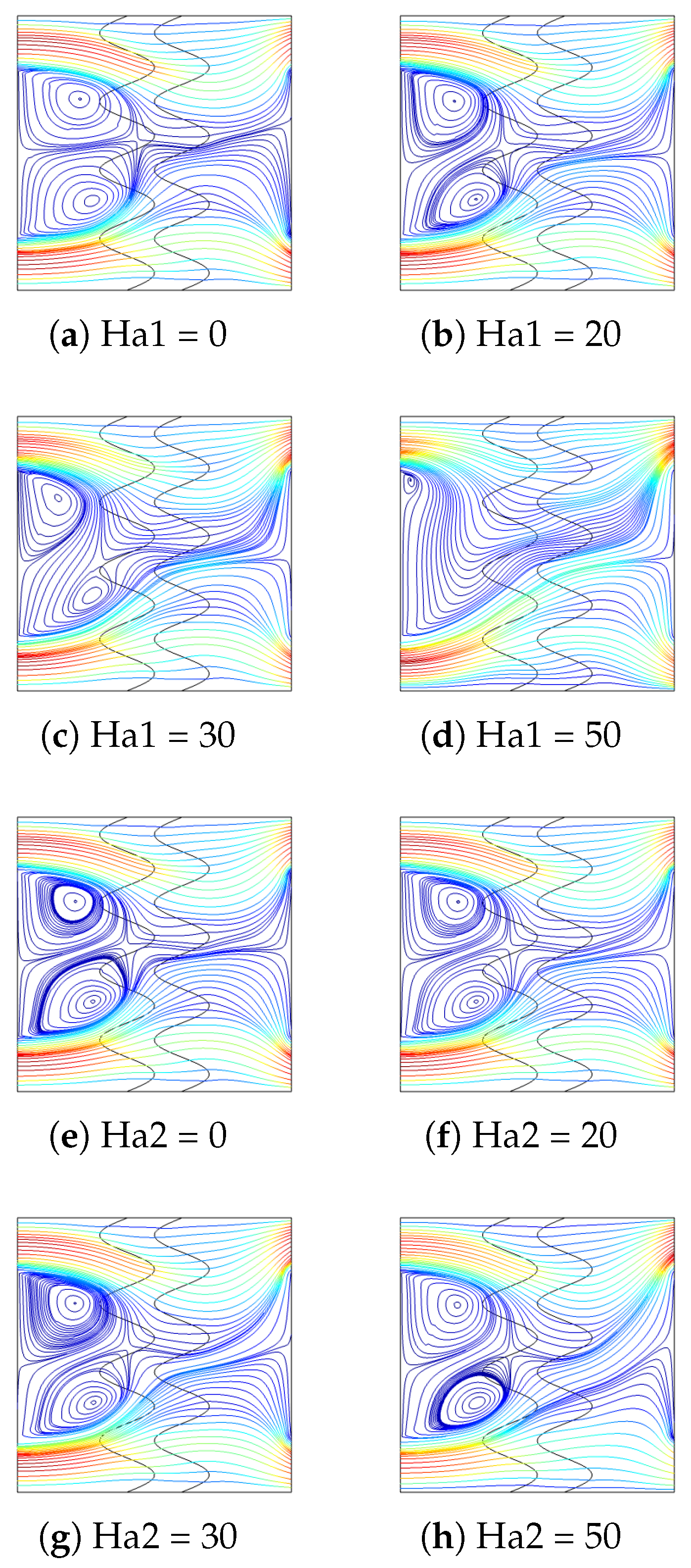
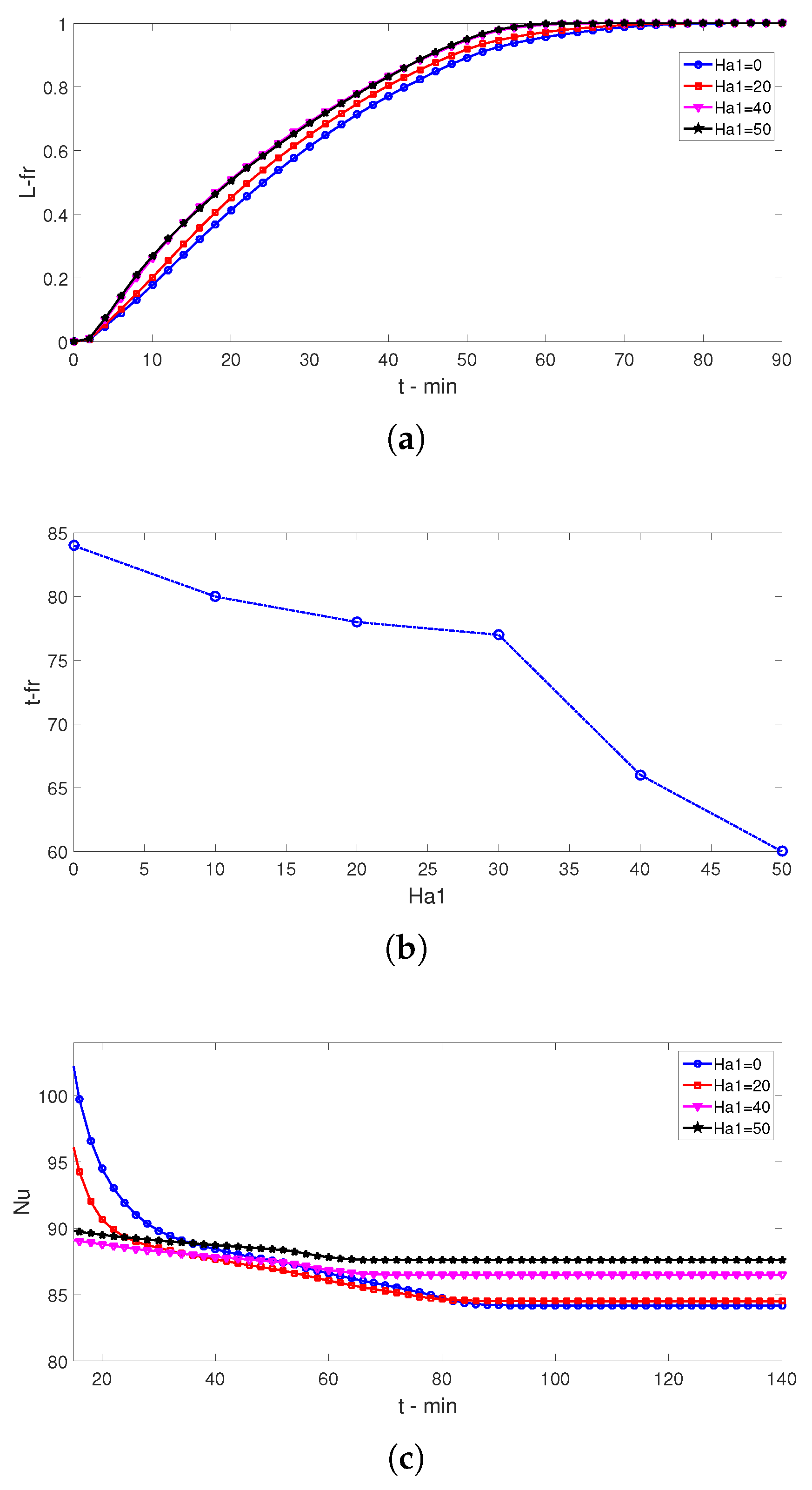
- When the MgF strength of the first domain rises, the PC-P process becomes fast due to the vortex suppression and rise of velocity in the near wall region. When the value of Ha1 rises from 0 to 30, reduction of t-fr is only 8.3%, whereas it is 22% when increasing Ha1 from 30 to 50.
- When cases without (Ha1 = 0) and with (Ha1 = 50) MgF in the VEN-C are compared, the average Nu is 9% higher at t = 18 min and 3.5% lower at t = 85 min.
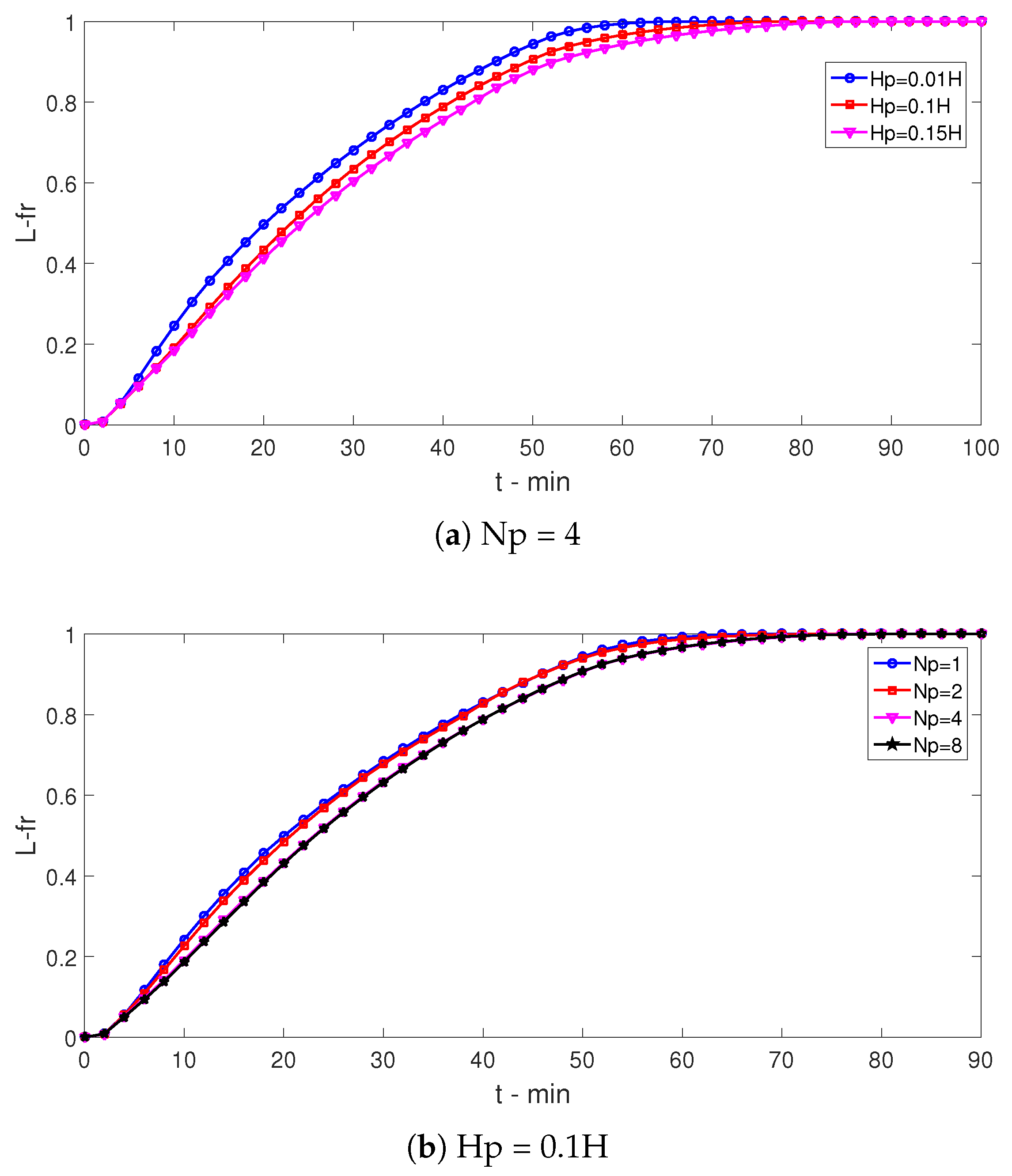
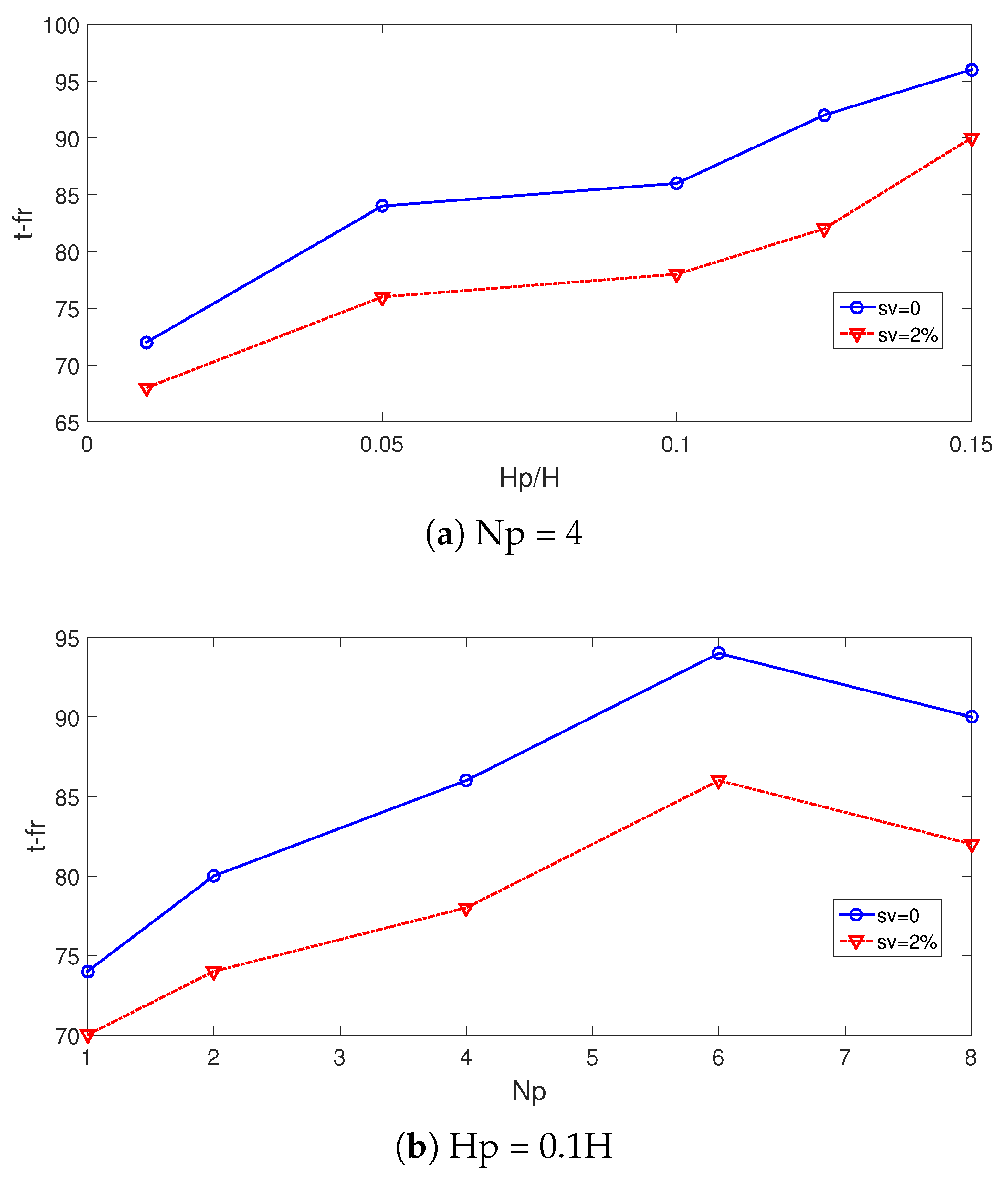
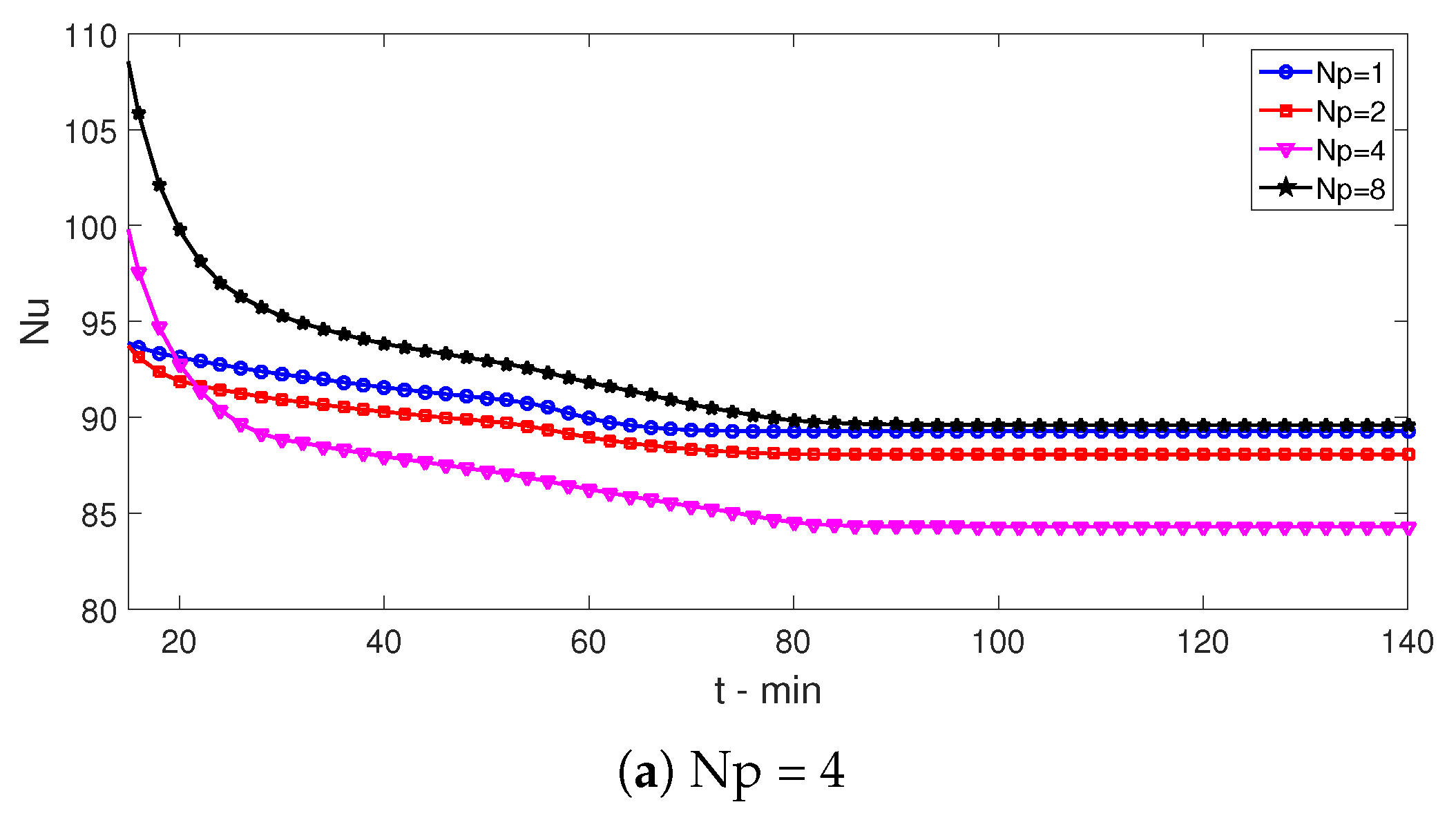
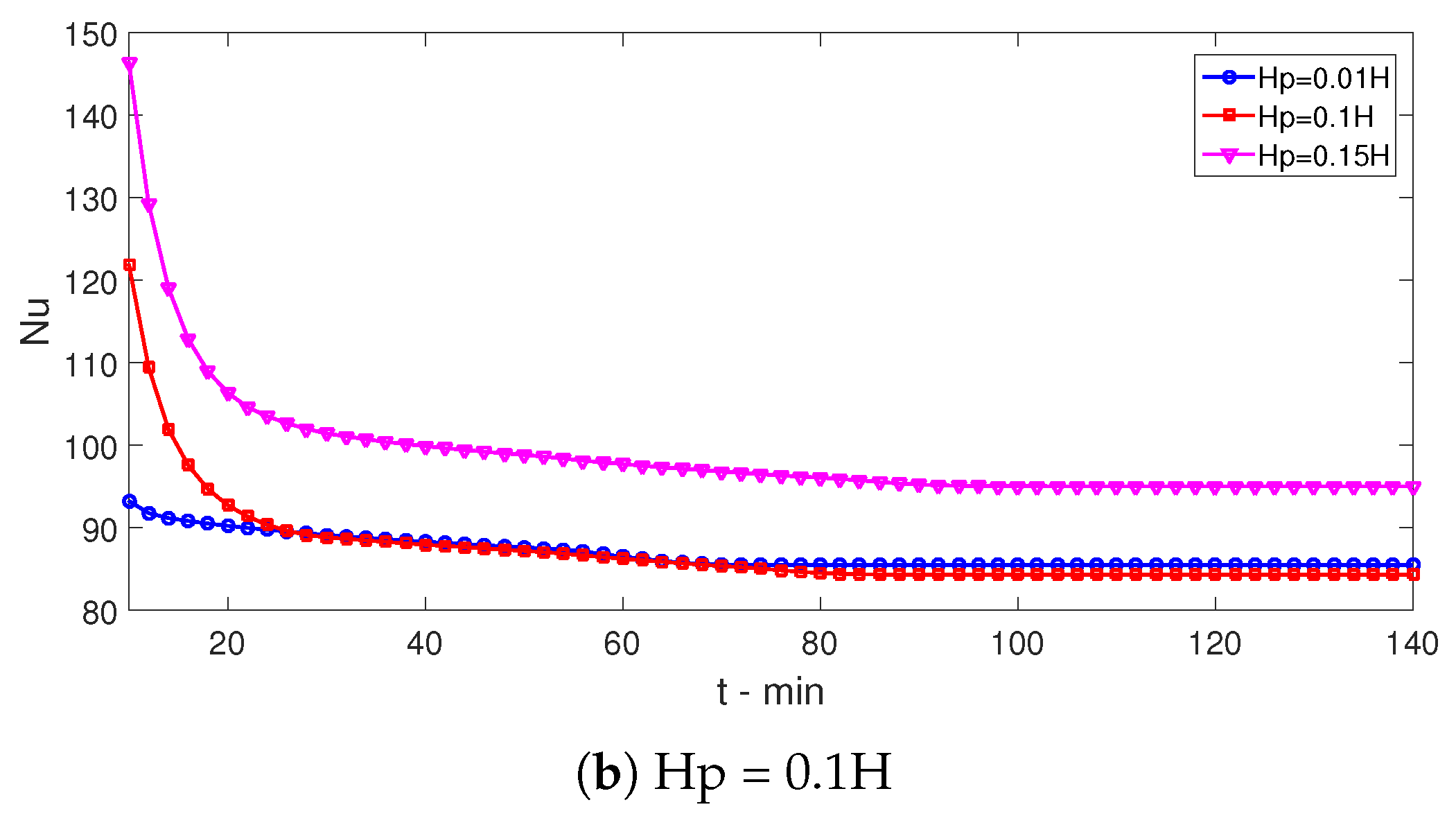
- When wave amplitude rises, complete transition time (t-fr) increases for nanofluid and pure fluid cases. The amount of the rise is about 33% when Hp rises from 0.01 H to 0.15 H. When wave number rises from Np = 1 to Np = 6, t-fr increases by about 23% with nanofluid as the HT fluid.
- Most favorable cases in terms of HT are obtained with higher amplitude and wave number. When wave amplitude rises, up to a 20% rise of HT is obtained at t = 20 min.
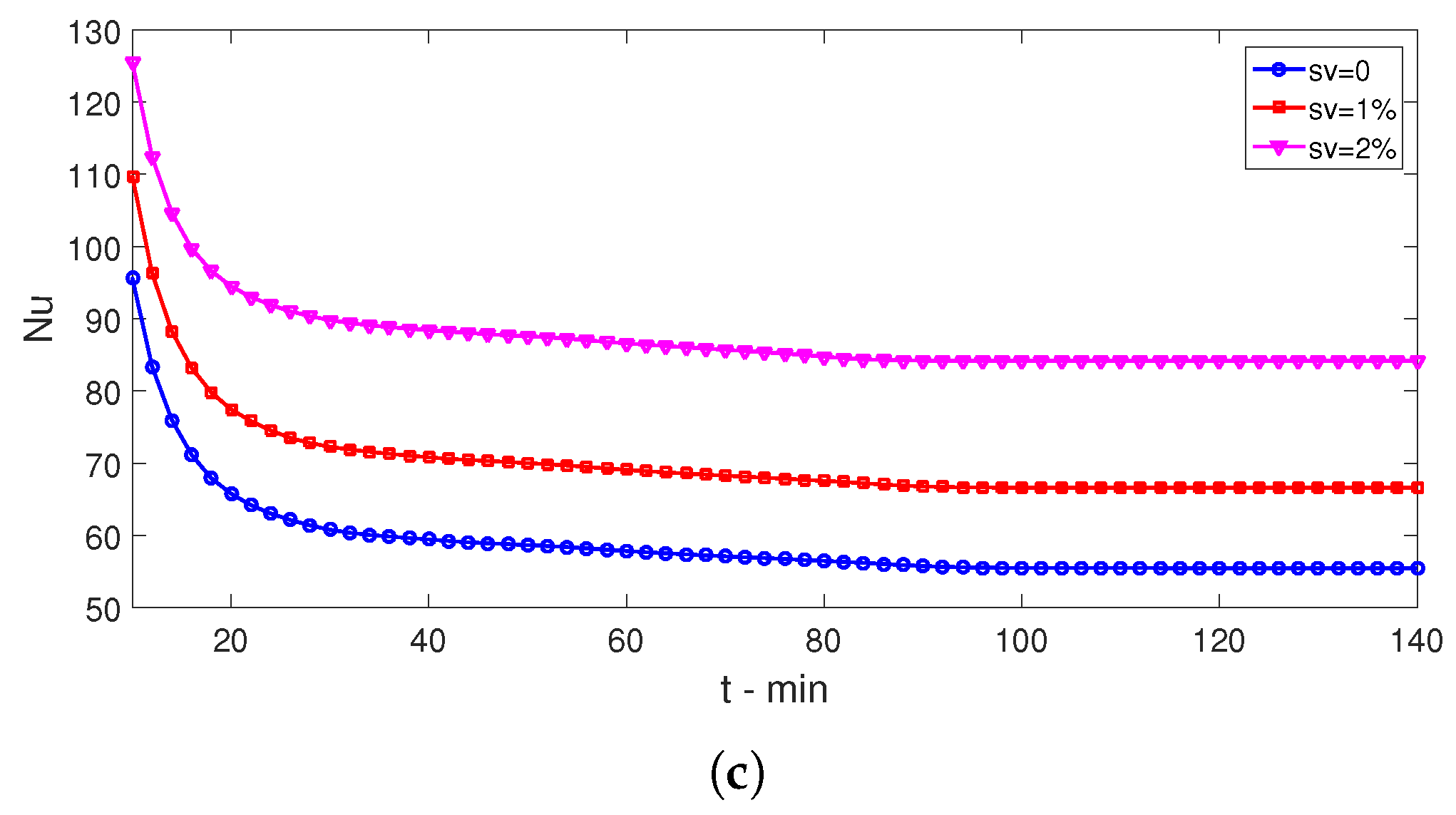
- When nanofluids are used, phase change is accelerated and thermal performance is also improved. Phase change process time is reduced by 15% at the highest nanoparticle loading as compared to the case with pure fluid while spatial average Nu rises by about 55%.
- The wavy shape of the PCM-PB region and varying its geometrical form provide good control opportunity for the phase change process and thermal performance improvement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| H | cavity size |
| Ha | Hartmann number |
| Hp | wave amplitude |
| k | thermal conductivity |
| L | latent heat of fusion |
| L-fr | liquid fraction |
| n | unit normal vector |
| Np | wave number |
| Nu | Nusselt number |
| p | pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| t | time |
| t-fr | complete transition time |
| T | temperature |
| T | melting temperature |
| w | inlet port size |
| w | outlet port size |
| u, v | velocity components |
| Greek Characters | |
| kinematic viscosity | |
| density of the fluid | |
| porosity | |
| permeability | |
| solid volume fraction | |
| magnetic field inclination | |
| Subscripts | |
| c | cold |
| h | hot |
| m | average |
| nf | nanofluid |
| p | solid particle |
| Abbreviations | |
| FEM | finite element method |
| HT | heat transfer |
| MgF | magnetic field |
| PB | packed bed |
| PCM | phase change material |
| VEN-C | vented cavity |
References
- Saeidi, S.; Khodadadi, J. Transient flow and heat transfer leading to periodic state in a cavity with inlet and outlet ports due to incoming flow oscillation. Int. J. Heat Mass Transf. 2007, 50, 530–538. [Google Scholar] [CrossRef]
- Ismael, M.A.; Jasim, H.F. Role of the fluid-structure interaction in mixed convection in a vented cavity. Int. J. Mech. Sci. 2018, 135, 190–202. [Google Scholar] [CrossRef]
- Saeidi, S.; Khodadadi, J. Forced convection in a square cavity with inlet and outlet ports. Int. J. Heat Mass Transf. 2006, 49, 1896–1906. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Fluid-solid interaction of elastic-step type corrugation effects on the mixed convection of nanofluid in a vented cavity with magnetic field. Int. J. Mech. Sci. 2019, 152, 185–197. [Google Scholar] [CrossRef]
- Shih, Y.C.; Khodadadi, J.; Nien, S.W.; Zeng, Y.; Huang, X.L. Impact of an oscillating guide vane on the thermo-hydraulic fields in a square cavity with single inlet and outlet ports. Int. J. Heat Mass Transf. 2019, 128, 1184–1200. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Magnetohydrodynamics forced convection of nanofluid in multi-layered U-shaped vented cavity with a porous region considering wall corrugation effects. Int. Commun. Heat Mass Transf. 2020, 113, 104551. [Google Scholar] [CrossRef]
- Hamzah, H.; Canpolat, C.; Jasim, L.M.; Sahin, B. Hydrothermal index and entropy generation of a heated cylinder placed between two oppositely rotating cylinders in a vented cavity. Int. J. Mech. Sci. 2021, 201, 106465. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. Simulation of nanofluid heat transfer in presence of magnetic field: A review. Int. J. Heat Mass Transf. 2017, 115, 1203–1233. [Google Scholar] [CrossRef]
- Kabeel, A.; El-Said, E.M.; Dafea, S. A review of magnetic field effects on flow and heat transfer in liquids: Present status and future potential for studies and applications. Renew. Sustain. Energy Rev. 2015, 45, 830–837. [Google Scholar] [CrossRef]
- Alghamdi, W.; Alsubie, A.; Kumam, P.; Saeed, A.; Gul, T. MHD hybrid nanofluid flow comprising the medication through a blood artery. Sci. Rep. 2021, 11, 11621. [Google Scholar] [CrossRef]
- Kefayati, G.R. Simulation of heat transfer and entropy generation of MHD natural convection of non-Newtonian nanofluid in an enclosure. Int. J. Heat Mass Transf. 2016, 92, 1066–1089. [Google Scholar] [CrossRef]
- Abbassi, H.; Nassrallah, S.B. MHD flow and heat transfer in a backward-facing step. Int. Commun. Heat Mass Transf. 2007, 34, 231–237. [Google Scholar] [CrossRef]
- Benzema, M.; Benkahla, Y.K.; Labsi, N.; Ouyahia, S.E.; El Ganaoui, M. Second law analysis of MHD mixed convection heat transfer in a vented irregular cavity filled with Ag–MgO/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 137, 1113–1132. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Chamkha, A.J. MHD mixed convection of nanofluid in a three-dimensional vented cavity with surface corrugation and inner rotating cylinder. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 1637–1660. [Google Scholar] [CrossRef]
- Ali, H.M.; Arshad, W. Effect of channel angle of pin-fin heat sink on heat transfer performance using water based graphene nanoplatelets nanofluids. Int. J. Heat Mass Transf. 2017, 106, 465–472. [Google Scholar] [CrossRef]
- Baïri, A. Experimental study on enhancement of free convective heat transfer in a tilted hemispherical enclosure by using Water-ZnO nanofluid saturated porous materials. Appl. Therm. Eng. 2019, 148, 992–998. [Google Scholar] [CrossRef]
- Esfe, M.H.; Esfandeh, S.; Saedodin, S.; Rostamian, H. Experimental evaluation, sensitivity analyzation and ANN modeling of thermal conductivity of ZnO-MWCNT/EG-water hybrid nanofluid for engineering applications. Appl. Therm. Eng. 2017, 125, 673–685. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Kasaeian, A.; Daneshazarian, R.; Mahian, O.; Kolsi, L.; Chamkha, A.J.; Wongwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Bashirnezhad, K.; Bazri, S.; Safaei, M.R.; Goodarzi, M.; Dahari, M.; Mahian, O.; Dalkılıça, A.S.; Wongwises, S. Viscosity of nanofluids: A review of recent experimental studies. Int. Commun. Heat Mass Transf. 2016, 73, 114–123. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Jena, S.K.; Mahapatra, S.K. MHD convection of nanofluids: A review. J. Nanofluids 2015, 4, 271–292. [Google Scholar] [CrossRef]
- Izadi, A.; Siavashi, M.; Rasam, H.; Xiong, Q. MHD enhanced nanofluid mediated heat transfer in porous metal for CPU cooling. Appl. Therm. Eng. 2020, 168, 114843. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. MHD Pulsating forced convection of nanofluid over parallel plates with blocks in a channel. Int. J. Mech. Sci. 2019, 157, 726–740. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Izadi, M.; Mohebbi, R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT–Fe3O4/water hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 132, 1087–1104. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castell, A.; Barreneche, C.d.; De Gracia, A.; Fernández, A. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Ebadi, S.; Tasnim, S.H.; Aliabadi, A.A.; Mahmud, S. Melting of nano-PCM inside a cylindrical thermal energy storage system: Numerical study with experimental verification. Energy Convers. Manag. 2018, 166, 241–259. [Google Scholar] [CrossRef]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal–external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical modeling of nano enhanced PCM solidification in an enclosure with metallic fin. J. Mol. Liq. 2018, 259, 424–438. [Google Scholar] [CrossRef]
- Madruga, S.; Mendoza, C. Heat transfer performance and thermal energy storage in nano-enhanced phase change materials driven by thermocapillarity. Int. Commun. Heat Mass Transf. 2021, 129, 105672. [Google Scholar] [CrossRef]
- Zhao, C.; Opolot, M.; Liu, M.; Bruno, F.; Mancin, S.; Hooman, K. Numerical study of melting performance enhancement for PCM in an annular enclosure with internal-external fins and metal foams. Int. J. Heat Mass Transf. 2020, 150, 119348. [Google Scholar] [CrossRef]
- Madruga, S.; Mischlich, G.S. Melting dynamics of a phase change material (PCM) with dispersed metallic nanoparticles using transport coefficients from empirical and mean field models. Appl. Therm. Eng. 2017, 124, 1123–1133. [Google Scholar] [CrossRef]
- Al-Jethelah, M.; Tasnim, S.H.; Mahmud, S.; Dutta, A. Nano-PCM filled energy storage system for solar-thermal applications. Renew. Energy 2018, 126, 137–155. [Google Scholar] [CrossRef]
- Kasaeian, A.; Bahrami, L.; Pourfayaz, F.; Khodabandeh, E.; Yan, W.M. Experimental studies on the applications of PCMs and nano-PCMs in buildings: A critical review. Energy Build. 2017, 154, 96–112. [Google Scholar] [CrossRef]
- Khodadadi, J.; Hosseinizadeh, S. Nanoparticle-enhanced phase change materials (NEPCM) with great potential for improved thermal energy storage. Int. Commun. Heat Mass Transf. 2007, 34, 534–543. [Google Scholar] [CrossRef]
- Rostami, S.; Afrand, M.; Shahsavar, A.; Sheikholeslami, M.; Kalbasi, R.; Aghakhani, S.; Shadloo, M.S.; Oztop, H.F. A review of melting and freezing processes of PCM/nano-PCM and their application in energy storage. Energy 2020, 211, 118698. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Analysis of hybrid nanofluid and surface corrugation in the laminar convective flow through an encapsulated PCM filled vertical cylinder and POD-based modeling. Int. J. Heat Mass Transf. 2021, 178, 121623. [Google Scholar] [CrossRef]
- Regin, A.F.; Solanki, S.; Saini, J. Heat transfer characteristics of thermal energy storage system using PCM capsules: A review. Renew. Sustain. Energy Rev. 2008, 12, 2438–2458. [Google Scholar] [CrossRef]
- Singh, H.; Saini, R.; Saini, J. A review on packed bed solar energy storage systems. Renew. Sustain. Energy Rev. 2010, 14, 1059–1069. [Google Scholar] [CrossRef]
- de Gracia, A.; Cabeza, L.F. Numerical simulation of a PCM packed bed system: A review. Renew. Sustain. Energy Rev. 2017, 69, 1055–1063. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Velraj, R. Numerical investigation of packed bed storage unit filled with PCM encapsulated spherical containers—A comparison between various mathematical models. Int. J. Therm. Sci. 2012, 60, 153–160. [Google Scholar] [CrossRef]
- Regin, A.F.; Solanki, S.; Saini, J. An analysis of a packed bed latent heat thermal energy storage system using PCM capsules: Numerical investigation. Renew. Energy 2009, 34, 1765–1773. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Zadeh, S.M.H.; Mehryan, S.; Pop, I.; Wen, D. Analysis of melting behavior of PCMs in a cavity subject to a non-uniform magnetic field using a moving grid technique. Appl. Math. Model. 2020, 77, 1936–1953. [Google Scholar] [CrossRef]
- Kohyani, M.T.; Ghasemi, B.; Raisi, A.; Aminossadati, S. Melting of cyclohexane–Cu nano-phase change material (nano-PCM) in porous medium under magnetic field. J. Taiwan Inst. Chem. Eng. 2017, 77, 142–151. [Google Scholar] [CrossRef]
- Ghachem, K.; Selimefendigil, F.; Öztop, H.F.; Almeshaal, M.; Alhadri, M.; Kolsi, L. Effects of magnetic field, binary particle loading and rotational conic surface on phase change process in a PCM filled cylinder. Case Stud. Therm. Eng. 2021, 28, 101456. [Google Scholar] [CrossRef]
- Gibanov, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Effect of uniform inclined magnetic field on mixed convection in a lid-driven cavity having a horizontal porous layer saturated with a ferrofluid. Int. J. Heat Mass Transf. 2017, 114, 1086–1097. [Google Scholar] [CrossRef]
- Cimpean, D.; Sheremet, M.; Pop, I. Mixed convection of hybrid nanofluid in a porous trapezoidal chamber. Int. Commun. Heat Mass Transf. 2020, 116, 104627. [Google Scholar] [CrossRef]
- Mohammadnejad, F.; Hossainpour, S. A CFD modeling and investigation of a packed bed of high temperature phase change materials (PCMs) with different layer configurations. J. Energy Storage 2020, 28, 101209. [Google Scholar] [CrossRef]
- Nield, D.; Bejan, A. Convection in Porous Media. In Convection Heat Transfer; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Comsol. Comsol User’s Guide; Comsol AB: Stockholm, Sweden, 2018. [Google Scholar]
- Wakao, N.; Kaguei, S.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds: Correlation of Nusselt numbers. Chem. Eng. Sci. 1979, 34, 325–336. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Nallusamy, N.; Sampath, S.; Velraj, R. Experimental investigation on a combined sensible and latent heat storage system integrated with constant/varying (solar) heat sources. Renew. Energy 2007, 32, 1206–1227. [Google Scholar] [CrossRef]
- Lewis, R.W.; Nithiarasu, P.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Rahman, M.M.; Parvin, S.; Rahim, N.; Islam, M.; Saidur, R.; Hasanuzzaman, M. Effects of Reynolds and Prandtl number on mixed convection in a ventilated cavity with a heat-generating solid circular block. Appl. Math. Model. 2012, 36, 2056–2066. [Google Scholar] [CrossRef]
- Ullah, N.; Nadeem, S.; Saleem, A. Finite element analysis of convective nanofluid equipped in enclosure having both inlet and outlet zones. J. Taiwan Inst. Chem. Eng. 2020, 113, 428–441. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Forced convection of ferrofluids in a vented cavity with a rotating cylinder. Int. J. Therm. Sci. 2014, 86, 258–275. [Google Scholar] [CrossRef]
- Ghasemi, B.; Aminossadati, S.; Raisi, A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int. J. Therm. Sci. 2011, 50, 1748–1756. [Google Scholar] [CrossRef]
- Wolff, F.; Viskanta, R. Solidification of a pure metal at a vertical wall in the presence of liquid superheat. Int. J. Heat Mass Transf. 1988, 31, 1735–1744. [Google Scholar] [CrossRef]

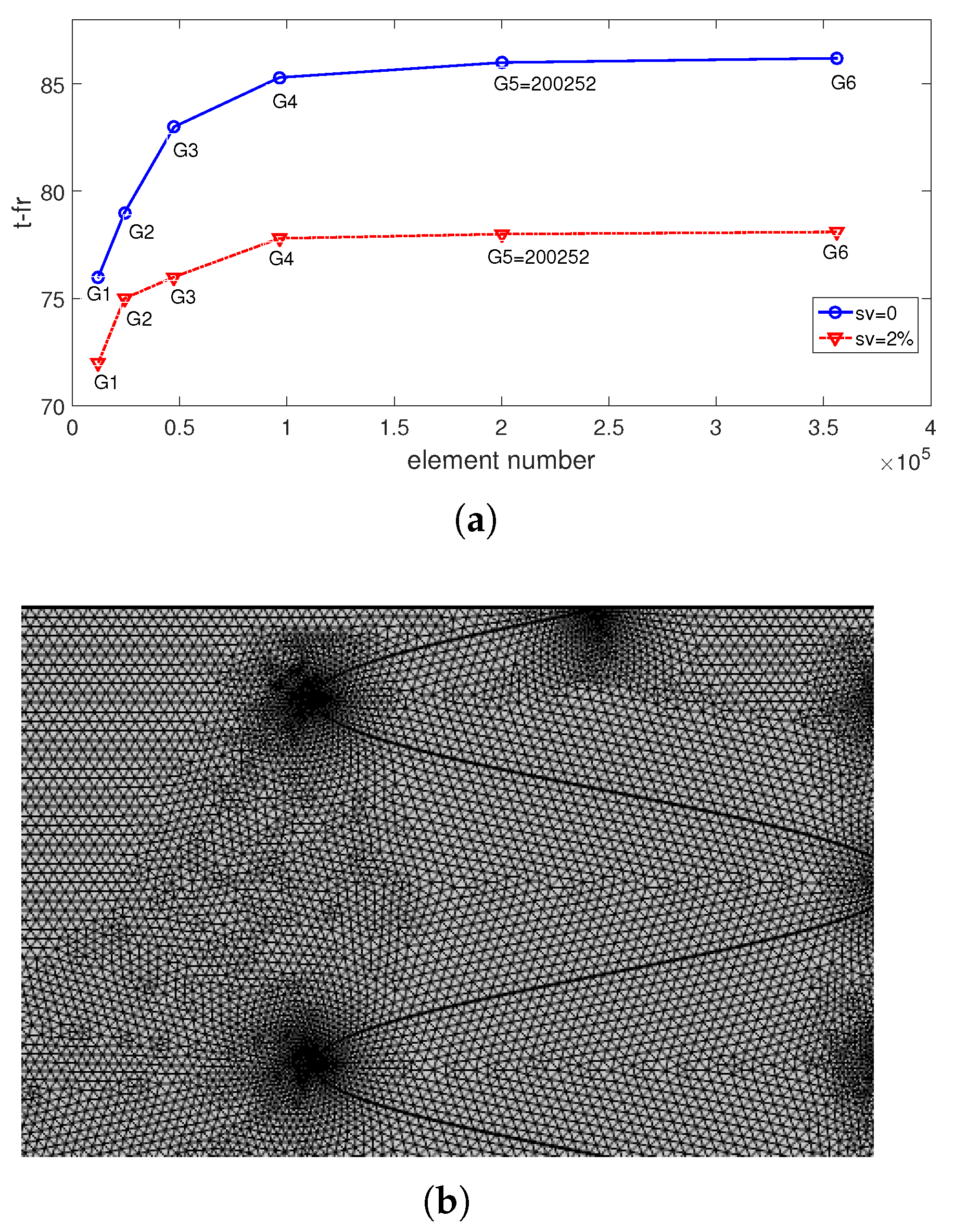
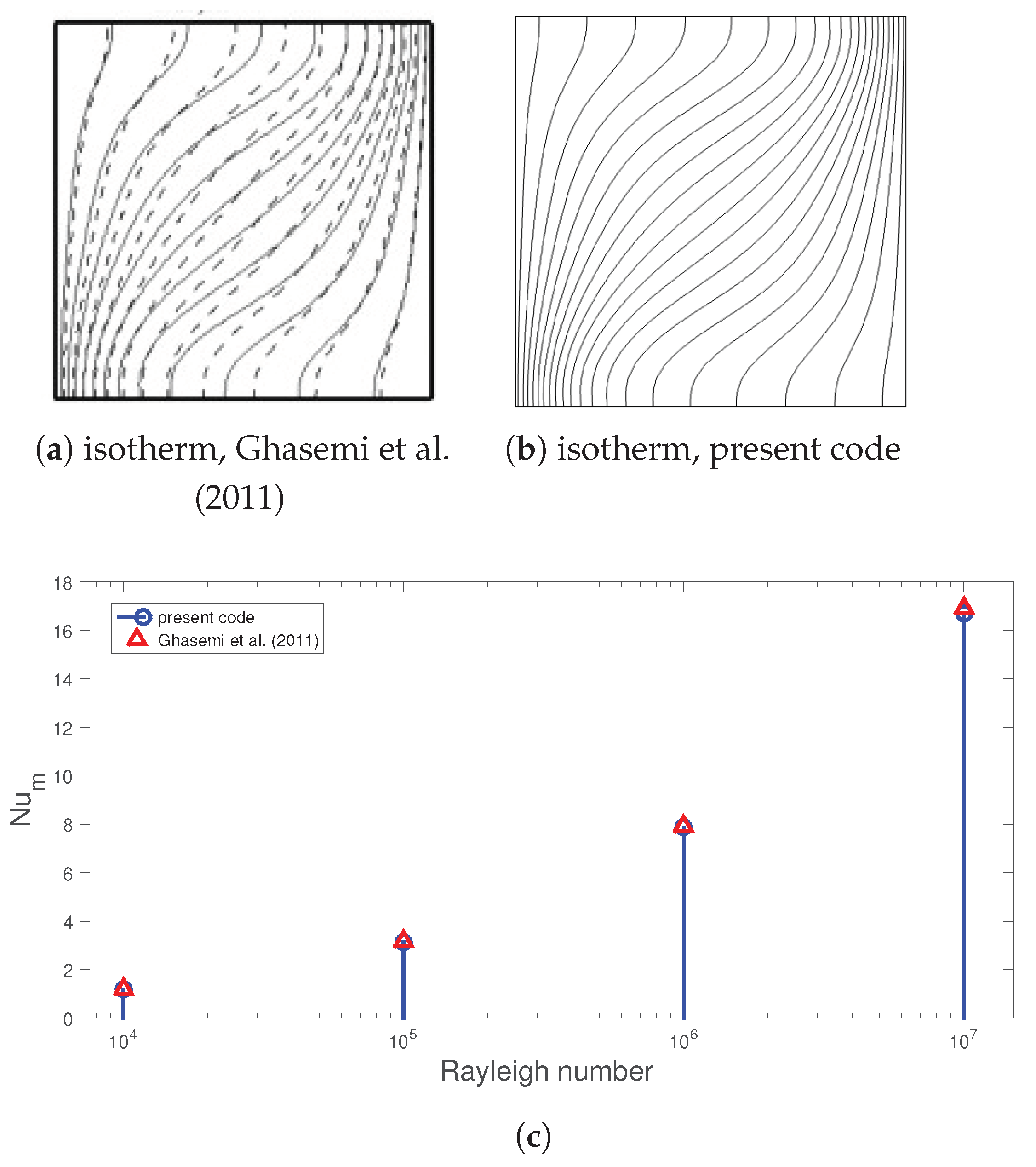
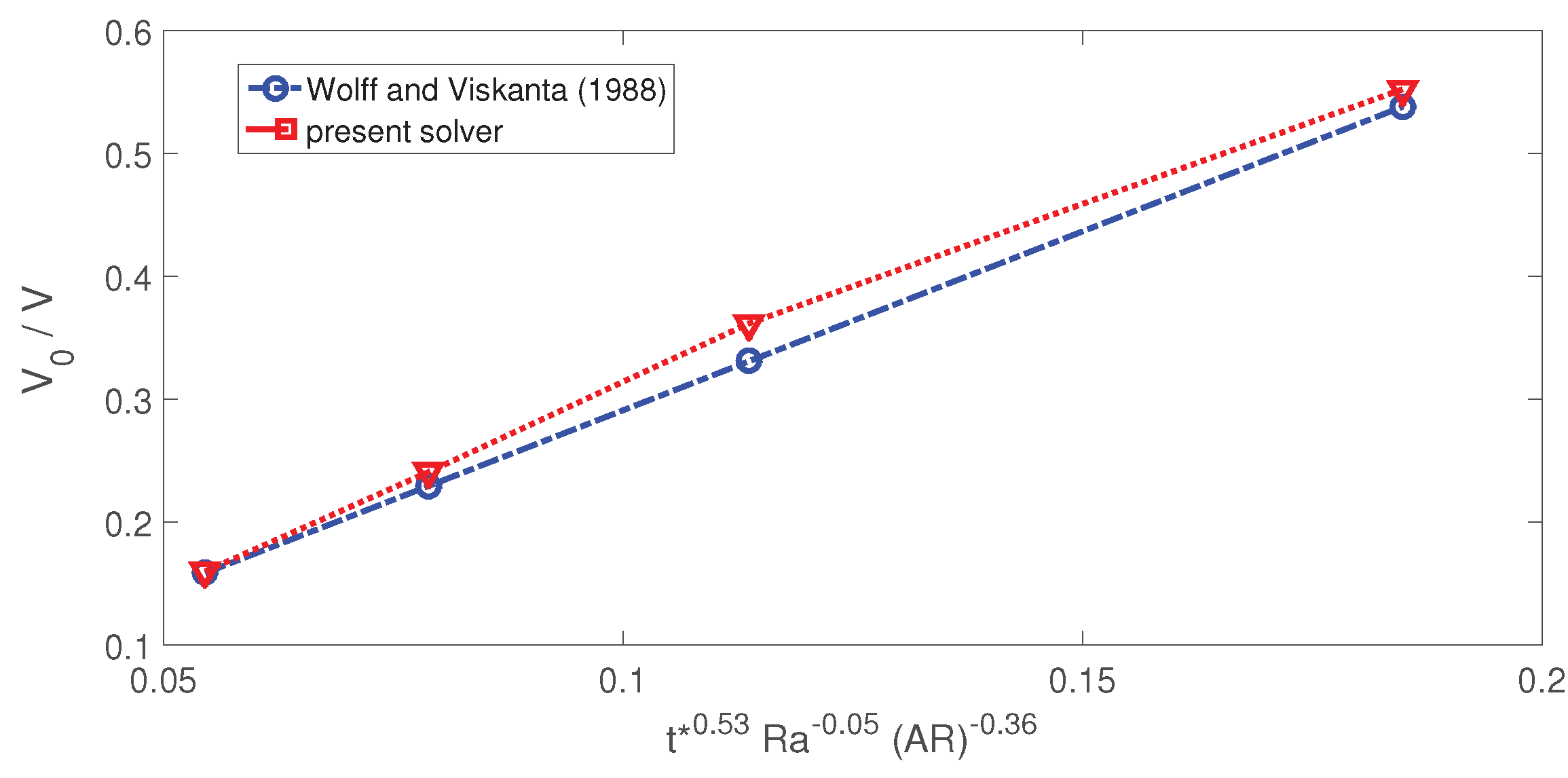



| Property | Value |
|---|---|
| Density-solid (, kg/m3) | 861 |
| Density-liquid (, kg/m3) | 778 |
| Specific heat-solid (Cp, J/kg °C) | 1850 |
| Specific heat-fluid (Cp, J/kg °C) | 2384 |
| Thermal conductivity-solid (k, W/m °C) | 0.40 |
| Thermal conductivity-fluid (k, W/m °C) | 0.15 |
| Melting temperature (Tm, °C) | 60 |
| Latent heat of fusion (L, kJ/kg) | 213 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selimefendigil, F.; Öztop, H.F. MHD Nanofluid Convection and Phase Change Dynamics in a Multi-Port Vented Cavity Equipped with a Sinusoidal PCM-Packed Bed System. Magnetochemistry 2022, 8, 190. https://doi.org/10.3390/magnetochemistry8120190
Selimefendigil F, Öztop HF. MHD Nanofluid Convection and Phase Change Dynamics in a Multi-Port Vented Cavity Equipped with a Sinusoidal PCM-Packed Bed System. Magnetochemistry. 2022; 8(12):190. https://doi.org/10.3390/magnetochemistry8120190
Chicago/Turabian StyleSelimefendigil, Fatih, and Hakan F. Öztop. 2022. "MHD Nanofluid Convection and Phase Change Dynamics in a Multi-Port Vented Cavity Equipped with a Sinusoidal PCM-Packed Bed System" Magnetochemistry 8, no. 12: 190. https://doi.org/10.3390/magnetochemistry8120190
APA StyleSelimefendigil, F., & Öztop, H. F. (2022). MHD Nanofluid Convection and Phase Change Dynamics in a Multi-Port Vented Cavity Equipped with a Sinusoidal PCM-Packed Bed System. Magnetochemistry, 8(12), 190. https://doi.org/10.3390/magnetochemistry8120190







