Mesostructure and Magnetic Properties of SiO2-Co Granular Film on Silicon Substrate
Abstract
1. Introduction
2. Experiment
2.1. Sample Preparation
- (1)
- Class of GFs (SiO2(x at.% Co), at x < 40 at.%) shows dielectric properties since isolated metal particles are dispersed in a dielectric continuum.
- (2)
- Class of GFs (SiO2(x at.% Co), at 40 at.% ≤ x ≤ 85 at.%) demonstrates semiconductor-like (intermediate) properties as metal particles with an increase in x become interconnected to form a maze structure. The electrical conductivity in this regime is due to percolation along the metallic maze and electron tunneling between isolated metal particles. The concentration of Co x ≈ 40 at.% is a percolation threshold, below which only the tunneling process contributes to the conductivity of the granular metal.
- (3)
- Class of GFs (SiO2(x at.% Co), at x > 85 at.%) can be attributed to metals as the volume fraction of the metal x is large, metal grains merge and form a metallic continuum with dielectric inclusions.
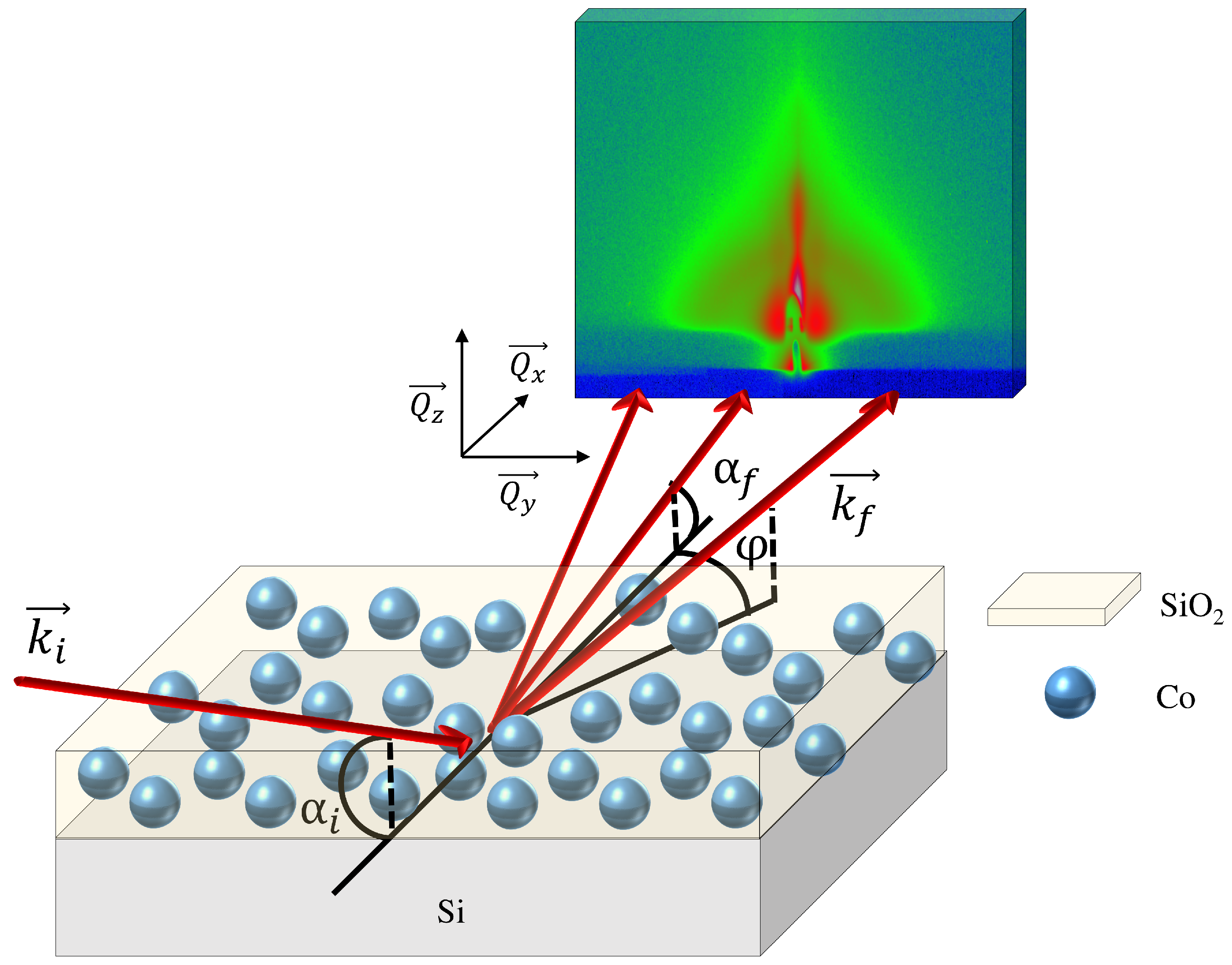
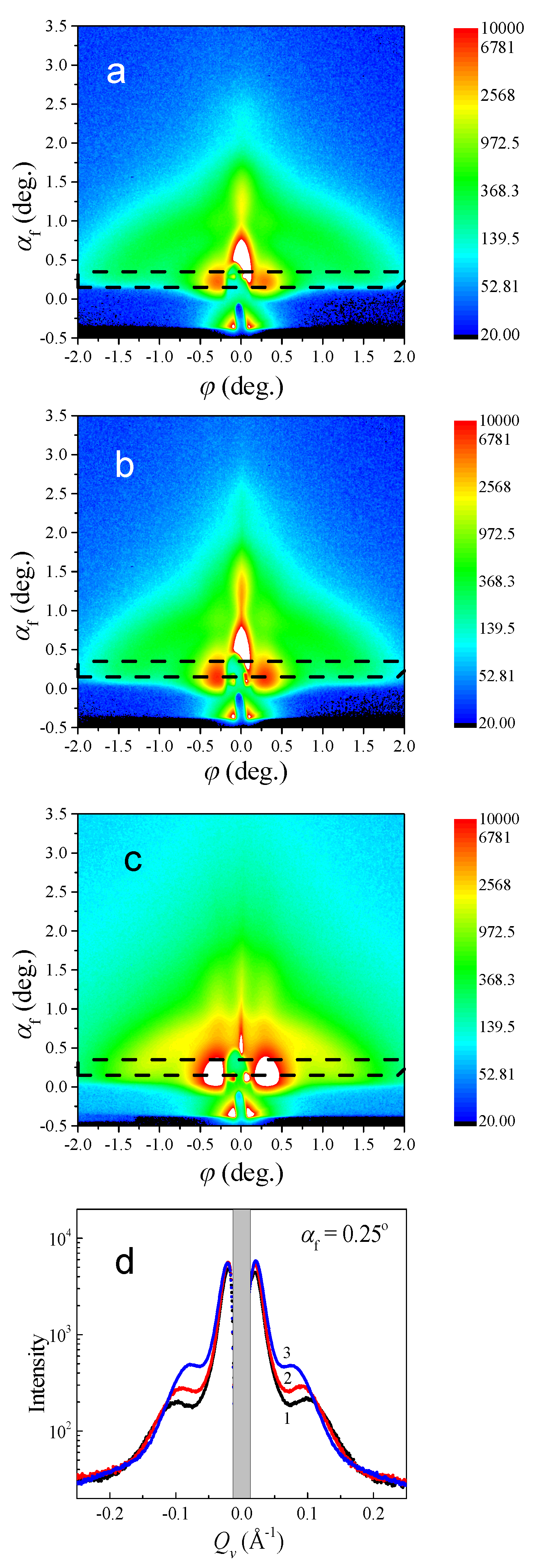
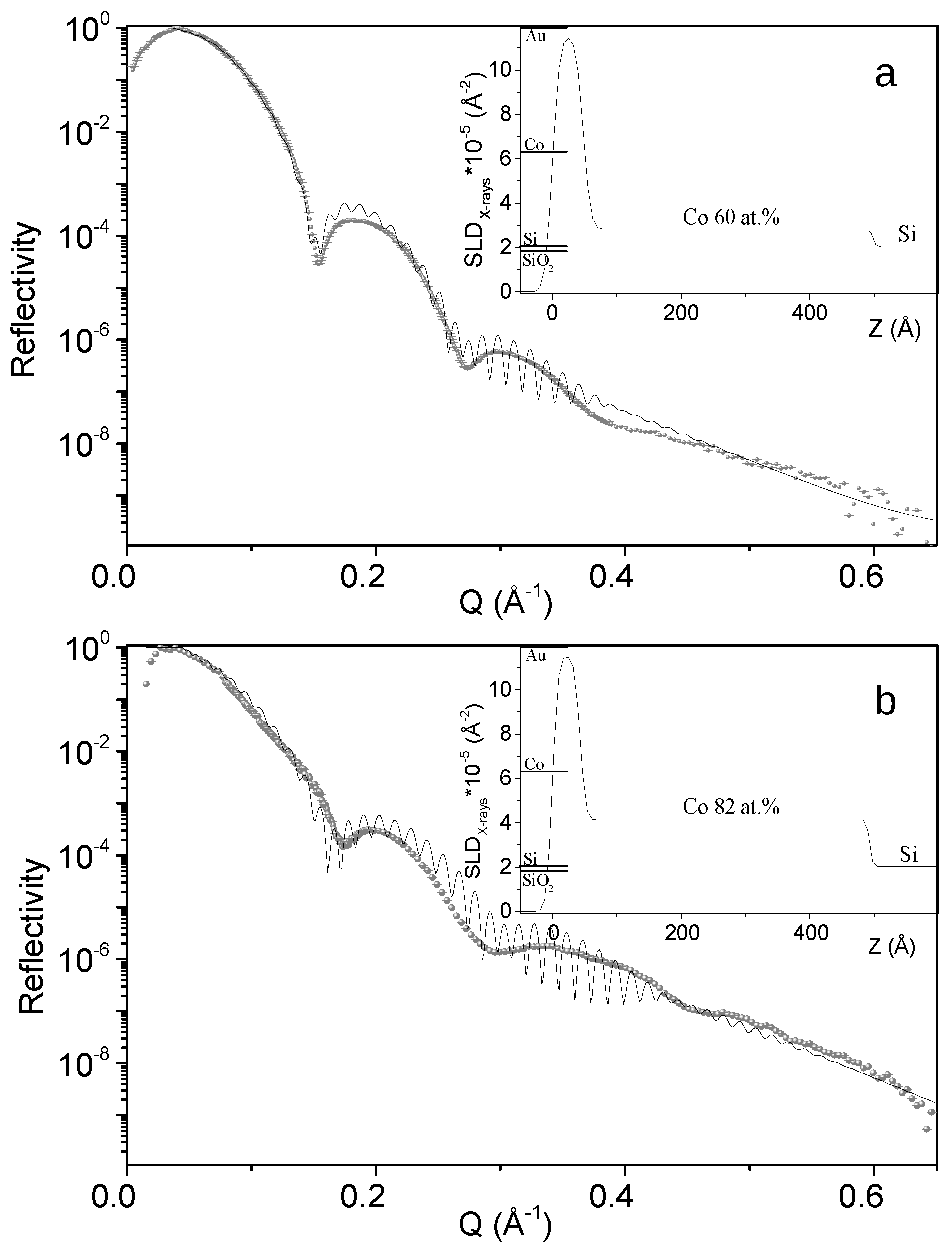
2.2. Grazing Incidence Small Angle X-ray Scattering and X-ray Reflectometry
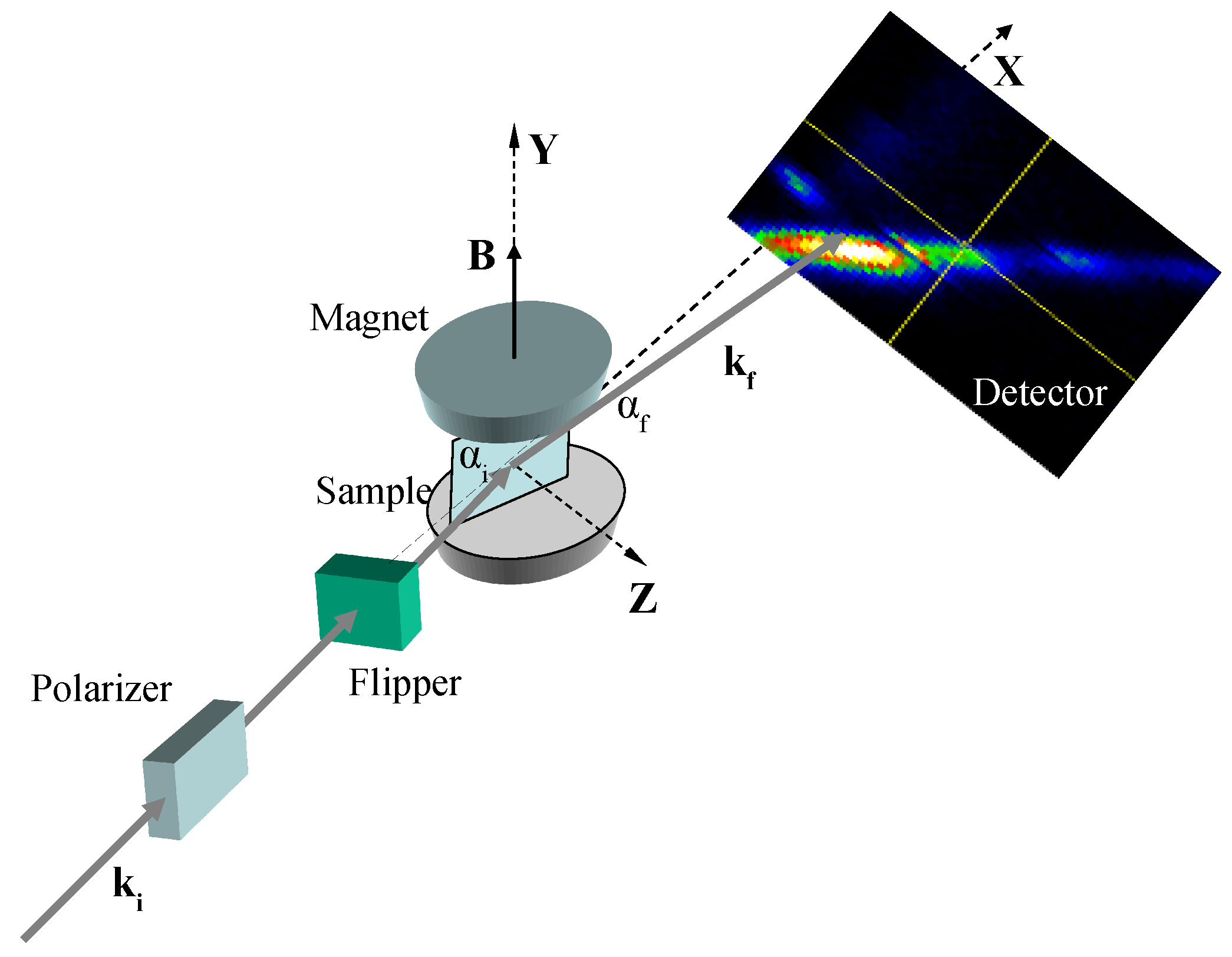
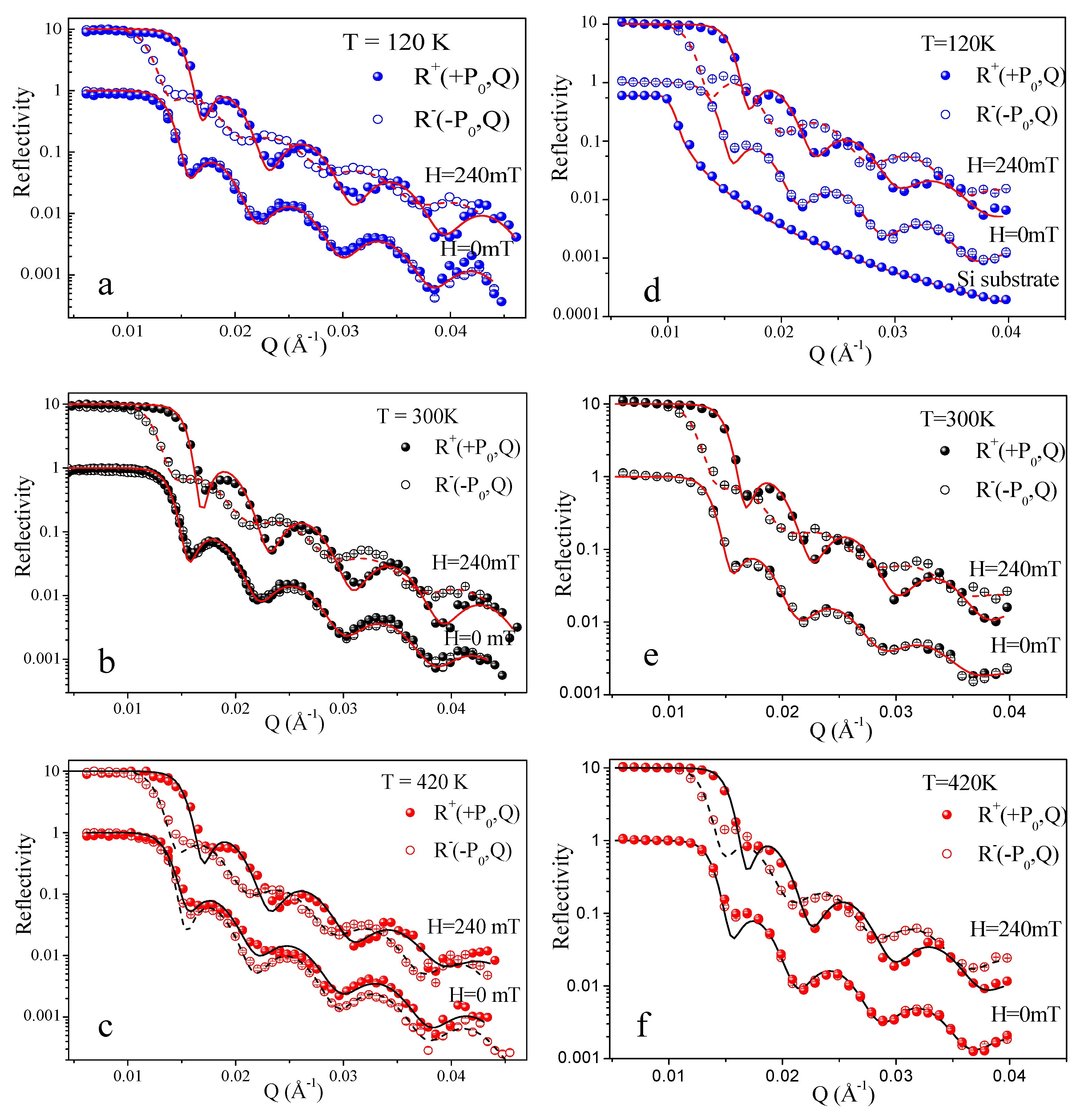
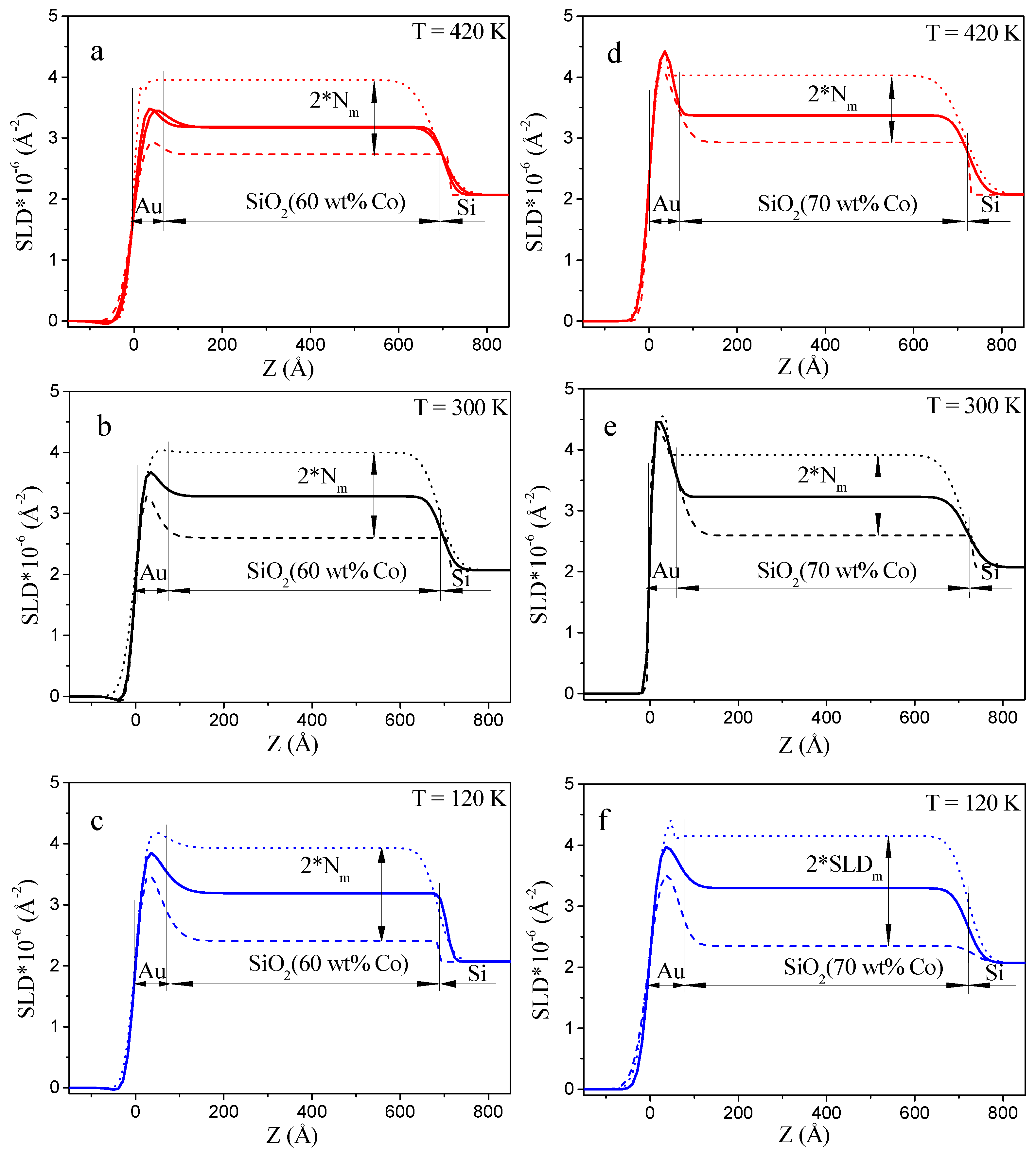
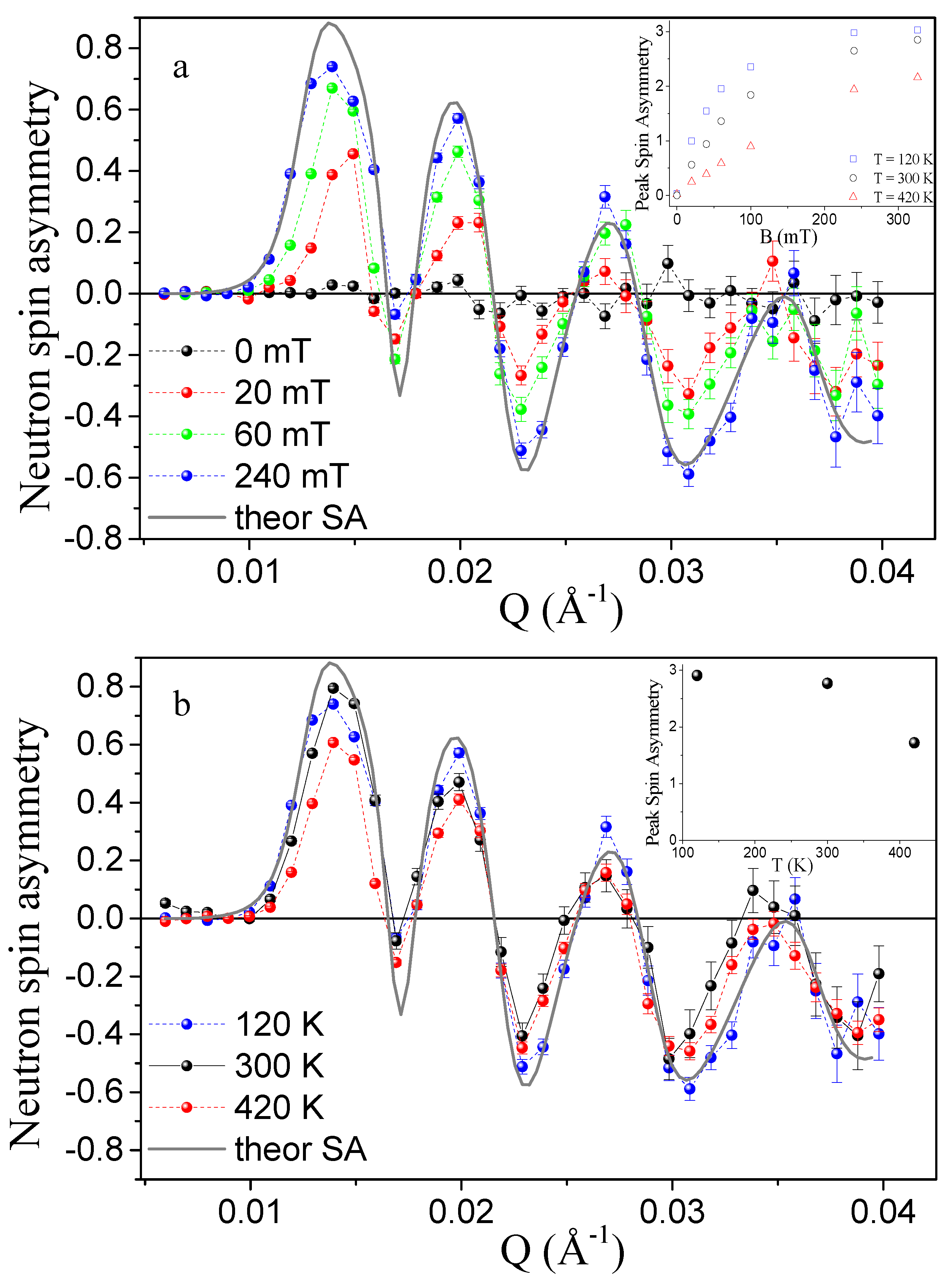
2.3. Polarized Neutron Reflectometry
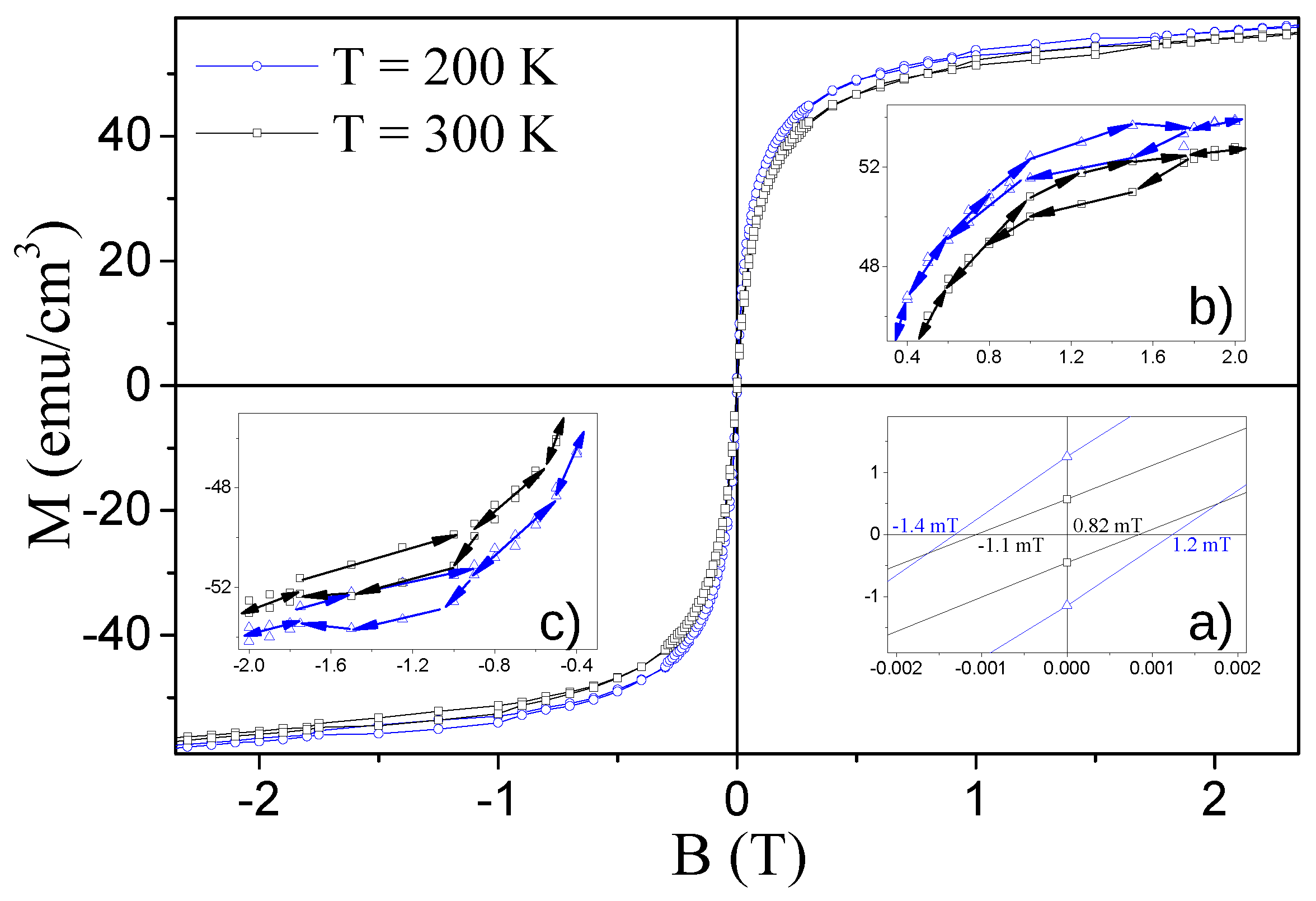
2.4. SQUID Magnetometry
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gerber, A.; Milner, A.; Groisman, B.; Karpovsky, M.; Sulpice, A. Magnetoresistance of granular ferromagnet-insulator films. Thin Solid Films 1997, 304, 319–322. [Google Scholar] [CrossRef]
- Stuart, H.R.; Hall, D.G. Island size effects in nanoparticle-enhanced photodetectors. Appl. Phys. Lett. 1998, 73, 3815–3817. [Google Scholar] [CrossRef]
- Kodama, R. Magnetic Nanoparticle. J. Magn. Magn. Mater. 1999, 200, 359–372. [Google Scholar] [CrossRef]
- Fujimori, H.; Ohnuma, S.; Kobayashi, N.; Masumoto, T. Spintronics in metal-insulator nanogranular magnetic thin films. J. Magn. Magn. Mater. 2006, 304, 32–35. [Google Scholar] [CrossRef]
- Žutić, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef]
- Lambert, C.-H.; Mangin, S.; Varaprasad, B.C.S.; Takahashi, Y.; Hehn, M.; Cinchetti, M.; Malinowski, G.; Hono, K.; Fainman, Y.; Aeschlimann, M.; et al. All-optical control of ferromagnetic thin films and nanostructures. Science 2014, 345, 1337–1340. [Google Scholar] [CrossRef]
- Lutsev, L.V.; Stognij, A.I.; Novitskii, N.N. Giant magnetoresistance in semiconductor/granular film heterostructures with cobalt nanoparticles. Phys. Rev. B 2009, 80, 184423. [Google Scholar] [CrossRef]
- Lutsev, L. Potential barrier for spin-polarized electrons induced by the exchange interaction at the interface in the ferromagnet/semiconductor heterostructure. J. Phys. Condens. Matter 2006, 18, 5881. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Miller, N.C.; Shirn, G.A. Co-sputtered Au-SiO2 cermet films. Appl. Phys. Lett. 1967, 10, 86. [Google Scholar] [CrossRef]
- Miller, N.C.; Hardiman, B.; Shirn, G.A. Transport properties, microstructure, and conduction model of cosputtered Au-SiO2 cermet films. J. Appl. Phys. 1970, 41, 1850. [Google Scholar] [CrossRef]
- Stognij, A.I.; Novitskii, N.N.; Stukalov, O.M. Separate cobalt-copper interface smoothening under the action of low-energy argon ion bombardment. Tech. Phys. Lett. 2003, 29, 43–46. [Google Scholar] [CrossRef]
- Smilgies, D.M.; Boudet, N.; Struth, B.; Konovalov, O. Troika II: A versatile beamline for the study of liquid and solid interfaces. J. Synchrotron Radiat. 2005, 12, 329–339. [Google Scholar] [CrossRef]
- Renaud, G.; Lazzari, R.; Leroy, F. Probing surface and interface morphology with Grazing Incidence Small Angle X-ray Scattering. Surf. Sci. Rep. 2009, 64, 255–380. [Google Scholar] [CrossRef]
- Renaud, G.; Lazzari, R.; Revenant, C.; Barbier, A.; Noblet, M.; Ulrich, O.; Leroy, F.; Jupille, J.; Borensztein, Y.; Henry, C.R.; et al. Real-time monitoring of growing nanoparticles. Science 2003, 300, 1416–1419. [Google Scholar] [CrossRef] [PubMed]
- Lazzari, R.; Renaud, G.; Revenant, C.; Jupille, J.; Borensztein, Y. Adhesion of growing nanoparticles at a glance: Surface differential reflectivity spectroscopy and grazing incidence small angle X-ray scattering. Phys. Rev. B 2009, 79, 125428. [Google Scholar] [CrossRef]
- Grigoreva, N.; Vorobev, A.; Ukleev, V.; Dyadkina, E.; Lutsev, L.; Stognij, A.; Novitskii, N.; Grigorev, S. Investigation of the SiO2 (Co)/GaAs heterostructures using the surface scattering of synchrotron radiation. JETP Lett. 2010, 92, 767–773. [Google Scholar] [CrossRef]
- Schwartzkopf, M.; Buet, A.; Körstgens, V.; Metwalli, E.; Schlage, K.; Benecke, G.; Perlich, J.; Rawolle, M.; Rothkirch, A.; Heidmann, B.; et al. From atoms to layers: In situ gold cluster growth kinetics during sputter deposition. Nanoscale 2013, 5, 5053–5062. [Google Scholar] [CrossRef] [PubMed]
- Parratt, L.G. Surface Studies of Solids by Total Reflection of X-rays. Phys. Rev. 1954, 95, 359. [Google Scholar] [CrossRef]
- Ankner, J.; Felcher, G. Polarized-neutron reflectometry. J. Magn. Magn. Mater. 1999, 200, 741–754. [Google Scholar] [CrossRef]
- Wolff, M.; Zhernenkov, K.; Zabel, H. Neutron reflectometery with ADAM at the ILL: Present status and future perspectives. Thin Solid Films 2007, 515, 5712–5715. [Google Scholar] [CrossRef]
- Devishvili, A.; Zhernenkov, K.; Dennison, A.J.; Toperverg, B.; Wol, M.; Hj¨orvarsson, B.; Zabel, H. SuperADAM: Upgraded polarized neutron reflectometer at the Institut Laue-Langevin. Rev. Sci. Instruments 2013, 84, 025112. [Google Scholar] [CrossRef]
- Vorobiev, A.; Devishvilli, A.; Palsson, G.; Rundlöf, H.; Johansson, N.; Olsson, A.; Dennison, A.; Wollf, M.; Giroud, B.; Aguettaz, O.; et al. Recent upgrade of the polarized neutron re?ectometer Super ADAM. Neutron News 2015, 26, 25–26. [Google Scholar] [CrossRef]
- Ukleev, V.A.; Grigoryeva, N.A.; Dyadkina, E.A.; Vorobiev, A.A.; Lott, D.; Lutsev, L.V.; Stognij, A.I.; Novitskiy, N.N.; Mistonov, A.A.; Menzel, D.; et al. Magnetic properties of the SiO2(Co)/GaAs interface: Polarized neutron reflectometry and SQUID magnetometry. Phys. Rev. B 2012, 86, 134424. [Google Scholar] [CrossRef]
- Ottavian, G.; Tu, K.N.; Psaras, P.; Nobili, C. In situ resistivity measurement of cobalt silicide formation. J. Appl. Phys. 1987, 62, 2290–2294. [Google Scholar] [CrossRef]
- Cabral, C., Jr.; Barmak, K.; Gupta, J.; Clevenger, L.A.; Arcot, B.; Smith, D.A.; Harper, J.M.E. Role of stress relief in the hexagona-clos-packed to face-centered-cubic phase transformation in cobalt thin films. J. Vac. Sci. Technol. 1993, A11, 1435–1440. [Google Scholar] [CrossRef]
- Colgan, E.G., Jr.; Cabral, C.; Kotecki, D.E. Activation energy for CoSi and CoSi2 formation measured during rapid thermal annealing. J. Appl. Phys. 1995, 77, 614–619. [Google Scholar] [CrossRef]
- Lowes, T.D.; Zinke-Allmang, M. Cobalt grain growth on clean Si(100) Surfaces. Scanning Microsc. 1998, 12, 119–129. [Google Scholar]
- Jaccodine, R.J. Surface energy of germanium and silicon. J. Electrochem. Soc. 1963, 110, 524. [Google Scholar] [CrossRef]
- Messmer, C.; Bilello, J.C. The surface energy of Si, GaAs, and GaP. J. Appl. Phys. 1981, 52, 4623. [Google Scholar] [CrossRef]
- Zinke-Allmang, M. Phase separation on solid surfaces: Nucleation, coarsening and coalescence kinetics. Thin Solid Films 1999, 346, 1–68. [Google Scholar] [CrossRef]
- Loncaric, M.; Sancho-Parramon, J.; Zorc, H. Optical properties of gold island films—A spectroscopic ellipsometry study. Thin Solid Films 2011, 519, 2946–2950. [Google Scholar] [CrossRef]
- Qian, H.; Xiao, Y.; Lepage, D.; Chen, L.; Liu, Z. Quantum electrostatic model for optical properties of nanoscale gold films. Nanophotonics 2015, 4, 413–418. [Google Scholar] [CrossRef]
- Yakubovsky, D.I.; Arsenin, A.V.; Stebunov, Y.V.; Fedyanin, D.Y.; Volkov, V.S. Optical constants and structural properties of thin gold films. Opt. Express 2017, 25, 25574. [Google Scholar] [CrossRef]
- Meiklejohn, W.H.; Bean, C.P. New Magnetic Anisotropy. Phys. Rev. 1957, 105, 904. [Google Scholar] [CrossRef]
- Gomoyunova, M.V.; Grebenyuk, G.S.; Pronin, I.I. Formation of ultrathin magnetic cobalt films on the Si(111)7 × 7 surface. Tech. Phys. 2011, 56, 865–868. [Google Scholar] [CrossRef]
- Katmis, F.; Lauter, V.; Nogueira, F.S.; Assaf, B.A.; Jamer, M.E.; Wei, P.; Satpati, B.; Freeland, J.W.; Eremin, I.; Heiman, D.; et al. A high-temperature ferromagnetic topological insulating phase by proximity coupling. Nature 2016, 533, 513–516. [Google Scholar] [CrossRef]
- Mogi, M.; Nakajima, T.; Ukleev, V.; Tsukazaki, A.; Yoshimi, R.; Kawamura, M.; Takahashi, K.S.; Hanashima, T.; Kakurai, K.; Arima, T.H.; et al. Large Anomalous Hall Effect in Topological Insulators with Proximitized Ferromagnetic Insulators. Phys. Rev. Lett. 2019, 123, 016804. [Google Scholar] [CrossRef] [PubMed]
- Cortie, D.L.; Lin, K.W.; Shueh, C.; Hsu, H.F.; Wang, X.L.; James, M.; Fritzsche, H.; Bruck, S.; Klose, F. Exchange bias in a nanocrystalline hematite/permalloy thin film investigated with polarized neutron reflectometry. Phys. Rev. B 2012, 86, 054408. [Google Scholar] [CrossRef]
- Saoudi, M.; Fritzsche, H.; Nieuwenhuys, G.J.; Hesselberth, M.B.S. Size Effect in the Spin Glass Magnetization of Thin AuFe Films as Studied by Polarized Neutron Reflectometry. Phys. Rev. Lett. 2008, 100, 057204. [Google Scholar] [CrossRef]
- Ankner, J.F.; Majrzak, C.F.; Homma, H. Magnetic dead layer in Fe/Si multilayer: Profile refinement of polarized neutron reflectivity data. J. Appl. Phys. 1993, 73, 6436. [Google Scholar] [CrossRef]
- Dyadkina, E.A.; Grigoriev, S.V.; Lott, D.; Sitnikov, A.V.; Kalinin, Y.E. Study of the [(Co45Fe45Zr10)x(Al2O3)100−x/a-Si:H]m multilayer nanostructure by polarized neutron reflectometry. Phys. B 2011, 406, 2397–2400. [Google Scholar] [CrossRef]
- Dyadkina, E.A.; Grigoryeva, N.A.; Vorobiev, A.A.; Grigoriev, S.V.; Lutsev, L.V.; Zhernenkov, K.; Wolff, M.; Lott, D.; Stognij, A.I.; Novitskii, N.N.; et al. Polarized neutron reflectometry from the interface of the heterostructures SiO2(Co)/Si and SiO2(Co)/GaAs. Phys. B 2009, 404, 2547–2549. [Google Scholar] [CrossRef]
- Lutsev, L. Magnetoresistance: Types, Roles and Research; Gonzalez, R., Ed.; Nova Science Publishers, Incorporated: New York, NY, USA, 2017; pp. 65–121. [Google Scholar]
- Fan, Z.; Li, P.; Zhang, L.; Mi, W.; Jiang, E.; Bai, H. Electrical transport properties and room-temperature positive magnetoresistance of Fe3O4/a-C/n-Si junctions. Thin Solid Films 2012, 520, 3641–3646. [Google Scholar] [CrossRef]
- Volkov, N.; Tarasov, A.; Eremin, E.; Baron, F.; Varnakov, S.; Ovchinnikov, S. Extremely large magnetoresistance induced by optical irradiation in the Fe/SiO2/p-Si hybrid structure with Schottky barrier. J. Appl. Phys. 2013, 114, 093903. [Google Scholar] [CrossRef]

| Layer | d (Å) | SLDX-rays · 10 −5 (Å−2) | (Å) |
|---|---|---|---|
| Au/SiO2(60 at.% Co)/Si | |||
| Au | 48 ± 2 | 11.5 ± 0.1 | 9.0 ± 0.2 |
| Granular film | 450 ± 2 | 2.83 ± 0.05 | 9.0 ± 0.2 |
| Si | – | 2.024 ± 0.05 | 3.8 ± 0.2 |
| Au/SiO2(82 at.% Co)/Si | |||
| Au | 43 ± 2 | 11.5 ± 0.1 | 7.0 ± 0.3 |
| Granular film | 450 ± 2 | 4.13 ± 0.05 | 7.0 ± 0.3 |
| Si | – | 2.024 ± 0.05 | 3.6 ± 0.2 |
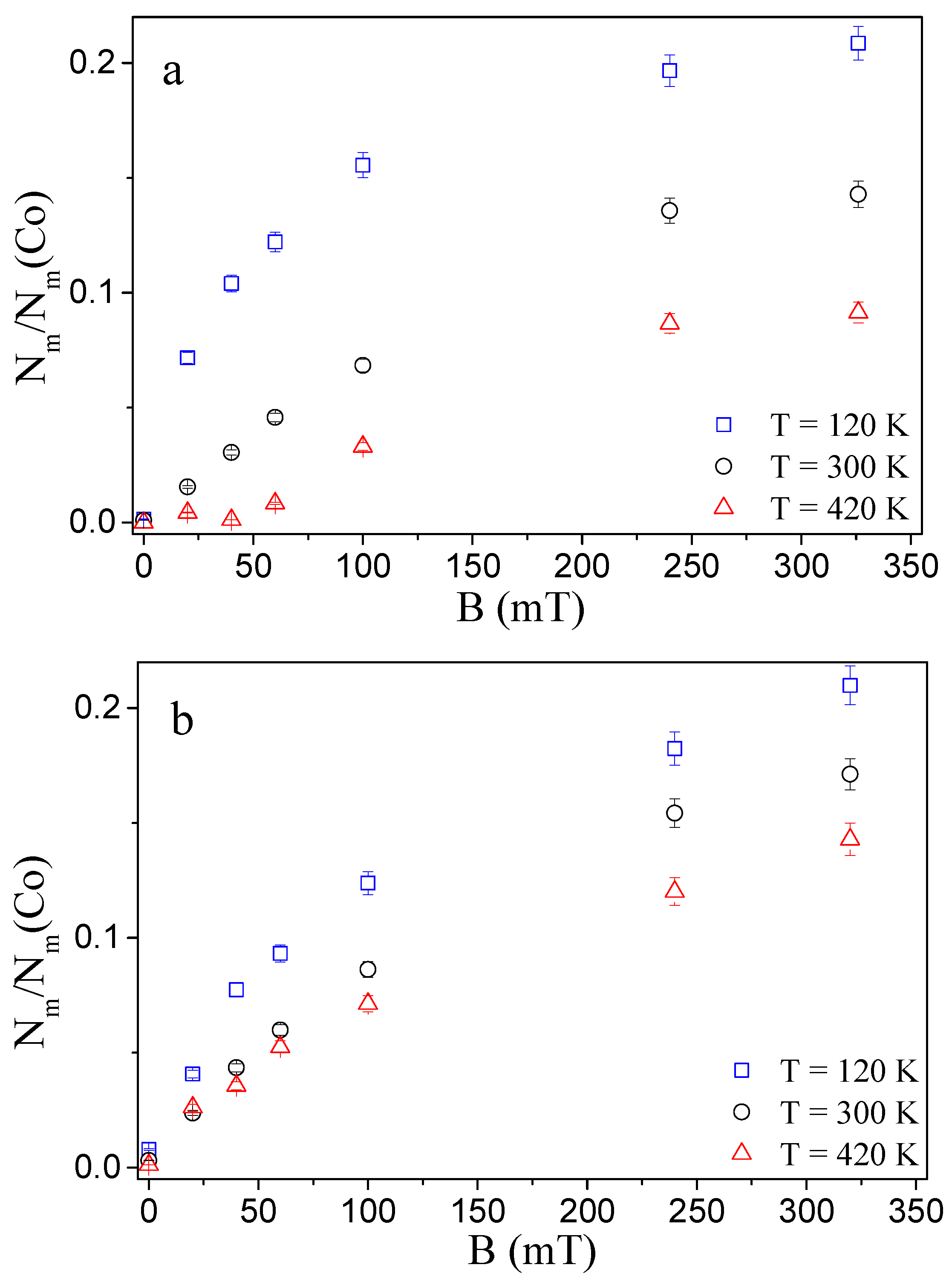
| Layer | d (Å) | Nn · 10−6 (Å−2) | Nm · −7 (Å−2) | H (mT) | (Å) |
|---|---|---|---|---|---|
| T = 120 K | |||||
| Au | 45 ± 2 | 3.8 ± 0.2 | – | 11.0 ± 1.0 | |
| 0.33 ± 0.02 | 0 | ||||
| 1.71 ± 0.02 | 20 | ||||
| 3.25 ± 0.02 | 40 | ||||
| GF | 680 ± 2 | 3.29 ± 0.03 | 3.91 ± 0.02 | 60 | 10.0 ± 1.0 |
| 5.02 ± 0.02 | 100 | ||||
| 7.66 ± 0.02 | 240 | ||||
| 8.82 ± 0.02 | 320 | ||||
| Si | 2.073 ± 0.02 | – | 40 ± 2 | ||
| T = 300 K | |||||
| Au | 45 ± 2 | 3.7 ± 0.2 | – | 11.0 ± 1.0 | |
| 0.13 ± 0.02 | 0 | ||||
| 0.99 ± 0.02 | 20 | ||||
| 1.83 ± 0.02 | 40 | ||||
| GF | 680 ± 2 | 3.29 ± 0.03 | 2.52 ± 0.02 | 60 | 10.0 ± 1.0 |
| 3.62 ± 0.02 | 100 | ||||
| 6.48 ± 0.02 | 240 | ||||
| 7.19 ± 0.02 | 320 | ||||
| Si | 2.073 ± 0.02 | – | 50 ± 2 | ||
| T = 420 K | |||||
| Au | 45 ± 2 | 3.5 ± 0.2 | – | 11.0 ± 1.0 | |
| 0.05 ± 0.02 | 0 | ||||
| 1.10 ± 0.02 | 20 | ||||
| 1.49 ± 0.02 | 40 | ||||
| GF | 680 ± 2 | 3.38 ± 0.03 | 2.21 ± 0.02 | 60 | 10.0 ± 1.0 |
| 2.99 ± 0.02 | 100 | ||||
| 5.05 ± 0.02 | 240 | ||||
| 6.00 ± 0.02 | 320 | ||||
| Si | 2.073 ± 0.02 | – | 50 ± 2 | ||
| Layer | d (Å) | Nn · 10−6 (Å−2) | Nm · 10 −7 (Å−2) | H (mT) | (Å) |
|---|---|---|---|---|---|
| T = 120 K | |||||
| Au | 45 ± 2 | 4.0 ± 0.2 | – | 11.0 ± 1.0 | |
| 0.06 ± 0.02 | 0 | ||||
| 3.01 ± 0.02 | 20 | ||||
| 4.37 ± 0.02 | 40 | ||||
| GF | 685 ± 2 | 3.29 ± 0.03 | 5.13 ± 0.02 | 60 | 10.0 ± 1.0 |
| 6.53 ± 0.02 | 100 | ||||
| 8.26 ± 0.02 | 240 | ||||
| 8.76 ± 0.02 | 320 | ||||
| Si | 2.073 ± 0.02 | – | 50 ± 2 | ||
| T = 300 K | |||||
| Au | 45 ± 2 | 3.7 ± 0.2 | – | 11.0 ± 1.0 | |
| 0.04 ± 0.02 | 0 | ||||
| 0.65 ± 0.02 | 20 | ||||
| 1.28 ± 0.02 | 40 | ||||
| GF | 685 ± 2 | 3.29 ± 0.03 | 1.92 ± 0.02 | 60 | 10.0 ± 1.0 |
| 2.87 ± 0.02 | 100 | ||||
| 5.70 ± 0.02 | 240 | ||||
| 6.00 ± 0.02 | 320 | ||||
| Si | 2.073 ± 0.02 | – | 50 ± 2 | ||
| T = 420 K | |||||
| Au | 45 ± 2 | 3.5 ± 0.2 | – | 11.0 ± 1.0 | |
| 0.00 ± 0.02 | 0 | ||||
| 0.005 ± 0.02 | 20 | ||||
| 0.02 ± 0.02 | 40 | ||||
| GF | 685 ± 2 | 3.29 ± 0.03 | 0.35 ± 0.02 | 60 | 10.0 ± 1.0 |
| 1.39 ± 0.02 | 100 | ||||
| 3.64 ± 0.02 | 240 | ||||
| 3.84 ± 0.02 | 320 | ||||
| Si | 2.073 ± 0.02 | – | 50 ± 2 | ||
| Ratio xCo/(1-x)SiO2 | xCo | xCoO | xCo2O3 | |||
|---|---|---|---|---|---|---|
| Nn, 10−6 Å−2 | SLDX-rays, 10−5 Å−2 | Nn, 10−6 Å−2 | SLDX-rays, 10−5 Å−2 | Nn, 10−6 Å−2 | SLDX-rays, 10−5 Å−2 | |
| 0.38/0.62 | 3.0 | 3.56 | 3.77 | 2.97 | 3.74 | 2.64 |
| 0.54/0.46 | 2.81 | 4.27 | 3.91 | 3.44 | 3.86 | 2.97 |
| 0.60/0.40 | 2.74 | 4.54 | 3.95 | 3.6 | 3.90 | 3.1 |
| 0.70/0.30 | 2.62 | 4.98 | 4.04 | 3.9 | 3.98 | 3.4 |
| 0.75/0.25 | 2.55 | 5.22 | 4.08 | 4.05 | 4.01 | 3.38 |
| 0.82/0.18 | 2.47 | 5.51 | 4.14 | 4.24 | 4.08 | 3.52 |
| Comp | D, g/ccm | MW, g/mole | n | Nn, 10−6 Å−2 | SLDX-rays, 10−5 Å−2 | Type of Magnetism at T = 300 K | Type of Conductivity at T = 300 K |
|---|---|---|---|---|---|---|---|
| Au | 19.3 | 196.97 | 0.059 | 4.5 | 12.47 | diamagnetic | metal |
| SiO2 | 2.2 | 60.08 | 0.022 | 3.46 | 1.88 | diamagnetic | insulator |
| CoO | 6.45 | 74.93 | 0.0518 | 4.29 | 4.77 | antiferromagnetic | semiconductor |
| Co2O3 | 5.18 | 165.86 | 0.0188 | 4.2 | 3.88 | antiferromagnetic | semiconductor |
| Co3O4 | 6.073 | 240.80 | 0.0152 | 4.66 | 4.53 | antiferromagnetic | semiconductor |
| Co | 8.9 | 58.933 | 0.091 | 2.26 | 6.3 | ferromagnetic | metal |
| CoSi | 6.3 | 87.02 | 0.0436 | 2.88 | 4.77 | diamagnetic | semimetal |
| Co2Si | 7.1 | 145.95 | 0.0293 | 2.67 | 5.23 | diamagnetic | metal |
| CoSi2 | 5.3 | 115.10 | 0.0277 | 2.97 | 4.15 | diamagnetic | metal |
| Si | 2.33 | 28.086 | 0.05 | 2.074 | 2.024 | diamagnetic | semiconductor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoryeva, N.A.; Ukleev, V.; Vorobiev, A.A.; Stognij, A.I.; Novitskii, N.N.; Lutsev, L.V.; Grigoriev, S.V. Mesostructure and Magnetic Properties of SiO2-Co Granular Film on Silicon Substrate. Magnetochemistry 2022, 8, 167. https://doi.org/10.3390/magnetochemistry8120167
Grigoryeva NA, Ukleev V, Vorobiev AA, Stognij AI, Novitskii NN, Lutsev LV, Grigoriev SV. Mesostructure and Magnetic Properties of SiO2-Co Granular Film on Silicon Substrate. Magnetochemistry. 2022; 8(12):167. https://doi.org/10.3390/magnetochemistry8120167
Chicago/Turabian StyleGrigoryeva, Natalia A., Victor Ukleev, Alexey A. Vorobiev, Alexander I. Stognij, Nikolay N. Novitskii, Leonid V. Lutsev, and Sergey V. Grigoriev. 2022. "Mesostructure and Magnetic Properties of SiO2-Co Granular Film on Silicon Substrate" Magnetochemistry 8, no. 12: 167. https://doi.org/10.3390/magnetochemistry8120167
APA StyleGrigoryeva, N. A., Ukleev, V., Vorobiev, A. A., Stognij, A. I., Novitskii, N. N., Lutsev, L. V., & Grigoriev, S. V. (2022). Mesostructure and Magnetic Properties of SiO2-Co Granular Film on Silicon Substrate. Magnetochemistry, 8(12), 167. https://doi.org/10.3390/magnetochemistry8120167






