Size and Ion-Doping Effects on Magnetic, Optical, and Phonon Properties of CuAlO2 Nanoparticles
Abstract
1. Introduction
2. The Model and Green’s Functions
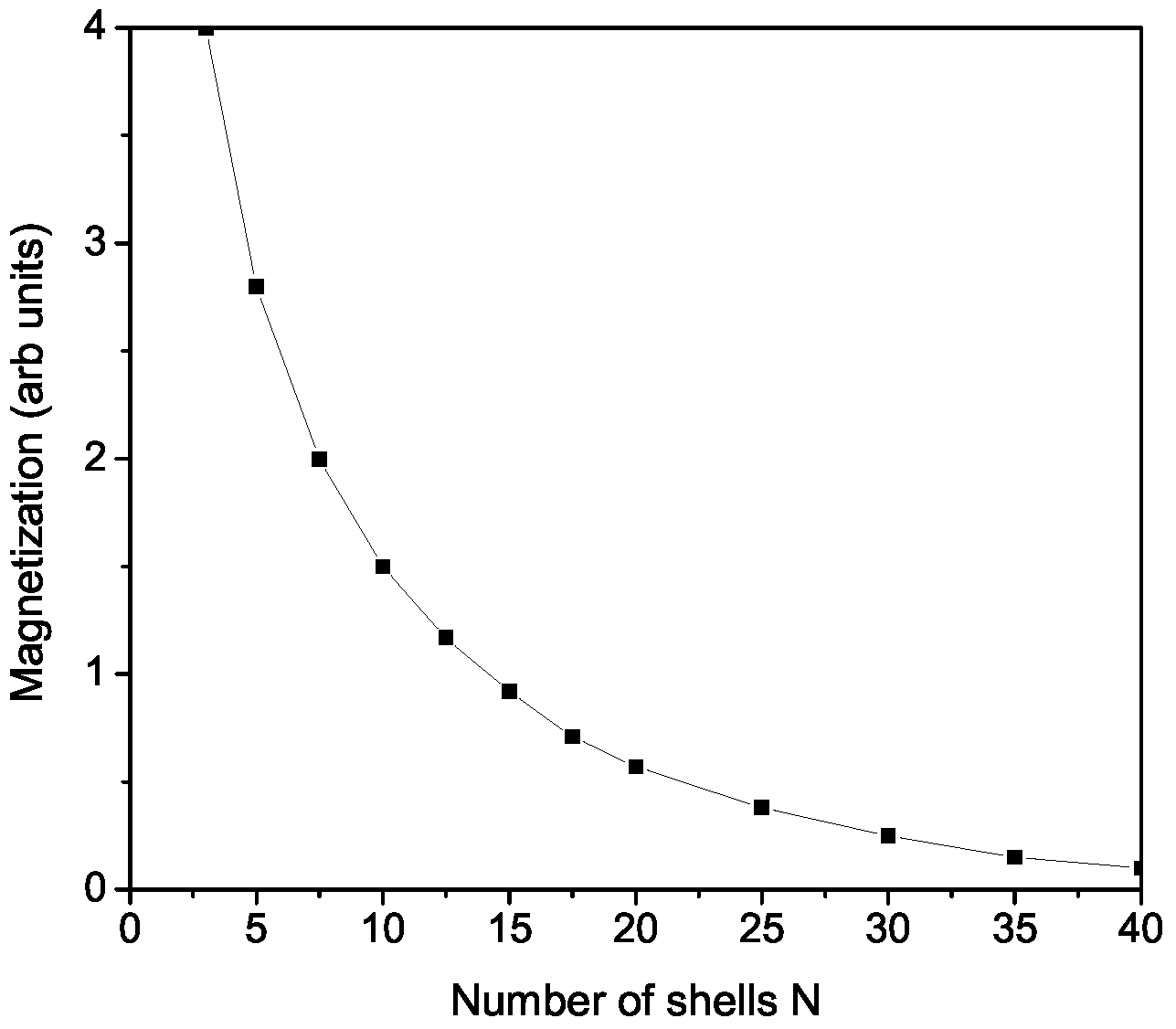
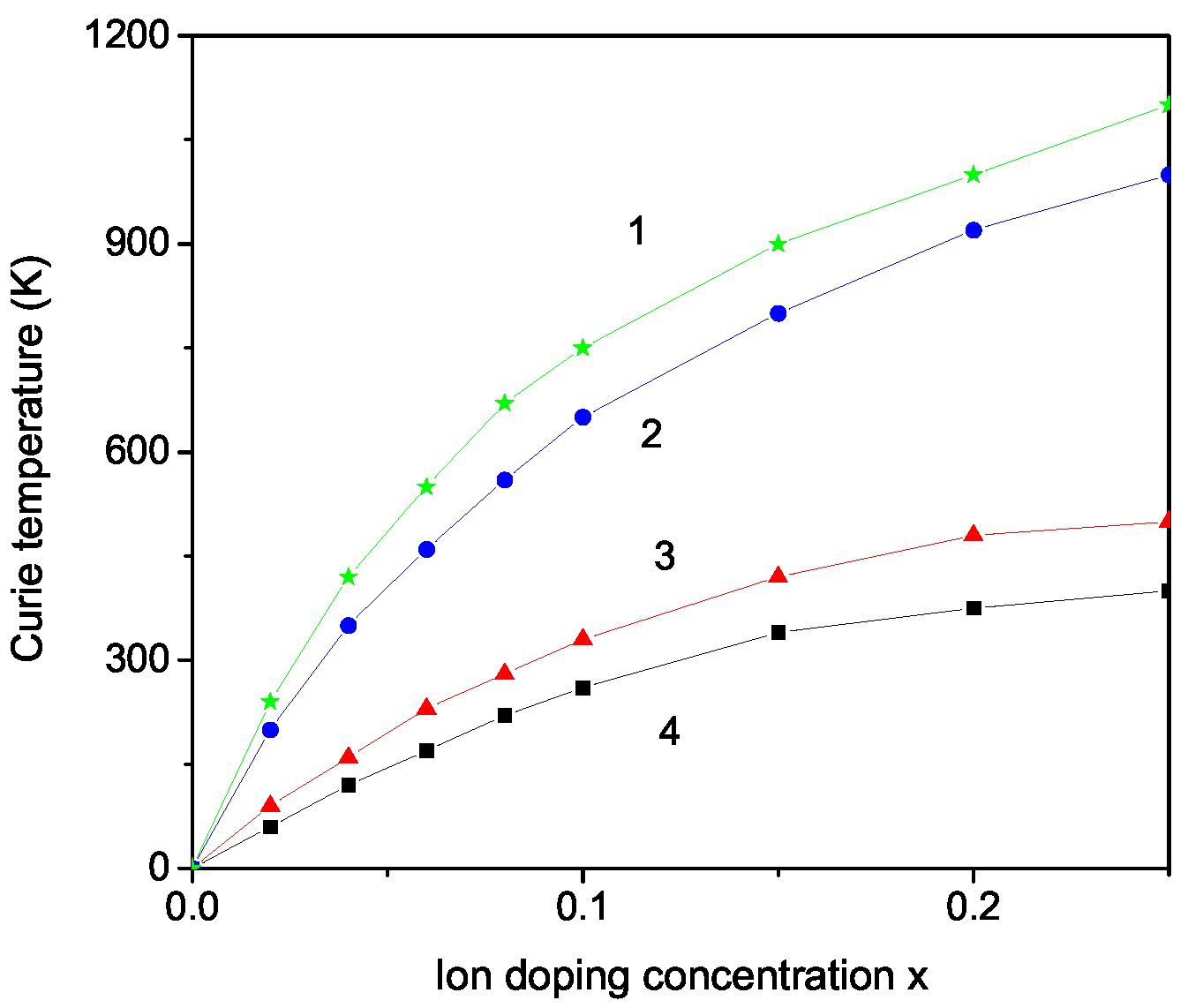
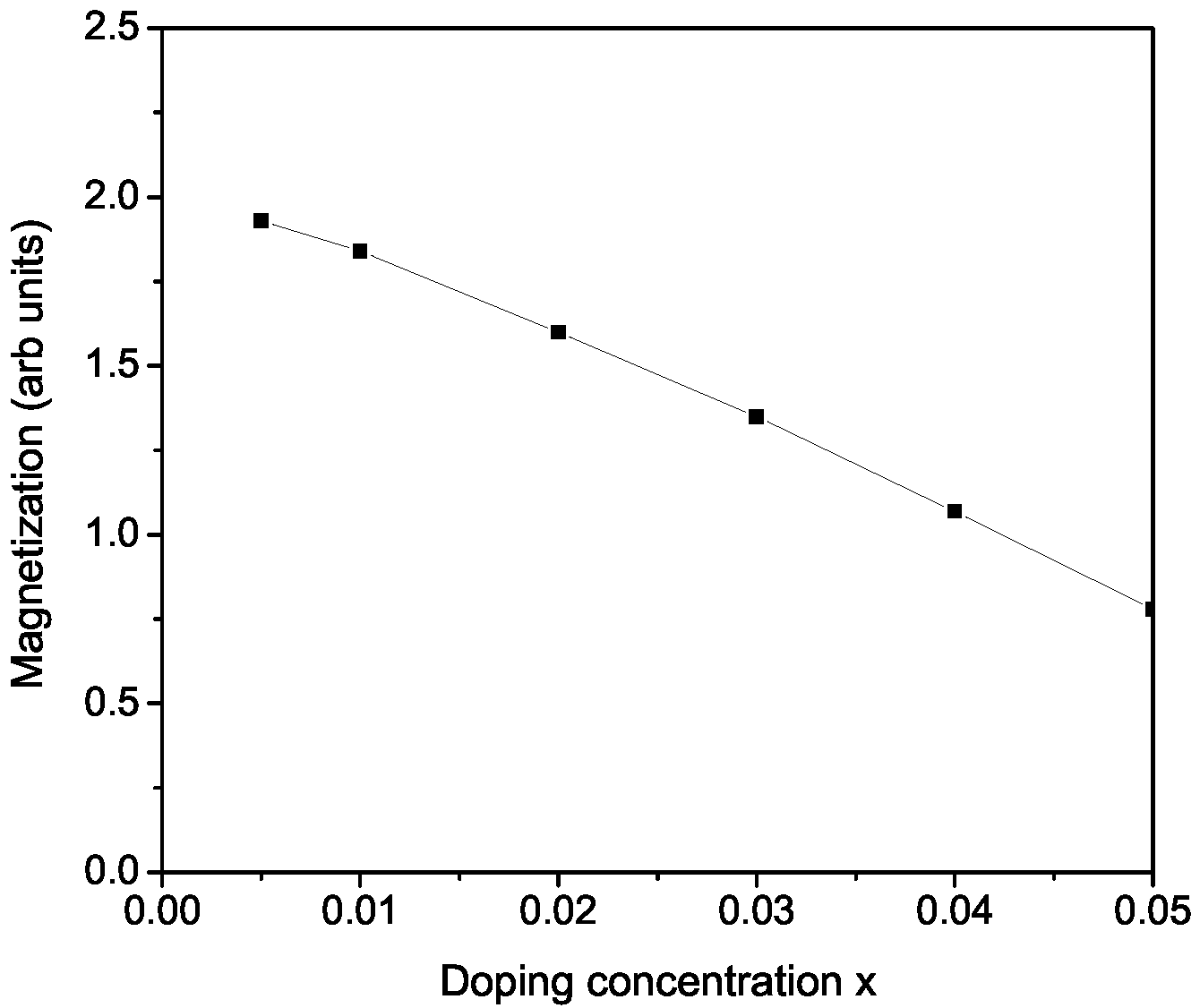
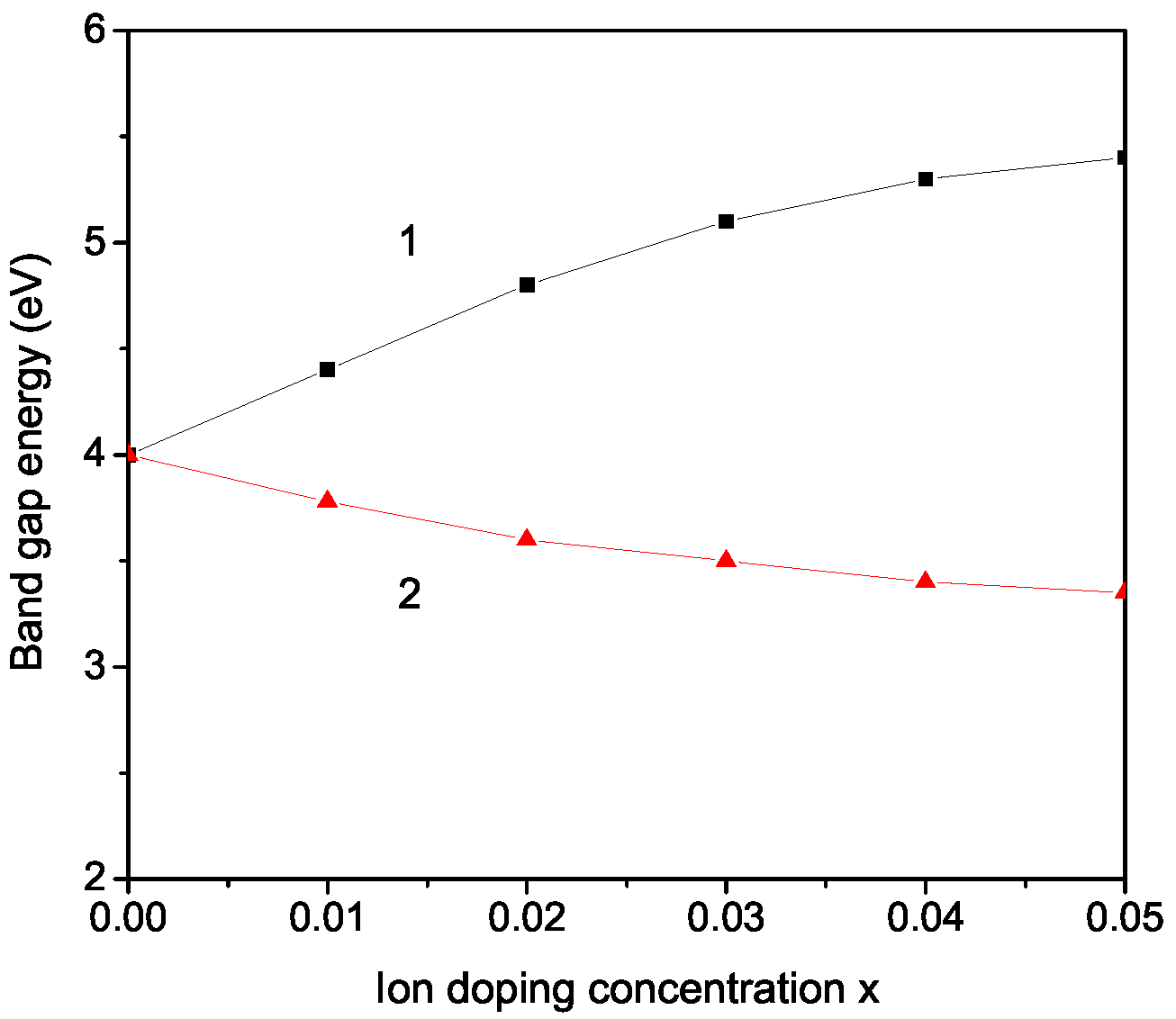
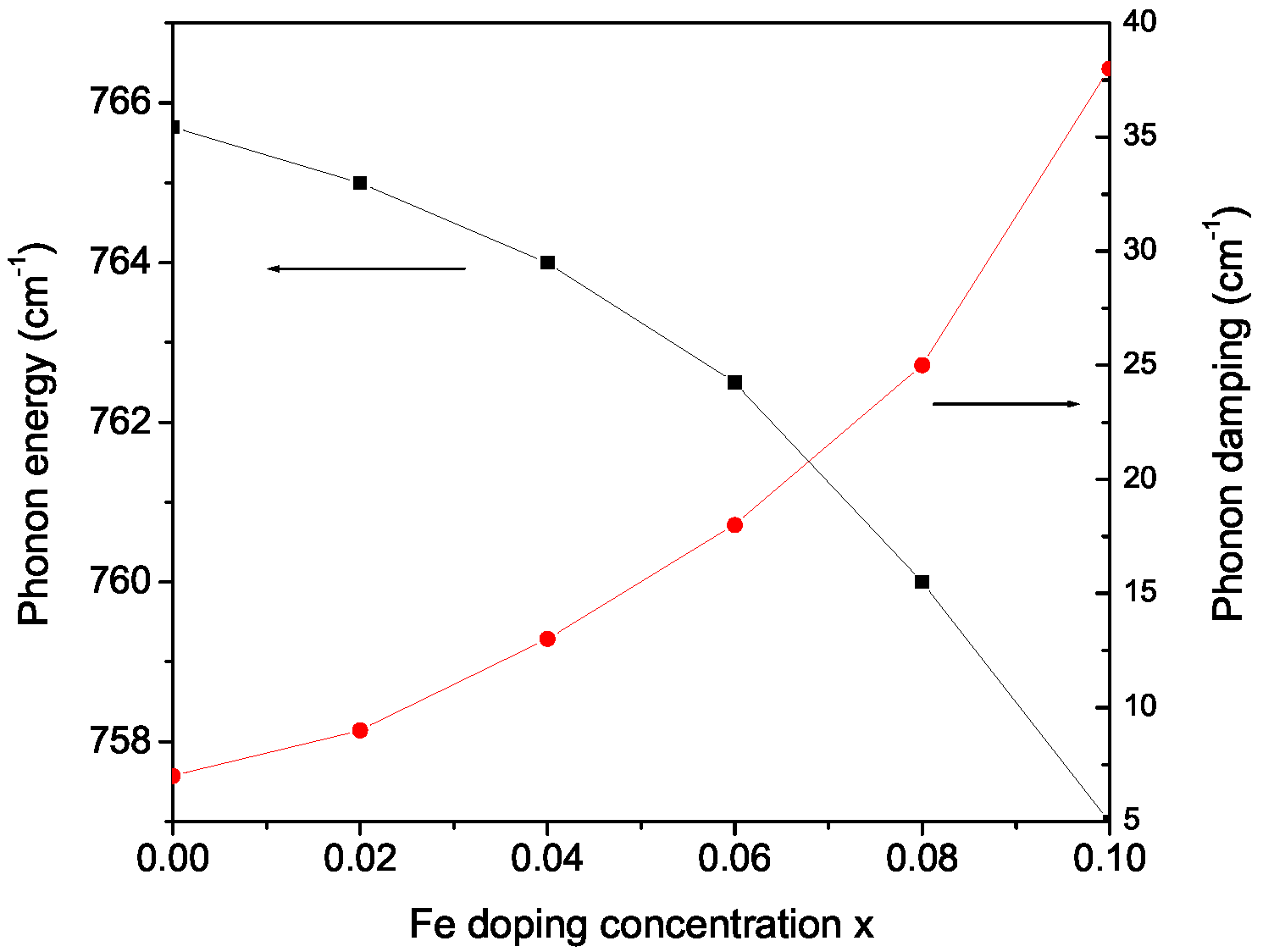
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dietl, T.; Ohno, H.; Matsukura, F.; Cibert, J.; Ferrand, D. Zener Model Description of Ferromagnetism in Zinc-Blende Magnetic Semiconductors. Science 2000, 287, 1019. [Google Scholar] [CrossRef]
- Sato, K.; Dederichs, P.H.; Katayama-Yoshida, H. Curie temperatures of III-V diluted magnetic semiconductors calculated from first principles. Europhys. Lett. 2003, 61, 403. [Google Scholar] [CrossRef]
- Sato, K.; Katayama-Yoshida, H. First principles materials design for semiconductor spintronics. Semicond. Sci. Technol. 2002, 2002. 17, 367. [Google Scholar] [CrossRef]
- Kizaki, H.; Sato, K.; Katayama-Yoshida, H. Materials Design of CuAlO2-Based Dilute Magnetic Semiconductors by First-Principles Calculations and Monte Carlo Simulations. Jpn. J. Appl. Phys. 2008, 47, 6488. [Google Scholar] [CrossRef]
- Iordanidou, K.; Persson, C. Stoner Ferromagnetism in Hole-Doped CuMIIIAO2 with MIIIA = Al, Ga, and In. ACS Appl. Mater. Interfaces 2021, 13, 29770. [Google Scholar] [CrossRef]
- Kawazoe, H.; Yasukawa, M.; Hyodo, H.; Kurita, M.; Yanagi, H.; Hosono, H. P-Type Electrical Conduction in Transparent Thin Films of CuAlO2. Nature 1997, 389, 939. [Google Scholar] [CrossRef]
- Kizaki, H.; Sato, K.; Katayama-Yoshida, H. Carrier concentration dependence of Curie temperature in CuAlO2 based dilute magnetic semiconductor by first-principles calculations. Phys. Stat. Sol. (c) 2007, 3, 4135. [Google Scholar] [CrossRef]
- Aziziha, M.; Byard, S.A.; Beesely, R.; Lewis, J.P.; Seehra, M.S.; Johnson, M.B. Magnetic properties of Fe-doped CuAlO2 and role of impurities. AIP Adv. 2019, 9, 035030. [Google Scholar] [CrossRef]
- Chen, C.; Dong, C.; Wang, B.; Huang, J.; Wang, Y. Synthesis and Room Temperature Ferromagnetism in Fe-Doped CuAlO2 Semiconductor. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2013, 28, 500. [Google Scholar] [CrossRef]
- Dong, C.J.; Yu, W.X.; Xu, M.; Cao, J.J.; Zhang, Y.; Chuai, Y.H.; Wang, Y.D. Evidence of room temperature ferromagnetism in Co-doped transparent CuAlO2 semiconductor. J. Alloys Compd. 2012, 512, 195. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, C.; Chuai, Y.; Wang, Y. Room temperature ferromagnetism in Codoped CuAlO2 nanofibers fabricated by electrospinning. J. Wuhan Univ. Technol.-Mater. Sci. 2015, 30, 1. [Google Scholar] [CrossRef]
- Ray, N.; Gupta, V.; Sarma, L.; Kush, P.; Nag, J.; Sapra, S. Tuning the Electronic and Magnetic Properties of CuAlO2 Nanocrystals Using Magnetic Dopants. ACS Omega 2018, 3, 509. [Google Scholar] [CrossRef]
- Hidetoshi, K.; Kazunori, S.; Akira, Y.; Katayama-Yoshida, H. First-Principles Materials Design of CuAlO2 Based Dilute Magnetic Semiconducting Oxide. Jpn. J. Appl. Phys. 2005, 44, L1187. [Google Scholar]
- Sun, C.Q. Dominance of broken bonds and nonbonding electrons at the nanoscale. Nanoscale 2010, 2, 1930. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.Y.; Li, P.G.; Chen, C.P.; Tu, Q.Y.; Tang, W.H. Magnetic properties of Mn-doped transparent CuAlO2 semiconductor. J. Alloys Compd. 2005, 396, 40. [Google Scholar]
- Lalic, M.V.; Mestnik-Filho, J.; Carbonari, A.W.; Saxena, R.N.; Moralles, M. Influence of Cd impurity on the electronic properties of CuAlO2 delafossite: First-principles calculations. J. Phys. Condens. Matter 2002, 14, 5517. [Google Scholar] [CrossRef]
- Jiang, H.F.; Zhu, X.B.; Lei, H.C.; Li, G.; Yang, Z.R.; Song, W.H.; Dai, J.M.; Sun, Y.P.; Fu, Y.K. Effect of Cr doping on the optical-electrical property of CuAlO2 thin films derived by chemical solution deposition. Thin Solid Films 2011, 519, 2559. [Google Scholar]
- Liu, Y.; Huang, Y.; Seo, H.J.; Wu, Y. Blueshift in near-band-edge emission in Y3+-doped CuAlO2 nanofibers. Opt. Mater. Express 2014, 4, 2602. [Google Scholar] [CrossRef]
- Liu, R.; Li, Y.; Yao, B.; Ding, Z.; Jiang, Y.; Meng, L.; Deng, R.; Zhang, L.; Zhang, Z.; Zhao, H.; et al. Shallow Acceptor State in Mg-Doped CuAlO2 and Its Effect on Electrical and Optical Properties: An Experimental and First-Principles Study. ACS Appl. Mater. Interfaces 2017, 9, 12608. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, M.; Bai, P.; Hou, X.; Liu, F.; Yan, H. Optical, electrical, and structural properties of Fe-doped CuAlO2 thin films. Funct. Mater. Lett. 2019, 12, 1850106. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, Y.; Mellott, N.P.; Wang, L.; Ye, H.; Wu, Y. Luminescence of delafossitetype CuAlO2 fibers with Eu substitution for Al cations. Sci. Technol. Adv. Mater. 2016, 17, 200. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.K.; Dussan, S.; Sharma, G.L.; Katiyar, R.S. Raman scattering measurements of phonon anharmonicity in thin films. J. Appl. Phys. 2008, 104, 113503. [Google Scholar] [CrossRef]
- Yassin, O.A.; Alamri, S.N.; Joraid, A.A. Effect of particle size and laser power on the Raman spectra of CuAlO2 delafossite nanoparticles. J. Phys. D Appl. Phys. 2013, 46, 235301. [Google Scholar] [CrossRef]
- Benreguia, N.; Barnabe, A.; Trari, M. Sol–gel synthesis and characterization of the delafossite CuAlO2. J. Sol-Gel Sci. Technol. 2015, 75, 670. [Google Scholar] [CrossRef]
- Byrne, D.; Cowley, A.; Bennettc, N.; McGlynn, E. The luminescent properties of CuAlO2. J. Mater. Chem. C 2014, 2, 7859. [Google Scholar] [CrossRef]
- Pellicer-Porres, J.; Martinez-Garcia, D.; Segura, A.; Rodriguez-Hernandez, P.; Munoz, A.; Chervin, J.C.; Garro, N.; Kim, D. Pressure and temperature dependence of the lattice dynamics of CuAlO2 investigated by Raman scattering experiments and abinitio calculations. Phys. Rev. B 2006, 74, 184301. [Google Scholar] [CrossRef]
- Wesselinowa, J.M.; Apostolov, A.T. Self-consistent theory of spin–phonon interactions in ferromagnetic semiconductors. J. Phys. Condens. Matter 1993, 5, 3555. [Google Scholar] [CrossRef]
- Agrawal, S.; Parveen, A.; Azam, A. Influence of Mg on structural, electrical and magnetic properties of CuAlO2 nanoparticles. Mater. Lett. 2016, 168, 125. [Google Scholar] [CrossRef]
- Luo, J.; Lin, Y.-J. Point defect-induced magnetic properties in CuAlO2 films without magnetic impurities. Appl. Phys. A 2016, 122, 163. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, M.; Lan, W.; Dong, P.; Yan, H. Structural and physical properties of Mg-doped CuAlO2 thin films. Vacuum 2008, 82, 1321. [Google Scholar] [CrossRef]
- Ghosh, C.K.; Popuri, S.R.; Sarkar, D.; Chattopadhyay, K.K. Sb-doped CuAlO2: Widening of band gap and nonlinear J-E characteristics. J. Mater. Sci. 2011, 46, 1613. [Google Scholar] [CrossRef]
- Zou, Y.S.; Wang, H.P.; Zhang, S.L.; Lou, D.; Dong, Y.H.; Song, X.F.; Zeng, H.B. Structural, electrical and optical properties of Mg-doped CuAlO2 films by pulsed laser deposition. RSC Adv. 2014, 4, 41294. [Google Scholar] [CrossRef]
- Daichakomphu, N.; Klongratog, B.; Rodpun, P.; Pluengphon, P.; Harnwunggmoung, A.; Poo-arporn, Y.; Sakulkalavek, A.; Sakdanuphab, R. Improving the photo-thermoelectric performance of CuAlO2via doping with Bi. Mater. Res. Bull. 2021, 144, 111479. [Google Scholar] [CrossRef]
- Wesselinowa, J.M.; Apostolov, A.T. Anharmonic effects in ferromagnetic semiconductors. J. Phys. Condens. Matter 1996, 8, 473. [Google Scholar] [CrossRef]
- Li, J.; Sleight, A.; Jones, C.Y.; Toby, B. Trends in negative thermal expansion behavior for AMO2 (A=Cu or Ag; M=Al, Sc, In, or La) compounds with the delafossite structure. J. Solid State Chem. 2005, 178, 285. [Google Scholar] [CrossRef]
- Miller, W.; Smith, C.W.; Mackenzie, D.S.; Evans, K.E. Negative Thermal Expansion: A Review. J. Mater. Sci. 2009, 44, 5441. [Google Scholar] [CrossRef]
- Salke, N.P.; Rao, R.; Achary, S.N.; Tyagi, A.K. Raman spectroscopic investigations on delafossite CuLaO2 at high pressures. J. Phys. Conf. Ser. 2012, 377, 012020. [Google Scholar] [CrossRef]
- Aziziha, M.; Akbarshahi, S.; Ghosh, S.; Pramanik, P.; Lewis, J.P.; Romero, A.H.; Thota, S.; Seehra, M.S.; Johnson, M.B. Phonon Dynamics in Anisotropic Dilute CuAl1−xFexO2 Delafossite Alloys by a Weighted Dynamical Matrix Approach. J. Phys. Chem. C 2019, 123, 30604. [Google Scholar] [CrossRef]
- Nakanishi, A.; Katayama-Yoshida, H. Chemical trend of superconducting transition temperature in hole-doped delafossite of CuAlO2, AgAlO2 and AuAlO2. Solid State Commun. 2012, 152, 2078. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apostolova, I.N.; Apostolov, A.T.; Wesselinowa, J.M. Size and Ion-Doping Effects on Magnetic, Optical, and Phonon Properties of CuAlO2 Nanoparticles. Magnetochemistry 2022, 8, 169. https://doi.org/10.3390/magnetochemistry8120169
Apostolova IN, Apostolov AT, Wesselinowa JM. Size and Ion-Doping Effects on Magnetic, Optical, and Phonon Properties of CuAlO2 Nanoparticles. Magnetochemistry. 2022; 8(12):169. https://doi.org/10.3390/magnetochemistry8120169
Chicago/Turabian StyleApostolova, Iliana Naumova, Angel Todorov Apostolov, and Julia Mihailova Wesselinowa. 2022. "Size and Ion-Doping Effects on Magnetic, Optical, and Phonon Properties of CuAlO2 Nanoparticles" Magnetochemistry 8, no. 12: 169. https://doi.org/10.3390/magnetochemistry8120169
APA StyleApostolova, I. N., Apostolov, A. T., & Wesselinowa, J. M. (2022). Size and Ion-Doping Effects on Magnetic, Optical, and Phonon Properties of CuAlO2 Nanoparticles. Magnetochemistry, 8(12), 169. https://doi.org/10.3390/magnetochemistry8120169





