Feasibility Study of Cooling a Bulk Acoustic Wave Resonator by Nanoparticle Enhanced Phase Change Material
Abstract
:1. Introduction
- 1
- Material;
- 2
- Geometry;
- 3
- Mechanical stability;
- 4
- Pad between electrode and transmission line;
- 5
- Temperature expansion coefficient.
2. Materials and Methods
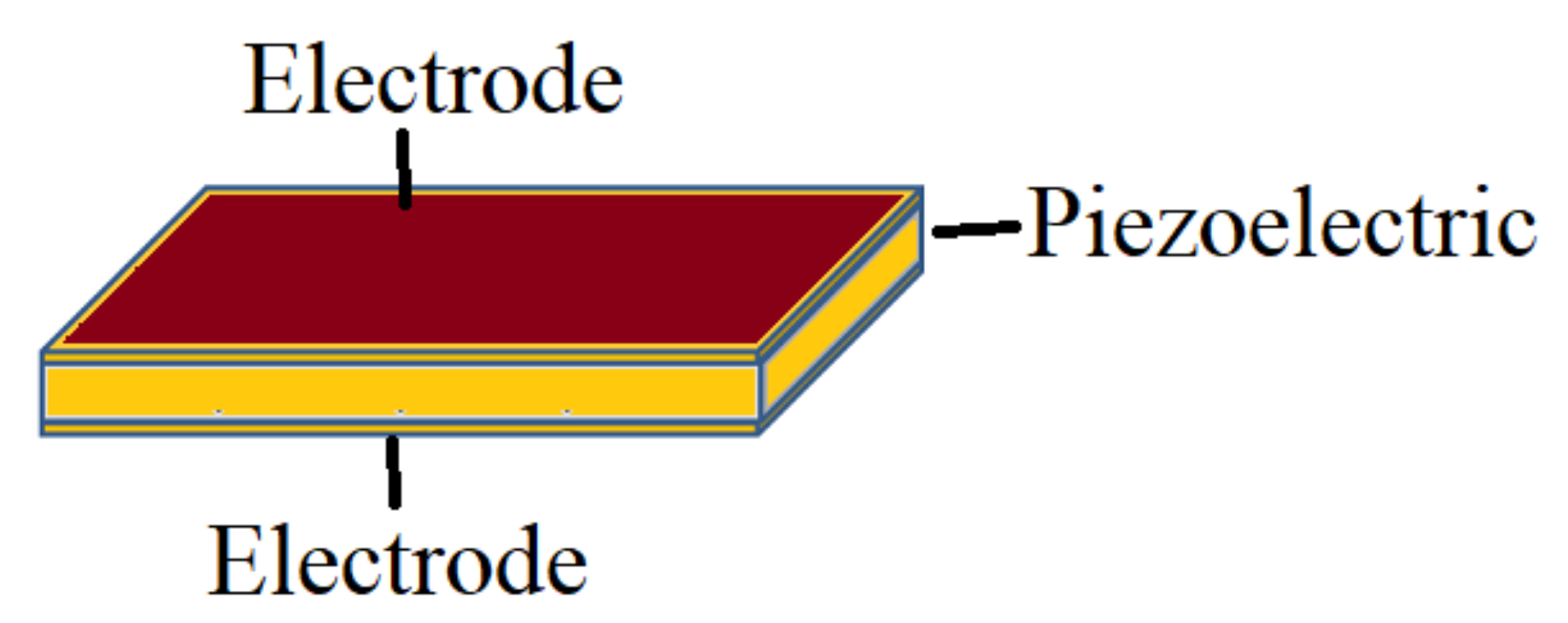
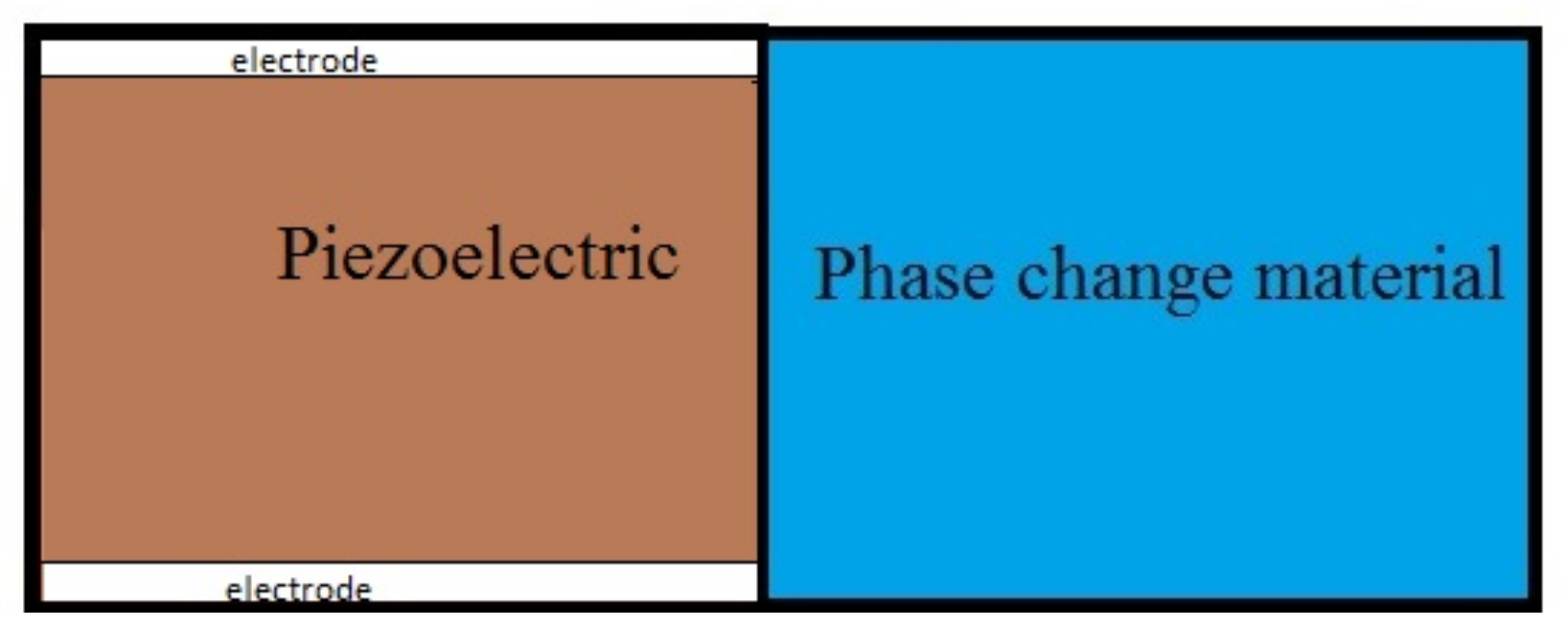
2.1. Cooling Part
2.2. Piezoelectric Induced Wave
3. Results
3.1. Validation of Used Code
3.1.1. Validation of Fluid Part
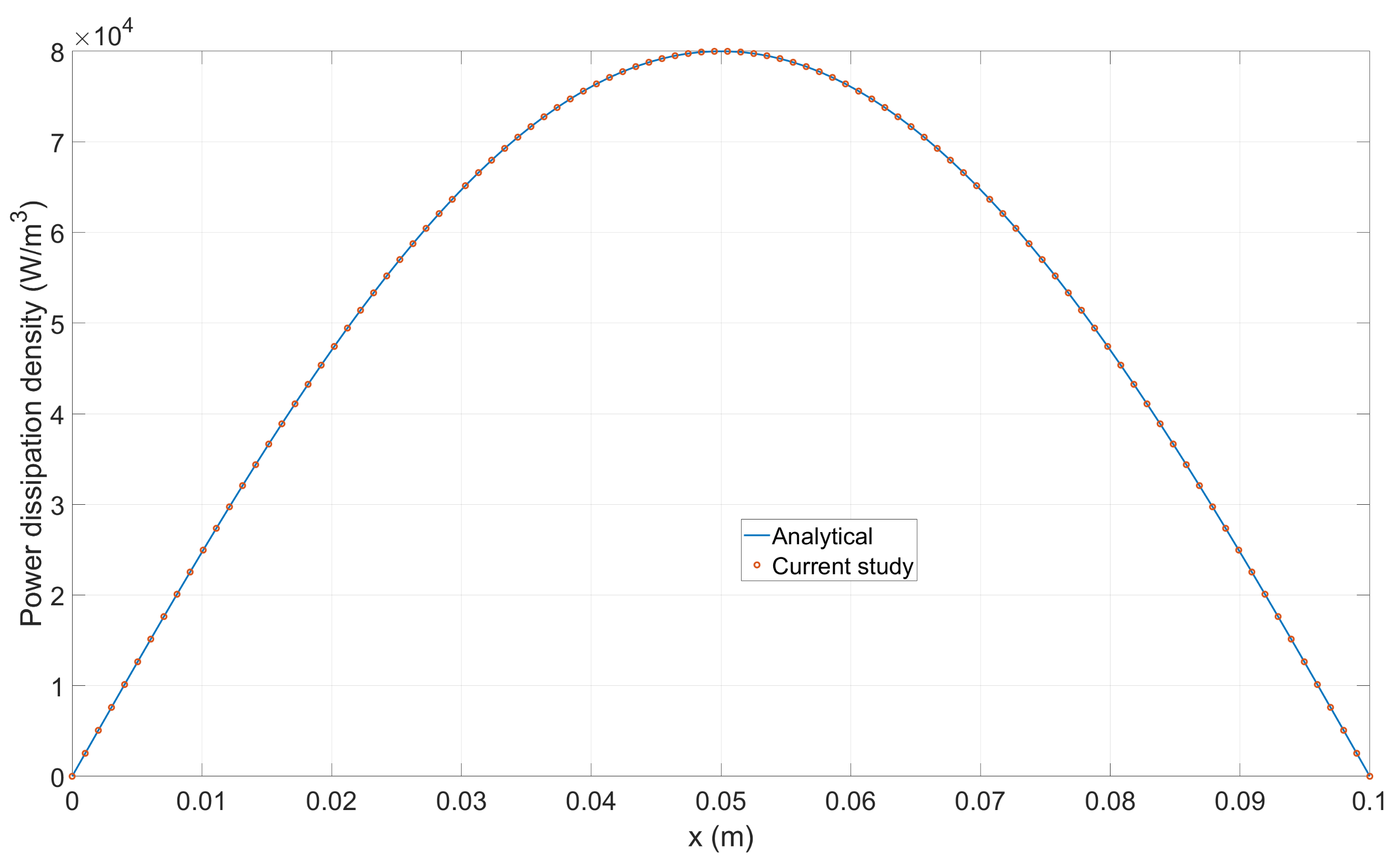
3.1.2. Validation of Heat Generation
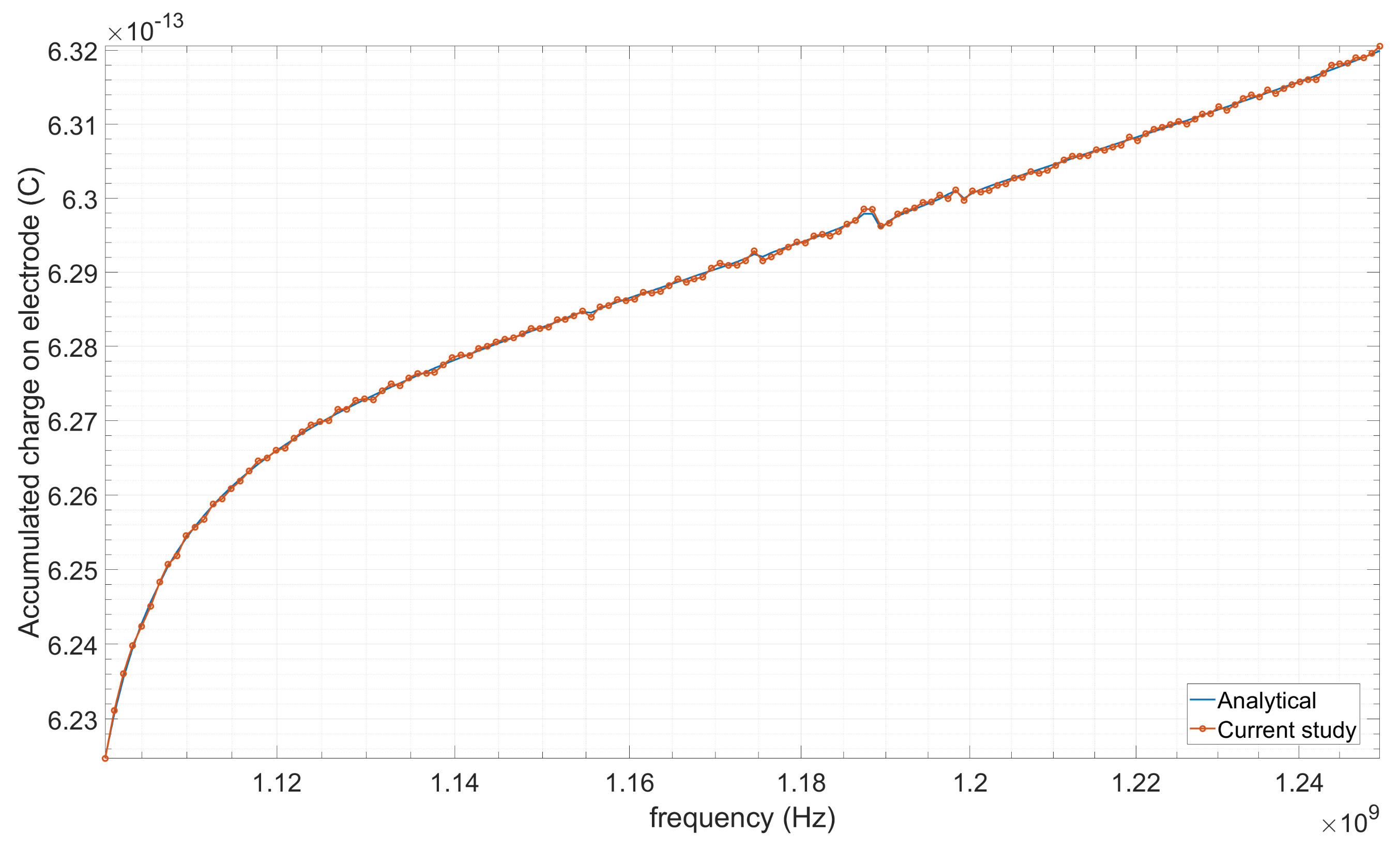
3.1.3. Validation of Charge Curve
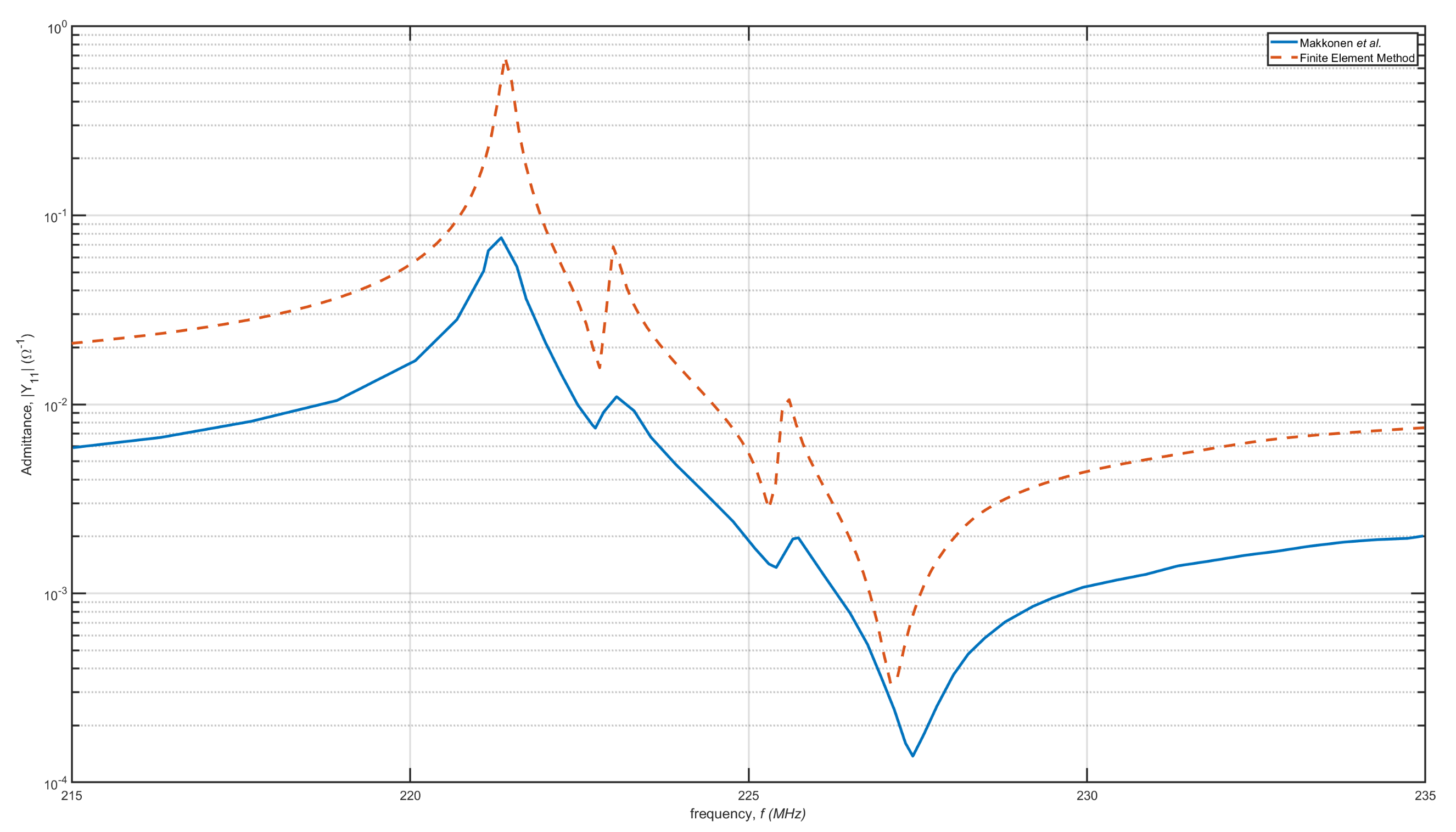
3.1.4. Validation of Dispersion Curve
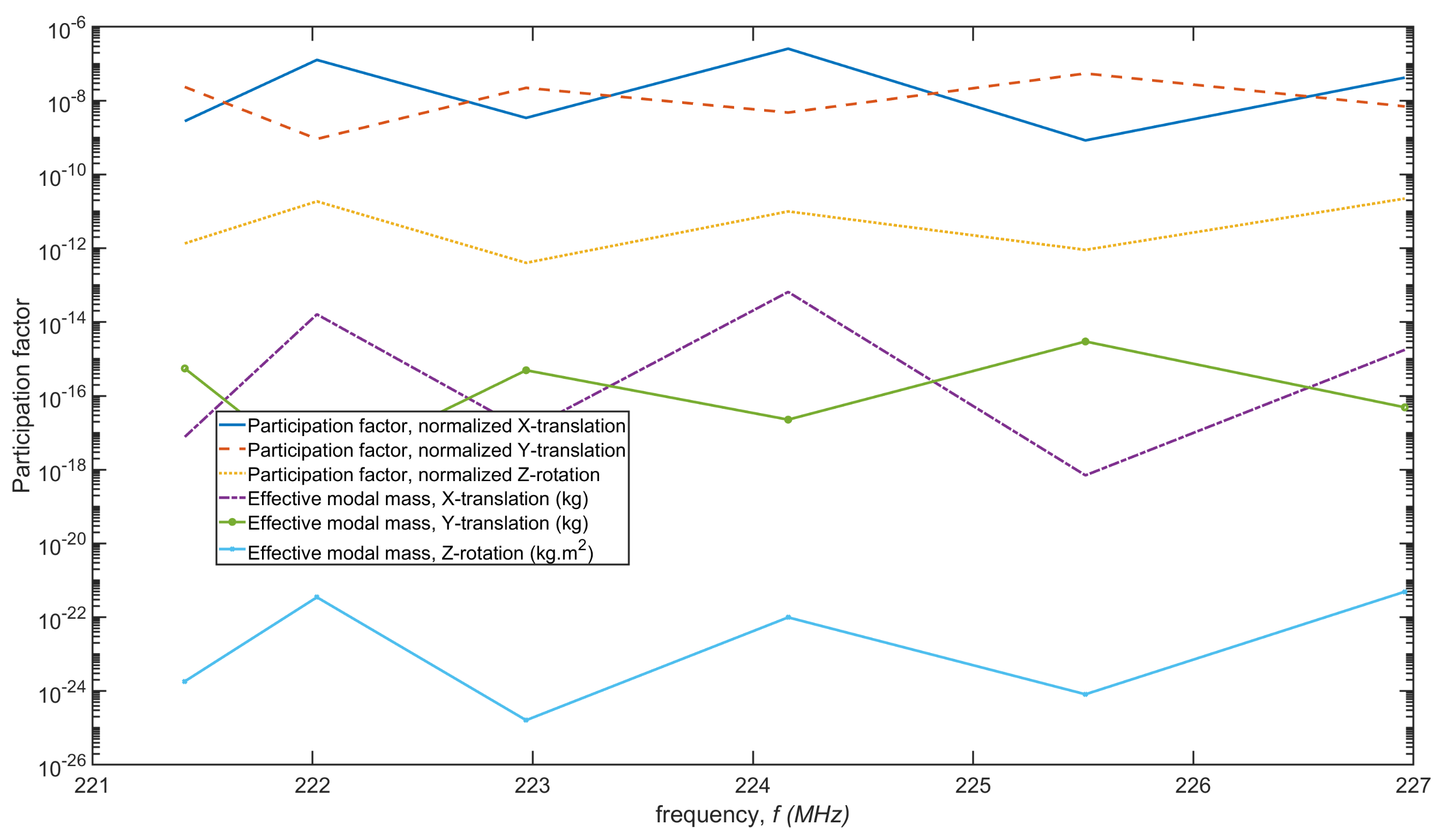
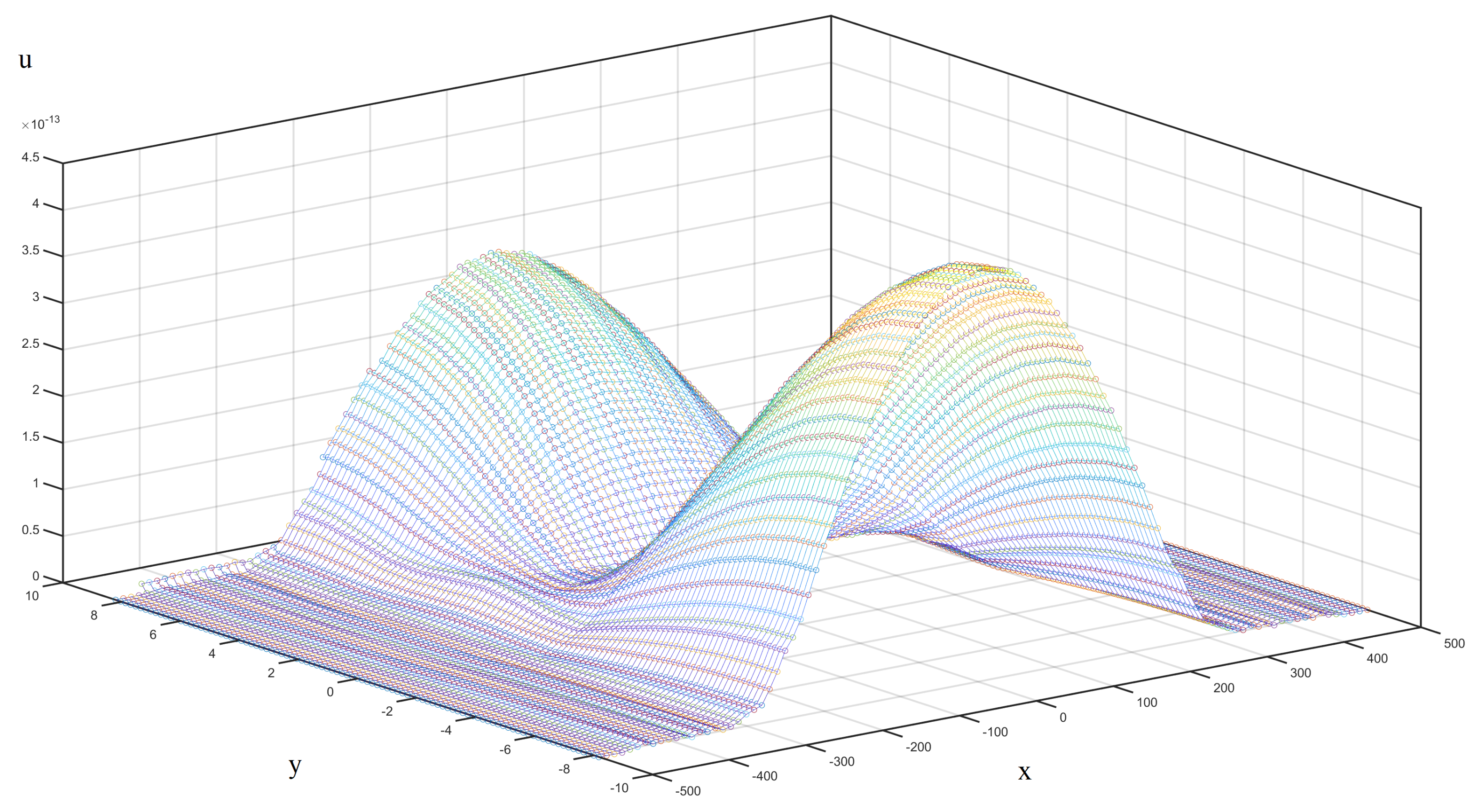
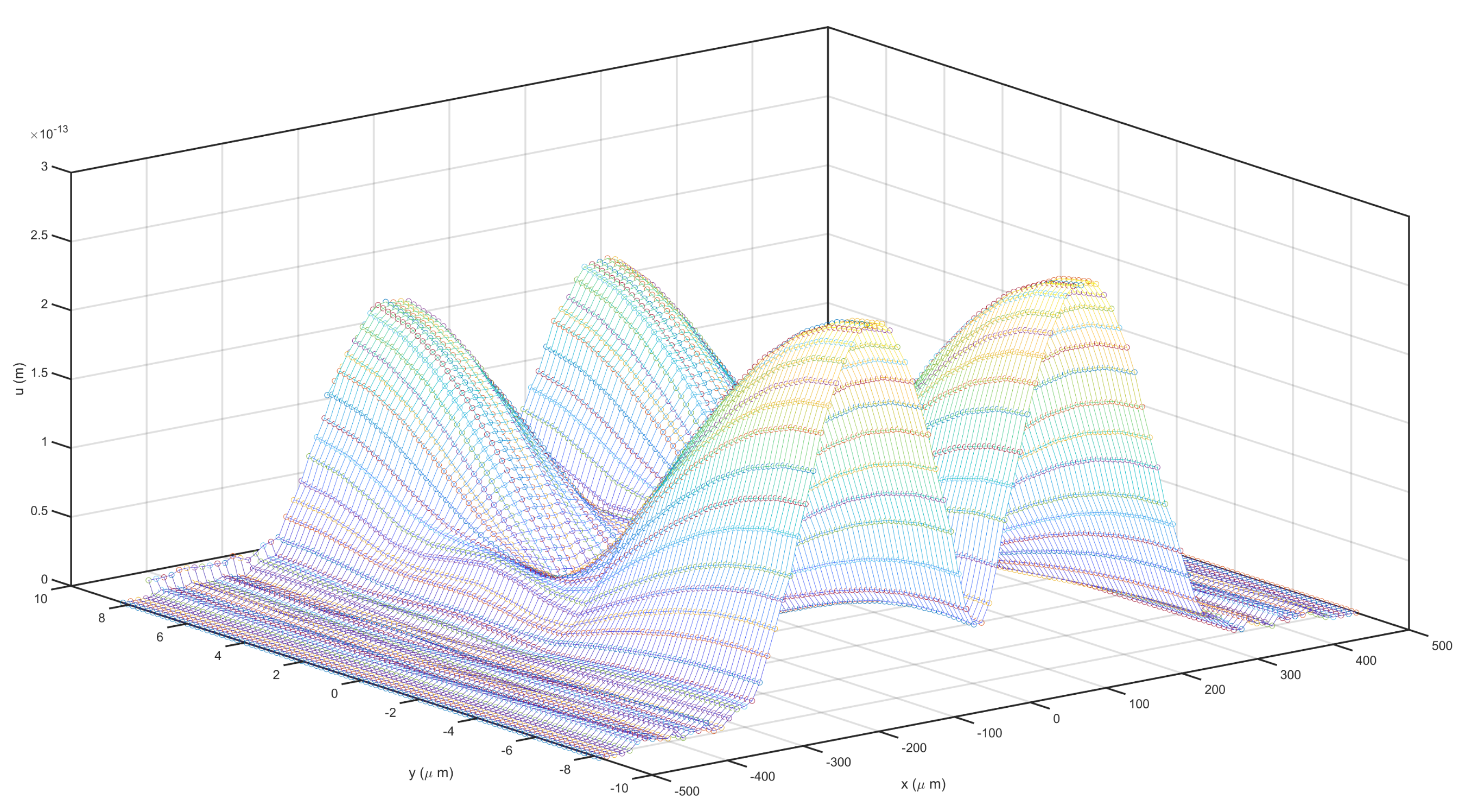
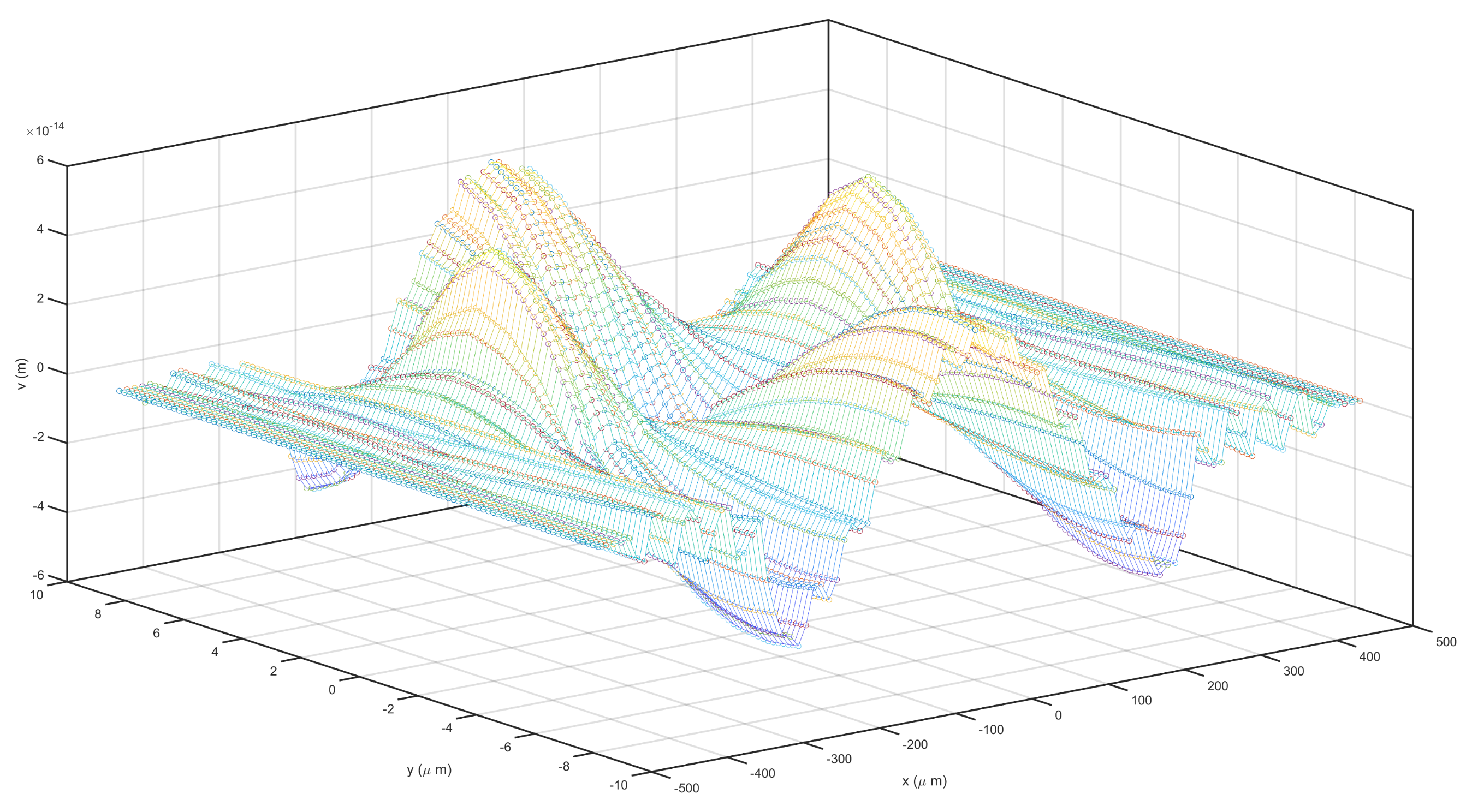
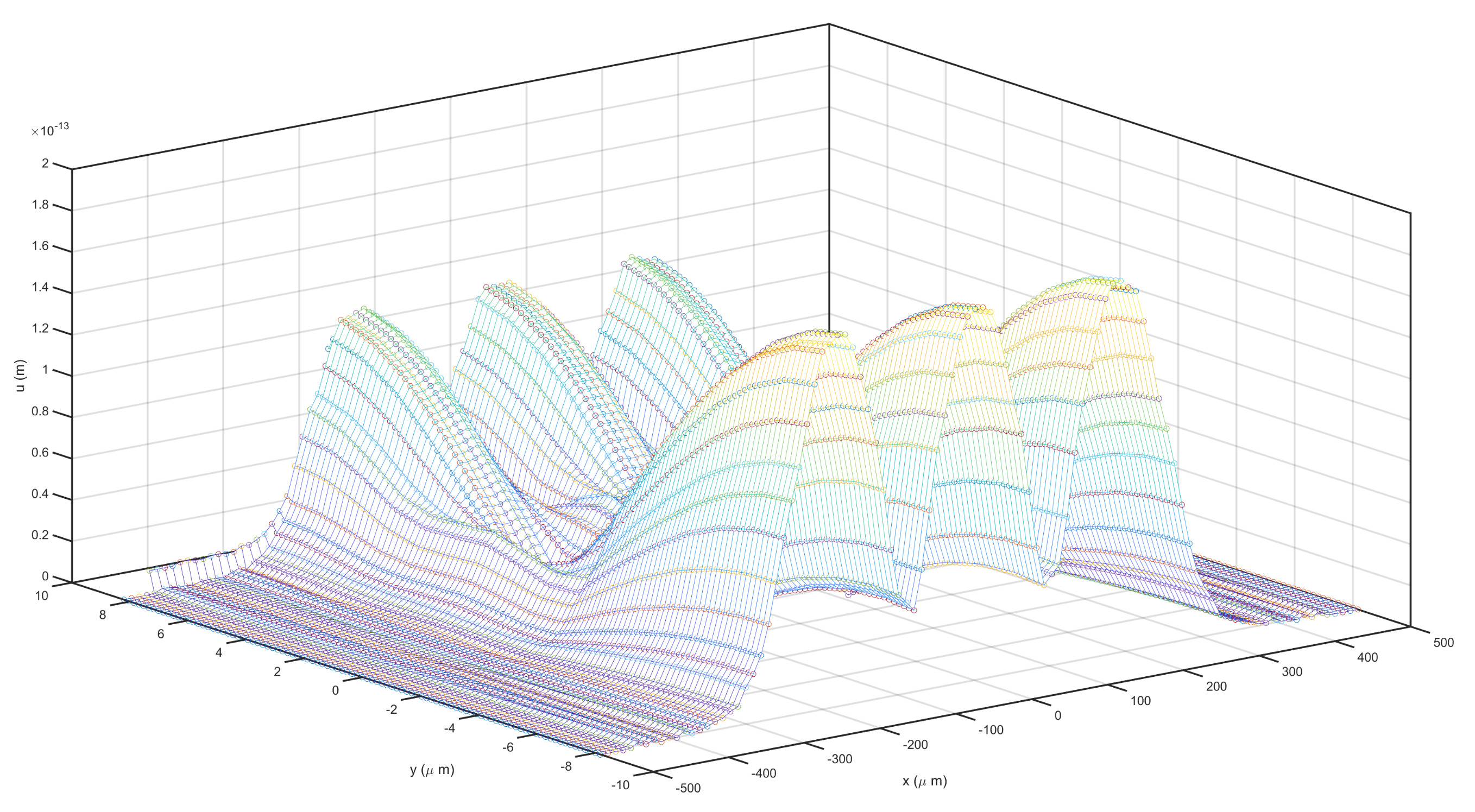
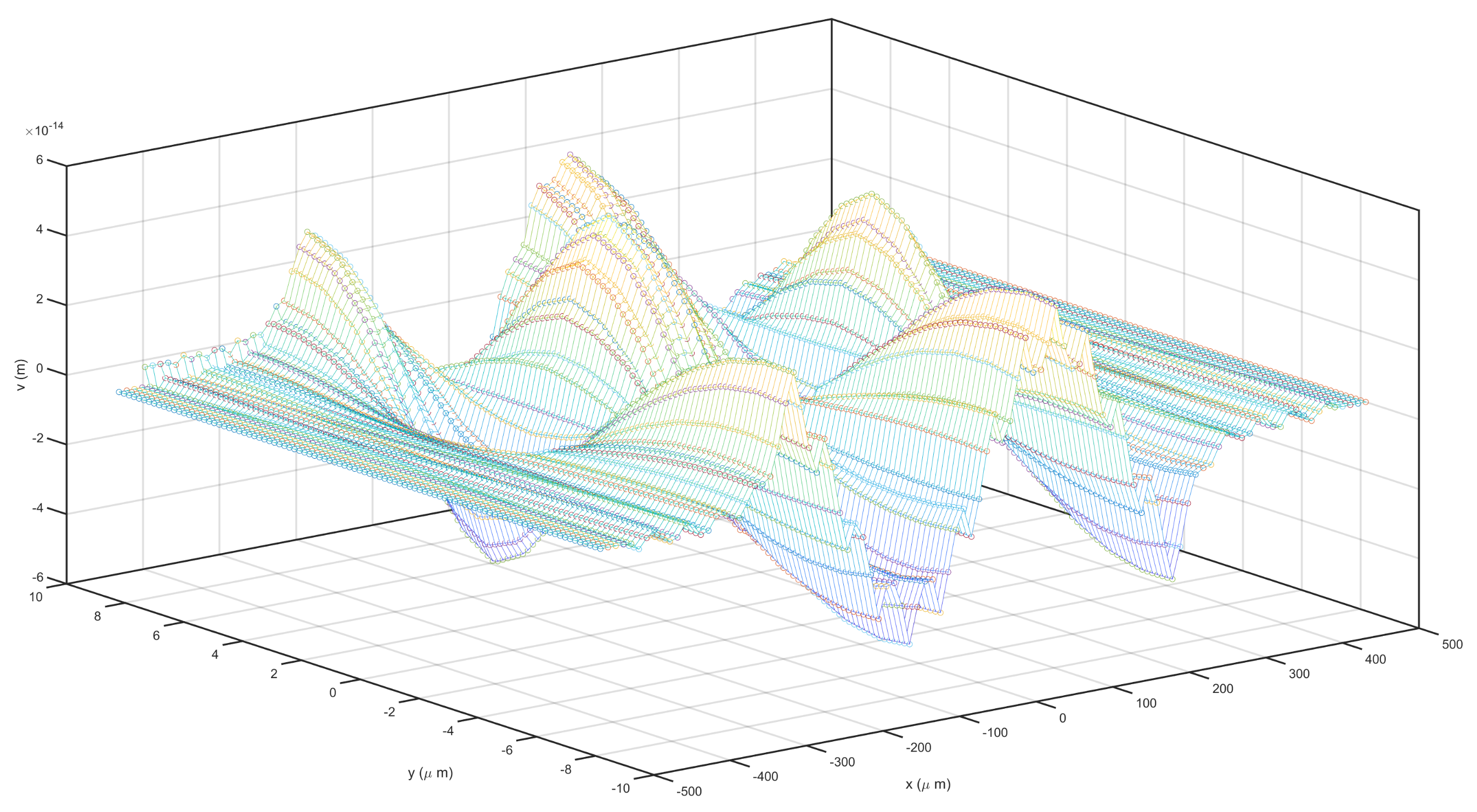
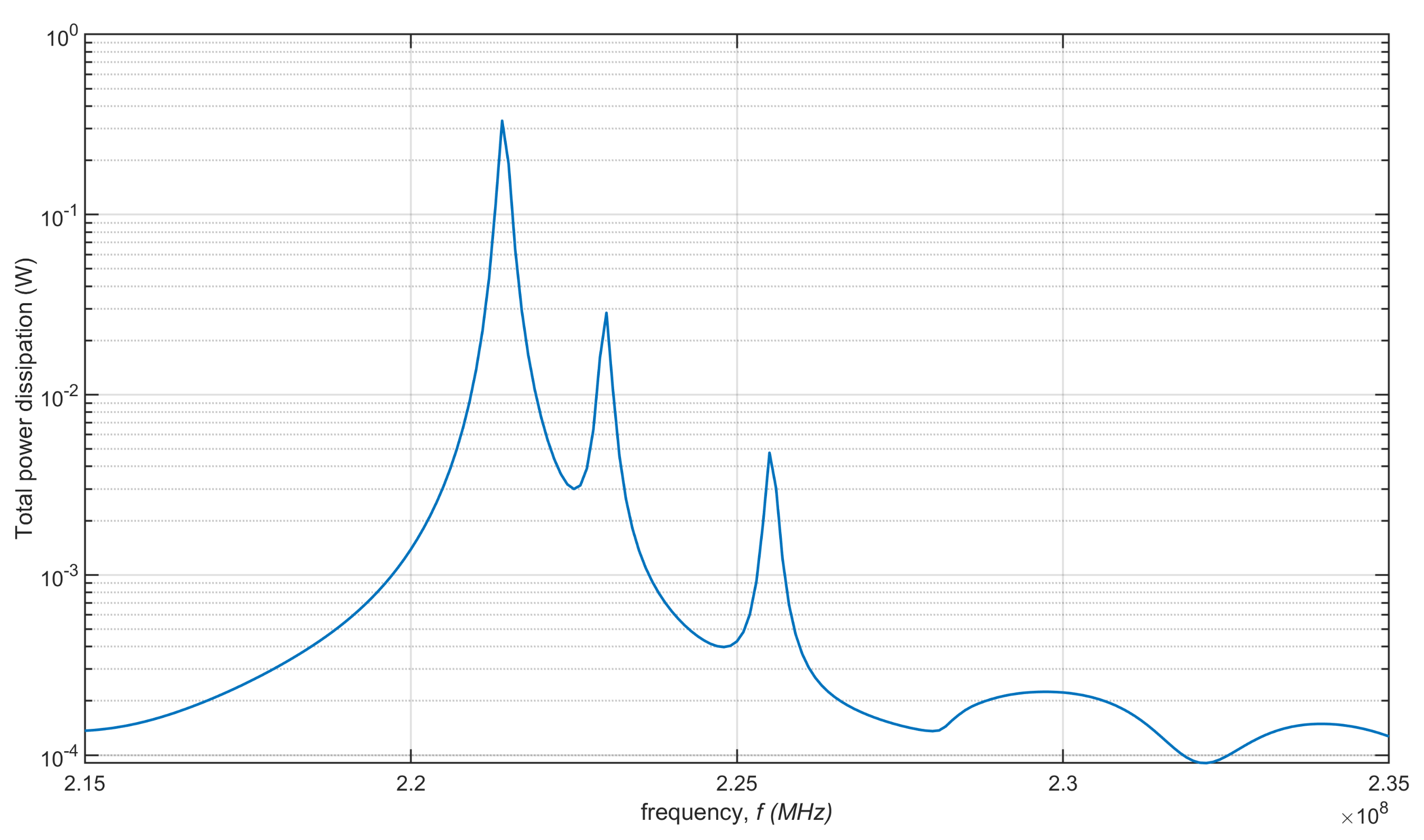
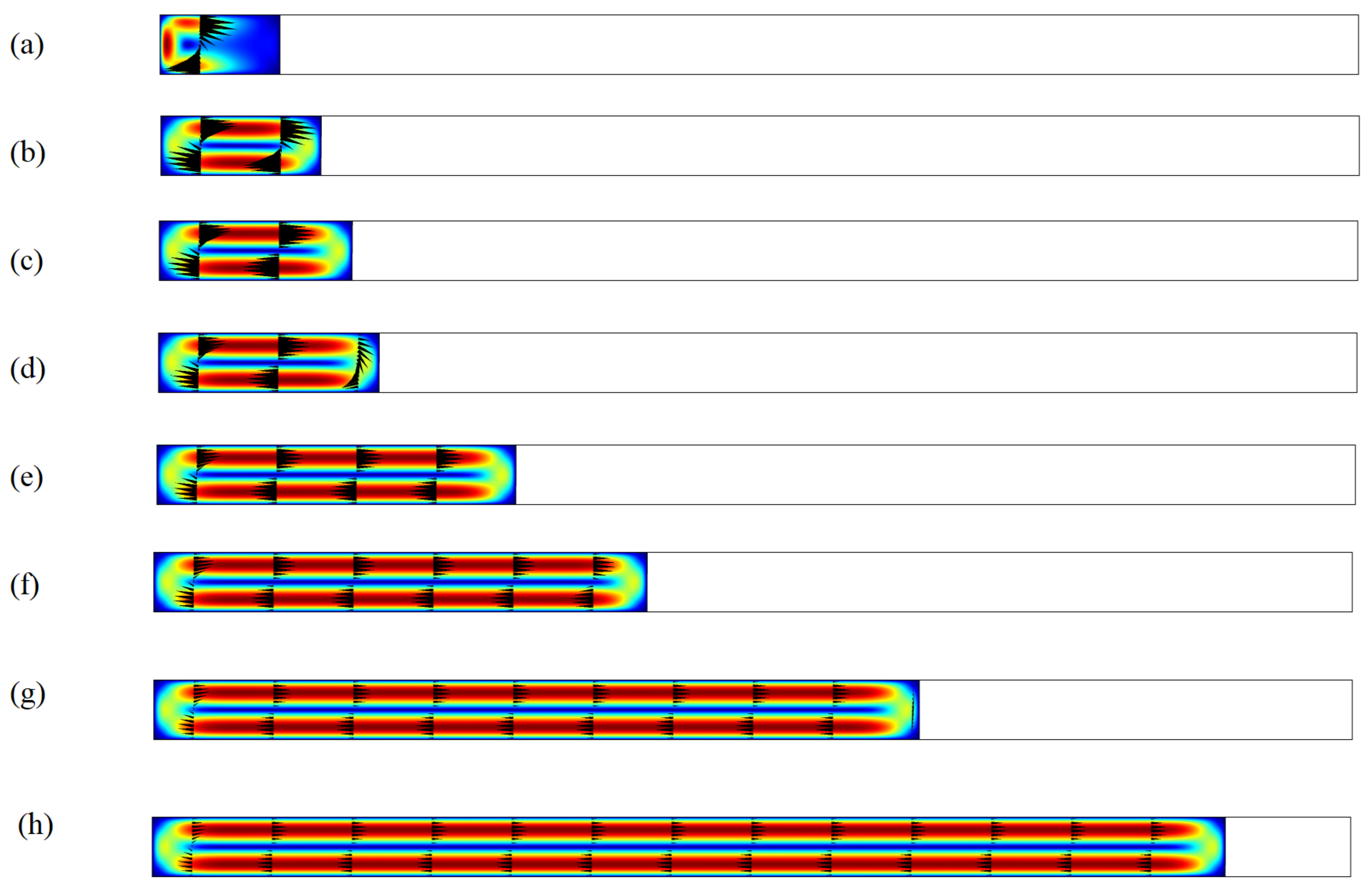
3.2. Eigenfrequency Analysis
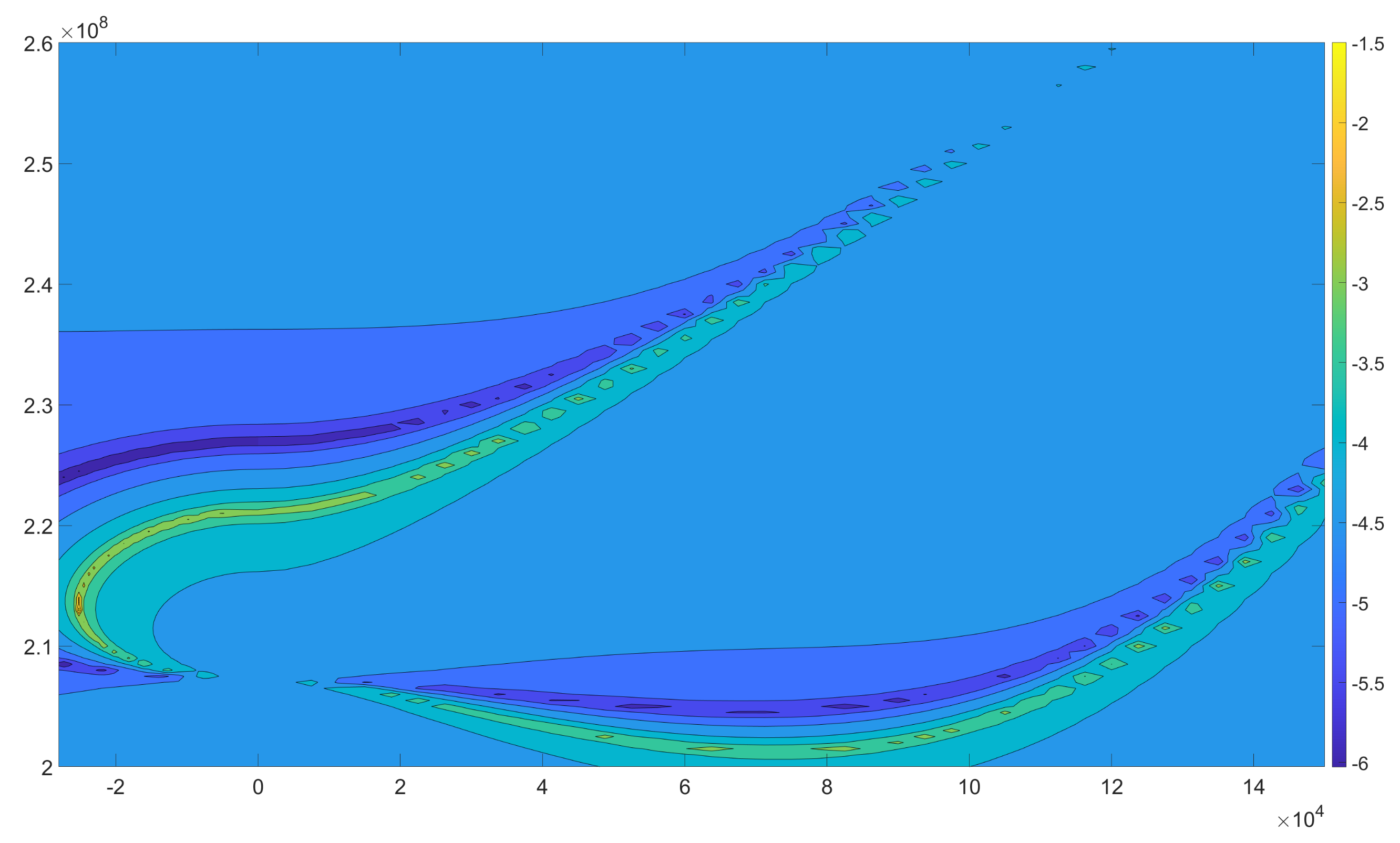
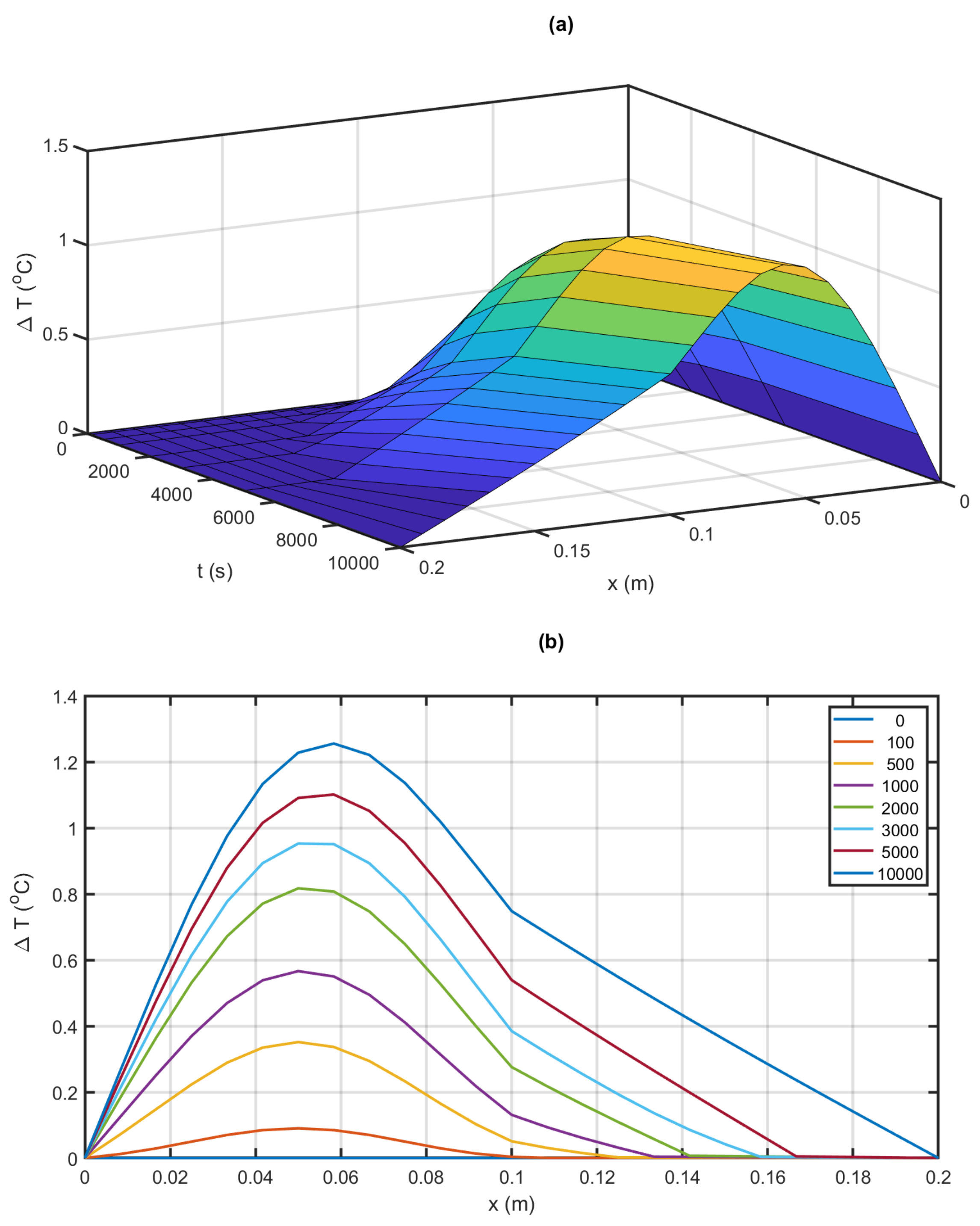
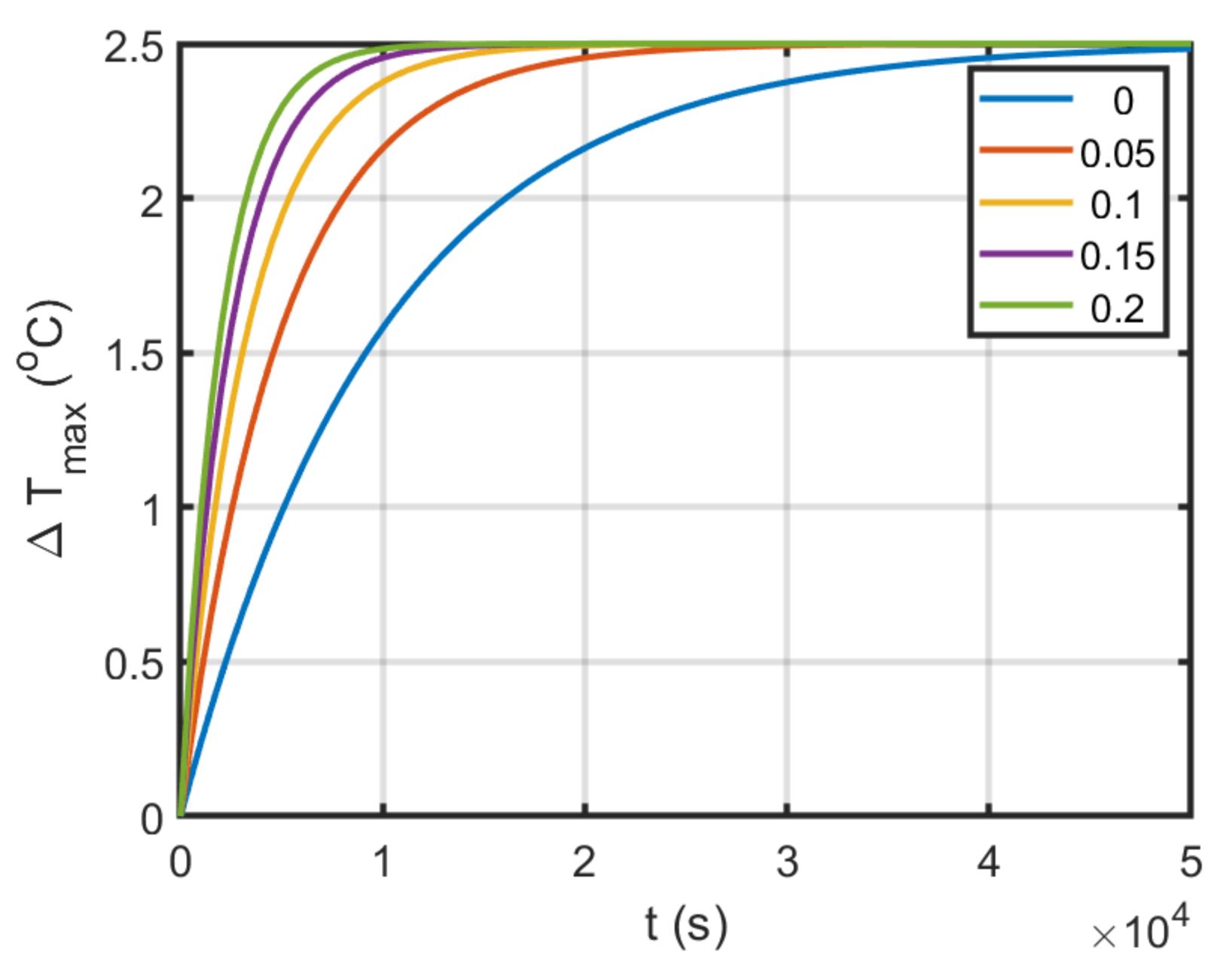
3.3. Fluid and Thermal Analysis
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two dimension |
| 3D | Three dimension |
| BAW | Bulk acoustic waves |
| BC | Boundary conditions |
| FEM | Finite element method |
| IoT | Internet of Things |
| IDT | Interdigital transducers |
| RFFE | Radio frequency front-end |
| SAW | Surface acoustic waves |
Nomenclature
| T | Stress |
| S | Strain |
| E | Electric field |
| D | Electric displacement |
| Elasticity matrix (rank 4 tensor ) | |
| e | Coupling matrix (rank 3 tensor ) |
| Permittivity matrix (rank 2 tensor ) | |
| Constant pressure specific heat (JkgK) | |
| g | Gravity constant (ms) |
| Nu | Nusselt number |
| p | Pressure (Pa) |
| Greek symbols | |
| Dynamic viscosity (kgsm) | |
| Electric potential | |
| s | Solid |
Appendix A. Analytical Solution in One Dimension
Appendix B. ANSYS APDL Input Files
References
- Abdollahzadeh Jamalabadi, M.Y. Rational Design Calculation of Surface Acoustic Wave Gas Sensor. Phys. J. 2020, 6, 63–87. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Park, J.H. Investigation of Property Variations on Freezing of PCM Containing Nanoparticles. World Appl. Sci. J. 2014, 32, 672–677. [Google Scholar]
- Makkonen, T.; Pensala, T.; Vartiainen, J.; Knuuttila, J.V.; Kaitila, J.; Salomaa, M.M. Estimating materials parameters in thin-film BAW resonators using measured dispersion curves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 42. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Park, J.H. Effects of Brownian motion on freezing of PCM containing nanoparticles. Therm. Sci. 2016, 20, 1533–1541. [Google Scholar] [CrossRef] [Green Version]
- Abdollahzadeh Jamalabadi, M.Y. MD Simulation of Brownian Motion of Buckminsterfullerene Trapping in nano-Optical Tweezers. Int. J. Opt. Appl. 2015, 5, 161–167. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y. Use of Nanoparticle Enhanced Phase Change Material for Cooling of Surface Acoustic Wave Sensor. Fluids 2021, 6, 31. [Google Scholar] [CrossRef]
- Singh, R.P.; Sze, J.Y.; Kaushik, S.C.; Rakshit, D.; Romagnoli, A. Thermal performance enhancement of eutectic PCM laden with functionalised graphene nanoplatelets for an efficient solar absorption cooling storage system. J. Energy Storage 2021, 33, 102092. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. A comprehensive review of thermal energy storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef] [Green Version]
- Khan, Z.; Khan, Z.; Ghafoor, A. A review of performance enhancement of PCM based latent heat storage system within the context of materials, thermal stability and compatibility. Energy Convers. Manag. 2016, 115, 132–158. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Qu, Z.G. Lithium-ion battery thermal management using heat pipe and phase change material during discharge—Charge cycle: A comprehensive numerical study. Appl. Energy 2019, 242, 378–392. [Google Scholar] [CrossRef]
- Tariq, S.L.; Ali, H.M.; Akram, M.A.; Janjua, M.M.; Ahmadlouydarab, M. Nanoparticles enhanced phase change materials (NePCMs)-A recent review. Appl. Therm. Eng. 2020, 176, 115305. [Google Scholar] [CrossRef]
- Raj, C.R.; Suresh, S.; Singh, V.K.; Bhavsar, R.R.; Chandrasekar, M.; Archita, V. Life cycle assessment of nanoalloy enhanced layered perovskite solid-solid phase change material till 10000 thermal cycles for energy storage applications. J. Energy Storage 2021, 35, 102220. [Google Scholar] [CrossRef]
- Tiari, S.; Hockins, A.; Mahdavi, M. Numerical study of a latent heat thermal energy storage system enhanced by varying fin configurations. Case Stud. Therm. Eng. 2021, 25, 100999. [Google Scholar] [CrossRef]
- Tiari, S.; Mahdavi, M. Computational study of a latent heat thermal energy storage system enhanced by highly conductive metal foams and heat pipes. J. Anal. Calorim. 2020, 141, 1741–1751. [Google Scholar] [CrossRef]
- Li, W.Q.; Guo, S.J.; Tan, L.; Liu, L.L.; Ao, W. Heat transfer enhancement of nano-encapsulated phase change material (NEPCM) using metal foam for thermal energy storage. Int. J. Heat Mass Transf. 2021, 166, 120737. [Google Scholar] [CrossRef]
- Dutkowski, K.; Kruzel, M.; Zajączkowski, B. Determining the heat of fusion and specific heat of microencapsulated phase change material slurry by thermal delay method. Energies 2021, 14, 179. [Google Scholar] [CrossRef]
- Abdulateef, A.M.; Jaszczur, M.; Hassan, Q.; Anish, R.; Niyas, H.; Sopian, K.; Abdulateef, J. Enhancing the melting of phase change material using a fins–nanoparticle combination in a triplex tube heat exchanger. J. Energy Storage 2021, 35, 102227. [Google Scholar] [CrossRef]
- Nie, C.; Liu, J.; Deng, S. Effect of geometric parameter and nanoparticles on PCM melting in a vertical shell-tube system. Appl. Therm. Eng. 2021, 184, 116290. [Google Scholar] [CrossRef]
- Aqib, M.; Hussain, A.; Ali, H.M.; Naseer, A.; Jamil, F. Experimental case studies of the effect of Al2O3 and MWCNTs nanoparticles on heating and cooling of PCM. Case Stud. Therm. Eng. 2020, 22, 100753. [Google Scholar] [CrossRef]
- Khatibi, M.; Nemati-Farouji, R.; Taheri, A.; Kazemian, A.; Ma, T.; Niazmand, H. Optimization and performance investigation of the solidification behavior of nano-enhanced phase change materials in triplex-tube and shell-and-tube energy storage units. J. Energy Storage 2021, 33, 102055. [Google Scholar] [CrossRef]
- Maher, H.; Rocky, K.A.; Bassiouny, R.; Saha, B.B. Synthesis and thermal characterization of paraffin-based nanocomposites for thermal energy storage applications. Therm. Sci. Eng. Prog. 2021, 22, 100797. [Google Scholar]
- Chen, G. Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons; Oxford University Press: Oxford, UK, 2005; ISBN 9780195159424. [Google Scholar]
- Santhosh, S.; Satish, M.; Yadav, A.; Anish Madhavan, A. Thermal analysis of Fe2O3—Myristic acid nanocomposite for latent heat storage. Mater. Today Proc. 2021, 52, 687. [Google Scholar]
- U Mekrisuh, K.; Giri, S.; Udayraj; Singh, D.; Rakshit, D. Optimal design of the phase change material based thermal energy storage systems: Efficacy of fins and/or nanoparticles for performance enhancement. J. Energy Storage 2021, 33, 102126. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Erfani Moghaddam, M.A.; Asadi, A.; Mogharrebi, A.R.; Jafari, B.; Hasani, M.R.; Ganji, D.D. Effect of two different fins (longitudinal-tree like) and hybrid nano-particles (MoS2-TiO2) on solidification process in triplex latent heat thermal energy storage system. Alex. Eng. J. 2021, 60, 1967–1979. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Hatami, M.; Rahmati, M. A numerical study on the effects of nanoparticles and stair fins on performance improvement of phase change thermal energy storages. Energy 2021, 215, 119112. [Google Scholar] [CrossRef]
- Li, F.; Almarashi, A.; Jafaryar, M.; Hajizadeh, M.R.; Chu, Y.-M. Melting process of nanoparticle enhanced PCM through storage cylinder incorporating fins. Powder Technol. 2021, 381, 551–560. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, C.; Lu, Y.; Kong, Q.; Wei, H.; Yang, Y.; Gao, Q.; Wu, Y.; Sciacovelli, A. Comprehensive performance of composite phase change materials based on eutectic chloride with SiO2 nanoparticles and expanded graphite for thermal energy storage system. Renew. Energy 2021, 172, 1120–1132. [Google Scholar] [CrossRef]
- Fang, Y. A Comprehensive Study of Phase Change Materials (PCMs) for Building Wall Applications. Ph.D. Dissertation, University of Kansas, Lawrence, KS, USA, 2009. [Google Scholar]





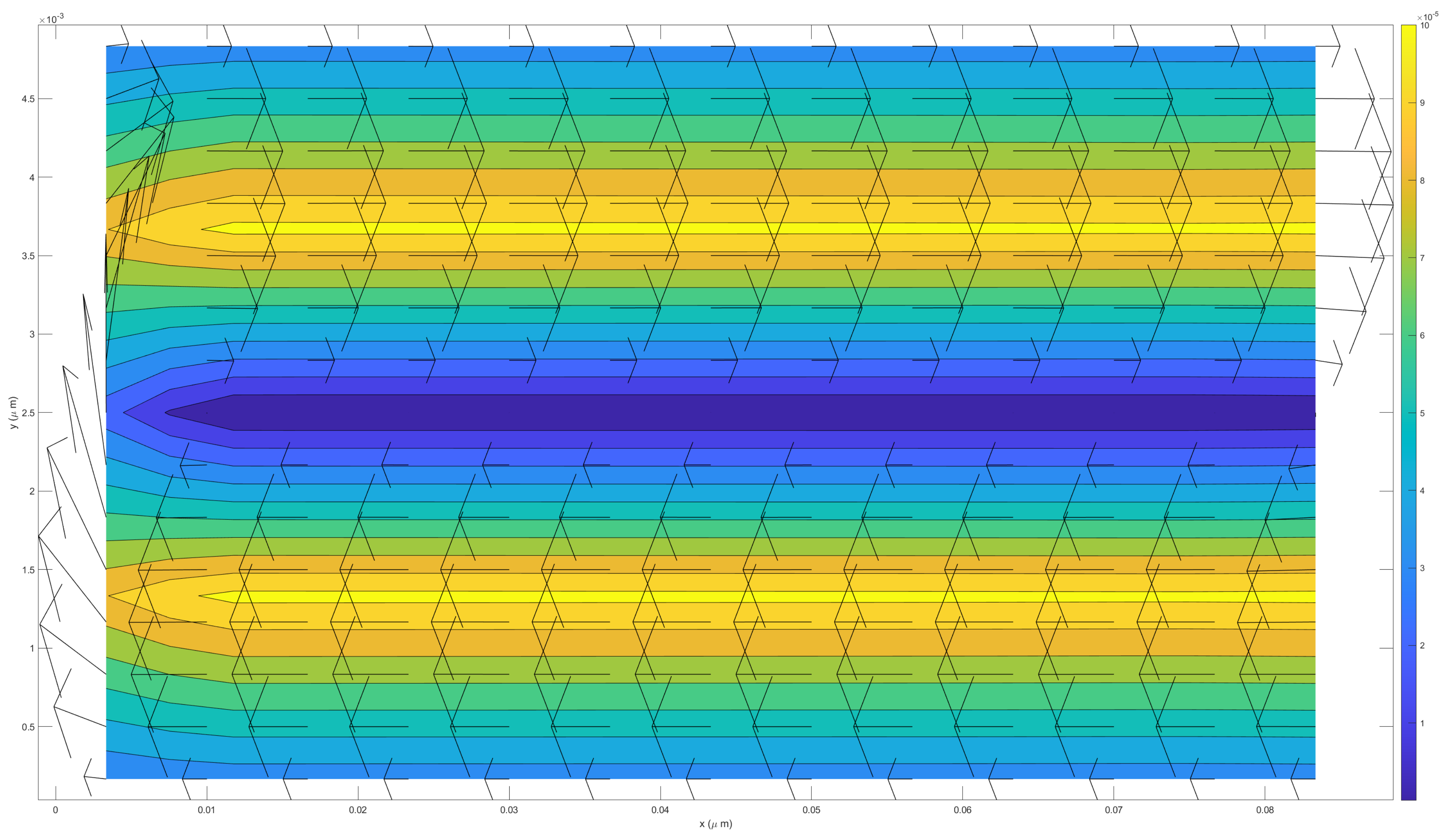
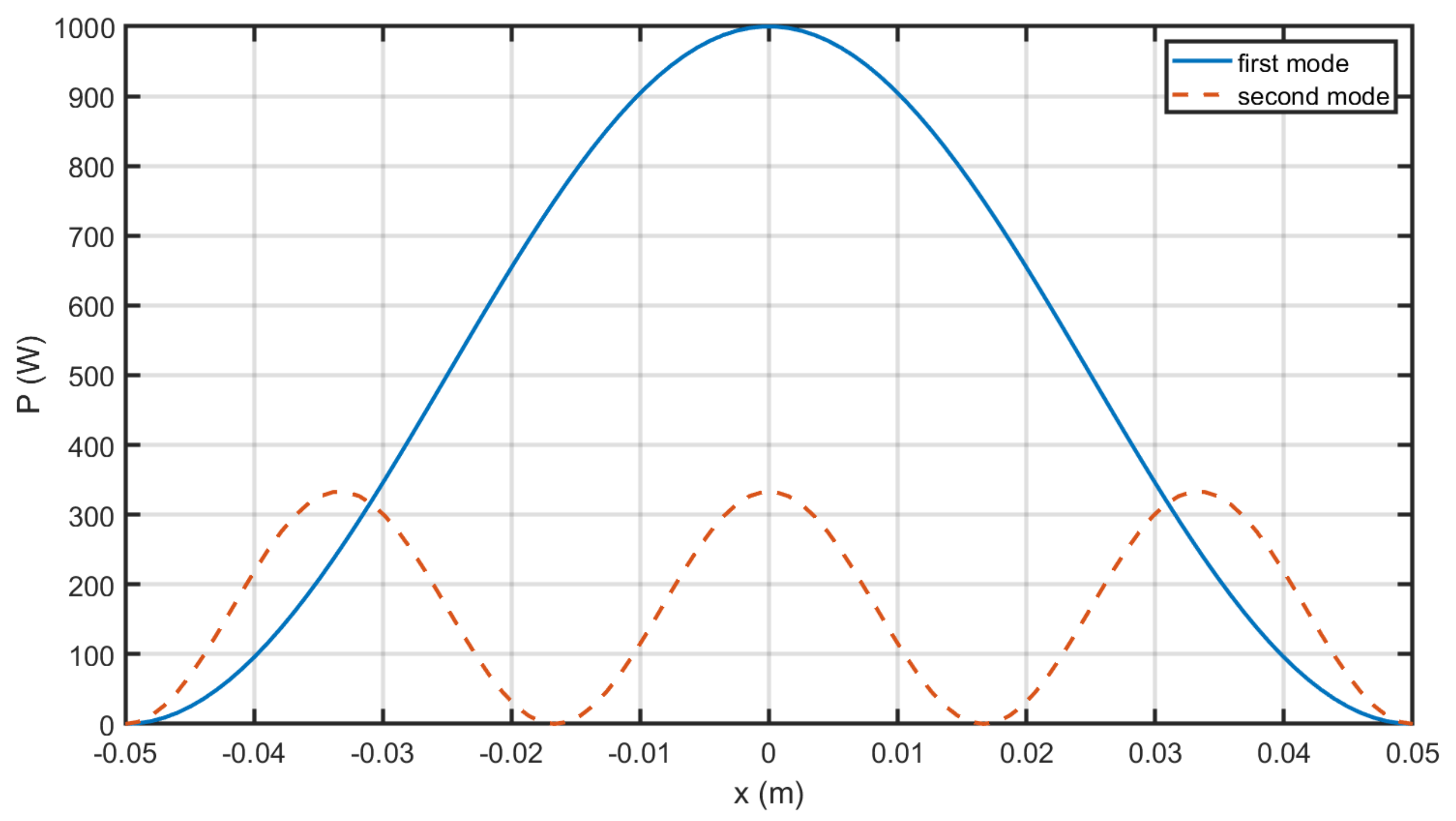
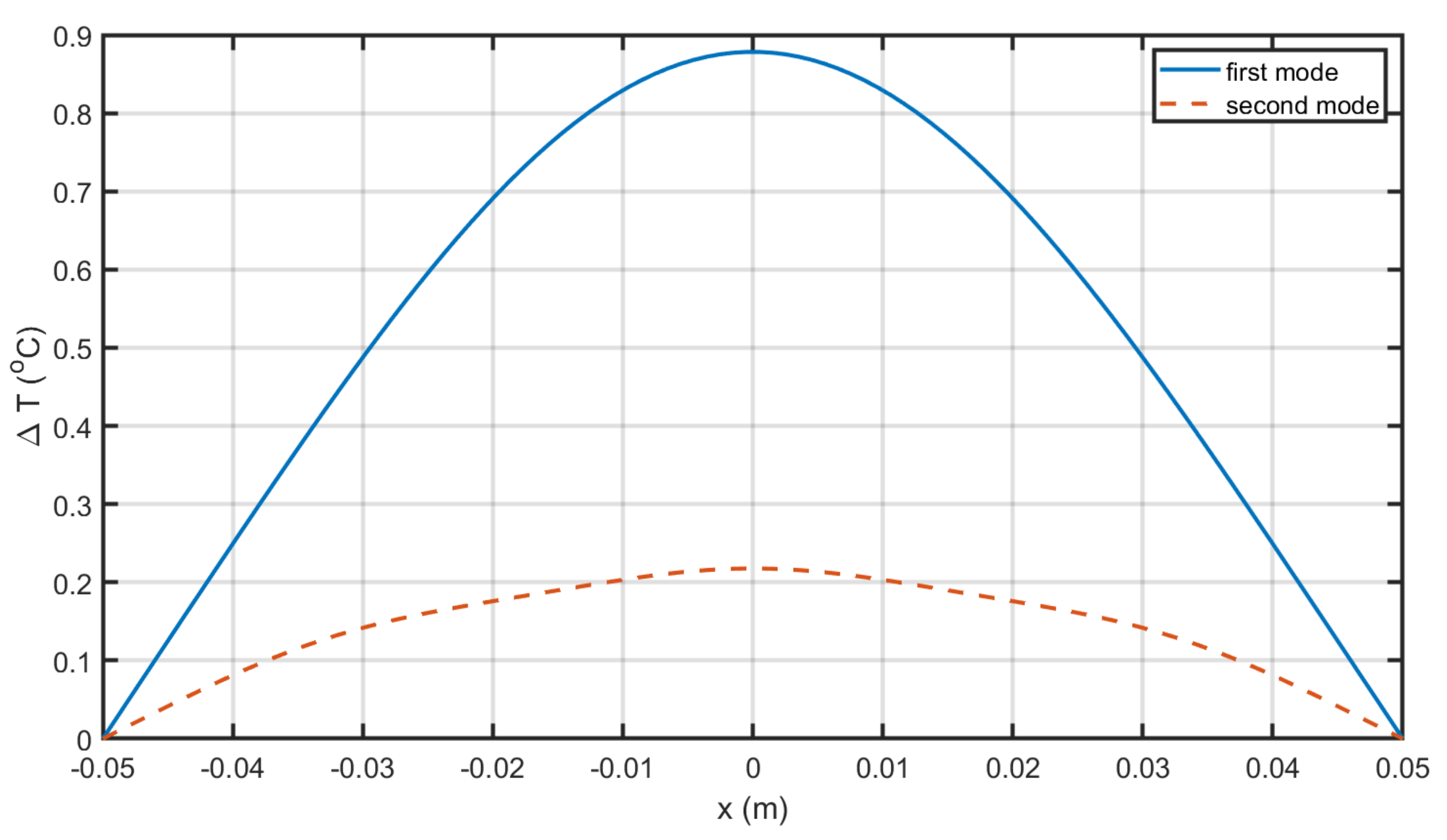
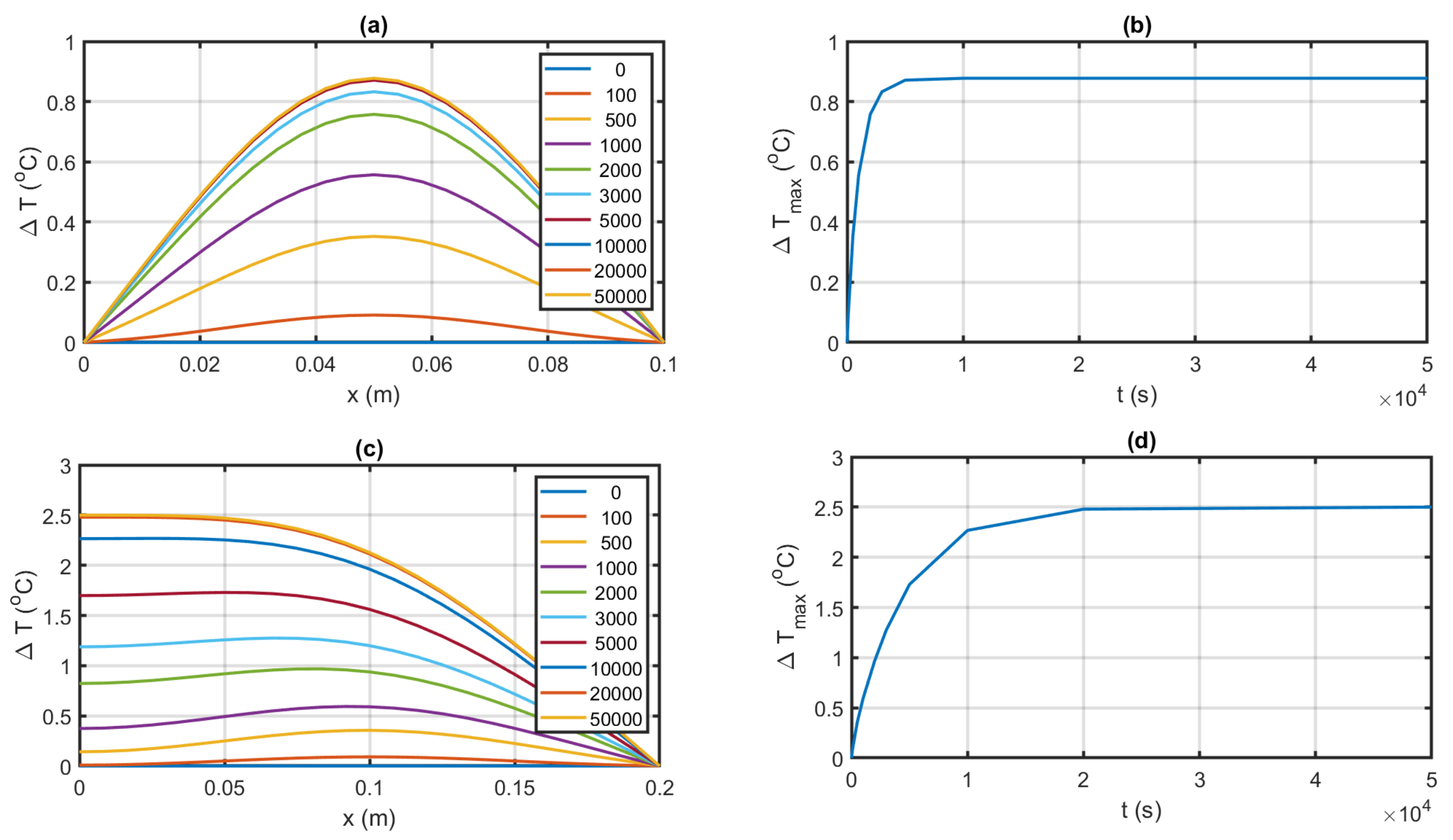
| Equation | Conservation of |
|---|---|
| (1) | mass |
| (2) | x momentums |
| (3) | y momentums |
| (4) | energy |
| x-Velocity | y-Velocity |
|---|---|
| (5) | (6) |
| (7) | (8) |
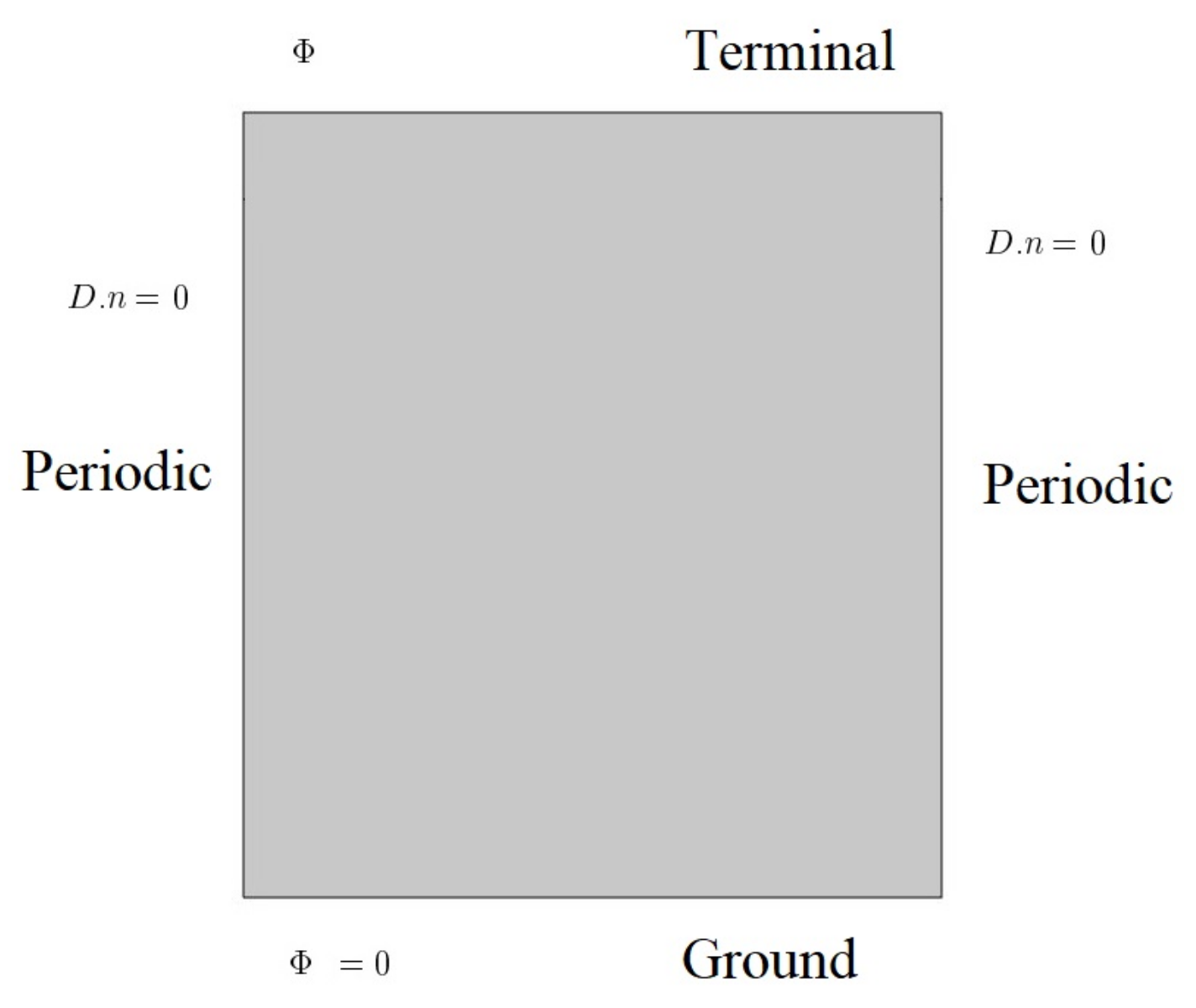
| Wall | Equation |
|---|---|
| left | (9) |
| right | (10) |
| top | (11) |
| bottom | (12) |
| Nano-Fluid Property | Formula |
|---|---|
| (13) | |
| (14) | |
| (15) | |
| (16) | |
| k | (17) |
| (18) | |
| (19) |
| Material | k (W/m·K) | C (kJ/kg·K) | (kg/m) | (K) | (J/kg ) | (Pa·s) |
|---|---|---|---|---|---|---|
| fluid TH29 | 0.53 | 2.2 | 1530 | 187 | ||
| solid TH29 | 1.09 | 1.4 | 1719 | 187 | ||
| Cu | 400 | 0.383 | 8954 |
| Zone | Equation |
|---|---|
| thermal balance over volume | (20) |
| left wall | (21) |
| right wall | (22) |
| top wall | (23) |
| bottom wall | (24) |
| Zone | Equation |
|---|---|
| momentum conservation | (25) |
| periodic left and right walls | (26) |
| top and bottom free surfaces | (27) |
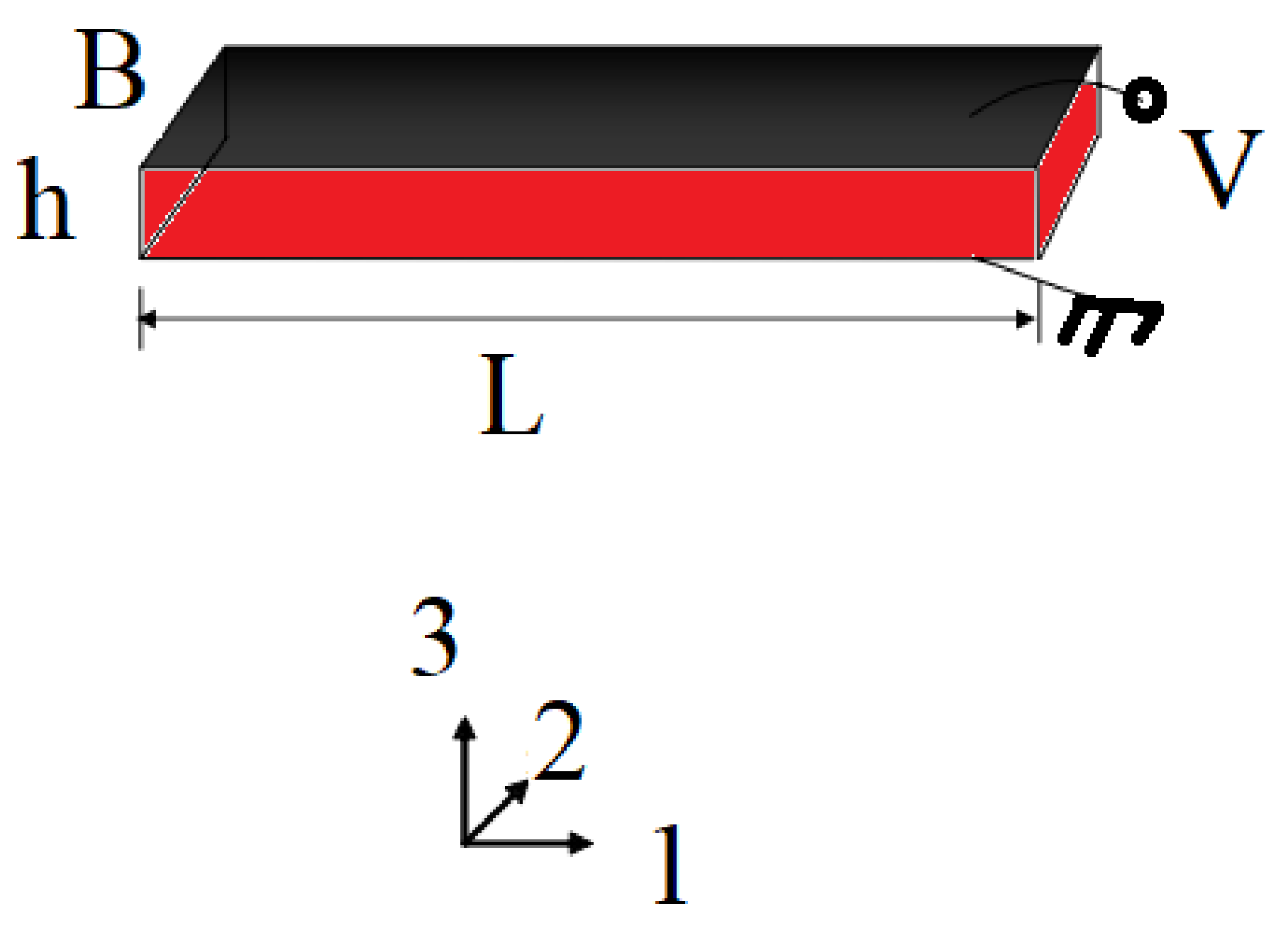
| Parameter | Value | Unit |
|---|---|---|
| L | 100 | mm |
| B | 10 | mm |
| h | 5 | mm |
| 7500 | kg/m | |
| C/N | ||
| F/m | ||
| F/m |
| Material Name | Parameter | Value |
|---|---|---|
| Aluminum Nitride | 3260 | |
| 8 | ||
| 8 | ||
| 10 | ||
| Silicon | 2181.5 | |
| E | ||
| 0.22 | ||
| G | ||
| Molybdenum | 10096 | |
| E | ||
| 0.362 | ||
| G |
| Variable Name | Value |
|---|---|
| Description | Units | Value |
|---|---|---|
| Eigenfrequency | Hz | 221.42 + 0.083574i |
| Participation factor, normalized, X-translation | - | −1.4177E−9−2.3951E−9i |
| Participation factor, normalized, Y-translation | - | 2.3391E−8−2.3982E−9i |
| Participation factor, normalized, Z-rotation | − | 1.3453E−12 + 1.4519E−13i |
| X-translation modal mass | kg | −3.7265E−18 + 6.7912E−18i |
| Y-translation modal mass | kg | 5.4141E−16−1.1219E−16i |
| Z-rotation modal mass | kg·m | 1.7886E−24 + 3.9064E−25i |
| Eigenfrequency | Hz | 222.02 + 0.084982i |
| Participation factor, normalized, X-translation | - | −1.2376E−7−2.2132E−8i |
| Participation factor, normalized, Y-translation | - | −6.3621E−10 + 1.2395E−9i |
| Participation factor, normalized, Z-rotation | − | −7.0904E−12 + 1.7065E−11i |
| X-translation modal mass | kg | 1.4827E−14 + 5.4782E−15i |
| Y-translation modal mass | kg | −1.1316E−18−1.5772E−18i |
| Z-rotation modal mass | kg·m | −2.4093E−22−2.4199E−22i |
| Eigenfrequency | Hz | 222.97 + 0.084029i |
| Participation factor, normalized, X-translation | - | 2.3988E−9−8.4602E−10i |
| Participation factor, normalized, Y-translation | - | −1.0829E−8−2.0163E−8i |
| Participation factor, normalized, Z-rotation | − | −1.1635E−13−1.7268E−13i |
| X-translation modal mass | kg | 5.0385E−18−4.0589E−18i |
| Y-translation modal mass | kg | −2.8925E−16 + 4.3670E−16i |
| Z-rotation modal mass | kg·m | −1.6281E−26 + 4.0181E−26i |
| Eigenfrequency | Hz | 224.16 + 0.090701i |
| Participation factor, normalized, X-translation | - | 5.3732E−8−2.4727E−7i |
| Participation factor, normalized, Y-translation | - | 6.2749E−10−1.0431E−9i |
| Participation factor, normalized, Z-rotation | − | −6.0091E−12−6.5558E−12i |
| X-translation modal mass | kg | −5.8254E−14−2.6572E−14i |
| Y-translation modal mass | kg | −6.9441E−19−1.3091E−18i |
| Z-rotation modal mass | kg·m | −6.8693E−24 + 7.8788E−23i |
| Eigenfrequency | Hz | 225.51 + 0.090162i |
| Participation factor, normalized, X-translation | - | −2.9494E−9−1.3085E−9i |
| Participation factor, normalized, Y-translation | - | −3.4432E−9 + 5.0666E−8i |
| Participation factor, normalized, Z-rotation | − | 6.7515E−13 + 6.2670E−13i |
| X-translation modal mass | kg | 6.9867E−18 + 7.7184E−18i |
| Y-translation modal mass | kg | −2.5551E−15−3.4891E−16i |
| Z-rotation modal mass | kg·m | 6.3072E−26 + 8.4624E−25i |
| Eigenfrequency | Hz | 226.96 + 0.090142i |
| Participation factor, normalized, X-translation | - | 3.8473E−8−1.7100E−8i |
| Participation factor, normalized, Y-translation | - | −1.0000E−9−9.8674E−10i |
| Participation factor, normalized, Z-rotation | − | −2.1903E−11 + 6.6730E−12i |
| X-translation modal mass | kg | 1.1878E−15−1.3158E−15i |
| Y-translation (modal mass | kg | 2.6426E−20 + 1.9736E−18i |
| Z-rotation modal mass | kg·m | 4.3522E−22−2.9232E−22i |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdollahzadeh Jamalabadi, M.Y. Feasibility Study of Cooling a Bulk Acoustic Wave Resonator by Nanoparticle Enhanced Phase Change Material. Magnetochemistry 2021, 7, 144. https://doi.org/10.3390/magnetochemistry7110144
Abdollahzadeh Jamalabadi MY. Feasibility Study of Cooling a Bulk Acoustic Wave Resonator by Nanoparticle Enhanced Phase Change Material. Magnetochemistry. 2021; 7(11):144. https://doi.org/10.3390/magnetochemistry7110144
Chicago/Turabian StyleAbdollahzadeh Jamalabadi, Mohammad Yaghoub. 2021. "Feasibility Study of Cooling a Bulk Acoustic Wave Resonator by Nanoparticle Enhanced Phase Change Material" Magnetochemistry 7, no. 11: 144. https://doi.org/10.3390/magnetochemistry7110144
APA StyleAbdollahzadeh Jamalabadi, M. Y. (2021). Feasibility Study of Cooling a Bulk Acoustic Wave Resonator by Nanoparticle Enhanced Phase Change Material. Magnetochemistry, 7(11), 144. https://doi.org/10.3390/magnetochemistry7110144





