Saturation of Specific Absorption Rate for Soft and Hard Spinel Ferrite Nanoparticles Synthesized by Polyol Process
Abstract
1. Introduction
2. Results and Discussion
2.1. Morphological and Structural Properties
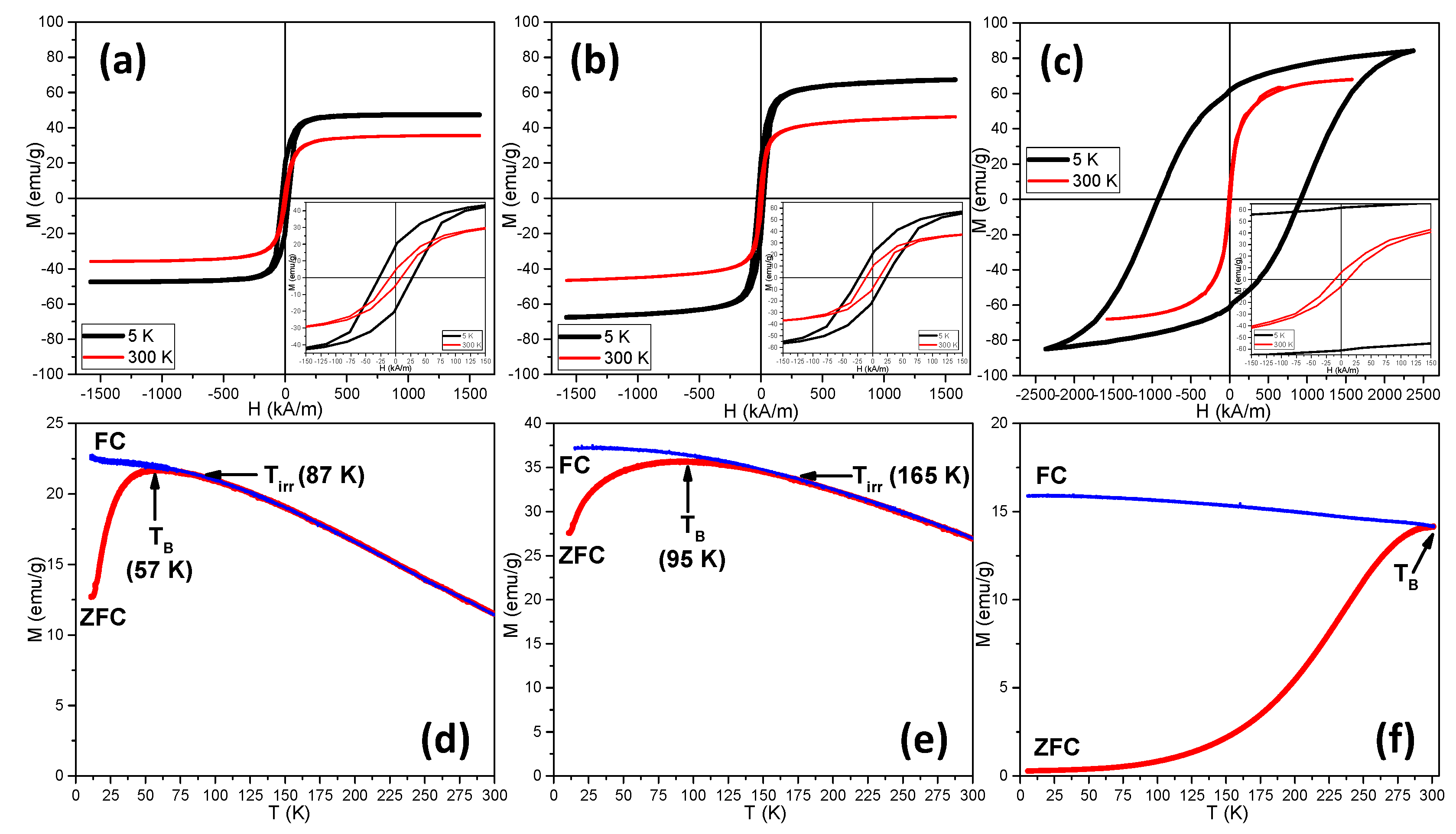
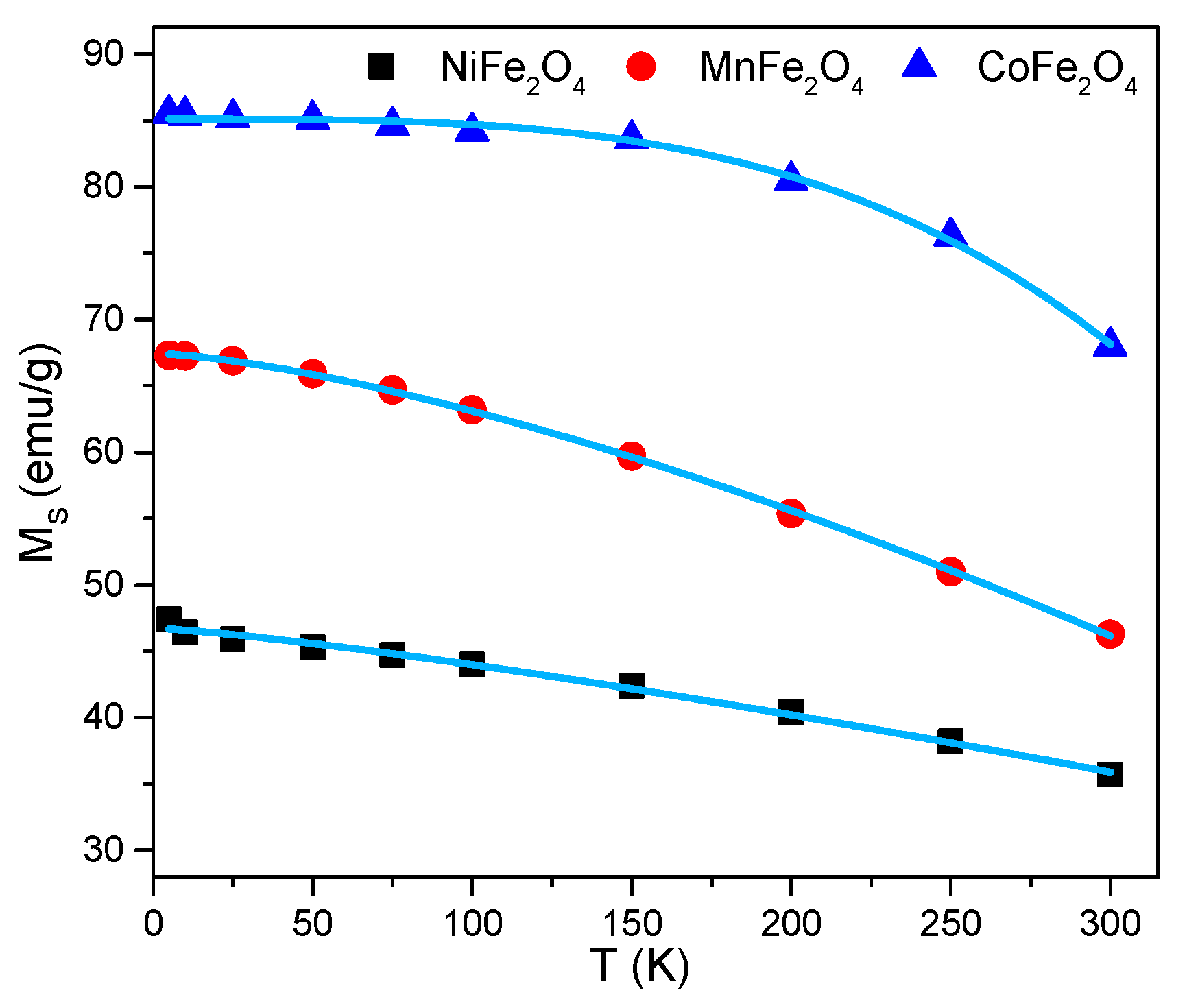
2.2. Magnetic Properties
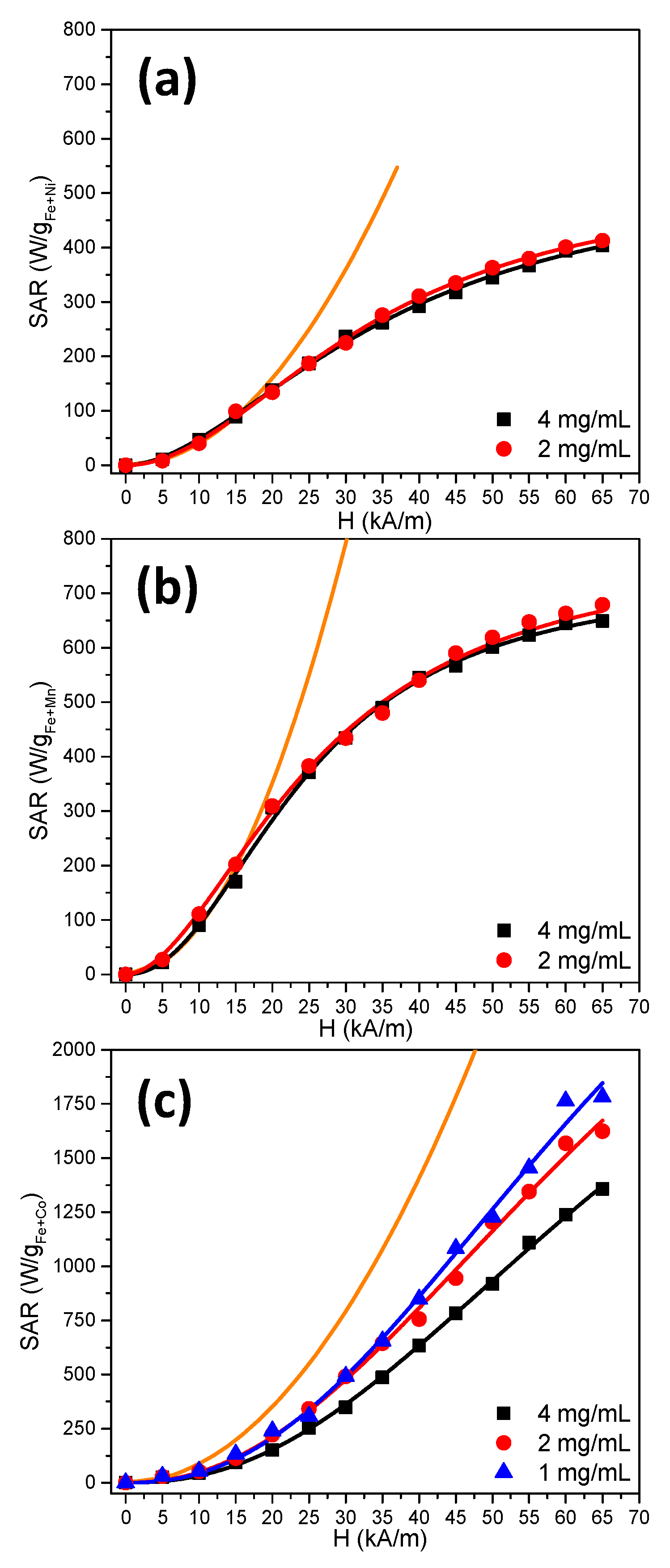
2.3. Hyperthermia Properties
3. Materials and Methods
3.1. Synthesis Method
3.2. Characterization Methods
3.3. Hyperthermia Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hepel, M. Magnetic Nanoparticles for Nanomedicine. Magnetochemistry 2020, 6, 3. [Google Scholar] [CrossRef]
- Katz, E. Synthesis, Properties and Applications of Magnetic Nanoparticles and Nanowires—A Brief Introduction. Magnetochemistry 2019, 5, 61. [Google Scholar] [CrossRef]
- Bilal, M.; Mehmood, S.; Rasheed, T.; Iqbal, H.M.N. Bio-Catalysis and Biomedical Perspectives of Magnetic Nanoparticles as Versatile Carriers. Magnetochemistry 2019, 5, 42. [Google Scholar] [CrossRef]
- Dulinska-Litewk, J.; Lazarczyk, A.; Halubiec, P.; Szafranski, O.; Karnas, K.; Karewicz, A. Superparamagnetic Iron Oxide Nanoparticles—Current and Prospective Medical Applications. Materials 2019, 12, 617. [Google Scholar] [CrossRef] [PubMed]
- Popescu, R.C.; Andronescu, E.; Vasile, B.S. Recent Advances in Magnetite Nanoparticle Functionalization for Nanomedicine. Nanomaterials 2019, 9, 1791. [Google Scholar] [CrossRef] [PubMed]
- Socoliuc, V.; Peddis, D.; Petrenko, V.I.; Avdeev, M.V.; Susan-Resiga, D.; Szabo, T.; Turcu, R.; Tombacz, E.; Vekas, L. Magnetic Nanoparticle Systems for Nanomedicine—A Materials Science Perspective. Magnetochemistry 2019, 6, 2. [Google Scholar] [CrossRef]
- Hosu, O.; Tertis, M.; Cristea, C. Implication of Magnetic Nanoparticles in Cancer Detection, Screening and Treatment. Magnetochemistry 2019, 5, 55. [Google Scholar] [CrossRef]
- Bruschi, M.L.; de Toledo, L.D.A.S. Pharmaceutical Applications of Iron-Oxide Magnetic Nanoparticles. Magnetochemistry 2019, 5, 50. [Google Scholar] [CrossRef]
- Obaidat, I.M.; Narayanaswamy, V.; Alaabed, S.; Sambasivam, S.; Muralee Gopi, C.V.V. Principles of Magnetic Hyperthermia: A Focus on Using Multifunctional Hybrid Magnetic Nanoparticles. Magnetochemistry 2019, 5, 67. [Google Scholar] [CrossRef]
- Obaidat, I.M.; Issa, B.; Haik, J. Magnetic Properties of Magnetic Nanoparticles for Efficient Hyperthermia. Nanomaterials 2015, 5, 63–89. [Google Scholar] [CrossRef]
- Gilchrist, R.K.; Medal, R.; Shorey, W.D.; Hanselman, R.C.; Parrot, J.C.; Taylor, C.B. Selective Inductive Heating of Lymph Nodes. J. Ann. Surg. 1957, 146, 596–606. [Google Scholar] [CrossRef]
- Maier-Hauff, K.; Ulrich, F.; Nestler, D.; Niehoff, H.; Wust, P.; Thiesen, B.; Orawa, H.; Budach, V.; Jordan, A. Efficacy and safety of intratumoral thermotherapy using magnetic iron oxide nanoparticles combined with external beam radiotherapy on patients with recurrent glioblastoma multiforme. J. Neurooncol. 2011, 103, 317–324. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating Magnetic Fluid with Alternating Magnetic Field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Glöckl, G.; Hergt, R.; Zeisberger, M.; Dutz, S.; Nagel, S.; Weitschies, W. The Effect of Field Parameters, Nanoparticle Properties and Immobilization on the Specific Heating Power in Magnetic Particle Hyperthermia. J. Phys. Condens. Matter 2006, 18, S2935. [Google Scholar]
- Hergt, R.; Dutz, S. Magnetic Particle Hyperthermia-Biophysical Limitations of a Visionary Tumour Therapy. J. Magn. Magn. Mater. 2007, 311, 187–192. [Google Scholar] [CrossRef]
- Pineiro, Y.; Vargas, Z.; Rivas, J.; López-Quintela, M.A. Iron Oxide Based Nanoparticles for Magnetic Hyperthermia Strategies in Biological Applications. Eur. J. Inorg. Chem. 2015, 27, 4495–4509. [Google Scholar] [CrossRef]
- Blanco-Andujar, C.; Walter, A.; Cotin, G.; Bordeianu, C.; Mertz, D.; Felder-Flesch, D.; Begin-Colin, S. Design of iron oxide-based nanoparticles for MRI and magnetic hyperthermia. Nanomedicine (London) 2016, 11, 1889–1910. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, J.; Xing, M.; Ping Liu, J. Inductive Thermal Effect of FerriteMagneticNanoparticles. Materials 2019, 12, 3208. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc. 1948, A240, 599–642. [Google Scholar] [CrossRef]
- Stiufiuc, R.; Iacovita, C.; Lucaciu, C.M.; Stiufiuc, G.; Dutu, A.G.; Braescu, C.; Leopold, N. SERS-active silver colloids prepared by reduction of silver nitrate with short-chain polyethylene glycol. Nanoscale Res. Lett. 2013, 8, 1–5. [Google Scholar] [CrossRef]
- Stiufiuc, R.; Iacovita, C.; Nicoara, R.; Stiufiuc, G.; Florea, A.; Achim, M.; Lucaciu, C.M. One-Step Synthesis of PEGylated Gold Nanoparticles with Tunable Surface Charge. J. Nanomater. 2013, 2013, 146031. [Google Scholar] [CrossRef]
- Iacovita, C.; Stiufiuc, R.; Radu, T.; Florea, A.; Stiufiuc, G.; Dutu, A.; Mican, S.; Tetean, R.; Lucaciu, C.M. Polyethylene glycol-mediated synthesis of cubic iron oxide nanoparticles with high heating power. Nanoscale Res. Lett. 2015, 10, 1–16. [Google Scholar] [CrossRef]
- Iacovita, C.; Florea, A.; Dudric, R.; Pall, E.; Moldovan, A.I.; Tetean, R.; Stiufiuc, R.; Lucaciu, C.M. Small versus Large Iron Oxide Magnetic Nanoparticles: Hyperthermia and Cell Uptake Properties. Molecules 2016, 21, 1357. [Google Scholar] [CrossRef] [PubMed]
- Iacovita, C.; Florea, A.; Scorus, L.; Pall, E.; Dudric, R.; Moldovan, A.I.; Stiufiuc, R.; Tetean, R.; Lucaciu, C.M. Hyperthermia, Cytotoxicity, and Cellular Uptake Properties of Manganese and Zinc Ferrite Magnetic Nanoparticles Synthesized by a Polyol-Mediated Process. Nanomaterials 2019, 9, 1489. [Google Scholar] [CrossRef] [PubMed]
- Iacovita, C.; Fizesan, I.; Pop, A.; Scorus, L.; Dudric, R.; Stiufiuc, G.; Vedeanu, N.; Tetean, R.; Loghin, F.; Stiufiuc, R.; et al. In Vitro Intracellular Hyperthermia of Iron Oxide Magnetic Nanoparticles, Synthesized at High Temperature by a Polyol Process. Pharmaceutics 2020, 12, 424. [Google Scholar] [CrossRef]
- Sabale, S.; Jadhav, V.; Khot, V.; Zhu, X.; Xin, M.; Chen, H. Superparamagnetic MFe2O4 (M = Ni, Co, Zn, Mn) nanoparticles: Synthesis, characterization, induction heating and cell viability studies for cancer hyperthermia applications. J. Mater. Sci. Mater. Med. 2015, 26, 1–9. [Google Scholar] [CrossRef]
- Patterson, A.L. The Scherrer formula for X-ray particle size determination. Phys. Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Lee, J.-H.; Huh, Y.-M.; Jun, Y.-W.; Seo, J.-W.; Jang, J.-T.; Song, H.-T.; Kim, S.; Cho, E.-J.; Yoon, H.-G.; Suh, J.-S.; et al. Artificially engineered magnetic nanoparticles for ultra-sensitive molecular imaging. Nat. Med. 2007, 13, 95–99. [Google Scholar] [CrossRef]
- Andersen, H.L.; Saura-Múzquiz, M.; Granados-Miralles, C.; Canévet, E.; Lock, N.; Christensen, M. Crystalline and magnetic structure-property relationship in spinel ferrite nanoparticles. Nanoscale 2018, 10, 14902–14914. [Google Scholar] [CrossRef]
- Menelaou, M.; Georgoula, K.; Simeonidis, K.; Dendrinou-Samara, C. Evaluation of nickel ferrite nanoparticles coated with oleylamine by NMR relaxation measurements and magnetic hyperthermia. Dalton Trans. 2014, 43, 3626–3636. [Google Scholar] [CrossRef]
- Vamvakidis, K.; Sakellari, D.; Angelakeris, M.; Dendrinou-Samara, C. Size and compositionally controlled manganese ferrite nanoparticles with enhanced magnetization. J. Nanopart. Res. 2013, 15, 1–11. [Google Scholar] [CrossRef]
- Li, X.-H.; Xu, C.-L.; Han, X.-H.; Qiao, L.; Wang, T.; Li, F.-S. Synthesis and Magnetic Properties of Nearly Monodisperse CoFe2O4 Nanoparticles Through a Simple Hydrothermal Condition. Nanoscale Res. Lett. 2010, 5, 1039–1044. [Google Scholar] [CrossRef]
- Demirci Donmez, C.E.; Manna, P.K.; Nickel, R.; Akturk, S.; van Lierop, J. Comparative Heating Efficiency of Cobalt-, Manganese-, and Nickel-Ferrite Nanoparticles for a Hyperthermia Agent in Biomedicines. ACS Appl. Mater. Interfaces 2019, 11, 6858–6866. [Google Scholar] [CrossRef] [PubMed]
- Baaziz, W.; Pichon, B.P.; Fleutot, S.; Liu, Y.; Lefevre, C.; Grenache, J.-M.; Toumi, M.; Mhiri, T.; Begin-Colin, S. Magnetic Iron Oxide Nanoparticles: Reproducible Tuning of the Size and Nanosized-Dependent Composition, Defects, and Spin Canting. J. Phys. Chem. C 2014, 118, 3795–3810. [Google Scholar] [CrossRef]
- Jiang, J.Z.; Goya, G.F.; Rechenberg, H.R. Magnetic properties of nanostructured CuFe2O4. J. Phys. Condens. Matter 1999, 11, 4063. [Google Scholar] [CrossRef]
- Weisz, R.S. Magnetic Anisotropy Constants of Ferromagnetic Spinels. Phys. Rew. 1954, 96, 800–801. [Google Scholar] [CrossRef]
- Pacakova, P.; Kubickova, S.; Reznickova, A.; Niznasky, D.; Vejpranova, J. Spinel Ferrite Nanoparticles: Correlation of Structure and Magnetism, Magnetic Spinels—Synthesis, Properties and Applications, Mohindar Singh Seehra; InTech Publishers: London, UK, March 2017; pp. 1–30. ISBN 978-953-51-2974-5. Print ISBN:978-953-51-2973-8. [Google Scholar] [CrossRef]
- Yelenich, O.; Solopan, S.; Kolodiazhnyi, T.; Tykhonenko, Y.; Tovstolytkin, A.; Belous, A. Magnetic Properties and AC Losses in AFe2O4 (A = Mn, Co, Ni, Zn) Nanoparticles Synthesized from Nonaqueous Solution. J. Chem. 2015, 2015, 532198. [Google Scholar] [CrossRef]
- Nayeb, C.; Manna, K.; Bhattacharjee, G.; Murugavel, P.; Obaidat, I. Investigating Size- and Temperature-Dependent Coercivity and Saturation Magnetization in PEG Coated Fe3O4 Nanoparticles. Magnetochemisty 2017, 3, 19. [Google Scholar]
- Enpuku, K.; Elrefai, A.L.; Yoshida, T.; Kahmann, T.; Zong, J.; Viereck, T.; Ludwig, F. Estimation of the effective magnetic anisotropy constant of multi-core based magnetic nanoparticles from the temperature dependence of the coercive field. J. Appl. Phys. 2020, 127, 133903. [Google Scholar] [CrossRef]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Chen, R.; Christiansen, M.G.; Anikeeva, P. Maximizing hysteretic losses in magnetic ferrite nanoparticles via model-driven synthesis and materials optimization. ACS Nano 2013, 7, 8990–9000. [Google Scholar] [CrossRef]
- Christiansen, M.G.; Senko, A.W.; Chen, R.; Romero, G.; Anikeeva, P. Magnetically multiplexed heating of single domain nanoparticles. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Morales, I.; Costo, R.; Mille, N.; da Silva, G.B.; Carrey, J.; Hernando, A.; de la Presa, P. High-Frequency Hysteresis Losses on γ-Fe2O3 and Fe3O4: Susceptibility as a Magnetic Stamp for Chain Formation. Nanomaterials 2018, 8, 970. [Google Scholar] [CrossRef] [PubMed]
- Wetterskog, E.; Johansson, C.; Smilgies, D.M.; Schaller, V.; Johansson, C.; Svedlindh, P. Colossal Anisotropy of the Dynamic Magnetic Susceptibility in Low-Dimensional Nanocube Assemblies. ACS Nano 2018, 12, 1403–1412. [Google Scholar] [CrossRef] [PubMed]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; Morales, M.D.; Baldomir, D.; Martinez-Boubeta, C. Multiplying Magnetic Hyperthermia Response by Nanoparticle Assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Teran, F.J.; Casado, C.; Mikuszeit, N.; Salas, G.; Bollero, A.; Morales, M.P.; Camarero, V.; Miranda, R. Accurate determination of the specific absorption rate in superparamagnetic nanoparticles under non-adiabatic conditions. Appl. Phys. Lett. 2012, 101, 062413. [Google Scholar] [CrossRef]
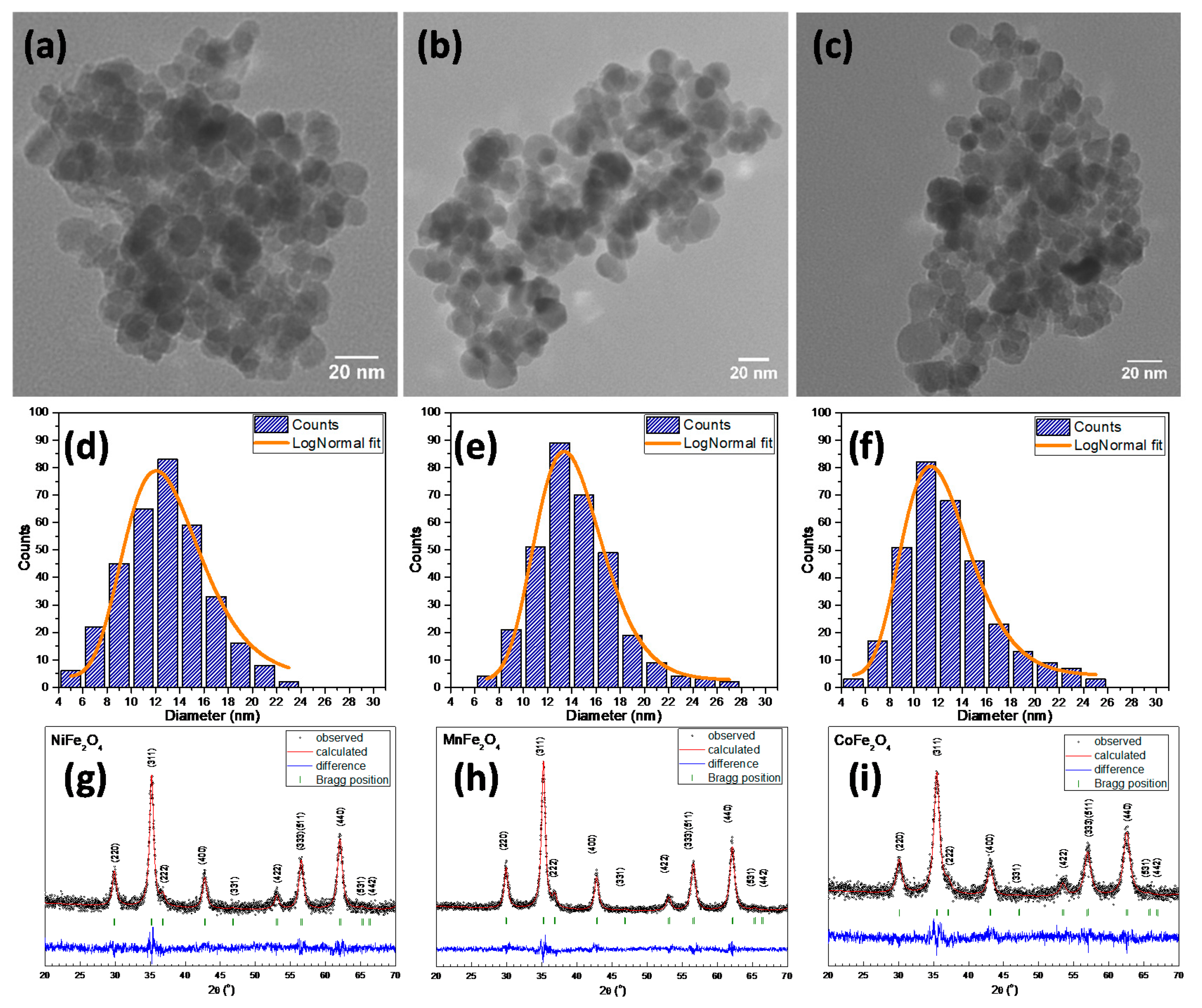
| Sample | DTEM (nm) | DXRD (nm) | A (Å) |
|---|---|---|---|
| NiFe2O4 | 12.9 ± 0.32 | 10.6 ± 2.44 | 8.349(9) |
| MnFe2O4 | 13.9 ± 0.13 | 11.5 ± 1.84 | 8.450(8) |
| CoFe2O4 | 12.1 ± 0.08 | 9.8 ± 1.53 | 8.397(9) |
| Sample | 5 K | 300 K | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ms (emu/g) | Hc (kA/m) | Mr (emu/g) | Mr/Ms | Ms (emu/g) | Hc (kA/m) | Mr (emu/g) | Mr/Ms | Keff (kJ/m3) | |
| NiFe2O4 | 47.4 | 27.75 | 19 | 0.40 | 35.7 | 9.4 | 4.8 | 0.13 | 8.6 |
| MnFe2O4 | 67.3 | 22.6 | 20.3 | 0.30 | 46.3 | 10.7 | 8.7 | 0.19 | 9.94 |
| CoFe2O4 | 85.5 | 922 | 61.5 | 0.72 | 68 | 11.2 | 7.4 | 0.11 | 515 |
| Sample | c (mg/mL) | SARMAX (W/g) | HcHyp (kA/m) | Power Coefficient n |
|---|---|---|---|---|
| NiFe2O4 | 4 | 541 ± 23 | 17.9 ± 1 | 1.8 ± 0.1 |
| 2 | 530 ± 18 | 19.6 ± 1.2 | 2 ± 0.1 | |
| MnFe2O4 | 4 | 733 ± 17 | 12.2 ± 0.5 | 2.15 ± 0.1 |
| 2 | 835 ± 27 | 14 ± 0.7 | 1.8 ± 0.1 | |
| CoFe2O4 | 4 | 3175 ± 366 | 48.8 ± 4 | 2.3 ± 0.1 |
| 2 | 3872 ± 909 | 47.1 ± 7 | 2.2 ± 0.2 | |
| 1 | 4142 ± 1061 | 47.6 ± 7 | 2.3 ± 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iacovita, C.; Stiufiuc, G.F.; Dudric, R.; Vedeanu, N.; Tetean, R.; Stiufiuc, R.I.; Lucaciu, C.M. Saturation of Specific Absorption Rate for Soft and Hard Spinel Ferrite Nanoparticles Synthesized by Polyol Process. Magnetochemistry 2020, 6, 23. https://doi.org/10.3390/magnetochemistry6020023
Iacovita C, Stiufiuc GF, Dudric R, Vedeanu N, Tetean R, Stiufiuc RI, Lucaciu CM. Saturation of Specific Absorption Rate for Soft and Hard Spinel Ferrite Nanoparticles Synthesized by Polyol Process. Magnetochemistry. 2020; 6(2):23. https://doi.org/10.3390/magnetochemistry6020023
Chicago/Turabian StyleIacovita, Cristian, Gabriela Fabiola Stiufiuc, Roxana Dudric, Nicoleta Vedeanu, Romulus Tetean, Rares Ionut Stiufiuc, and Constantin Mihai Lucaciu. 2020. "Saturation of Specific Absorption Rate for Soft and Hard Spinel Ferrite Nanoparticles Synthesized by Polyol Process" Magnetochemistry 6, no. 2: 23. https://doi.org/10.3390/magnetochemistry6020023
APA StyleIacovita, C., Stiufiuc, G. F., Dudric, R., Vedeanu, N., Tetean, R., Stiufiuc, R. I., & Lucaciu, C. M. (2020). Saturation of Specific Absorption Rate for Soft and Hard Spinel Ferrite Nanoparticles Synthesized by Polyol Process. Magnetochemistry, 6(2), 23. https://doi.org/10.3390/magnetochemistry6020023





