The Hydrodynamic Behavior of Vortex Shedding behind Circular Cylinder in the Presence of Group Focused Waves
Abstract
:1. Introduction
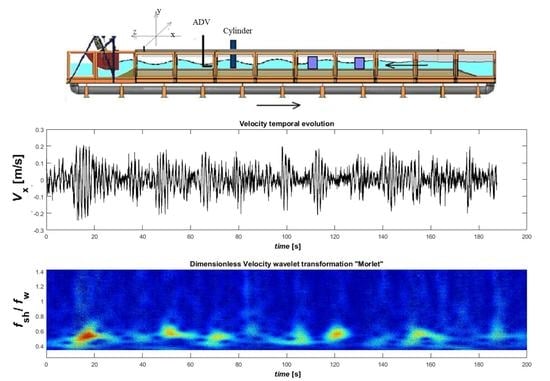
2. Materials and Methods
3. Results and Discussions
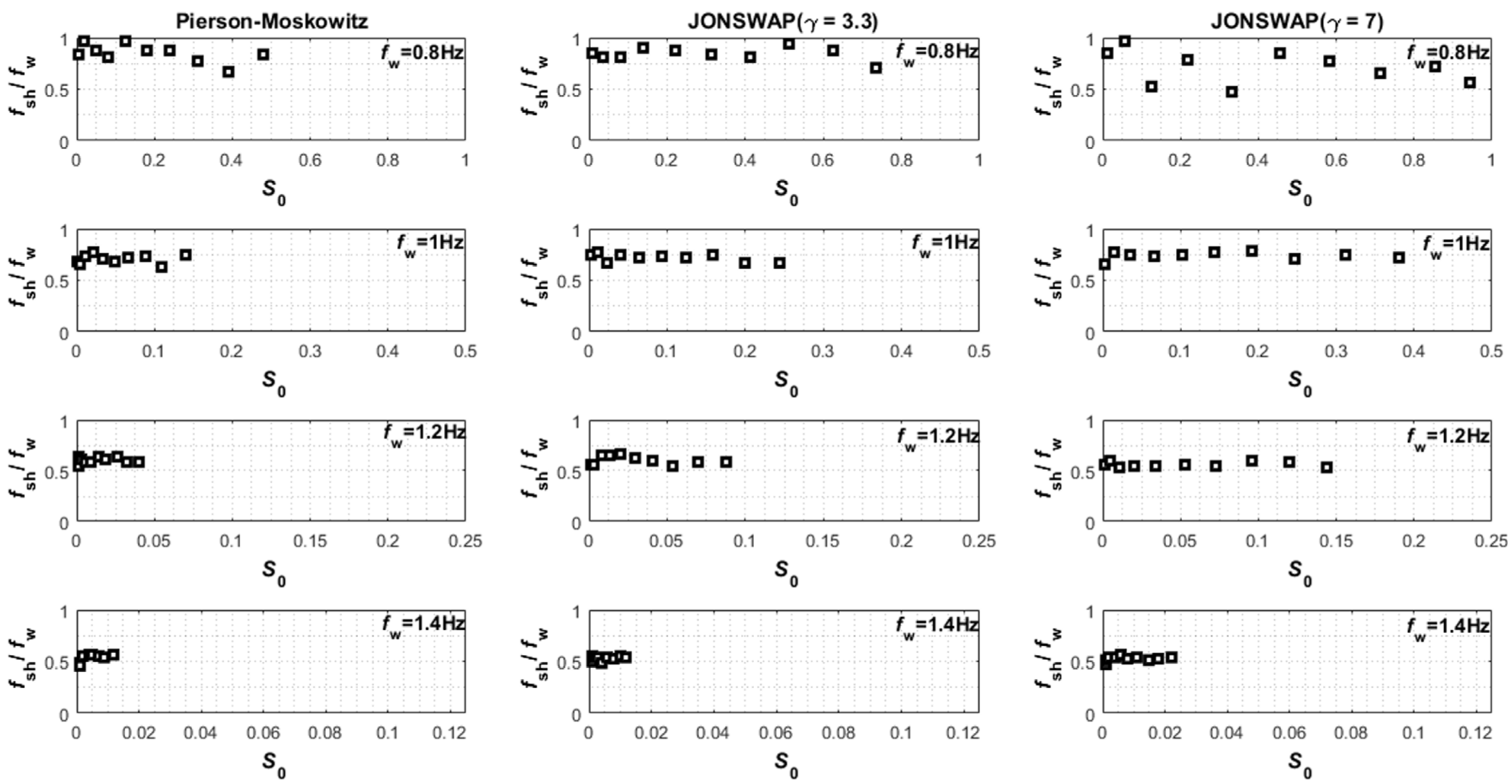
3.1. Fourier Analysis
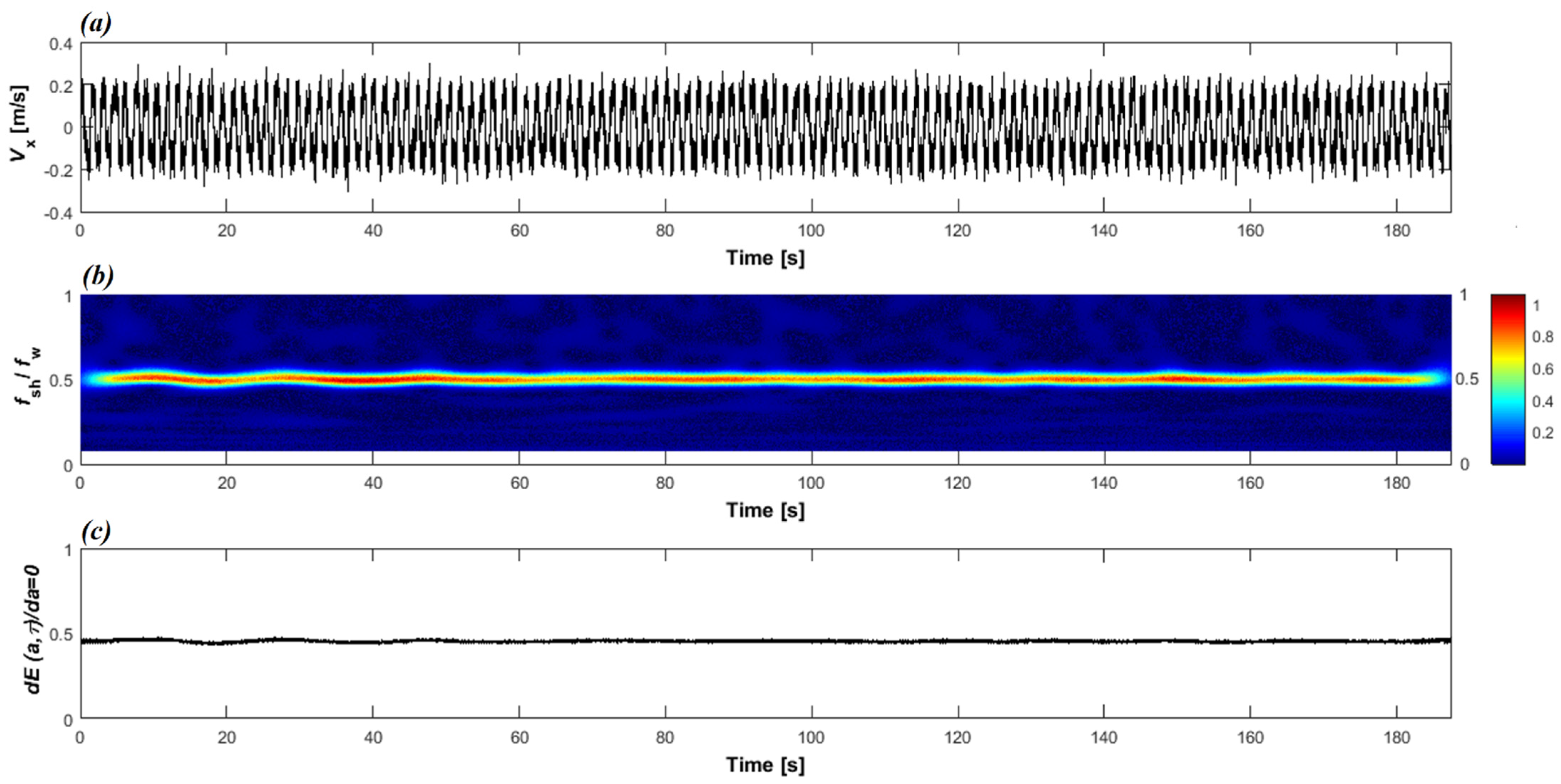
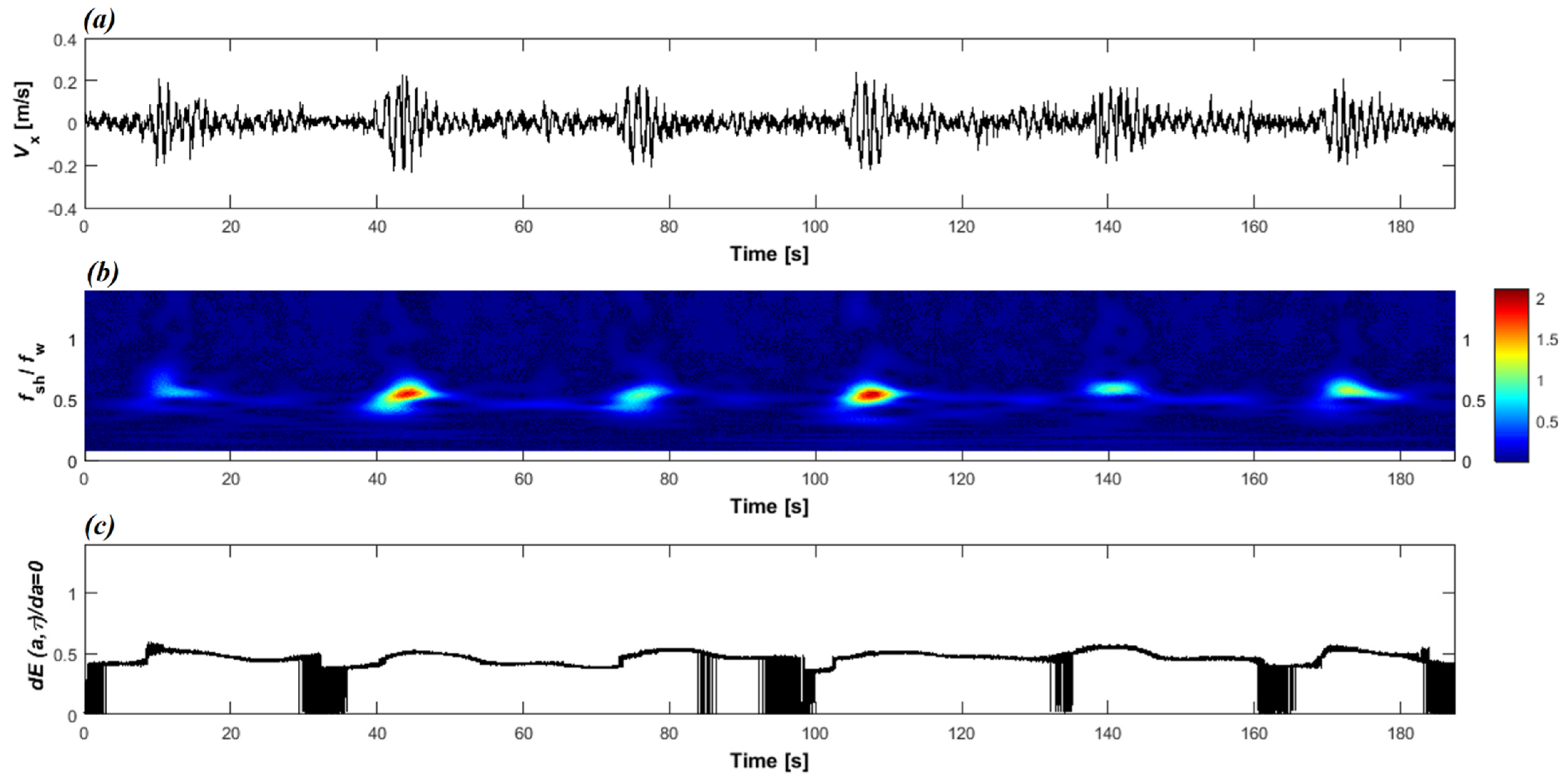
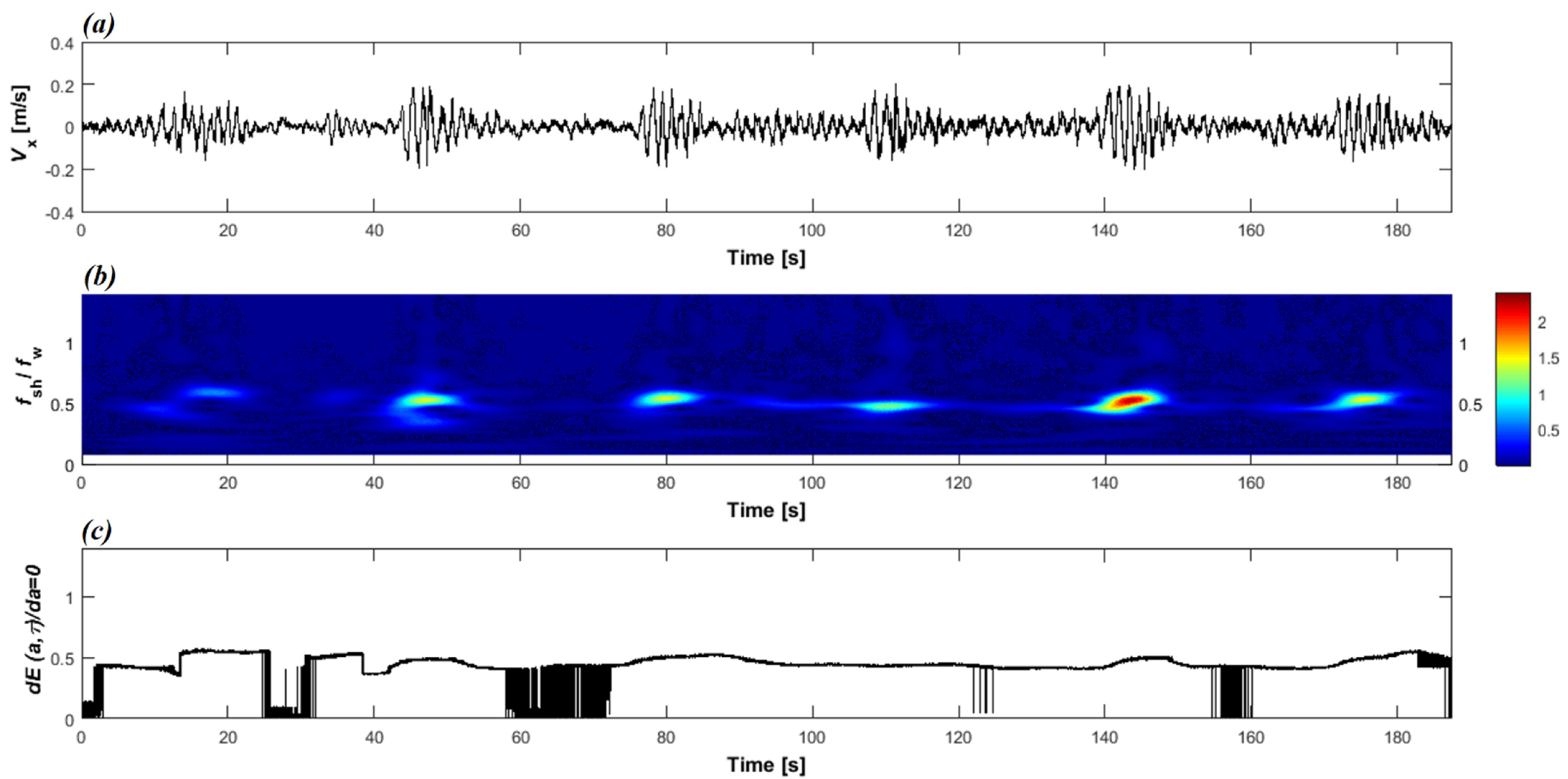
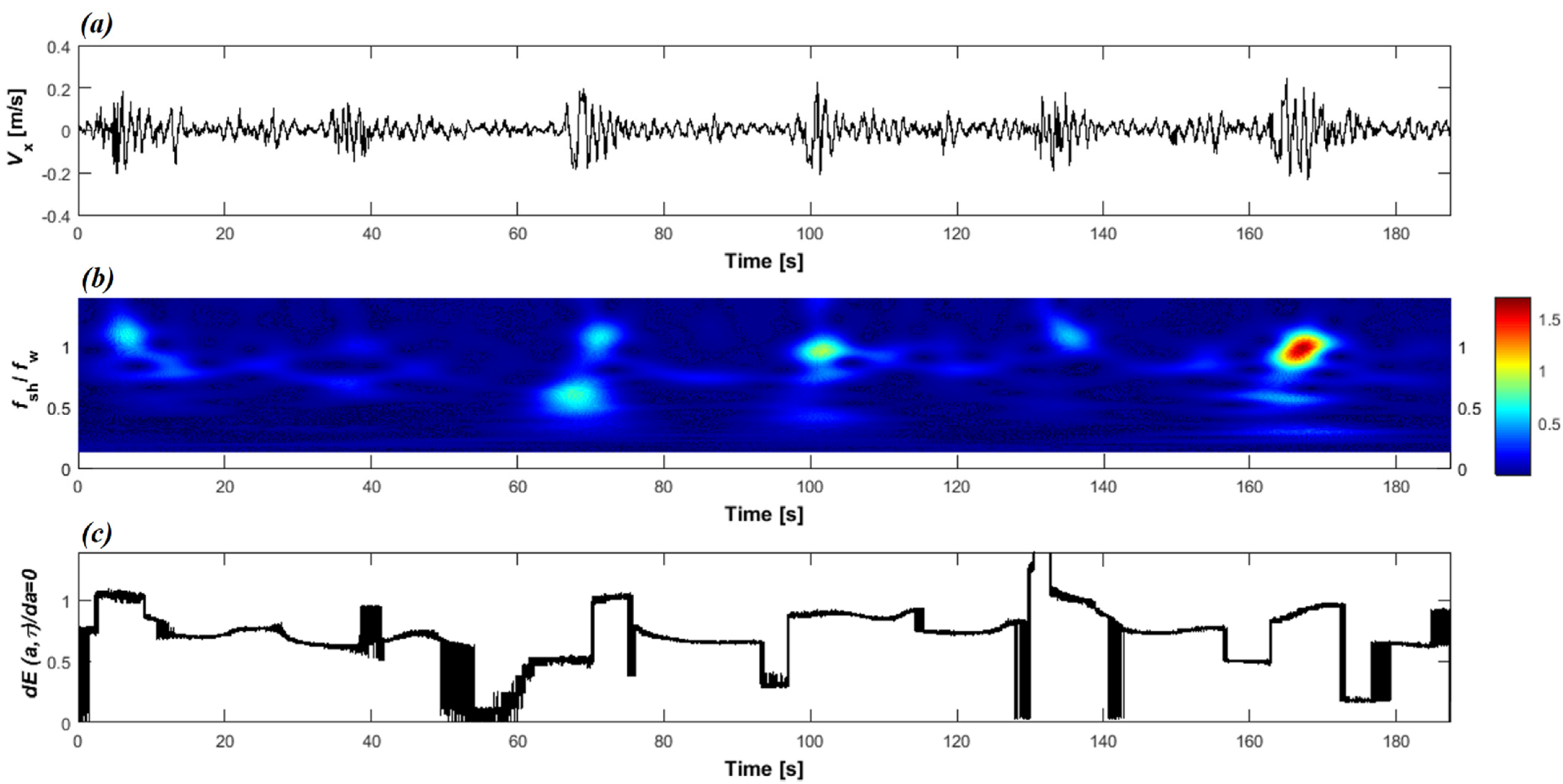
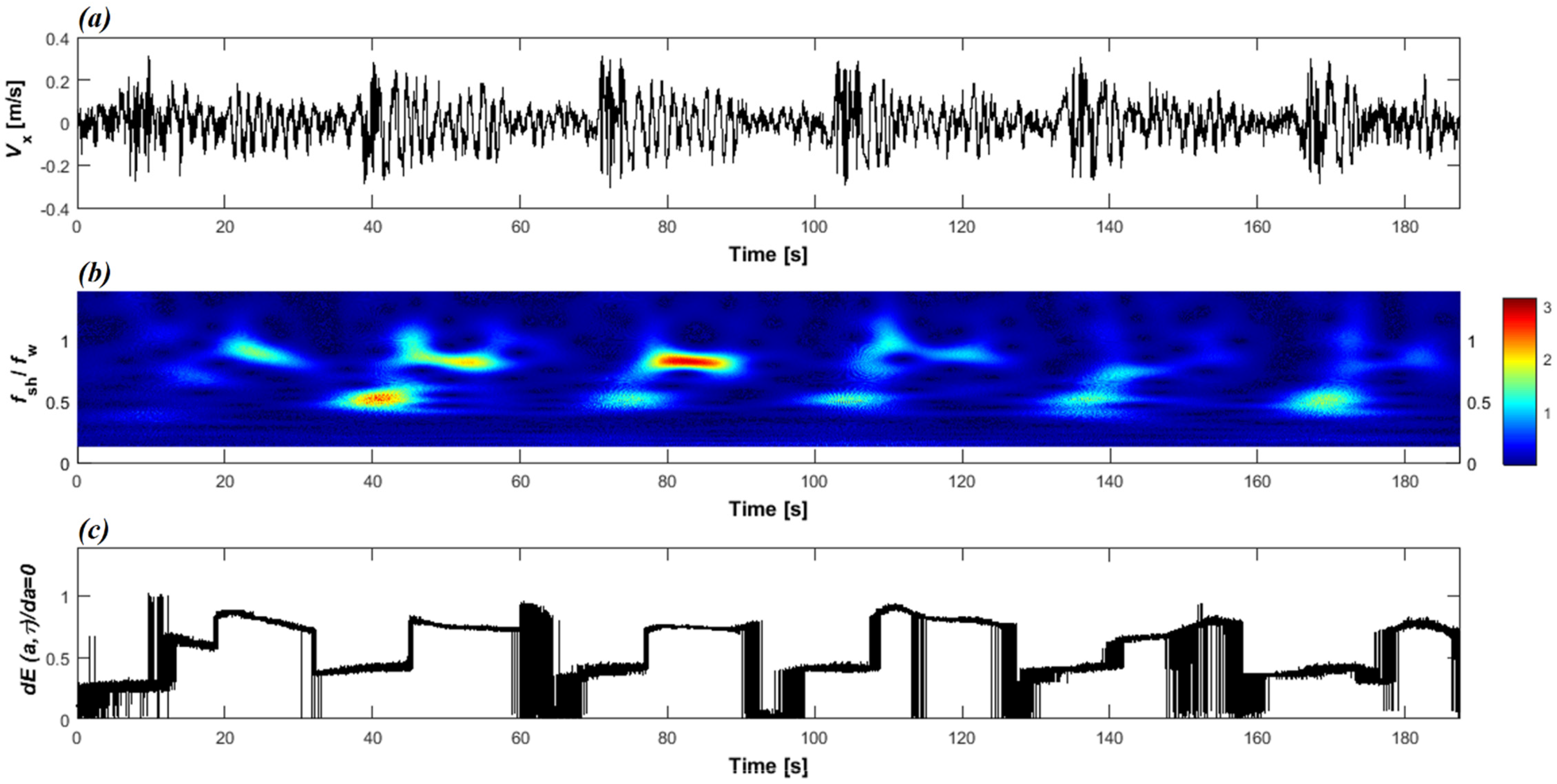
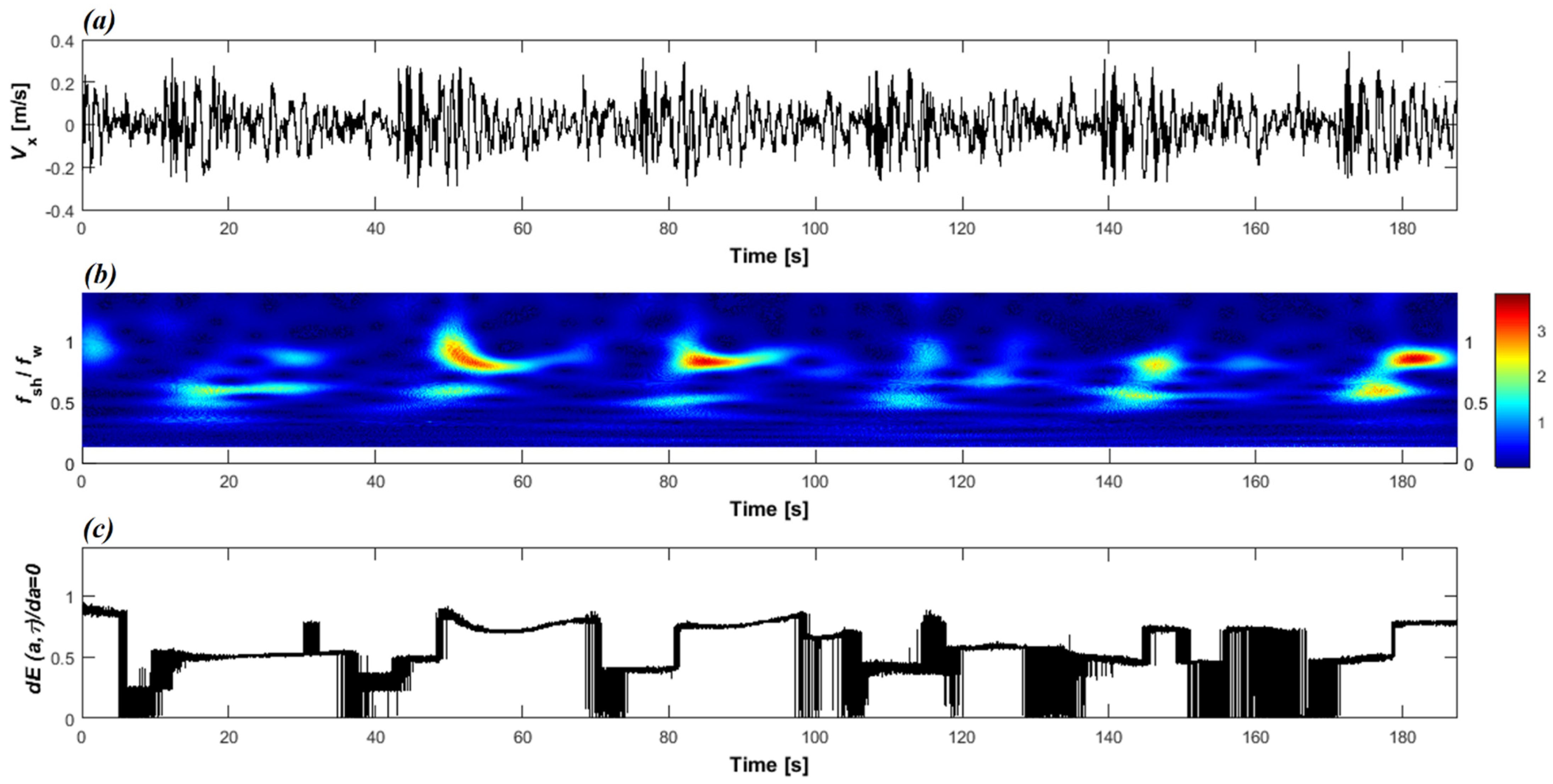
3.2. Wavelet Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jungsoo, S.; Yang, J.; Stern, F. The effect of air-water interface on the vortex shedding from a vertical circular cylinder. J. Fluid Struct. 2011, 27, 1–22. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Olsen, J.F.; Rajagopalan, S. Vortex shedding behind modified circular cylinders. J. Wind Eng. Ind. Aerod. 2000, 86, 55–63. [Google Scholar] [CrossRef]
- Hildebrandt, A.; Sriram, V. Pressure Distribution and Vortex Shedding Around a Cylinder due to a Steep Wave at the Onset of Breaking from Physical and Numerical Modeling. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Konstantinidis, E.; Balabani, S.; Yianneskis, M. Bimodal vortex shedding in a perturbed cylinder wake. Phys. Fluids 2007, 19, 011701. [Google Scholar] [CrossRef]
- Lam, K.M. Vortex shedding flow behind a slowly rotating circular cylinder. J. Fluid Struct. 2009, 25, 245–262. [Google Scholar] [CrossRef]
- Hans, G.; Abcha, N.; Ezersky, A. Frequency lock-in and phase synchronization of vortex shedding behind circular cylinder due to surface waves. Phys. Lett. A 2016, 380, 863–868. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B-Fluid 2003, 22, 603–635. [Google Scholar] [CrossRef] [Green Version]
- Kharif, C.; Pelinovsky, E.; Slunayev, A. Rogue Waves in the Ocean: Observations, Theories and Modelling; Springer: New York, NY, USA, 2009; Volume 255. [Google Scholar] [CrossRef]
- Fedele, F.; Herterich, J.; Tayfun, A.; Dias, F. Large nearshore storm waves off the Irish coast. Sci. Rep. 2019, 9, 15406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vyzikas, T.; Stagonas, D.; Buldakov, E.; Greaves, D. The evolution of free and bound waves during dispersive focusing in a numerical and physical flume. Coast. Eng. 2018, 132, 95–109. [Google Scholar] [CrossRef]
- Xu, G.; Hao, H.; Ma, Q. An experimental study of focusing wave generation with improved wave amplitude spectra. Water 2019, 11, 2521. [Google Scholar] [CrossRef] [Green Version]
- Abroug, I.; Abcha, N.; Dutykh, D.; Jarno, A.; Marin, F. Experimental and numerical study of the propagation of focused wave groups in the nearshore zone. Phys. Lett. A 2020, 6, 126144. [Google Scholar] [CrossRef] [Green Version]
- Tromans, P.S.; Anaturk, A.R.; Hagemeijer, P. A new model for the kinematics of large ocean waves-application as a design wave. In Proceedings of the First International Offshore and Polar Engineering Conference, Edinburgh, UK, 11–16 August 1991. [Google Scholar]
- Milligen, B.P.V.; Sanchez, E.; Estrada, T.; Hidalgo, C.; Branas, B.; Carrersa, B.; Garcia, L. Wavelet bicoherence: A new turbulence analysis tool. Phys. Plasma 1995, 2, 3017–3032. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Xia, X.; Li, X.; Wang, Y.; Yang, Y.; Liu, Y.; Liang, Z.; He, J. Spinal cord stimulation modulates frontal delta and gamma in patients of minimally consciousness state. Neuroscience 2017, 346, 247–254. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geoph. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Young, I.R.; Eldeberky, Y. Observations of triad coupling of finite depth wind waves. Coast. Eng. 1998, 33, 137–154. [Google Scholar] [CrossRef]
- Becq-Girard, F.; Forget, P.; Benoit, M. Nonlinear propagation of unidirectional wave fields over varying topography. Coast. Eng. 1999, 38, 91–113. [Google Scholar] [CrossRef]
- Abroug, I.; Abcha, N.; Jarno, A.; Marin, F. Laboratory study of non-linear wave-wave interactions of extreme focused waves in the nearshore zone. Nat. Hazard Earth Syst. 2020, 20, 3279–3291. [Google Scholar] [CrossRef]
- Tiscareno, M.S.; Hedman, M.H. A review of Morlet wavelet analysis of radial profiles of Saturn’s rings. Philos. Trans. R. Soc. A 2018, 376, 2126. [Google Scholar] [CrossRef] [Green Version]
- Farge, M. Wavelet transforms and their applications to turbulence. Ann. Rev. Fluid Mech. 1992, 24, 395–457. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef] [Green Version]
- Shark, L.K.; Yu, C. Design of matched wavelets based on generalized Mexican_hat function. Signal Process. 2006, 7, 1469–1475. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Springer: Philadelphia, PA, USA, 1992. [Google Scholar] [CrossRef]
- Ortiz-Gracia, L.; Oosterlee, A. A highly efficient Shannon wavelet inverse Fourier technique for pricing european options. AIP Conf. Proc. 2016, 38, 118–143. [Google Scholar] [CrossRef] [Green Version]
- Turki, I.; Massei, N.; Laignel, B. Linking sea level dynamic and exceptional events to large-scale atmospheric circulation variability: Case of Seine Bay, France. Oceanologia 2019, 61, 321–330. [Google Scholar] [CrossRef]
- Addison, P.S.; Watson, J.N.; Feng, T. Low-oscillation complex wavelets. J. Sound Vib. 2002, 254, 733–762. [Google Scholar] [CrossRef]
- Feng, X.; Yunfei, L.; Xiping, W.; Brian, K.B.; Lon, A.Y.; Robert, J.R. Evaluation internal condition of hardwood logs based on AR-minimum entropy deconvolution combined with wavelet based spectral kurtosis approach. Holzforschung 2021, 75, 237–249. [Google Scholar] [CrossRef]
- Turki, I.; Massei, N.; Laignel, B. Effects of global climate oscillations on Intermonthly to interannual variability of sea levels along the English channel coasts (NW France). Oceanologia 2020, 62, 226–242. [Google Scholar] [CrossRef]
- Turki, I.; Baulon, L.; Massei, N.; Laignel, B.; Costa, S.; Fournier, M.; Maquaire, O. A nonstationary analysis for investigating the multiscale variability of extreme surges: Case of the English Channel coasts. Nat. Hazard Earth Syst. 2020, 20, 3225–3243. [Google Scholar] [CrossRef]
- Christou, M.; Ewans, K. Field Measurements of rogue water waves. J. Phys. Oceanogr. 2014, 44, 2317–2335. [Google Scholar] [CrossRef]
- Kolahan, A.; Roohi, E.; Pendar, M.R. Wavelet analysis and frequency spectrum of cloud cavitation around a sphere. Ocean Eng. 2019, 182, 235–247. [Google Scholar] [CrossRef]
- Pendar, M.R.; Roohi, E. Cavitation characteristics around a sphere: An LES investigation. Int. J. Multiph. Flow 2018, 98, 1–23. [Google Scholar] [CrossRef]





| fw (Hz) | kwh0 | S0 | fw (H) | kwh0 | S0 | ||
| Case 1 | 0.8 | 0.9 | 0.005 | Case 11 | 1 | 1.2 | 0.001 |
| Case 2 | 0.9 | 0.021 | Case 12 | 1.2 | 0.005 | ||
| Case 3 | 0.9 | 0.050 | Case 13 | 1.2 | 0.012 | ||
| Case 4 | 0.9 | 0.081 | Case 14 | 1.2 | 0.021 | ||
| Case 5 | 0.9 | 0.125 | Case 15 | 1.2 | 0.034 | ||
| Case 6 | 0.9 | 0.180 | Case 16 | 1.2 | 0.050 | ||
| Case 7 | 0.9 | 0.240 | Case 17 | 1.2 | 0.067 | ||
| Case 8 | 0.9 | 0.310 | Case 18 | 1.2 | 0.088 | ||
| Case 9 | 0.9 | 0.390 | Case 19 | 1.2 | 0.110 | ||
| Case 10 | 0.9 | 0.480 | Case 20 | 1.2 | 0.140 | ||
| fw (Hz) | kwh0 | S0 | fw (H) | kwh0 | S0 | ||
| Case 21 | 1.2 | 1.58 | 0.001 | Case 31 | 1.4 | 2.04 | 0.001 |
| Case 22 | 1.58 | 0.001 | Case 32 | 2.04 | 0.001 | ||
| Case 23 | 1.58 | 0.003 | Case 33 | 2.04 | 0.001 | ||
| Case 24 | 1.58 | 0.006 | Case 34 | 2.04 | 0.001 | ||
| Case 25 | 1.58 | 0.009 | Case 35 | 2.04 | 0.002 | ||
| Case 26 | 1.58 | 0.014 | Case 36 | 2.04 | 0.004 | ||
| Case 27 | 1.58 | 0.019 | Case 37 | 2.04 | 0.005 | ||
| Case 28 | 1.58 | 0.026 | Case 38 | 2.04 | 0.007 | ||
| Case 29 | 1.58 | 0.032 | Case 39 | 2.04 | 0.009 | ||
| Case 30 | 1.58 | 0.040 | Case 40 | 2.04 | 0.012 |
| fw (Hz) | kwh0 | S0 | fw (H) | kwh0 | S0 | ||
| Case 41 | 0.8 | 0.9 | 0.010 | Case 51 | 1 | 1.2 | 0.002 |
| Case 42 | 0.9 | 0.036 | Case 52 | 1.2 | 0.011 | ||
| Case 43 | 0.9 | 0.080 | Case 53 | 1.2 | 0.024 | ||
| Case 44 | 0.9 | 0.140 | Case 54 | 1.2 | 0.041 | ||
| Case 45 | 0.9 | 0.220 | Case 55 | 1.2 | 0.065 | ||
| Case 46 | 0.9 | 0.313 | Case 56 | 1.2 | 0.093 | ||
| Case 47 | 0.9 | 0.412 | Case 57 | 1.2 | 0.124 | ||
| Case 48 | 0.9 | 0.514 | Case 58 | 1.2 | 0.159 | ||
| Case 49 | 0.9 | 0.624 | Case 59 | 1.2 | 0.199 | ||
| Case 50 | 0.9 | 0.734 | Case 60 | 1.2 | 0.244 | ||
| fw (Hz) | kwh0 | S0 | fw (H) | kwh0 | S0 | ||
| Case 61 | 1.2 | 1.58 | 0.001 | Case 71 | 1.4 | 2.04 | 0.001 |
| Case 62 | 1.58 | 0.003 | Case 72 | 2.04 | 0.001 | ||
| Case 63 | 1.58 | 0.008 | Case 73 | 2.04 | 0.001 | ||
| Case 64 | 1.58 | 0.013 | Case 74 | 2.04 | 0.002 | ||
| Case 65 | 1.58 | 0.020 | Case 75 | 2.04 | 0.003 | ||
| Case 66 | 1.58 | 0.030 | Case 76 | 2.04 | 0.004 | ||
| Case 67 | 1.58 | 0.041 | Case 77 | 2.04 | 0.006 | ||
| Case 68 | 1.58 | 0.054 | Case 78 | 2.04 | 0.008 | ||
| Case 69 | 1.58 | 0.070 | Case 79 | 2.04 | 0.010 | ||
| Case 70 | 1.58 | 0.088 | Case 80 | 2.04 | 0.012 |
| fw (Hz) | kwh0 | S0 | fw (Hz) | kwh0 | S0 | ||
| Case 81 | 0.8 | 0.9 | 0.014 | Case 91 | 1 | 1.2 | 0.003 |
| Case 82 | 0.9 | 0.058 | Case 92 | 1.2 | 0.014 | ||
| Case 83 | 0.9 | 0.125 | Case 93 | 1.2 | 0.035 | ||
| Case 84 | 0.9 | 0.218 | Case 94 | 1.2 | 0.066 | ||
| Case 85 | 0.9 | 0.332 | Case 95 | 1.2 | 0.102 | ||
| Case 86 | 0.9 | 0.457 | Case 96 | 1.2 | 0.144 | ||
| Case 87 | 0.9 | 0.584 | Case 97 | 1.2 | 0.191 | ||
| Case 88 | 0.9 | 0.715 | Case 98 | 1.2 | 0.247 | ||
| Case 89 | 0.9 | 0.853 | Case 99 | 1.2 | 0.312 | ||
| Case 90 | 0.9 | 0.944 | Case 100 | 1.2 | 0.381 | ||
| fw (Hz) | kwh0 | S0 | fw (Hz) | kwh0 | S0 | ||
| Case 101 | 1.2 | 1.58 | 0.001 | Case 111 | 1.4 | 2.04 | 0.001 |
| Case 102 | 1.58 | 0.005 | Case 112 | 2.04 | 0.001 | ||
| Case 103 | 1.58 | 0.011 | Case 113 | 2.04 | 0.002 | ||
| Case 104 | 1.58 | 0.020 | Case 114 | 2.04 | 0.004 | ||
| Case 105 | 1.58 | 0.034 | Case 115 | 2.04 | 0.006 | ||
| Case 106 | 1.58 | 0.053 | Case 116 | 2.04 | 0.008 | ||
| Case 107 | 1.58 | 0.073 | Case 117 | 2.04 | 0.011 | ||
| Case 108 | 1.58 | 0.096 | Case 118 | 2.04 | 0.015 | ||
| Case 109 | 1.58 | 0.120 | Case 119 | 2.04 | 0.018 | ||
| Case 110 | 1.58 | 0.144 | Case 120 | 2.04 | 0.022 |
| Cases | Spectrum | fw | kwh0 | S0 | Lock-In |
|---|---|---|---|---|---|
| 2 | PM | 0.8 | 0.9 | 0.021 | Absence |
| 35 | PM | 1.4 | 2.04 | 0.002 | Presence |
| 46 | JS (3.3) | 0.8 | 0.9 | 0.313 | Absence |
| 72 | JS (3.3) | 1.4 | 2.04 | 0.001 | Presence |
| 90 | JS (7) | 0.8 | 0.9 | 0.944 | Absence |
| 111 | JS (7) | 1.4 | 2.04 | 0.001 | Presence |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abroug, I.; Abcha, N.; Mejri, F.; Turki, E.I.; Ojeda, E. The Hydrodynamic Behavior of Vortex Shedding behind Circular Cylinder in the Presence of Group Focused Waves. Fluids 2022, 7, 4. https://doi.org/10.3390/fluids7010004
Abroug I, Abcha N, Mejri F, Turki EI, Ojeda E. The Hydrodynamic Behavior of Vortex Shedding behind Circular Cylinder in the Presence of Group Focused Waves. Fluids. 2022; 7(1):4. https://doi.org/10.3390/fluids7010004
Chicago/Turabian StyleAbroug, Iskander, Nizar Abcha, Fahd Mejri, Emma Imen Turki, and Elena Ojeda. 2022. "The Hydrodynamic Behavior of Vortex Shedding behind Circular Cylinder in the Presence of Group Focused Waves" Fluids 7, no. 1: 4. https://doi.org/10.3390/fluids7010004
APA StyleAbroug, I., Abcha, N., Mejri, F., Turki, E. I., & Ojeda, E. (2022). The Hydrodynamic Behavior of Vortex Shedding behind Circular Cylinder in the Presence of Group Focused Waves. Fluids, 7(1), 4. https://doi.org/10.3390/fluids7010004