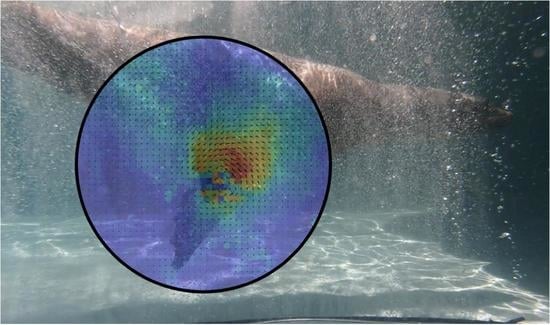
Velocity Field Measurements of the California Sea Lion Propulsive Stroke Using Bubble PIV
Abstract
:1. Introduction
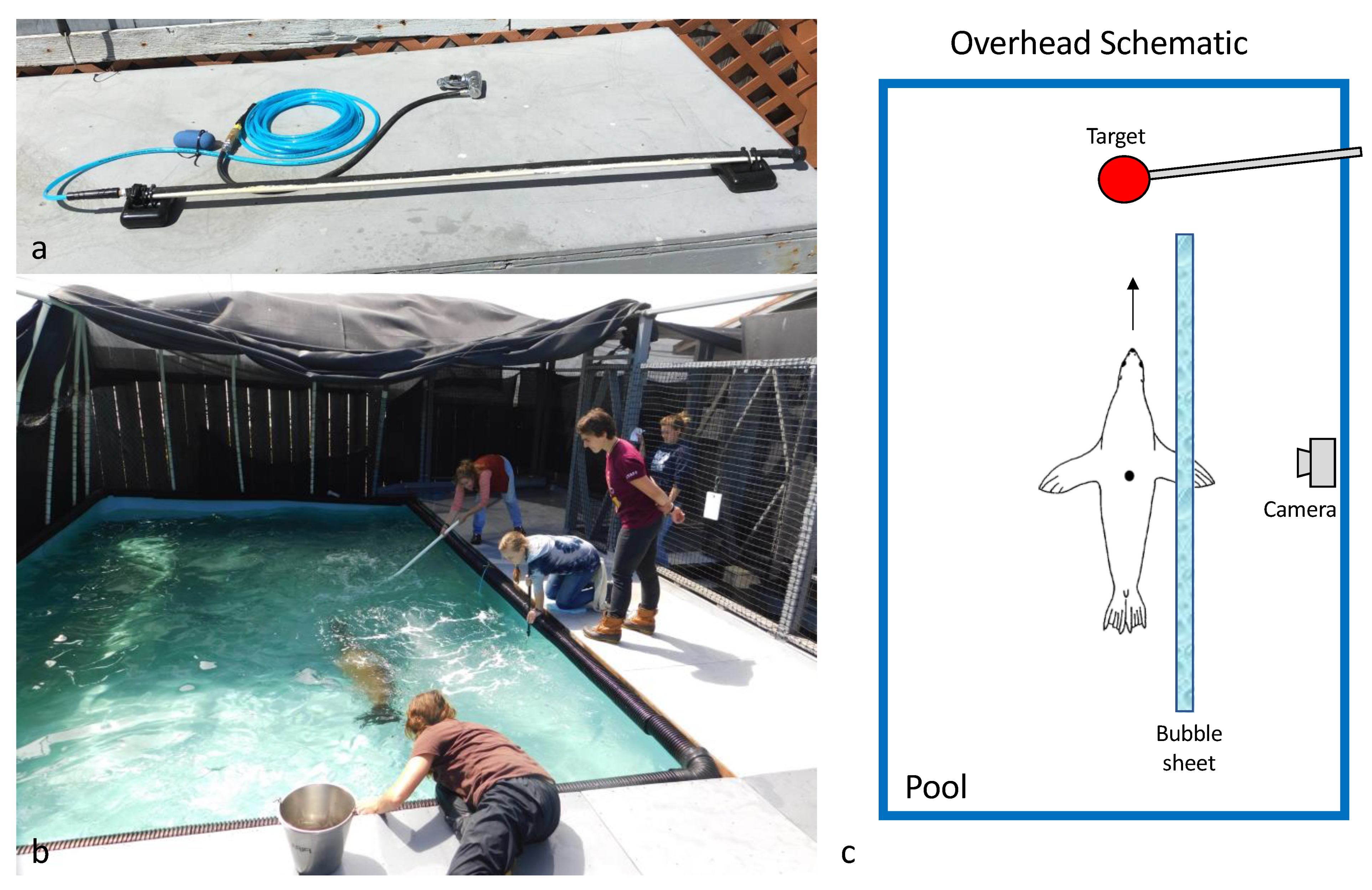
2. Materials and Methods
2.1. Data Collection
2.2. Image Processing
2.2.1. Image Channel Mixing
2.2.2. Sliding Minimum Subtraction
2.2.3. Spatial Median Subtraction
2.2.4. Heuristic Refinement
2.3. Two-Dimensional PIV
3. Results
3.1. Velocity Fields
3.2. Vorticity Fields
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Drucker, E.G.; Lauder, G.V. Locomotor forces on a swimming fish: Three-dimensional vortex wake dynamics quantified using digital particle image velocimetry. J. Exp. Biol. 1999, 202, 2393–2412. [Google Scholar] [CrossRef]
- Lauder, G.V.; Drucker, E.G. Forces, fishes, and fluids: Hydrodynamic mechanisms of aquatic locomotion. Physiology 2002, 17, 235–240. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming: I. Wake structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D. The hydrodynamics of eel swimming II. Effect of swimming speed. J. Exp. Biol. 2004, 207, 3265–3279. [Google Scholar] [CrossRef] [Green Version]
- Siddiqui, M.H.K. Velocity measurements around a freely swimming fish using PIV. Meas. Sci. Technol. 2006, 18, 96–105. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Colin, S.P.; Gemmell, B.J.; Lucas, K.N.; Leftwich, M.C.; Costello, J.H. Jellyfish and Fish Solve the Challenges of Turning Dynamics Similarly to Achieve High Maneuverability. Fluids 2020, 5, 106. [Google Scholar] [CrossRef]
- Mendelson, L.; Techet, A.H. Quantitative wake analysis of a freely swimming fish using 3D synthetic aperture PIV. Exp. Fluids 2015, 56, 135. [Google Scholar] [CrossRef] [Green Version]
- Mendelson, L.; Techet, A.H. Multi-camera volumetric PIV for the study of jumping fish. Exp. Fluids 2017, 59, 10. [Google Scholar] [CrossRef] [Green Version]
- Triantafyllou, M.S.; Yue, D.K.P. Hydrodynamics of Fishlike Swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Wu, T.Y. Fish Swimming and Bird/Insect Flight. Annu. Rev. Fluid Mech. 2011, 43, 25–58. [Google Scholar] [CrossRef]
- Lauder, G.V. Fish Locomotion: Recent Advances and New Directions. Annu. Rev. Mar. Sci. 2015, 7, 521–545. [Google Scholar] [CrossRef] [Green Version]
- Costello, J.H.; Colin, S.P.; Dabiri, J.O.; Gemmell, B.J.; Lucas, K.N.; Sutherland, K.R. The Hydrodynamics of Jellyfish Swimming. Annu. Rev. Mar. Sci. 2021, 13, 375–396. [Google Scholar] [CrossRef] [PubMed]
- Katija, K.; Dabiri, J.O. In situ field measurements of aquatic animal-fluid interactions using a Self-Contained Underwater Velocimetry Apparatus (SCUVA). Limnol. Oceanogr. Methods 2008, 6, 162–171. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Gharib, M.; Colin, S.P.; Costello, J.H. Vortex motion in the ocean: In situ visualization of jellyfish swimming and feeding flows. Phys. Fluids 2005, 17, 091108. [Google Scholar] [CrossRef] [Green Version]
- Troutman, V.A.; Dabiri, J.O. Single-camera three-dimensional tracking of natural particulate and zooplankton. Meas. Sci. Technol. 2018, 29, 075401. [Google Scholar] [CrossRef] [Green Version]
- Katija, K.; Sherlock, R.E.; Sherman, A.D.; Robison, B.H. New technology reveals the role of giant larvaceans in oceanic carbon cycling. Sci. Adv. 2017, 3, e1602374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tolkoff, S.W. Robotics and Power Measurements of the RoboTuna. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- Hultmark, M.; Leftwich, M.; Smits, A.J. Flowfield measurements in the wake of a robotic lamprey. Exp. Fluids 2007, 43, 683–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ijspeert, A.J.; Crespi, A.; Ryczko, D.; Cabelguen, J.-M. From Swimming to Walking with a Salamander Robot Driven by a Spinal Cord Model. Science 2007, 315, 1416–1420. [Google Scholar] [CrossRef] [Green Version]
- Leftwich, M.C.; Smits, A.J. Thrust production by a mechanical swimming lamprey. Exp. Fluids 2010, 50, 1349–1355. [Google Scholar] [CrossRef]
- Tangorra, J.L.; Lauder, G.V.; Hunter, I.W.; Mittal, R.; Madden, P.G.A.; Bozkurttas, M. The effect of fin ray flexural rigidity on the propulsive forces generated by a biorobotic fish pectoral fin. J. Exp. Biol. 2010, 213, 4043–4054. [Google Scholar] [CrossRef] [Green Version]
- Esposito, C.J.; Tangorra, J.L.; Flammang, B.; Lauder, G.V. A robotic fish caudal fin: Effects of stiffness and motor program on locomotor performance. J. Exp. Biol. 2012, 215, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Kashi, E.; Kulkarni, A.; Perrotta, G.M.; Leftwich, M.C. Flowfields produced by a robotic sea lion foreflipper starting from rest. Bioinspir. Biomim. 2020, 15, 035002. [Google Scholar] [CrossRef]
- Fish, F.E.; Legac, P.; Williams, T.M.; Wei, T. Measurement of hydrodynamic force generation by swimming dolphins using bubble DPIV. J. Exp. Biol. 2014, 217, 252–260. [Google Scholar] [CrossRef] [Green Version]
- Fish, F.E.; Williams, T.M.; Sherman, E.; Moon, Y.E.; Wu, V.; Wei, T. Experimental Measurement of Dolphin Thrust Generated during a Tail Stand Using DPIV. Fluids 2018, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Ryu, Y.; Chang, K.-A.; Lim, H.-J. Use of bubble image velocimetry for measurement of plunging wave impinging on structure and associated greenwater. Meas. Sci. Technol. 2005, 16, 1945–1953. [Google Scholar] [CrossRef]
- Friedman, C.; Leftwich, M.C. The kinematics of the California sea lion foreflipper during forward swimming. Bioinspir. Biomim. 2014, 9, 046010. [Google Scholar] [CrossRef] [PubMed]
- Godfrey, S.J. Additional observations of subaqueous locomotion in the California Sea Lion (Zalophus californianus). Aquat. Mamm. 1985, 11, 53–57. [Google Scholar]
- Feldkamp, S.D. Foreflipper propulsion in the California sea lion, Zalophus californianus. J. Zool. 1987, 212, 43–57. [Google Scholar] [CrossRef]
- Adrian, R.J.; Westerweel, J. Particle Image Velocimetry (No. 30); Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perrotta, G.; Fish, F.E.; Adams, D.S.; Leahy, A.M.; Downs, A.M.; Leftwich, M.C. Velocity Field Measurements of the California Sea Lion Propulsive Stroke Using Bubble PIV. Fluids 2022, 7, 3. https://doi.org/10.3390/fluids7010003
Perrotta G, Fish FE, Adams DS, Leahy AM, Downs AM, Leftwich MC. Velocity Field Measurements of the California Sea Lion Propulsive Stroke Using Bubble PIV. Fluids. 2022; 7(1):3. https://doi.org/10.3390/fluids7010003
Chicago/Turabian StylePerrotta, Gino, Frank E. Fish, Danielle S. Adams, Ariel M. Leahy, Abigal M. Downs, and Megan C. Leftwich. 2022. "Velocity Field Measurements of the California Sea Lion Propulsive Stroke Using Bubble PIV" Fluids 7, no. 1: 3. https://doi.org/10.3390/fluids7010003
APA StylePerrotta, G., Fish, F. E., Adams, D. S., Leahy, A. M., Downs, A. M., & Leftwich, M. C. (2022). Velocity Field Measurements of the California Sea Lion Propulsive Stroke Using Bubble PIV. Fluids, 7(1), 3. https://doi.org/10.3390/fluids7010003