Variable Energy Fluxes and Exact Relations in Magnetohydrodynamics Turbulence
Abstract
:1. Introduction
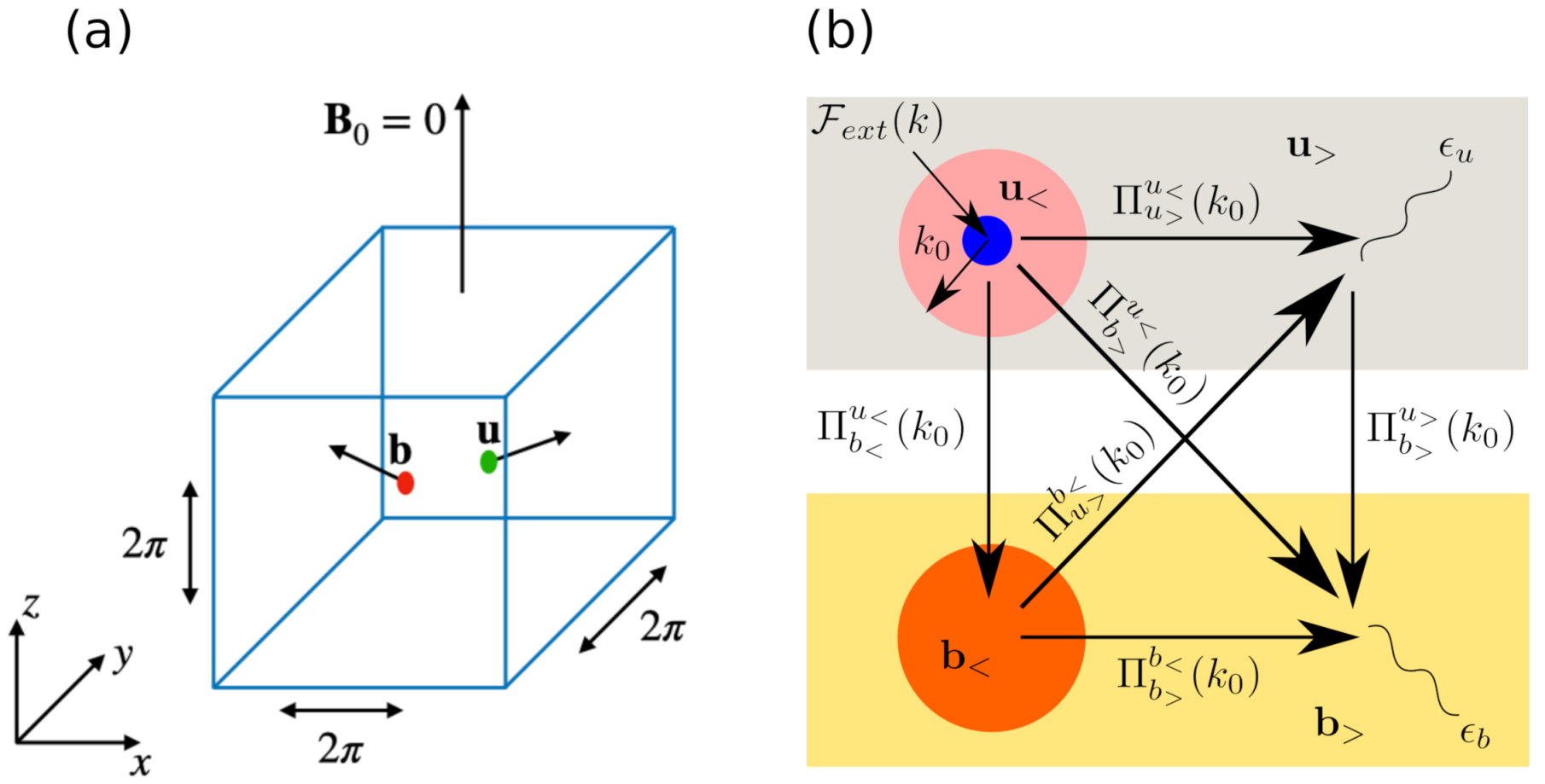
2. Energy Fluxes and Exact Relations
3. Governing Equations and Simulation Method
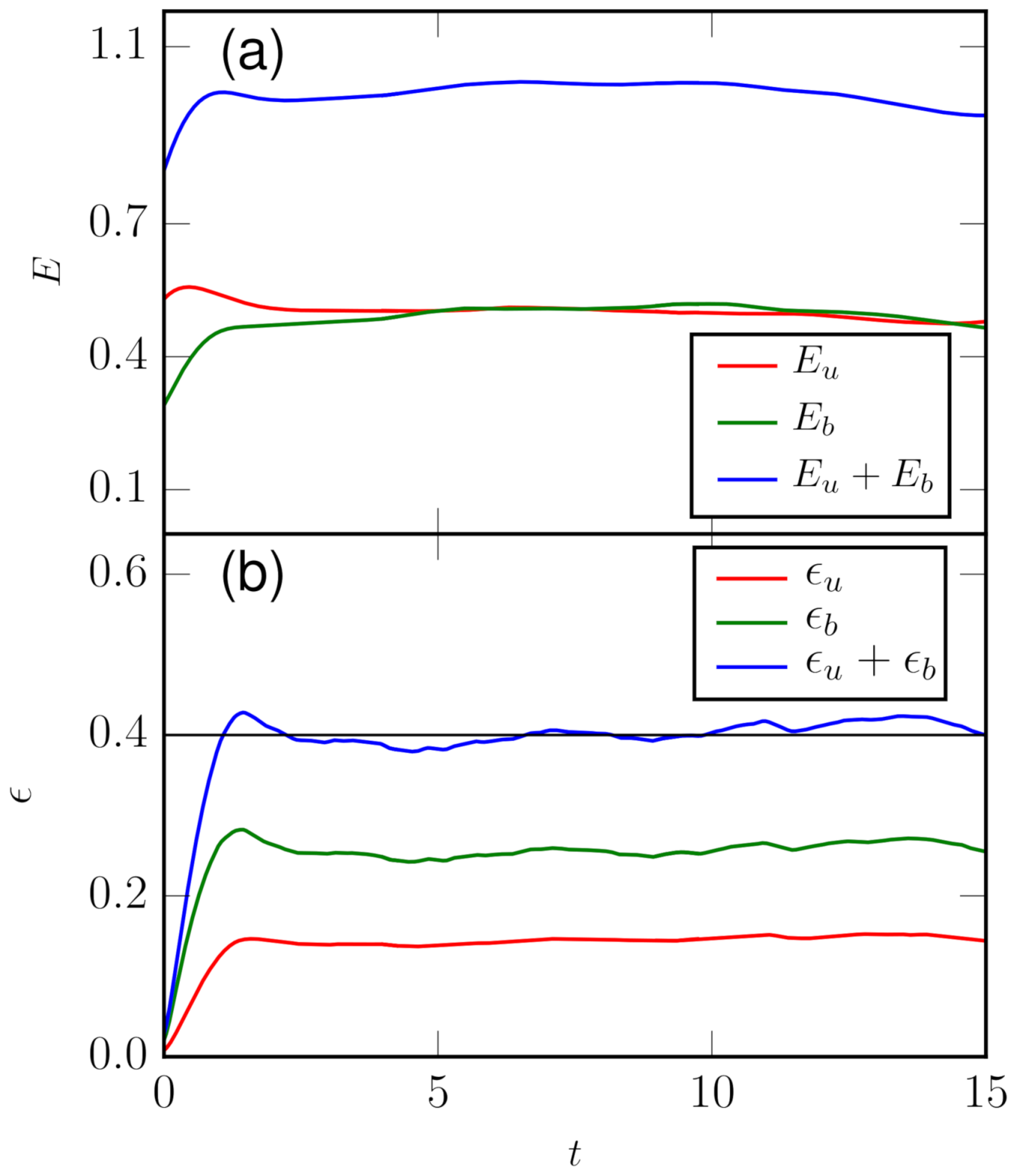
4. Numerical Results on the Energy Fluxes
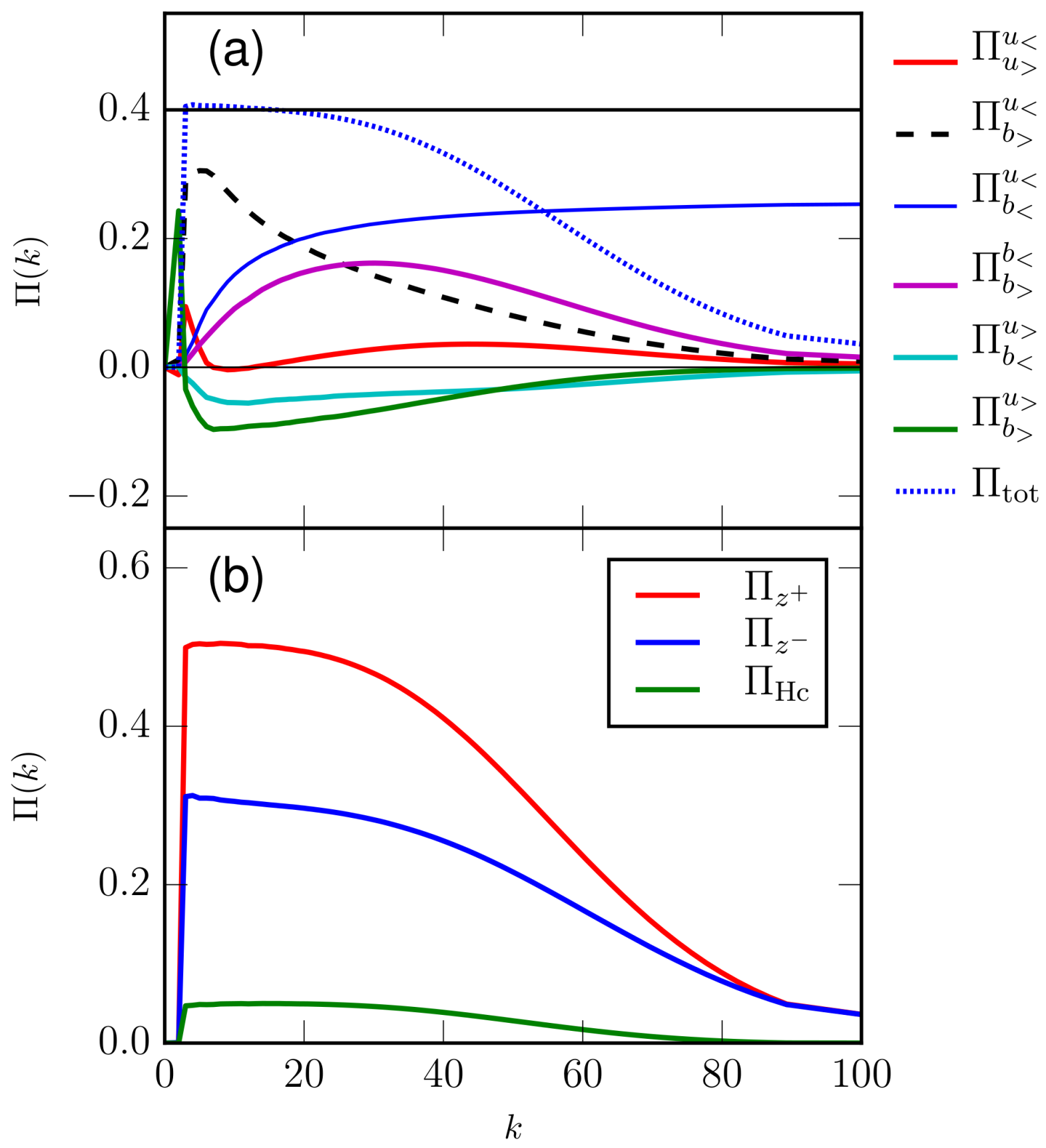
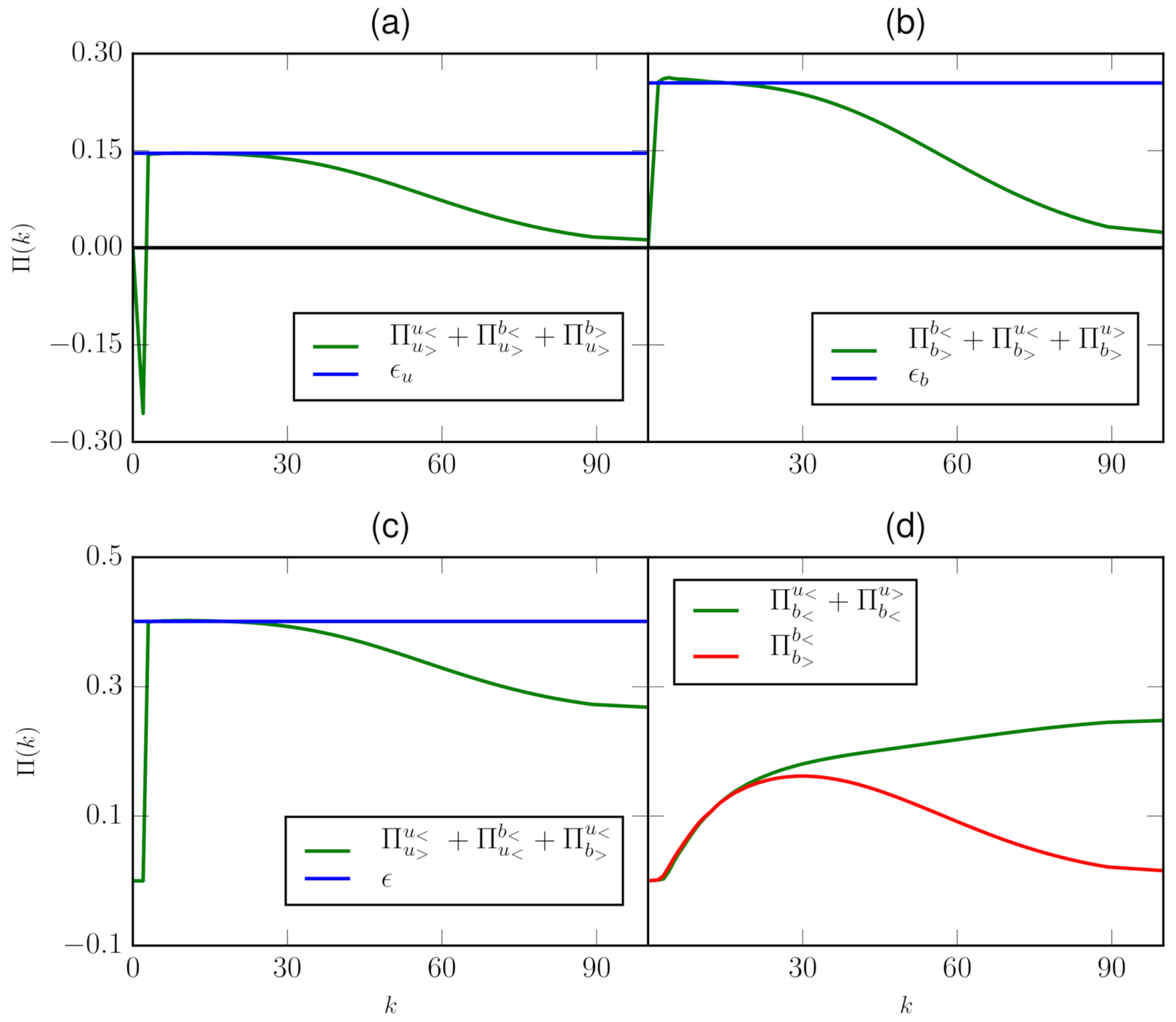
- The energy fluxes corresponding to the total energy and are nearly constant in the wavenumber band (3, 20), consistent with the power-law regime of the energy spectra discussed earlier. Note that the inertial-range energy flux of the total energy matches with ; in addition, these fluxes are equal to the energy supply rate and the total-energy dissipation rate, consistent with the conservation of energy.
- As shown in Figure 4a, in the wavenumber band , the kinetic energy flux dips sharply, while the magnetic energy fluxes, and , grow rapidly. This observation indicates energy transfer from u to b. Note that picks up significantly after this band ().
- The energy fluxes and are negative and become significant beyond wavenumber band (3, 6). These fluxes indicate energy transfers from the magnetic field to the intermediate-scale velocity field. Consequently, grows and becomes significant beyond .
- The energy fluxes corresponding to the velocity and magnetic fields exhibit significant variability due to cross energy transfers. However, the fluxes of are nearly constant in the inertial range due to lack of such transfers. We also compute the flux of cross helicity, which is , and exhibit this flux in Figure 4b. We need to further explore the evolution of cross helicity flux in MHD turbulence.
- Figure 5a demonstrates that in the inertial range, the sum matches with the kinetic energy dissipation rate . Note that the sum represents the total energy transfer to the inertial-range velocity modes that gets dissipated in the dissipation range; this is the reason for the equality of Equation (26).
- The magnetic field is not forced externally. Instead, the large-scale magnetic modes () receive energy from the velocity modes as . The energy received by the large-scale magnetic modes cascades to the inertial range of the magnetic field as . Hence, . This relation is verified for the wavenumber range . See Figure 5d for an illustration.
5. Conclusions
- Our work is focused on the energy fluxes of forced MHD turbulence, in contrast to those of decaying MHD turbulence, studied earlier by Debliquy et al. [16]. A close comparison between the two sets of energy fluxes shows that the decaying and the forced MHD turbulence have several critical differences. For example, we observe positive , while Debliquy et al. [16] reported negative .
- We employed hyperviscous and hyperdiffusive terms in our simulation to increase the extent of the inertial range. For our simulation, the flux for the total energy is nearly constant in the inertial range, which is . The extent of our inertial range is larger than that of Debliquy et al. [16], who do not employ hyperdiffusion.
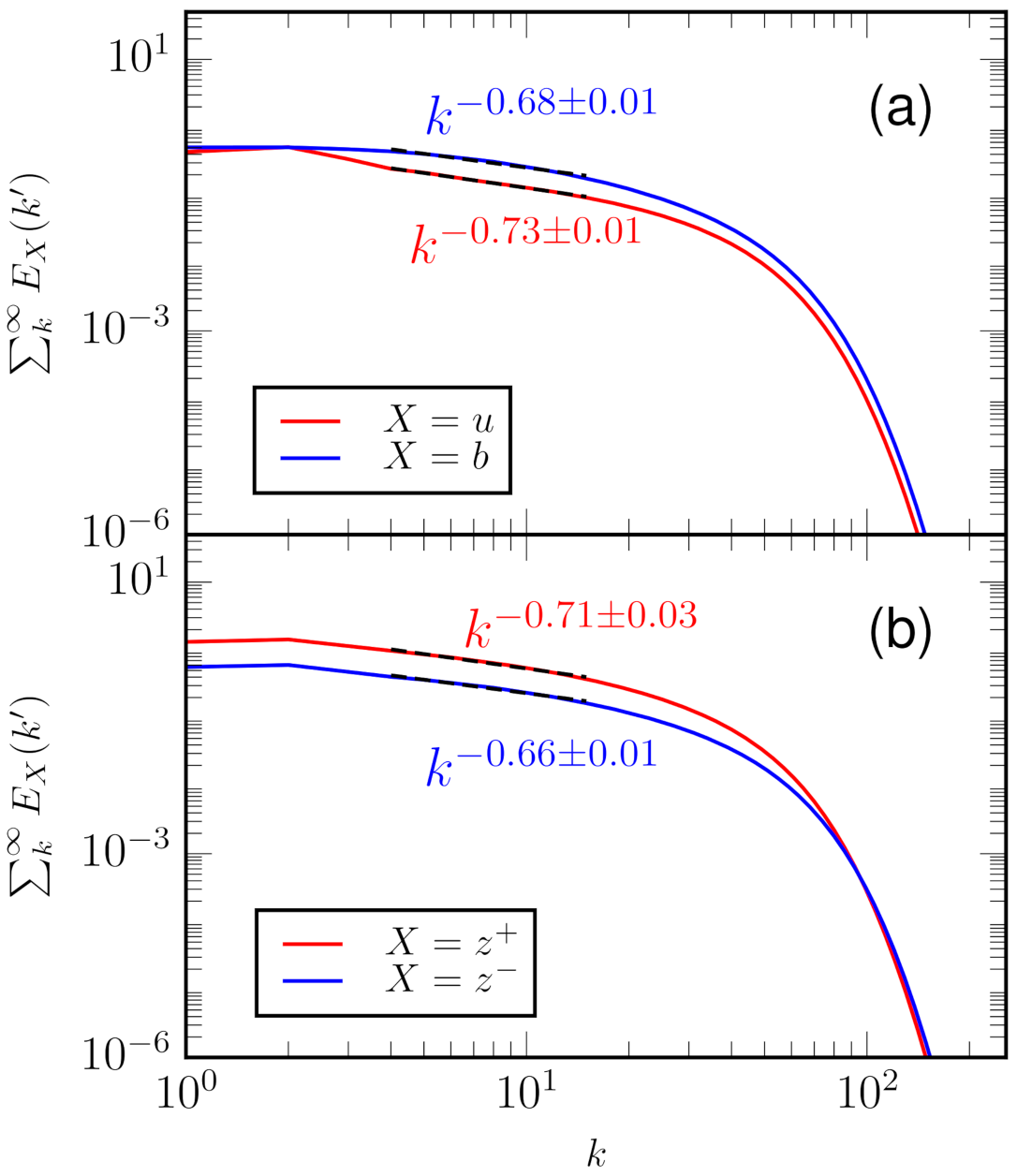
- For our numerical simulations, the spectral indices for and are close to −5/3, rather than [10]. A word of caution, however, is that the inertial range is quite narrow due to the moderate resolution of our simulation. For a better understanding of the spectral indices and the energy fluxes, we need a broader inertial range that is possible with high-resolution simulations; we plan for such simulations in the near future.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MHD | Magnetohydrodynamics |
| 3D | Three dimensions |
| 2D | Two dimensions |
Nomenclature
| Fourier wavenumbers | |
| Velocity field | |
| Magnetic field | |
| Elsässer variables | |
| t | Time |
| p | Pressure |
| Random large-scale force | |
| Lorentz force | |
| Stretching of magnetic field by velocity field | |
| Modal kinetic energy | |
| Modal magnetic energy | |
| Kinetic energy spectrum | |
| Magnetic energy spectrum | |
| Elsässer energy spectra | |
| Nonlinear modal energy transfers | |
| Modal kinetic energy dissipation rate | |
| Modal magnetic energy dissipation rate | |
| External modal energy injection rate | |
| Cross energy transfers among velocity and magnetic modes | |
| Kinetic energy dissipation rate | |
| Magnetic energy dissipation rate | |
| Total dissipation rate | |
| Kinetic energy injection rate | |
| Energy flux from the wavenumbers inside the sphere of radius of field X to outside the sphere of field of field Y, e.g., | |
| Unit vectors in Craya–Herring basis | |
| Characteristic velocity | |
| Velocity components in Craya–Herring basis | |
| Mean magnetic field | |
| Total energy flux | |
| L | Periodic box size used in simulation |
| N | Grid size |
| Kinematic hyperviscosity, magnetic hyperdiffusivity | |
| Kinematic viscosity, magnetic diffusivity | |
| Kinetic Reynolds number | |
| Magnetic Reynolds number | |
| Magnetic Prandtl number | |
| Cumulative spectra, where | |
| Radius of ith intermediate sphere | |
| n | Total no. of spheres |
| Radius of target wavenumber sphere |
References
- Choudhuri, A.R. Physics of Fluids and Plasmas; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Frisch, U. Turbulence; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Kolmogorov, A.N. Dissipation of Energy in Locally Isotropic Turbulence. Dokl. Akad. Nauk. SSSR 1941, 32, 16. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk. SSSR 1941, 30, 301. [Google Scholar]
- Dar, G.; Verma, M.K.; Eswaran, V. Energy transfer in two-dimensional magnetohydrodynamic turbulence: Formalism and numerical results. Physica D 2001, 157, 207. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.K. Statistical theory of magnetohydrodynamic turbulence: Recent results. Phys. Rep. 2004, 401, 229. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.K.; Alam, S.; Chatterjee, S. Turbulent drag reduction in magnetohydrodynamic and quasi-static magnetohydrodynamic turbulence. Phys. Plasmas 2020, 27, 052301. [Google Scholar] [CrossRef]
- Verma, M.K. Energy Transfers in Fluid Flows: Multiscale and Spectral Perspectives; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Verma, M.K. Variable energy flux in turbulence. arXiv 2020, arXiv:2011.07291. [Google Scholar]
- Kraichnan, R.H. Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 1965, 7, 1385. [Google Scholar] [CrossRef] [Green Version]
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Astron. 1964, 7, 566. [Google Scholar]
- Dobrowolny, M.; Mangeney, A.; Veltri, P. Fully developed anisotropic hydromagnetic turbulence in interplanetary space. Phys. Rev. Lett. 1980, 45, 144. [Google Scholar] [CrossRef]
- Marsch, E. Turbulence in the Solar Wind. In Reviews in Modern Astronomy; Springer: Berlin/Heidelberg, Germany, 1991; pp. 145–156. [Google Scholar]
- Verma, M.K. Mean magnetic field renormalization and Kolmogorov’s energy spectrum in magnetohydrodynamic turbulence. Phys. Plasmas 1999, 6, 1455–1460. [Google Scholar] [CrossRef] [Green Version]
- Goldreich, P.; Sridhar, S. Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence. Astrophys. J 1995, 463, 763–775. [Google Scholar] [CrossRef]
- Debliquy, O.; Verma, M.K.; Carati, D. Energy fluxes and shell-to-shell transfers in three-dimensional decaying magnetohydrodynamic turbulence. Phys. Plasmas 2005, 12, 042309. [Google Scholar] [CrossRef]
- Alexakis, A.; Mininni, P.D.; Pouquet, A. Shell-to-shell energy transfer in magnetohydrodynamics. I. steady state turbulence. Phys. Rev. E 2005, 72, 046301. [Google Scholar] [CrossRef] [Green Version]
- Carati, D.; Debliquy, O.; Knaepen, B.; Teaca, B.; Verma, M.K. Energy transfers in forced MHD turbulence. J. Turbul. 2006, 7, 1. [Google Scholar] [CrossRef]
- Verma, M.K.; Roberts, D.A.; Goldstein, M.L.; Ghosh, S.; Stribling, W.T. A numerical study of the nonlinear cascade of energy in magnetohydrodynamic turbulence. J. Geophys. Res. Space Phys. 1996, 101, 21619–21625. [Google Scholar] [CrossRef]
- Teaca, B.; Verma, M.K.; Knaepen, B.; Carati, D. Energy transfer in anisotropic magnetohydrodynamic turbulence. Phys. Rev. E 2009, 79, 046312. [Google Scholar] [CrossRef] [Green Version]
- Sundar, S.; Verma, M.K.; Alexakis, A.; Chatterjee, A.G. Dynamic anisotropy in MHD turbulence induced by mean magnetic field. Phys. Plasmas 2017, 24, 022304. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.K. Field theoretic calculation of renormalized viscosity, renormalized resistivity, and energy fluxes of magnetohydrodynamic turbulence. Phys. Rev. E 2001, 64, 026305. [Google Scholar] [CrossRef] [Green Version]
- Verma, M. Field theoretic calculation of energy cascade rates in non-helical magnetohydrodynamic turbulence. Pramana 2003, 61, 577–594. [Google Scholar] [CrossRef] [Green Version]
- Verma, M. Energy fluxes in helical magnetohydrodynamics and dynamo action. Pramana 2003, 61, 707–724. [Google Scholar] [CrossRef] [Green Version]
- Matthaeus, W.H.; Goldstein, M.L. Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. Space Phys. 1982, 87, 6011–6028. [Google Scholar] [CrossRef]
- Tu, C.Y.; Marsch, E. MHD structures, waves and turbulence in the solar wind: Observations and theories. Space Sci. Rev. 1995, 73, 1–210. [Google Scholar] [CrossRef]
- Parashar, T.N.; Chasapis, A.; Bandyopadhyay, R.; Chhiber, R.; Matthaeus, W.H.; Maruca, B.; Shay, M.A.; Burch, J.L.; Moore, T.E.; Giles, B.L.; et al. Kinetic Range Spectral Features of Cross Helicity Using the Magnetospheric Multiscale Spacecraft. Phys. Rev. Lett. 2018, 121, 265101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, M.K.; Roberts, D.A.; Goldstein, M.L. Turbulent heating and temperature evolution in the solar wind plasma. J. Geophys. Res. Space Phys. 1995, 100, 1989–19850. [Google Scholar] [CrossRef]
- Politano, H.; Pouquet, A. von Kármán-Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 1998, 57, R21–R24. [Google Scholar] [CrossRef]
- Sorriso-Valvo, L.; Marino, R.; Carbone, V.; Noullez, A.; Lepreti, F.; Veltri, P.; Bruno, R.; Bavassano, B.; Pietropaolo, E. Observation of inertial energy cascade in interplanetary space plasma. Phys. Rev. Lett. 2007, 99, 115001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bandyopadhyay, R.; Goldstein, M.L.; Maruca, B.A.; Matthaeus, W.H.; Parashar, T.N.; Ruffolo, D.; Chhiber, R.; Usmanov, A.; Chasapis, A.; Qudsi, R.; et al. Enhanced Energy Transfer Rate in Solar Wind Turbulence Observed near the Sun from Parker Solar Probe. Astrophys. J. 2020, 246, 48. [Google Scholar] [CrossRef] [Green Version]
- Kothandapani, M.; Pushparaj, V.; Prakash, J. Effect of magnetic field on peristaltic flow of a fourth grade fluid in a tapered asymmetric channel. J. King Saud Univ. Eng. Sci. 2018, 30, 86–95. [Google Scholar] [CrossRef] [Green Version]
- Elkoumy, S.R.; Barakat, E.I.; Abdelsalam, S.I. Hall and transverse magnetic field effects on peristaltic flow of a Maxwell fluid through a porous medium. Glob. J. Pure Appl. Math 2013, 9, 187–203. [Google Scholar]
- Eldesoky, I.; Abdelsalam, S.; El-Askary, W.; El-Refaey, A.M.; Ahmed, M. Joint Effect of Magnetic Field and Heat Transfer on Particulate Fluid Suspension in a Catheterized Wavy Tube. Bionanoscience 2019, 9, 723–739. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M. Anomalous reactivity of thermo-bioconvective nanofluid towards oxytactic microorganisms. Appl. Math. Mech. 2020, 41, 711–724. [Google Scholar] [CrossRef]
- Abdelsalam, S.; Sohail, M. Numerical approach of variable thermophysical features of dissipated viscous nanofluid comprising gyrotactic micro-organisms. Pramana 2020, 94, 67. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Velasco-Hernández, J.X.; Zaher, A.Z. Electro-magnetically modulated self-propulsion of swimming sperms via cervical canal. Biomech. Model. Mechanobiol. 2021. [Google Scholar] [CrossRef] [PubMed]
- Elmaboud, Y.; Mekheimer, K.S.; Abdelsalam, S.I. A study of nonlinear variable viscosity in finite-length tube with peristalsis. Appl. Bionics Biomech. 2014, 11, 197–206. [Google Scholar] [CrossRef] [Green Version]
- Eldesoky, I.M.; Abdelsalam, S.I.; Abumandour, R.M.; Kamel, M.H.; Vafai, K. Interaction between compressibility and particulate suspension on peristaltically driven flow in planar channel. Appl. Math. Mech. Engl. Ed. 2017, 38, 137–154. [Google Scholar] [CrossRef]
- Sadal, H.; Abdelsalam, S.I. Adverse effects of a hybrid nanofluid in a wavy nonuniform annulus with convective boundary conditions. RSC Adv. 2020, 10, 15035–15043. [Google Scholar]
- Alexakis, A.; Mininni, P.D.; Pouquet, A. Turbulent cascades, transfer, and scale interactions in magnetohydrodynamics. New J. Phys. 2007, 9, 298. [Google Scholar] [CrossRef] [Green Version]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magnetohydrodynamic Darcy–Forchheimer nanofluid flow over a nonlinear stretching sheet. Phys. Scr. 2019, 94, 105221. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy Generation and Consequences of Binary Chemical Reaction on MHD Darcy–Forchheimer Williamson Nanofluid Flow Over Non-Linearly Stretching Surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef] [Green Version]
- Rasool, G.; Shafiq, A.; Durur, H. Darcy-Forchheimer relation in Magnetohydrodynamic Jeffrey nanofluid flow over stretching surface. Discret. Contin. Dyn. Syst. Ser. S 2020. [Google Scholar] [CrossRef]
- Ali, B.; Rasool, G.; Hussain, S.; Baleanu, D.; Bano, S. Finite Element Study of Magnetohydrodynamics (MHD) and Activation Energy in Darcy–Forchheimer Rotating Flow of Casson Carreau Nanofluid. Processes 2020, 8, 1185. [Google Scholar] [CrossRef]
- Rasool, G.; Khan, W.A.; Bilal, S.M.; Khan, I. MHD squeezed darcy–forchheimer nanofluidflow between two h–distance aparthorizontal plates. Open Phys. 2020, 18, 1100–1107. [Google Scholar] [CrossRef]
- Rasool, G.; Wakif, A. Numerical spectral examination of EMHD mixed convective flow of second-grade nanofluid towards a vertical Riga plate using an advanced version of the revised Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2020, 1143, 2379–2393. [Google Scholar]
- Rasool, G.; Shafiq, A.; Alqarni, M.; Wakif, A.; Khan, I.; Bhutta, M.S. Numerical Scrutinization of Darcy-Forchheimer Relation in Convective Magnetohydrodynamic Nanofluid Flow Bounded by Nonlinear Stretching Surface in the Perspective of Heat and Mass Transfer. Micromachines 2021, 12, 374. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Roberts, D.A.; Matthaeus, W.H. Magnetohydrodynamic turbulence in the solar wind. Annu. Rev. Astron. Astrophys. 1995, 33, 283–325. [Google Scholar] [CrossRef]
- Verma, M.K.; Chatterjee, A.G.; Yadav, R.K.; Paul, S.; Chandra, M.; Samtaney, R. Benchmarking and scaling studies of pseudospectral code Tarang for turbulence simulations. Pramana 2013, 81, 617. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, A.G.; Verma, M.K.; Kumar, A.; Samtaney, R.; Hadri, B.; Khurram, R. Scaling of a Fast Fourier Transform and a pseudo-spectral fluid solver up to 196608 cores. J. Parallel Distrib. Comput. 2018, 113, 77–91. [Google Scholar] [CrossRef] [Green Version]
- Craya, A. Contribution À l’analyse de la Turbulence Associée à Des Vitesses Moyennes. Ph.D. Thesis, Université de Granoble, Saint-Martin-d’Hères, France, 1958. [Google Scholar]
- Herring, J.R. Approach of axisymmetric turbulence to isotropy. Phys. Fluids 1974, 17, 859–872. [Google Scholar] [CrossRef]
- Kida, S.; Yanase, S.; Mizushima, J. Statistical properties of MHD turbulence and turbulent dynamo. Phys. Fluids A 1991, 3, 457–465. [Google Scholar] [CrossRef]
- Alvelius, K. Random forcing of three-dimensional homogeneous turbulence. Phys. Fluids 1999, 11, 1880–1889. [Google Scholar] [CrossRef]
- Maffioli, A. Vertical spectra of stratified turbulence at large horizontal scales. Phys. Rev. Fluids 2017, 2, 104802. [Google Scholar] [CrossRef] [Green Version]
- Beresnyak, A.; Lazarian, A. Comparison of spectral slopes of magnetohydrodynamic and hydrodynamic turbulence and measurements of alignment effects. APJ 2009, 702, 1190–1198. [Google Scholar] [CrossRef]
- Beresnyak, A. Spectral Slope and Kolmogorov Constant of MHD Turbulence. Phys. Rev. Lett. 2011, 106, 075001. [Google Scholar] [CrossRef] [Green Version]
- Beresnyak, A. Basic properties of magnetohydrodynamic turbulence in the inertial range. Mon. Not. R. Astron. Soc. 2012, 422, 3495–3502. [Google Scholar] [CrossRef] [Green Version]
- Beresnyak, A. MHD turbulence. Living Rev. Comput. Astrophys. 2019, 5, 2. [Google Scholar] [CrossRef] [Green Version]
| N | ||||||
|---|---|---|---|---|---|---|
| 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, M.; Sharma, M.; Chatterjee, S.; Alam, S. Variable Energy Fluxes and Exact Relations in Magnetohydrodynamics Turbulence. Fluids 2021, 6, 225. https://doi.org/10.3390/fluids6060225
Verma M, Sharma M, Chatterjee S, Alam S. Variable Energy Fluxes and Exact Relations in Magnetohydrodynamics Turbulence. Fluids. 2021; 6(6):225. https://doi.org/10.3390/fluids6060225
Chicago/Turabian StyleVerma, Mahendra, Manohar Sharma, Soumyadeep Chatterjee, and Shadab Alam. 2021. "Variable Energy Fluxes and Exact Relations in Magnetohydrodynamics Turbulence" Fluids 6, no. 6: 225. https://doi.org/10.3390/fluids6060225






