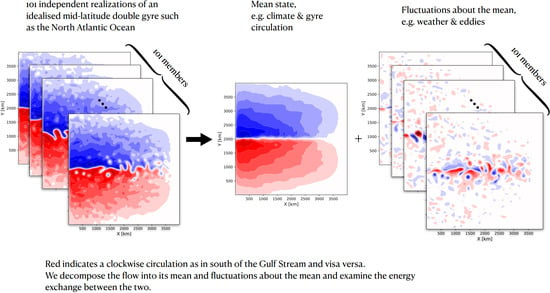
The Seasonal Variability of the Ocean Energy Cycle from a Quasi-Geostrophic Double Gyre Ensemble
Abstract
1. Introduction
2. Model Description
3. Derivation of the Lorenz Energy Cycle
4. Results
4.1. The Domain Integrated Lorenz Energy Cycle
4.2. Time Lag in Lower-Layer Energetics
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Layered Quasi-Geostrophic Potential Vorticity
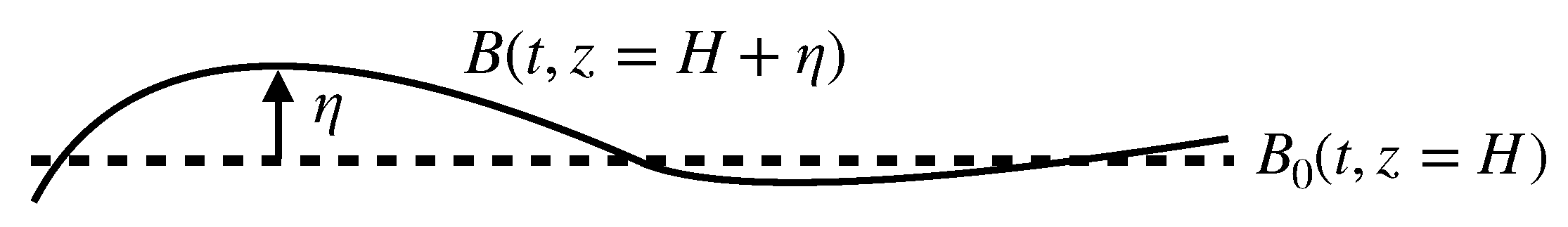
Appendix B. The Omega Equation with a Temporally Varying Background Stratification
Appendix C. Decomposing the Mean and Eddy Energetics
Appendix D. The Three-Layer QG Lorenz Energy Cycle
References
- Phillips, N.A. The general circulation of the atmosphere: A numerical experiment. Q. J. R. Meteorol. Soc. 1956, 82, 123–164. [Google Scholar] [CrossRef]
- Lorenz, E.N. The Nature and Theory of the General Circulation of the Atmosphere; World Meteorological Organization: Geneva, Switzerland, 1967; Volume 218. [Google Scholar]
- Holland, W.R. The role of mesoscale eddies in the general circulation of the ocean—Numerical experiments using a wind-driven quasi-geostrophic model. J. Phys. Oceanogr. 1978, 8, 363–392. [Google Scholar] [CrossRef]
- Holland, W.R.; Schmitz, W.J. Zonal penetration scale of model midlatitude jets. J. Phys. Oceanogr. 1985, 15, 1859–1875. [Google Scholar] [CrossRef][Green Version]
- Kang, D.; Curchitser, E.N. Energetics of Eddy–Mean Flow Interactions in the Gulf Stream Region. J. Phys. Oceanogr. 2015, 45, 1103–1120. [Google Scholar] [CrossRef]
- McWilliams, J.C. A perspective on the legacy of Edward Lorenz. Earth Space Sci. 2019, 6, 336–350. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Su, Z.; Wang, J.; Klein, P.; Thompson, A.F.; Menemenlis, D. Ocean submesoscales as a key component of the global heat budget. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Ajayi, A.; Le Sommer, J.; Chassignet, E.; Molines, J.M.; Xu, X.; Albert, A.; Cosme, E. Spatial and Temporal Variability of the North Atlantic Eddy Field From Two Kilometric-Resolution Ocean Models. J. Geophys. Res. Ocean. 2020, 125, e2019JC015827. [Google Scholar] [CrossRef]
- Lévy, M.; Franks, P.J.; Smith, K.S. The role of submesoscale currents in structuring marine ecosystems. Nat. Commun. 2018, 9, 1–16. [Google Scholar] [CrossRef]
- Thomas, L.N.; Tandon, A.; Mahadevan, A. Submesoscale processes and dynamics. Ocean Model. Eddying Regime 2008, 177, 17–38. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, C.E.; Naveira Garabato, A.C.; Thompson, A.F.; Brannigan, L.; Lazar, A.; Marshall, D.P.; George Nurser, A.; Damerell, G.; Heywood, K.J.; Belcher, S.E. Seasonality of submesoscale flows in the ocean surface boundary layer. Geophys. Res. Lett. 2016, 43, 2118–2126. [Google Scholar] [CrossRef]
- Uchida, T.; Balwada, D.; Abernathey, R.; McKinley, G.; Smith, S.; Levy, M. The contribution of submesoscale over mesoscale eddy iron transport in the open Southern Ocean. J. Adv. Model. Earth Syst. 2019, 11, 3934–3958. [Google Scholar] [CrossRef]
- Siegelman, L.; Klein, P.; Rivière, P.; Thompson, A.F.; Torres, H.S.; Flexas, M.; Menemenlis, D. Enhanced upward heat transport at deep submesoscale ocean fronts. Nat. Geosci. 2020, 13, 50–55. [Google Scholar] [CrossRef]
- Tagklis, F.; Bracco, A.; Ito, T.; Castelao, R. Submesoscale modulation of deep water formation in the Labrador Sea. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Charney, J.G. Geostrophic turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- Arbic, B.K.; Polzin, K.L.; Scott, R.B.; Richman, J.G.; Shriver, J.F. On eddy viscosity, energy cascades, and the horizontal resolution of gridded satellite altimeter products. J. Phys. Oceanogr. 2013, 43, 283–300. [Google Scholar] [CrossRef]
- Aluie, H.; Hecht, M.; Vallis, G.K. Mapping the Energy Cascade in the North Atlantic Ocean: The Coarse-Graining Approach. J. Phys. Oceanogr. 2018, 48, 225–244. [Google Scholar] [CrossRef]
- Yang, Y.; McWilliams, J.C.; Liang, X.S.; Zhang, H.; Weisberg, R.H.; Liu, Y.; Menemenlis, D. Spatial and Temporal Characteristics of the Submesoscale Energetics in the Gulf of Mexico. J. Phys. Oceanogr. 2020. [Google Scholar] [CrossRef]
- Font, J.; Garcialadona, E.; Gorriz, E. The seasonality of mesoscale motion in the northern current of the western mediterranean-several years of evidence. Oceanol. Acta 1995, 18, 207–219. [Google Scholar]
- Strub, P.T.; James, C. Altimeter-derived variability of surface velocities in the California Current System: 2. Seasonal circulation and eddy statistics. Deep Sea Res. Part II Top. Stud. Oceanogr. 2000, 47, 831–870. [Google Scholar] [CrossRef]
- Eden, C.; Böning, C. Sources of eddy kinetic energy in the Labrador Sea. J. Phys. Oceanogr. 2002, 32, 3346–3363. [Google Scholar] [CrossRef]
- Pujol, M.I.; Larnicol, G. Mediterranean sea eddy kinetic energy variability from 11 years of altimetric data. J. Mar. Syst. 2005, 58, 121–142. [Google Scholar] [CrossRef]
- Jouanno, J.; Sheinbaum, J.; Barnier, B.; Molines, J.M.; Candela, J. Seasonal and interannual modulation of the eddy kinetic energy in the Caribbean Sea. J. Phys. Oceanogr. 2012, 42, 2041–2055. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Sasaki, H.; Sasai, Y. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent. J. Phys. Oceanogr. 2014, 44, 3079–3098. [Google Scholar] [CrossRef]
- Sasaki, H.; Klein, P.; Qiu, B.; Sasai, Y. Impact of oceanic-scale interactions on the seasonal modulation of ocean dynamics by the atmosphere. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Uchida, T.; Abernathey, R.; Smith, S. Seasonality of eddy kinetic energy in an eddy permitting global climate model. Ocean Model. 2017, 118, 41–58. [Google Scholar] [CrossRef]
- Dong, J.; Fox-Kemper, B.; Zhang, H.; Dong, C. The seasonality of submesoscale energy production, content, and cascade. Geophys. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Schubert, R.; Jonathan, G.; Greatbatch, R.J.; Baschek, B.; Biastoch, A. The Submesoscale Kinetic Energy Cascade: Mesoscale Absorption of Submesoscale Mixed-Layer Eddies and Frontal Downscale Fluxes. J. Phys. Oceanogr. 2020. [Google Scholar] [CrossRef]
- Ajayi, A.; Le Sommer, J.; Chassignet, E.; Molines, J.M.; Xu, X.; Albert, A.; Dewar, W.K. Diagnosing cross-scale kinetic energy exchanges from two submesoscale permitting ocean models. J. Adv. Model. Earth Syst. 2021. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Ferrari, R.; Hallberg, R. Parameterization of mixed layer eddies. Part I: Theory and diagnosis. J. Phys. Oceanogr. 2008, 38, 1145–1165. [Google Scholar] [CrossRef]
- Johnson, L.; Lee, C.M.; D’Asaro, E.A. Global Estimates of Lateral Springtime Restratification. J. Phys. Oceanogr. 2016, 46, 1555–1573. [Google Scholar] [CrossRef]
- Thompson, A.F.; Lazar, A.; Buckingham, C.; Naveira Garabato, A.C.; Damerell, G.M.; Heywood, K.J. Open-Ocean Submesoscale Motions: A Full Seasonal Cycle of Mixed Layer Instabilities from Gliders. J. Phys. Oceanogr. 2016, 46, 1285–1307. [Google Scholar] [CrossRef]
- Rieck, J.K.; Böning, C.W.; Greatbatch, R.J.; Scheinert, M. Seasonal variability of eddy kinetic energy in a global high-resolution ocean model. Geophys. Res. Lett. 2015, 42, 9379–9386. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: New York, NY, USA, 1987. [Google Scholar]
- Bachman, S.; Fox-Kemper, B.; Bryan, F. A tracer-based inversion method for diagnosing eddy-induced diffusivity and advection. Ocean Model. 2015, 86, 1–14. [Google Scholar] [CrossRef]
- Young, W.R. An Exact Thickness-Weighted Average Formulation of the Boussinesq Equations. J. Phys. Oceanogr. 2012, 42, 692–707. [Google Scholar] [CrossRef]
- Deremble, B.; Martinez, E.M. MSOM: Multiple Scale Ocean Model; MEOM Research Group: Grenoble, France, 2020. [Google Scholar] [CrossRef]
- Popinet, S. A quadtree-adaptive multigrid solver for the Serre-Green-Naghdi equations. J. Comput. Phys. 2015, 302, 336–358. [Google Scholar] [CrossRef]
- Verron, J. Nudging satellite altimeter data into quasi-geostrophic ocean models. J. Geophys. Res. Ocean. 1992, 97, 7479–7491. [Google Scholar] [CrossRef]
- Barnier, B.; Le Provost, C. Influence of bottom topography roughness on the jet and inertial recirculation of a mid-latitude gyre. Dyn. Atmos. Ocean. 1993, 18, 29–65. [Google Scholar] [CrossRef]
- Arakawa, A. Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I. J. Comput. Phys. 1997, 135, 103–114. [Google Scholar] [CrossRef]
- Karabasov, S.; Berloff, P.S.; Goloviznin, V. CABARET in the ocean gyres. Ocean Model. 2009, 30, 155–168. [Google Scholar] [CrossRef]
- Hallberg, R. Using a resolution function to regulate parameterizations of oceanic mesoscale eddy effects. Ocean Model. 2013, 72, 92–103. [Google Scholar] [CrossRef]
- Rhines, P.B.; Schopp, R. The wind-driven circulation: Quasi-geostrophic simulations and theory for nonsymmetric winds. J. Phys. Oceanogr. 1991, 21, 1438–1469. [Google Scholar] [CrossRef][Green Version]
- Hogg, A.M.C.; Killworth, P.D.; Blundell, J.R.; Dewar, W.K. Mechanisms of decadal variability of the wind-driven ocean circulation. J. Phys. Oceanogr. 2005, 35, 512–531. [Google Scholar] [CrossRef]
- Simonnet, E. Quantization of the low-frequency variability of the double-gyre circulation. J. Phys. Oceanogr. 2005, 35, 2268–2290. [Google Scholar] [CrossRef]
- Berloff, P.; Hogg, A.M.C.; Dewar, W. The turbulent oscillator: A mechanism of low-frequency variability of the wind-driven ocean gyres. J. Phys. Oceanogr. 2007, 37, 2363–2386. [Google Scholar] [CrossRef]
- Chelton, D.B.; DeSzoeke, R.A.; Schlax, M.G.; El Naggar, K.; Siwertz, N. Geographical variability of the first baroclinic Rossby radius of deformation. J. Phys. Oceanogr. 1998, 28, 433–460. [Google Scholar] [CrossRef]
- Dijkstra, H.A.; Wubs, F.W.; Cliffe, A.K.; Doedel, E.; Dragomirescu, I.F.; Eckhardt, B.; Gelfgat, A.Y.; Hazel, A.L.; Lucarini, V.; Salinger, A.G.; et al. Numerical bifurcation methods and their application to fluid dynamics: Analysis beyond simulation. Commun. Comput. Phys. 2014, 15, 1–45. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Draghici, I.; Davies, H.C. A new look at the ω-equation. Q. J. R. Meteorol. Soc. 1978, 104, 31–38. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: Cambridge, MA, USA, 1982; Volume 30, 662p. [Google Scholar]
- Grooms, I.; Julien, K.; Fox-Kemper, B. On the interactions between planetary geostrophy and mesoscale eddies. Dyn. Atmos. Ocean. 2011, 51, 109–136. [Google Scholar] [CrossRef]
- Jamet, Q.; Deremble, B.; Wienders, N.; Uchida, T.; Dewar, W.K. On Wind-driven Energetics of Subtropical Gyres. J. Adv. Model. Earth Syst. 2021, e2020MS002329. [Google Scholar] [CrossRef]
- Sérazin, G.; Jaymond, A.; Leroux, S.; Penduff, T.; Bessières, L.; Llovel, W.; Barnier, B.; Molines, J.M.; Terray, L. A global probabilistic study of the ocean heat content low-frequency variability: Atmospheric forcing versus oceanic chaos. Geophys. Res. Lett. 2017, 44, 5580–5589. [Google Scholar] [CrossRef]
- Leroux, S.; Penduff, T.; Bessières, L.; Molines, J.M.; Brankart, J.M.; Sérazin, G.; Barnier, B.; Terray, L. Intrinsic and Atmospherically Forced Variability of the AMOC: Insights from a Large-Ensemble Ocean Hindcast. J. Clim. 2018, 31, 1183–1203. [Google Scholar] [CrossRef]
- Jamet, Q.; Dewar, W.K.; Wienders, N.; Deremble, B. Spatiotemporal Patterns of Chaos in the Atlantic Overturning Circulation. Geophys. Res. Lett. 2019, 46, 7509–7517. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Marshall, D.P. Gulf Stream separation in numerical ocean models. Geophys. Monogr. Ser. 2008, 177. [Google Scholar] [CrossRef]
- Hoyer, S.; Hamman, J.; Roos, M.; Cherian, D.; Fitzgerald, C.; Fujii, K.; Maussion, F.; Crusaderky; Kleeman, A.; Clark, S.; et al. xarray: N-D Labeled Arrays and Datasets; USA. 2020. Available online: http://doi.org/10.5281/zenodo.4299126 (accessed on 9 April 2021).
- Griffies, S.M. The Gent–McWilliams skew flux. J. Phys. Oceanogr. 1998, 28, 831–841. [Google Scholar] [CrossRef]
| Parameter | Notation | Value | Unit |
|---|---|---|---|
| Number of horizontal grids | N | 1024 | - |
| Number of vertical layers | 3 | - | |
| Non-dim. horizontal domain size | 80 | - | |
| Non-dim. horizontal resolution | - | ||
| Background Rossby number | - | ||
| Non-dim. Coriolis parameter | - | ||
| Bottom Ekman number | - | ||
| Non-dim. surface Ekman pumping | - | ||
| Biharmonic Reynolds number | 4000 | - | |
| Non-dim. beta | - | ||
| Background Froude number | - | ||
| Amplitude of | - | ||
| Non-dim. frequency of | - | ||
| Non-dim. layer thickness | - | ||
| Non-dim. reduced gravity | - | ||
| Non-dim. maximum time stepping | - | ||
| CFL condition | - | - | |
| Horizontal velocity | U | [m s] | |
| Length scale | L | 50 | [km] |
| Total layer thickness | H | 5000 | [m] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uchida, T.; Deremble, B.; Penduff, T. The Seasonal Variability of the Ocean Energy Cycle from a Quasi-Geostrophic Double Gyre Ensemble. Fluids 2021, 6, 206. https://doi.org/10.3390/fluids6060206
Uchida T, Deremble B, Penduff T. The Seasonal Variability of the Ocean Energy Cycle from a Quasi-Geostrophic Double Gyre Ensemble. Fluids. 2021; 6(6):206. https://doi.org/10.3390/fluids6060206
Chicago/Turabian StyleUchida, Takaya, Bruno Deremble, and Thierry Penduff. 2021. "The Seasonal Variability of the Ocean Energy Cycle from a Quasi-Geostrophic Double Gyre Ensemble" Fluids 6, no. 6: 206. https://doi.org/10.3390/fluids6060206
APA StyleUchida, T., Deremble, B., & Penduff, T. (2021). The Seasonal Variability of the Ocean Energy Cycle from a Quasi-Geostrophic Double Gyre Ensemble. Fluids, 6(6), 206. https://doi.org/10.3390/fluids6060206