Five-Wave Resonances in Deep Water Gravity Waves: Integrability, Numerical Simulations and Experiments
Abstract
1. Introduction
2. Deep-Water Surface Waves in One-Dimensional Propagation
2.1. Fifth-Order Hamiltonian Theory in Natural Variables
2.2. The Simplest Arrangement of Five-Wave Resonances
- Explicit formulae for the five-wave resonant manifold, leading to five different types of resonance, numbered from (i) to (v).
- Closed-form expressions for the five-wave interaction coefficients evaluated at the resonant manifold. In particular, it was shown that these interaction coefficients are equal to zero in resonance types (iii) and (iv), and nonzero in the resonance types (i), (ii) and (v).
- First resonant quintet:along with its negative version . In terms of linear frequencies via the dispersion relation , this resonance reads , where .
- Second resonant quintet:along with its negative version . In terms of linear frequencies via the dispersion relation , this resonance reads , where .
- Third resonant quintet (vanishing interaction coefficient):along with its negative version . Notice that one of the wavenumbers (), along with its negative, do not appear explicitly in this resonant quintet.
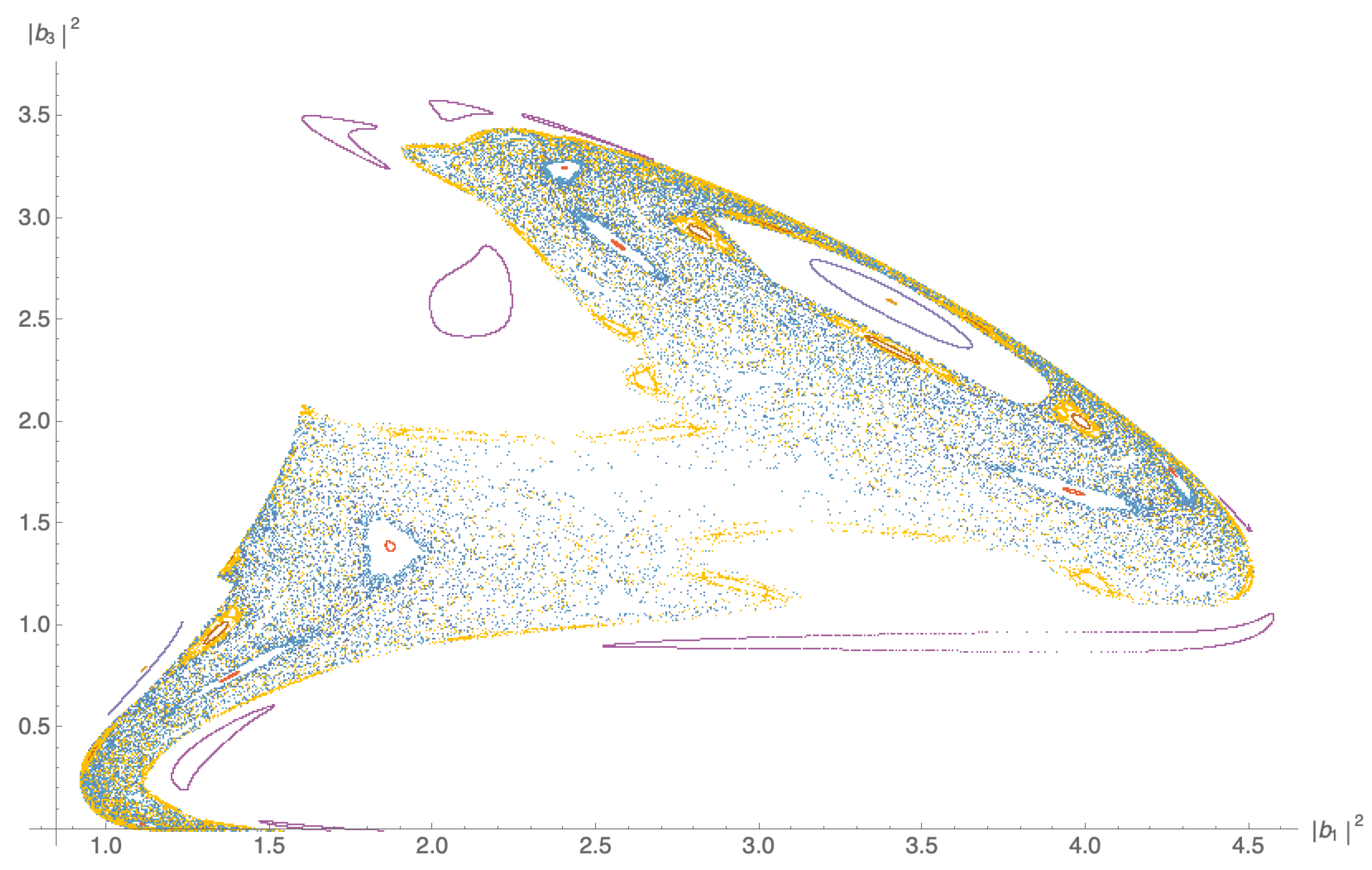
2.3. Non-Integrability of the Five-Wave Resonance in the Case of Encountering Waves
2.4. Analysis of the Scenario of Encountering Waves in the Small-Steepness Case
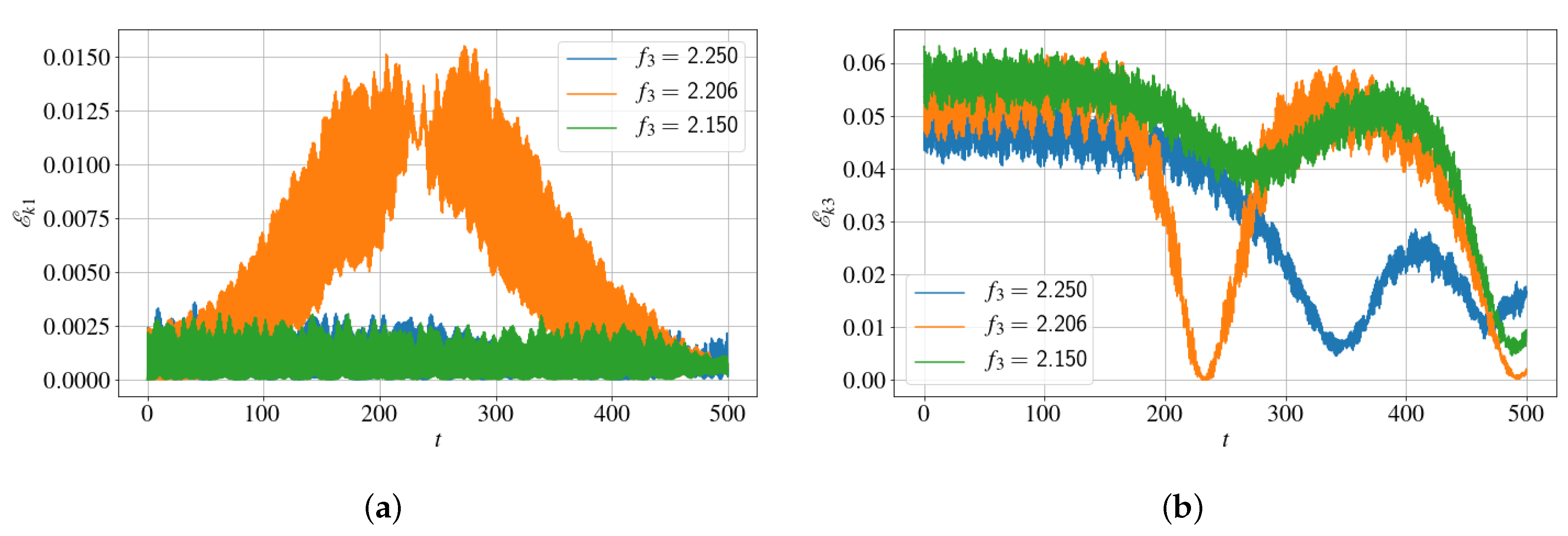
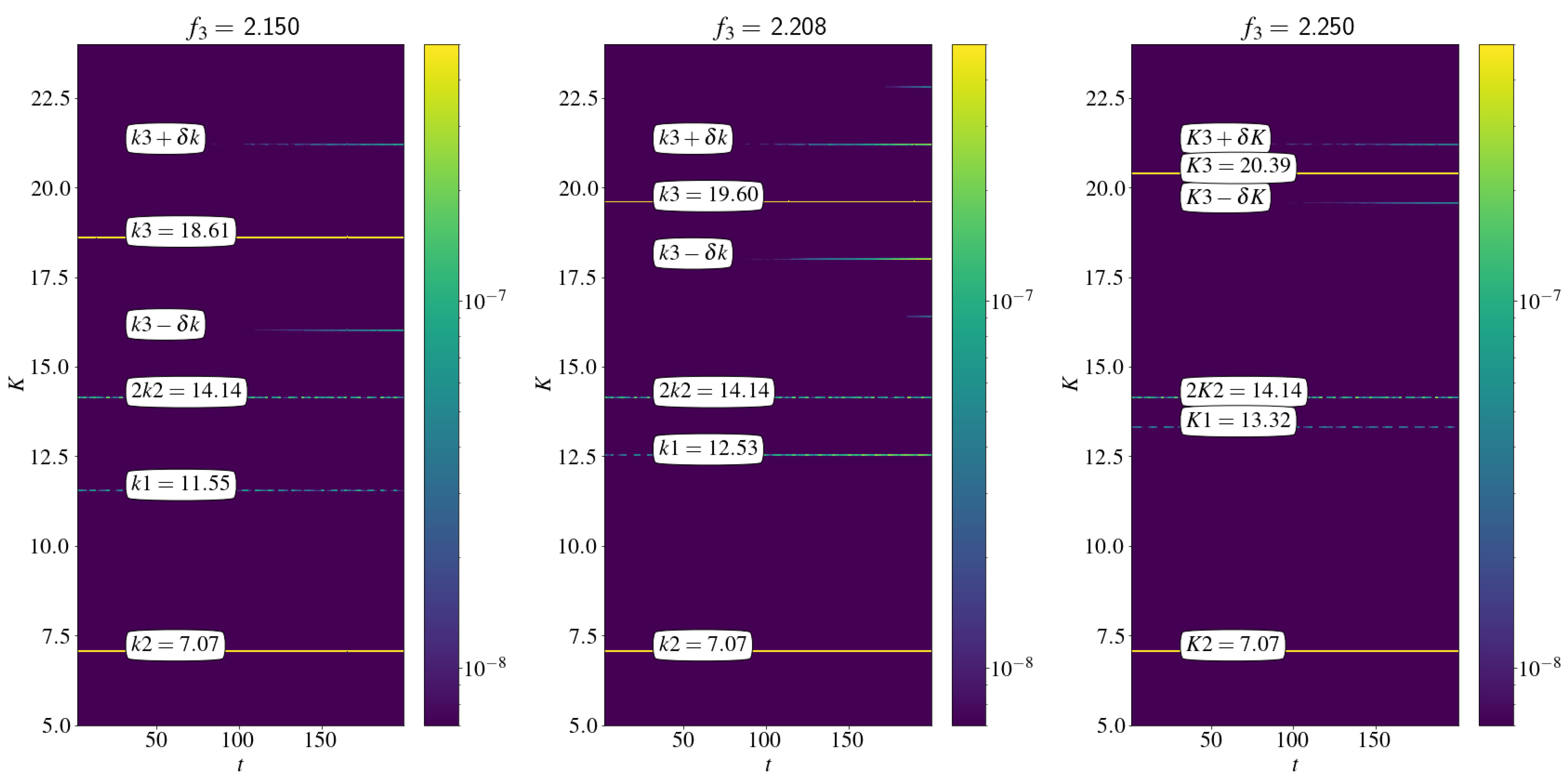
3. Numerical Simulations of the Fifth-Order Governing Equations in Natural Variables
3.1. Encountering Plane Waves
3.2. Encountering Wave Packets
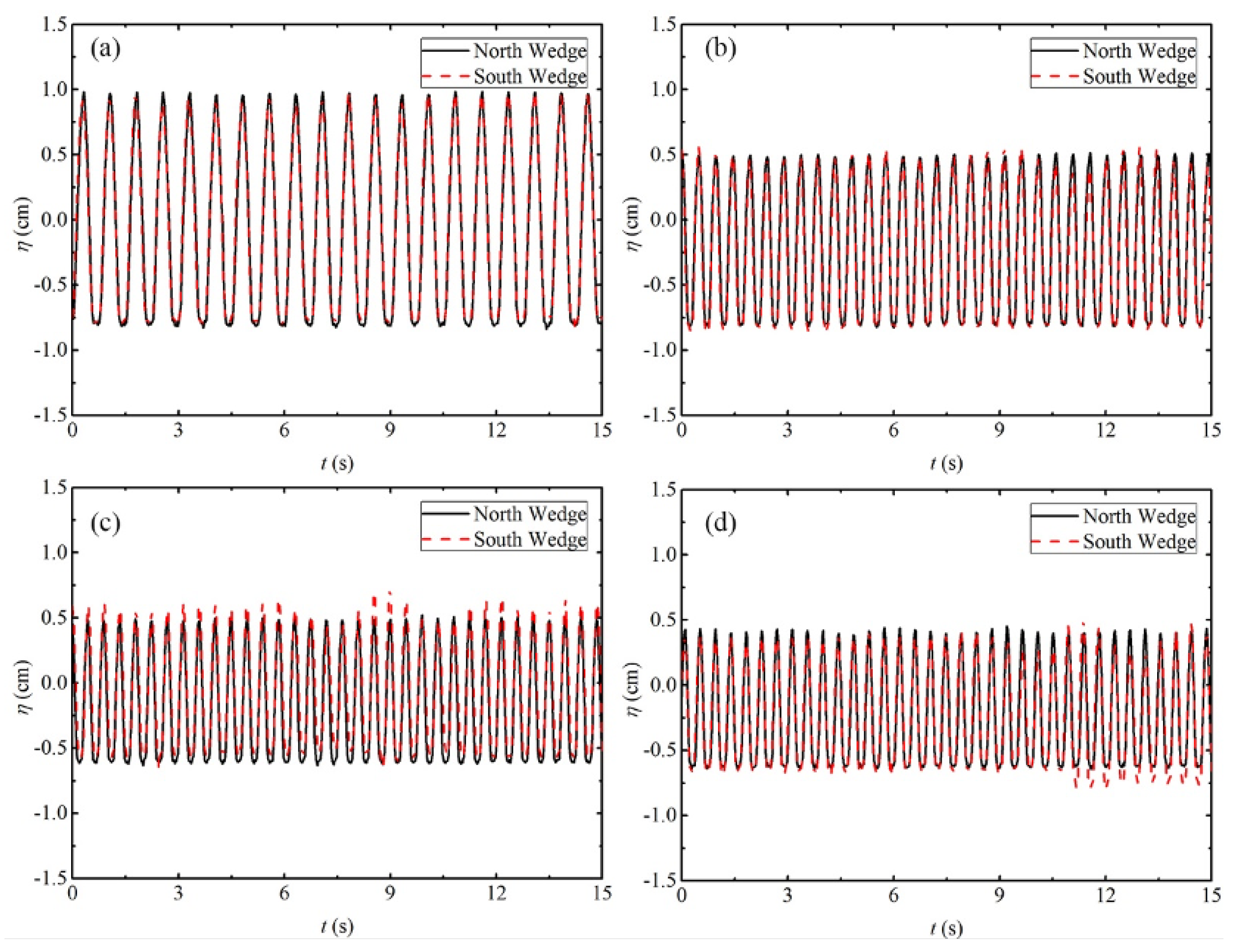
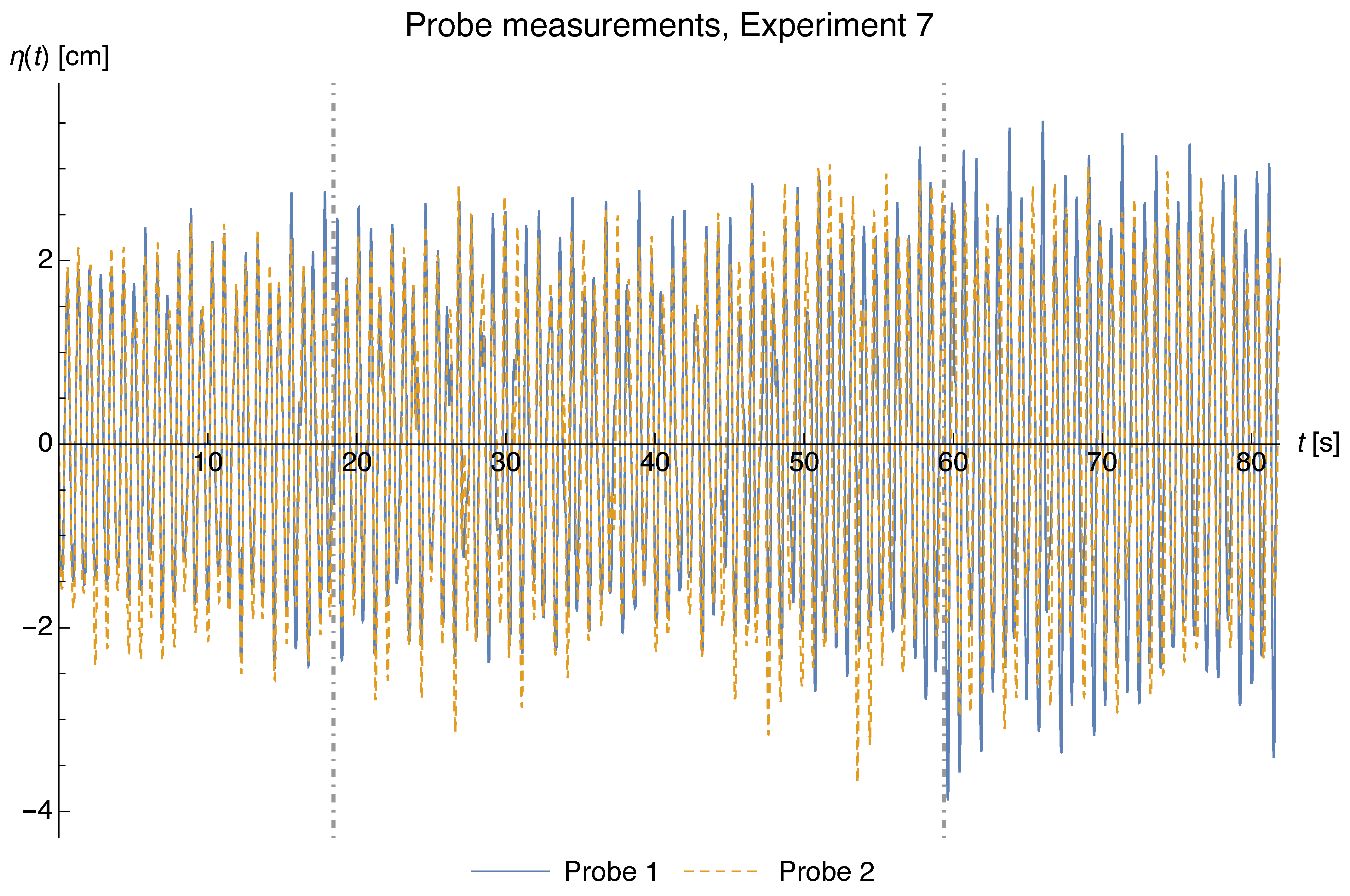
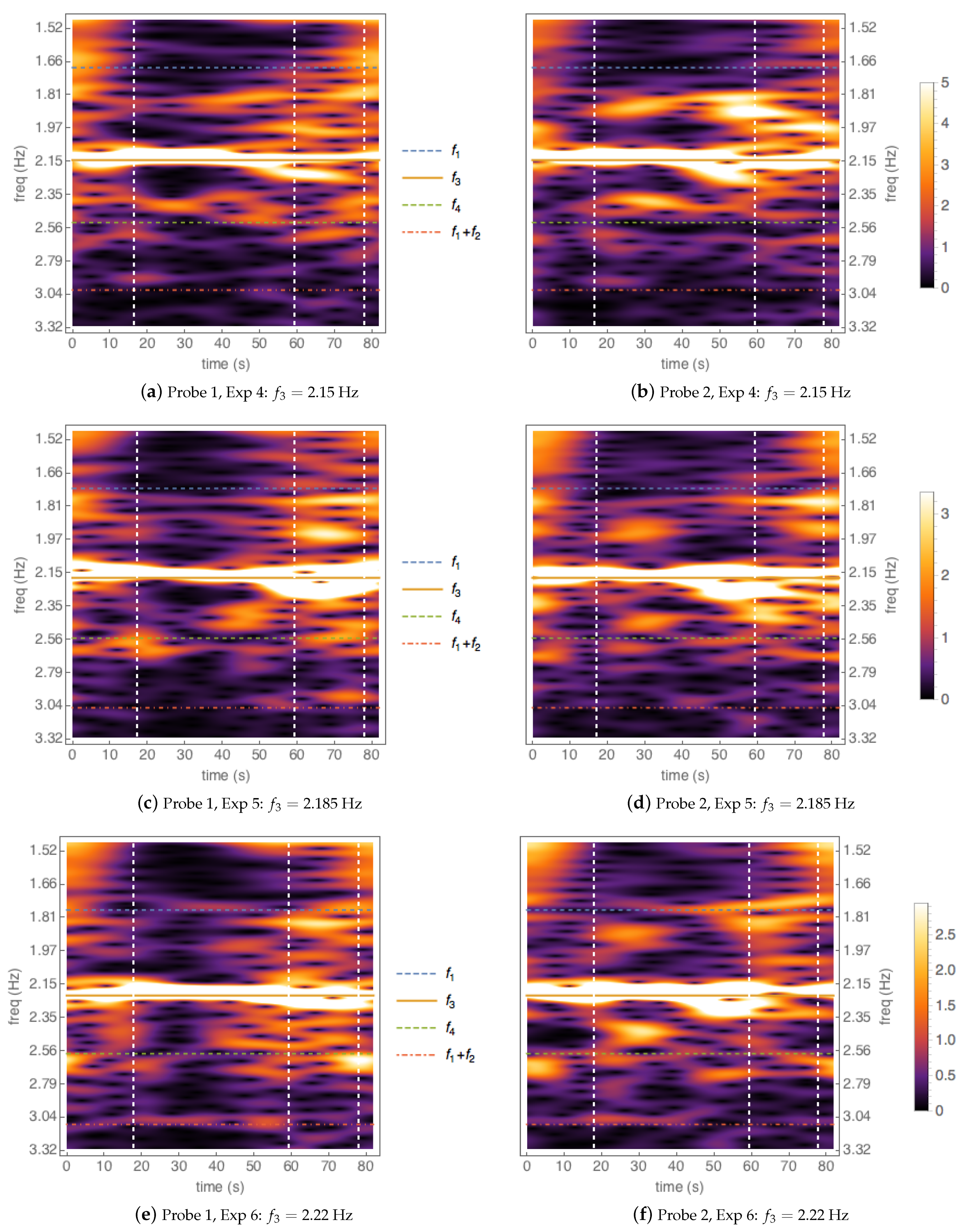
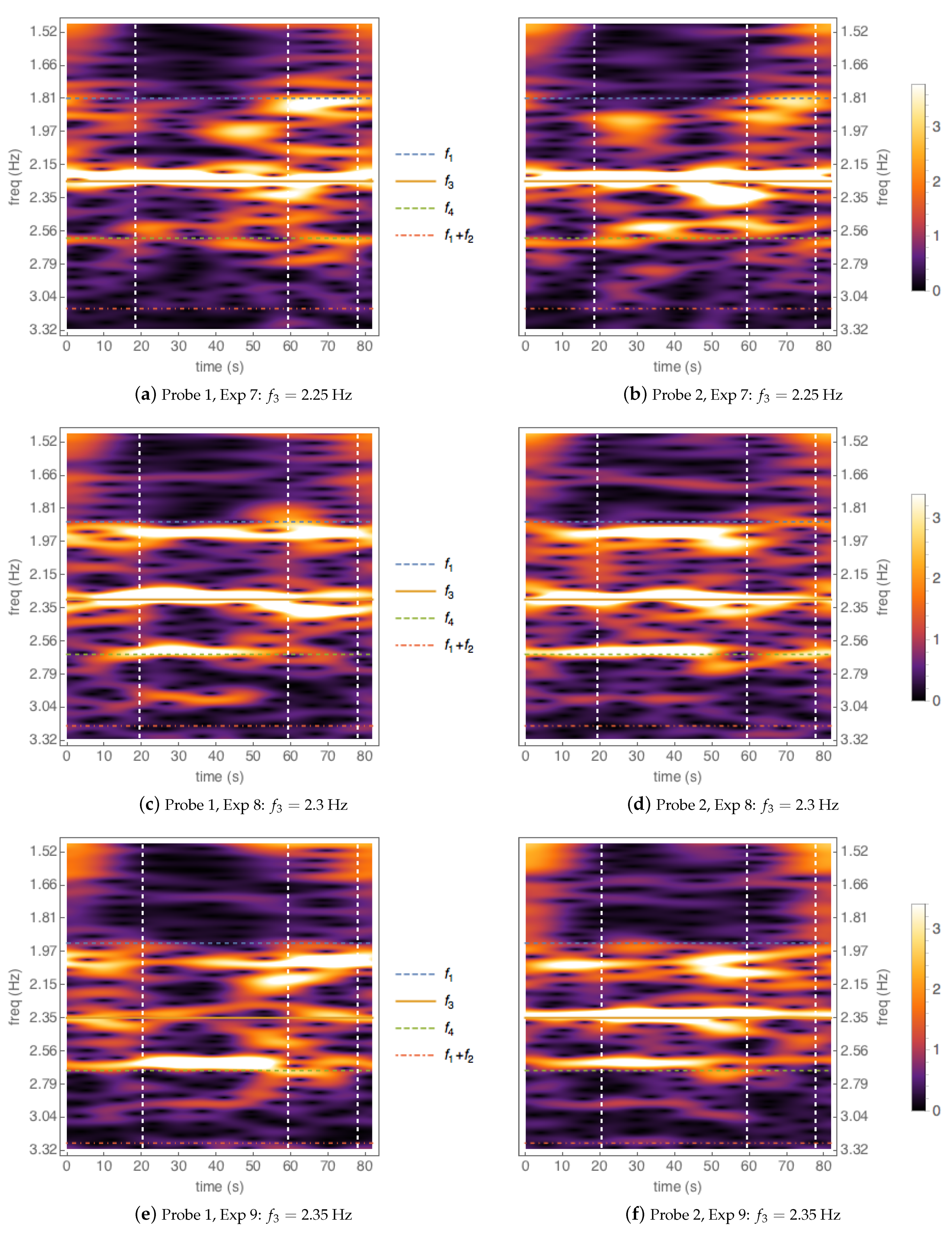
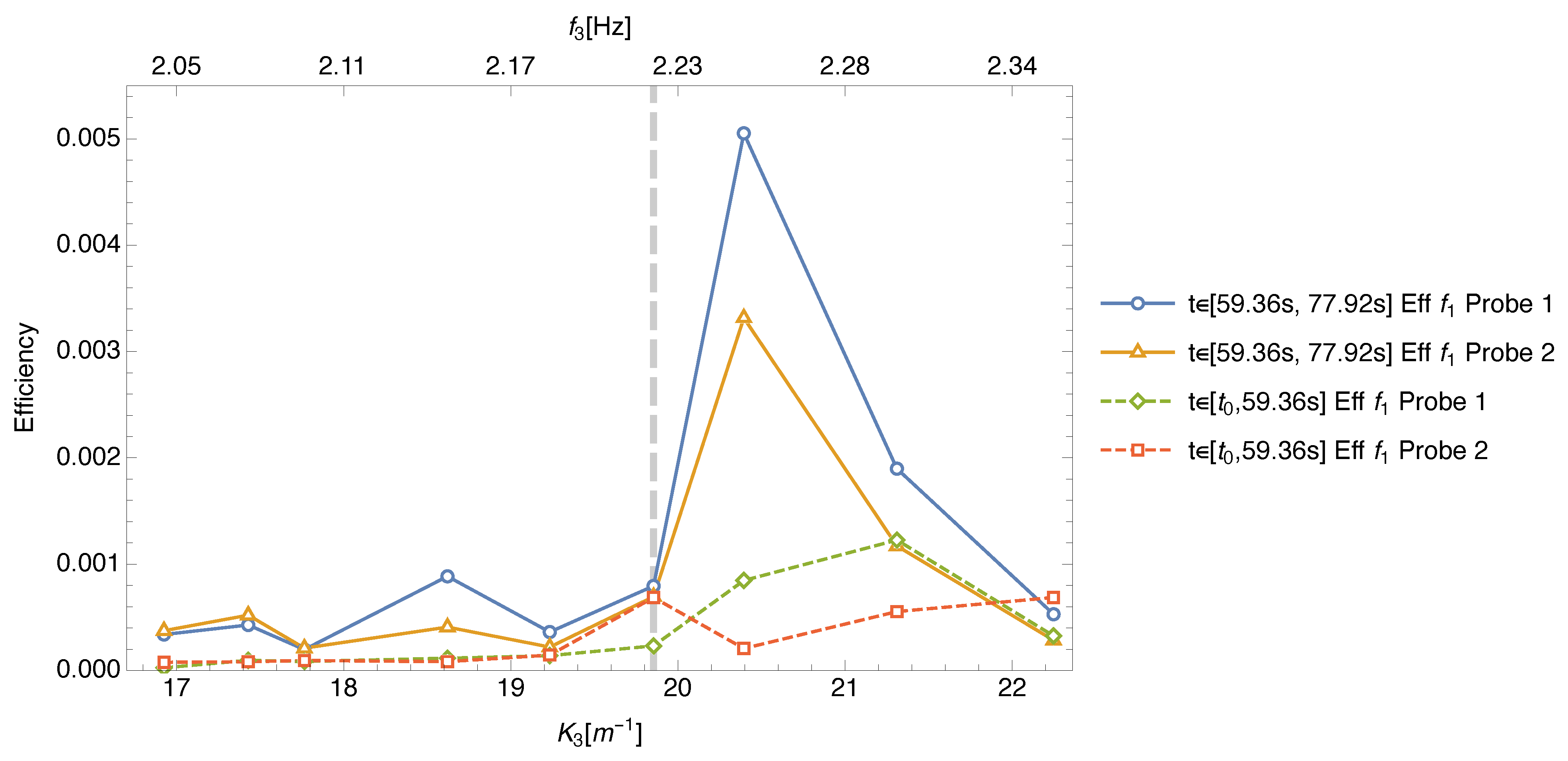
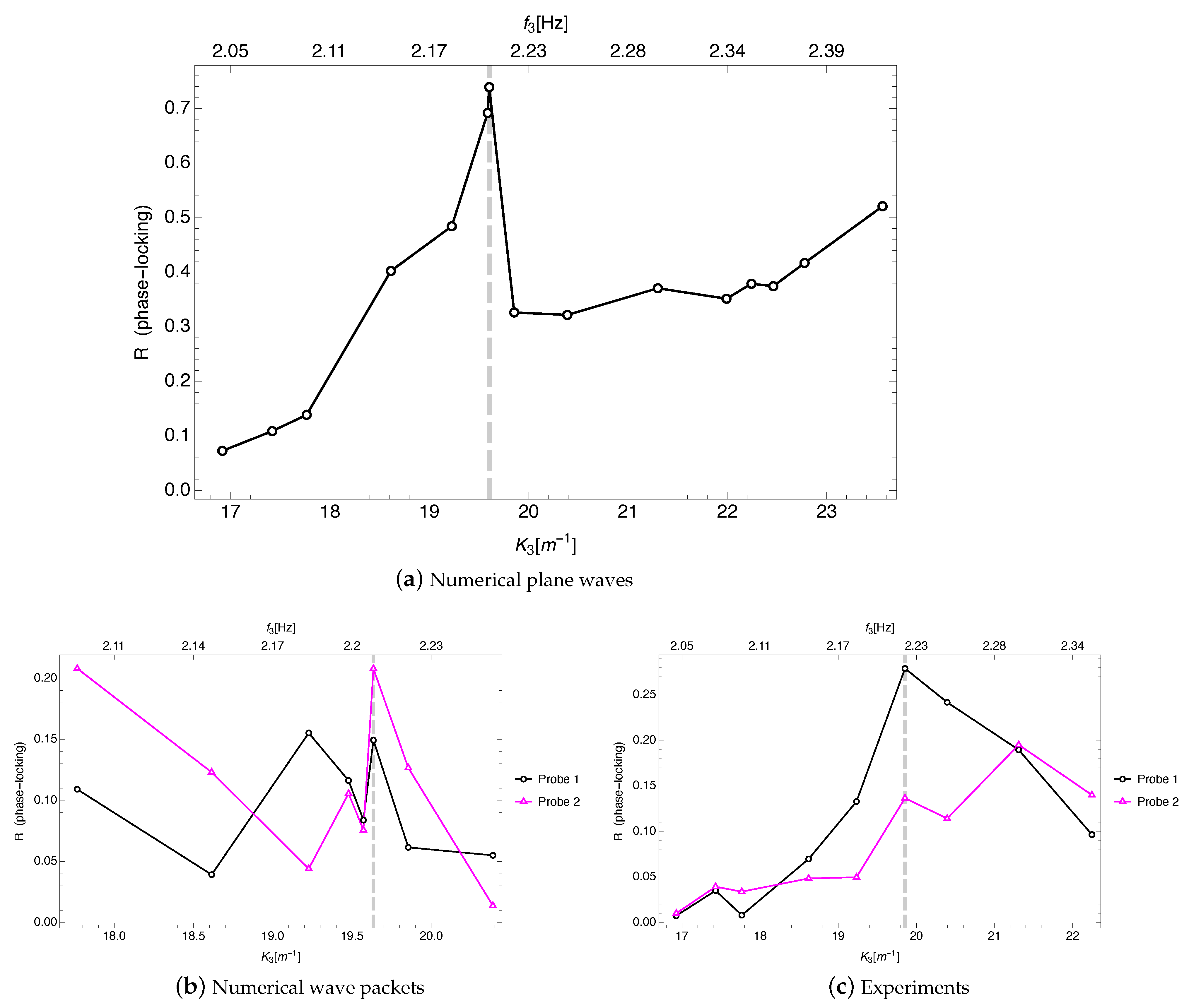
4. Experiments
Encountering Wavepacket Experiments
5. Conclusions and Discussion
- On the theoretical front, the 5-wave resonant manifold and the interaction coefficients on this resonant manifold had been obtained in a series of papers over two decades ago [4,5,6], triggered by the discovery that the interaction coefficients vanish identically on the 4-wave resonant manifold for one-dimensional propagation of water gravity waves [3]. We used these results to find the simplest 5-wave resonance that can be made out of a triad of wavevectors and their negatives, and calculated its normal-form Hamiltonian. We proved that the system is not integrable, but it lacks just one constant of motion to become integrable, so symmetric scenarios can produce integrable systems.
- On the front of numerical simulations of the governing partial differential equations, the equations had been obtained over five decades ago [15], as a power series in terms of the steepness effectively. The numerical implementation we needed to use in order to accurately resolve 5-wave interactions is the one that uses up to 6-wave interactions in a pseudo-spectral setting [40]. Such an implementation requires a higher-than-usual dealiasing and thus can get quite expensive in terms of the required spectral resolution. We managed to validate our implementation against some benchmarks, and were able to establish the existence of the resonance and quantify its effects in terms of the energy transferred to target modes. We considered encountering plane waves and also encountering wave packets, in a simulated tank that is 300 m long. The plane-wave case provided the most efficient energy transfer in terms of Hamiltonian energy, while the wavepackets case provided a higher efficiency in terms of the probe measurements of surface elevation at a point along the tank.
- On the experimental front the main difficulty is to fine tune the amplitudes and frequencies in order to capture the resonance, but we got this from hindsight. Our preliminary experiments seem to show that the resonance exists physically, although as can be seen in Figure 18, the efficiency is relatively small.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Construction of 5-Wave Resonances Using Only Three Different Positive Wavevectors J1, J2, J3 (with 0 < J2 < J1 and J3 = J1 + J2) Along with Their Negatives
- (i)
- All wavevectors are positive.
- (ii)
- , and one of the is negative.
- (iii)
- , and two of the are negative.
- (iv)
- have different signs, and .
- (v)
- have different signs, and one of the is negative.
- (i)
- As all wavevectors are positive, we need to restrict . As we must impose (A1) we conclude . Therefore we have two subcases: (i.1) and (i.2) . In subcase (i.1) the option leads to the momentum equation but the resonance condition is which contradicts the momentum equation. The only other option is . We have the following three instances:(i.1.a) . Here, the momentum equation is which implies and thus , so the resonance condition is , which has no solution.(i.1.b) . Here, the momentum equation is which implies and thus , so the resonance condition is , which has no solution.(i.1.c) . Here, the momentum equation is which implies , with no solution.In conclusion subcase (i.1) has no solution. We now study subcase (i.2) . In this subcase we must have for all . We have the following six instances:(i.2.a) . Here, the momentum equation is which implies , with no solution.(i.2.b) . Here, the momentum equation is which implies , with no solution.(i.2.c) . Here, the momentum equation is which implies and thus , so the resonance condition is , which has no solution.(i.2.d) . Here, the momentum equation is which implies which has no solution (because ).(i.2.e) . Here, the momentum equation is which implies , with no solution.(i.2.f) . Here, the momentum equation is which implies , with no solution.In conclusion subcase (i.2) has no solution. Therefore, case (i) has no solution.
- (ii)
- In this case we restrict and , with following from (A1). The momentum condition reads . As in case (i) we have two subcases: (ii.1) and (ii.2) . In subcase (ii.1) the option leads to the momentum condition , leading to , so . However, the resonance condition reads , leading to , so , a contradiction.The only other option is . We have the following three instances:(ii.1.a) . Here, the momentum condition is which implies , with no solution (because ).(ii.1.b) . Here, the momentum condition is which implies , with only solution , leading to and thus . Thus, the resonance condition reads , with no solution.(ii.1.c) . Here, the momentum condition is which implies . The resonance condition reads , or . Squaring this gives , thus . Squaring again gives , with no real solution.In conclusion subcase (ii.1) has no solution. We now study subcase (ii.2) . In this subcase we must have for all . We have the following three instances:(ii.2.a) . Here, the momentum equation is , which implies , with no solution.(ii.2.b) . Here, the momentum equation is , which implies , so . As , we can check that is not possible as it implies , a contradiction. We can check that the two remaining choices or imply . So we conclude and thus . Thus, the resonance condition reads , with no solution.(ii.2.c) . Here, the momentum equation is , which implies . As , we can check that implies and , so the resonance condition reads , with no solution. The two remaining choices or imply and . Thus, the resonance condition reads , with no solution.In conclusion subcase (ii.2) has no solution. Therefore, case (ii) has no solution.
- (iii)
- This case has zero interaction coefficients so it will not be considered.
- (iv)
- This case has zero interaction coefficients so it will not be considered.
- (v)
- In this case we restrict and , with and following from (A1). Instead of considering explicitly all 27 possible instances we will use the results from [5] regarding inequalities amongst frequencies. These translate directly to inequalities amongst wavevectors, which in our notation can be summarised as:As we assume without loss of generality , it follows that and because is the smallest wavenumber. Thus, there are two subcases: (v.1) , and (v.2) .In subcase (v.1) , inequalities (A2) imply and , with the now strict inequality . There are three options:(v.1.a) . Here the momentum condition reads , which simplifies to , a contradiction.(v.1.b) . Here the momentum condition reads , which simplifies to , a contradiction.(v.1.c) . Here the momentum condition reads , which is identically satisfied (because ). We turn to the resonance condition to find , or . Squaring this gives , or . Squaring again gives . Thus and . In summary this leads to a 5-wave resonance parameterised by as follows:In subcase (v.2) , inequalities (A2) imply with the now strict inequality , while . There are thus two options:(v.2.a) . Here the momentum condition reads , which simplifies to , a contradiction.(v.2.b) . Here the momentum condition reads , which simplifies to , thus . We turn to the resonance condition to find , which is satisfied. In summary this leads to a 5-wave resonance parameterised by as follows:
Appendix B. Probe Calibration and Wavemaker Tests


References
- Hammack, J.L.; Henderson, D.M. Resonant Interactions Among Surface-Water Waves. Annu. Rev. Fluid Mech. 1993, 25, 55–97. [Google Scholar]
- Nazarenko, S.; Lukaschuk, S. Wave Turbulence on Water Surface. Annu. Rev. Condens. Matter Phys. 2016, 7, 61–88. [Google Scholar]
- Dyachenko, A.; Zakharov, V.E. Is free-surface hydrodynamics an integrable system? Phys. Lett. A 1994, 190, 144–148. [Google Scholar] [CrossRef]
- Dyachenko, A.; Lvov, Y.; Zakharov, V.E. Five-wave interaction on the surface of deep fluid. Physica D 1995, 87, 233–261. [Google Scholar] [CrossRef]
- Lvov, Y. Effective five-wave Hamiltonian for surface water waves. Phys. Lett. A 1997, 230, 38–44. [Google Scholar] [CrossRef]
- Krasitskii, V.P. On reduced equations in the Hamiltonian theory of weakly nonlinear surface waves. J. Fluid Mech. 1994, 272, 1–20. [Google Scholar]
- Caponi, E.A.; Yuen, H.C.; Saffman, P.G. Instability and confined chaos in a nonlinear dispersive wave system. Phys. Fluids 1982, 25, 2159–2166. [Google Scholar] [CrossRef]
- Holmes, P. Chaotic motions in a weakly nonlinear model for surface waves. J. Fluid Mech. 1986, 162, 365–388. [Google Scholar]
- Trillo, S.; Wabnitz, S. Modulational Polarization Instabilities and Disorder in Birefringent Optical Fibers. In Nonlinearity with Disorder; Springer: Berlin/Heidelberg, Germany, 1992; pp. 269–281. [Google Scholar]
- Kim, W.; West, B.J. Chaotic properties of internal wave triad interactions. Phys. Fluids (1994-Present) 1997, 9, 632–647. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity wave spectrum Part 2. Conservation theorems; wave-particle analogy; irrevesibility. J. Fluid Mech. 1963, 15, 273–281. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum. Part 3. Evaluation of the energy flux and swell-sea interaction for a Neumann spectrum. J. Fluid Mech. 1963, 15, 385–398. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Filonenko, N.N. Weak turbulence of capillary waves. J. Appl. Mech. Tech. Phys. 1967, 8, 37–40. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Newell, A.C.; Rumpf, B. Wave turbulence. Annu. Rev. Fluid Mech. 2011, 43, 59–78. [Google Scholar] [CrossRef]
- Janssen, P.A. Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 2003, 33, 863–884. [Google Scholar] [CrossRef]
- Annenkov, S.Y.; Shrira, V.I. Role of non-resonant interactions in the evolution of nonlinear random water wave fields. J. Fluid Mech. 2006, 561, 181–208. [Google Scholar] [CrossRef]
- Bustamante, M.D.; Quinn, B.; Lucas, D. Robust energy transfer mechanism via precession resonance in nonlinear turbulent wave systems. Phys. Rev. Lett. 2014, 113, 084502. [Google Scholar] [CrossRef]
- Raphaldini, B.; Teruya, A.S.; Raupp, C.F.; Bustamante, M.D. Nonlinear Rossby wave–wave and wave–mean flow theory for long-term solar cycle modulations. Astrophys. J. 2019, 887, 1. [Google Scholar] [CrossRef]
- Walsh, S.G.; Bustamante, M.D. On the convergence of the normal form transformation in discrete Rossby and drift wave turbulence. J. Fluid Mech. 2020, 884. [Google Scholar] [CrossRef]
- Perlin, M.; Henderson, D.; Hammack, J. Experiments on ripple instabilities. Part 2 Selective amplification of resonant triads. J. Fluid Mech. 1990, 219, 51–80. [Google Scholar] [CrossRef]
- Perlin, M.; Hammack, J. Experiments on ripple instabilities. Part 3. Resonant quartets of the Benjamin–Feir type. J. Fluid Mech. 1991, 229, 229–268. [Google Scholar] [CrossRef]
- Perlin, M.; Ting, C.L. Steep gravity–capillary waves within the internal resonance regime. Phys. Fluids A 1992, 4, 2466–2478. [Google Scholar] [CrossRef]
- Haudin, F.; Cazaubiel, A.; Deike, L.; Jamin, T.; Falcon, E.; Berhanu, M. Experimental study of three-wave interactions among capillary-gravity surface waves. Phys. Rev. E 2016, 93, 043110-12. [Google Scholar] [CrossRef]
- Aubourg, Q.; Mordant, N. Nonlocal Resonances in Weak Turbulence of Gravity-Capillary Waves. Phys. Rev. Lett. 2015, 114, 144501. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, T.B.; Feir, J.E. The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Tulin, M.P.; Waseda, T. Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 1999, 378, 197–232. [Google Scholar] [CrossRef]
- Shemer, L.; Chamesse, M. Experiments on nonlinear gravity–capillary waves. J. Fluid Mech. 1999, 380, 205–232. [Google Scholar] [CrossRef][Green Version]
- Waseda, T.; Kinoshita, T.; Cavaleri, L.; Toffoli, A. Third-order resonant wave interactions under the influence of background current fields. J. Fluid Mech. 2015, 784, 51–73. [Google Scholar] [CrossRef]
- Hammack, J.L.; Henderson, D.M.; Segur, H. Progressive waves with persistent two-dimensional surface patterns in deep water. J. Fluid Mech. 2005, 532, 1–52. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, D.; Li, J.; Peng, T.; Alsaedi, A.; Liao, S. On the existence of steady-state resonant waves in experiments. J. Fluid Mech. 2015, 763, 1–23. [Google Scholar] [CrossRef][Green Version]
- Bonnefoy, F.; Haudin, F.; Michel, G.; Semin, B.; Humbert, T.; Aumaître, S.; Berhanu, M.; Falcon, E. Observation of resonant interactions among surface gravity waves. J. Fluid Mech. 2016, 805, R3. [Google Scholar] [CrossRef]
- Bustamante, M.D.; Hutchinson, K.; Lvov, Y.V.; Onorato, M. Exact discrete resonances in the Fermi-Pasta-Ulam–Tsingou system. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 437–471. [Google Scholar] [CrossRef]
- Pistone, L.; Chibbaro, S.; Bustamante, M.D.; Lvov, Y.V.; Onorato, M. Universal route to thermalization in weakly-nonlinear one-dimensional chains. Math. Eng. 2019, 1, 672–698. [Google Scholar] [CrossRef]
- Choi, W. Nonlinear evolution equations for two-dimensional surface waves in a fluid of finite depth. J. Fluid Mech. 1995, 295, 381–394. [Google Scholar] [CrossRef]
- Choi, W.; Kent, C.P. A pseudo-spectral method for nonlinear wave hydrodynamics. In Proceedings of the 25th ONR Symposium, St. John’s, NL, Canada, 8–13 August 2004. [Google Scholar]
- Tian, Z.; Perlin, M.; Choi, W. Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J. Fluid Mech. 2010, 655, 217–257. [Google Scholar] [CrossRef]
- Tian, Z.; Perlin, M.; Choi, W. Evaluation of a deep-water wave breaking criterion. Phys. Fluids 2008, 20, 066604. [Google Scholar] [CrossRef]
- Choi, W. Fifth-order nonlinear spectral model for surface gravity waves: From pseudo-spectral to spectral formulations (Workshop on Nonlinear Water Waves). RIMS Kokyuroku 2019, 2109, 47–60. [Google Scholar]
- Craig, W.; Sulem, C. Numerical simulation of gravity waves. J. Comput. Phys. 1993, 108, 73–83. [Google Scholar] [CrossRef]
- Craig, W.; Worfolk, P.A. An integrable normal form for water waves in infinite depth. Physica D 1995, 84, 513–531. [Google Scholar] [CrossRef]
- Verheest, F. Proof of integrability for five-wave interactions in a case with unequal coupling constants. J. Phys. Math. Gen. 1988, 21, L545–L549. [Google Scholar] [CrossRef]
- Yoshida, H. Necessary condition for the existence of algebraic first integrals. Celest. Mech. 1983, 31, 363–379. [Google Scholar] [CrossRef]
- Goriely, A. Integrability and Nonintegrability of Dynamical Systems; World Scientific: Singapore, 2001; Volume 19. [Google Scholar]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng. Part III 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Boccaletti, S.; Pisarchik, A.N.; Del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]




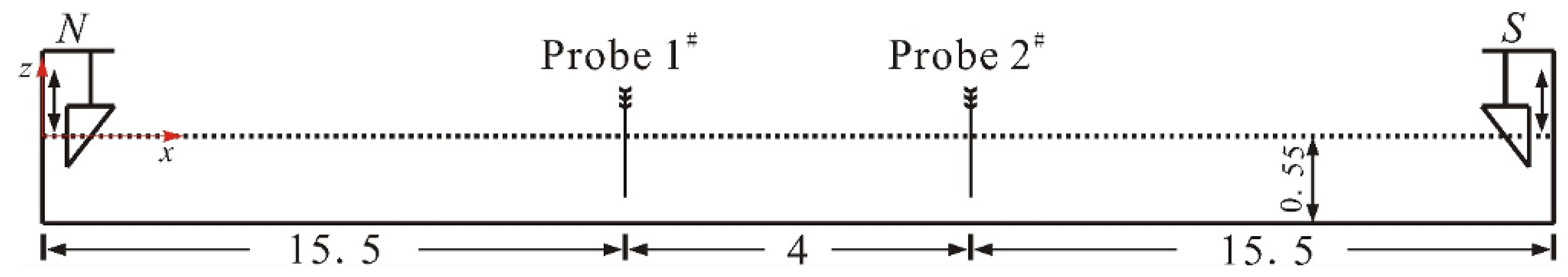
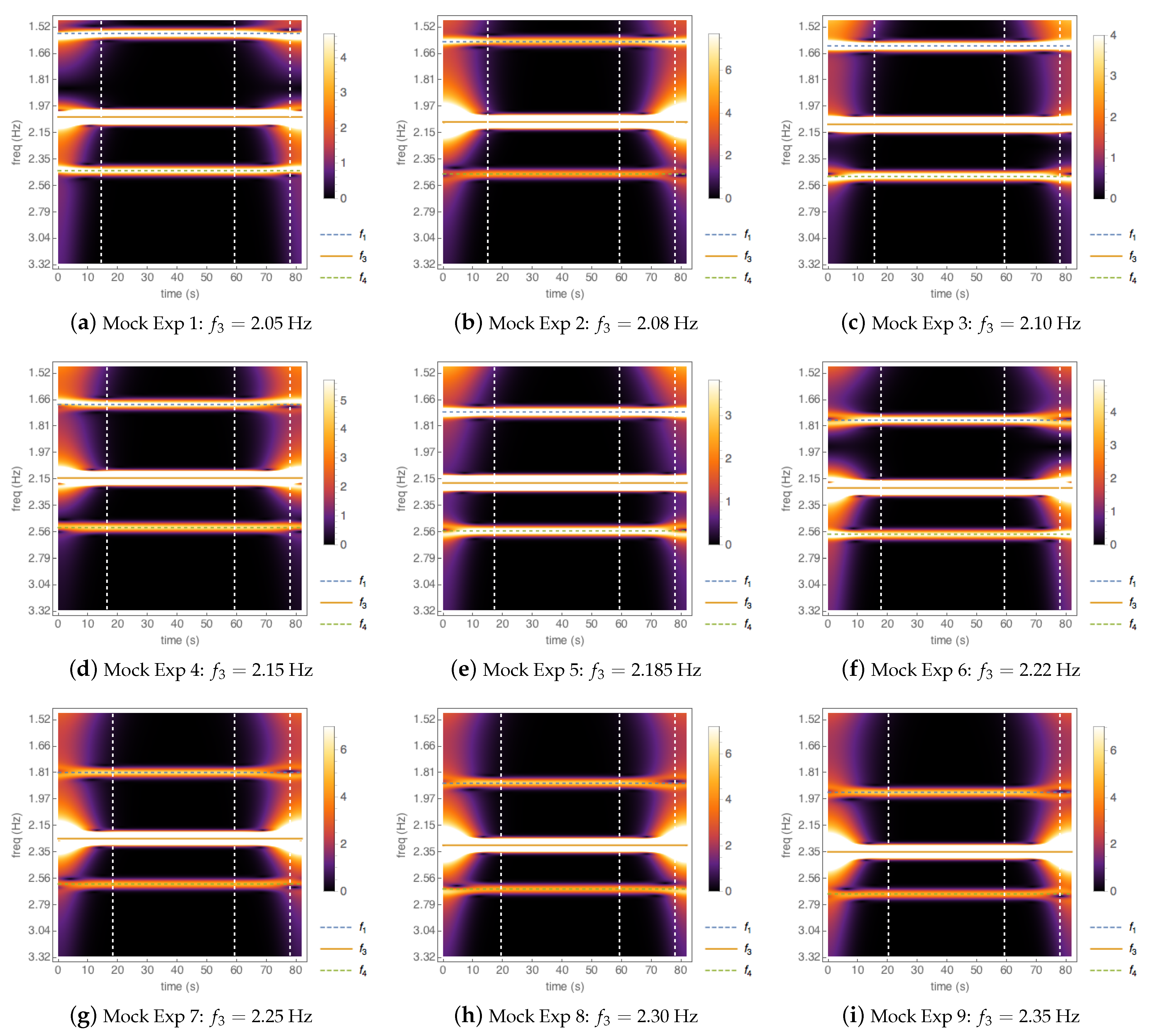

| Experiment | (Hz) | (cm) | Target (Hz) |
|---|---|---|---|
| Exp 1 | 2.05 | 0.71 | 1.56 |
| Exp 2 | 2.08 | 0.69 | 1.60 |
| Exp 3 | 2.10 | 0.68 | 1.62 |
| Exp 4 | 2.15 | 0.64 | 1.69 |
| Exp 5 | 2.185 | 0.62 | 1.73 |
| Exp 6 | 2.22 | 0.60 | 1.78 |
| Exp 7 | 2.25 | 0.59 | 1.81 |
| Exp 8 | 2.30 | 0.56 | 1.88 |
| Exp 9 | 2.35 | 0.54 | 1.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucas, D.; Perlin, M.; Liu, D.-Y.; Walsh, S.; Ivanov, R.; Bustamante, M.D. Five-Wave Resonances in Deep Water Gravity Waves: Integrability, Numerical Simulations and Experiments. Fluids 2021, 6, 205. https://doi.org/10.3390/fluids6060205
Lucas D, Perlin M, Liu D-Y, Walsh S, Ivanov R, Bustamante MD. Five-Wave Resonances in Deep Water Gravity Waves: Integrability, Numerical Simulations and Experiments. Fluids. 2021; 6(6):205. https://doi.org/10.3390/fluids6060205
Chicago/Turabian StyleLucas, Dan, Marc Perlin, Dian-Yong Liu, Shane Walsh, Rossen Ivanov, and Miguel D. Bustamante. 2021. "Five-Wave Resonances in Deep Water Gravity Waves: Integrability, Numerical Simulations and Experiments" Fluids 6, no. 6: 205. https://doi.org/10.3390/fluids6060205
APA StyleLucas, D., Perlin, M., Liu, D.-Y., Walsh, S., Ivanov, R., & Bustamante, M. D. (2021). Five-Wave Resonances in Deep Water Gravity Waves: Integrability, Numerical Simulations and Experiments. Fluids, 6(6), 205. https://doi.org/10.3390/fluids6060205






