Phase Evolution of the Time- and Space-Like Peregrine Breather in a Laboratory
Abstract
:1. Introduction
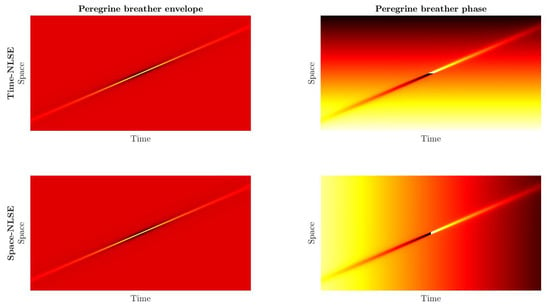
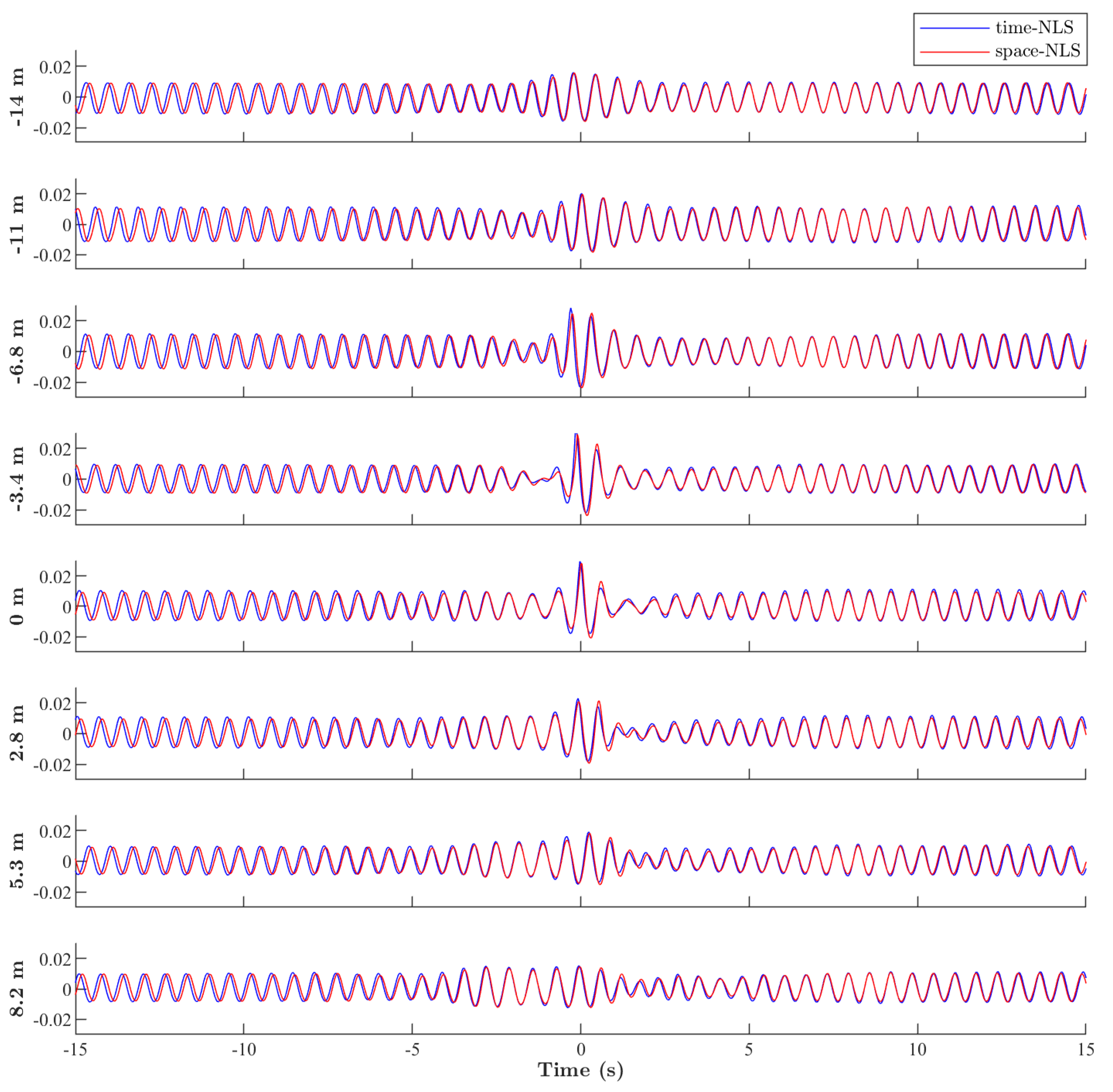
2. The Time- and Space-Like Peregrine Breather within the NLSE Framework
3. Experimental Investigation
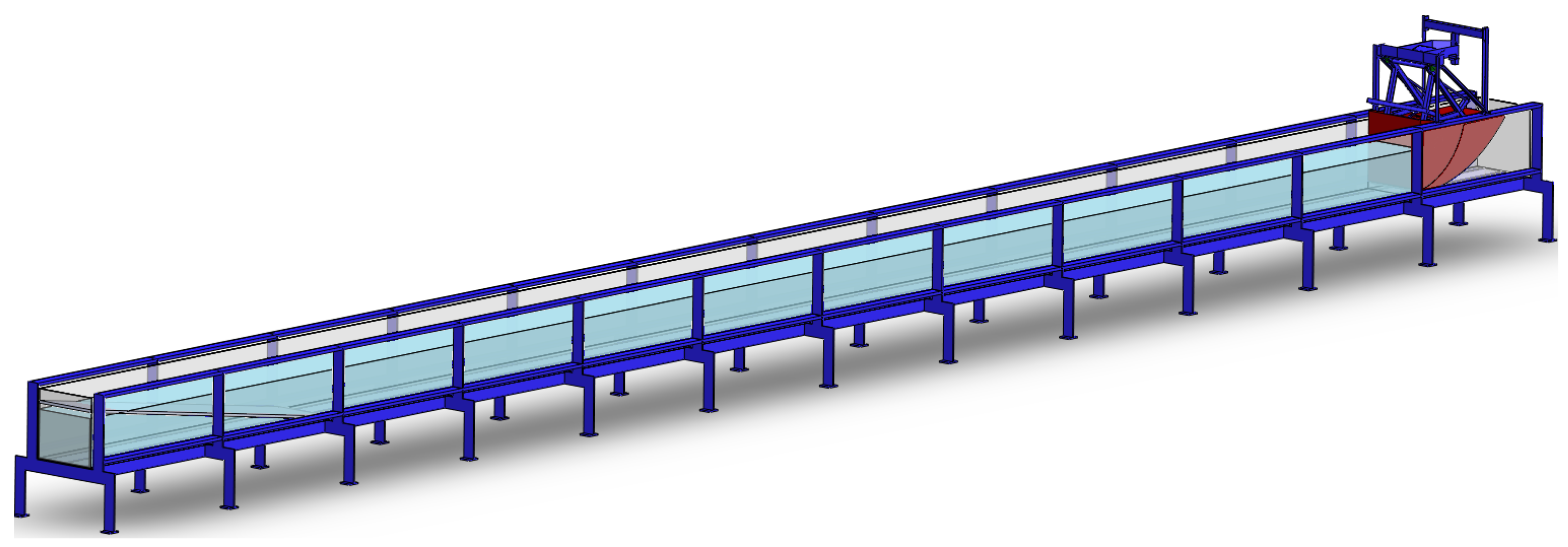
3.1. Experimental Setup
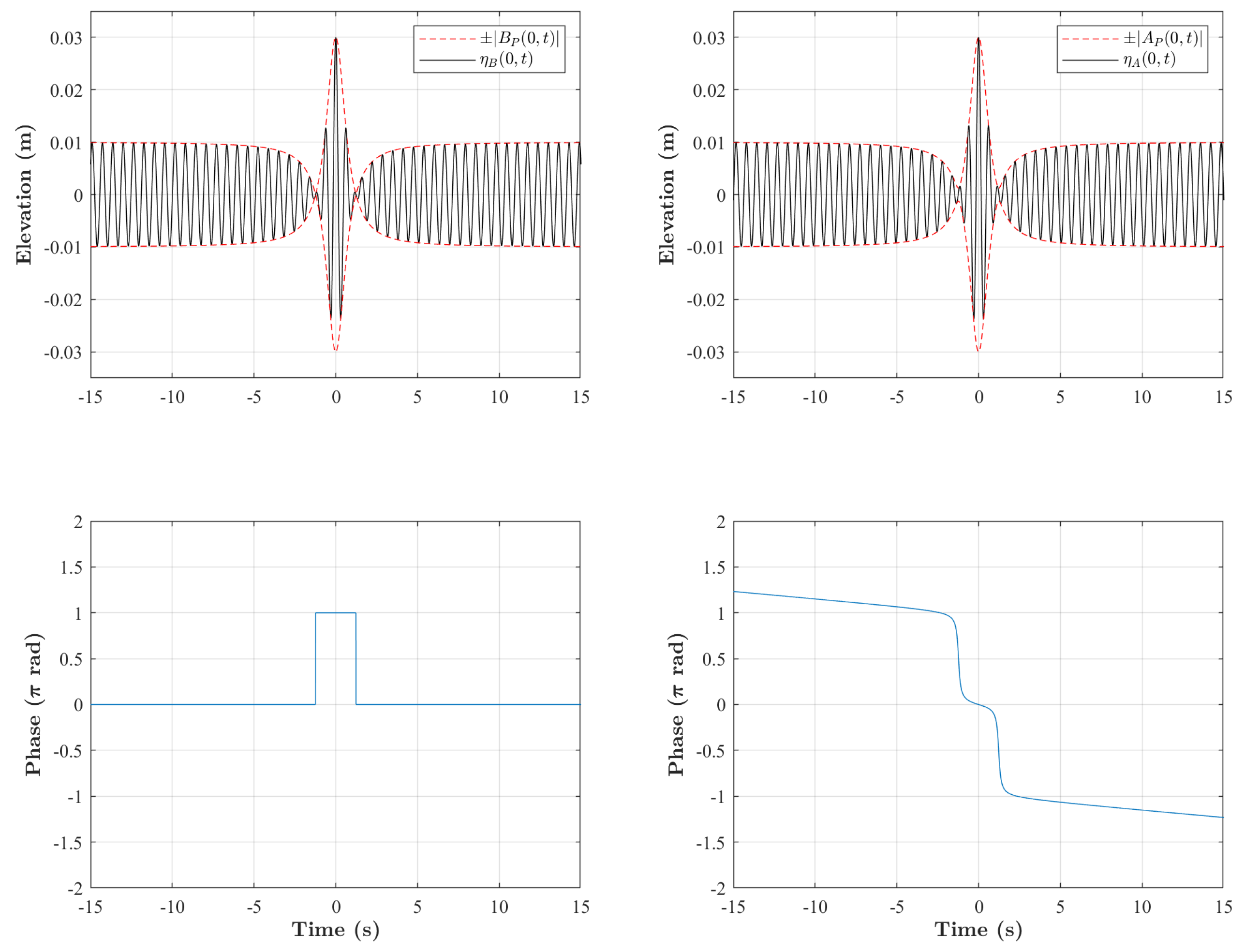
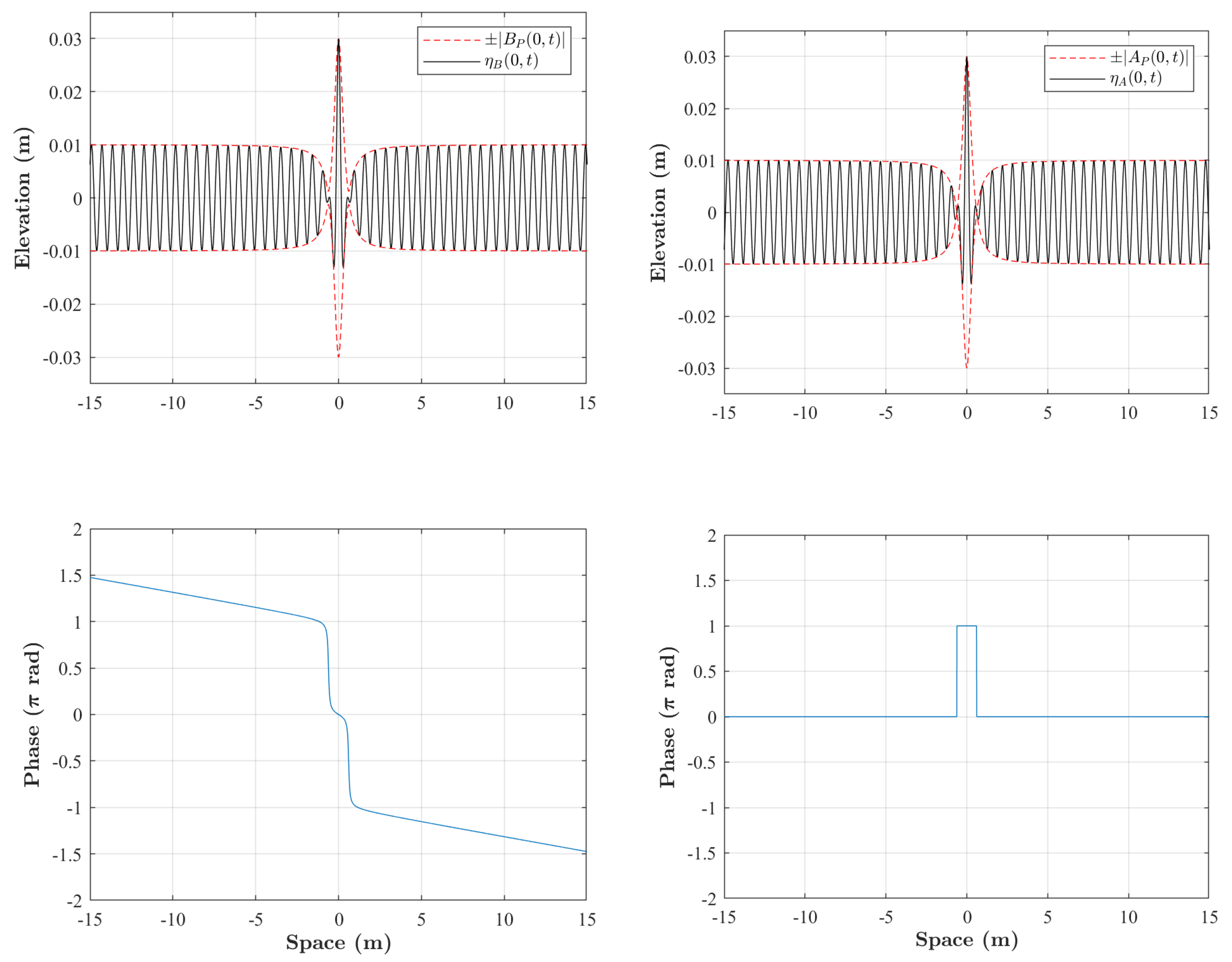
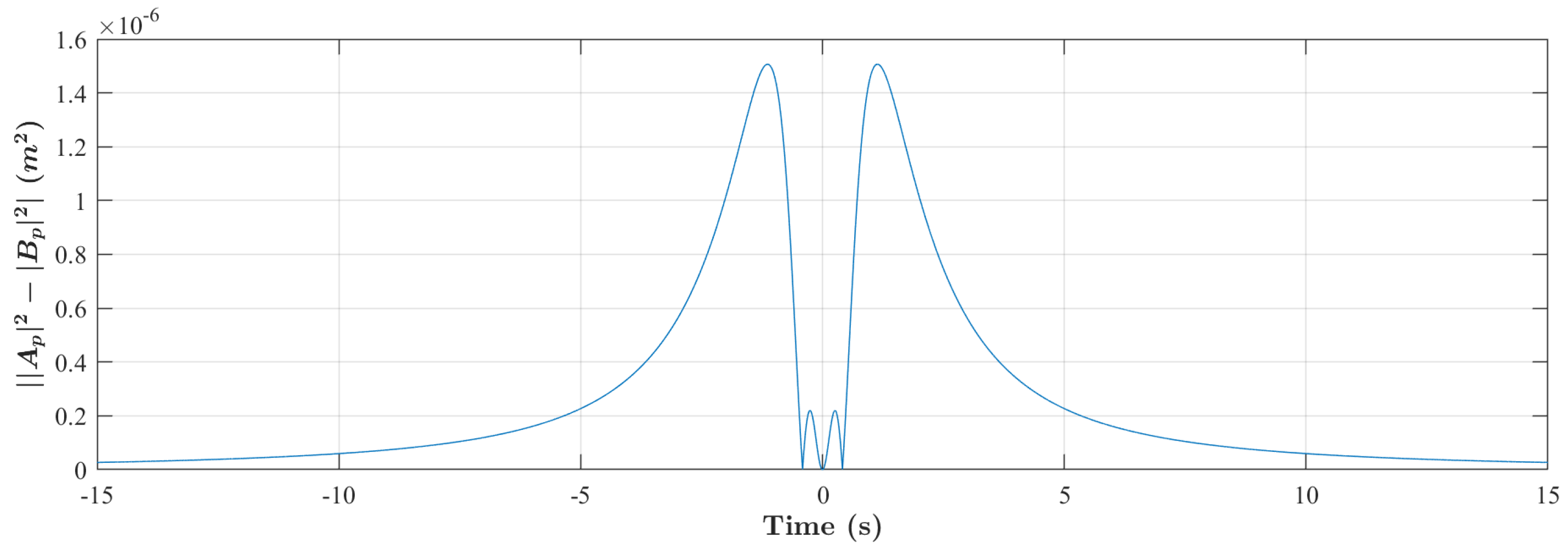
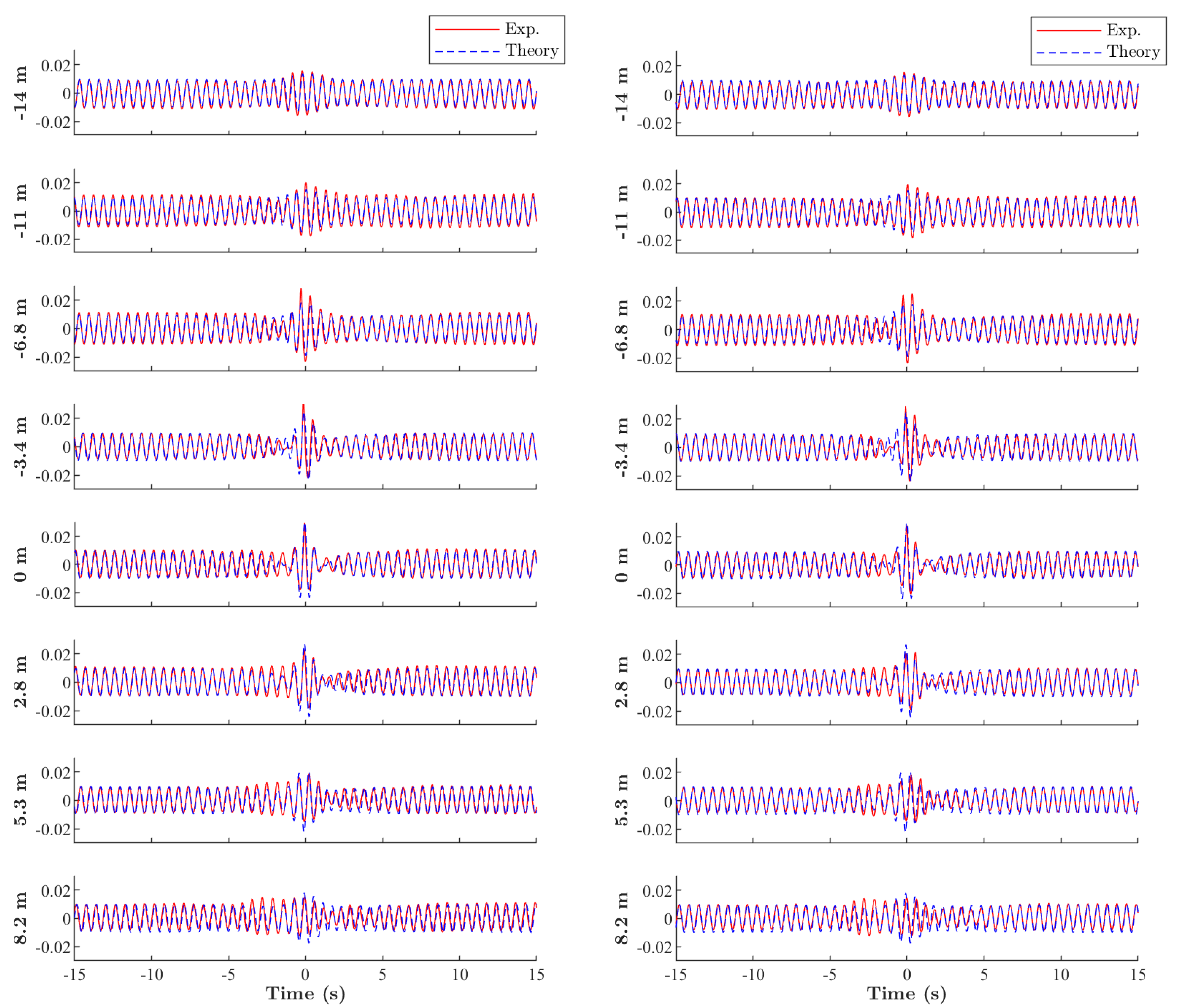
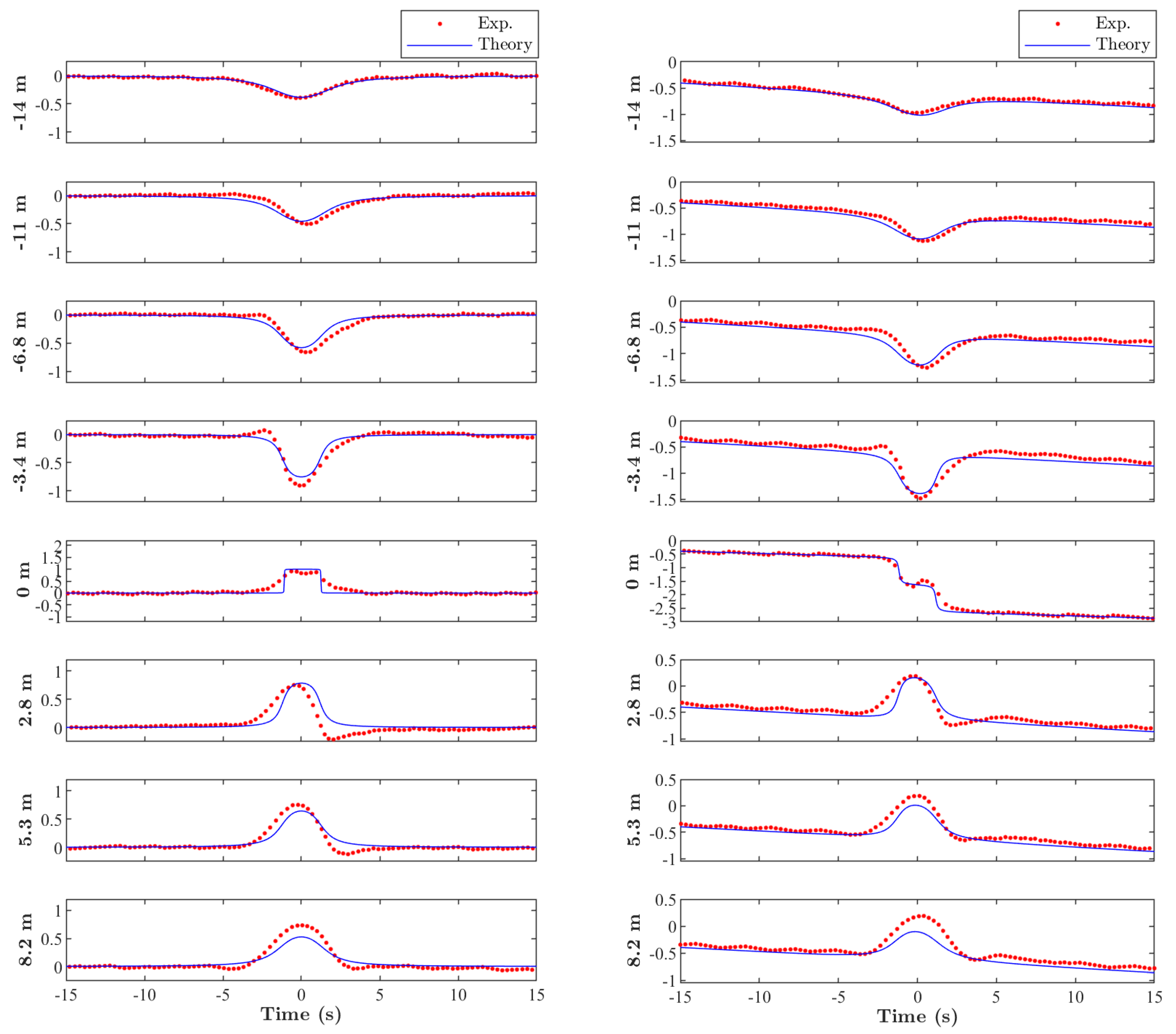
3.2. Evolution of the Time- and Space-Like Peregrine Breather in a Water Wave Flume
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Osborne, A. Nonlinear Ocean Waves and the Inverse Scattering Transform; Academic Press: New York, NY, USA, 2010; Volume 97. [Google Scholar]
- Agrawal, G. Nonlinear Fiber Optics; Optics and Photonics; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Walczak, P.; Randoux, S.; Suret, P. Optical Rogue Waves in Integrable Turbulence. Phys. Rev. Lett. 2015, 114, 143903. [Google Scholar] [CrossRef] [PubMed]
- Suret, P.; El Koussaifi, R.; Tikan, A.; Evain, C.; Randoux, S.; Szwaj, C.; Bielawski, S. Single-shot observation of optical rogue waves in integrable turbulence using time microscopy. Nat. Commun. 2016, 7, 13136. [Google Scholar] [CrossRef] [Green Version]
- Tikan, A.; Billet, C.; El, G.; Tovbis, A.; Bertola, M.; Sylvestre, T.; Gustave, F.; Randoux, S.; Genty, G.; Suret, P.; et al. Universality of the Peregrine soliton in the focusing dynamics of the cubic nonlinear Schrödinger equation. Phys. Rev. Lett. 2017, 119, 033901. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Balachandran, B. Extreme wave formation in unidirectional sea due to stochastic wave phase dynamics. Phys. Lett. A 2018, 382, 1864–1872. [Google Scholar] [CrossRef]
- Tikan, A.; Bielawski, S.; Szwaj, C.; Randoux, S.; Suret, P. Single-shot measurement of phase and amplitude by using a heterodyne time-lens system and ultrafast digital time-holography. Nat. Photonics 2018, 12, 228–234. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Mussot, A.; Chabchoub, A.; Dias, F. Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 2019, 1, 675–689. [Google Scholar] [CrossRef]
- Tikan, A. Effect of local Peregrine soliton emergence on statistics of random waves in the one-dimensional focusing nonlinear Schrödinger equation. Phys. Rev. E 2020, 101, 012209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasimoto, H.; Ono, H. Nonlinear modulation of gravity waves. J. Phys. Soc. Jpn. 1972, 33, 805–811. [Google Scholar] [CrossRef]
- Mei, C.C.; Stiassnie, M.; Yue, D.K.P. Theory and Applications of Ocean Surface Waves: Nonlinear Aspects; World Scientific: Singapore, 2005; Volume 23. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011; Volume 47. [Google Scholar]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Le Touzé, D.; Ferrant, P. A modified high-order spectral method for wavemaker modeling in a numerical wave tank. Eur. J. Mech.-B/Fluids 2012, 34, 19–34. [Google Scholar] [CrossRef]
- Chabchoub, A.; Mozumi, K.; Hoffmann, N.; Babanin, A.V.; Toffoli, A.; Steer, J.N.; van den Bremer, T.S.; Akhmediev, N.; Onorato, M.; Waseda, T. Directional soliton and breather beams. Proc. Natl. Acad. Sci. USA 2019, 116, 9759–9763. [Google Scholar] [CrossRef] [Green Version]
- Slunyaev, A.; Pelinovsky, E.; Sergeeva, A.; Chabchoub, A.; Hoffmann, N.; Onorato, M.; Akhmediev, N. Super-rogue waves in simulations based on weakly nonlinear and fully nonlinear hydrodynamic equations. Phys. Rev. E 2013, 88, 012909. [Google Scholar] [CrossRef] [Green Version]
- Shemer, L.; Alperovich, L. Peregrine breather revisited. Phys. Fluids 2013, 25, 051701. [Google Scholar] [CrossRef] [Green Version]
- Chabchoub, A.; Grimshaw, R.H. The hydrodynamic nonlinear Schrödinger equation: Space and time. Fluids 2016, 1, 23. [Google Scholar] [CrossRef] [Green Version]
- Akhmediev, N.; Eleonskii, V.; Kulagin, N. Generation of periodic trains of picosecond pulses in an optical fiber: Exact solutions. Sov. Phys. JETP 1985, 62, 894–899. [Google Scholar]
- Houtani, H.; Waseda, T.; Tanizawa, K. Experimental and numerical investigations of temporally and spatially periodic modulated wave trains. Phys. Fluids 2018, 30, 034101. [Google Scholar] [CrossRef]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef] [Green Version]
- Kedziora, D.J.; Ankiewicz, A.; Akhmediev, N. The phase patterns of higher-order rogue waves. J. Opt. 2013, 15, 064011. [Google Scholar] [CrossRef]
- Xu, G.; Hammani, K.; Chabchoub, A.; Dudley, J.M.; Kibler, B.; Finot, C. Phase evolution of Peregrine-like breathers in optics and hydrodynamics. Phys. Rev. E 2019, 99, 012207. [Google Scholar] [CrossRef] [Green Version]
- Bailung, H.; Sharma, S.; Nakamura, Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 2011, 107, 255005. [Google Scholar] [CrossRef]
- Randoux, S.; Suret, P.; Chabchoub, A.; Kibler, B.; El, G. Nonlinear spectral analysis of Peregrine solitons observed in optics and in hydrodynamic experiments. Phys. Rev. E 2018, 98, 022219. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Ma, Q.; Yan, S.; Chabchoub, A. Persistence of Peregrine Breather in Random Sea States. Phys. Rev. Appl. 2018, 9, 014016. [Google Scholar] [CrossRef]
- Michel, G.; Bonnefoy, F.; Ducrozet, G.; Prabhudesai, G.; Cazaubiel, A.; Copie, F.; Tikan, A.; Suret, P.; Randoux, S.; Falcon, E. Emergence of Peregrine solitons in integrable turbulence of deep water gravity waves. Phys. Rev. Fluids 2020, 5, 082801. [Google Scholar] [CrossRef]
- Shabat, A.; Zakharov, V. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62. [Google Scholar]
- Akhmediev, N.N.; Ankiewicz, A. Solitons: Nonlinear Pulses and Beams; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Shrira, V.I.; Geogjaev, V.V. What makes the Peregrine soliton so special as a prototype of freak waves? J. Eng. Math. 2010, 67, 11–22. [Google Scholar] [CrossRef]
- Chabchoub, A.; Akhmediev, N.; Hoffmann, N. Experimental study of spatiotemporally localized surface gravity water waves. Phys. Rev. E 2012, 86, 016311. [Google Scholar] [CrossRef] [Green Version]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A Math. Phys. Sci. 1979, 369, 105–114. [Google Scholar]
- Trulsen, K.; Dysthe, K.B. A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 1996, 24, 281–289. [Google Scholar] [CrossRef]
- Waseda, T.; Fujimoto, W.; Chabchoub, A. On the Asymmetric Spectral Broadening of a Hydrodynamic Modulated Wave Train in the Optical Regime. Fluids 2019, 4, 84. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Suret, P.; Chabchoub, A. Phase Evolution of the Time- and Space-Like Peregrine Breather in a Laboratory. Fluids 2021, 6, 308. https://doi.org/10.3390/fluids6090308
He Y, Suret P, Chabchoub A. Phase Evolution of the Time- and Space-Like Peregrine Breather in a Laboratory. Fluids. 2021; 6(9):308. https://doi.org/10.3390/fluids6090308
Chicago/Turabian StyleHe, Yuchen, Pierre Suret, and Amin Chabchoub. 2021. "Phase Evolution of the Time- and Space-Like Peregrine Breather in a Laboratory" Fluids 6, no. 9: 308. https://doi.org/10.3390/fluids6090308
APA StyleHe, Y., Suret, P., & Chabchoub, A. (2021). Phase Evolution of the Time- and Space-Like Peregrine Breather in a Laboratory. Fluids, 6(9), 308. https://doi.org/10.3390/fluids6090308