Investigation of a Light Boxplane Model Using Tuft Flow Visualization and CFD
Abstract
:1. Introduction
2. Materials and Methods
2.1. Wind Tunnel Experiment
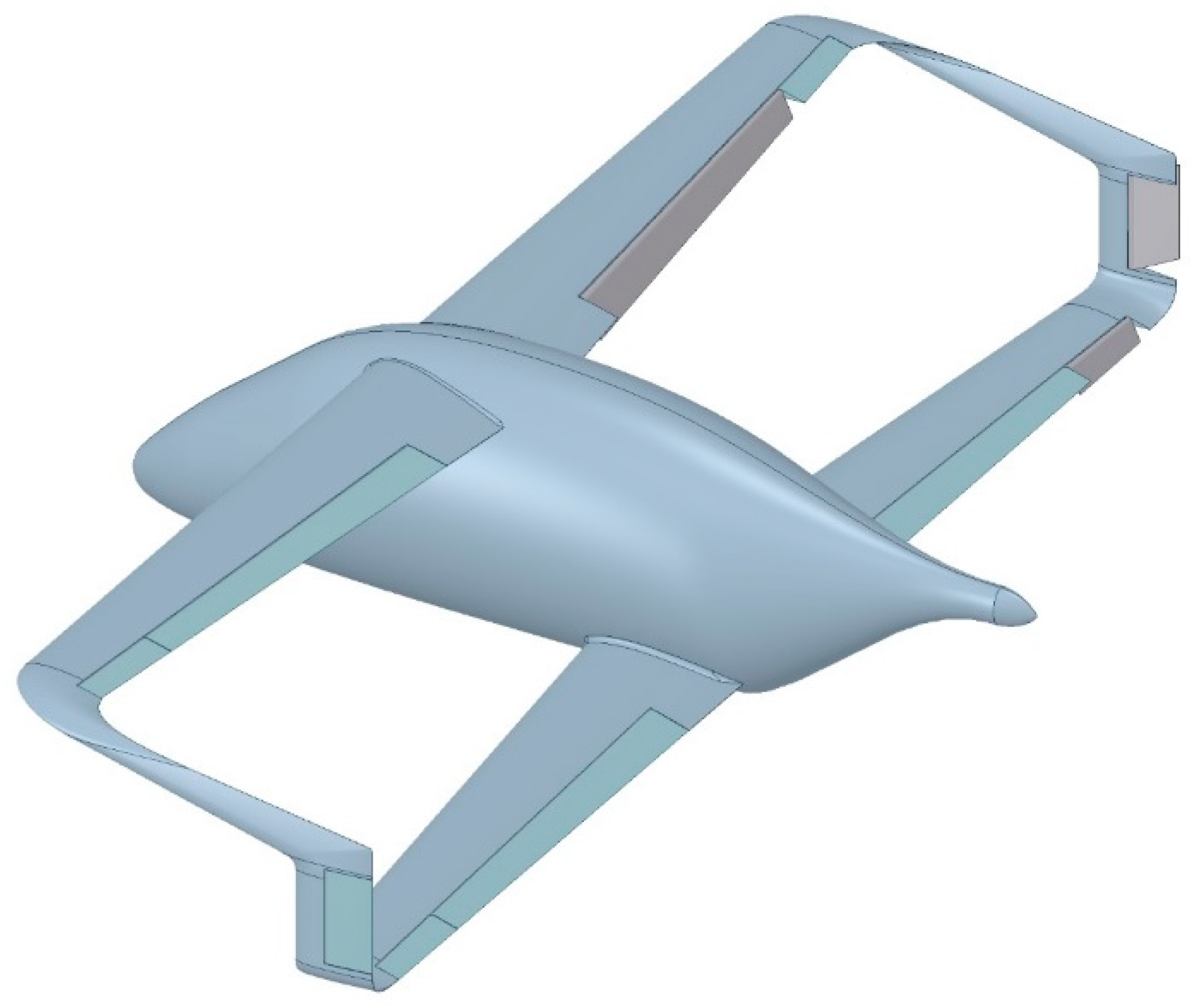
2.1.1. Geometry
- ‑
- Dimensions (fuselage length x wingspan x fuselage height): 0.709 × 1.1 × 0.207 m;
- ‑
- Wing aspect ratio: 12 (both wings);
- ‑
- Fuselage aspect ratio: 3.42;
- ‑
- Wing sweep angle at ¼ chord: 1.6° (fore wing), 3.2° (aft wing);
- ‑
- Airfoil: NACA 3413 (fore wing), NACA 4415 (aft wing);
- ‑
- Airfoil relative thickness: 15% (both wings);
- ‑
- Wing incidence angle: 2.5° (fore wing), 2° (aft wing);
- ‑
- Elevator-to-wing area ratio: 0.17 (both wings);
- ‑
- Flaperon-to-wing area ratio: 0.03 (both wings).
- α = 15° (aircraft stall angle in cruise configuration, non-linearity in dependence Cm = f(α));
- α = 10° (local stall, bend in Cnβ (α) and Cyβ (α), reduced elevator efficiency);
- Additionally, we set α = 0°, 5°, 20°, 25°.
- ‑
- Investigate why the model has a large value of Cm0;
- ‑
- Evaluate the fuselage contribution to lateral divergence of the aircraft;
- ‑
- Determine why the rear elevators generate lift twice as large as that of the front elevators;
- ‑
- Explore why the flaperons do not perform as expected.
2.1.2. Wind Tunnel Test Conditions
- Incipient detachment (ID) occurring with instantaneous backflow 1% of the time;
- Intermittent transitory detachment (ITD) occurring with instantaneous backflow 20% of the time;
- Transitory detachment (TD) occurring with instantaneous backflow 50% of the time;
- Detachment (D) occurring where the time-averaged wall shearing stress is zero.
- Unseparated flow;
- Separated flow;
- “Momentarily separated”;
- “Intermittently separated”.
2.2. CFD Model
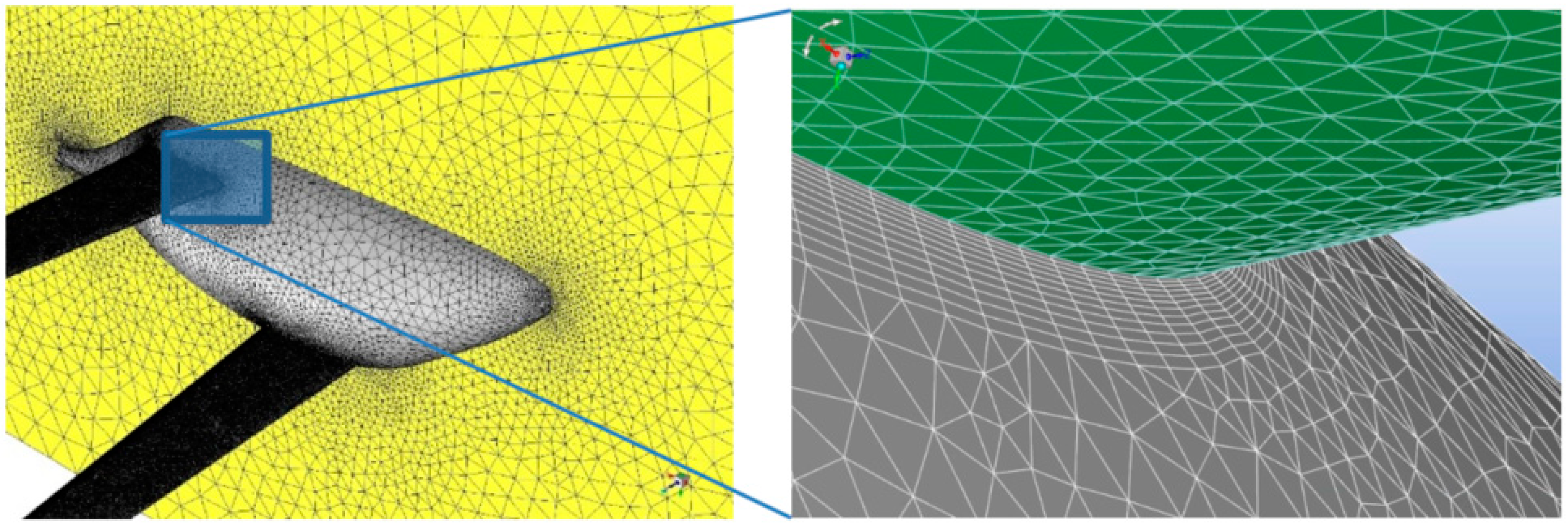
2.2.1. Meshing
2.2.2. Governing Equations and CFD Setup
Turbulence Modelling
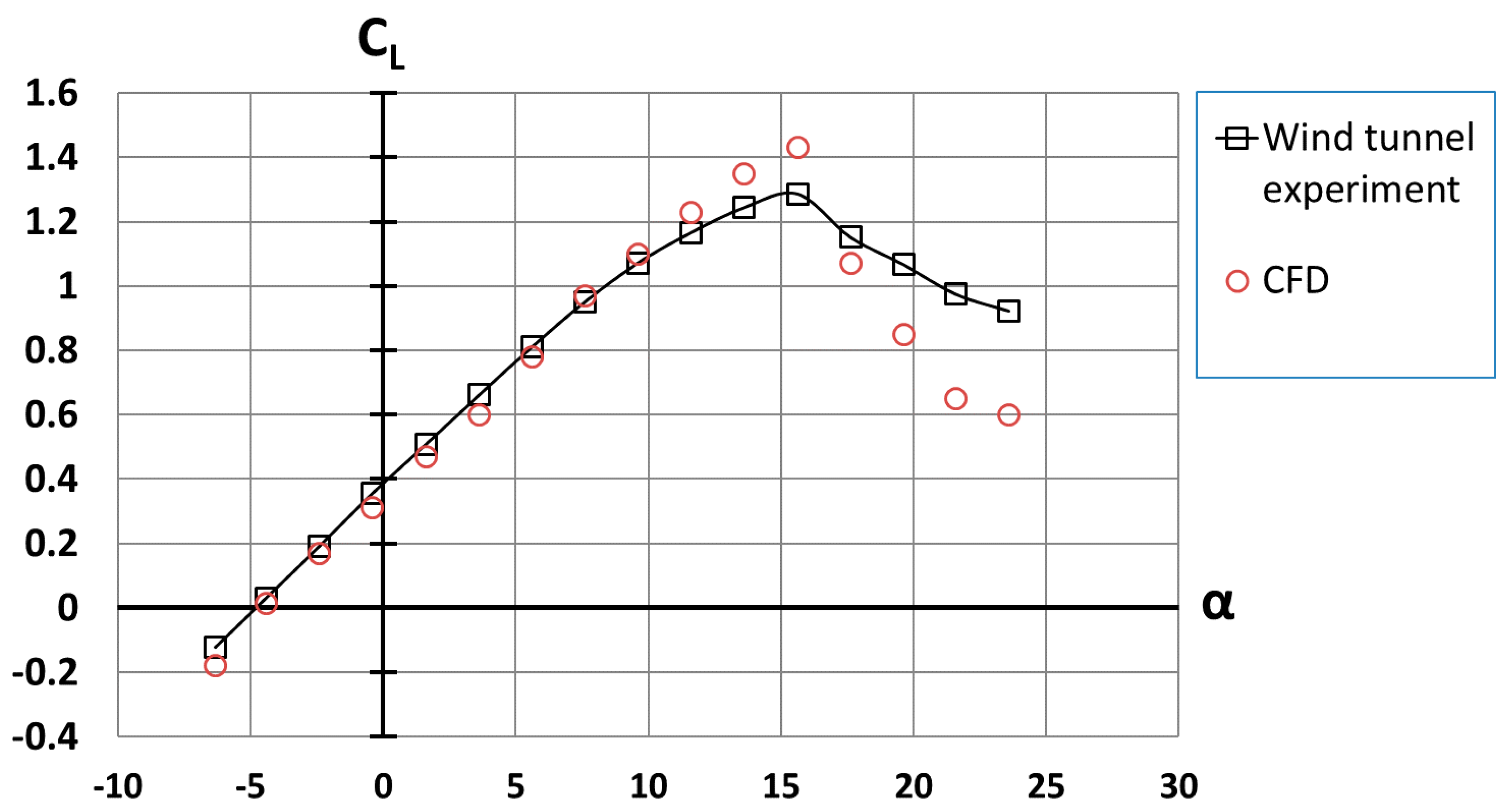
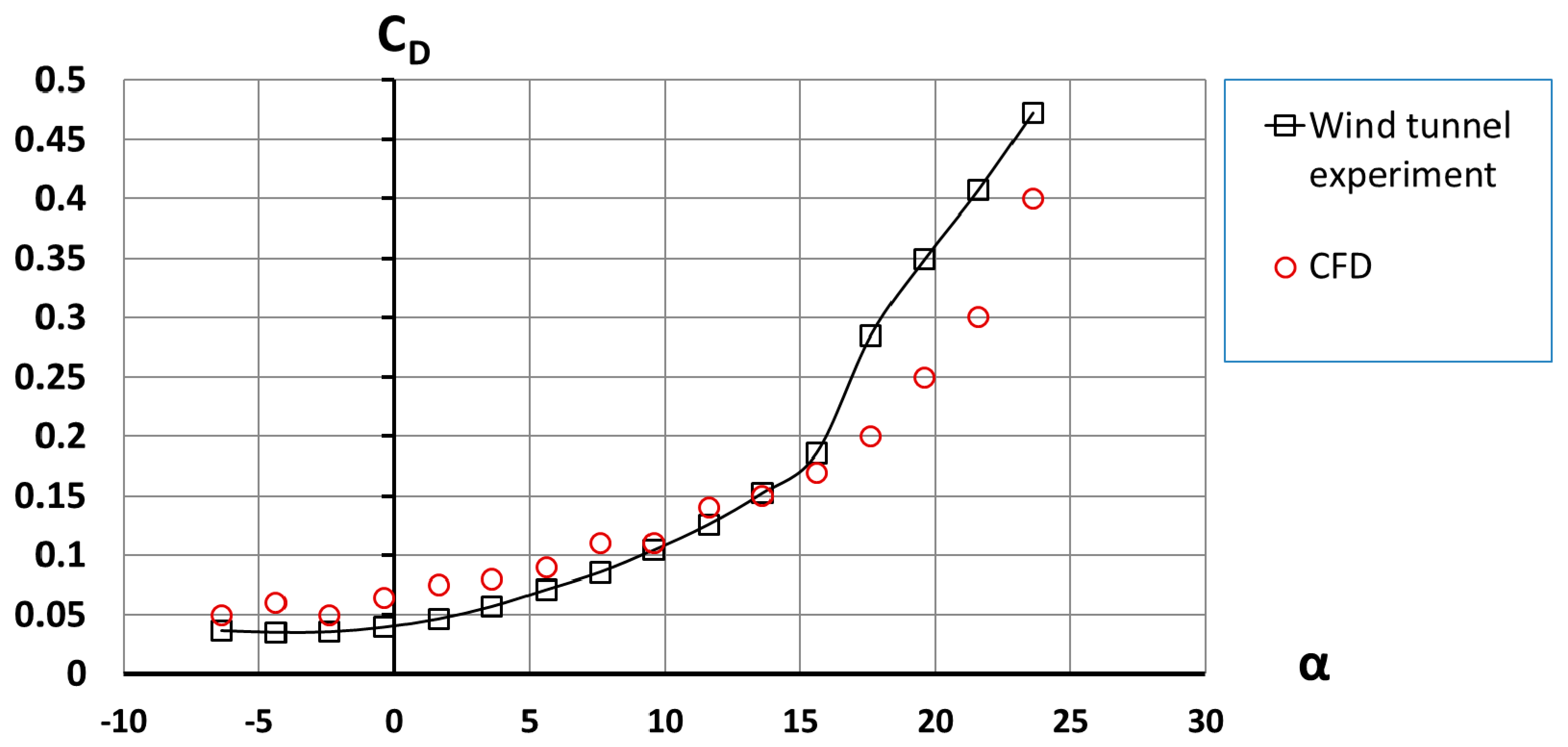
2.2.3. Validation of the CFD Model against Wind Tunnel Data
3. Results
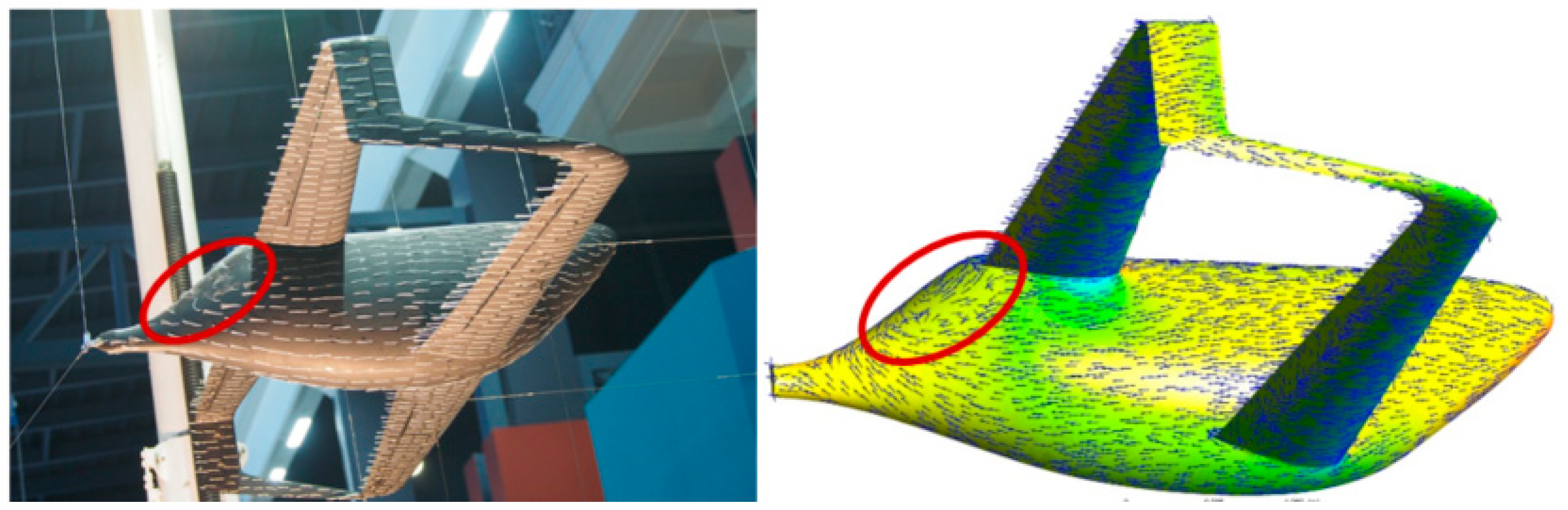
3.1. General Overview
- The possibility that tufts’ presence may change the flow nature. This effect is believed to be small enough.
- The flow pattern resolution dependency on the size of tufts. Relatively long tufts fail to show local separations, indicating a shallow reversed flow instead.
- The low reproducibility of tuft visualization due to the fact that geometry, bending stiffness, and spacing of the tufts are not identical.
- In some cases, the interpretation of tuft patterns is doubtful.
- Characteristic deflection behavior of the tufts changes over time as irreversible deformation of the tufts occurs after being exposed to air flow.
- Development of turbulent boundary layer and separated flow on the scale model (CFD and wind tunnel visualizations).
3.2. Large Value of Cm0
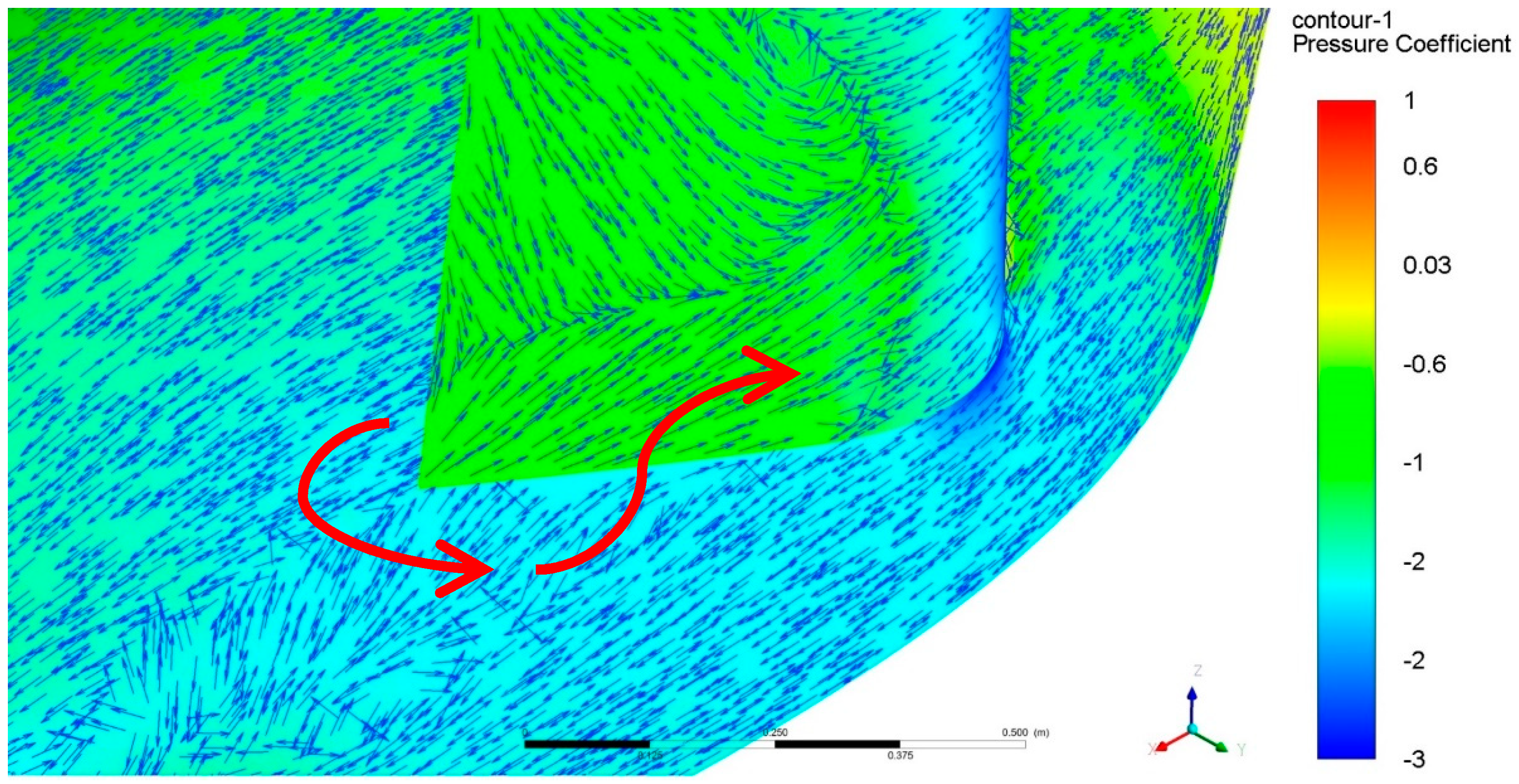
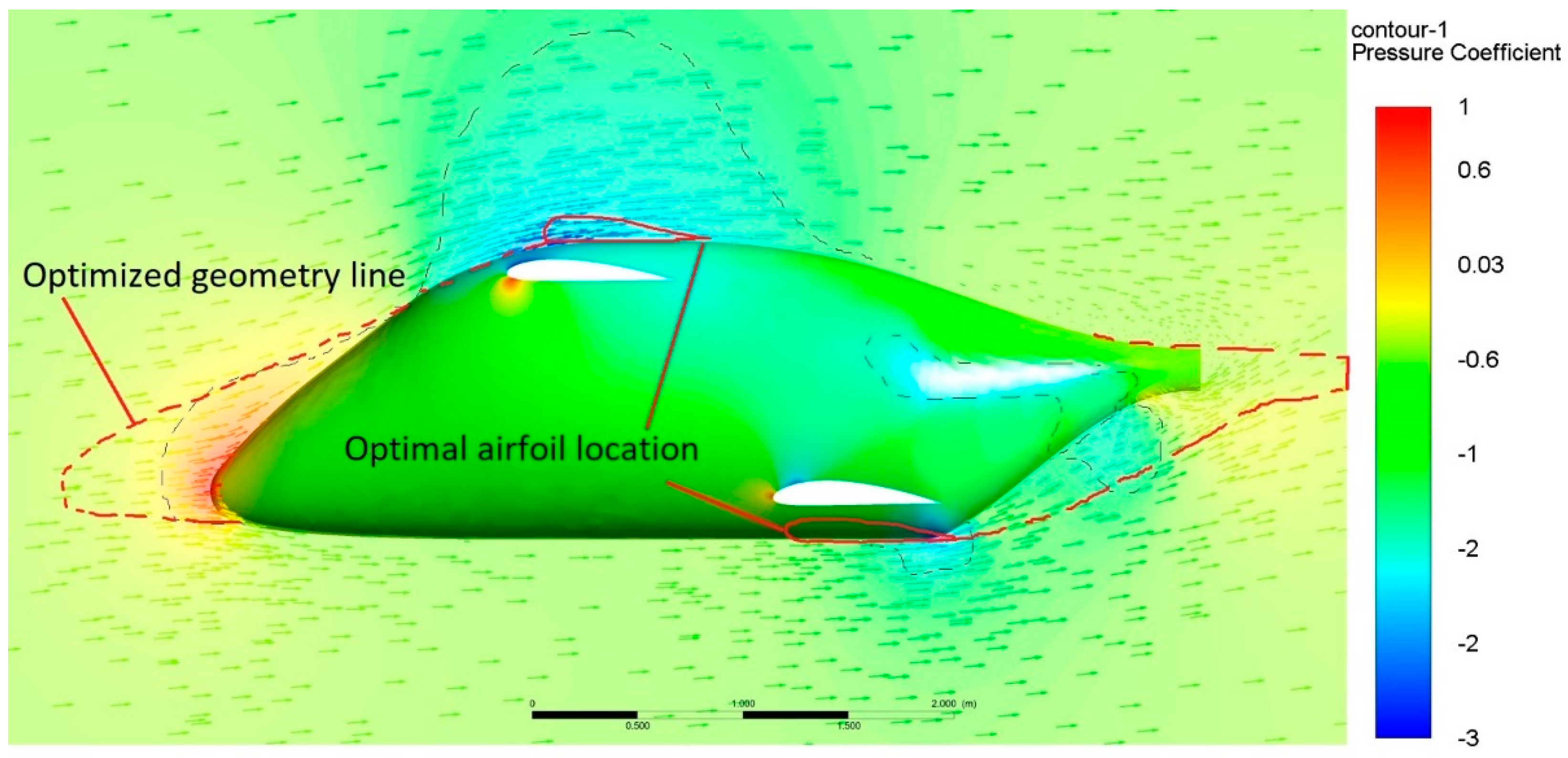
3.3. Fuselage Contribution to the Lateral Instability of the Aircraft
- Increased area of the fairing covering the aft wing–fuselage junction area (at the cost of increased wetted area and viscous drag).
- Giving the fuselage shape a flattened top line for a reduced flow acceleration on its front upper surface.
- Increased length of the fuselage (at the cost of a significantly increased wetted area, increased aircraft weight, and reduced performance).
- Increased sidewing area.
- Increased sidewing arm through aft and fore wing planform modifications.
- Additional small stabilizers mounted on the aft fuselage.
- Wing vertical arrangement modification with low front wings and high aft wings mounted on a vertical stabilizer (as proposed in several large boxwing transport aircraft concepts).
- Distributed electric propulsion system with a differential thrust control of the propellers.
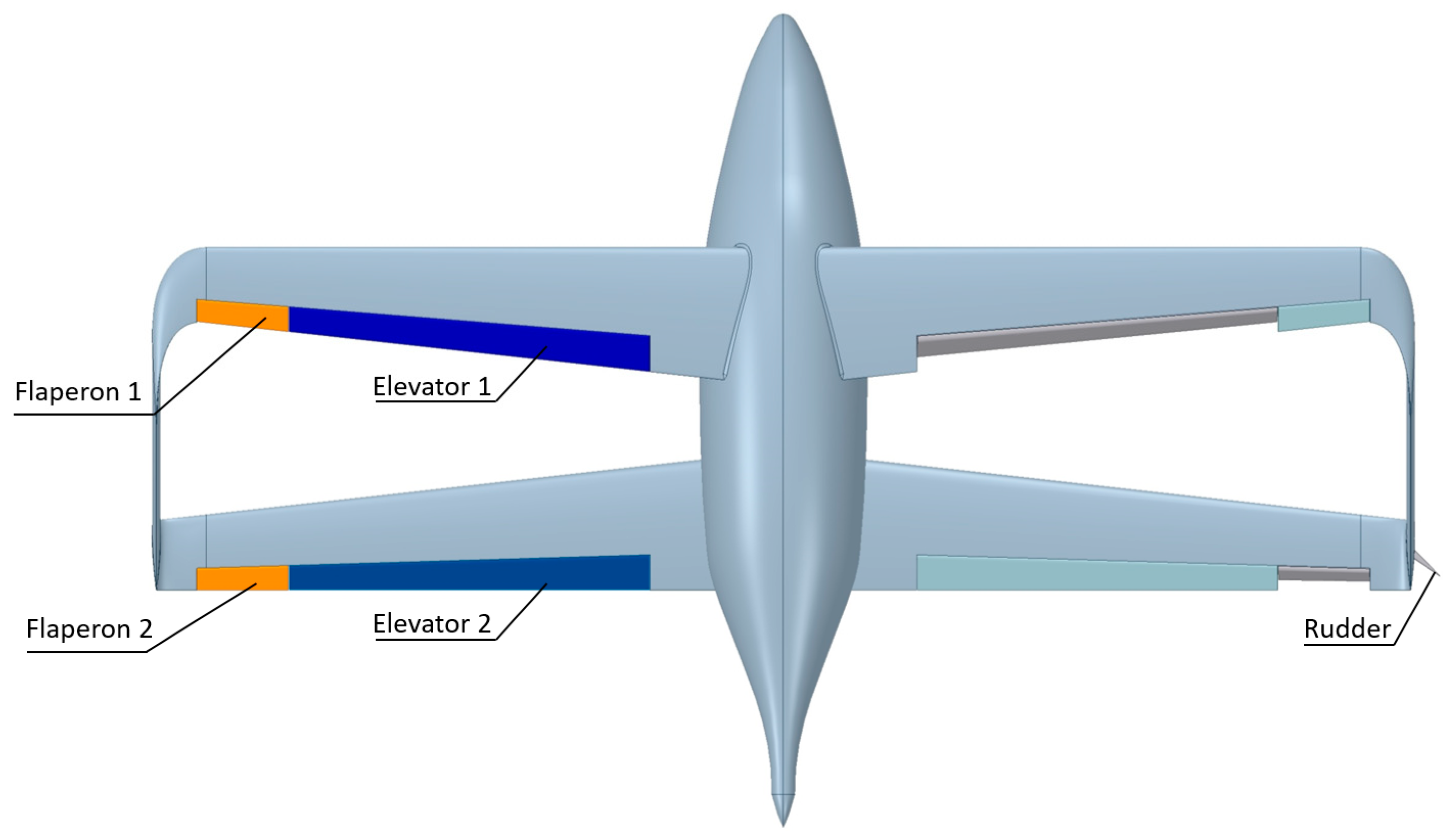
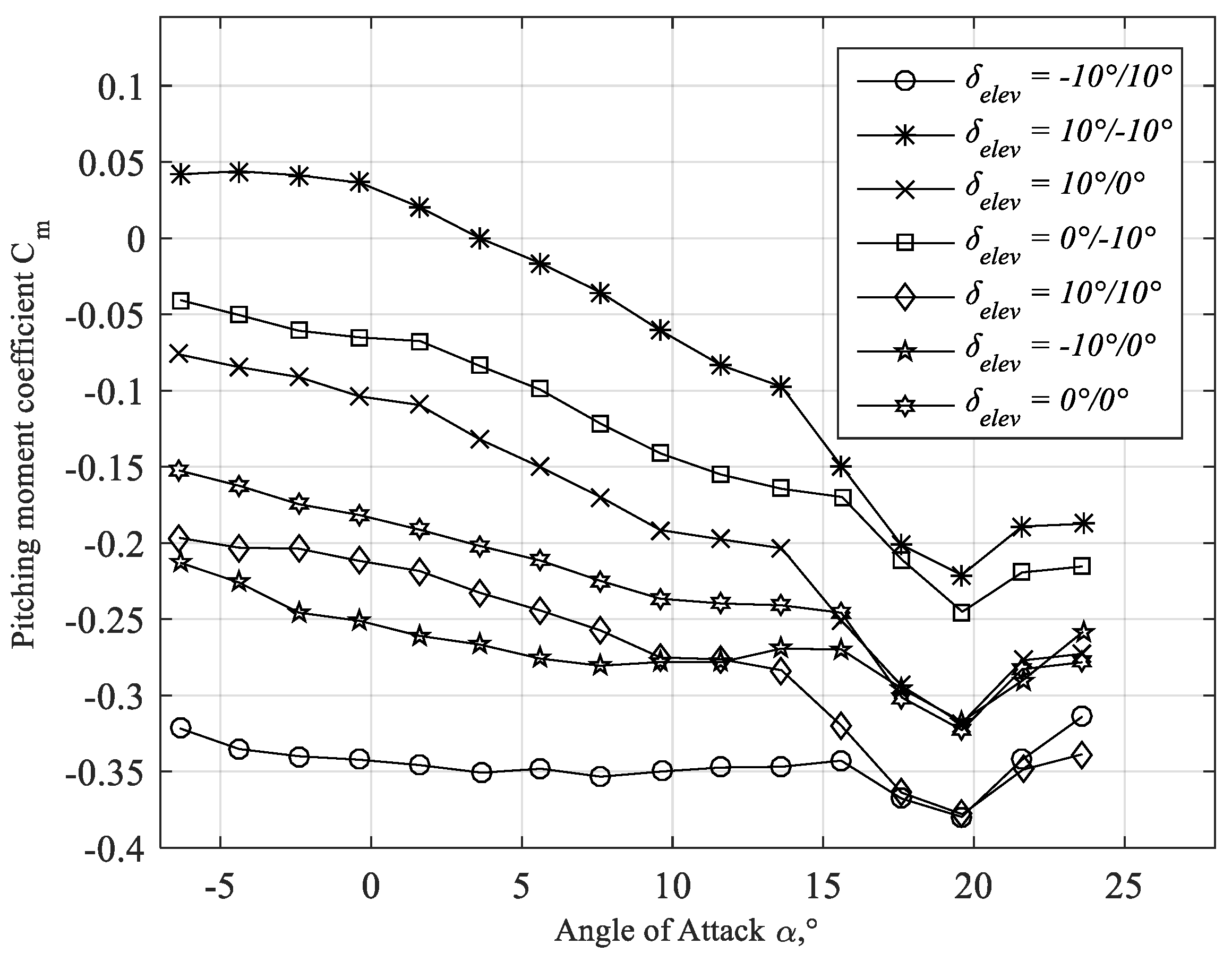
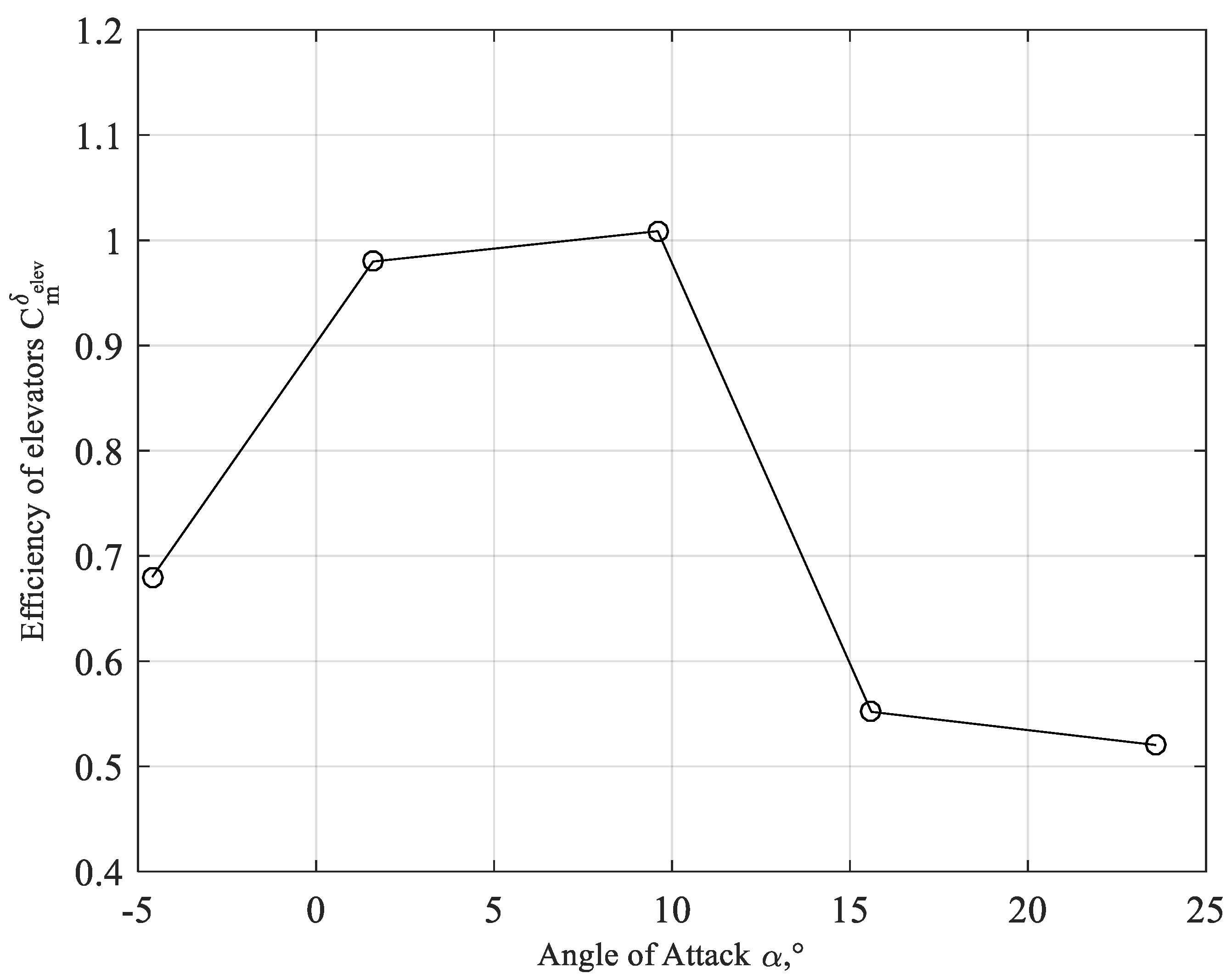
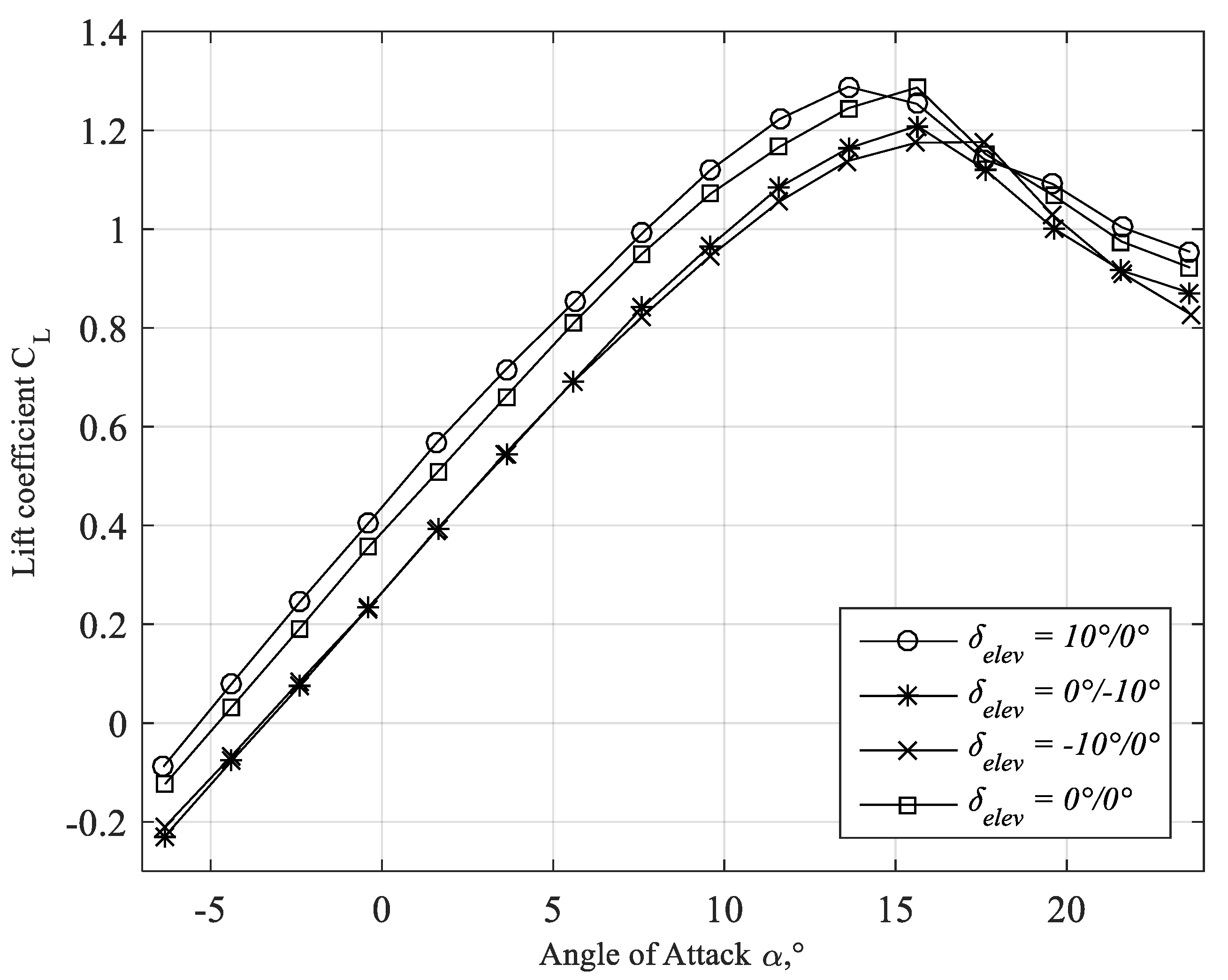
3.4. Elevators
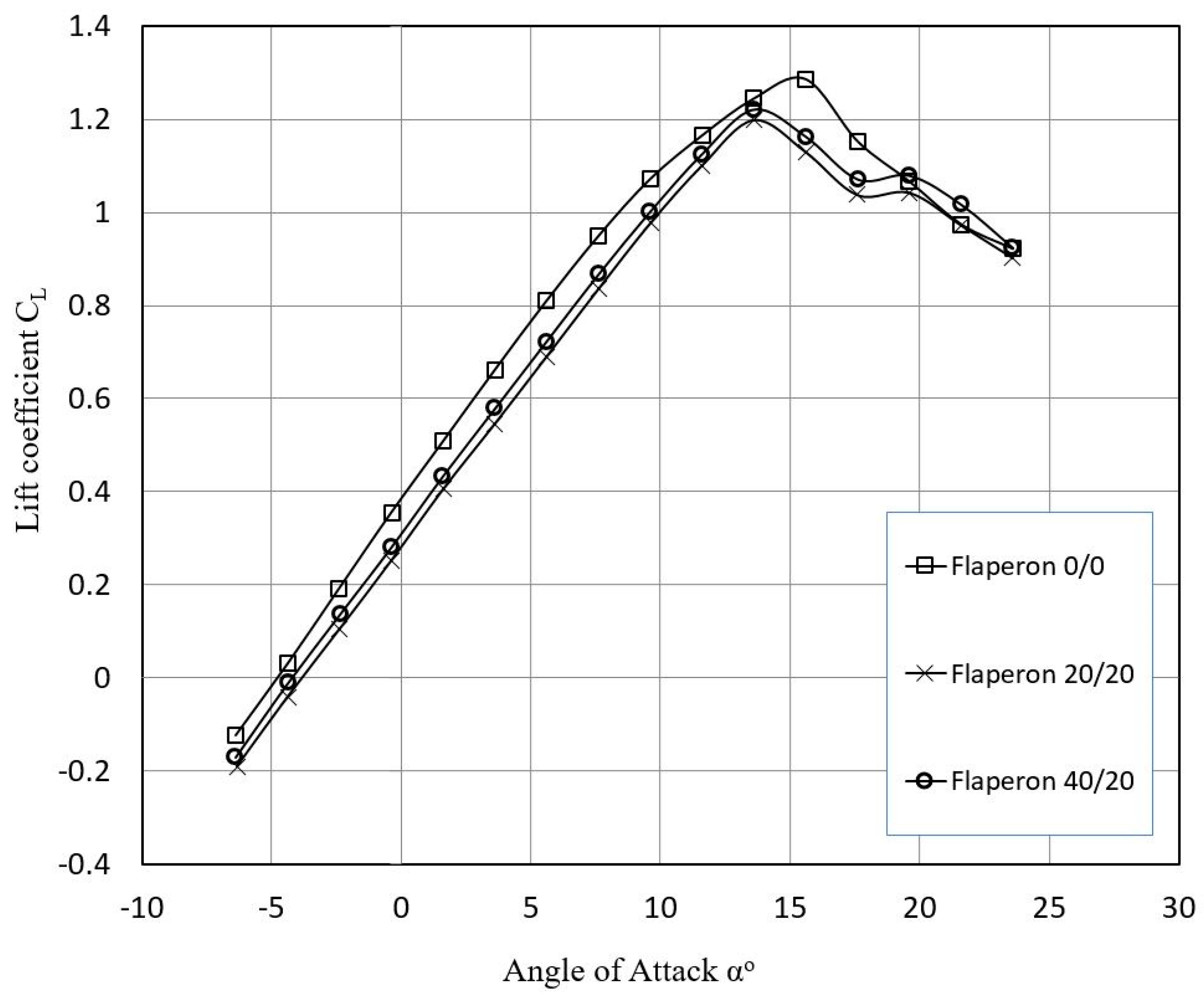
3.5. Flaperon Performance
4. Discussion
- Refinement of the analytical predictive models for a light boxplane;
- Trade studies and optimization of the aircraft geometry to better meet the performance requirements;
- Development of a code, specifically designing a light boxplane;
- Investigation of the effect of the airframe on the efficiency of the pusher propeller for this layout;
- Flight tests of the boxplane model.
Author Contributions
Funding
Conflicts of Interest
References
- Lange, R.H.; Cahill, J.F.; Bradley, E.S.; Eudaily, R.R.; Jenness, C.M.; Macwilkinson, D.G. Feasibility Study of the Transonic Biplane Concept for Transport Aircraft Application. 1974. Available online: https://archive.org/details/NASA_NTRS_Archive_19740026364/mode/2up (accessed on 6 September 2021).
- Prandtl, L. Induced Drag of Multiplanes. Available online: https://archive.org/details/nasa_techdoc_19930080964/mode/2upttps://archive.org/details/nasa_techdoc_19930080964/mode/2up (accessed on 6 September 2021).
- Spohr, A.; Schirra, J.C.; Hoefling, J.; Schedl, A. Wing Weight estimation methodology for highly non-planar lifting systems during conceptual design. Dtsch. Luft-Und Raumfahrtkongress 2013. [Google Scholar] [CrossRef]
- Kalinovwski, M.J. Structural optimization of box wing aircraft. Arch. Mech. Eng. 2015, LXII, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Schiktanz, D.; Scholts, D. Maximum Glide Ratio of Box Wing Aircraft—Fundamental Considerations. J. Hambg. Univ. Appl. Sci. 2001, 18. Available online: https://www.fzt.haw-hamburg.de/pers/Scholz/Airport2030/Airport2030_M_BoxWing_E_max_12-06-14.pdf (accessed on 6 September 2021).
- van Ginneken, D.; Voskuijl, M.; van Tooren, M.; Frediani, A. Automated Control Surface Design and Sizing for the Prandtl Plane. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 18th AIAA/ASME/AHS Adaptive Structures Conference, Orlando, FL, USA, 12–15 April 2010. [Google Scholar]
- Miranda, L. Boxplane Wing and Aircraft. U.S. Patent Application No. US3834654A, 10 September 1974. Available online: https://patents.google.com/patent/US3834654A/ (accessed on 6 September 2021).
- Peters, S.E. Aircraft Structure to Improve Directional Stability. U.S. Patent Application No. US6098923A, 8 August 2008. Available online: https://patents.google.com/patent/US6098923A/ (accessed on 6 September 2021).
- Frediani, A.; Gasperini, M.; Saporito, G.; Rimondi, A. The development of a PrandtlPlane aircraft configuration. In Proceedings of the 17th AIDAA Congress, Roma, Italy, 15–19 September 2003. [Google Scholar]
- Frediani, A.; Rizzo, E.; Cipolla, V.; Chiavacci, L.; Bottoni, C.; Scanu, J.; Iezzi, G. Development of ULM PrandtlPlane aircraft and flight tests on scaled models. In Proceedings of the Xix Aidaa Congress, XIX CONGRESSO NAZIONALE AIDAA, Milan, Italy, 17–21 September 2007. [Google Scholar]
- Airkraft Sunny–Wikipedia. Available online: https://en.wikipedia.org/wiki/Airkraft_Sunny (accessed on 6 September 2021).
- Ligeti Stratos—Nest of Dragons. Available online: https://www.nestofdragons.net/weird-airplanes/tandemwings/ligeti-stratos/ (accessed on 6 September 2021).
- Andrews, S.A.; Perez, R.E. Analytic Study of the Conditions Required for Longitudinal Stability of Dual-Wing Aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 232, 958–972. [Google Scholar] [CrossRef]
- Frediani, A. The Prandtl Wing: Innovative Configurations and Advanced Concepts for Future Civil Transport Aircraft; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2005. [Google Scholar]
- Parsifal Project. Available online: https://parsifalproject.eu/ (accessed on 6 September 2021).
- IDINTOS: Light Amphibious PrandtlPlane. Available online: http://www.idintos.eu/eng/ (accessed on 6 September 2021).
- Karpovich, E.A.; Liseitsev, N.K. Analytical Evaluation of Box Wing Aircraft Aerodynamic Characteristics at Early Design Stages. Russ. Aeronaut. 2019, 62, 417–422. [Google Scholar] [CrossRef]
- Karpovich, E.; Liseitsev, N. Revisiting the Longitudinal Stability and Balance of a Boxwing Aircraft. PNRPU Aerosp. Eng. Bull. 2019, 56, 29–44. [Google Scholar] [CrossRef]
- Karpovich, E.A.; Kochurova, N.I.; Kuznetsov, A.V. Experimental Study of Aerodynamic Characteristics of a Boxplane Wind-Tunnel Model. Russ. Aeronaut. 2020, 63, 659–668. [Google Scholar] [CrossRef]
- Steinfurth, B.; Cura, C.; Gehring, J.; Weiss, J. Tuft deflection velocimetry: A simple method to extract quantitative flow field information. Exp. Fluids 2020, 61, 1–11. [Google Scholar] [CrossRef]
- Simpson, R.L. Aspects of turbulent boundary-layer separation. Prog. Aerosp. Sci. 1996, 32, 457–521. [Google Scholar] [CrossRef]
- Abbott, I.; Sherman, A. Flow Observations with Tufts and Lampblack of the Stalling of Four Typical Airfoil Sections in the N.A.C.A. Variable-Density Tunnel; Technical Note No. 672; National Advisory Committee for Aeronautics: Washington, DC, USA, 1938. [Google Scholar]
- Ruchała, P. Aerodynamic Interference between Pusher Propeller Slipstream and An Airframe: Literature Review. J. KONES Powertrain Transp. 2017, 24, 237–244. [Google Scholar] [CrossRef]
- Vey, S.; Lang, H.M.; Nayeri, C.N.; Paschereit, C.O.; Pechlivanoglou, G. Extracting quantitative data from tuft flow visualizations on utility scale wind turbines. J. Phys. Conf. Ser. 2014, 524, 012011. [Google Scholar] [CrossRef] [Green Version]
- Bardina, J.; Huang, P.; Coakley, T. Turbulence modeling validation. In Proceedings of the 28th AIAA Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. [Google Scholar] [CrossRef]
- Zhang, C.; Bounds, C.P.; Foster, L.; Uddin, M. Turbulence Modeling Effects on the CFD Predictions of Flow over a Detailed Full-Scale Sedan Vehicle. Fluids 2019, 4, 148. [Google Scholar] [CrossRef] [Green Version]
- Gueraiche, D.; Popov, S. Winglet Geometry Impact on DLR-F4 Aerodynamics and an Analysis of a Hyperbolic Winglet Concept. Aerospace 2017, 4, 60. [Google Scholar] [CrossRef] [Green Version]
- Sclafani, A.; DeHaan, M.; Vassberg, J.; Rumsey, C.; Pulliam, T. Drag Prediction for the NASA CRM Wing-Body-Tail Using CFL3D and OVERFLOW on an Overset Mesh. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar]
- Wilcox, D.C. Multiscale model for turbulent flows. AIAA J. 1988, 26, 1311–1320. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Velocity, V∞ | 37 m/s |
| Pressure, p∞ | 100,500 Pa |
| Temperature, T∞ | 293 K |
| Turbulence intensity, ε | 0.35% |
| Reynolds number, Re | 328,433 |
| Average Angular Deviation of the Tufts, ° | Flow State |
|---|---|
| 180° ± 5° | Attached turbulent or laminar |
| 180° ± 40° | Attached flow, increased turbulence |
| 270° ± 40° 90° ± 40° | Turbulent crossflow |
| The separation line is where the chordwise velocity component is zero. | |
| α° | 5° | 10° | 15° |
|---|---|---|---|
| Cp scale |  | ||
| Top surface pressure coefficient visualization |  | 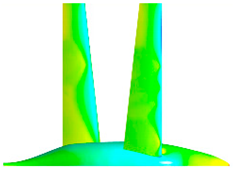 | 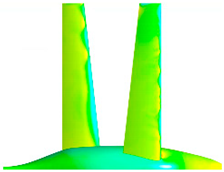 |
| Remarks | Front wing lift advantage; both wings attached; important fuselage lift contribution. | Equal lift generated with a slight fore wing advantage. Both wings attached. | Fore wing partially separated; aft wing lift advantage despite separation onset spots. |
| Conclusion | Fore wing maintains lift advantage until α° = 10–15°, where it begins to separate. | ||
| α° | 20° | 25° |
|---|---|---|
| Cp scale |  | |
| Top surface pressure coefficient visualization | 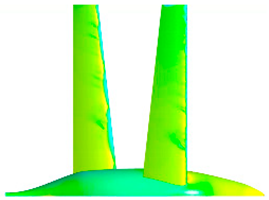 | 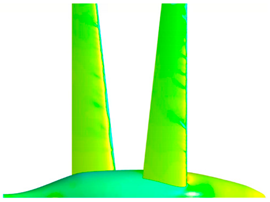 |
| Remarks | Fore wing fully separated; aft wing almost fully separated. | Both wings fully separated. |
| Conclusion | Further increasing α shifts lift contribution towards the aft wing, which maintains unseparated flow up until 17.5°. Above 20°, both wings are separated. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpovich, E.; Gueraiche, D.; Sergeeva, N.; Kuznetsov, A. Investigation of a Light Boxplane Model Using Tuft Flow Visualization and CFD. Fluids 2021, 6, 451. https://doi.org/10.3390/fluids6120451
Karpovich E, Gueraiche D, Sergeeva N, Kuznetsov A. Investigation of a Light Boxplane Model Using Tuft Flow Visualization and CFD. Fluids. 2021; 6(12):451. https://doi.org/10.3390/fluids6120451
Chicago/Turabian StyleKarpovich, Elena, Djahid Gueraiche, Natalya Sergeeva, and Alexander Kuznetsov. 2021. "Investigation of a Light Boxplane Model Using Tuft Flow Visualization and CFD" Fluids 6, no. 12: 451. https://doi.org/10.3390/fluids6120451
APA StyleKarpovich, E., Gueraiche, D., Sergeeva, N., & Kuznetsov, A. (2021). Investigation of a Light Boxplane Model Using Tuft Flow Visualization and CFD. Fluids, 6(12), 451. https://doi.org/10.3390/fluids6120451





