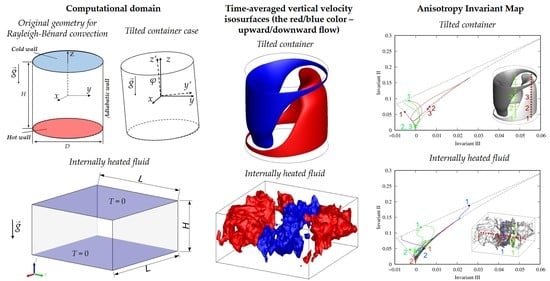
The Emergence and Identification of Large-Scale Coherent Structures in Free Convective Flows of the Rayleigh-Bénard Type
Abstract
:1. Introduction
- Are the flows self-organized (in the sense of CS presence) or constitute the sequence of irregular “thermals”?
- If CS are present, what factors govern their stability and temporal variability?
- Are the turbulence archetypes similar for two chosen types of forcing?
- What are the CS fingerprints (if any) on AIM?
2. Problem Definition, Mathematical Model and Numerical Aspects
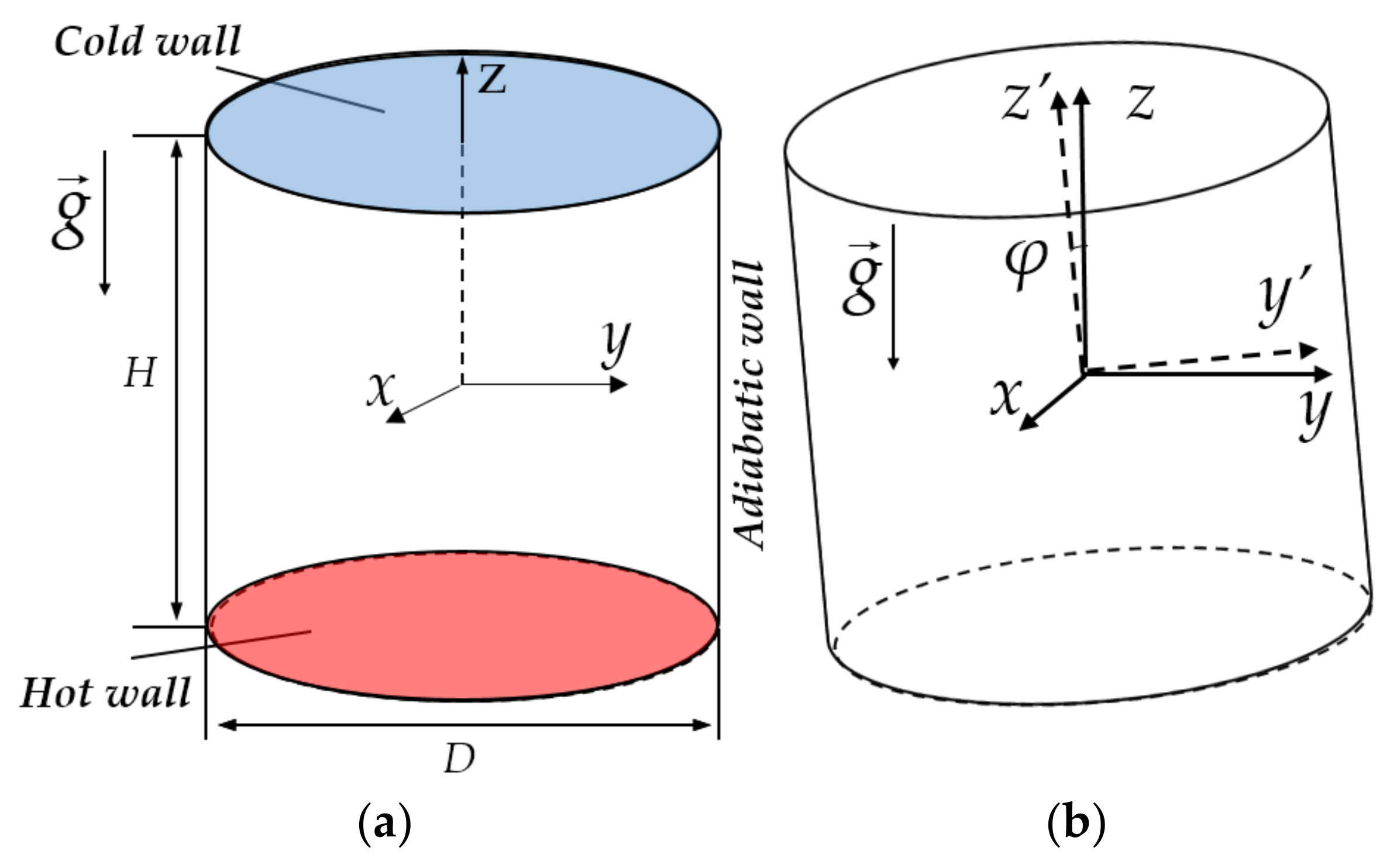
2.1. Rayleigh-Bénard Convection in a Cylinder
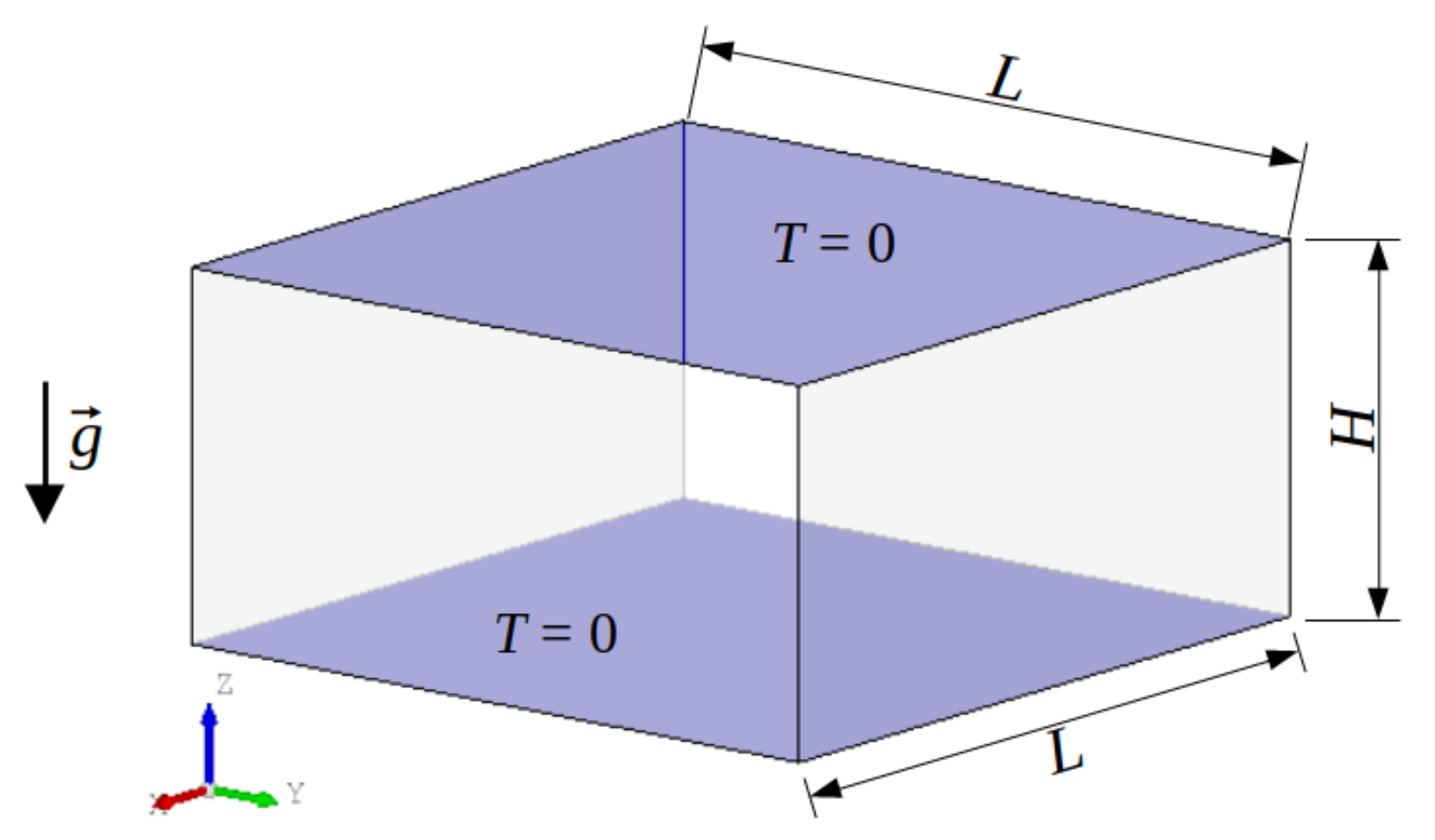
2.2. Convection of an Internally Heated Fluid
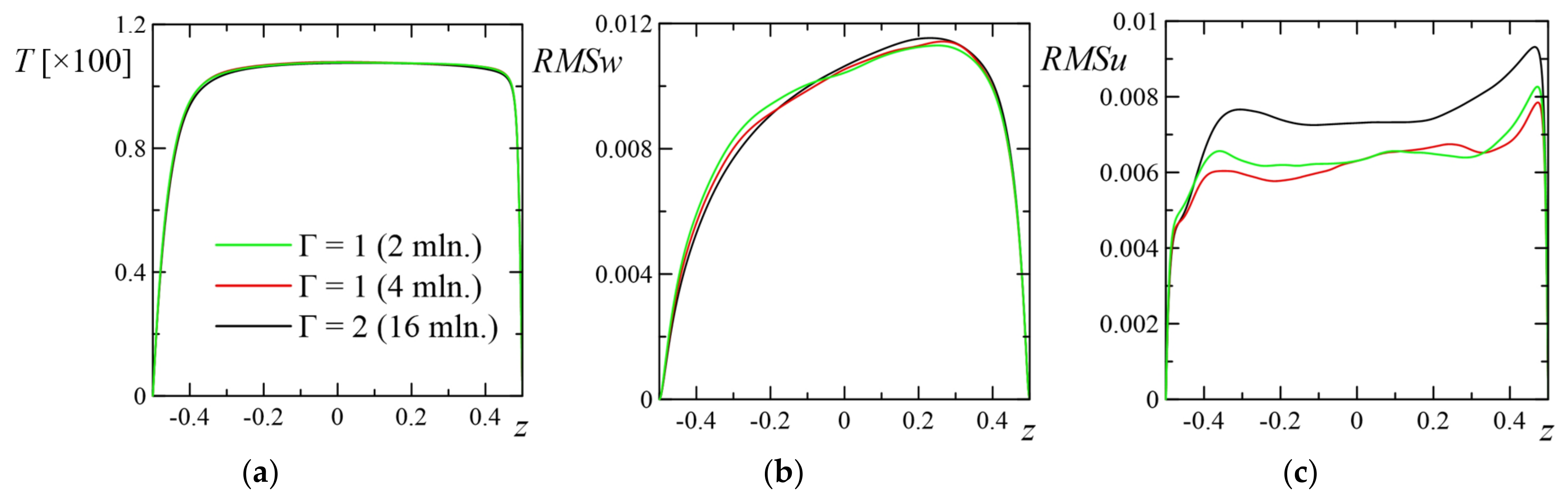
2.3. Computational Aspects
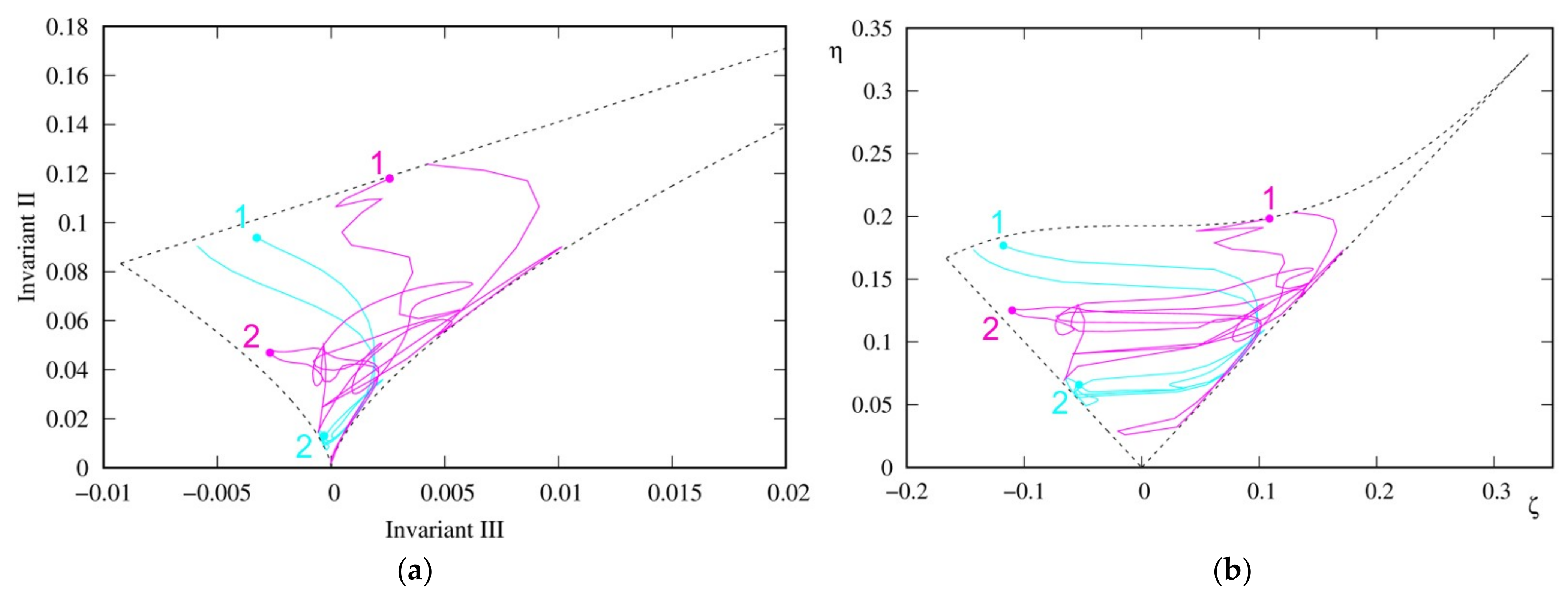
3. Results
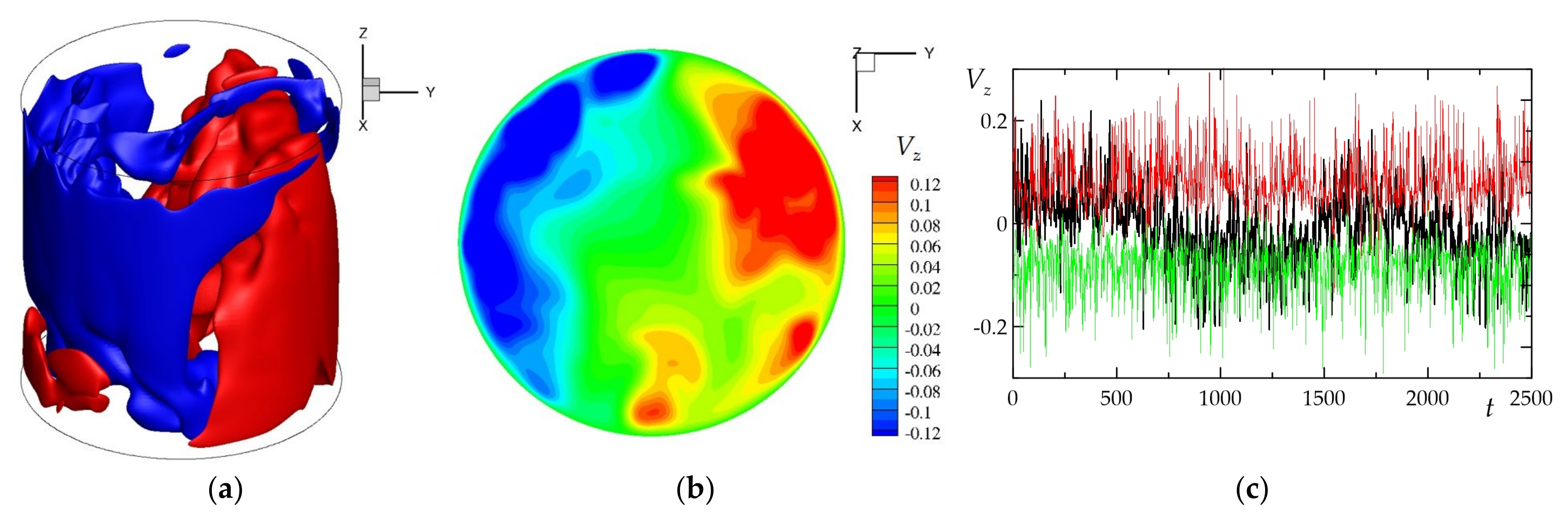
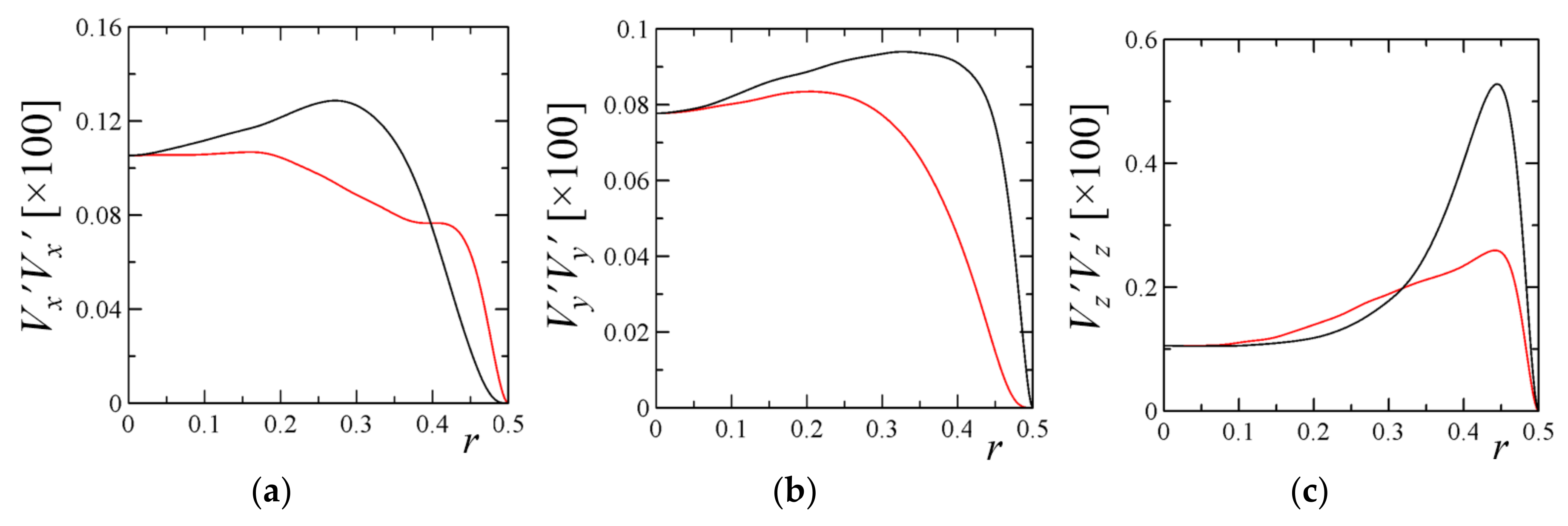
3.1. Rayleigh-Bénard Convection in a Cylinder
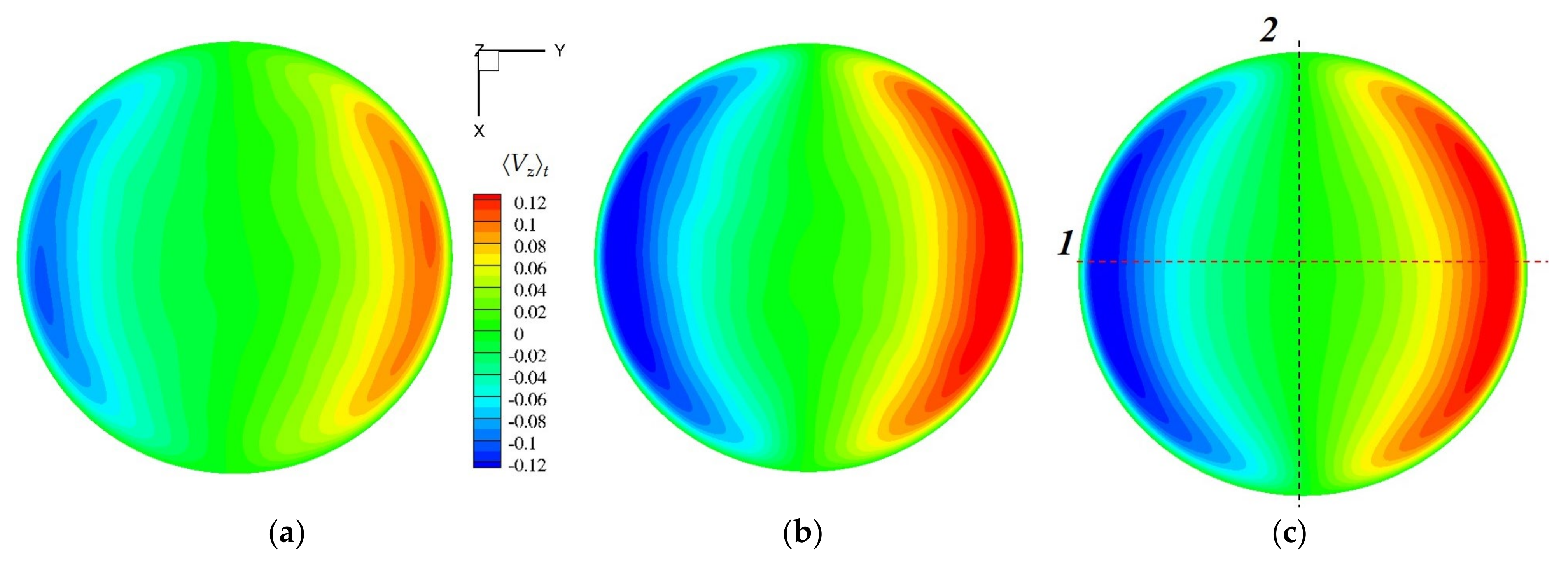
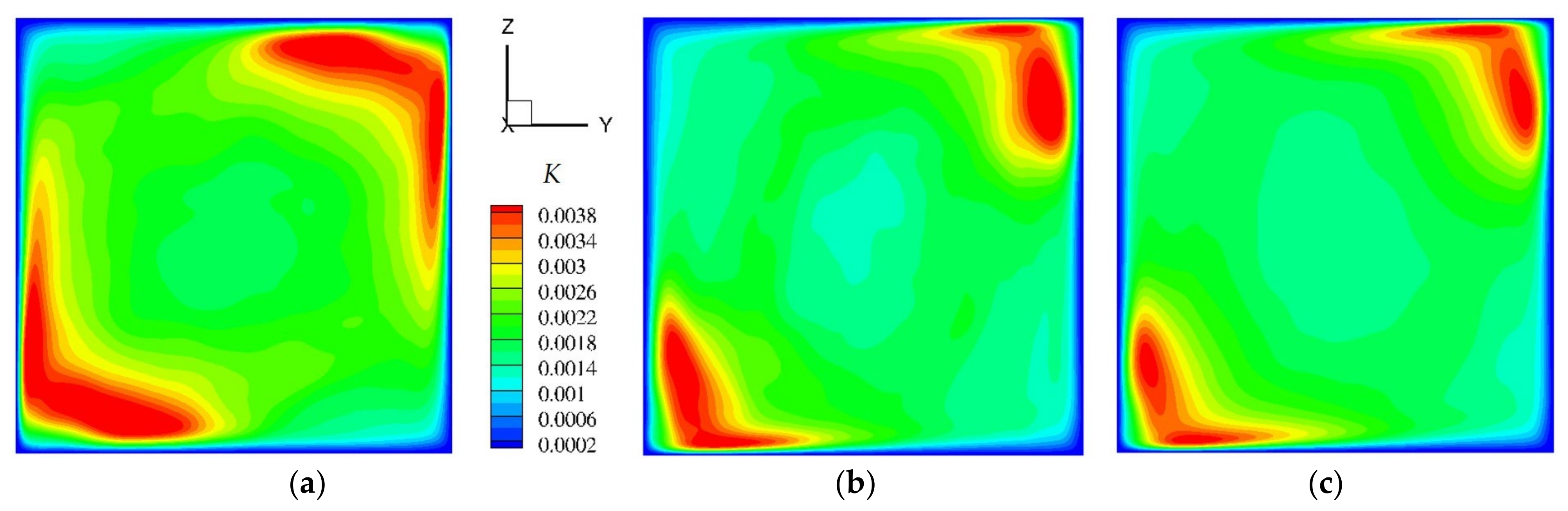
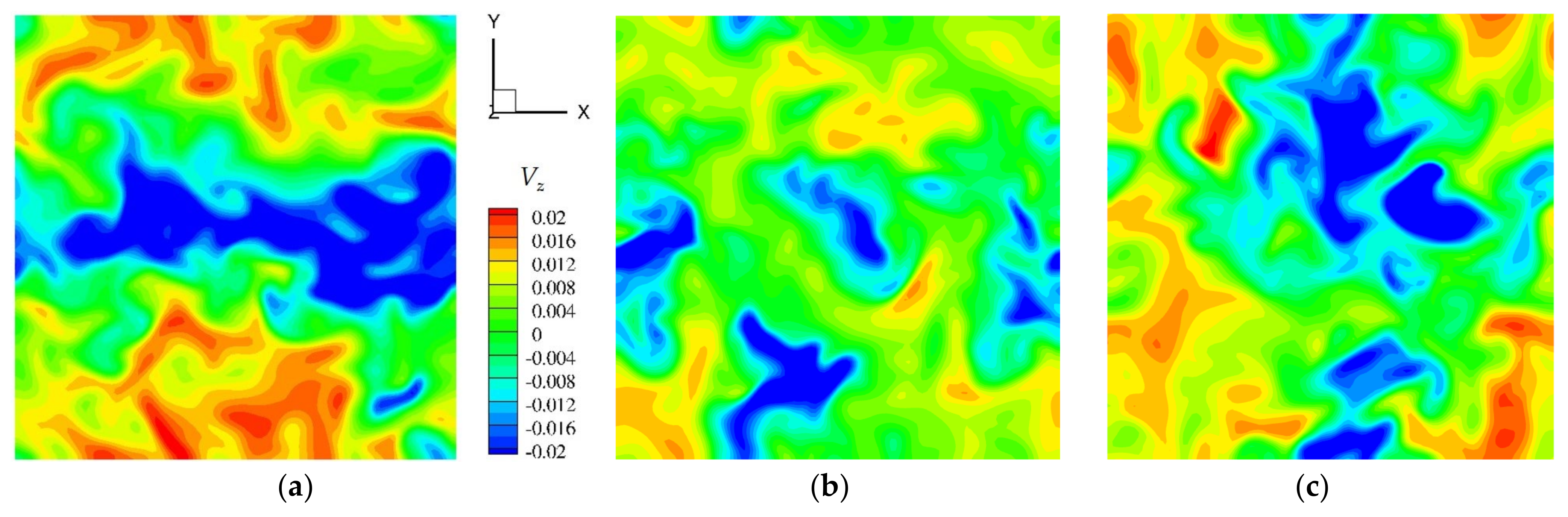
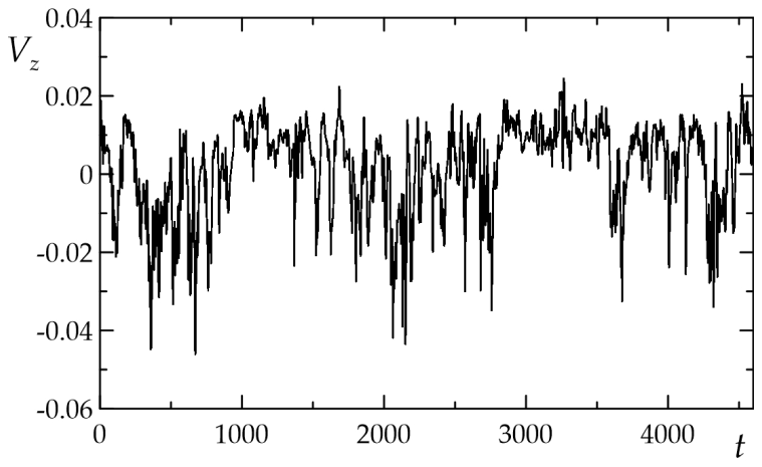
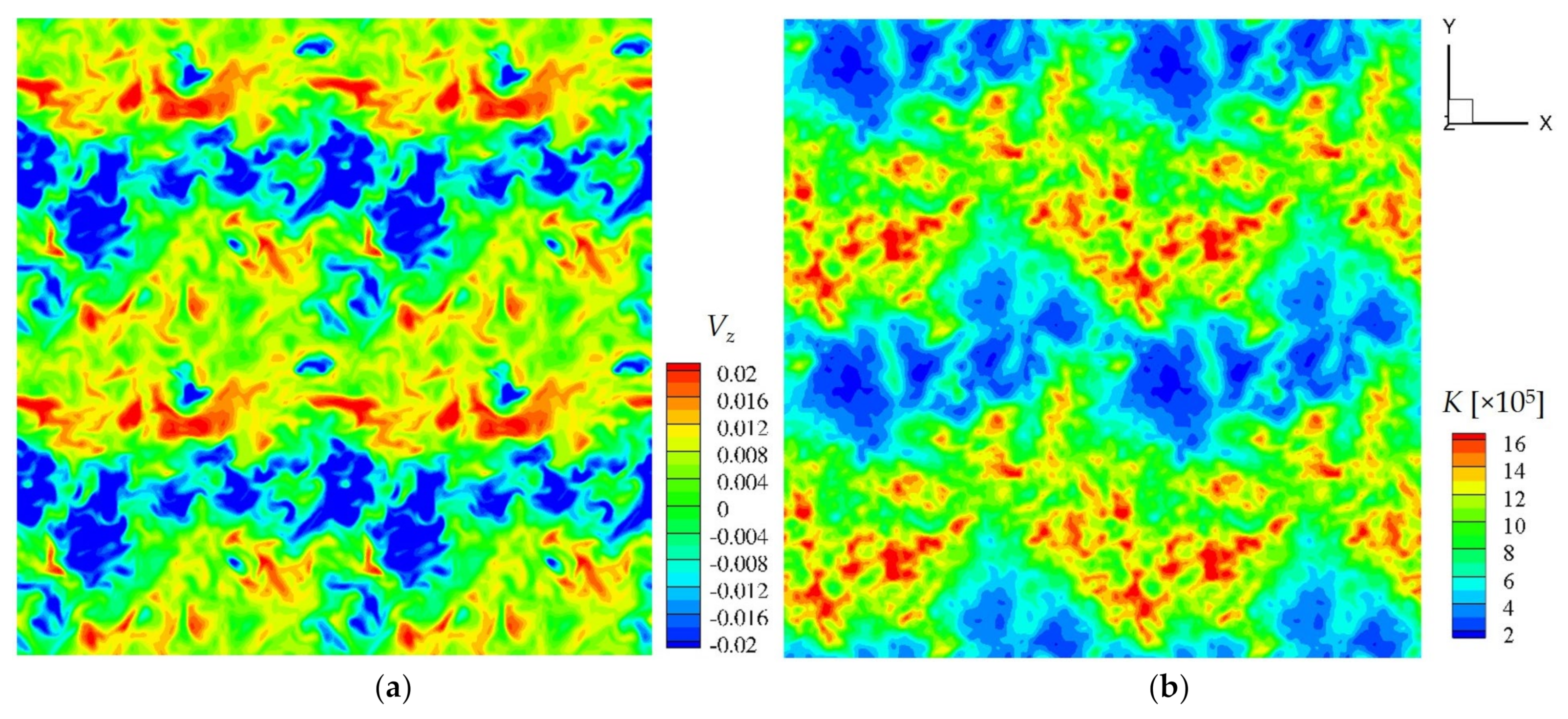
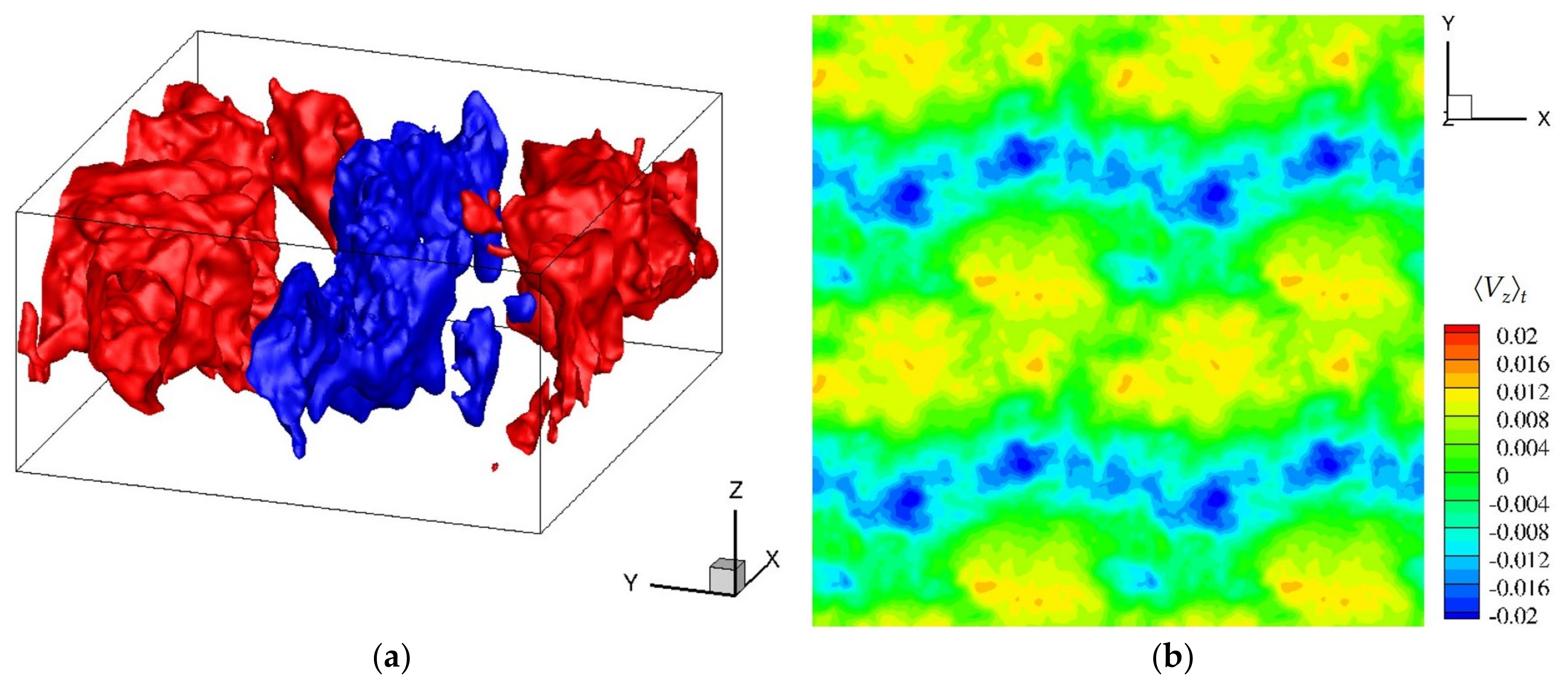
3.2. Convection of an Internally Heated Fluid
4. Discussion
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gargett, A.E.; Grosch, C.E. Turbulence Process Domination under the Combined Forcings of Wind Stress, the Langmuir Vortex Force, and Surface Cooling. J. Phys. Oceanogr. 2014, 44, 44–67. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, MA, USA, 2000; 771p. [Google Scholar] [CrossRef]
- Emory, M.; Iaccarino, G. Visualizing turbulence anisotropy in the spatial domain with componentality contours. Cent. Turbul. Res. Annu. Res. Briefs 2014, 123–138. [Google Scholar]
- Bluteau, C.E.; Jones, N.L.; Ivey, G.N. Turbulent mixing efficiency at an energetic ocean site. JGR Oceans 2013, 118, 4662–4672. [Google Scholar] [CrossRef] [Green Version]
- Ulloa, H.; Wüest, A.; Bouffard, D. Mechanical energy budget and mixing efficiency for a radiatively heated ice-covered waterbody. J. Fluid Mech. 2018, 852, R1. [Google Scholar] [CrossRef] [Green Version]
- Maffioli, A.; Brethouwer, G.; Lindborg, E. Mixing efficiency in stratified turbulence. J. Fluid Mech. 2016, 794, R3. [Google Scholar] [CrossRef] [Green Version]
- Lumley, J.L. Computational modeling of turbulent flows. Adv. Appl. Mech. 1978, 18, 123–176. [Google Scholar]
- Choi, K.-S.; Lumley, J.L. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 2001, 436, 59–84. [Google Scholar] [CrossRef]
- Simonsen, A.J.; Krogstad, P.-A. Turbulent stress invariant analysis: Clarification of existing terminology. Phys. Fluids 2005, 17, 088103. [Google Scholar] [CrossRef] [Green Version]
- Kunnen, R.P.J. Turbulent Rotating Convection; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Anisotropy in the Free Stream Region of Turbulent Flows through Emergent Rigid Vegetation on Rough Beds. Water 2020, 12, 2464. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, H.; Lu, L.; Li, Q. Investigation of Vortical Structures and Turbulence Characteristics in Corner Separation in a Linear Compressor Cascade Using DDES. J. Fluids Eng. 2017, 139, 021107. [Google Scholar] [CrossRef]
- Font, B.; Weymouth, G.D.; Nguyen, V.-T.; Tutty, O.R. Span effect on the turbulence nature of flow past a circular cylinder. J. Fluid Mech. 2019, 878, 306–323. [Google Scholar] [CrossRef]
- Gargett, A.; Wells, J.; Tejada-Martínez, A.E.; Grosch, C.E. Langmuir supercells: A mechanism for sediment resuspension and transport in shallow seas. Science 2004, 306, 1925–1928. [Google Scholar] [CrossRef] [PubMed]
- Smyth, W.D.; Moum, J.N. Anistropy of turbulence in stably stratified mixing layers. Phys. Fluids 2000, 12, 1343–1362. [Google Scholar] [CrossRef] [Green Version]
- Ye, Q.Y.; Wörner, M.; Grötzbach, G. Modelling Turbulent Dissipation Correlations for Rayleigh-Bénard Convection Based on Two-Point Correlation Technique and Invariant Theory; Karlsruhe FZKA: Karlsruhe, Germany, 1998; 54p. [Google Scholar]
- Brown, E.; Ahlers, G. Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 2006, 568, 351–386. [Google Scholar] [CrossRef] [Green Version]
- Mishra, P.K.; De, A.K.; Verma, M.K.; Eswaran, V. Dynamics of reorientations and reversals of large-scale flow in Rayleigh–Bénard convection. J. Fluid Mech. 2011, 668, 480–499. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.K. Physics of Buoyant Flows: From Instabilities to Turbulence; World Scientific: Singapore, 2018; 352p. [Google Scholar] [CrossRef]
- Kelley, D.E. Convection in ice-covered lakes: Effects on algal suspension. J. Plankton Res. 1997, 19, 1859–1880. [Google Scholar] [CrossRef]
- D’Asaro, E.A. Convection and the seeding of the North Atlantic bloom. J. Marine Syst. 2008, 69, 233–237. [Google Scholar] [CrossRef]
- Woodward, J.R.; Pitchford, J.W.; Bees, M.A. Physical flow effects can dictate plankton population dynamics. J. R. Soc. Interface 2019, 16, 20190247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martinat, G.; Grosch, C.E.; Gatski, T.B. Modeling of Langmuir Circulation: Triple Decomposition of the Craik–Leibovich Model. Flow Turbul. Combust. 2011, 92, 395–411. [Google Scholar] [CrossRef]
- Pernica, P.; North, R.L.; Baulch, H.M. In the cold light of day: The potential importance of under-ice convective mixed layers to primary producers. Inland Waters 2017, 7, 138–150. [Google Scholar] [CrossRef]
- Ahlers, G.; Grossmann, S.; Lohse, D. Heat transfer and large-scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 2009, 81, 503–538. [Google Scholar] [CrossRef] [Green Version]
- Chillà, F.; Schumacher, J. New perspectives in turbulent Rayleigh-Bénard convection. Eur. Phys. J. E 2012, 35, 1–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, X.-Z.; Libchaber, A. Scaling relations in thermal turbulence: The aspect-ratio dependence. Phys. Rev. A 1992, 45, 842–845. [Google Scholar] [CrossRef]
- Cioni, S.; Ciliberto, S.; Sommeria, J. Experimental study of high-Rayleigh-number convection in mercury and water. Dyn. Atmos. Oceans 1996, 24, 117–127. [Google Scholar] [CrossRef]
- Niemela, J.J.; Skrbek, L.; Sreenivasan, K.R.; Donnelly, R.J. Turbulent convection at very high Rayleigh numbers. Nature 2000, 404, 837–840. [Google Scholar] [CrossRef] [PubMed]
- Ahlers, G.; Bodenschatz, E.; Funfschilling, D.; Hogg, J. Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid Mech. 2009, 641, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Verzicco, R.; Camussi, R. Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 2003, 477, 19–49. [Google Scholar] [CrossRef]
- Shishkina, O.; Thess, A. Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 2009, 633, 449–460. [Google Scholar] [CrossRef] [Green Version]
- Scheel, J.D.; Kim, E.; White, K.R. Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 2012, 711, 281–305. [Google Scholar] [CrossRef]
- Chillà, F.; Rastello, M.; Chaumat, S.; Castaing, B. Long relaxation times and tilt sensitivity in Rayleigh-Bénard turbulence. Eur. Phys. J. B. 2004, 40, 223–227. [Google Scholar] [CrossRef]
- Ahlers, G.; Brown, E.; Nikolaenko, A. The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 2006, 557, 347–367. [Google Scholar] [CrossRef] [Green Version]
- Xi, H.-D.; Xia, K.-Q. Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: A comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 2008, 78, 036326. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, S.I.; Abramov, A.G.; Smirnov, E.M. Numerical simulation of turbulent Rayleigh-Bénard mercury convection in a circular cylinder with introducing small deviations from the axisymmetric formulation. J. Phys. Conf. Ser. 2019, 1359, 012077. [Google Scholar] [CrossRef]
- Smirnov, S.I.; Smirnov, E.M. Direct numerical simulation of the turbulent Rayleigh-Bénard convection in a slightly tilted cylindrical container. St. Petersburg State Polytech. Univ. J. Phys. Math. 2020, 13, 14–25. [Google Scholar] [CrossRef]
- Zwirner, L.; Khalilov, R.; Kolesnichenko, I.; Mamykin, A.; Mandrykin, S.; Pavlinov, A.; Shestakov, A.; Teimurazov, A.; Frick, P.; Shishkina, O. The influence of the cell inclination on the heat transport and large-scale circulation in liquid metal convection. J. Fluid Mech. 2020, 884, A18. [Google Scholar] [CrossRef] [Green Version]
- Goluskin, D. Internally Heated Convection and Rayleigh-Bénard Convection; Springer Briefs in Thermal Engineering and Applied Science; Springer: Berlin/Heidelberg, Germany, 2016; 66p. [Google Scholar] [CrossRef]
- Kerr, R.M.; Herring, J.R. Prandtl number dependence of Nusselt number in direct numerical simulations. J. Fluid Mech. 2000, 419, 325–344. [Google Scholar] [CrossRef]
- Hartlep, T.; Tilgner, A.; Busse, F.H. Large Scale Structures in Rayleigh-Bénard Convection at High Rayleigh Numbers. Phys. Rev. Lett. 2003, 91, 064501. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.; Scheel, J.D.; Schumacher, J. Turbulent superstructures in Rayleigh-Bénard convection. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hardenberg, J.V.; Parodi, A.; Passoni, G.; Provenzale, A.; Spiegel, E.A. Large-scale patterns in Rayleigh–Bénard convection. Phys. Lett. A 2008, 372, 2223–2229. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Blass, A.; Zhu, X.; Verzicco, R.; Lohse, D. Turbulent thermal superstructures in Rayleigh-Bénard convection. Phys. Rev. Fluids 2018, 3, 041501. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Petschel, K.; Wilczek, M.; Breuer, M.; Friedrich, R.; Hansen, U. Statistical analysis of global wind dynamics in vigorous Rayleigh–Bénard convection. Phys. Rev. E 2011, 84, 026309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, A.; Chen, X.; Wang, F.; Xi, H.-D. Correlation of internal flow structure with heat transfer efficiency in turbulent Rayleigh–Bénard convection. Phys. Fluids 2020, 32, 105112. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Verma, M.K.; Samtaney, R. Prandtl number dependence of the small-scale properties in turbulent Rayleigh-Bénard convection. Phys. Rev. Fluids 2021, 6, 063501. [Google Scholar] [CrossRef]
- Xu, A.; Chen, X.; Xi, H.-D. Tristable flow states and reversal of the large-scale circulation in two-dimensional circular convection cells. J. Fluid Mech. 2021, 910, A33. [Google Scholar] [CrossRef]
- Kulacki, F.A.; Goldstein, R.J. Thermal convection in a horizontal fluid layer with uniform volumetric energy sources. J. Fluid Mech. 1972, 55, 271–287. [Google Scholar] [CrossRef]
- Goluskin, D.; van der Poel, E.P. Penetrative internally heated convection in two and three dimensions. J. Fluid Mech. 2016, 791, R6. [Google Scholar] [CrossRef] [Green Version]
- Lepot, S.; Aumaître, S.; Gallet, B. Radiative heating achieves the ultimate regime of thermal convection. Proc. Natl. Acad. Sci. USA 2018, 115, 8937–8941. [Google Scholar] [CrossRef] [Green Version]
- Bouillaut, V.; Lepot, S.; Aumaître, S.; Gallet, B. Transition to the ultimate regime in a radiatively driven convection experiment. J. Fluid Mech. 2019, 861, R5. [Google Scholar] [CrossRef]
- Creyssels, M. Model for classical and ultimate regimes of radiatively driven turbulent convection. J. Fluid Mech. 2020, 900, A39. [Google Scholar] [CrossRef]
- Smirnov, S.I.; Smirnov, E.M.; Smirnovsky, A.A. Endwall heat transfer effects on the turbulent mercury convection in a rotating cylinder. St. Petersburg Polytech. Univ. J. Phys. Math. 2017, 3, 83–94. [Google Scholar] [CrossRef]
- Kooij, G.L.; Botchev, M.A.; Geurts, B.J. Direct numerical simulation of Nusselt number scaling in rotating Rayleigh–Bénard convection. Int. J. Heat Fluid Flow 2015, 55, 26–33. [Google Scholar] [CrossRef]
- Ahn, J.; Kim, K.-H.; Pan, X.; Choi, J.-I. Contribution of Reynolds shear stress to near-wall turbulence in Rayleigh–Bénard convection. Int. J. Heat Mass Transfer 2021, 181, 121873. [Google Scholar] [CrossRef]
- Vasilev, A.; Frick, P.; Kumar, A.; Stepanov, R.; Sukhanovskii, A.; Verma, M.K. Transient flows and reorientations of large-scale convection in a cubic cell. Int. Commun. Heat Mass Transf. 2019, 108, 104319. [Google Scholar] [CrossRef] [Green Version]
- Mironov, D.; Danilov, S.; Olbers, D. Large-eddy simulation of radiatively-driven convection in ice-covered lakes. In Proceedings of the 6th International Workshop on ‘Physical Processes in Natural Waters’, Girona, Spain, 27–29 June 2001; pp. 71–75. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, S.; Smirnovsky, A.; Bogdanov, S. The Emergence and Identification of Large-Scale Coherent Structures in Free Convective Flows of the Rayleigh-Bénard Type. Fluids 2021, 6, 431. https://doi.org/10.3390/fluids6120431
Smirnov S, Smirnovsky A, Bogdanov S. The Emergence and Identification of Large-Scale Coherent Structures in Free Convective Flows of the Rayleigh-Bénard Type. Fluids. 2021; 6(12):431. https://doi.org/10.3390/fluids6120431
Chicago/Turabian StyleSmirnov, Sergei, Alexander Smirnovsky, and Sergey Bogdanov. 2021. "The Emergence and Identification of Large-Scale Coherent Structures in Free Convective Flows of the Rayleigh-Bénard Type" Fluids 6, no. 12: 431. https://doi.org/10.3390/fluids6120431
APA StyleSmirnov, S., Smirnovsky, A., & Bogdanov, S. (2021). The Emergence and Identification of Large-Scale Coherent Structures in Free Convective Flows of the Rayleigh-Bénard Type. Fluids, 6(12), 431. https://doi.org/10.3390/fluids6120431