Abstract
This research investigates laser-induced convection through a stream function-vorticity formulation. Specifically, this paper considers a solution to the steady Boussinesq Navier–Stokes equations in two dimensions with a slip boundary condition on a finite box. A fixed-point algorithm is introduced in stream function-vorticity variables, followed by a proof of the existence of steady solutions for small laser amplitudes. From this analysis, an asymptotic relationship is demonstrated between the nondimensional fluid parameters and least upper bounds for laser amplitudes that guarantee existence, which accords with numerical results implementing the algorithm in a finite difference scheme. The findings indicate that the upper bound for laser amplitude scales by when , and by when . These results suggest that the existence of steady solutions is heavily dependent on the size of the Reynolds (Re) and Peclet (Pe) numbers, as noted in previous studies. The simulations of steady solutions indicate the presence of symmetric vortex rings, which agrees with experimental results described in the literature. From these results, relevant implications to thermal blooming in laser propagation simulations are discussed.
1. Introduction
In this article, we investigate steady Boussinesq fluid convection driven by a laser source. More precisely, we present and interrogate a solution to the steady-state case of a buoyancy-driven fluid with a forcing term due to heat transfer from a laser. The Boussinesq approximation is highly accurate for such buoyancy-driven flows and is commonplace in laser propagation studies, especially those involving thermal blooming [1]. This phenomenon of thermal blooming plays an important role in dictating the behavior of laser-fluid interaction within the context of laser propagation, and especially in domains such as manufacturing, remote sensing, directed energy, imaging, and several others [2,3,4]. Motivated by the applications in these respective fields, we will consider steady-state laser convection within a 2D setting. Several authors have elucidated the means by which laser-induced convection, both in steady and unsteady regimes, can be applied to engineering and applied science problems. For example, Vela [5] describes a method to manipulate micro-beads at mesoscale velocities within a convection chamber. In a similar analysis, Flores–Flores [6] considers microparticle transport driven by laser-induced convective currents in gas at microscale velocities. In nanofluids, Mourad et al. [7] and Jamshed et al. [8] consider the thermal characteristics of fluid flow undergoing natural convection. At larger fluid velocities, Masoomi [9] considered steady-state convective heat transfer from lasers in the context of additive manufacturing, and Rennie [10] has discussed the impact laser-induced convection can have on material heating times in directed energy applications.
In treating the steady-state laser convection problem, we introduce an iterative numerical method to simulate steady solutions over a 2D finite grid. We provide a proof of existence of steady solutions for small enough laser amplitudes and we give a theorem to describe the scaling between nondimensional fluid parameters and a least upper bound for laser amplitude which permits computable solutions. There exist several papers in the relevant literature that prove convergence of iterations in weak and strong formulations for the Navier–Stokes equations. Work has already been done [11,12] to prove the existence of weak solutions in the 2D and 3D steady Navier–Stokes equations with a Boussinesq approximation and slip boundary conditions, but all in the primitive variable setting and without an implementable iteration to find the solutions. Other studies each considered an unforced problem or a problem with forcing along the boundary of the considered domain [13,14]. By choosing an appropriate function space, convergent iterations exist in at least two dimensions for steady and unsteady cases [15,16,17,18]. The iteration presented in this work, however, is unique in that it provides solutions to an internally forced convection problem. In our formulation, we establish a fixed-point iteration with existence in Sobolev spaces in two dimensions. From this iteration, we implement a finite-difference numerical algorithm to compute solutions over a grid. Previous work surrounding the simulation of laser-induced convection has included discussions about free versus forced convection [19], difficulties with nondimensional scaling [20], difficulties with deriving proper boundary conditions [21], and several other associated problems. Similar finite difference algorithms do exist [22,23] along with methods that implement finite elements [24] and radial basis functions [25]; however, these algorithms do not consider a convection problem with internal forcing. Furthermore, in our analysis of the induced finite-difference scheme, we give particular consideration to the asymptotic scaling of the nondimensional fluid parameters.
Since the Navier–Stokes equations may be represented in either primitive variables (temperature, velocity, pressure), or in stream function-vorticity form, the chosen formulation informs on the techniques used to analyze potential solution methods. Both representations have their benefits. The stream function-vorticity formulation, however, is advantageous in that it implicitly guarantees divergence-free flow without the requirement of a pressure-correction term. In numerical implementations of the primitive Navier–Stokes equations, this pressure correction term often leads to solution inaccuracies arising from inappropriate choices in pressure boundary conditions [26]. With the stream function-vorticity formulation, the choice of boundary conditions for each fluid variable is thus simplified. We consider here a no-friction slip condition in stream function-vorticity variables with homogeneous Dirichlet conditions for temperature. The slip condition is easily manifested in stream-function vorticity form as a homogeneous Dirichlet condition on the fluid stream function and vorticity. This condition allows for free tangential movement along the boundary, allowing for the development of vortex rings within the domain.
The novel findings from this study will include the existence of solutions arising from a numerically implementable iteration, as well as the asymptotic relationship between nondimensional fluid parameters and a maximum laser amplitude. In the following chapters, we discuss the relationship between the physical problem and the stream function-vorticity representation, we introduce and prove convergence of an iteration to solve the Boussinesq Navier–Stokes equations, and we conclude with results and a discussion on the asymptotic scaling of nondimensional fluid parameters with respect to convergence. Following this analysis, we provide numerical solutions to the steady-state and we examine the applications to laser beam propagation.
2. Formulation
We now introduce our approach to mathematically describing the laser-fluid interaction of interest. We consider a model for laser-fluid interaction on a finite, 2D domain such that this domain represents a rectangular cross section along the propagation path (z coordinate) of the laser beam. That is, the domain will be a rectangular subsection of the plane where we assume the Gaussian laser intensity profile is centered on the origin of the domain. This assumption would be most valid when considering thermal blooming at the laser aperture. We denote the domain as and the boundary of the domain as , where we begin by considering a square domain as depicted in Figure 1.
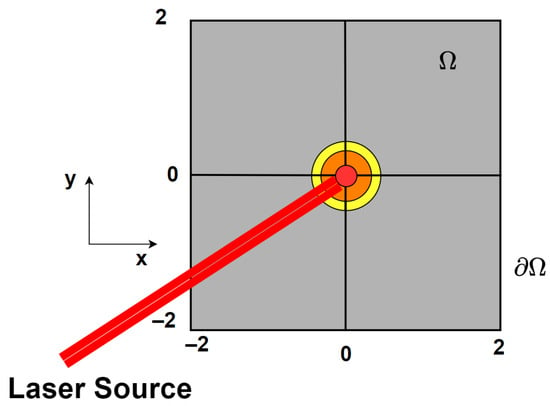
Figure 1.
The above figure provides a visualization of the fluid boundary and domain with laser forcing centered on the origin. Both the x and y coordinates range from −2 to 2.
Several assumptions on the fluid and laser properties must be imposed in the pursuit of governing equations which dictate fluid behavior. We assume an incompressible, Newtonian fluid which is governed by the Boussinesq approximation for buoyancy-driven flows. This Boussinesq model assumes that variations in fluid density have a linear relationship with temperature. Further, we assume a representation of the normalized laser irradiance as a function defined over the domain such that the laser heats the fluid and induces temperature variations. We first introduce the governing equations for fluid flow in primitive variables where we seek the functions
representing the nondimensional temperature fluctuation, pressure, and velocity field of the fluid which obey the incompressible, Boussinesq Navier–Stokes equations undergoing forcing [27]:
where represents the laser forcing and represents the unit vector in the vertical y direction. For a characteristic length scale L, characteristic velocity scale U, force due to gravity g, kinematic viscosity , and thermal diffusivity , the Reynolds, Peclet, and Richardson numbers are respectively defined as
We seek steady-state solutions such that all temporal variation is negligible and each . In two dimensions, it is often easier to consider the stream function-vorticity form of the Boussinesq equations. This formulation reduces the total number of fluid variables by one, and often allows for easier treatment of boundary conditions. The transformation from the primitive form to the stream function-vorticity form is a well established procedure, where the two representations are equivalent for valid boundary data [28]. We state the equivalent stream function-vorticity form of the steady Boussinesq equations below:
where is the vorticity and is the stream function of the fluid. Like the primitive formulation, we may interpret the system as a type of vector-valued, nonlinear Poisson equation over the domain .
In this study, we consider a slip boundary condition on a finite box corresponding to zero shear stress along the boundary. This slip condition enforces boundary impermeability and assumes that the coefficient of friction between the fluid and the boundary is zero. That is, the normal component of velocity at the boundary vanishes but the tangential component is unrestricted. This boundary condition is useful in investigating laser-fluid interaction as it localizes the fluid within a finite domain without having to consider boundary layer effects. In primitive variables, where , this is satisfied through the condition
Based on the definitions for the stream function
and the definition for vorticity
we may transform the primitive slip condition into an equivalent condition on the stream function and vorticity. First, if on the top and bottom and on the left and right, then
and
which is satisfied by taking on all of . For the vorticity, if on the top and bottom, then on the top and bottom. Similarly, if on the left and right, then on the left and right. It thus follows that the slip condition in primitive variables is equivalent to a homogeneous Dirichlet condition on the stream function and vorticity. For simplicity, we impose a homogeneous Dirichlet condition on the temperature, but a Neumann condition can also yield useful results. The slip condition in stream function-vorticity form is thus stated as
With the stream function-vorticity formulation posed as a system of coupled Poisson boundary value problems, we now define , , and as the exact temperature fluctuation, vorticity, and stream function, respectively. We restate Equation (3) for the steady Navier–Stokes equations in the Boussinseq approximation as
We then introduce the fixed-point iteration for as
where the laser irradiance takes the form of an amplitude scaled by a normalized Gaussian f
and we initialize the solution as
This initialization is the linearization of the system of equations and thus should serve as a strong initial guess for small amplitude solutions. We show in the following section that unique, convergent solutions exist for this iteration when laser amplitude is small.
In the numerical implementation of this iteration, we employ a finite difference scheme to successively solve the Poisson equations in each fluid variable at each step n. We proceed by uniformly discretizing the domain with step size h, and we utilize a second order, centered difference approximation to discretize the Laplacian
For an discrete grid, the solution to the discrete Poisson equation solution can be found in flops [29]. Since this represents the most computationally expensive step in the iteration, we thus conclude that the scheme (9) has an asymptotic cost of when it converges to a unique solution. In a MATLAB implementation, we establish stopping criteria based on the Cauchy error of successive iterations. That is, the algorithm terminates when the numerical solutions converge based on the criterion
using vector 2-norms for some appropriately small p. The following section is dedicated to demonstrating that these convergent solutions exist for small enough laser amplitudes.
3. Existence Proof
Recall that the iteration (9) was constructed so that its fixed points are steady solutions of (8), so this convergence of the scheme gives existence of solutions. We state this result as a theorem:
Theorem 1
(Convergence of Steady Solutions to the Stream Function-Vorticity Form of the Boussinesq Navier–Stokes equations). The iteration defined in (9) and (11) converges to unique solutions for small forcing and Dirichlet boundary conditions.
Proof.
We begin by stating a definition from Brezis [30] and two lemmas which assist in our analysis:
Definition 1
(Sobolev Spaces). Let and let with . If is an integer, then the Sobolev space is defined for all α with ,
where we employ the multi-index notation such that
We assign the . The space equipped with the norm
is a Banach space and we define the space
originally defined by Sobolev in [31,32].
Lemma 1
( is an algebra). Let . Suppose and . Then and gives that , and that
where M depends only on and d.
See [33] for proof.
Lemma 2
(Elliptic Estimate). If then there exists a unique solution to
with
And that solution satisfies where is a positive constant.
(see [34] for proof. A similar result also exists for inhomogeneous and Neumann boundary conditions for boundary data which satisfy compatibility conditions as described in [35,36].)
We now introduce the small amplitude assumption on the dynamics, where each is represented by a perturbation from the resting fluid case:
The key result of the proof involves constructing the equation for the difference between two iterations and (and similarly and , and ) by applying the representation in (18) and subtracting (9) at the two indices m and n:
We proceed by investigating the form of Equation (19a) first. Define
where we manipulate the form of the equation to arrive at a more convenient expression:
We now prove that the function such that the norm by showing that each for .
Lemma 3
(Sobolev Inclusion). Let be a laser forcing such that . Then for all , each and as defined in (20).
Proof.
Suppose that . By recalling the initialization (11), we apply Lemma 2 to see that . By the definition of the Sobolev space (14), it follows that and thus by applying Lemma 2 again it follows that and similarly . We now hypothesize for induction that each . The base case was just shown. Based on the iteration (9) and by applying the small amplitude assumption (18), we see that
Since and by assumption, we apply Lemma 1 with and on the derivatives and on the derivatives to see that the right hand side is an function such that from Lemma 2. A similar argument holds for each so we conclude that . Based on this Sobolev inclusion, we may again apply Lemma 1 to the terms in the expression for to see that . □
We now apply the triangle inequality to the norm of the expression (21) which yields
Recall that we can define the Sobolev space
The norm for is then
By this definition, it then follows that
Hence, by applying Lemma 1 with and , we can establish the following inequalities on the norms:
Note that by definition of the norm (16) in the Sobolev space for some , we can establish the inequality
Finally, by applying Lemma 2 to the Equation (19a), we see that for , with . We now establish the inequality on by:
With a similar approach, we provide the equivalent inequalities for and :
With a bound established on the difference between two terms in the iteration, we now show that for small enough the entire sequence remains in a small ball.
Lemma 4
(Bounded Sequence). There exists and for which the sequence defined by the iteration (9) with initialization (11) is bounded in a ball for all n.
Proof.
We show by strong induction that the sequence (9) is bounded by the ball centered at zero with radius R. Hence, let be defined such that
where we say
to keep R sufficiently large where each norm is measured over the domain . This establishes the base case for induction. Now, we hypothesize by induction that each
where we seek to show that . Thus, by the inequality (23), it follows that
By applying the definition of R and the inductive hypothesis it follows that , , , and . Hence, we can apply the inequality
where we select such that for , . Hence, let
and it follows that if then by the reverse triangle inequality
so
We now proceed by finding the similar terms and such that each respective term stays within the ball of radius R. From the inequality (24):
We recall that and we then apply a similar analysis to obtain:
To force , we then pick
From the inequality (25), we have:
So from applying the result for , we obtain
We now let where for all ,
so we conclude by induction that there exists such that the sequence remains bounded in a ball of radius R. □
Theorem 2
(Contraction Mapping). The iteration defined by (9) and (11) is a contraction mapping.
Proof.
From the above lemma, we establish by the triangle inequality that each
Hence, by the inequality (23) for , we have:
Similarly, the other variables satisfy
We now consider the space consisting of triples of functions with metric defined by:
Thus, for our set of fluid variables, we establish a new inequality for the sum of differences of index:
Now, define
such that
where we note that . Setting and defining by for functions then ensures the Lipschitz condition such that for :
Hence, the iteration is a contraction mapping. □
Since is a contraction mapping, we thus conclude by the Banach fixed-point theorem that F converges to a unique fixed-point such that the sequence . It then follows that this is the steady solution to the stream function-vorticity formulation of the Boussinesq Navier–Stokes equations for small amplitude forcing. □
Since the sequence is a convergent, Cauchy sequence, it follows that the inequality of the form (30) is equivalent to the inequality
which implies linear convergence to the unique solution for which satisfies the Lipschitz condition. From this result, we conclude that the iteration defined by (9) guarantees linear convergence for a sufficiently small amplitude forcing. The following section considers the relationship between the laser amplitudes for convergent solutions and the Re, Ri, and Pe numbers.
4. Numerical Results
4.1. Maximum Laser Amplitude
Based on the condition that the laser amplitude must be small enough for the iteration (9) to converge, we are motivated to find the relationship between the maximum allowable laser amplitude and the nondimensional fluid parameters Re, Ri, and Pe. We first consider a lemma which describes the asymptotic size of solutions as a function of these numbers.
Lemma 5
(Asymptotic Size of Solutions). Let be the norm and let f be normalized such that . If , then for ,
Similarly, if , then
Proof.
The proof proceeds by a simple inductive argument on the iteration (9). □
We now introduce a theorem which identifies an upper bound for laser amplitude as an asymptotic of the Re, Ri, Pe numbers.
Theorem 3
(Upper Bound for Laser Amplitude). Let E be the set of all amplitudes ε such that the iteration (9) converges. If , then
Similarly, if , then
Proof.
Recall from Theorem 2 that for the fixed-point iteration to converge, we require
for an such that the entire sequence of solutions stay bounded in a ball of size R. A least upper bound for the allowable laser amplitude, then, may be determined by finding a greatest lower bound for R such that the sequence of solutions stays bounded. This will thus be a least upper bound for solutions in the norm for a given . Suppose that . Then from the above lemma, we observe that the size of the nth iteration may be bounded by the asymptotic . Then for the supremum of the amplitude,
Now, suppose that . By again applying Lemma 5, we observe that the size of the nth iteration may now be bounded by the asymptotic . Then for the supremum of the amplitude,
□
Based on the relationships defined in Theorem 3, we expect the maximum computable amplitude in a numerical implementation of the iteration to adhere to an asymptotic relationship in these dimensionless parameters. By considering the homogeneous Dirichlet boundary condition in the stream function-vorticity formulation, we run the algorithm for increasing laser amplitudes until the iteration diverges to determine the max amplitude within an error of . Figure 2 and Figure 3 provide these numerical results with a comparison to the expected asymptotic relationship.
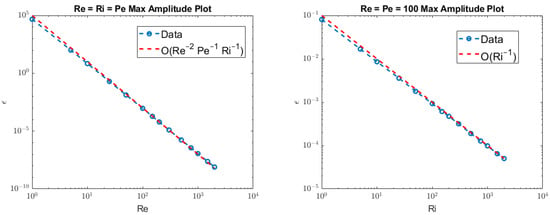
Figure 2.
These figures provide a log-log plot of maximum amplitude as a function of on the left and as a function of Ri with on the right. Based on the asymptotic relationship, we expect the max amplitude to scale by on the left figure and by on the right figure, both of which are seen here.
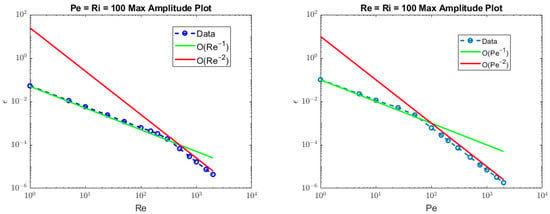
Figure 3.
These figures provide a log-log plot of maximum amplitude as a function of Re with on the left and as a function of Pe with on the right. Based on the asymptotic relationship, we expect the max amplitude to scale by when and when on the left figure and by when and when on the right figure. This is observed for both cases since the asymptotic relationship changes when .
From these results, we observe that the convergence analysis gives accurate predictions for the maximum laser amplitude as computed in the numerical algorithm. This is significant, since we see that the maximum allowable laser amplitude scales by the inverse square of the Reynolds number or Peclet number depending on their relative size. For physical laser-fluid setups, this result suggests that the computation of steady solutions is particularly sensitive to fluid viscosity and fluid thermal diffusivity. Physical intuition suggests that this is true, since less viscous flows with lower rates of heat transfer will have a more elusive steady state. Hence, finding convergent solutions for both large amplitude laser forcing and large Reynolds and Peclet numbers proves difficult.
4.2. Numerical Simulations
We now consider the convergent solutions found through a numerical implementation of the iteration (9) in the slip boundary condition. First, we specify the Re, Ri, Pe numbers to appropriately characterize fluid flow. Akers and Reeger [1] provide a discussion on the relationship between these parameters and the fluid behavior in thermal blooming. For the normalized laser forcing , we pick to represent rapid Gaussian decay from the origin towards the boundary of the domain. This parameter, however, can also be changed based on the exact laser specifications. We assign and with a grid spacing of and a laser amplitude of . Figure 4 provides a streamline plot to the left and a plot of the temperature fluctuation to the right for the steady-state solution to the slip boundary condition.
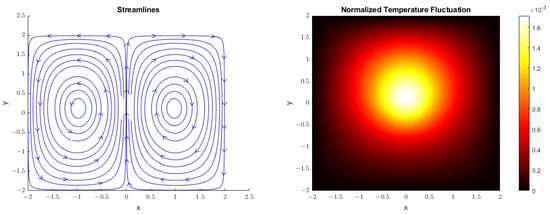
Figure 4.
These figures provide a streamline and temperature plot for the no-slip boundary condition. We see that the streamlines imply a symmetric circulation of the flow which extends to the boundary of the domain. The peak temperature fluctuation is shifted upwards in the domain due to the gravitational convection of the fluid.
We can clearly see here the result of the buoyancy driven convection within the domain. Fluid heated by the laser in the center of the domain rises until it contacts the top, then travels along the boundary to satisfy the slip condition. Steady vortex rings are formed to the left and right of center, which are centered horizontally at the halfway point between the middle and the edge of the domain. The vertical center of the vortex rings shift with the peak temperature fluctuation, which occurs just above the domain center due to the heated fluid rising in a buoyancy driven flow. Figure 5 provides a plot of the temperature fluctuation along the line as a function of the vertical position.
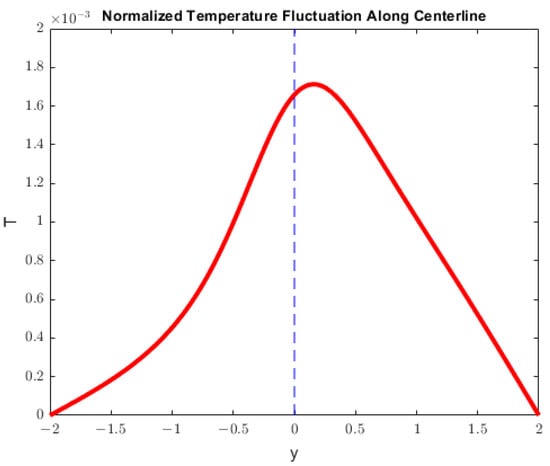
Figure 5.
This figure provides the normalized steady-state temperature fluctuation along the line as a function of the vertical position. The peak temperature fluctuation is shifted upwards and experiences asymmetric decay due to the influence of gravity.
Due to the influence of gravity in the steady-state, the temperature fluctuation exhibits asymmetry in the vertical direction. The peak temperature is shifted slightly upwards in the domain before asymmetric decay in temperature forces temperature to zero along the boundary.
5. Conclusions
This study considered the existence of solutions to a 2D steady, Boussinesq fluid flow problem in a stream function-vorticity formulation. Motivated by the fact that thermal blooming often plays an immense role in the simulation of laser propagation, the algorithm introduced in this paper provides a rapid numerical method for computing the steady-state of a buoyancy driven fluid while heated by a laser. For a small enough laser amplitude, we showed with a fixed-point argument that steady solutions indeed exist in an appropriate function space. The threshold which determines how small this amplitude must be is related to the nondimensional fluid parameters Re, Ri, Pe through an established asymptotic relationship. The theoretical derivation of this relationship was corroborated by numerical simulations, with a key result being that high amplitude convergent solutions are difficult to find for large Re and Pe numbers. We showed that the slip boundary condition for fluid velocity is equivalent to a homogeneous Dirichlet condition on the stream function and vorticity based on their respective definitions. The numerical simulations of these steady solutions described the existence of symmetric vortex rings in the left and right sides of the domain, implying that the fluid heated by the laser rises in a circulatory fashion before being recirculated within the domain. The peak temperature fluctuation was shifted upwards in the domain due to the same convective behavior, which prognosticates asymmetric laser propagation when slip boundary conditions are imposed in a finite box. In building upon this work, the authors are seeking to couple the presented fluid iteration with a laser propagation model to determine how buoyancy driven thermal blooming impacts on-target laser irradiance. Included in this pursuit is the investigation of more apt boundary conditions around the domain for a free-space laser propagation setup.
Author Contributions
Conceptualization, B.F.A.; methodology, B.F.A. and J.S.L.; software, J.S.L.; validation, B.F.A. and J.S.L.; formal analysis, J.S.L.; investigation, J.S.L.; resources, B.F.A.; data curation, J.S.L.; writing—original draft preparation, J.S.L.; writing—review and editing, B.F.A. and J.S.L.; visualization, J.S.L.; supervision, B.F.A.; project administration, B.F.A.; funding acquisition, B.F.A. All authors have read and agreed to the published version of the manuscript.
Funding
B. Akers acknowledges support from the Air Force Office of Sponsored Research under the project Radial Basis Functions for Numerical Simulation and the Office of Naval Research under the project A Machine Learning Approach for Simulation of Atmospheric Propagation of High Energy Lasers.
Conflicts of Interest
The authors declare no conflict of interest.
Disclaimer
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, make any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
References
- Akers, B.F.; Reeger, J.A. Numerical simulation of thermal blooming with laser-induced convection. J. Electromagn. Waves Appl. 2019, 33, 96–106. [Google Scholar] [CrossRef]
- Chakraborty, S. Order parameter modeling of fluid dynamics in narrow confinements subjected to hydrophobic interactions. Phys. Rev. Lett. 2007, 99, 1–4. [Google Scholar] [CrossRef]
- Chan, K.L.; Sofia, S. Turbulent compressible convection in a deep atmosphere. iii. tests on the validity and limitation of the numerical approach. Astrophys. J. 1986, 307, 222–241. [Google Scholar] [CrossRef]
- Karimzadeh, R. Spatial self-phase modulation of a laser beam propagating through liquids with self-induced natural convection flow. J. Opt. 2012, 14, 095701. [Google Scholar] [CrossRef]
- Vela, E.; Hafez, M.; Régnier, S. Laser-induced thermocapillary convection for mesoscale manipulation. Int. J. Optomechatron. 2009, 3, 289–302. [Google Scholar] [CrossRef]
- Flores-Flores, E.; Torres-Hurtado, S.A.; Páez, R.; Ruiz, U.; Beltrán-Pérez, G.; Neale, S.L.; Ramirez-San-Juan, J.C.; Ramos-García, R. Trapping and manipulation of microparticles using laser-induced convection currents and photophoresis. Biomed. Opt. Express 2015, 6, 4079. [Google Scholar] [CrossRef] [PubMed]
- Mourad, A.; Aissa, A.; Mebarek-Oudina, F.; Jamshed, W.; Ahmed, W.; Ali, H.M.; Rashad, A.M. Galerkin finite element analysis of thermal aspects of Fe3O4-MWCNT/water hybrid nanofluid filled in wavy enclosure with uniform magnetic field effect. Int. Commun. Heat Mass Transf. 2021, 126, 105461. [Google Scholar] [CrossRef]
- Jamshed, W.; Goodarzi, M.; Prakash, M.; Nisar, K.S.; Zakarya, M.; Abdel-Aty, A.H. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud. Therm. Eng. 2021, 26, 101160. [Google Scholar] [CrossRef]
- Masoomi, M.; Pegues, J.W.; Thompson, S.M.; Shamsaei, N. A numerical and experimental investigation of convective heat transfer during laser-powder bed fusion. Addit. Manuf. 2018, 22, 729–745. [Google Scholar] [CrossRef]
- Rennie, R.M.; Jumper, E.J.; Marineau, E.C. Investigation of the importance of convective heat transfer on laser-induced heating. J. Thermophys. Heat Transf. 2010, 24, 573–580. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Domnich, A.A. Model of a Nonuniformly Heated Viscous Flow through a Bounded Domain. Differ. Equ. 2020, 56, 304–314. [Google Scholar] [CrossRef]
- Artemov, M.A.; Baranovskii, E.S. Solvability of the Boussinesq approximation for water polymer solutions. Mathematics 2019, 7, 611. [Google Scholar] [CrossRef]
- Larios, A.; Lunasin, E.; Titi, E.S. Global well-posedness for the 2D Boussinesq system with anisotropic viscosity and without heat diffusion. J. Differ. Equ. 2013, 255, 2636–2654. [Google Scholar] [CrossRef]
- Li, J.; Titi, E.S. Global Well-Posedness of the 2D Boussinesq Equations with Vertical Dissipation. Arch. Ration. Mech. Anal. 2016, 220, 983–1001. [Google Scholar] [CrossRef]
- Ferreira, L.C.; Villamizar Roa, E.J. Existence of solutions to the convection problem in a pseudomeasure-type space. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 1983–1999. [Google Scholar] [CrossRef]
- Kacprzyk, P. Long-time existence of solutions to the Navier-Stokes equations with inflow-outflow and heat convection. Math. Methods Appl. Sci. 2012, 35, 1000–1013. [Google Scholar] [CrossRef]
- Hao, C.; Li, H.L. Global existence for compressible Navier-Stokes-Poisson equations in three and higher dimensions. J. Differ. Equ. 2009, 246, 4791–4812. [Google Scholar] [CrossRef]
- Hishida, T. Global Exstence and Exponential Stability of Convection. J. Math. Anal. Appl. 1995, 196, 699–721. [Google Scholar] [CrossRef]
- Livingston, P.M. Thermally Induced Modifications of a High Power cw Laser Beam. Appl. Opt. 1971, 10, 426. [Google Scholar] [CrossRef]
- Ahmad, R.A. Steady-state numerical solution of the navier-stokes and energy equations around a horizontal cylinder at moderate reynolds numbers from 100 to 500. Heat Transf. Eng. 1996, 17, 31–81. [Google Scholar] [CrossRef]
- Bjorland, C.; Schonbek, M.E. Existence and stability of steady-state solutions with finite energy for the navier-stokes equation in the whole space. Nonlinearity 2009, 22, 1615–1637. [Google Scholar] [CrossRef][Green Version]
- Bruneau, C.H.; Jouron, C. An efficient scheme for solving steady incompressible Navier-Stokes equations. J. Comput. Phys. 1990, 89, 389–413. [Google Scholar] [CrossRef]
- Tian, Z.; Ge, Y. A fourth-order compact finite difference scheme for the steady stream function–vorticity formulation of the Navier–Stokes Boussinesq equations. Int. J. Numer. Methods Fluids 2003, 518, 495–518. [Google Scholar] [CrossRef]
- Deparis, S.; Rozza, G. Reduced basis method for multi-parameter-dependent steady Navier-Stokes equations: Applications to natural convection in a cavity. J. Comput. Phys. 2009, 228, 4359–4378. [Google Scholar] [CrossRef]
- Chandhini, G.; Sanyasiraju, Y.V.S.S. Local RBF-FD solutions for steady convection–diffusion problems. Int. J. Numer. Methods Eng. 2007, 72, 352–378. [Google Scholar] [CrossRef]
- Gresho, P.M.; Sani, R.L. On pressure boundary conditions for the incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 1987, 7, 1111–1145. [Google Scholar] [CrossRef]
- Acheson, D. Elementary Fluid Dynamics; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Quartapelle, L. Numerical Solution of the Incompressible Navier-Stokes Equations, 1st ed.; Birkhauser Verlag: Basel, Switzerland; Boston, MA, USA; Berlin, Germany, 1993; p. 283. [Google Scholar]
- Novak, K.A. Numerical Methods for Scientific Computing; Lulu Press, Inc.: Raleigh, NC, USA, 2017. [Google Scholar]
- Brezis, H. Functional Analysis, Sobolev Spaces, and Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Sobolev, S. On a Theorem of Functional Analysis. Am. Math. Soc. Transl. Ser. 2 1963, 33, 39–68. [Google Scholar]
- Sobolev, S. Some applications of functional analysis in mathematical physics. Transl. Math. Monogr. 1963, 7, 239. [Google Scholar]
- Behzadan, A.; Holst, M. Multiplication in Sobolev Spaces, Revisited. arXiv 2015, arXiv:1512.07379. [Google Scholar] [CrossRef]
- Villavert, J. Elementary Theory and Methods for Elliptic Partial Differential Equations; University of Texas: Austin, TX, USA, 2015. [Google Scholar]
- Langford, J. Comparison Theorems in Elliptic Partial Differential Equations with Neumann Boundary Conditions. Ph.D. Thesis, Washington University, St. Louis, MO, USA, 2012. [Google Scholar]
- Yu, X. Poisson Equation in Sobolev Spaces; Lecture Notes; University of Alberta: Edmonton, AB, Canada, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).