Flow Dynamics in a Model of a Left Ventricle with Different Mitral Valve Orientations
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
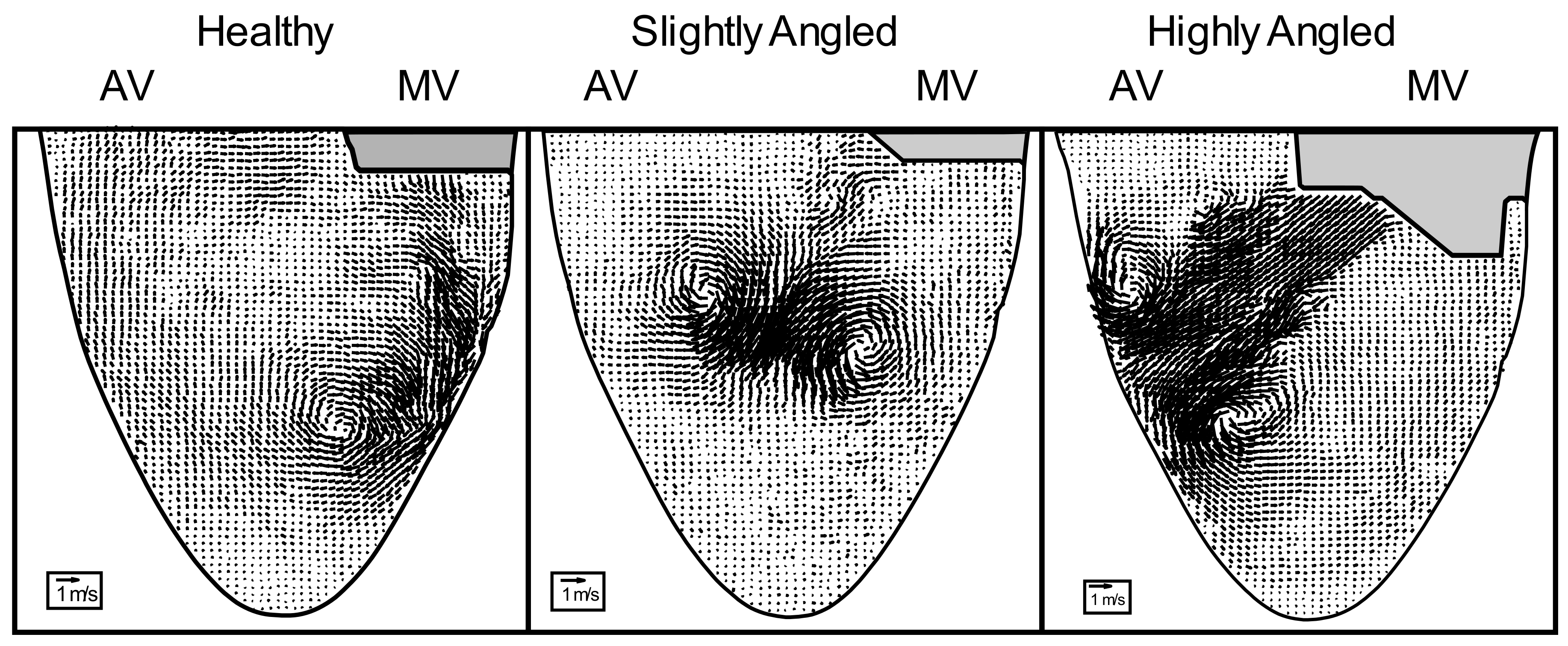
3.1. Effects of Misalignment
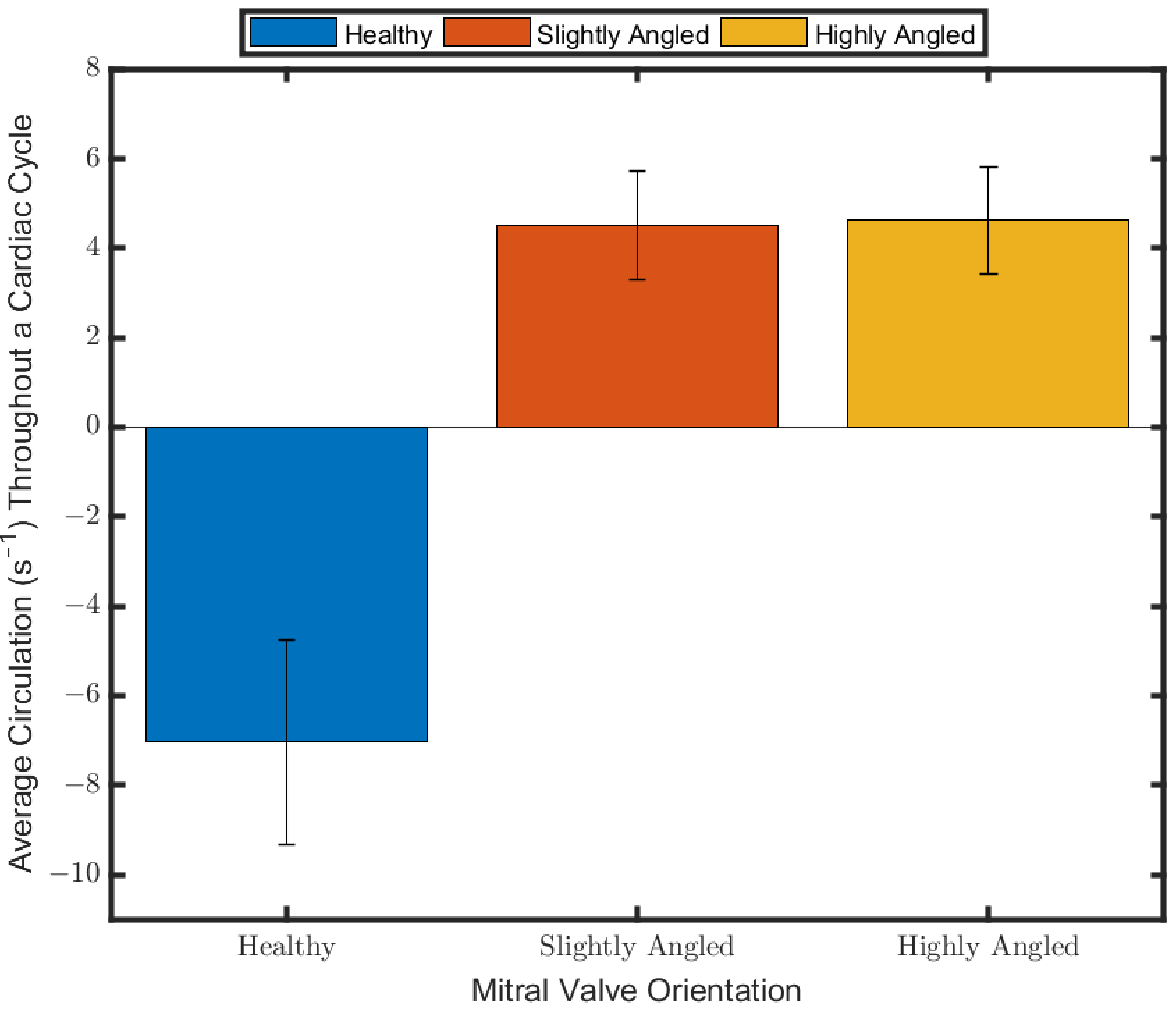
3.2. Circulation
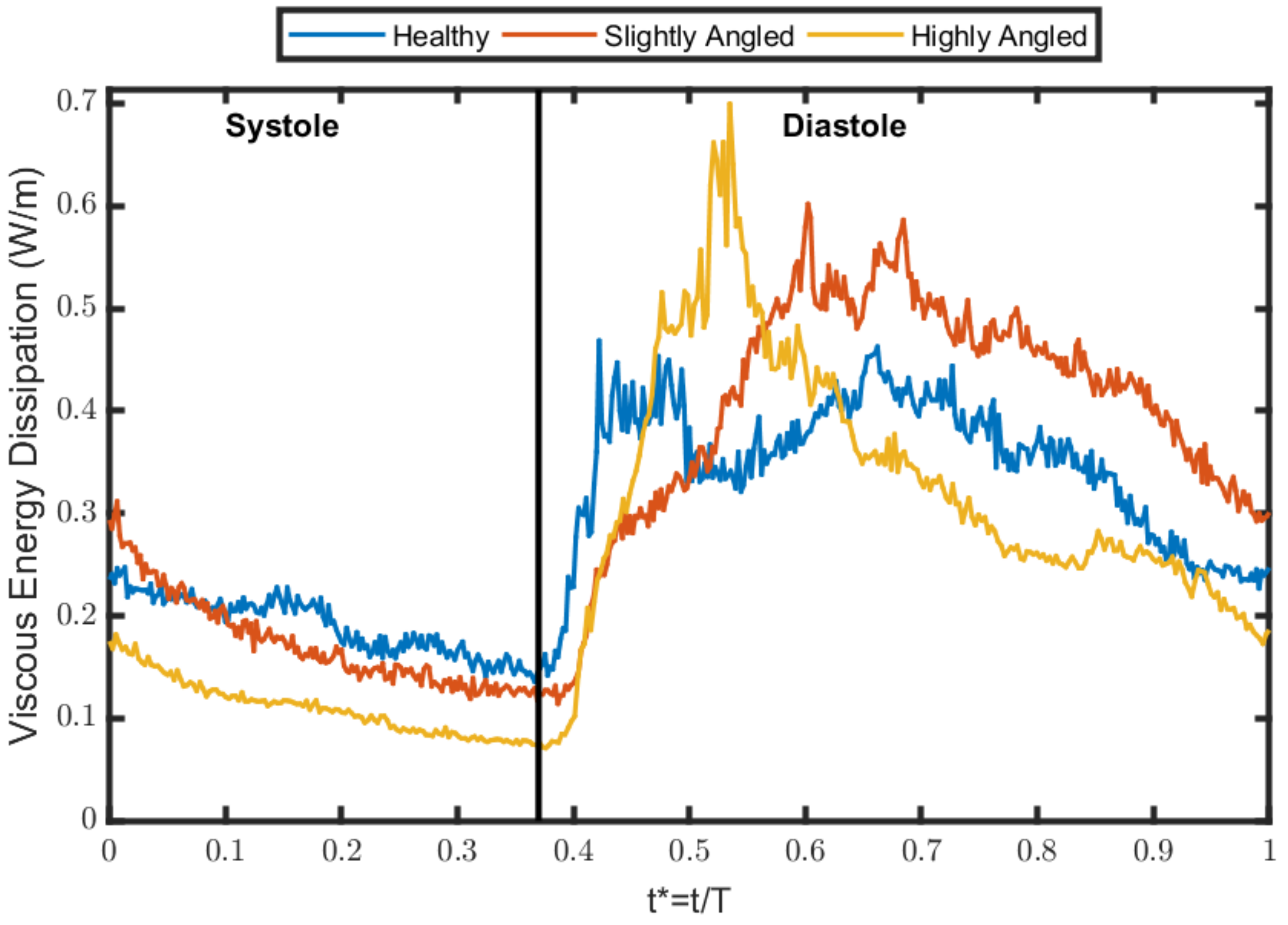
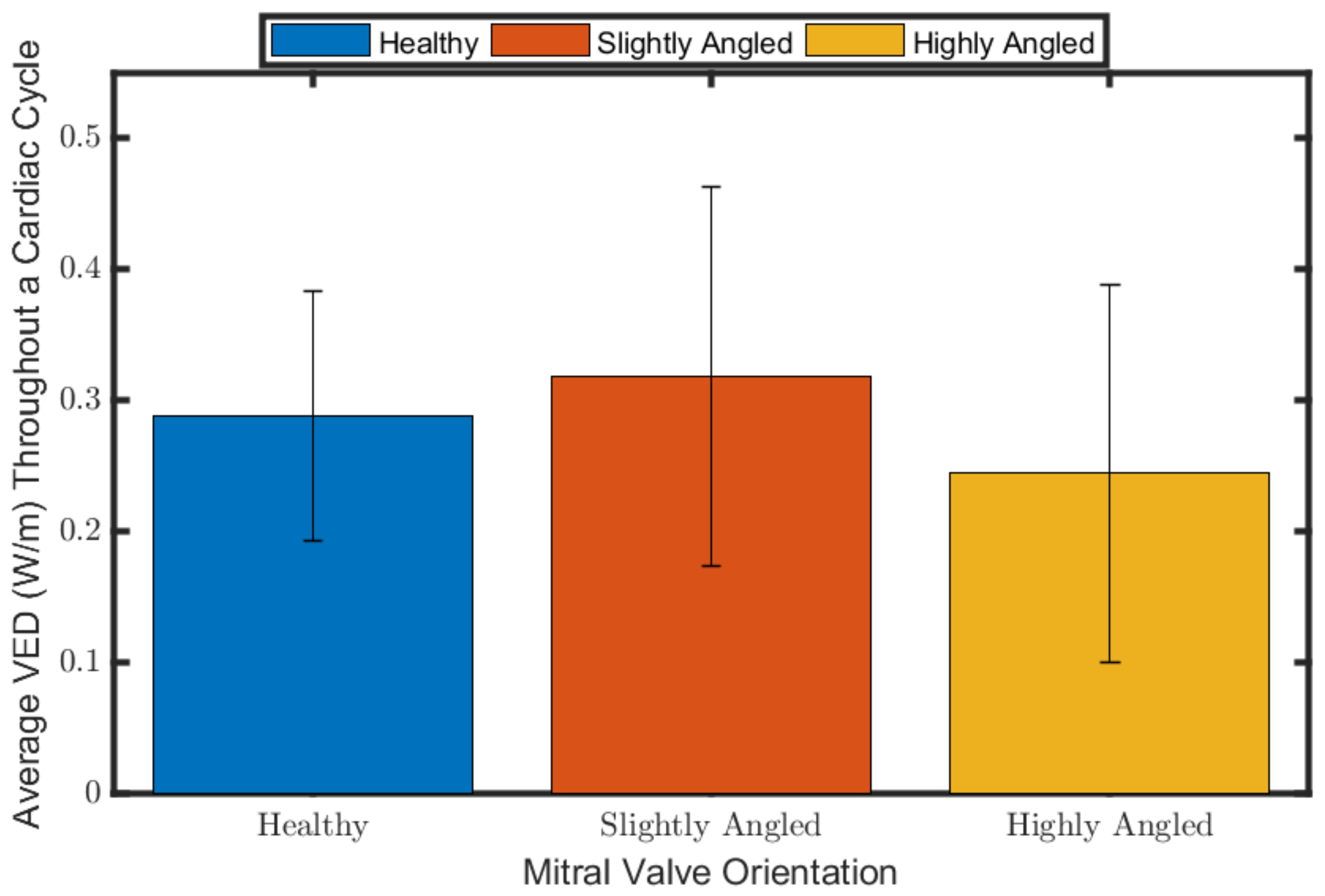
3.3. Viscous Energy Dissipation
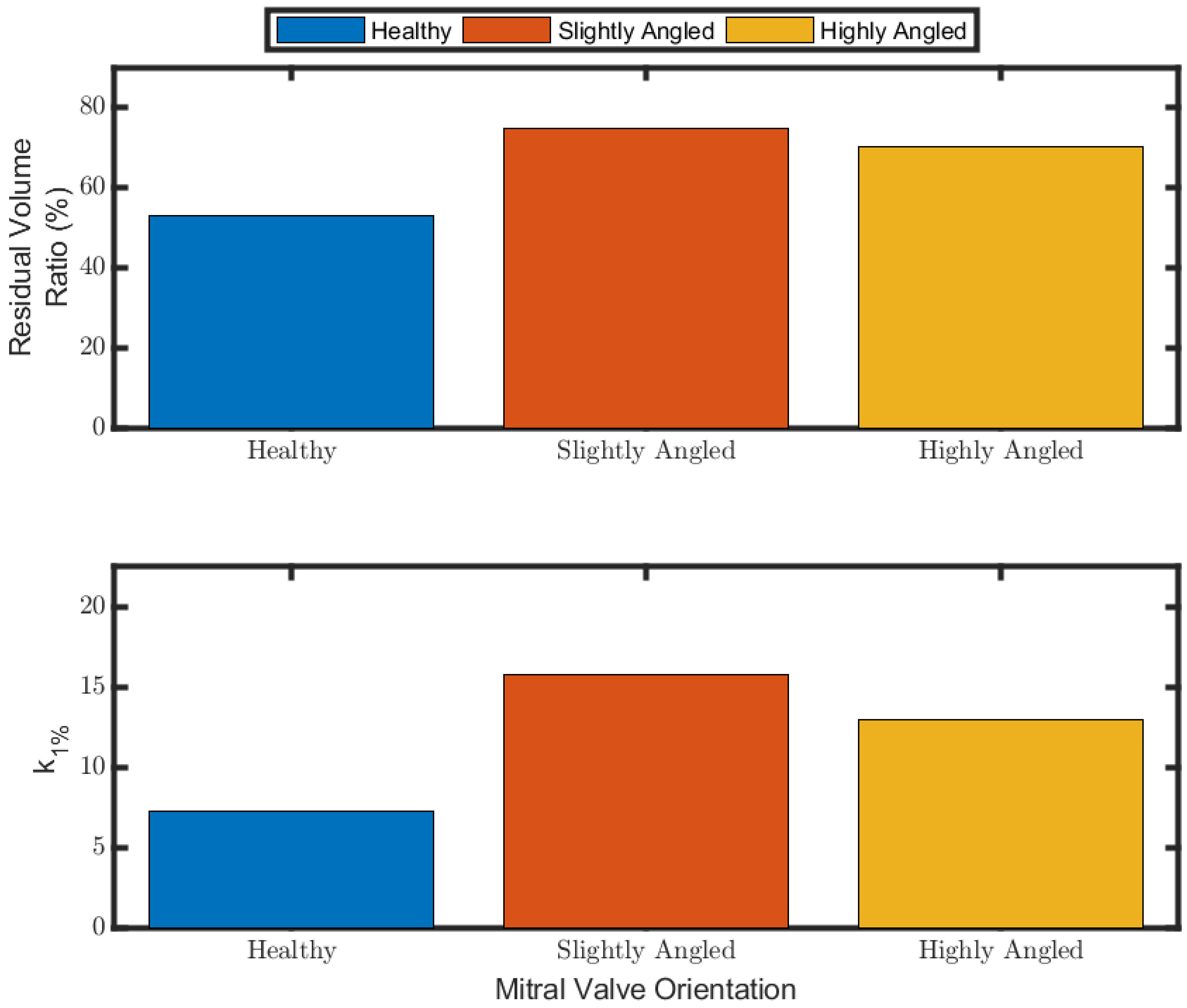
3.4. Ventricular Washout
3.5. Discussion
4. Limitations of the Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kilner, P.J.; Yang, G.-Z.; Wilkes, A.J.; Mohiaddin, R.H.; Firmin, D.; Yacoub, M.H. Asymmetric redirection of flow through the heart. Nature 2000, 404, 759–761. [Google Scholar] [CrossRef]
- Bellhouse, B.J. Fluid mechanics of a model mitral valve and left ventricle. Cardiovasc. Res. 1972, 6, 199–210. [Google Scholar] [CrossRef]
- Di Labbio, G.; Vétel, J.; Kadem, L. Material transport in the left ventricle with aortic valve regurgitation. Phys. Rev. Fluids 2018, 3, 113101. [Google Scholar] [CrossRef] [Green Version]
- Pedrizzetti, G.; Domenichini, F. Nature Optimizes the Swirling Flow in the Human Left Ventricle. Phys. Rev. Lett. 2005, 95, 108101. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Gao, Q.; Wei, R.; Wang, J. Experimental study on the effect of an artificial cardiac valve on the left ventricular flow. Exp. Fluids 2017, 58, 1–17. [Google Scholar] [CrossRef]
- Di Labbio, G.; Kadem, L. Jet collisions and vortex reversal in the human left ventricle. J. Biomech. 2018, 78, 155–160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kheradvar, A.; Houle, H.; Pedrizzetti, G.; Tonti, G.; Belcik, T.; Ashraf, M.; Lindner, J.R.; Gharib, M.; Sahn, D. Echocardiographic Particle Image Velocimetry: A Novel Technique for Quantification of Left Ventricular Blood Vorticity Pattern. J. Am. Soc. Echocardiogr. 2010, 23, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.C.; Hong, G.R. Intraventricular Flow: More than Pretty Pictures. Heart Fail. Clin. 2019, 15, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, K.; Nakamura, N.; Itatani, K.; Naito, Y.; Kinoshita, M.; Shimizu, M.; Hamaoka, S.; Kato, H.; Yasumoto, H.; Nakajima, Y.; et al. Flow-dynamics assessment of mitral-valve surgery by intraoperative vector flow mapping. Interact. Cardiovasc. Thorac. Surg. 2017, 24, 869–875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakashima, K.; Itatani, K.; Kitamura, T.; Oka, N.; Horai, T.; Miyazaki, S.; Nie, M.; Miyaji, K. Energy dynamics of the intraventricular vortex after mitral valve surgery. Heart Vessel. 2017, 32, 1123–1129. [Google Scholar] [CrossRef]
- Pedrizzetti, G.; Domenichini, F.; Tonti, G. On the Left Ventricular Vortex Reversal after Mitral Valve Replacement. Ann. Biomed. Eng. 2010, 38, 769–773. [Google Scholar] [CrossRef]
- Kheradvar, A.; Gharib, M. On Mitral Valve Dynamics and its Connection to Early Diastolic Flow. Ann. Biomed. Eng. 2008, 37, 1–13. [Google Scholar] [CrossRef]
- Espa, S.; Badas, M.G.; Fortini, S.; Querzoli, G.; Cenedese, A. A Lagrangian investigation of the flow inside the left ventricle. Eur. J. Mech. B Fluids 2012, 35, 9–19. [Google Scholar] [CrossRef]
- Reul, H.; Talukder, N.; Mu¨ller, E. Fluid mechanics of the natural mitral valve. J. Biomech. 1981, 14, 361–372. [Google Scholar] [CrossRef]
- Voorneveld, J.; Saaid, H.; Schinkel, C.; Radeljic, N.; Lippe, B.; Gijsen, F.J.; van der Steen, A.F.; de Jong, N.; Claessens, T.; Vos, H.J.; et al. 4-D Echo-Particle Image Velocimetry in a Left Ventricular Phantom. Ultrasound Med. Biol. 2020, 46, 805–817. [Google Scholar] [CrossRef] [Green Version]
- Warner, H.R.; Toronto, A.F. Effect of Heart Rate on Aortic Insufficiency as Measured by a Dye-Dilution Technique. Circ. Res. 1961, 9, 413–417. [Google Scholar] [CrossRef] [Green Version]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Scharnowski, S.; Kähler, C.J. Particle image velocimetry—Classical operating rules from today’s perspective. Opt. Lasers Eng. 2020, 135, 106185. [Google Scholar] [CrossRef]
- Faludi, R.; Szulik, M.; D’Hooge, J.; Herijgers, P.; Rademakers, F.; Pedrizzetti, G.; Voigt, J.-U. Left ventricular flow patterns in healthy subjects and patients with prosthetic mitral valves: An in vivo study using echocardiographic particle image velocimetry. J. Thorac. Cardiovasc. Surg. 2010, 139, 1501–1510. [Google Scholar] [CrossRef] [Green Version]
- Akiyama, K.; Maeda, S.; Matsuyama, T.; Kainuma, A.; Ishii, M.; Naito, Y.; Kinoshita, M.; Hamaoka, S.; Kato, H.; Nakajima, Y.; et al. Vector flow mapping analysis of left ventricular energetic performance in healthy adult volunteers. BMC Cardiovasc. Disord. 2017, 17, 21. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, H.; Sugiura, S.; Hisada, T. The looped heart does not save energy by maintaining the momentum of blood flowing in the ventricle. Am. J. Physiol. Circ. Physiol. 2008, 294, H2191–H2196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seo, J.H.; Mittal, R. Effect of diastolic flow patterns on the function of the left ventricle. Phys. Fluids 2013, 25, 110801. [Google Scholar] [CrossRef]
- Suh, G.-Y.; Les, A.S.; Tenforde, A.S.; Shadden, S.C.; Spilker, R.L.; Yeung, J.J.; Cheng, C.P.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Quantification of Particle Residence Time in Abdominal Aortic Aneurysms Using Magnetic Resonance Imaging and Computational Fluid Dynamics. Ann. Biomed. Eng. 2010, 39, 864–883. [Google Scholar] [CrossRef] [Green Version]
- De Vecchi, A.; Marlevi, D.; Nordsletten, D.A.; Ntalas, I.; Leipsic, J.; Bapat, V.; Rajani, R.; Niederer, S.A. Left ventricular outflow obstruction predicts increase in systolic pressure gradients and blood residence time after transcatheter mitral valve replacement. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Reza, M.M.S.; Arzani, A. A critical comparison of different residence time measures in aneurysms. J. Biomech. 2019, 88, 122–129. [Google Scholar] [CrossRef]
- Bolger, A.F.; Heiberg, E.; Karlsson, M.; Wigström, L.; Engvall, J.; Sigfridsson, A.; Ebbers, T.; Kvitting, J.-P.; Carlhäll, C.J.; Wranne, B. Transit of Blood Flow Through the Human Left Ventricle Mapped by Cardiovascular Magnetic Resonance. J. Cardiovasc. Magn. Reson. 2007, 9, 741–747. [Google Scholar] [CrossRef]
- Hendabadi, S.; Bermejo, J.; Benito, Y.; Yotti, R.; Fernández-Avilés, F.; Del Alamo, J.C.; Shadden, S.C. Topology of blood transport in the human left ventricle by novel processing of Doppler echocardiography. Ann. Biomed. Eng. 2013, 41, 2603–2616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossini, L.; Martinez-Legazpi, P.; Vu, V.; Friera, L.F.; del Villar, C.P.; Rodríguez-López, S.; Benito, Y.; Borja, M.-G.; Pastor-Escuredo, D.; Yotti, R.; et al. A clinical method for mapping and quantifying blood stasis in the left ventricle. J. Biomech. 2015, 49, 2152–2161. [Google Scholar] [CrossRef] [Green Version]
- Goode, D.; Dhaliwal, R.; Mohammadi, H. Transcatheter Mitral Valve Replacement: State of the Art. Cardiovasc. Eng. Technol. 2020, 11, 229–253. [Google Scholar] [CrossRef]
- Domenichini, F.; Pedrizzetti, G.; Baccani, B. Three-dimensional filling flow into a model left ventricle. J. Fluid Mech. 2005, 539, 179–198. [Google Scholar] [CrossRef]
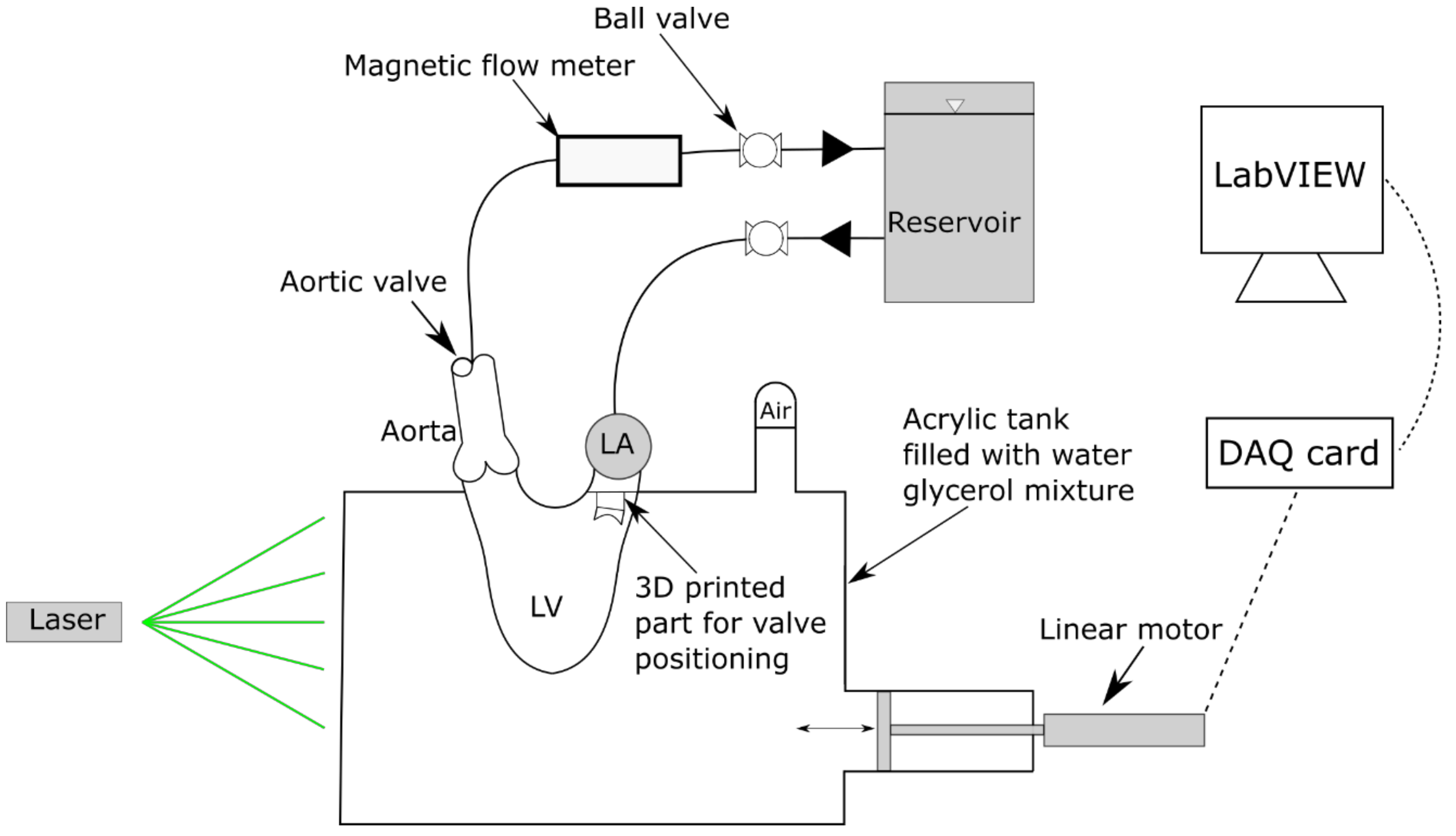
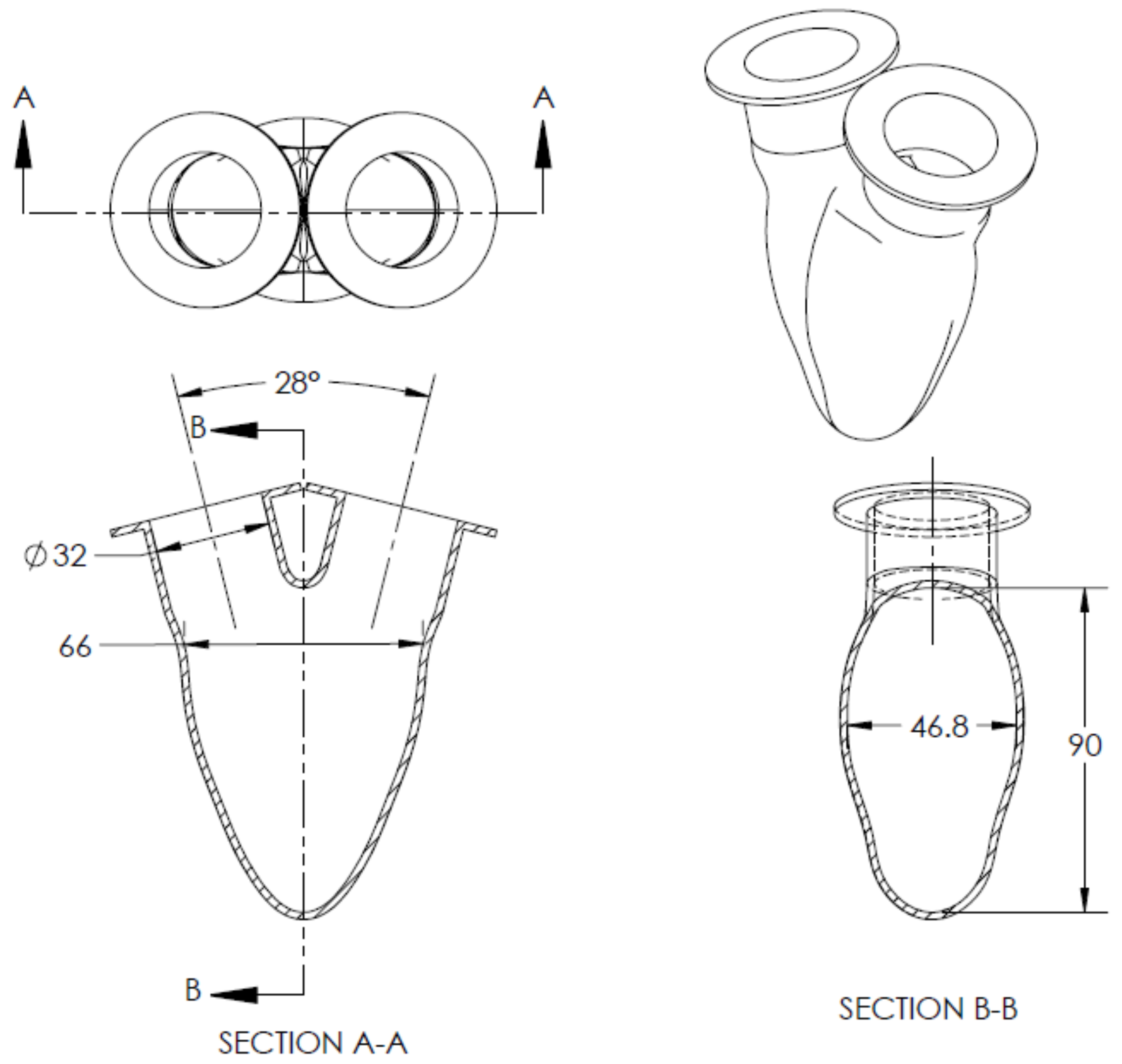
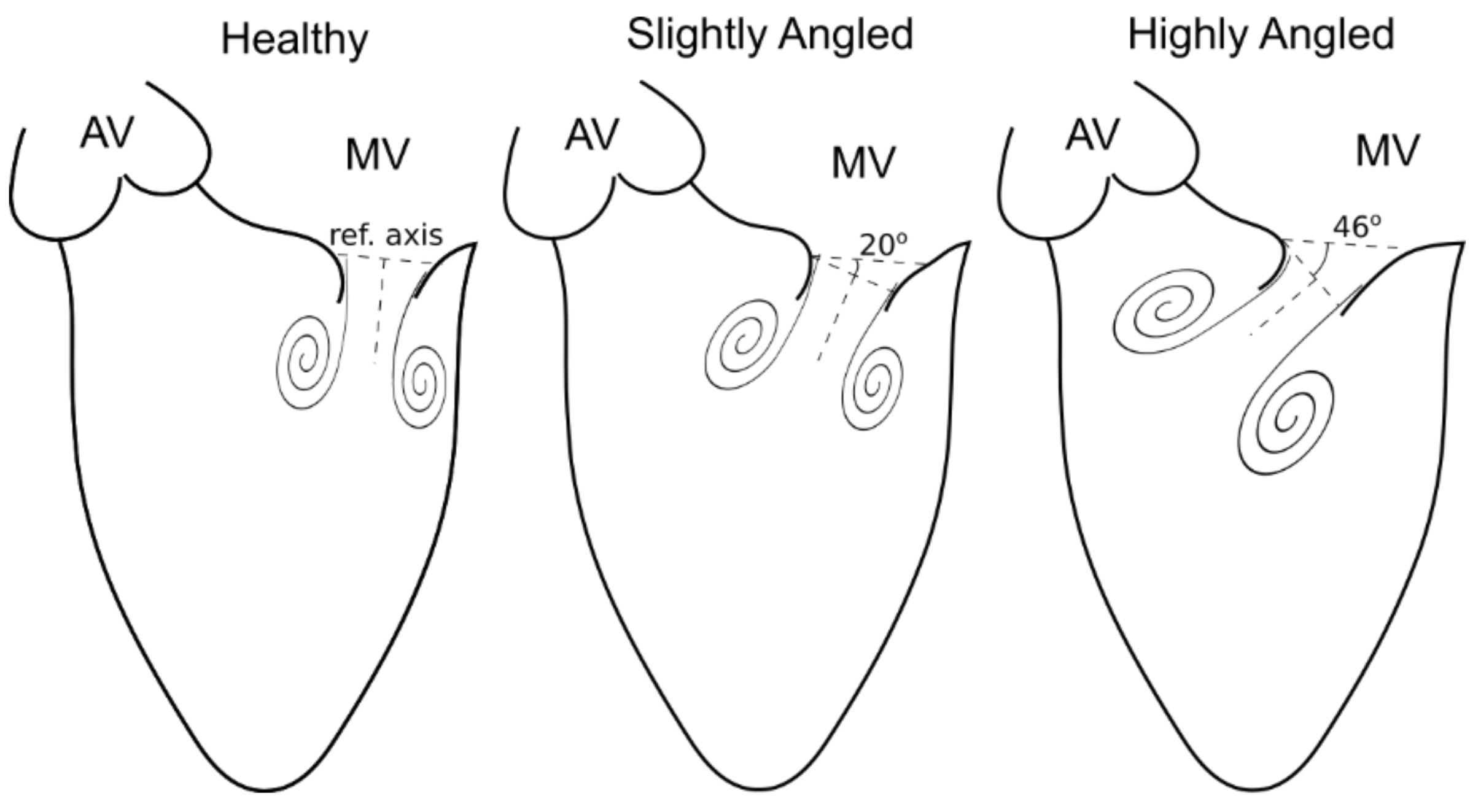
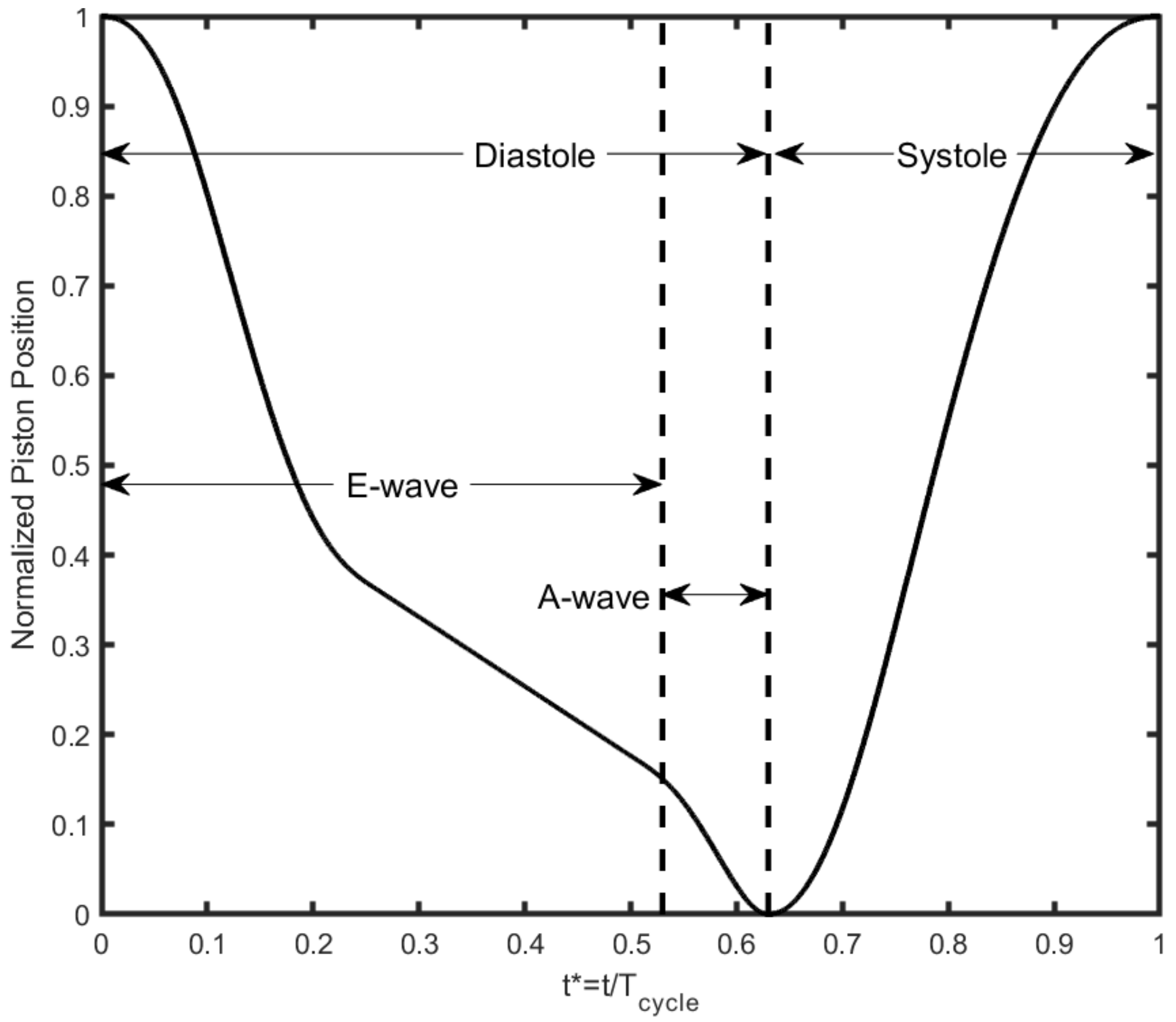


| Working Fluid Conditions | Simulator Conditions | ||
|---|---|---|---|
| Water–glycerol ratio | 60:40 | Heart rate | 80 bpm |
| Density (ρ) | 1100 kg/m3 | Cardiac cycle period | 0.75 s |
| Dynamic viscosity (μ) | 0.0042 Pa∙s | Systole duration | 0.28 s |
| Mitral valve diameter | 25 mm | ||
| Aortic valve diameter | 25 mm | ||
| Cardiac output | 3.1 ± 0.31 L/min | ||
| Mitral inflow Womersley number (Wo) a | 18.52 | ||
| Mitral inflow mean Reynolds number (Re) a | 689.17 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maraouch, G.; Kadem, L. Flow Dynamics in a Model of a Left Ventricle with Different Mitral Valve Orientations. Fluids 2021, 6, 428. https://doi.org/10.3390/fluids6120428
Maraouch G, Kadem L. Flow Dynamics in a Model of a Left Ventricle with Different Mitral Valve Orientations. Fluids. 2021; 6(12):428. https://doi.org/10.3390/fluids6120428
Chicago/Turabian StyleMaraouch, Ghassan, and Lyes Kadem. 2021. "Flow Dynamics in a Model of a Left Ventricle with Different Mitral Valve Orientations" Fluids 6, no. 12: 428. https://doi.org/10.3390/fluids6120428
APA StyleMaraouch, G., & Kadem, L. (2021). Flow Dynamics in a Model of a Left Ventricle with Different Mitral Valve Orientations. Fluids, 6(12), 428. https://doi.org/10.3390/fluids6120428






