1. Introduction
In this article, we investigate steady Boussinesq fluid convection driven by a laser source. More precisely, we present and interrogate a solution to the steady-state case of a buoyancy-driven fluid with a forcing term due to heat transfer from a laser. The Boussinesq approximation is highly accurate for such buoyancy-driven flows and is commonplace in laser propagation studies, especially those involving thermal blooming [
1]. This phenomenon of thermal blooming plays an important role in dictating the behavior of laser-fluid interaction within the context of laser propagation, and especially in domains such as manufacturing, remote sensing, directed energy, imaging, and several others [
2,
3,
4]. Motivated by the applications in these respective fields, we will consider steady-state laser convection within a 2D setting. Several authors have elucidated the means by which laser-induced convection, both in steady and unsteady regimes, can be applied to engineering and applied science problems. For example, Vela [
5] describes a method to manipulate micro-beads at mesoscale velocities within a convection chamber. In a similar analysis, Flores–Flores [
6] considers microparticle transport driven by laser-induced convective currents in gas at microscale velocities. In nanofluids, Mourad et al. [
7] and Jamshed et al. [
8] consider the thermal characteristics of fluid flow undergoing natural convection. At larger fluid velocities, Masoomi [
9] considered steady-state convective heat transfer from lasers in the context of additive manufacturing, and Rennie [
10] has discussed the impact laser-induced convection can have on material heating times in directed energy applications.
In treating the steady-state laser convection problem, we introduce an iterative numerical method to simulate steady solutions over a 2D finite grid. We provide a proof of existence of steady solutions for small enough laser amplitudes and we give a theorem to describe the scaling between nondimensional fluid parameters and a least upper bound for laser amplitude which permits computable solutions. There exist several papers in the relevant literature that prove convergence of iterations in weak and strong formulations for the Navier–Stokes equations. Work has already been done [
11,
12] to prove the existence of weak solutions in the 2D and 3D steady Navier–Stokes equations with a Boussinesq approximation and slip boundary conditions, but all in the primitive variable setting and without an implementable iteration to find the solutions. Other studies each considered an unforced problem or a problem with forcing along the boundary of the considered domain [
13,
14]. By choosing an appropriate function space, convergent iterations exist in at least two dimensions for steady and unsteady cases [
15,
16,
17,
18]. The iteration presented in this work, however, is unique in that it provides solutions to an internally forced convection problem. In our formulation, we establish a fixed-point iteration with existence in Sobolev spaces in two dimensions. From this iteration, we implement a finite-difference numerical algorithm to compute solutions over a grid. Previous work surrounding the simulation of laser-induced convection has included discussions about free versus forced convection [
19], difficulties with nondimensional scaling [
20], difficulties with deriving proper boundary conditions [
21], and several other associated problems. Similar finite difference algorithms do exist [
22,
23] along with methods that implement finite elements [
24] and radial basis functions [
25]; however, these algorithms do not consider a convection problem with internal forcing. Furthermore, in our analysis of the induced finite-difference scheme, we give particular consideration to the asymptotic scaling of the nondimensional fluid parameters.
Since the Navier–Stokes equations may be represented in either primitive variables (temperature, velocity, pressure), or in stream function-vorticity form, the chosen formulation informs on the techniques used to analyze potential solution methods. Both representations have their benefits. The stream function-vorticity formulation, however, is advantageous in that it implicitly guarantees divergence-free flow without the requirement of a pressure-correction term. In numerical implementations of the primitive Navier–Stokes equations, this pressure correction term often leads to solution inaccuracies arising from inappropriate choices in pressure boundary conditions [
26]. With the stream function-vorticity formulation, the choice of boundary conditions for each fluid variable is thus simplified. We consider here a no-friction slip condition in stream function-vorticity variables with homogeneous Dirichlet conditions for temperature. The slip condition is easily manifested in stream-function vorticity form as a homogeneous Dirichlet condition on the fluid stream function and vorticity. This condition allows for free tangential movement along the boundary, allowing for the development of vortex rings within the domain.
The novel findings from this study will include the existence of solutions arising from a numerically implementable iteration, as well as the asymptotic relationship between nondimensional fluid parameters and a maximum laser amplitude. In the following chapters, we discuss the relationship between the physical problem and the stream function-vorticity representation, we introduce and prove convergence of an iteration to solve the Boussinesq Navier–Stokes equations, and we conclude with results and a discussion on the asymptotic scaling of nondimensional fluid parameters with respect to convergence. Following this analysis, we provide numerical solutions to the steady-state and we examine the applications to laser beam propagation.
2. Formulation
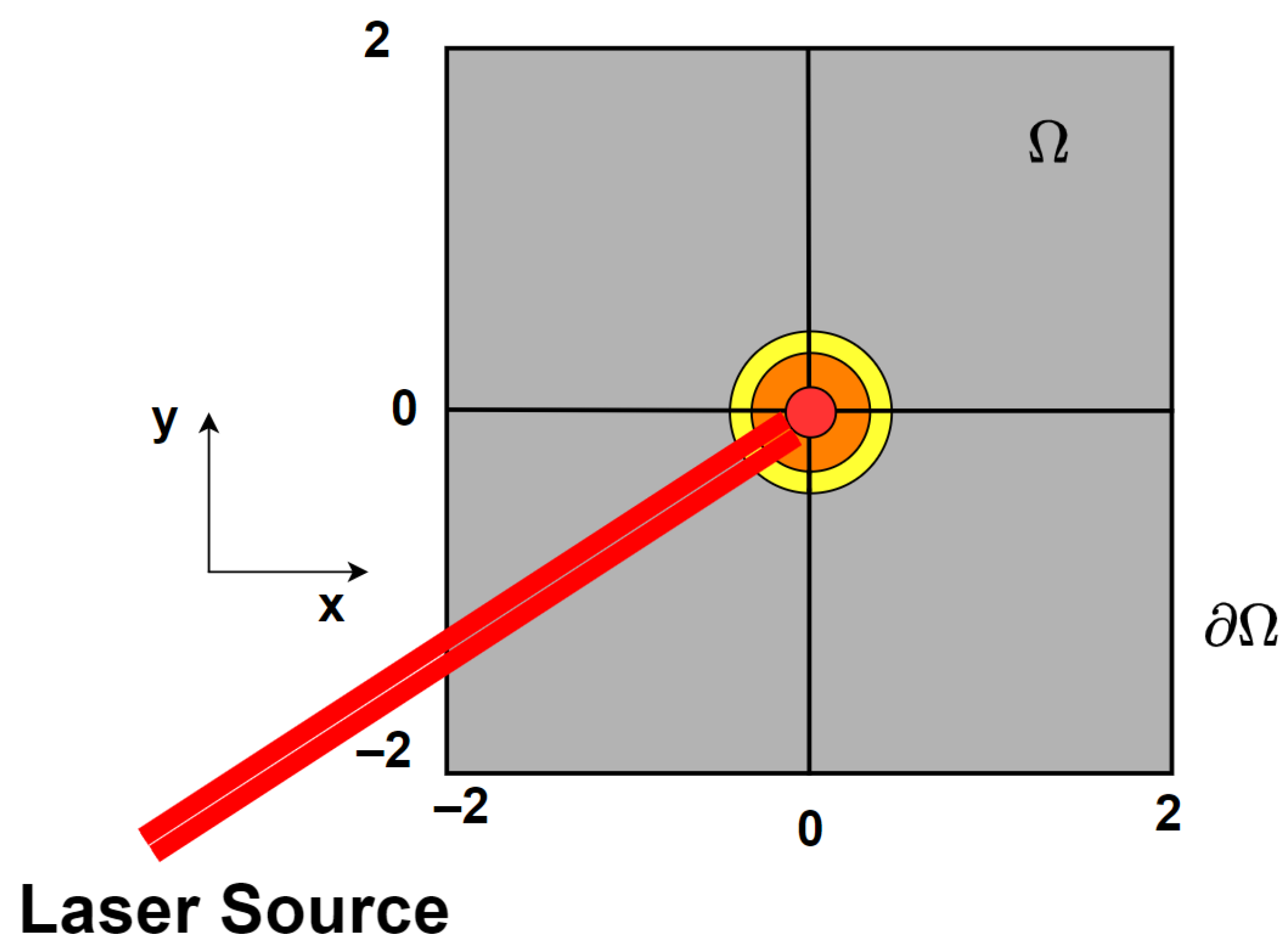
We now introduce our approach to mathematically describing the laser-fluid interaction of interest. We consider a model for laser-fluid interaction on a finite, 2D domain such that this domain represents a rectangular cross section along the propagation path (z coordinate) of the laser beam. That is, the domain will be a rectangular subsection of the
plane where we assume the Gaussian laser intensity profile is centered on the origin of the domain. This assumption would be most valid when considering thermal blooming at the laser aperture. We denote the domain as
and the boundary of the domain as
, where we begin by considering a square domain
as depicted in
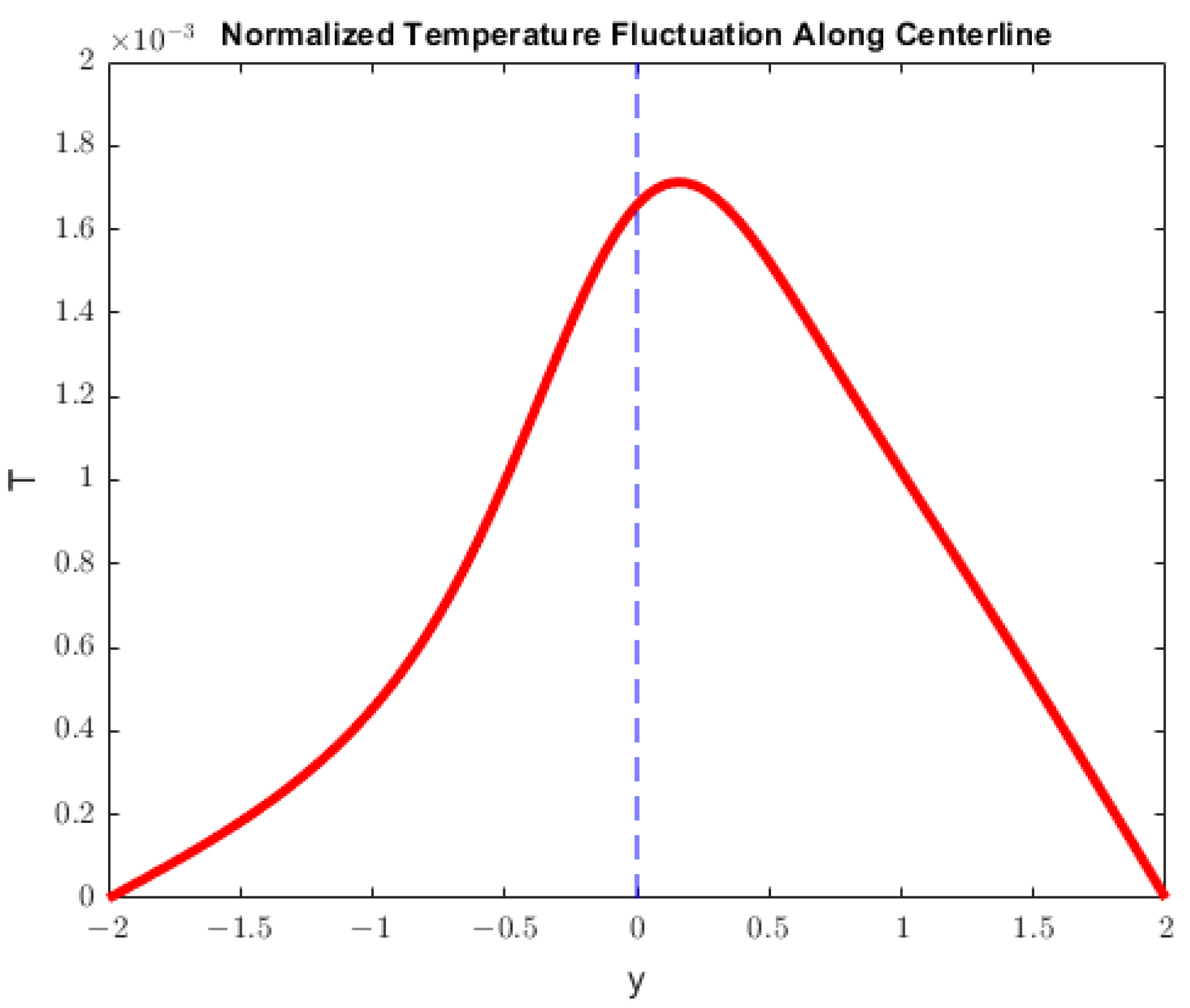
Figure 1.
Several assumptions on the fluid and laser properties must be imposed in the pursuit of governing equations which dictate fluid behavior. We assume an incompressible, Newtonian fluid which is governed by the Boussinesq approximation for buoyancy-driven flows. This Boussinesq model assumes that variations in fluid density have a linear relationship with temperature. Further, we assume a representation of the normalized laser irradiance as a function defined over the domain
such that the laser heats the fluid and induces temperature variations. We first introduce the governing equations for fluid flow in primitive variables where we seek the functions
representing the nondimensional temperature fluctuation, pressure, and velocity field of the fluid which obey the incompressible, Boussinesq Navier–Stokes equations undergoing forcing [
27]:
where
represents the laser forcing and
represents the unit vector in the vertical
y direction. For a characteristic length scale
L, characteristic velocity scale
U, force due to gravity
g, kinematic viscosity
, and thermal diffusivity
, the Reynolds, Peclet, and Richardson numbers are respectively defined as
We seek steady-state solutions such that all temporal variation is negligible and each
. In two dimensions, it is often easier to consider the stream function-vorticity form of the Boussinesq equations. This formulation reduces the total number of fluid variables by one, and often allows for easier treatment of boundary conditions. The transformation from the primitive form to the stream function-vorticity form is a well established procedure, where the two representations are equivalent for valid boundary data [
28]. We state the equivalent stream function-vorticity form of the steady Boussinesq equations below:
where
is the vorticity and
is the stream function of the fluid. Like the primitive formulation, we may interpret the system as a type of vector-valued, nonlinear Poisson equation over the domain
.
In this study, we consider a slip boundary condition on a finite box corresponding to zero shear stress along the boundary. This slip condition enforces boundary impermeability and assumes that the coefficient of friction between the fluid and the boundary is zero. That is, the normal component of velocity at the boundary vanishes but the tangential component is unrestricted. This boundary condition is useful in investigating laser-fluid interaction as it localizes the fluid within a finite domain without having to consider boundary layer effects. In primitive variables, where
, this is satisfied through the condition
Based on the definitions for the stream function
and the definition for vorticity
we may transform the primitive slip condition into an equivalent condition on the stream function and vorticity. First, if
on the top and bottom and
on the left and right, then
and
which is satisfied by taking
on all of
. For the vorticity, if
on the top and bottom, then
on the top and bottom. Similarly, if
on the left and right, then
on the left and right. It thus follows that the slip condition in primitive variables is equivalent to a homogeneous Dirichlet condition on the stream function and vorticity. For simplicity, we impose a homogeneous Dirichlet condition on the temperature, but a Neumann condition can also yield useful results. The slip condition in stream function-vorticity form is thus stated as
With the stream function-vorticity formulation posed as a system of coupled Poisson boundary value problems, we now define
,
, and
as the exact temperature fluctuation, vorticity, and stream function, respectively. We restate Equation (3) for the steady Navier–Stokes equations in the Boussinseq approximation as
We then introduce the fixed-point iteration for
as
where the laser irradiance takes the form of an amplitude
scaled by a normalized Gaussian
f
and we initialize the solution as
This initialization is the linearization of the system of equations and thus should serve as a strong initial guess for small amplitude solutions. We show in the following section that unique, convergent solutions exist for this iteration when laser amplitude is small.
In the numerical implementation of this iteration, we employ a finite difference scheme to successively solve the Poisson equations in each fluid variable at each step
n. We proceed by uniformly discretizing the domain
with step size
h, and we utilize a second order, centered difference approximation to discretize the Laplacian
For an
discrete grid, the solution to the discrete Poisson equation solution can be found in
flops [
29]. Since this represents the most computationally expensive step in the iteration, we thus conclude that the scheme (9) has an asymptotic cost of
when it converges to a unique solution. In a MATLAB implementation, we establish stopping criteria based on the Cauchy error of successive iterations. That is, the algorithm terminates when the numerical solutions converge based on the criterion
using vector 2-norms for some appropriately small
p. The following section is dedicated to demonstrating that these convergent solutions exist for small enough laser amplitudes.
3. Existence Proof
Recall that the iteration (9) was constructed so that its fixed points are steady solutions of (8), so this convergence of the scheme gives existence of solutions. We state this result as a theorem:
Theorem 1 (Convergence of Steady Solutions to the Stream Function-Vorticity Form of the Boussinesq Navier–Stokes equations). The iteration defined in (9) and (11) converges to unique solutions for small forcing and Dirichlet boundary conditions.
Proof. We begin by stating a definition from Brezis [
30] and two lemmas which assist in our analysis:
Definition 1 (Sobolev Spaces)
. Let and let with . If is an integer, then the Sobolev space is defined for all α with ,where we employ the multi-index notation such thatWe assign the . The space equipped with the normis a Banach space and we define the spaceoriginally defined by Sobolev in [31,32]. Lemma 1 (
is an algebra)
. Let . Suppose and . Then and gives that , and thatwhere M depends only on and d. Lemma 2 (Elliptic Estimate)
. If then there exists a unique solution towithAnd that solution satisfies where is a positive constant.
(see [34] for proof. A similar result also exists for inhomogeneous and Neumann boundary conditions for boundary data which satisfy compatibility conditions as described in [35,36].) We now introduce the small amplitude assumption on the dynamics, where each
is represented by a perturbation from the resting fluid case:
The key result of the proof involves constructing the equation for the difference between two iterations
and
(and similarly
and
,
and
) by applying the representation in (18) and subtracting (9) at the two indices
m and
n:
We proceed by investigating the form of Equation (19a) first. Define
where we manipulate the form of the equation to arrive at a more convenient expression:
We now prove that the function such that the norm by showing that each for .
Lemma 3 (Sobolev Inclusion)
. Let be a laser forcing such that . Then for all , each and as defined in (20). Proof. Suppose that
. By recalling the initialization (11), we apply Lemma 2 to see that
. By the definition of the Sobolev space (14), it follows that
and thus by applying Lemma 2 again it follows that
and similarly
. We now hypothesize for induction that each
. The base case was just shown. Based on the iteration (9) and by applying the small amplitude assumption (18), we see that
Since and by assumption, we apply Lemma 1 with and on the derivatives and on the derivatives to see that the right hand side is an function such that from Lemma 2. A similar argument holds for each so we conclude that . Based on this Sobolev inclusion, we may again apply Lemma 1 to the terms in the expression for to see that . □
We now apply the triangle inequality to the norm of the expression (21) which yields
Recall that we can define the Sobolev space
The norm for
is then
By this definition, it then follows that
Hence, by applying Lemma 1 with
and
, we can establish the following inequalities on the norms:
Note that by definition of the norm (16) in the Sobolev space
for some
, we can establish the inequality
Finally, by applying Lemma 2 to the Equation (19a), we see that for
,
with
. We now establish the inequality on
by:
With a similar approach, we provide the equivalent inequalities for
and
:
With a bound established on the difference between two terms in the iteration, we now show that for small enough the entire sequence remains in a small ball.
Lemma 4 (Bounded Sequence). There exists and for which the sequence defined by the iteration (9) with initialization (11) is bounded in a ball for all n.
Proof. We show by strong induction that the sequence (9) is bounded by the ball
centered at zero with radius
R. Hence, let
be defined such that
where we say
to keep
R sufficiently large where each
norm is measured over the domain
. This establishes the base case for induction. Now, we hypothesize by induction that each
where we seek to show that
. Thus, by the inequality (
23), it follows that
By applying the definition of
R and the inductive hypothesis it follows that
,
,
, and
. Hence, we can apply the inequality
where we select
such that for
,
. Hence, let
and it follows that if
then by the reverse triangle inequality
so
We now proceed by finding the similar terms
and
such that each respective term stays within the ball of radius
R. From the inequality (
24):
We recall that
and we then apply a similar analysis to obtain:
To force
, we then pick
From the inequality (
25), we have:
So from applying the result for
, we obtain
We now let
where for all
,
so we conclude by induction that there exists
such that the sequence remains bounded in a ball of radius
R. □
Theorem 2 (Contraction Mapping). The iteration defined by (9) and (11) is a contraction mapping.
Proof. From the above lemma, we establish by the triangle inequality that each
Hence, by the inequality (
23) for
, we have:
Similarly, the other variables satisfy
We now consider the space
consisting of triples
of
functions with metric defined by:
Thus, for our set of fluid variables, we establish a new inequality for the sum of differences of index:
Now, define
such that
where we note that
. Setting
and defining
by
for functions
then ensures the Lipschitz condition such that for
:
Hence, the iteration is a contraction mapping. □
Since is a contraction mapping, we thus conclude by the Banach fixed-point theorem that F converges to a unique fixed-point such that the sequence . It then follows that this is the steady solution to the stream function-vorticity formulation of the Boussinesq Navier–Stokes equations for small amplitude forcing. □
Since the sequence
is a convergent, Cauchy sequence, it follows that the inequality of the form (
30) is equivalent to the inequality
which implies linear convergence to the unique solution
for
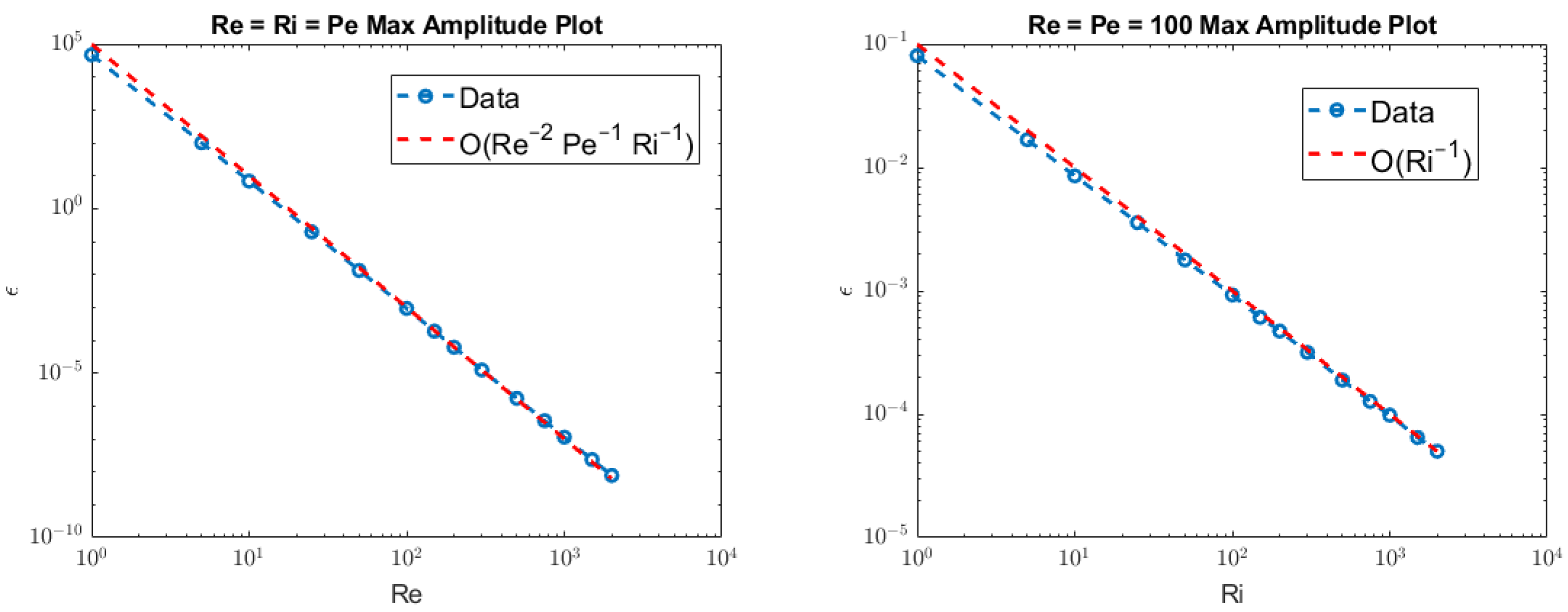
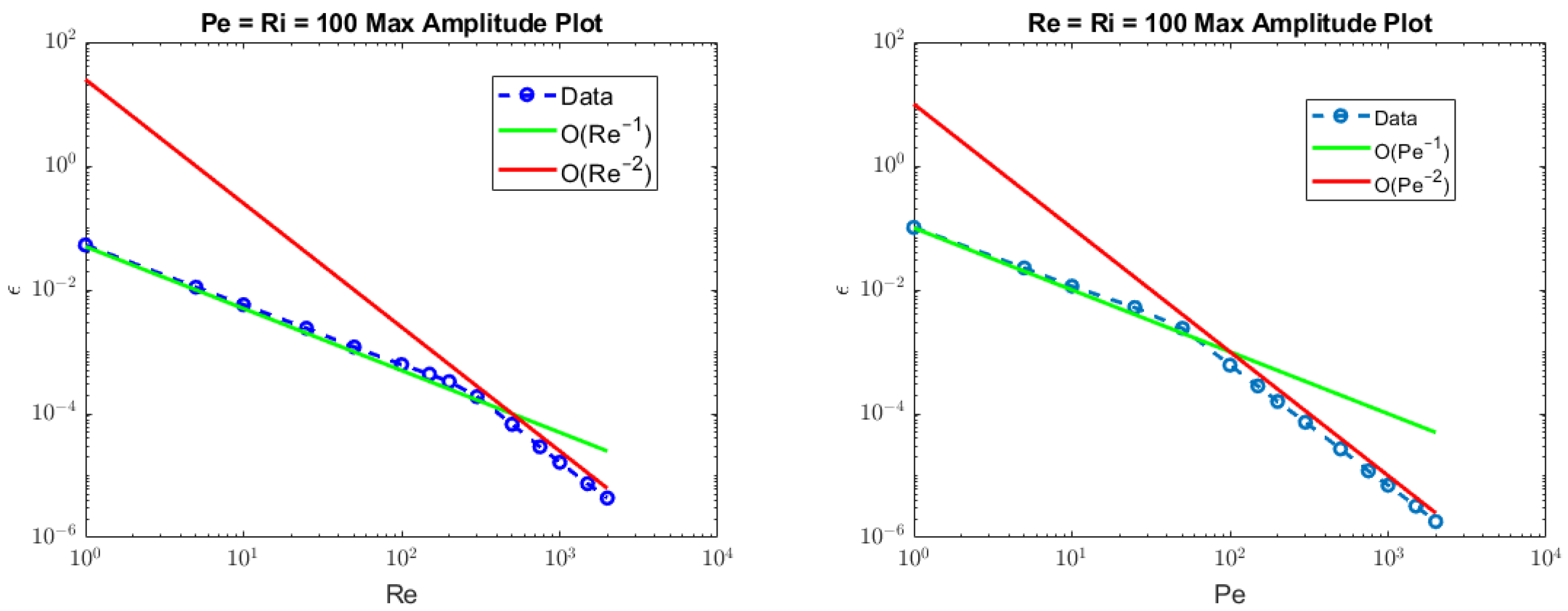
which satisfies the Lipschitz condition. From this result, we conclude that the iteration defined by (9) guarantees linear convergence for a sufficiently small amplitude forcing. The following section considers the relationship between the laser amplitudes for convergent solutions and the Re, Ri, and Pe numbers.