Parametric Study of Unsteady Flow and Heat Transfer of Compressible Helium–Xenon Binary Gas through a Porous Channel Subjected to a Magnetic Field
Abstract
1. Introduction
2. Problem Formulation and Methodology
2.1. Mathematical Model
2.2. Nondimensionalization Process
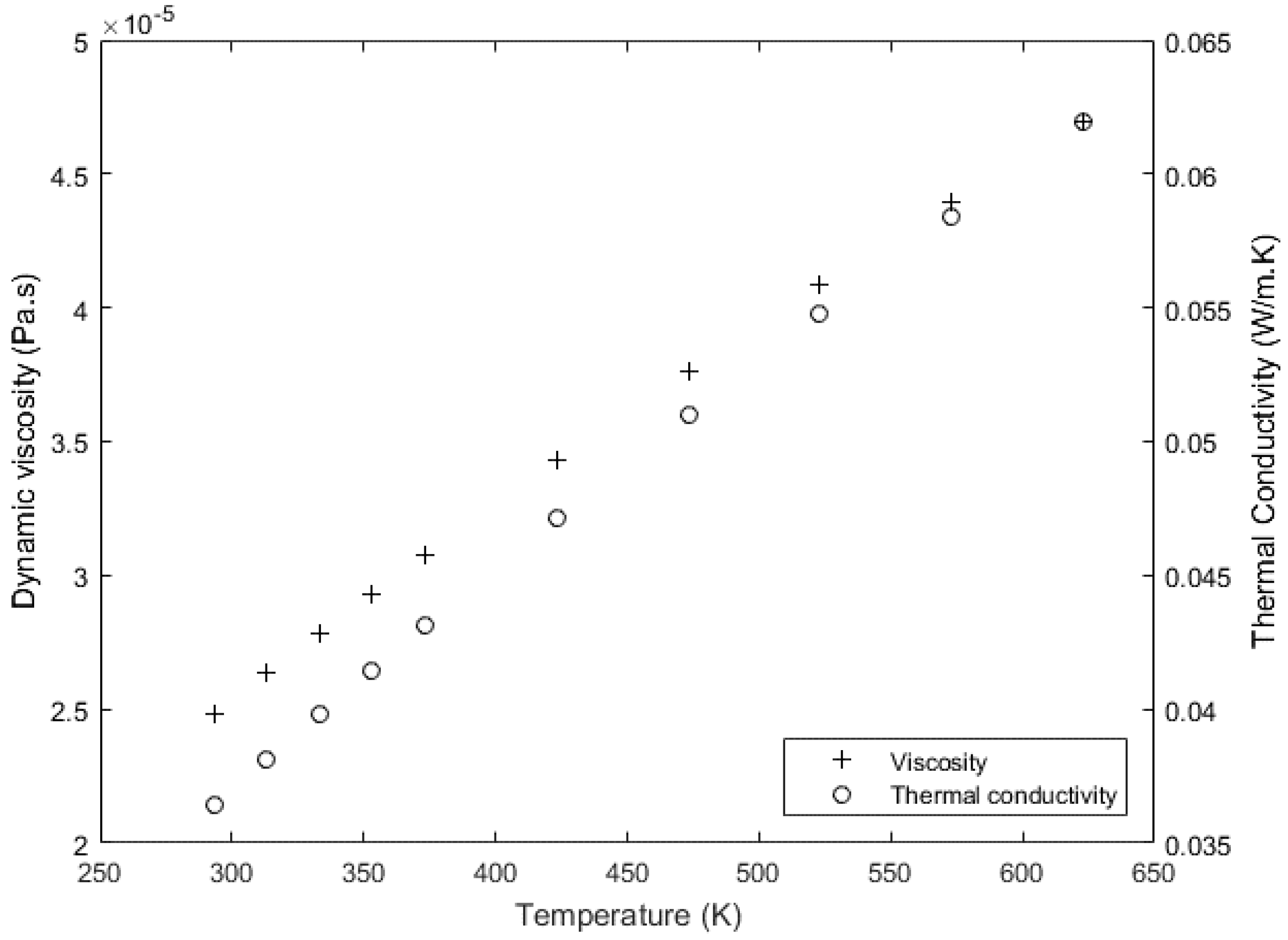
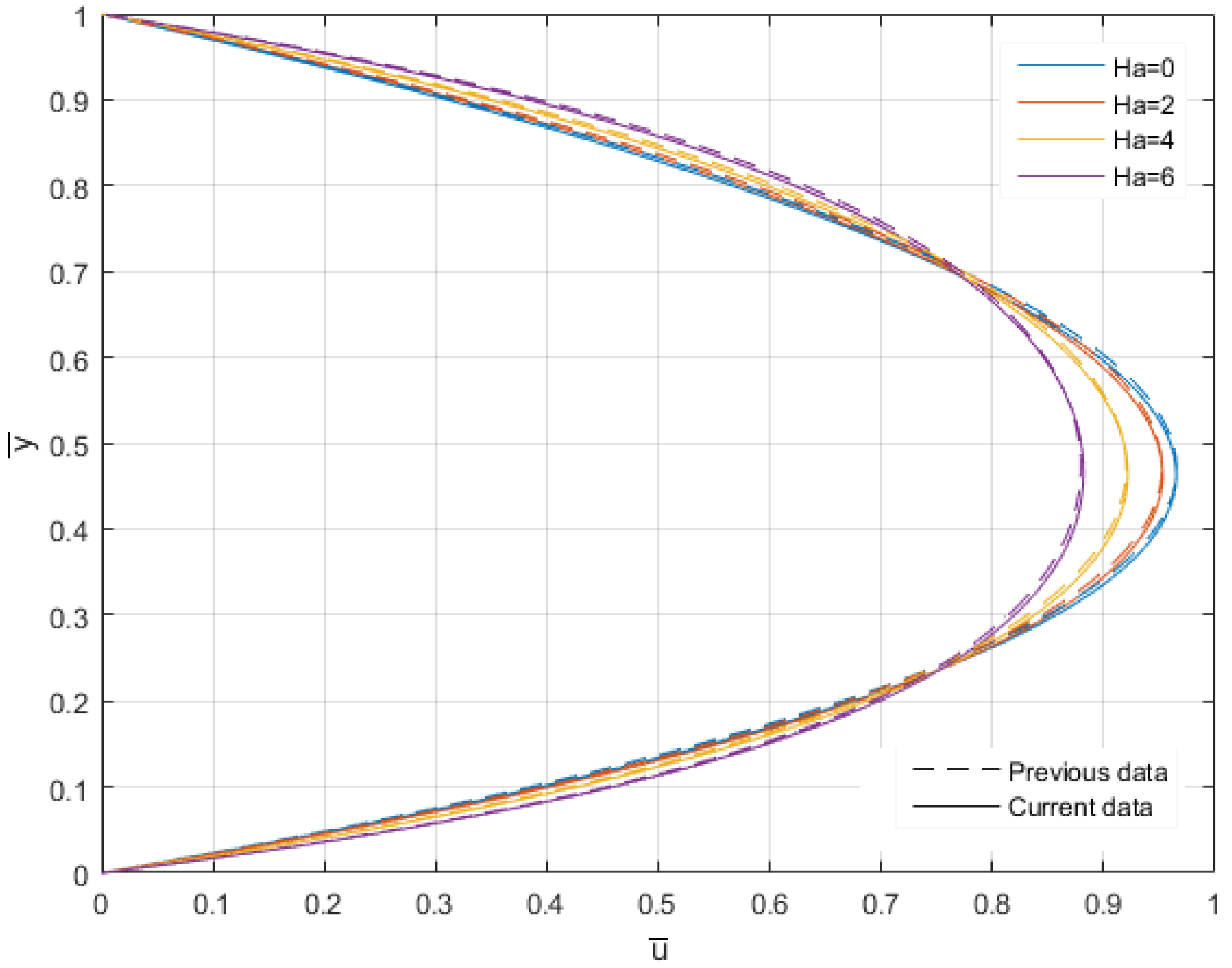
2.3. Numerical Procedure and Model Validation
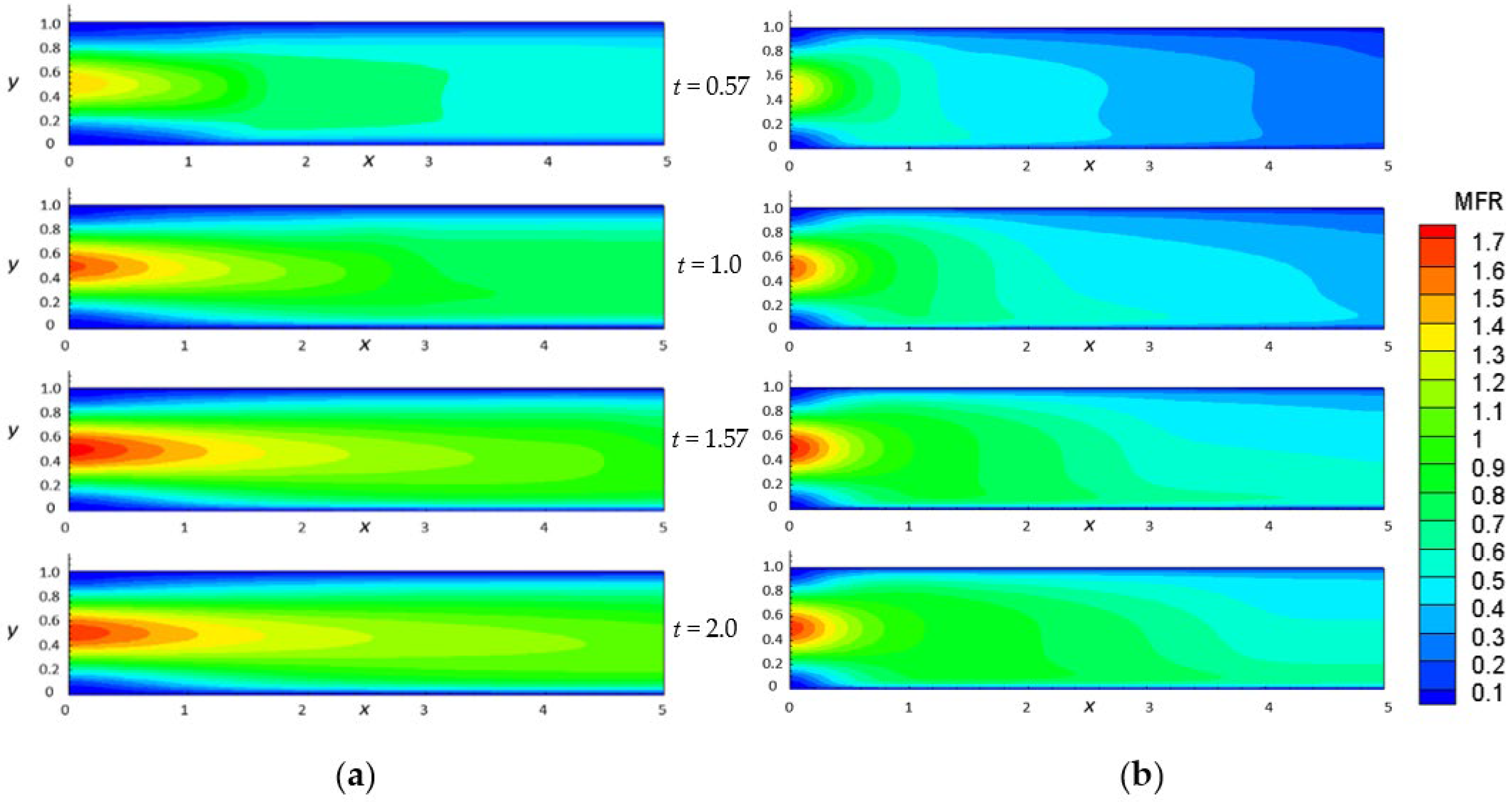
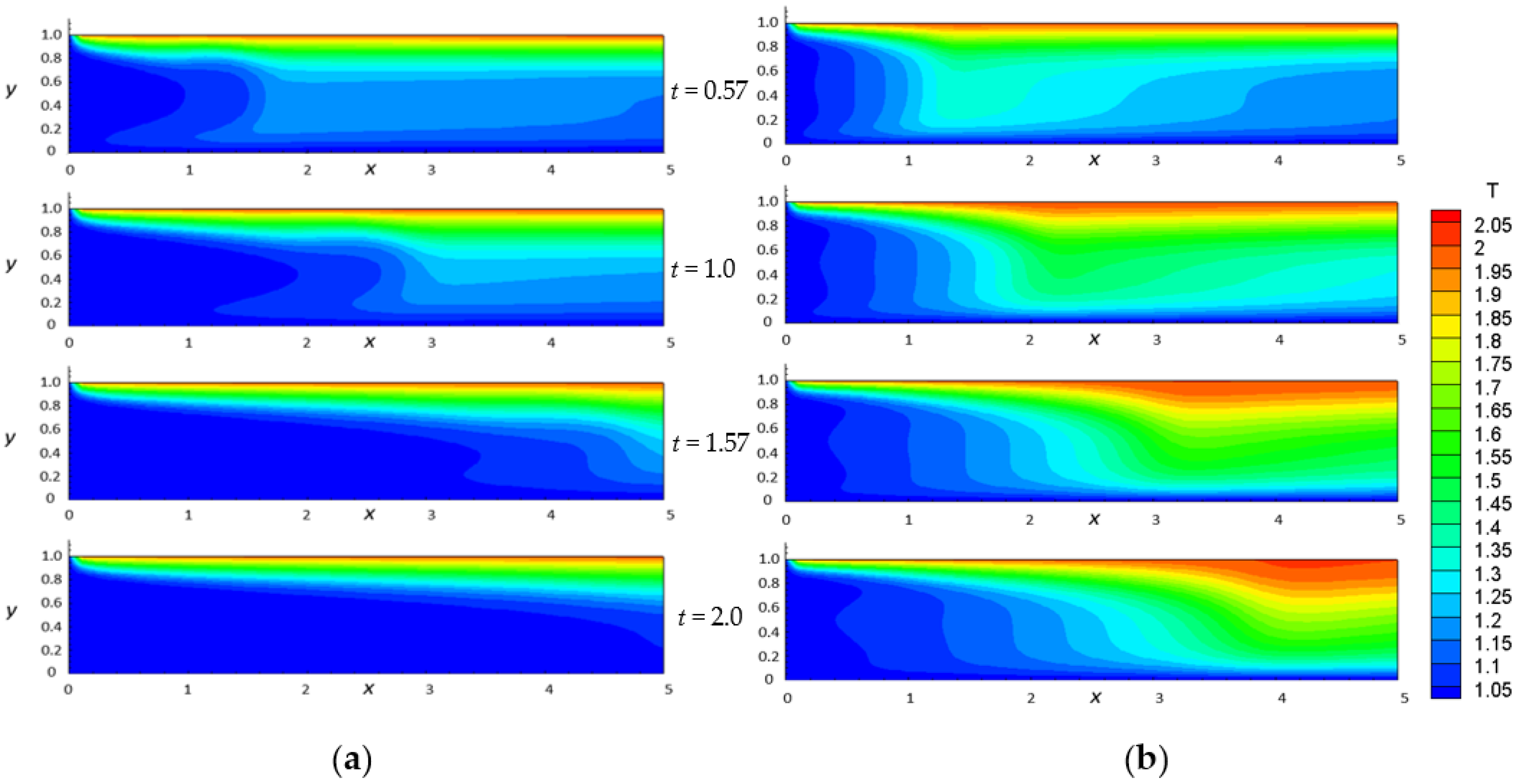
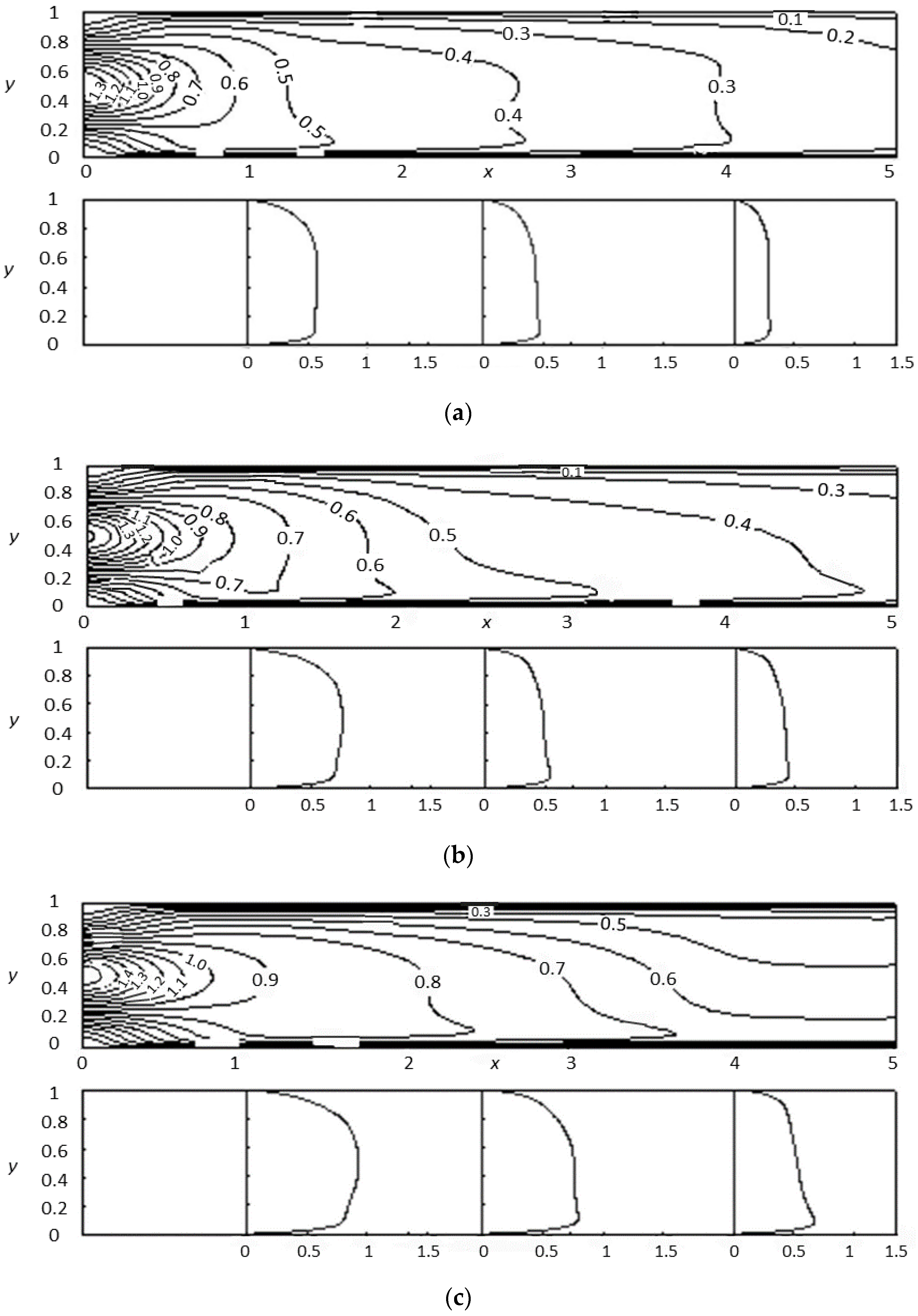
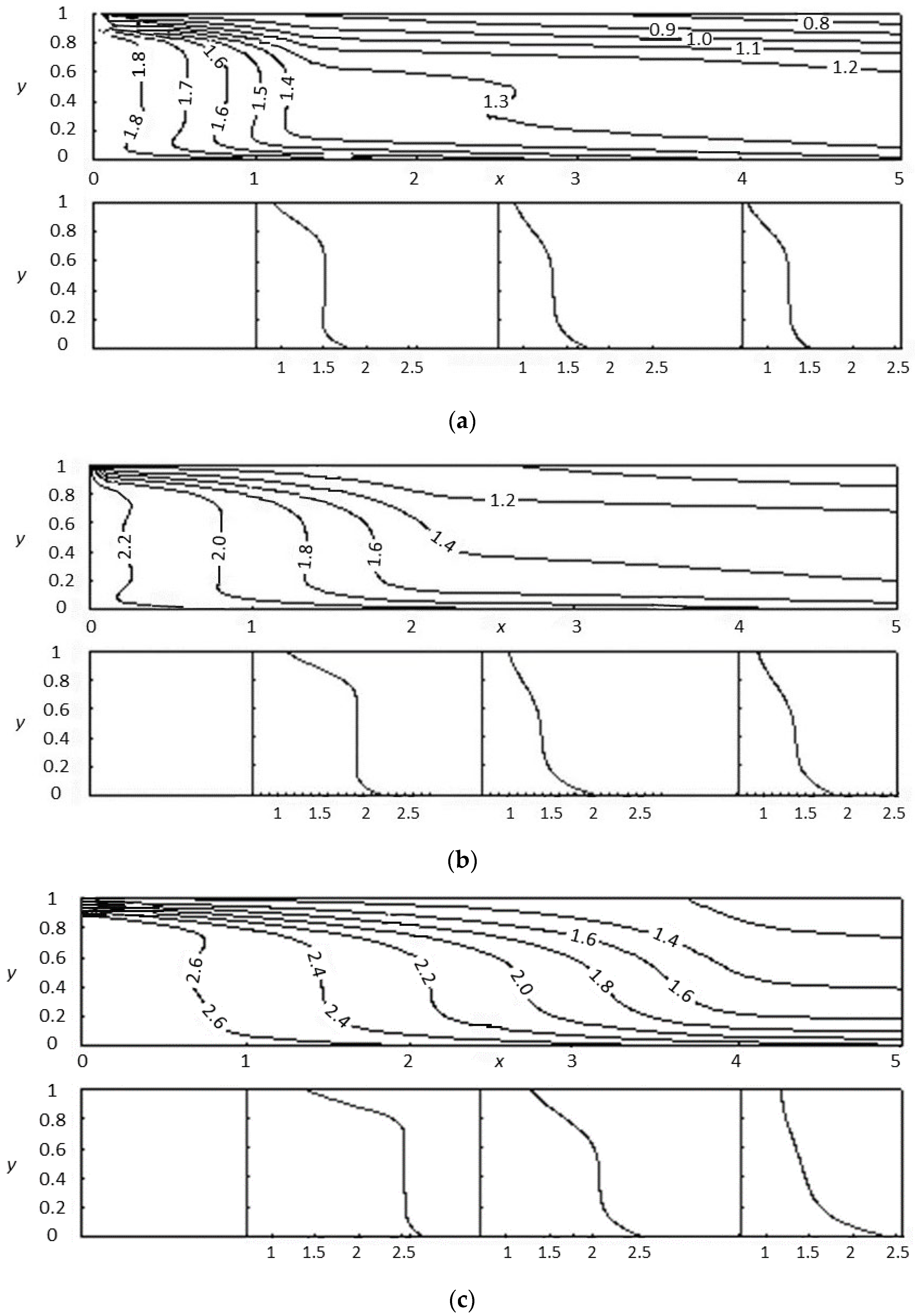
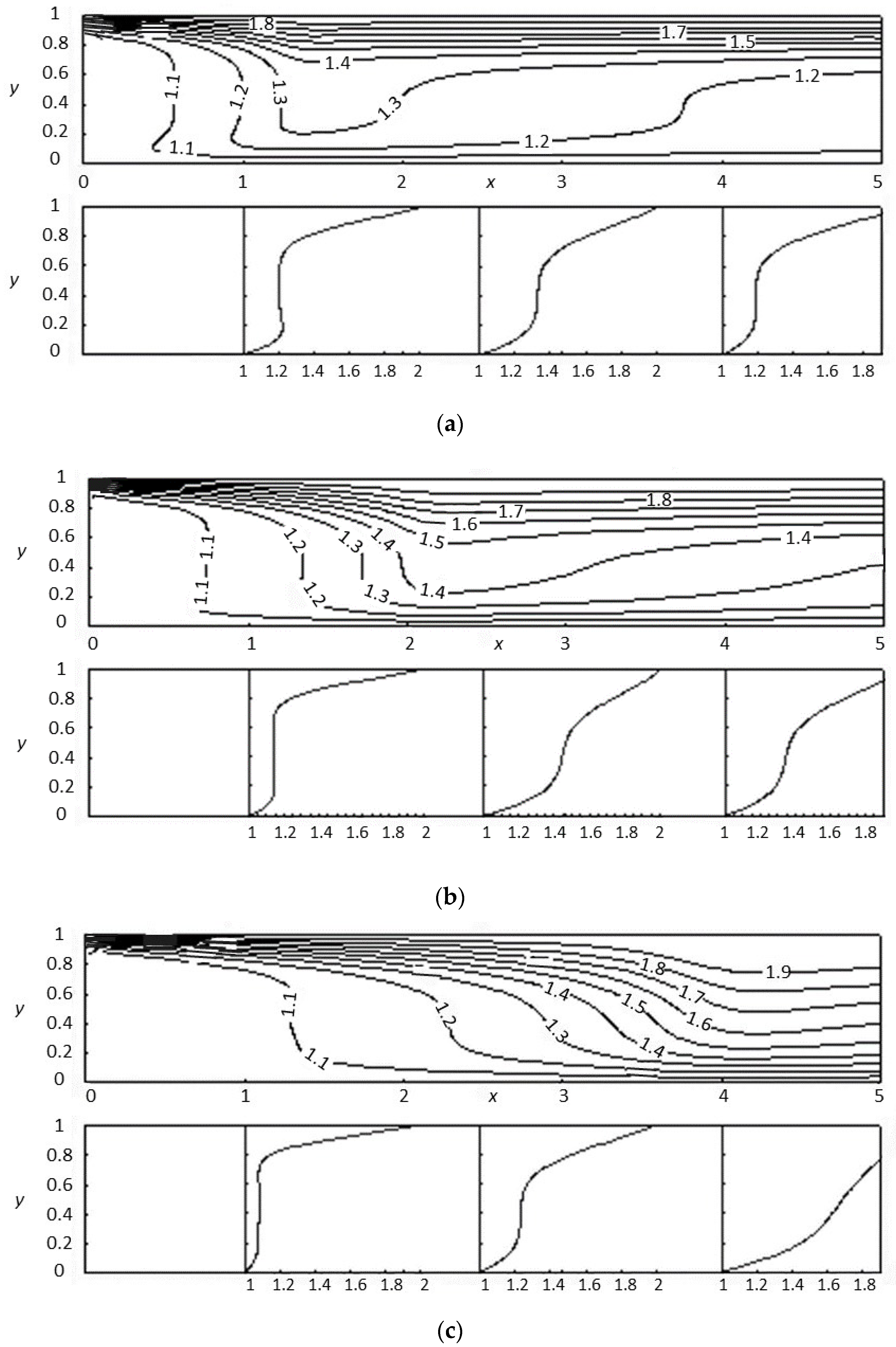
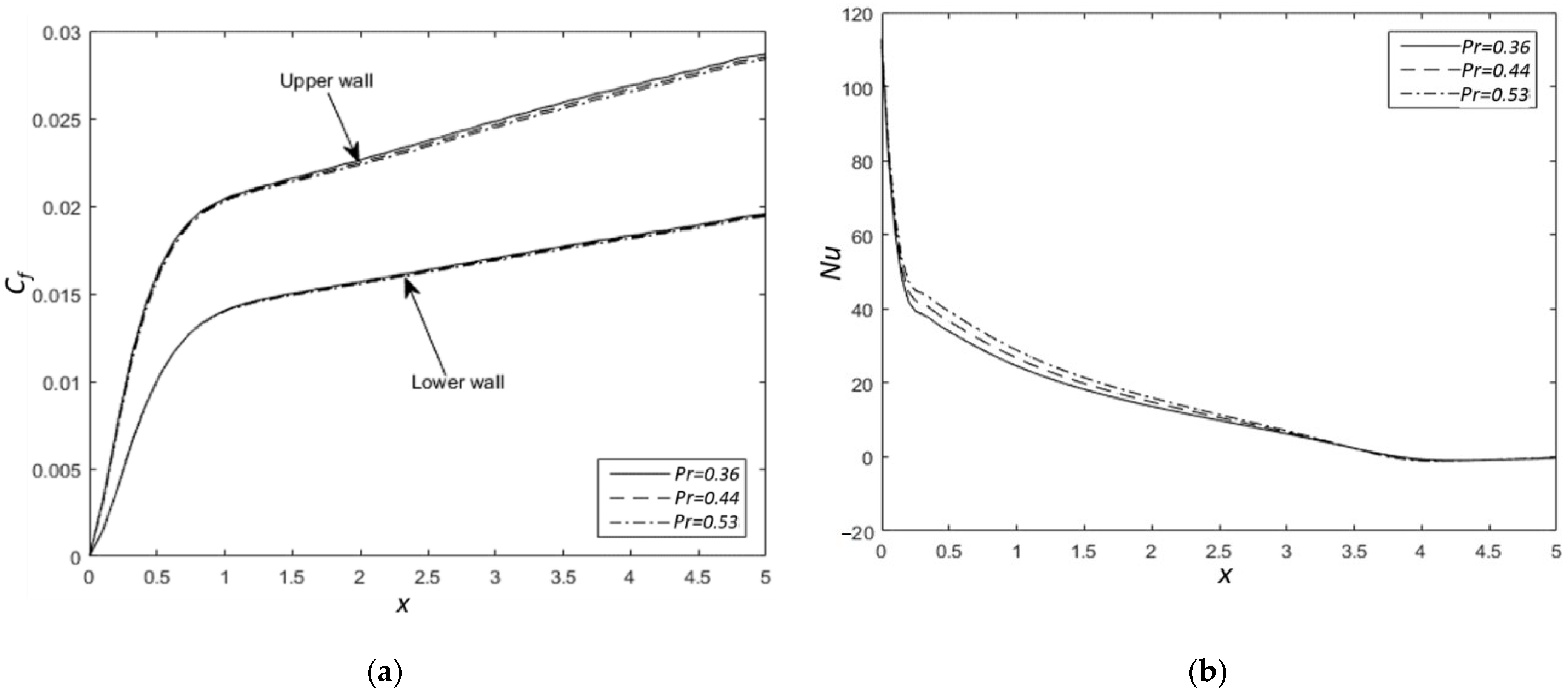
3. Results and Discussion
4. Conclusions
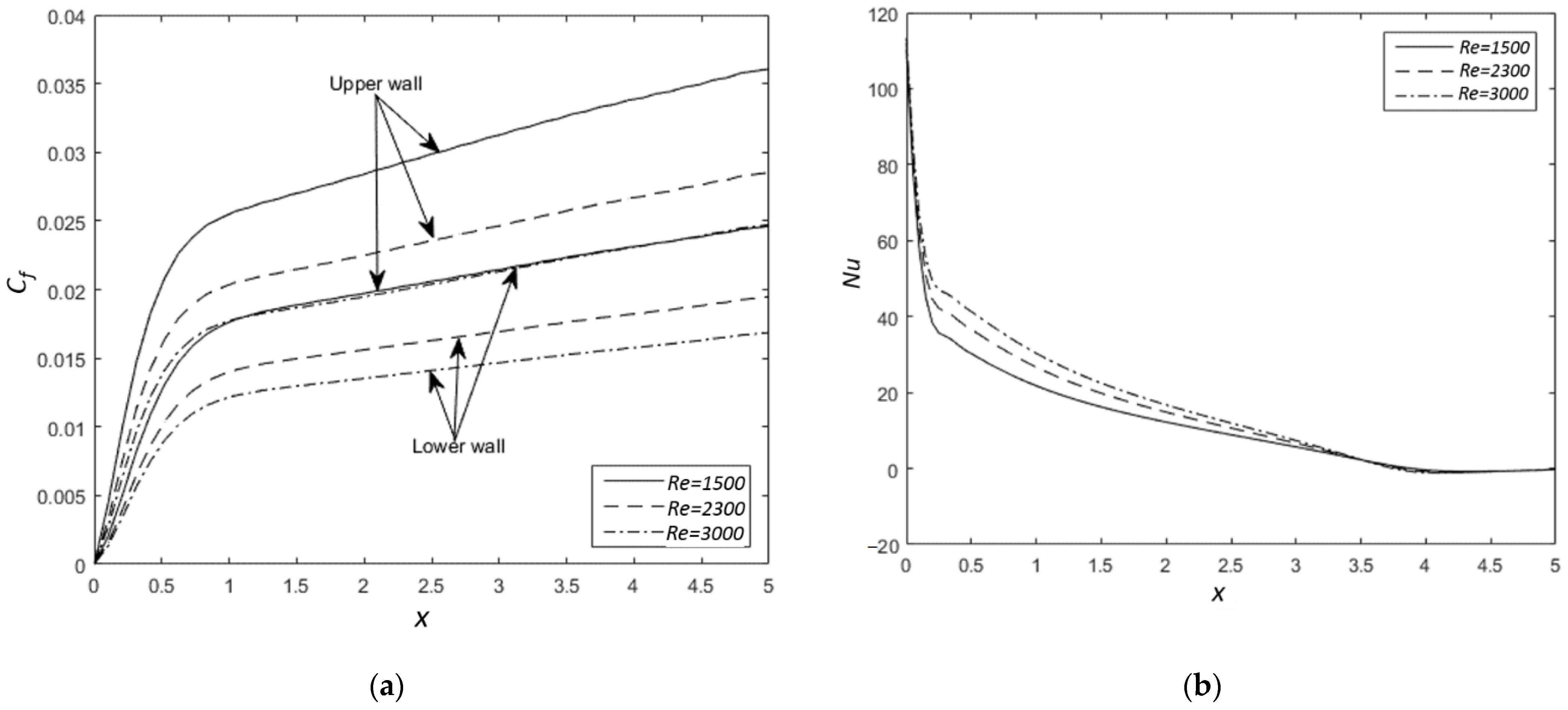
- The friction coefficient increases for a greater Reynolds number, as the velocity gradient gets larger while the boundary layer becomes thinner. The Nusselt number () rises with an increased , caused a thinner thermal boundary layer.
- The friction coefficient is increased with a decreased Prandtl number , due to a higher ratio of momentum diffusivity to thermal diffusivity. However, this effect on can be considered small. On the other hand, is increased with , since the inertial force of fluid flow is larger.
- The friction coefficient is found to vary with the Stuart number near the channel entrance in the developing region. However, this trend reverses at a certain distance inside the channel, as decreases with an increased . As increases, also increases at the entrance region; however, it in turn decreases downstream towards the fully developed region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, S.; Bau, H. Magneto-hydrodynamics based microfluidics. Mech. Res. Commun. 1998, 36, 10–21. [Google Scholar] [CrossRef]
- Mishra, S.R.; Dash, G.C.; Acharya, M. Mass and heat transfer effect on MHD flow of a visco-elastic fluid through porous medium with oscillatory suction and heat source. Int. J. Heat Mass Transf. 2013, 57, 433–438. [Google Scholar] [CrossRef]
- Rebhi, R.; Mamou, M.; Hadidi, N. Onset of linear and nonlinear thermosolutal convection with soret and dufour effects in a porous collector under a uniform magnetic field. Fluids 2021, 6, 243. [Google Scholar] [CrossRef]
- Vasu, B.; Gorla, R.S.R.; Murthy, P.V.S.N.; Prasad, V.R.; Bég, O.A.; Siddiqa, S. MHD Free Convection-Radiation Interaction in a Porous Medium—Part I: Numerical Investigation. Int. J. Appl. Mech. Eng. 2020, 25, 198–218. [Google Scholar] [CrossRef]
- Buhler, L.; Mistrangelo, C.; Najuch, T. Magnetohydrodynamic flows in porous structures. Fusion Eng. Des. 2015, 98, 1239–1243. [Google Scholar] [CrossRef]
- Manna, N.K.; Mondal, C.; Biswas, N.; Sarkar, U.K.; Öztop, H.F.; Abu-Hamdeh, N.H. Effect of multibanded magnetic field on convective heat transport in linearly heated porous systems filled with hybrid nanofluid. Phys. Fluids 2021, 33, 053604. [Google Scholar] [CrossRef]
- Geindreau, C.; Auriault, J.L. Magnetohydrodynamic Flows in porous media. J. Fluid Mech. 2002, 466, 343–363. [Google Scholar] [CrossRef]
- Lehmann, P.; Moreau, R.; Camel, D.; Bolcato, R. A simple analysis of the effect of convection on the structure of the mushy zone in the case of horizontal Bridgman solidification. Comparison with experimental results. J. Cryst. Growth 1998, 183, 690–704. [Google Scholar] [CrossRef]
- Evtikhin, V.A.; Vertkov, A.V.; Lyublinski, I.E.; Khripunov, B.I.; Petrov, V.B.; Mirnov, S.V. Research of lithium capillary-pore systems for fusion reactor plasma facing components. J. Nucl. Mater. 2002, 307–311, 1664–1669. [Google Scholar] [CrossRef]
- Nithyadevi, N.; Rajarathinam, M. Effect of inclination angle and magnetic field on convection heat transfer for nanofluid in a porous cavity. J. Appl. Fluid Mech. 2016, 9, 2347–2358. [Google Scholar] [CrossRef]
- Kumari, P.; Nigam, M.; Kumar, S.; Kumar, V.; Raturi, S.; Pargaei, M.; Krishna Murthy, S.V.S.S.; Rathish Kumar, B.V. Magnetic field effect on non-darcy mixed convection from a horizontal plate in a nanofluid-saturated porous medium. J. Porous Media 2019, 22, 599–610. [Google Scholar] [CrossRef]
- Mondal, M.K.; Biswas, N.; Manna, N.K.; Chamkha, A.J. Enhanced magnetohydrodynamic thermal convection in a partially driven cavity packed with a nanofluid-saturated porous medium. Math. Methods Appl. Sci. 2021. Article in Press. [Google Scholar] [CrossRef]
- Balla, C.S.; Haritha, C.; Kishan, N.; Rashad, A.M. Magnetohydrodynamic nanofluid flow and heat transfer in a porous cavity containing heated surface. J. Nanofluids 2019, 8, 577–588. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Mansour, M.A.; Rashad, A.M.; Morsy, Z. MHD free convection and sinusoidal heating in a wavy cavity filled with a heat-generating porous medium using Cu–water nanofluids. Comput. Therm. Sci. 2020, 12, 217–232. [Google Scholar] [CrossRef]
- Shah, N.A.; Al-Zubaidi, A.; Saleem, S. Study of Magnetohydrodynamic Pulsatile Blood Flow through an Inclined Porous Cylindrical Tube with Generalized Time-Nonlocal Shear Stress. Adv. Math. Phys. 2021, 2021, 5546701. [Google Scholar] [CrossRef]
- Ponalagusamy, R.; Manchi, R. Mathematical modeling of electro-magnetohydrodynamic pulsatile flow of an elastico-viscous fluid through an inclined porous tapered arterial stenosis. Math. Eng. Sci. Aerosp. 2020, 11, 237–254. [Google Scholar]
- Taklifi, A.; Aghanajafi, C. MHD non-Darcian flow through a non-isothermal vertical surface embedded in a porous medium with radiation. Meccanica 2012, 47, 929–937. [Google Scholar] [CrossRef]
- Chamkha, A.J. Unsteady laminar hydromagnetic flow and heat transfer in porous channels with temperature-dependent properties. Int. J. Numer. Methods Heat Fluid Flow 2001, 11, 430–448. [Google Scholar] [CrossRef]
- El-Amin, M.F. Combined effect of viscous dissipation and Joule heating on MHD forced convection over a non-isothermal horizontal cylinder embedded in a fluid saturated porous medium. J. Magn. Magn. Mater. 2003, 263, 337–343. [Google Scholar] [CrossRef]
- Haq, S.U.; Khan, M.A.; Khan, Z.A.; Ali, F. MHD effects on the channel flow of a fractional viscous fluid through a porous medium: An application of the Caputo-Fabrizio time-fractional derivative. Chin. J. Phys. 2020, 65, 14–23. [Google Scholar] [CrossRef]
- Sunil; Sharma, R.C.; Chan, T. Combined effect of magnetic field and rotation on thermosolutal instability of a compressible fluid in porous medium. Polym. Plast. Technol. Eng. 1996, 35, 377–391. [Google Scholar] [CrossRef]
- Rana, G.C.; Patial, M. Thermal instability of compressible rivlin-ericksen rotating fluid permeated with suspended dust particles in the presence of vertical magnetic field in porous medium. Int. J. Heat Technol. 2011, 29, 51–55. [Google Scholar]
- Islam, M.M.; Tusher Mollah, M.; Hasan, M.S.; Mahmud Alam, M. Numerical solution of unsteady viscous compressible fluid flow along a porous plate with induced magnetic field. Model. Meas. Control B 2017, 86, 850–863. [Google Scholar] [CrossRef]
- Ganesh, S.; Patil, V.S.; Delhi Babu, R.; Chandrasekar, P.; Anish, M. Unsteady magnetohydrodynamic flow of a compressible liquid through a stainless steel plate of porous medium. In Proceedings of the 3rd International Conference on Frontiers in Automobile & Mechanical Engineering, FAME 2020, Chennai, India, 7–9 August 2020. [Google Scholar]
- Pakdee, W.; Yuvakanit, B.; Hussein, A.K. Numerical Analysis on the Two-dimensional Unsteady Magnetohydrodynamic Compressible Flow through a Porous Medium. J. Appl. Fluid Mech. 2017, 10, 1153–1159. [Google Scholar] [CrossRef]
- Zhou, B.; Ji, Y.; Sun, J.; Sun, Y. Modified turbulent Prandtl number model for helium–xenon gas mixture with low Prandtl number. Nucl. Eng. Des. 2020, 366, 110738. [Google Scholar] [CrossRef]
- Harada, N.; Le Kien, C.; Tashiro, T. Closed cycle MHD generator using He/Xe working plasma. In Proceedings of the 33rd AIAA Plasmadynamics and Lasers Conference 2020, Maui, HI, USA, 20–23 May 2002. [Google Scholar]
- El-Genk, M.S.; Tournier, J.-M. Noble-gas binary mixtures for closed-Brayton-cycle space reactor power systems. J. Propuls. Power 2007, 23, 863–873. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Tournier, J.-M. On the use of noble gases and binary mixtures as reactor coolants and CBC working fluids. Energy Convers. Manag. 2008, 49, 1882–1891. [Google Scholar] [CrossRef]
- Pakdee, W.; Mahalingam, S. Accurate Method to Implement Boundary Conditions for Reacting Flows Based on Characteristic Wave Analysis. Combust. Theory Model. 2003, 7, 705–712. [Google Scholar] [CrossRef][Green Version]
- Pakdee, W.; Sakkarangkoon, T. Numerical study of an unsteady non-premixed flame in a porous medium based on the thermal equilibrium model. J. Theor. Appl. Mech. 2021, 59, 401–412. [Google Scholar] [CrossRef]
- Vafai, K. Handbook of Porous Media; CRC Press: New York, NY, USA, 2005. [Google Scholar]
- Marpu, D.R. Forchheimer and Brinkman extended Darcy flow model on natural convection in a vertical cylindrical porous annulus. Acta Mech. 1995, 109, 41–48. [Google Scholar] [CrossRef]
- Kestin, J.; Kniernim, K.; Mason, E.A.; Najafi, B.; Ro, S.T.; Waldman, M. Equilibrium and Transport Properties of the Noble Gases and Their Mixtures at Low Density. J. Phys. Chem. Ref. Data 1984, 13, 229–303. [Google Scholar] [CrossRef]
- Anderson, K.R.; Mahalingam, S.; Hertzberg, J. A Two-Dimensional Planar Computational Investigation of Flame Broadening in Confined Non-Premixed Jets. Combust. Flame 1999, 118, 233–247. [Google Scholar] [CrossRef]
- Cimolin, F.; Discacciati, M. Navier-Stokes/Forchheimer models for filtration through porous media. Appl. Numer. Math. 2013, 72, 205–224. [Google Scholar] [CrossRef]
- Lele, S.K. Compact Finite Difference Schemes with Spectral-like Resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]


| Variable | Definition |
|---|---|
| Length | |
| Velocity | |
| Temperature | |
| Total Energy | |
| Time | |
| Density | |
| Pressure [35] | |
| Thermal Conductivity | |
| Stress |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pattanavanitkul, P.; Pakdee, W. Parametric Study of Unsteady Flow and Heat Transfer of Compressible Helium–Xenon Binary Gas through a Porous Channel Subjected to a Magnetic Field. Fluids 2021, 6, 392. https://doi.org/10.3390/fluids6110392
Pattanavanitkul P, Pakdee W. Parametric Study of Unsteady Flow and Heat Transfer of Compressible Helium–Xenon Binary Gas through a Porous Channel Subjected to a Magnetic Field. Fluids. 2021; 6(11):392. https://doi.org/10.3390/fluids6110392
Chicago/Turabian StylePattanavanitkul, Pornthep, and Watit Pakdee. 2021. "Parametric Study of Unsteady Flow and Heat Transfer of Compressible Helium–Xenon Binary Gas through a Porous Channel Subjected to a Magnetic Field" Fluids 6, no. 11: 392. https://doi.org/10.3390/fluids6110392
APA StylePattanavanitkul, P., & Pakdee, W. (2021). Parametric Study of Unsteady Flow and Heat Transfer of Compressible Helium–Xenon Binary Gas through a Porous Channel Subjected to a Magnetic Field. Fluids, 6(11), 392. https://doi.org/10.3390/fluids6110392





