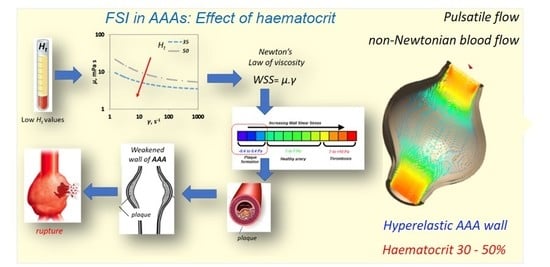
Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effect of Haematocrit
Abstract
1. Introduction
2. Methodology
2.1. About FSI
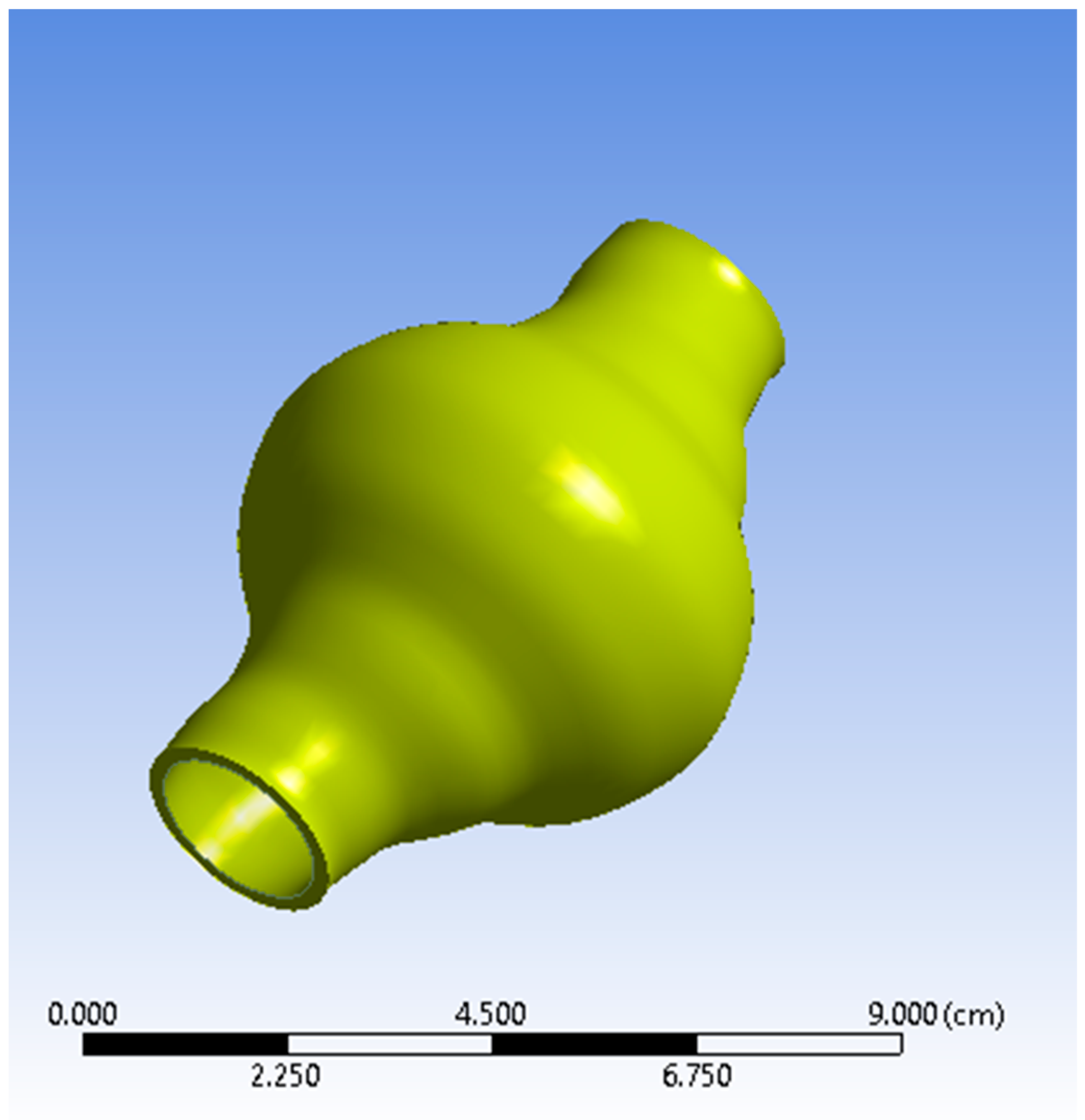
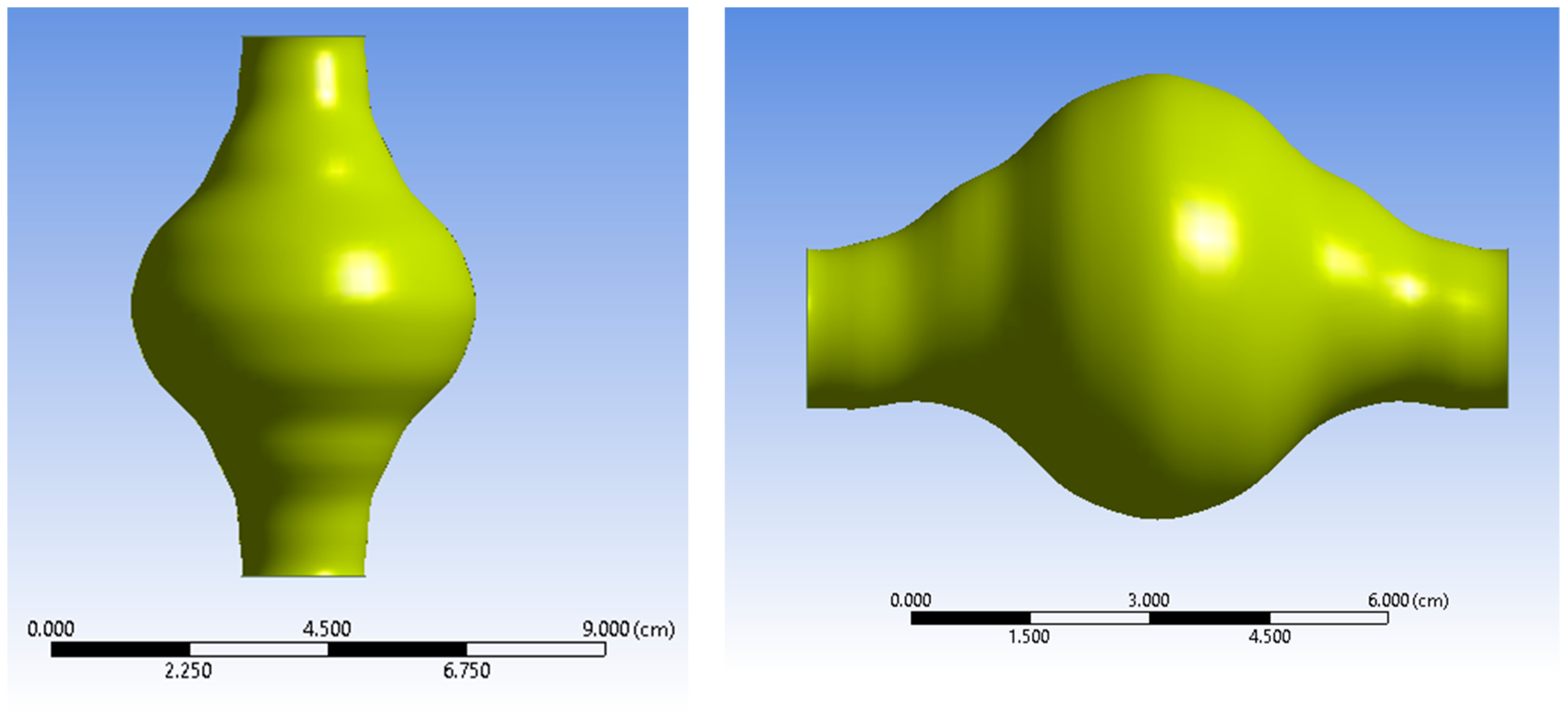
2.2. Geometry
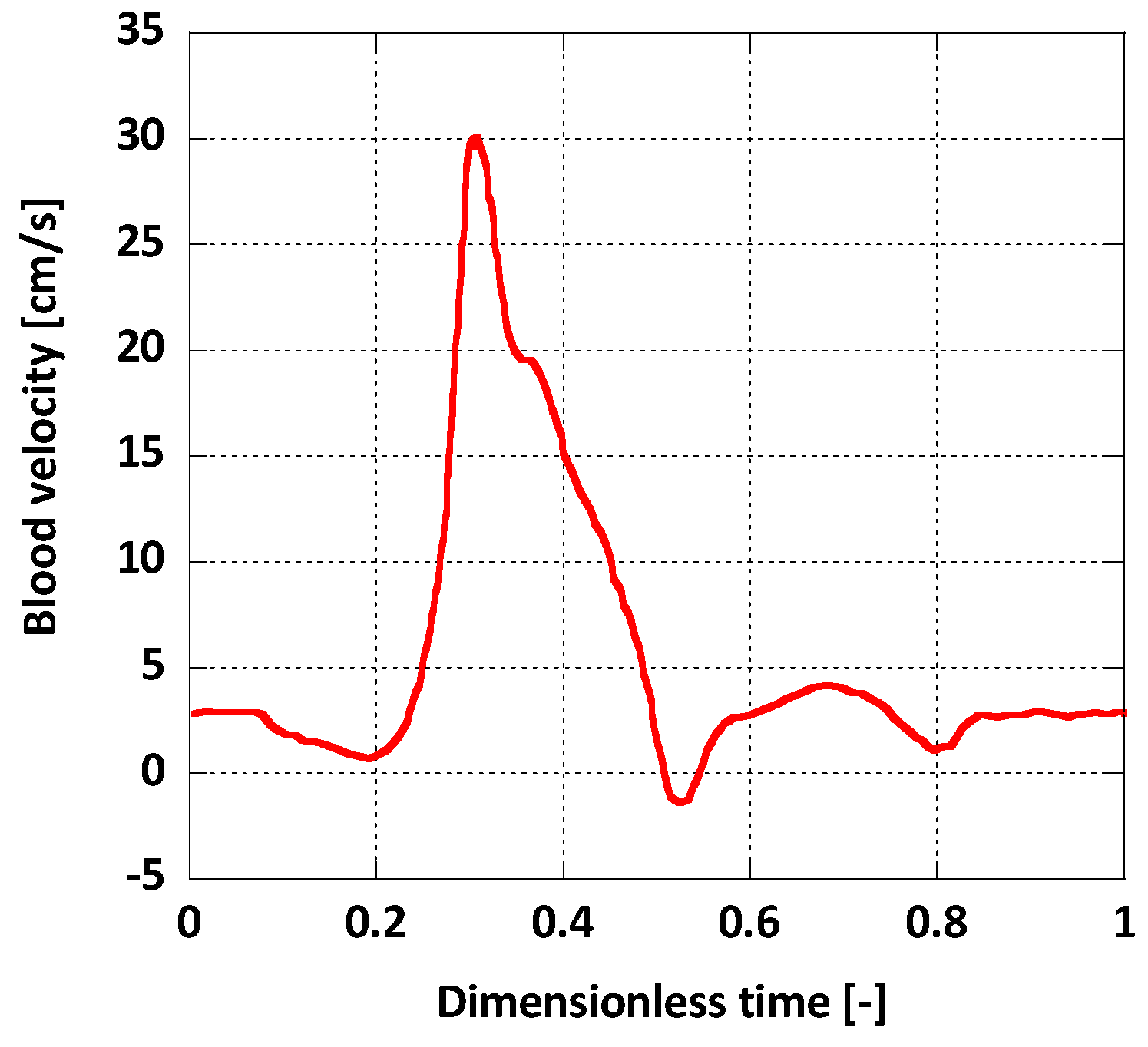
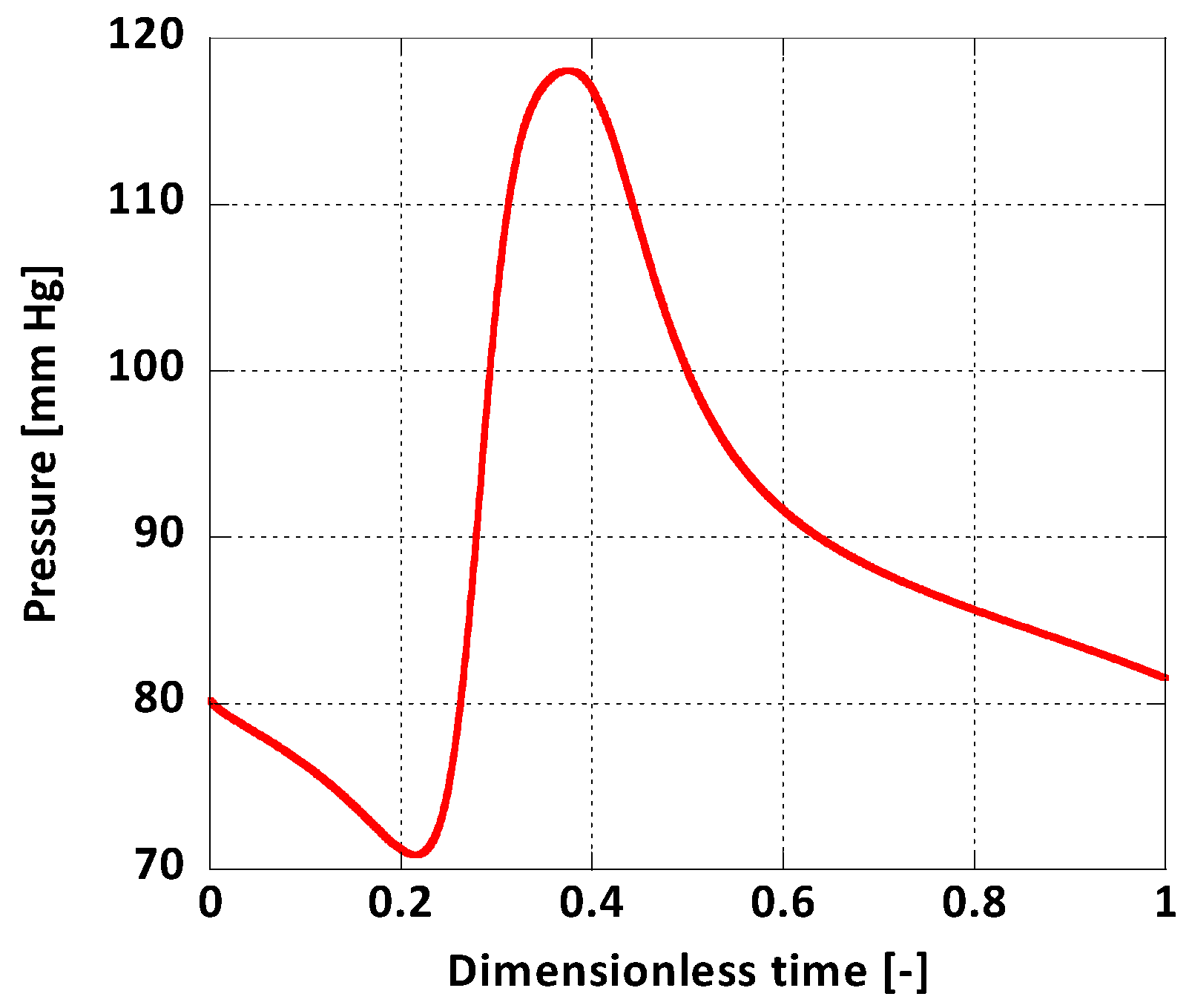
2.3. Governing Equations and Boundary Conditions
3. CFD Modelling
4. Results
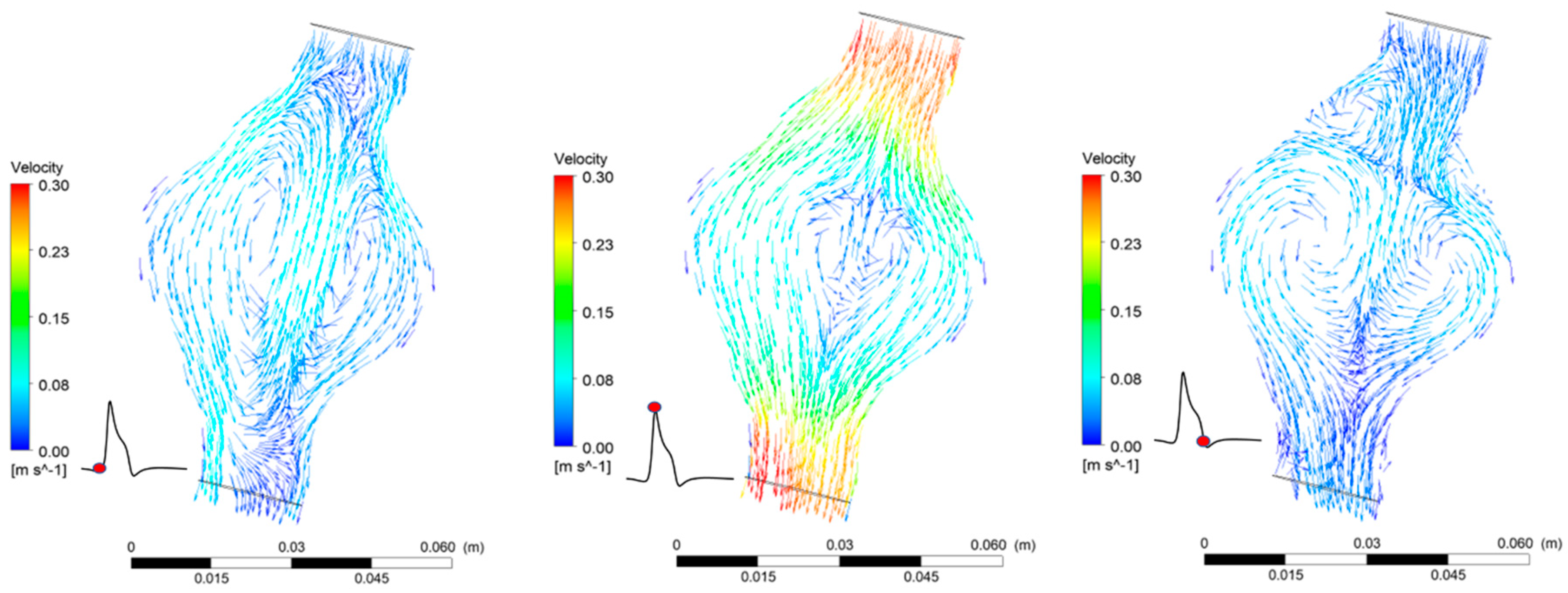
4.1. Blood flow in the AAA
4.2. AAA Wall Displacement
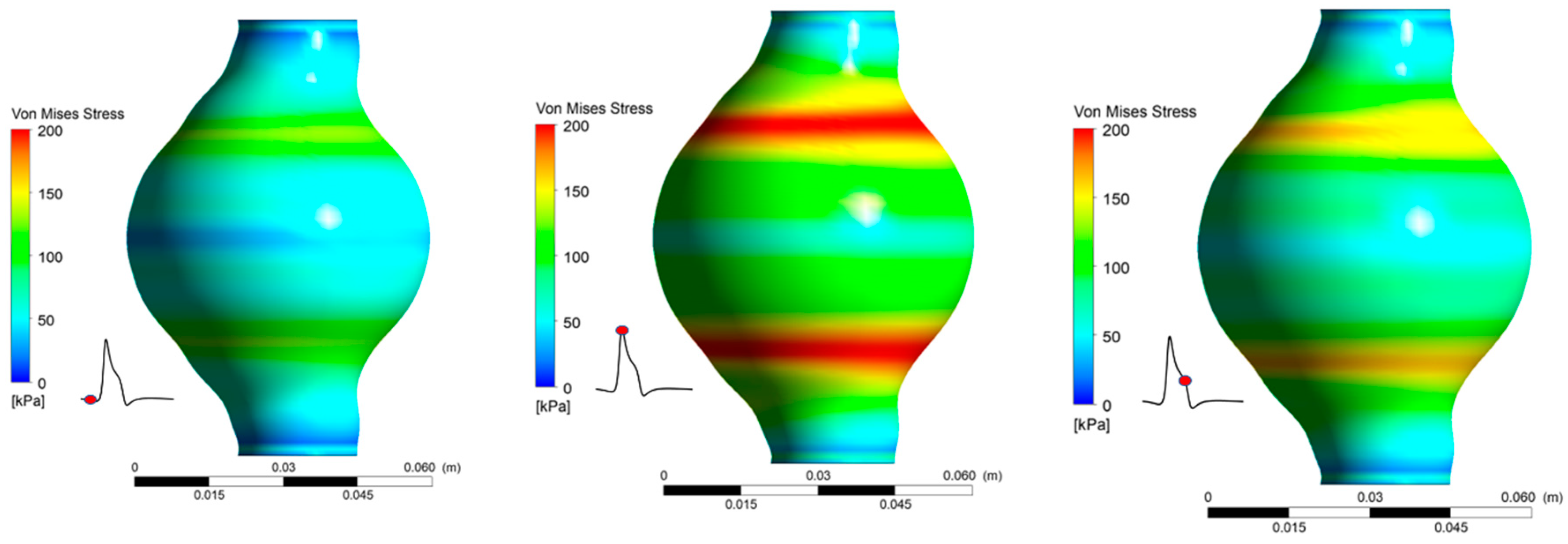
4.3. von Mises Stress () Distribution on AAA Wall
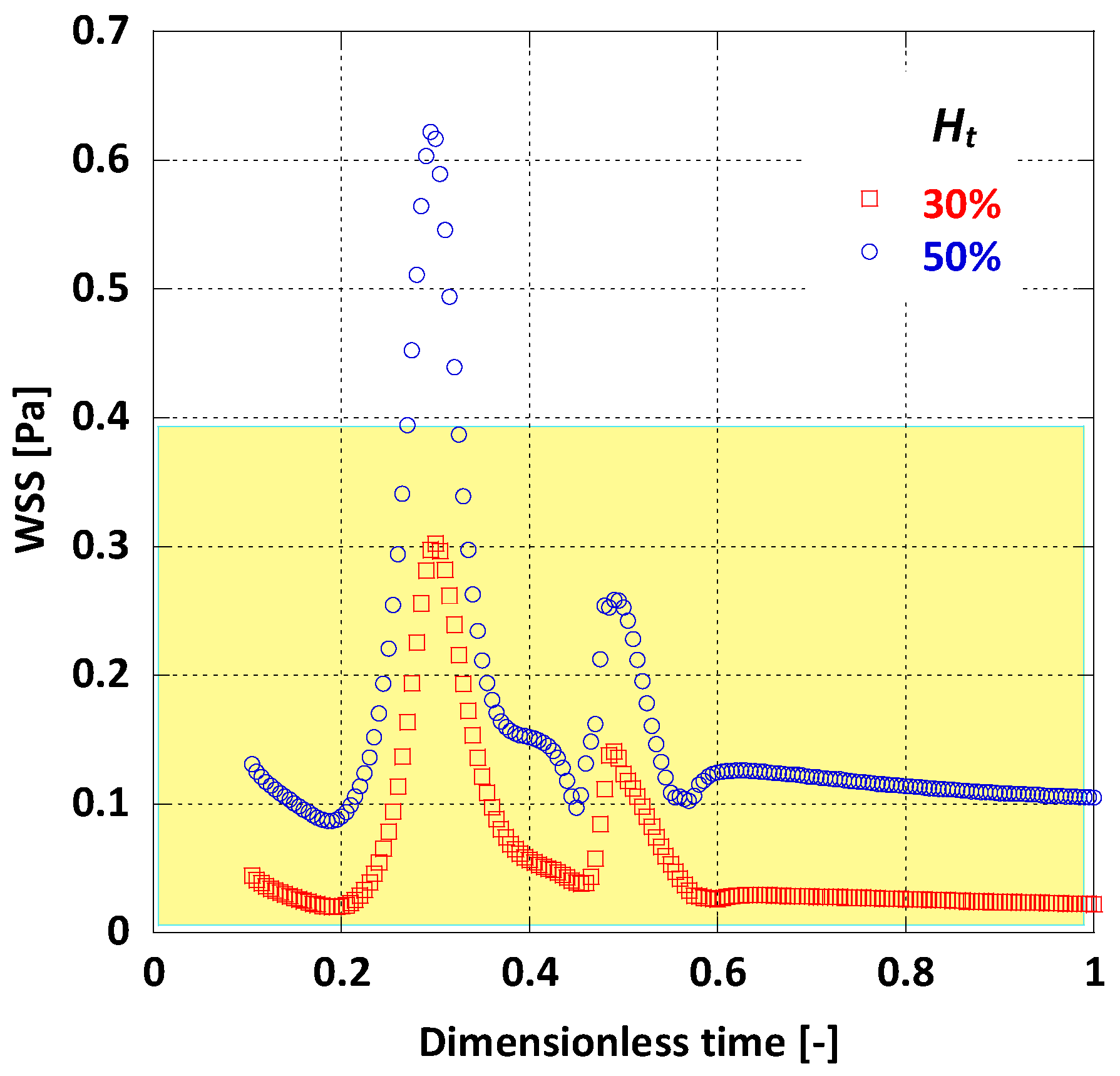
4.4. WSS in the AAA
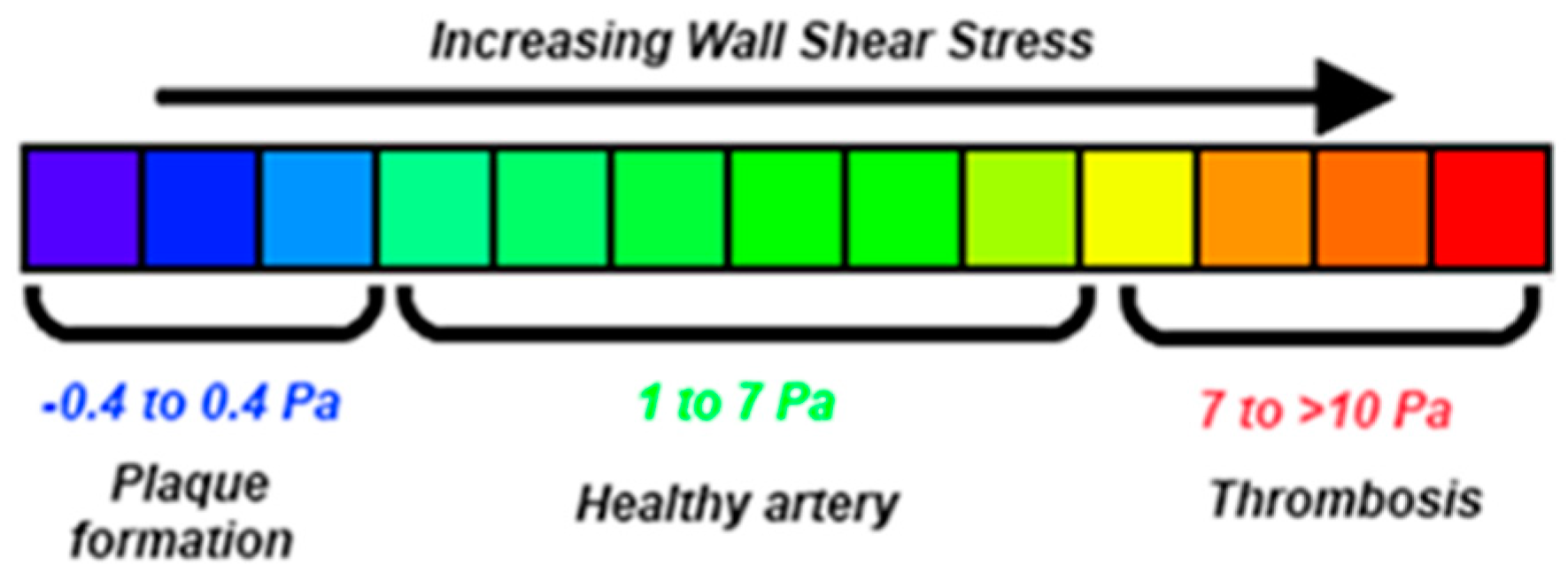
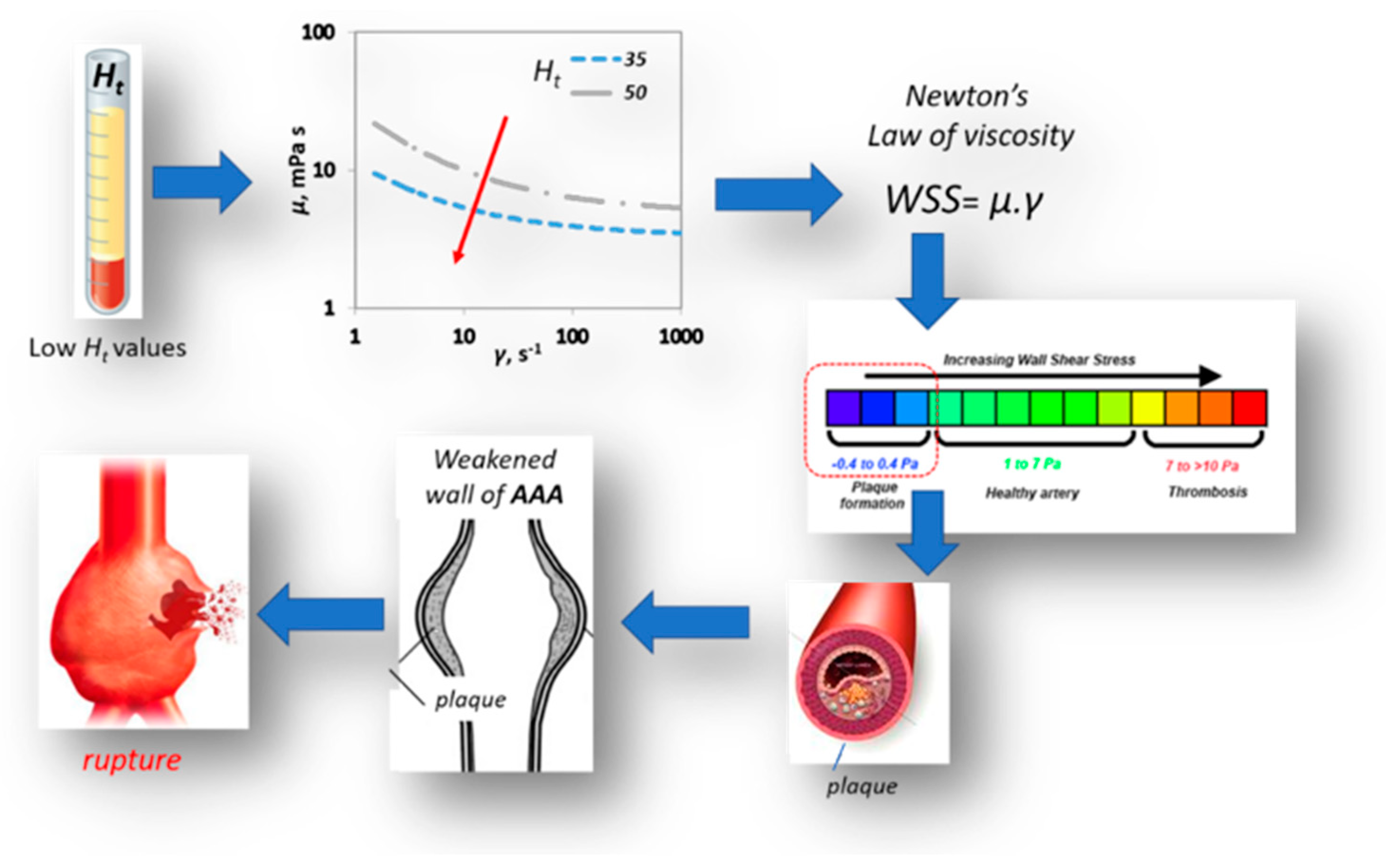
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Yield stress constant, Pa |
| C1 | Mooney-Rivlin constant 1, N/cm2 |
| C2 | Mooney-Rivlin constant 2, N/cm2 |
| Dmax | Maximum aneurismal diameter, mm |
| Di | Internal inlet AAA diameter, mm |
| d | FSI interface displacement, m |
| FSI interface velocity, m/s | |
| FSI interface acceleration, m/s2 | |
| f | Arterial wall force per volume, N/m3 |
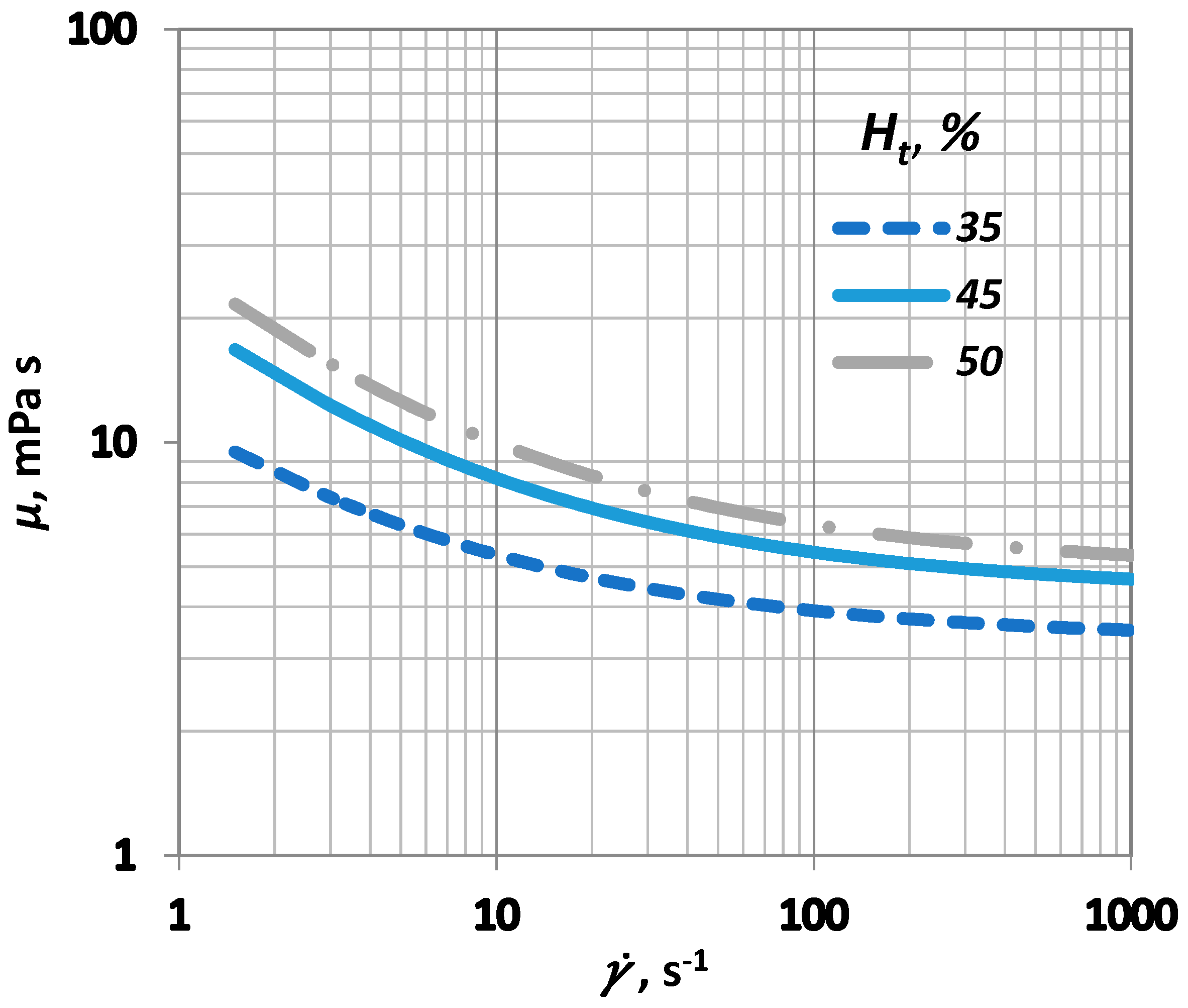
| Ht | Haematocrit, % |
| k | Arterial wall thickness, mm |
| L | Total length of the AAA, mm |
| P | Pressure, Pa |
| Re | Reynolds number, dimensionless |
| t | Time, s |
| T | Heart rate period, s |
| u | Velocity, m/s |
| Wo | Womersley number, dimensionless |
| WSS | Wall shear stress, Pa |
| Greek letters | |
| Shear rate, s−1 | |
| Δt | Timestep, s |
| μ | Viscosity, Pa·s |
| ρ | Density, kg/m3 |
| von Mises stress, Pa | |
| τ | Shear stress, Pa |
| τy | Yield stress, Pa |
| Ψ | Strain energy density, J/m3 |
References
- Keisler, B.; Carter, C. Abdominal aortic aneurysm. Am. Fam. Physician 2015, 91, 538–543. [Google Scholar] [PubMed]
- Singh, K.; Bønaa, K.H.; Jacobsen, B.K.; Bjørk, L.; Solberg, S. Prevalence of and risk factors for abdominal aortic aneurysms in a population-based study: The Tromsø Study. Am. J. Epidemiol. 2001, 154, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Assar, A.N.; Zarins, C.K. Ruptured abdominal aortic aneurysm: A surgical emergency with many clinical presentations. Postgrad. Med. J. 2009, 85, 268–273. [Google Scholar] [CrossRef] [PubMed]
- Chervu, A.; Clagett, G.P.; Valentine, R.J.; Myers, S.I.; Rossi, P.J. Role of physical examination in detection of abdominal aortic aneurysms. Surgery 1995, 117, 454–457. [Google Scholar] [CrossRef]
- Vorp, D.A. Biomechanics of abdominal aortic aneurysm. J. Biomech. 2007, 40, 1887–1902. [Google Scholar] [CrossRef] [PubMed]
- Fillinger, M.F.; Marra, S.P.; Raghavan, M.L.; Kennedy, F.E. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J. Vasc. Surg. 2003, 37, 724–732. [Google Scholar] [CrossRef] [PubMed]
- Georgakarakos, E.; Ioannou, C.V.; Kamarianakis, Y.; Papaharilaou, Y.; Kostas, T.; Manousaki, E.; Katsamouris, A.N. The Role of Geometric Parameters in the Prediction of Abdominal Aortic Aneurysm Wall Stress. Eur. J. Vasc. Endovasc. Surg. 2010, 39, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Xenos, M.; Rambhia, S.H.; Alemu, Y.; Einav, S.; Labropoulos, N.; Tassiopoulos, A.; Ricotta, J.J.; Bluestein, D. Patient-Based Abdominal Aortic Aneurysm Rupture Risk Prediction with Fluid Structure Interaction Modeling. Ann. Biomed. Eng. 2010, 38, 3323–3337. [Google Scholar] [CrossRef]
- Diehm, N.; Benenati, J.F.; Becker, G.J.; Quesada, R.; Tsoukas, A.I.; Katzen, B.T.; Kovacs, M. Anemia is associated with abdominal aortic aneurysm (AAA) size and decreased long-term survival after endovascular AAA repair. J. Vasc. Surg. 2007, 46, 676–681. [Google Scholar] [CrossRef] [PubMed]
- Errill, E.W. Rheology of blood. Physiol. Rev. 1969, 49, 863–888. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, X. Computational simulation of aortic aneurysm using FSI method: Influence of blood viscosity on aneurismal dynamic behaviors. Comput. Biol. Med. 2011, 41, 812–821. [Google Scholar] [CrossRef] [PubMed]
- Kanaris, A.G.; Anastasiou, A.D.; Paras, S.V. Modeling the effect of blood viscosity on hemodynamic factors in a small bifurcated artery. Chem. Eng. Sci. 2012, 71, 202–211. [Google Scholar] [CrossRef]
- Scotti, C.M.; Shkolnik, A.D.; Muluk, S.C.; Finol, E.A. Fluid-structure interaction in abdominal aortic aneurysms: Effects of asymmetry and wall thickness. Biomed. Eng. Online 2005, 4, 64. [Google Scholar] [CrossRef] [PubMed]
- Scotti, C.M.; Jimenez, J.; Muluk, S.C.; Finol, E.A. Wall stress and flow dynamics in abdominal aortic aneurysms: Finite element analysis vs. fluid–structure interaction. Comput. Methods Biomech. Biomed. Eng. 2008, 11, 301–322. [Google Scholar] [CrossRef] [PubMed]
- Leung, J.H.; Wright, A.R.; Cheshire, N.; Crane, J.; Thom, S.A.; Hughes, A.D.; Xu, Y. Fluid structure interaction of patient specific abdominal aortic aneurysms: A comparison with solid stress models. Biomed. Eng. Online 2006, 5, 33. [Google Scholar] [CrossRef]
- Lin, S.; Han, X.; Bi, Y.; Ju, S.; Gu, L. Fluid-Structure Interaction in Abdominal Aortic Aneurysm: Effect of Modeling Techniques. BioMed. Res. Int. 2017, 2017, 7023078. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E. Computational Fluid-Structure Interaction: Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-118-48357-2. [Google Scholar]
- Malek, A.M.; Alper, S.L.; Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. JAMA 1999, 282, 2035–2042. [Google Scholar] [CrossRef]
- Boyd, A.J.; Kuhn, D.C.S.; Lozowy, R.J.; Kulbisky, G.P. Low wall shear stress predominates at sites of abdominal aortic aneurysm rupture. J. Vasc. Surg. 2016, 63, 1613–1619. [Google Scholar] [CrossRef]
- Finol, E.A.; Amon, C.H. Blood Flow in Abdominal Aortic Aneurysms: Pulsatile Flow Hemodynamics. J. Biomech. Eng. 2001, 123, 474–484. [Google Scholar] [CrossRef]
- Khanafer, K.M.; Gadhoke, P.; Berguer, R.; Bull, J.L. Modeling pulsatile flow in aortic aneurysms: Effect of non-Newtonian properties of blood. Biorheology 2006, 43, 661–679. [Google Scholar]
- Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non-Newtonian blood flow in human right coronary arteries: Transient simulations. J. Biomech. 2006, 39, 1116–1128. [Google Scholar] [CrossRef] [PubMed]
- Mesri, Y.; Niazmand, H.; Deyranlou, A.; Sadeghi, M.R. Fluid-structure interaction in abdominal aortic aneurysms: Structural and geometrical considerations. Int. J. Mod. Phys. C 2014, 26, 1550038. [Google Scholar] [CrossRef]
- Sharzehee, M.; Khalafvand, S.S.; Han, H.-C. Fluid-structure interaction modeling of aneurysmal arteries under steady-state and pulsatile blood flow: A stability analysis. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 219–231. [Google Scholar] [CrossRef] [PubMed]
- Joh, J.H.; Ahn, H.-J.; Park, H.-C. Reference diameters of the abdominal aorta and iliac arteries in the Korean population. Yonsei Med. J. 2013, 54, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Syed, M.N.; Ahmad, M.M.; Ahmad, M.N.; Hussaini, S.; Muhammad, M.N.; Pir, S.H.A.; Khandheria, B.K.; Tajik, A.J.; Ammar, K.A. Normal Diameter of the Ascending Aorta in Adults: The Impact of Stricter Criteria on Selection of Subjects Free of Disease. J. Am. Coll. Cardiol. 2017, 69, 2075. [Google Scholar] [CrossRef]
- Leotta, D.F.; Paun, M.; Beach, K.W.; Kohler, T.R.; Zierler, R.E.; Strandness, D.E. Measurement of abdominal aortic aneurysms with three-dimensional ultrasound imaging: Preliminary report. J. Vasc. Surg. 2001, 33, 700–707. [Google Scholar] [CrossRef] [PubMed]
- Brown, P.M.; Zelt, D.T.; Sobolev, B. The risk of rupture in untreated aneurysms: The impact of size, gender, and expansion rate. J. Vasc. Surg. 2003, 37, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Lederle, F.A.; Johnson, G.R.; Wilson, S.E.; Ballard, D.J.; William, D.; Jordan, J.; Blebea, J.; Littooy, F.N.; Freischlag, J.A.; Bandyk, D.; et al. Rupture Rate of Large Abdominal Aortic Aneurysms in Patients Refusing or Unfit for Elective Repair. JAMA 2002, 287, 2968–2972. [Google Scholar] [CrossRef]
- Janela, J.; Moura, A.; Sequeira, A. A 3D non-Newtonian fluid–structure interaction model for blood flow in arteries. J. Comput. Appl. Math. 2010, 234, 2783–2791. [Google Scholar] [CrossRef]
- Neofytou, P. Comparison of blood rheological models for physiological flow simulation. Biorheology 2004, 41, 693–714. [Google Scholar]
- Fournier, R.L. Basic Transport Phenomena in Biomedical Engineering, 3rd ed.; CRC Press: New York, NY, USA, 2011; ISBN 978-1-4398-2670-6. [Google Scholar]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. Lond. A 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Vorp, D.A. Toward a biomechanical tool to evaluate rupture potential of abdominal aortic aneurysm: Identification of a finite strain constitutive model and evaluation of its applicability. J. Biomech. 2000, 33, 475–482. [Google Scholar] [CrossRef]
- Mills, C.J.; Gabe, I.T.; Gault, J.H.; Mason, D.T.; Ross, J.; Braunwald, E.; Shillingford, J.P. Pressure-flow relationships and vascular impedance in man. Cardiovasc. Res. 1970, 4, 405–417. [Google Scholar] [CrossRef] [PubMed]
- Nichols, W.W.; McDonald, D.A.; O’Rourke, M.F. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles, 5th ed.; Taylor & Francis: Milton Park, UK, 2005; ISBN 978-0-340-80941-9. [Google Scholar]
- Maday, Y. Analysis of coupled models for fluid-structure interaction of internal flows. In Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Formaggia, L., Quarteroni, A., Veneziani, A., Eds.; Springer-Verlag: Mailand, Italy, 2009; ISBN 978-88-470-1152-6. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007; ISBN 978-0-13-127498-3. [Google Scholar]
- Von Mises, R. Mechanik der festen Körper im plastisch- deformablen Zustand. Nachr. Ges. Wiss. Gött. Math.-Phys. Kl. 1913, 1913, 582–592. [Google Scholar]
- Shaaban, A.M.; Duerinckx, A.J. Wall shear stress and early atherosclerosis: A review. Am. J. Roentgenol. 2000, 174, 1657–1665. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Tempel, D.; van Haperen, R.; van der Baan, A.; Grosveld, F.; Daemen, M.J.A.P.; Krams, R.; de Crom, R. Atherosclerotic lesion size and vulnerability are determined by patterns of fluid shear stress. Circulation 2006, 113, 2744–2753. [Google Scholar] [CrossRef]
- Hsiai, T.K.; Cho, S.K.; Honda, H.M.; Hama, S.; Navab, M.; Demer, L.L.; Ho, C.-M. Endothelial Cell Dynamics under Pulsating Flows: Significance of High Versus Low Shear Stress Slew Rates (∂τ/∂τ). Ann. Biomed. Eng. 2002, 30, 646–656. [Google Scholar] [CrossRef]
- Millon, A.; Sigovan, M.; Boussel, L.; Mathevet, J.-L.; Louzier, V.; Paquet, C.; Geloen, A.; Provost, N.; Majd, Z.; Patsouris, D.; et al. Low WSS Induces Intimal Thickening, while Large WSS Variation and Inflammation Induce Medial Thinning, in an Animal Model of Atherosclerosis. PLoS ONE 2015, 10, e0141880. [Google Scholar] [CrossRef]
- O’Leary, S.A.; Mulvihill, J.J.; Barrett, H.E.; Kavanagh, E.G.; Walsh, M.T.; McGloughlin, T.M.; Doyle, B.J. Determining the influence of calcification on the failure properties of abdominal aortic aneurysm (AAA) tissue. J. Mech. Behav. Biomed. Mater. 2015, 42, 154–167. [Google Scholar] [CrossRef]
- Chatziprodromou, I.; Tricoli, A.; Poulikakos, D.; Ventikos, Y. Haemodynamics and wall remodelling of a growing cerebral aneurysm: A computational model. J. Biomech. 2007, 40, 412–426. [Google Scholar] [CrossRef] [PubMed]
- Sheidaei, A.; Hunley, S.C.; Zeinali-Davarani, S.; Raguin, L.G.; Baek, S. Simulation of abdominal aortic aneurysm growth with updating hemodynamic loads using a realistic geometry. Med. Eng. Phys. 2011, 33, 80–88. [Google Scholar] [CrossRef]
- Reed, D.; Reed, C.; Stemmermann, G.; Hayashi, T. Are aortic aneurysms caused by atherosclerosis? Circulation 1992, 85, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Boussel, L.; Rayz, V.; McCulloch, C.; Martin, A.; Acevedo-Bolton, G.; Lawton, M.; Higashida, R.; Smith, W.S.; Young, W.L.; Saloner, D. Aneurysm growth occurs at region of low wall shear stress: Patient-specific correlation of hemodynamics and growth in a longitudinal study. Stroke 2008, 39, 2997–3002. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zarins, C.K.; Glagov, S. Aneurysmal and occlusive atherosclerosis of the human abdominal aorta. J. Vasc. Surg. 2001, 33, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Drewe, C.J.; Parker, L.P.; Kelsey, L.J.; Norman, P.E.; Powell, J.T.; Doyle, B.J. Haemodynamics and stresses in abdominal aortic aneurysms: A fluid-structure interaction study into the effect of proximal neck and iliac bifurcation angle. J. Biomech. 2017, 60, 150–156. [Google Scholar] [CrossRef]
- De Heer, L.M.; Budde, R.P.J.; Mali, W.P.T.M.; de Vos, A.M.; van Herwerden, L.A.; Kluin, J. Aortic root dimension changes during systole and diastole: Evaluation with ECG-gated multidetector row computed tomography. Int. J. Cardiovasc. Imaging 2011, 27, 1195–1204. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Total length of the AAA, L | 90 mm |
| Internal inlet diameter of the AAA, Di | 20 mm |
| Maximum aneurismal diameter, Dmax | 55 mm |
| Arterial thickness, k | 2 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stergiou, Y.G.; Kanaris, A.G.; Mouza, A.A.; Paras, S.V. Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effect of Haematocrit. Fluids 2019, 4, 11. https://doi.org/10.3390/fluids4010011
Stergiou YG, Kanaris AG, Mouza AA, Paras SV. Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effect of Haematocrit. Fluids. 2019; 4(1):11. https://doi.org/10.3390/fluids4010011
Chicago/Turabian StyleStergiou, Yorgos G., Athanasios G. Kanaris, Aikaterini A. Mouza, and Spiros V. Paras. 2019. "Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effect of Haematocrit" Fluids 4, no. 1: 11. https://doi.org/10.3390/fluids4010011
APA StyleStergiou, Y. G., Kanaris, A. G., Mouza, A. A., & Paras, S. V. (2019). Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effect of Haematocrit. Fluids, 4(1), 11. https://doi.org/10.3390/fluids4010011