Effects of Lewis Number on the Evolution of Curvature in Spherically Expanding Turbulent Premixed Flames
Abstract
1. Introduction
- To demonstrate the effects of Lewis number on the terms of the transport equation of flame curvature in spherically expanding turbulent premixed flames.
- To identify the mechanisms, which lead to the effects of thermo-diffusive instability (i.e., augmentation of burning rate and flame wrinkling and a positive correlation between local burning rate and flame curvature) in the flames with .
2. Mathematical Background
3. Numerical Implementation
4. Results and Discussion
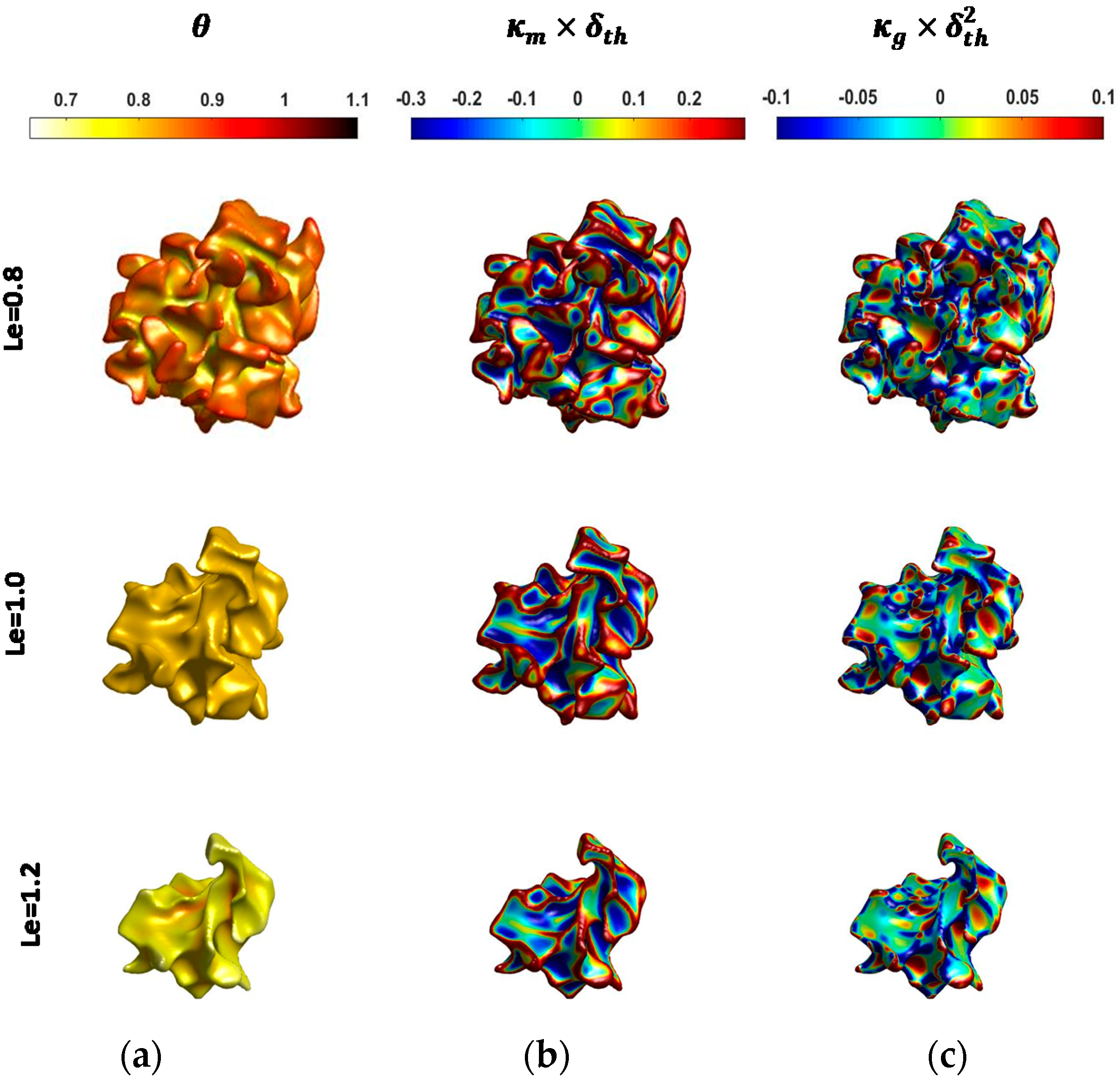
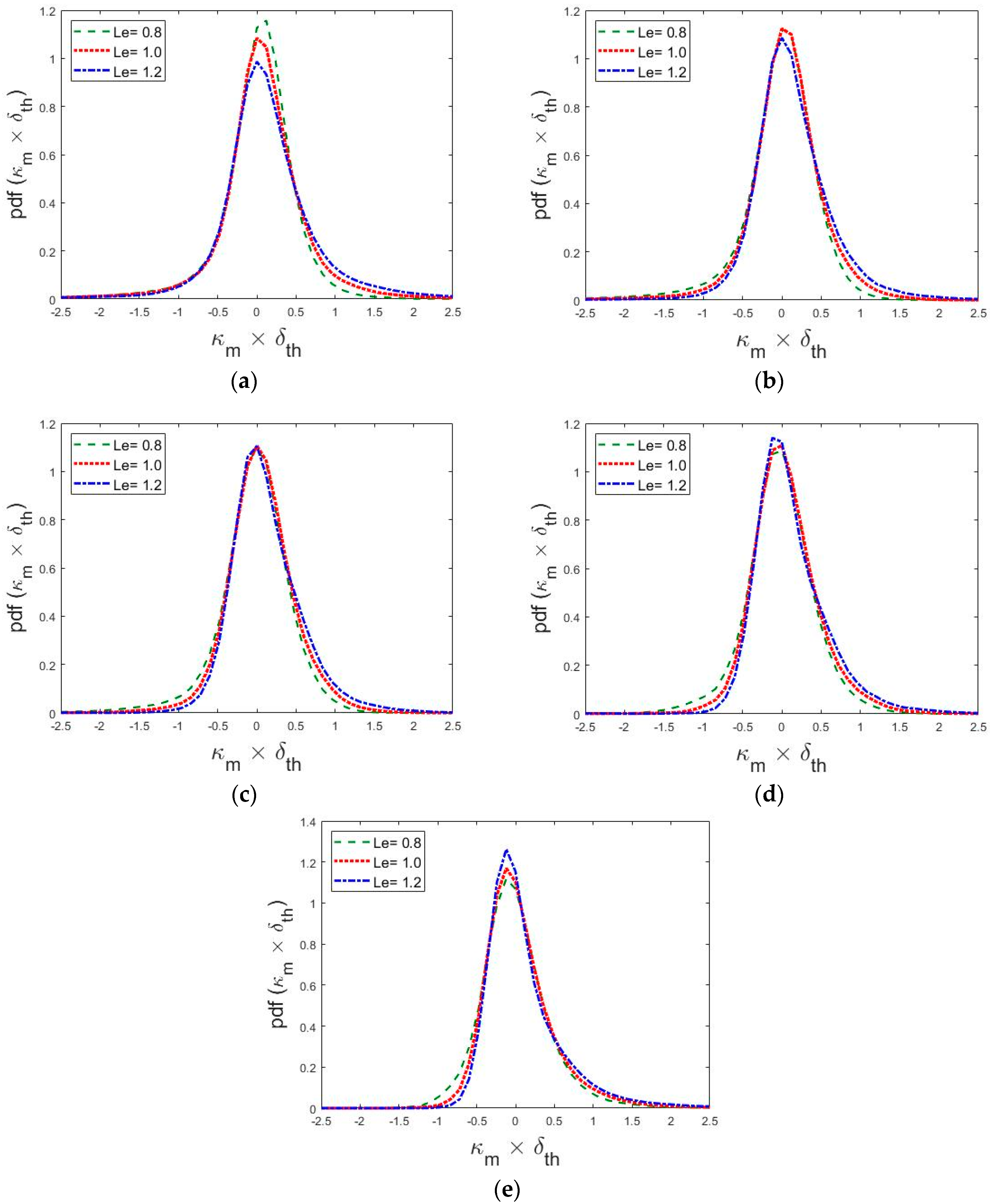
4.1. Curvature Characterisation
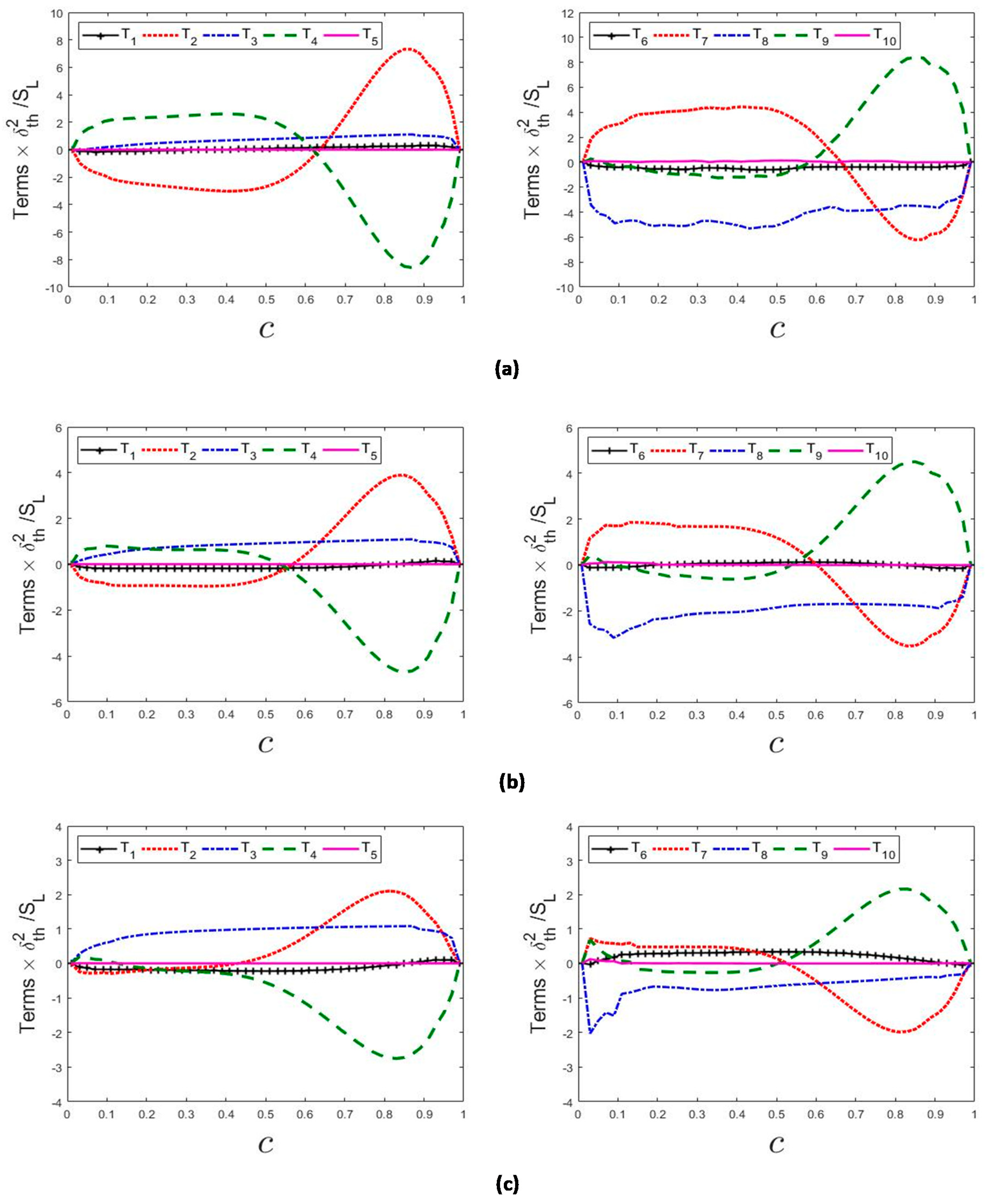
4.2. Mean Profiles of Source/Sink Terms of the Curvature Transport Equation
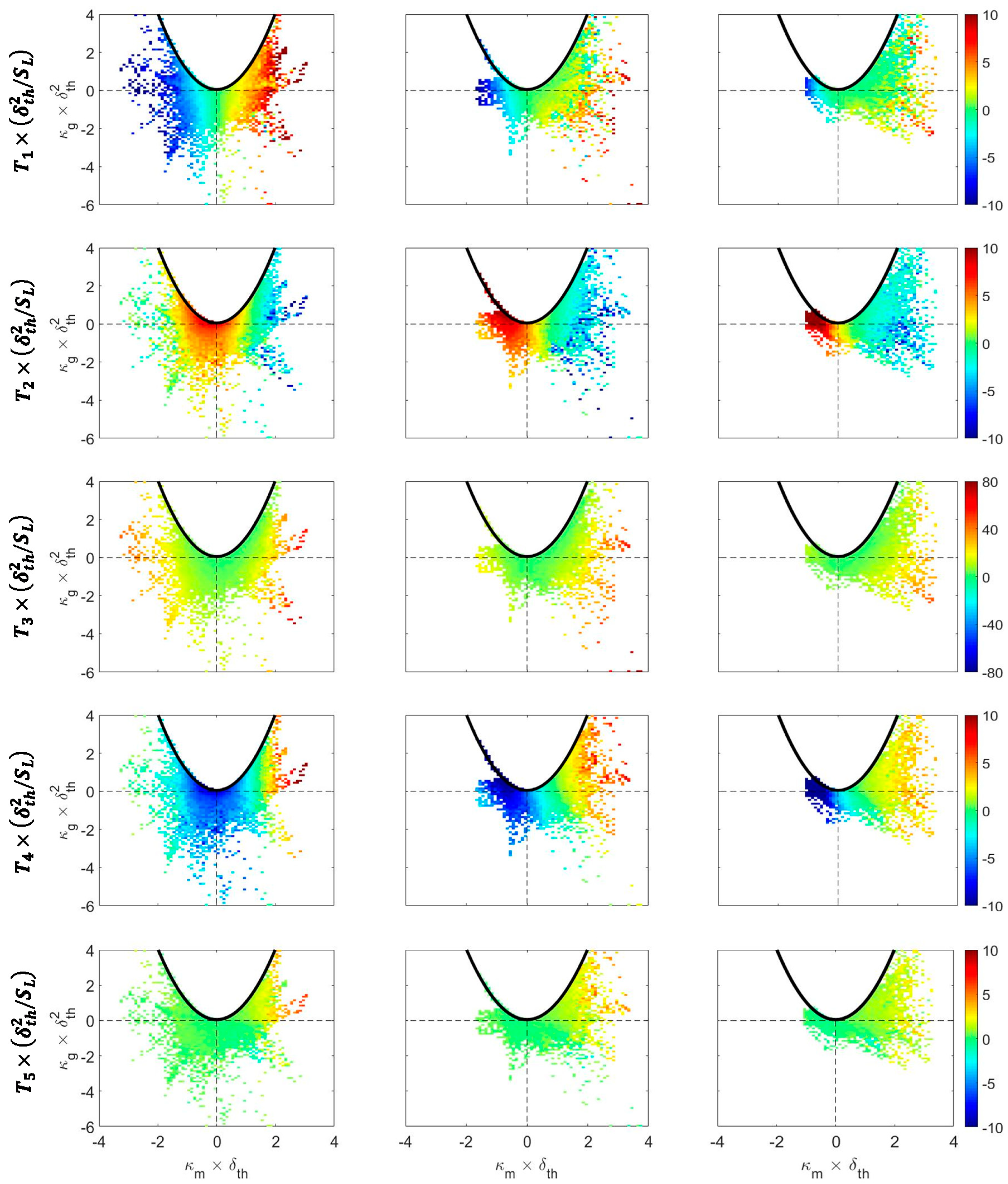
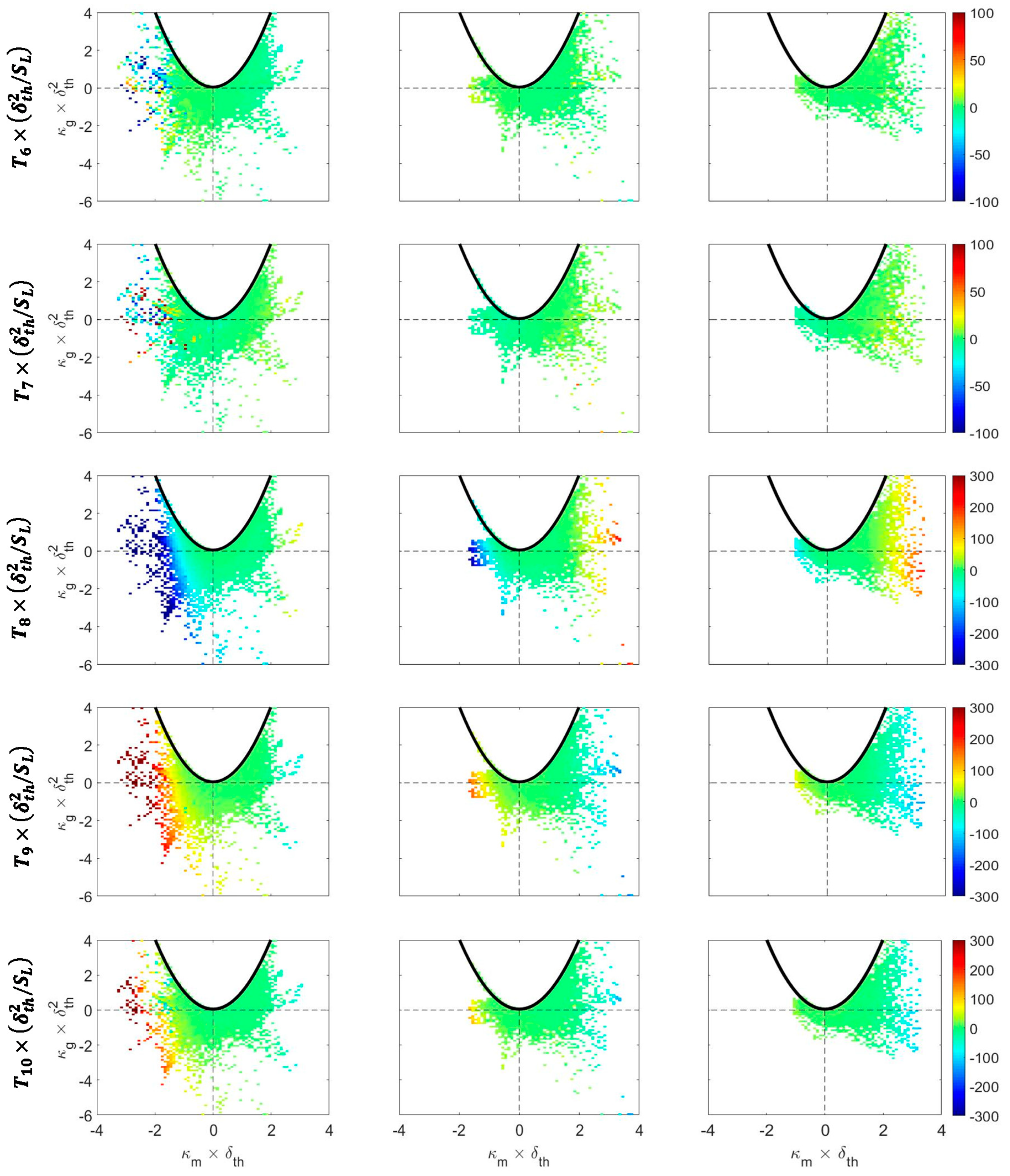
4.3. Mean Profiles of the Terms of the Curvature Transport Equation Conditioned Upon Curvature
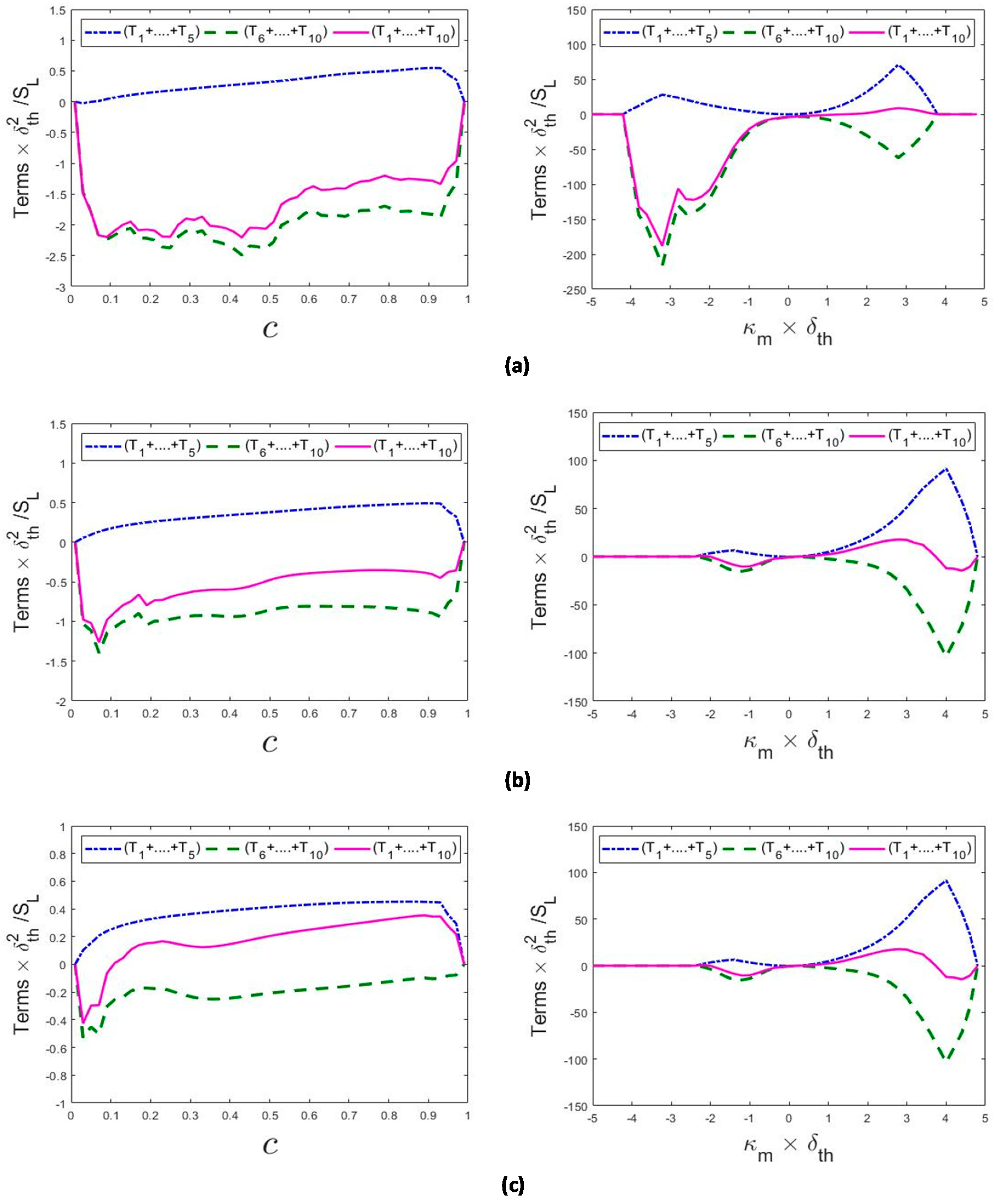
4.4. Overall Behaviour of the Terms in the Curvature Transport Equation
4.5. Relations of the Terms of the Curvature Transport Equation with Local Curvature
4.6. Modelling Implications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdel-Gayed, R.G.; Al-Khishali, K.J.; Bradley, D. Turbulent burning velocities and flame straining in explosions. Proc. R. Soc. Lond. A 1984, 391, 393–414. [Google Scholar] [CrossRef]
- Beretta, G.P.; Rashidi, M.; Keck, J.C. Turbulent flame propagation and combustion in spark ignition engines. Combust. Flame 1983, 52, 217–245. [Google Scholar] [CrossRef]
- Bradley, D.; Gaskell, P.H.; Gu, X.J. Burning velocities, Markstein lengths, and flame quenching for spherical methane-air flames: A computational study. Combust. Flame 1996, 104, 176–198. [Google Scholar] [CrossRef]
- Renou, B.; Boukhalfa, A.; Puechberty, D.; Trinit’e, M. Local scalar flame properties of freely propagating premixed turbulent flames at various Lewis numbers. Combust. Flame 2000, 123, 507–521. [Google Scholar] [CrossRef]
- Haq, M.Z.; Sheppard, C.G.W.; Woolley, R.; Greenhalgh, D.A.; Lockett, R.D. Wrinkling and curvature of laminar and turbulent premixed flames. Combust. Flame 2002, 131, 1–15. [Google Scholar] [CrossRef]
- Bradley, D.; Haq, M.Z.; Hicks, R.A.; Kitagawa, T.; Lawes, M.; Sheppard, C.G.W.; Woolley, R. Turbulent burning velocity, burned gas distribution, and associatedflame surface definition. Combust. Flame 2002, 133, 415–430. [Google Scholar] [CrossRef]
- Lawes, M.; Ormsby, M.P.; Sheppard, C.G.W.; Woolley, R. The turbulent burning velocity of iso-octane/air mixtures. Combust. Flame 2012, 159, 1949–1959. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Wu, F.; Zhu, D.; Law, C.K. Flame speed and self-similar propagation of expanding turbulent premixed flames. Phys. Rev. Lett. 2012, 108, 044503. [Google Scholar] [CrossRef]
- Akkerman, V.; Chaudhuri, S.; Law, C.K. Accelerative propagation and explosion triggering by expanding turbulent premixed flames. Phys. Rev. E 2013, 87, 23008. [Google Scholar] [CrossRef]
- Pope, S.B.; Cheng, W.K. Statistical calculations of spherical turbulent flames. Proc. Combust. Inst. 1986, 21, 1473–1481. [Google Scholar]
- Baum, M.; Poinsot, T. Effects of mean flow on premixed flame ignition. Combust. Sci. Technol. 1995, 106, 19–39. [Google Scholar] [CrossRef]
- Poinsot, T.; Candel, S.; Trouve, A. Applications of direct numerical simulation to premixed turbulent combustion. Prog. Energy Combust. Sci. 1995, 21, 531–576. [Google Scholar] [CrossRef]
- Schmid, H.-P.; Habisreuther, P.; Leuckel, W. A model for calculating heat release in premixed turbulent flames. Combust. Flame 1998, 113, 79–91. [Google Scholar] [CrossRef]
- Nwagwe, I.K.; Weller, H.G.; Tabor, G.R.; Gosman, A.D.; Lawes, M.; Sheppard, C.G.W.; Wooley, R. Measurements and large eddy simulations of turbulent premixed flame kernel growth. Proc. Combust. Inst. 2000, 28, 59–65. [Google Scholar] [CrossRef]
- Jenkins, K.W.; Cant, R.S. Curvature effects on flame kernels in a turbulent environment. Proc. Combust. Inst. 2002, 29, 2023–2029. [Google Scholar] [CrossRef]
- Tabor, G.; Weller, H.G. Large eddy simulation of premixed turbulent combustion using flame surface wrinkling model. Flow Turbul. Combust. 2004, 72, 1–27. [Google Scholar] [CrossRef]
- van Oijen, J.A.; Groot, G.R.A.; Bastiaans, R.J.M.; de Goey, L.P.H. A flamelet analysis of the burning velocity of premixed turbulent expanding flames. Proc. Combust. Inst. 2005, 30, 657–664. [Google Scholar] [CrossRef]
- Gashi, S.; Hult, J.; Jenkins, K.W.; Chakraborty, N.; Cant, R.S.; Kaminski, C.F. Curvature and Wrinkling of Premixed Flame Kernels-Comparisons of OH PLIF and DNS data. Proc. Combust. Inst. 2005, 30, 809–817. [Google Scholar] [CrossRef]
- Thevenin, D. Three-dimensional direct simulations and structure of expanding turbulent methane flames. Proc. Combust. Inst. 2005, 30, 629–637. [Google Scholar] [CrossRef]
- Klein, M.; Chakraborty, N.; Jenkins, K.W.; Cant, R.S. Effects of initial radius on the propagation of premixed flame kernels in a turbulent environment. Phys. Fluids 2006, 18, 055102. [Google Scholar] [CrossRef]
- Jenkins, K.W.; Klein, M.; Chakraborty, N.; Cant, R.S. Effects of strain rate and curvature on the propagation of a spherical flame kernel in the thin-reactionzones regime. Combust. Flame 2006, 145, 415–434. [Google Scholar] [CrossRef]
- Klein, M.; Chakraborty, N.; Cant, R.S. Effects of turbulence on self-sustained combustion in premixed flame kernels: A direct numerical simulation (DNS) study. Flow Turbul. Combust. 2008, 81, 583–607. [Google Scholar] [CrossRef]
- Hult, J.; Gashi, S.; Chakraborty, N.; Klein, M.; Jenkins, K.W.; Cant, R.S.; Kaminski, C. Measurement of Flame Surface Density for Turbulent Premixed Flames using PLIF and DNS. Proc. Combust. Inst. 2007, 31, 1319–1326. [Google Scholar] [CrossRef]
- Chakraborty, N.; Klein, M.; Cant, R.S. Stretch rate effects on displacement speed in turbulent premixed flame kernels in the thin reaction zones regime. Proc. Combust. Inst. 2007, 31, 1385–1392. [Google Scholar] [CrossRef]
- Dunstan, T.D.; Jenkins, K.W. Flame surface density distribution in turbulent flame kernels during the early stages of growth. Proc. Combust. Inst. 2009, 32, 1427–1434. [Google Scholar] [CrossRef]
- Dunstan, T.D.; Jenkins, K.W. The effects of hydrogen substitution on turbulent premixed methane-air kernels using direct numerical simulation. Int. J. Hydrogen Energy 2009, 34, 8389–8404. [Google Scholar] [CrossRef]
- Chakraborty, N.; Rogerson, J.W.; Swaminathan, N. The scalar gradient alignment statistics of flame kernels and its modelling implications for turbulent premixed combustion. Flow Turbul. Combust. 2010, 85, 25–55. [Google Scholar] [CrossRef]
- Lecocq, G.; Richard, S.; Colin, O.; Vervisch, L. Hybrid presumed PDF and flame surface density approaches for large-eddy simulation of premixed turbulent combustion. part 2: Early flame development after sparking. Combust. Flame 2011, 158, 1215–1226. [Google Scholar] [CrossRef]
- Colin, O.; Truffin, K. A spark ignition model for large eddy simulation based on an FSD transport equation (ISSIM-LES). Proc. Combust. Inst. 2011, 33, 3097–3104. [Google Scholar] [CrossRef]
- Ahmed, I.; Swaminathan, N. Simulation of spherically expanding turbulent premixed flames. Combust. Sci.Technol. 2013, 185, 1509–1540. [Google Scholar] [CrossRef]
- Ahmed, I.; Swaminathan, N. Simulation of turbulent explosion of hydrogen-air mixtures. Int. J. Hydrogen Energy 2014, 39, 9562–9572. [Google Scholar] [CrossRef]
- Peters, N.; Terhoeven, P.; Chen, J.H.; Echekki, T. Statistics of flame displacement speeds from computations of 2-D unsteady methane-air flames. Proc. Combust. Inst. 1998, 27, 833–839. [Google Scholar] [CrossRef]
- Echekki, T.; Chen, J.H. Analysis of the contributions of curvature to premixed flame propagation. Combust. Flame 1999, 118, 308–311. [Google Scholar] [CrossRef]
- Chen, J.H.; Im, H.G. Correlation of flame speed with stretch in turbulent premixed Methane/Air flames. Proc. Combust. Inst. 1998, 27, 819–826. [Google Scholar] [CrossRef]
- Chen, J.H.; Im, H.G. Stretch effects on the burning velocity of turbulent premixed Hydrogen/Air flames. Proc. Combust. Inst. 2000, 28, 211–218. [Google Scholar] [CrossRef]
- Hawkes, E.R.; Chen, J.H. Direct numerical simulation of hydrogen-enriched lean premixed methane air flames. Combust. Flame 2004, 138, 242–258. [Google Scholar] [CrossRef]
- Hawkes, E.R.; Chen, J.H. Evaluation of models for flame stretch due to curvature in the thin reaction zones regime. Proc. Combust. Inst. 2005, 30, 647–655. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, S. Unsteady effects of strain rate and curvature on turbulent premixed flames in inlet-outlet configuration. Combust. Flame 2004, 137, 129–147. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R.S. Influence of Lewis number on curvature effects in turbulent premixed flame propagation in the thin reaction zones regime. Phys. Fluids 2005, 17, 105105. [Google Scholar] [CrossRef]
- Chakraborty, N. Comparison of displacement speed statistics of turbulent premixed flames in the regimes representing combustion in corrugated flamelets and thin reaction zones. Phys. Fluids 2007, 19, 105109. [Google Scholar] [CrossRef]
- Han, I.; Huh, K.Y. Roles of displacement speed on evolution of flame surface density for different turbulent intensities and Lewis numbers in turbulent premixed combustion. Combust. Flame 2008, 152, 194–205. [Google Scholar] [CrossRef]
- Rutland, C.; Trouvé, A. Direct Simulations of premixed turbulent flames with nonunity Lewis numbers. Combust. Flame 1993, 94, 41–57. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R.S. Effects of strain rate and curvature on surface density function transport in turbulent premixed flames in the thin reaction zones regime. Phys. Fluids 2005, 17, 065108. [Google Scholar] [CrossRef]
- Chakraborty, N.; Klein, M. Influence of Lewis number on the Surface Density Function transport in the thin reaction zones regime for turbulent premixed flames. Phys. Fluids 2008, 20, 065102. [Google Scholar] [CrossRef]
- Chakraborty, N.; Klein, M. Effects of global flame curvature on surface density function transport in turbulent premixed flame kernels in the thin reaction zone regime. Proc. Combust. Inst. 2009, 32, 1435–1443. [Google Scholar] [CrossRef]
- Sandeep, A.; Proch, F.; Kempf, A.M.; Chakraborty, N. Statistics of strain rates and Surface Density Function in a flame-resolved high-fidelity simulation of a turbulent premixed bluff body burner. Phys. Fluids 2018, 30, 065101. [Google Scholar] [CrossRef]
- Chakraborty, N.; Hawkes, E.R.; Chen, J.H.; Cant, R.S. Effects of strain rate and curvature on Surface Density Function transport in turbulent premixed CH4-air and H2-air flames: A comparative study. Combust. Flame 2008, 154, 259–280. [Google Scholar] [CrossRef]
- Klein, M.; Alwazzan, D.; Chakraborty, N. A Direct Numerical Simulation analysis of pressure variation in turbulent premixed Bunsen burner flames-Part 1: Scalar gradient and strain rate statistics. Comput. Fluids 2018. [Google Scholar] [CrossRef]
- Klein, M.; Alwazzan, D.; Chakraborty, N. A Direct Numerical Simulation analysis of pressure variation in turbulent premixed Bunsen burner flames-Part 2: Surface Density Function transport statistics. Comput. Fluids 2018. [Google Scholar] [CrossRef]
- Reddy, H.; Abraham, J. Two-dimensional direct numerical simulation evaluation of the flame-surface density model for flames developing from an ignition kernel in lean methane/air mixtures under engine conditions. Phys. Fluids 2012, 24, 105108. [Google Scholar] [CrossRef]
- Pope, S.B. The evolution of surfaces in turbulence. Int. J. Eng. Sci. 1988, 26, 445–469. [Google Scholar] [CrossRef]
- Dopazo, C.; Martin, J.; Cifuentes, L.; Hierro, J. Strain, rotation and curvature of non-material propagating iso-scalar surfaces in homogeneous turbulence. Flow Turbul. Combust. 2018. [Google Scholar] [CrossRef]
- Cifuentes, L.; Dopazo, C.; Karichedu, A.; Chakraborty, N.; Kempf, A.M. Analysis of flame curvature evolution in a turbulent premixed bluff Body burner. Phys. Fluids 2018, 30, 095101. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. Diffusional-thermal theory of cellular flames. Combust. Sci. Technol. 1977, 16, 137–146. [Google Scholar] [CrossRef]
- Clavin, P.; Williams, F.A. Effects of molecular diffusion and thermal expansion on the structure and dynamics of turbulent premixed flames in turbulent flows of large scale and small intensity. J. Fluid Mech. 1982, 128, 251–282. [Google Scholar] [CrossRef]
- Ashurst, W.T.; Peters, N.; Smooke, M.D. Numerical simulation of turbulent flame structure with non-unity Lewis number. Combust. Sci. Technol. 1987, 53, 339–375. [Google Scholar] [CrossRef]
- Haworth, D.C.; Poinsot, T.J. Numerical simulations of Lewis number effects in turbulent premixed flames. J. Fluid Mech. 1992, 244, 405–436. [Google Scholar] [CrossRef]
- Trouvé, A.; Poinsot, T. The evolution equation for flame surface density in turbulent premixed combustion. J. Fluid Mech. 1994, 278, 1–31. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L.; Chakraborty, N. Vorticity budgets in premixed combusting turbulent flows at different Lewis numbers. Phys. Fluids 2017, 29, 045106. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L.; Martin, J.; Jimenez, C. Strain rates normal to approaching isoscalar surfaces in a turbulent premixed flame. Combust. Flame 2015, 162, 1729–1736. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L.; Alwazzan, D.; Chakraborty, N. Influence of the Lewis number on effective strain rates in weakly turbulent premixed combustion. Combust. Sci. Technol. 2018, 190, 591–614. [Google Scholar] [CrossRef]
- Chakraborty, N.; Kolla, H.; Sankaran, R.; Hawkes, E.R.; Chen, J.H.; Swaminathan, N. Determination of three-dimensional quantities related to scalar dissipation rate and its transport from two-dimensional measurements: Direct Numerical Simulation based validation. Proc. Combust. Inst. 2013, 34, 1151–1162. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. A direct numerical study of vorticity transformation in weakly turbulent premixed flames. Phys. Fluids 2014, 26, 105104. [Google Scholar] [CrossRef]
- Gao, Y.; Chakraborty, N.; Klein, M. Assessment of sub-grid scalar flux modelling in premixed flames for Large Eddy Simulations: A-priori Direct Numerical Simulation. Eur. J. Mech. Fluids-B 2015, 52, 97–108. [Google Scholar] [CrossRef]
- Papapostolou, V.; Wacks, D.H.; Klein, M.; Chakraborty, N.; Im, H.G. Enstrophy transport conditional on local flow topologies in different regimes of premixed turbulent combustion. Sci. Rep. 2017, 7, 11545. [Google Scholar] [CrossRef] [PubMed]
- Klein, M.; Kasten, C.; Chakraborty, N.; Mukhadiyev, N.; Im, H.G. Turbulent scalar fluxes in Hydrogen-Air premixed flames at low and high Karlovitz numbers. Combust. Theory Model. 2018, 22, 1033–1048. [Google Scholar] [CrossRef]
- Gao, Y.; Chakraborty, N. Modelling of Lewis Number dependence of Scalar dissipation rate transport for Large Eddy Simulations of turbulent premixed combustion. Numer. Heat Trans. A 2016, 69, 1201–1222. [Google Scholar] [CrossRef]
- Lai, J.; Chakraborty, N. Effects of Lewis Number on head on quenching of turbulent premixed flame: A Direct Numerical Simulation analysis. Flow Turbul. Combust. 2016, 96, 279–308. [Google Scholar] [CrossRef]
- Gao, Y.; Minamoto, Y.; Tanahashi, M.; Chakraborty, N. A priori assessment of scalar dissipation rate closure for Large Eddy Simulations of turbulent premixed combustion using a detailed chemistry Direct Numerical Simulation database. Combust. Sci. Technol. 2016, 188, 1398–1423. [Google Scholar] [CrossRef]
- Lai, J.; Klein, M.; Chakraborty, N. Direct Numerical Simulation of head-on quenching of statistically planar turbulent premixed methane-air flames using a detailed chemical mechanism. Flow Turbul. Combust. 2018, 101, 1073–1091. [Google Scholar] [CrossRef]
- Jenkins, K.W.; Cant, R.S. DNS of turbulent flame kernels. In Proceedings of the 2nd AFOSR Conference on DNS and LES; Liu, C., Sakell, L., Beautner, T., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 192–202. [Google Scholar]
- Muppala, S.R.; Aluri, N.K.; Dinkelacker, F.; Leipertz, A. Development of an Algebraic Reaction rate approach for the Numerical Calculation of Turbulent Premixed Methane, Ethylene and Propane/air flames at Pressures up to 1.0 MPa. Combust. Flame 2005, 140, 257–266. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tamura, H.; Maruta, K.; Nikola, T.; Williams, F.A. Burning velocity of turbulent premixed flames in a high-pressure environment. Proc. Combust. Inst. 1996, 26, 389–396. [Google Scholar] [CrossRef]
- Wray, A.A. Minimal Storage Time Advancement Schemes for Spectral Methods; NASA Ames Research Center: Mountain View, CA, USA, 1990; Unpublished work.
- Poinsot, T.; Lele, S.K. Boundary conditions for direct simulation of compressible viscous flows. J. Comp. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Rogallo, R.S. Numerical Experiments in Homogeneous Turbulence; NASA Technical Memorandum 81315; NASA Ames Research Center: Mountain View, CA, USA, 1981.
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Peters, N. Turbulent Combustion, Cambridge Monograph on Mechanics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dopazo, C.; Martin, J.; Hierro, J. Local geometry of isoscalar surfaces. Phys. Rev. E 2007, 76, 056316. [Google Scholar] [CrossRef]
- Hartung, G.; Hult, J.; Kaminski, C.F.; Rogerson, J.W.; Swaminathan, N. Effect of heat release on turbulence and scalar-turbulence interaction in premixed combustion. Phys. Fluids 2008, 20, 035110. [Google Scholar] [CrossRef]
- Chakraborty, N.; Swaminathan, N. Influence of Damköhler number on turbulence-scalar interaction in premixed flames, Part I: Physical Insight. Phys. Fluids 2007, 19, 045103. [Google Scholar] [CrossRef]
- Chakraborty, N.; Klein, M.; Swaminathan, N. Effects of Lewis number on reactive scalar gradient alignment with local strain rate in turbulent premixed flames. Proc. Combust. Inst. 2009, 32, 1409–1417. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R.S. A-Priori Analysis of the curvature and propagation terms of the Flame Surface Density transport equation for Large Eddy Simulation. Phys. Fluids 2007, 19, 105101. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R.S. Direct Numerical Simulation analysis of the Flame Surface Density transport equation in the context of Large Eddy Simulation. Proc. Combust. Inst. 2009, 32, 1445–1453. [Google Scholar] [CrossRef]
- Gao, Y.; Chakraborty, N.; Swaminathan, N. Local strain rate and curvature dependences of scalar dissipation rate transport in turbulent premixed flames: A Direct Numerical Simulation analysis. J. Combust. 2014, 2014, 280671. [Google Scholar] [CrossRef]
- Gao, Y.; Chakraborty, N.; Swaminathan, N. Scalar dissipation rate transport and its modelling for Large Eddy Simulations of turbulent premixed combustion. Combust. Sci. Technol. 2015, 187, 362–383. [Google Scholar] [CrossRef]


| Description | Term |
|---|---|
| Total strain rate tensor | |
| Total rotation rate tensor | |
| Flow strain rate tensor | |
| Flow rotation rate tensor | |
| Added strain rate tensor | |
| Added rotation rate tensor |
| Flow Terms | Added Terms | ||
|---|---|---|---|
| Terms | Description | Terms | Description |
| Contribution due to curvature and flow normal strain rate correlation | Term due to curvature and added normal strain rate correlation | ||
| Contribution due to flow normal strain rate normal variation | Contribution due to added normal strain rate normal variation | ||
| Flow stretching term | Added stretching term | ||
| Contribution of flow strain rate gradients | Contribution of added strain rate gradients | ||
| Contribution of flow vorticity curl | Contribution of added vorticity curl | ||
| Le | ΩT/ΩL | AT/AL |
|---|---|---|
| 0.8 | 13.75 | 13.22 |
| 1.0 | 6.86 | 7.30 |
| 1.2 | 3.86 | 4.66 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqallaf, A.; Klein, M.; Chakraborty, N. Effects of Lewis Number on the Evolution of Curvature in Spherically Expanding Turbulent Premixed Flames. Fluids 2019, 4, 12. https://doi.org/10.3390/fluids4010012
Alqallaf A, Klein M, Chakraborty N. Effects of Lewis Number on the Evolution of Curvature in Spherically Expanding Turbulent Premixed Flames. Fluids. 2019; 4(1):12. https://doi.org/10.3390/fluids4010012
Chicago/Turabian StyleAlqallaf, Ahmad, Markus Klein, and Nilanjan Chakraborty. 2019. "Effects of Lewis Number on the Evolution of Curvature in Spherically Expanding Turbulent Premixed Flames" Fluids 4, no. 1: 12. https://doi.org/10.3390/fluids4010012
APA StyleAlqallaf, A., Klein, M., & Chakraborty, N. (2019). Effects of Lewis Number on the Evolution of Curvature in Spherically Expanding Turbulent Premixed Flames. Fluids, 4(1), 12. https://doi.org/10.3390/fluids4010012







