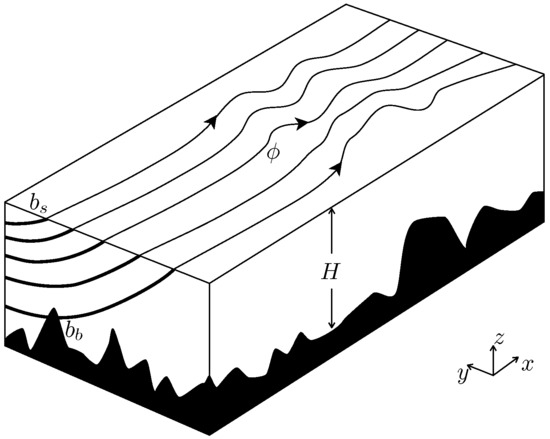
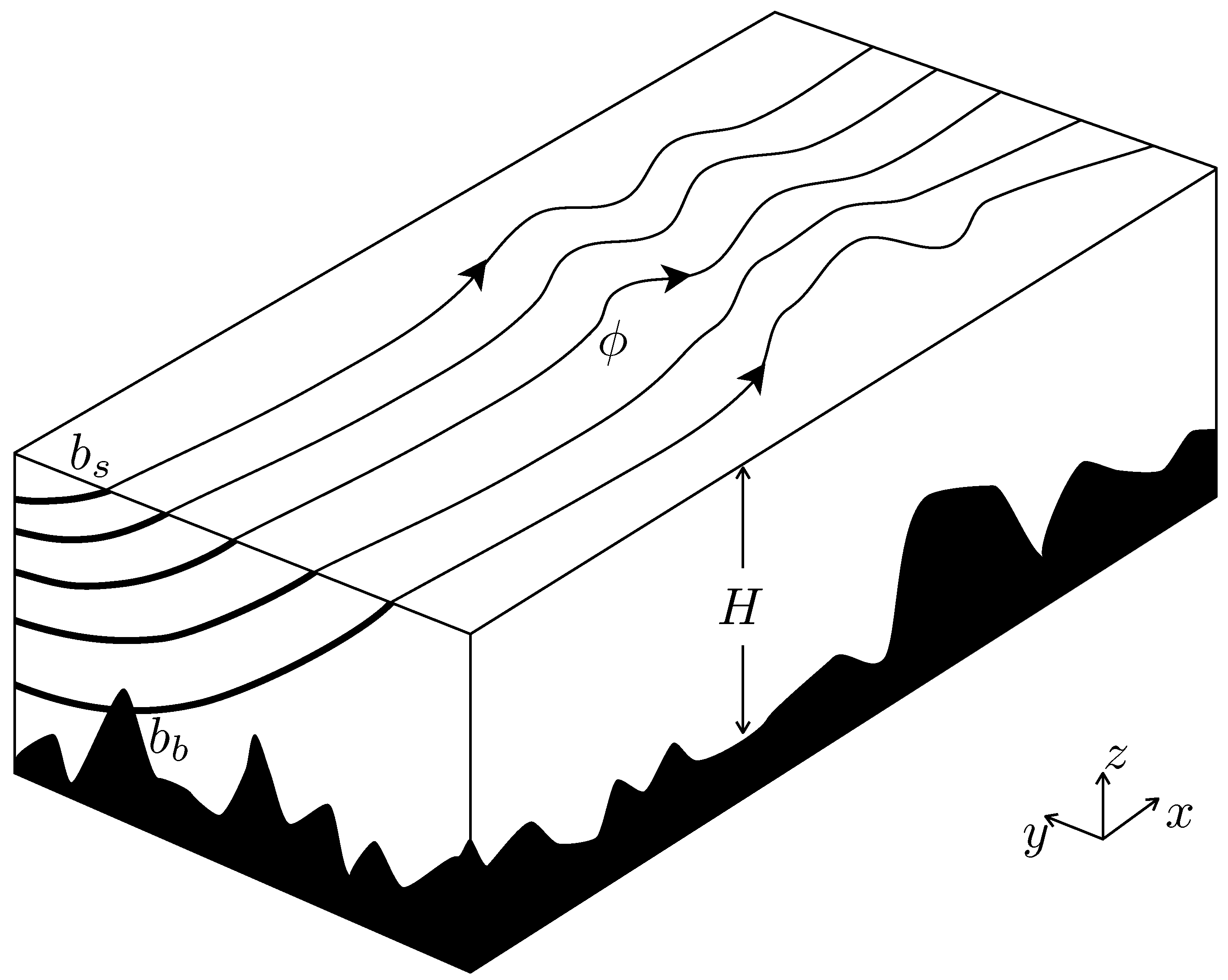
A Theoretical Model of Long Rossby Waves in the Southern Ocean and Their Interaction with Bottom Topography
Abstract
:1. Introduction
- Long Rossby waves are “steered” by the bottom topography in precisely the same manner as the time-mean surface streamlines. In the limit in which the surface flow is relatively unaffected by the bottom topography, so are the long Rossby waves. This concept is made rigorous through comparison of the mathematical equations for long Rossby waves in the present continuously-stratified model with variable bottom topography and the the equivalent equations for long Rossby waves in a two-layer model, linearised about a state of rest.
- The result that long Rossby waves propagate quasi-zonally breaks down catastrophically wherever contours close, irrespective of the stratification. This is demonstrated through the derivation of an integral constraint in which a weighted integral of the dominant Rossby propagation term vanishes over any area enclosed by an contour. Such behaviour has been studied in the analogous two-layer model [16] and has been shown to result in the long Rossby waves partially “jumping” across the closed contour.
- Following the approach of Salmon [15], a nonlinear long Rossby wave equation can be derived which demonstrates, in this model, that the long Rossby wave speed is Doppler shifted by the depth-mean flow. For realistic ACC parameters, the latter term dominates and causes eastward propagation relative to the sea floor, at speeds consistent with the observed eastward propagation of Southern Ocean surface anomalies.
2. Planetary Geostrophic Equations
3. Application to the Southern Ocean
3.1. Interior Dynamics
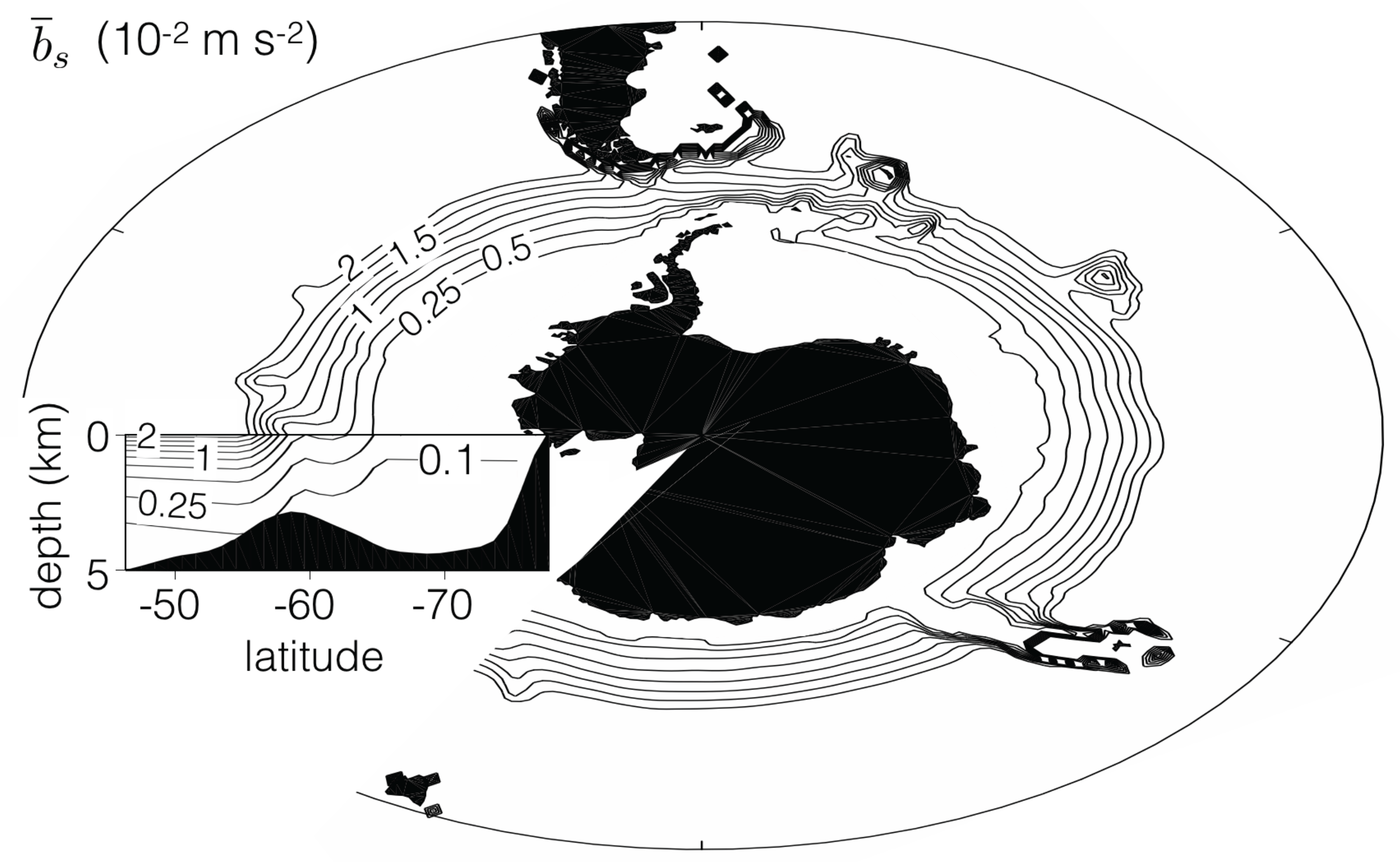
3.2. Boundary Conditions
4. Steady State
4.1. Characteristics
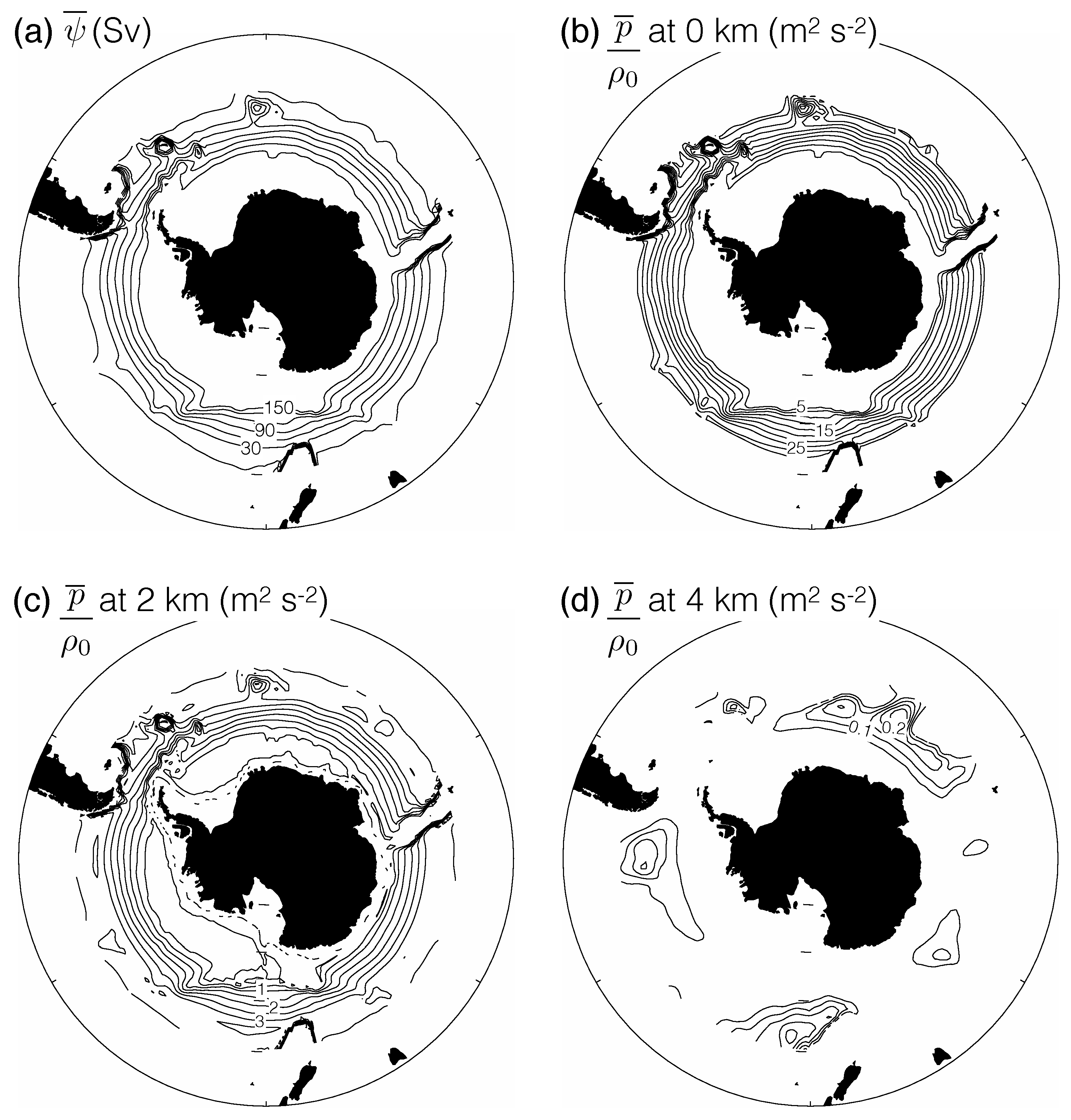
4.2. An Illustrative Solution
5. Linear Rossby Waves
5.1. Linear Wave Equations
5.2. Relation to the Two-Layer Model
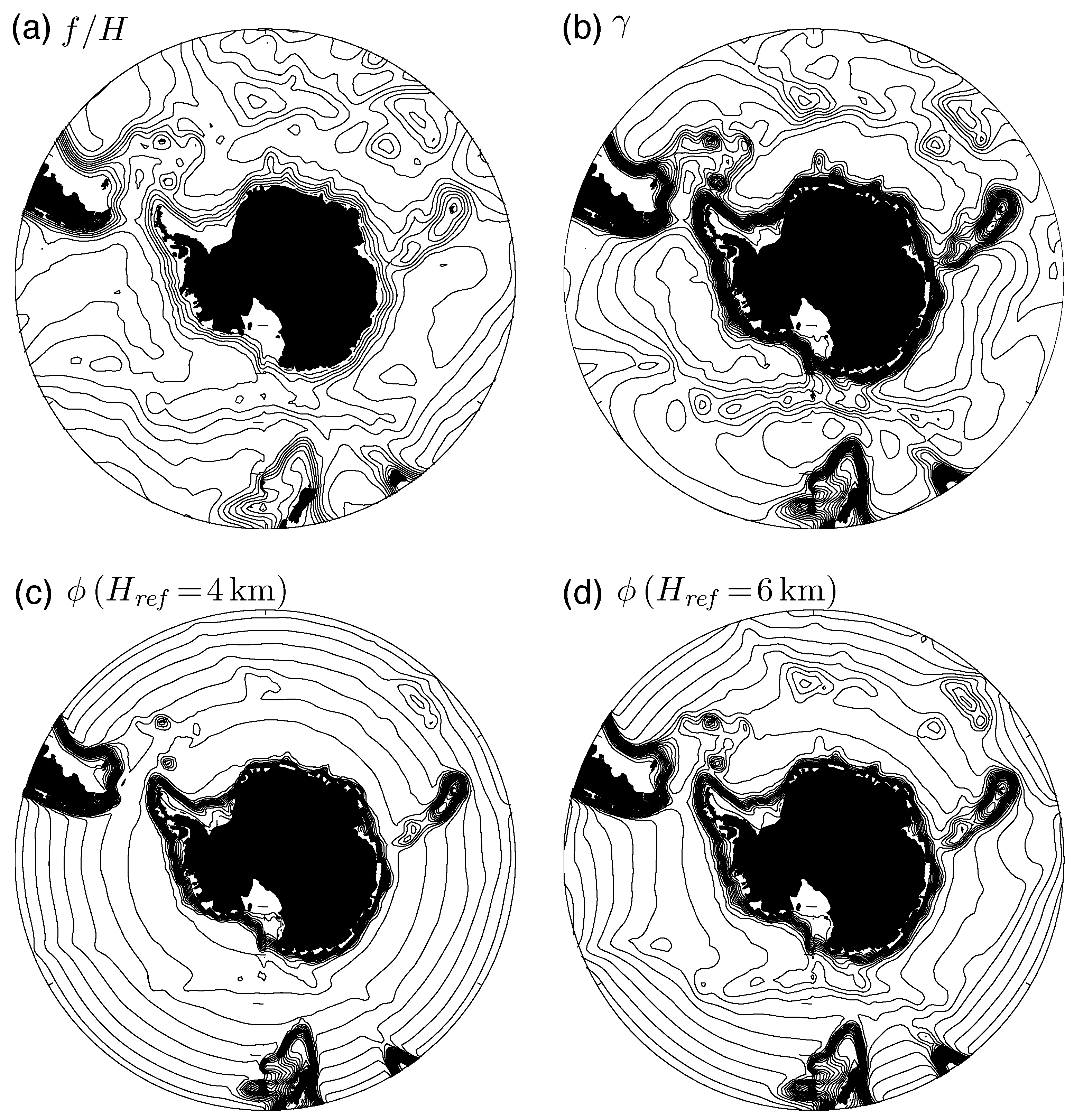
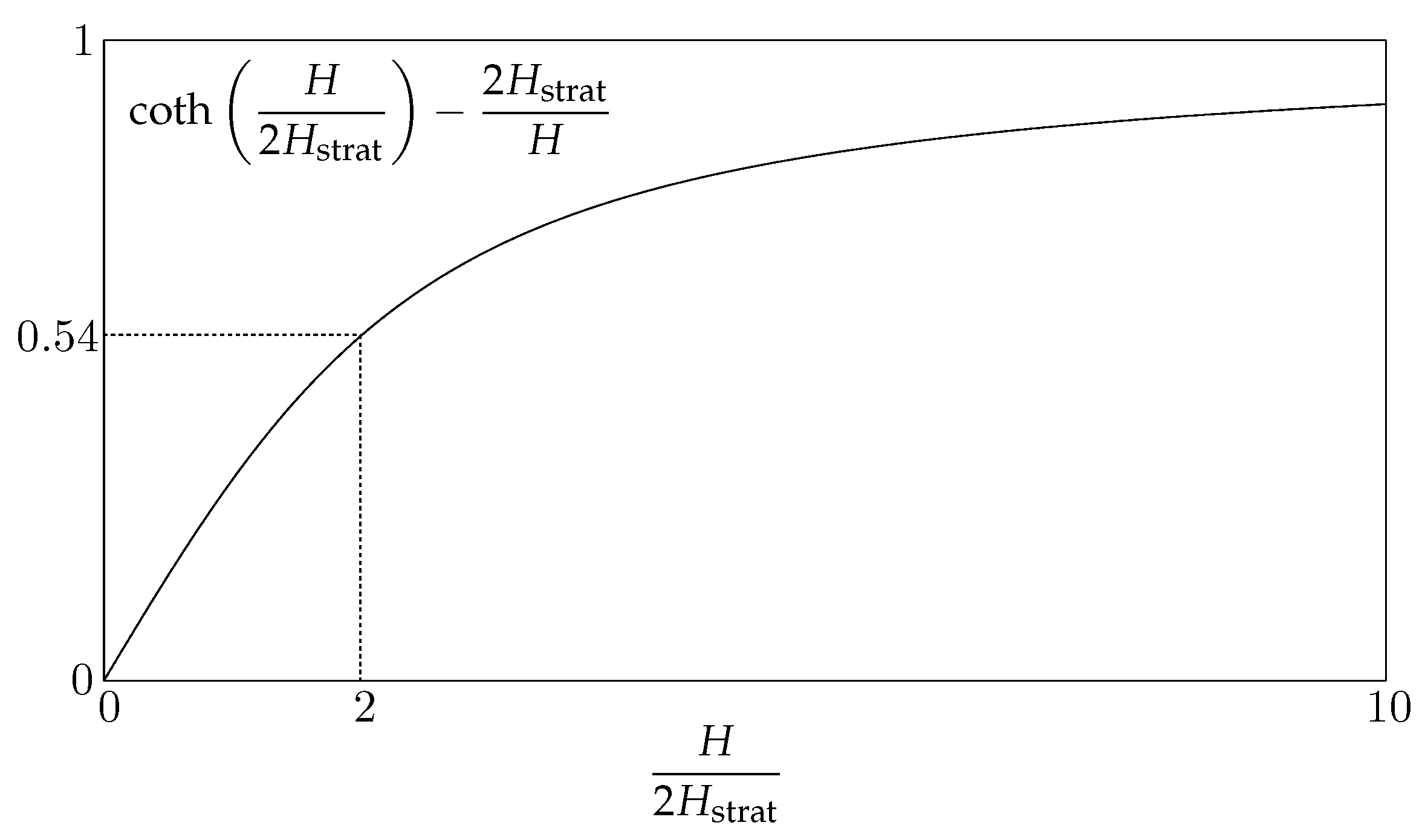
5.3. Shallow Pycnocline Limit: Topographic Shielding and Rossby Wormholes
6. Nonlinear Rossby Wave Equation
7. Conclusions
- Long Rossby waves propagate along the same path as followed by the mean surface geostrophic flow, characteristics that are intermediate to f and contours. For realistic Southern Ocean parameters, these characteristics are nearly zonal, with only slight deflections over major topographic features, aside from the Kerguelan Plateau which represents a more substantial obstacle.
- The quasi-zonal propagation of long Rossby waves breaks down catastrophically in regions of closed contours where, by analogy with the simpler two-layer model, the long Rossby waves can be expected to partially jump across the closed contour.
- In the absence of topographic variations, the Rossby propagation speed consists of an intrinsic Rossby speed, slightly modified from the classical Rossby speed to account for finite ocean depth, and Doppler shifting by the depth-mean flow, consistent with an earlier result obtained by Salmon [15]. This Doppler shift dominates for realistic Southern Ocean parameters, consistent with the observed eastward propagation of Southern Ocean anomalies in surface altimetric observations.
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| ACC | Antarctic Circumpolar Current |
| JEBAR | Joint Effect of Baroclinicity and Relief |
Appendix A. Derivation of Streamfunction of the Depth-Integrated Flow
References
- Munk, W.H.; Palmén, E. Note on the dynamics of the Antarctic Circumpolar Current. Tellus 1951, 3, 53–55. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Hughes, C.W.; Jones, M.S.; Carnochan, S. Use of transient features to identify eastward currents in the Southern Ocean. J. Geophys. Res. 1998, 103, 2929–2942. [Google Scholar] [CrossRef]
- Hughes, C.W. Nonlinear vorticity balance of the Antarctic Circumpolar Current. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Klocker, A.; Marshall, D.P. Advection of baroclinic eddies by depth mean flow. Geophys. Res. Lett. 2014, 41, 3517–3521. [Google Scholar] [CrossRef]
- Sarkisyan, A.S. Principles of Theory and Computation of Ocean Currents; Gidrometeoizdat: Leningrad, Russia, 1966. [Google Scholar]
- Sarkisyan, A.S.; Ivanov, V.F. Joint effect of baroclinicity and bottom relief as an important factor in the dynamics of sea currents. Izv. Akad. Nauk. SSSR Fiz. Atmos. Okeana 1971, 7, 173–188. [Google Scholar]
- Cane, M.A.; Kamenkovitch, V.M.; Krupiysky, A. On the utility and disutility of JEBAR. J. Phys. Oceanogr. 1998, 28, 519–526. [Google Scholar] [CrossRef]
- Marshall, D. Influence of topography on the large-scale ocean circulation. J. Phys. Oceanogr. 1995, 25, 1622–1635. [Google Scholar] [CrossRef]
- Marshall, D. Topographic steering of the Antarctic Circumpolar Current. J. Phys. Oceanogr. 1995, 25, 1636–1650. [Google Scholar] [CrossRef]
- Marshall, D.P.; Stephens, J.C. On the insensitivity of the wind-driven circulation to bottom topography. J. Mar. Res. 2001, 59, 1–27. [Google Scholar] [CrossRef]
- Killworth, P.D.; Hughes, C.W. The Antarctic Circumpolar Current as a free equivalent-barotropic jet. J. Mar. Res. 2002, 60, 19–45. [Google Scholar] [CrossRef]
- de Szoeke, R.A. Wind-driven mid-ocean baroclinic gyres over topography: A circulation equation extending the Sverdrup relation. J. Mar. Res. 1985, 43, 793–824. [Google Scholar] [CrossRef]
- Salmon, R. Generalized two-layer models of ocean circulation. J. Mar. Res. 1994, 52, 865–908. [Google Scholar] [CrossRef]
- Marshall, D.P. Rossby wormholes. J. Mar. Res. 2011, 69, 309–330. [Google Scholar] [CrossRef]
- Welander, P. An advective model of the ocean thermocline. Tellus 1959, 11, 309–318. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer-Verlag: New York, NY, USA, 1987. [Google Scholar]
- De Verdiere, A. On mean flow instabilities within the planetary geostrophic equations. J. Phys. Oceanogr. 1986, 16, 1981–1984. [Google Scholar] [CrossRef]
- Welander, P. Some exact solutions to the equations describing an ideal-fluid thermocline. J. Mar. Res. 1971, 29, 60–68. [Google Scholar]
- Marshall, J.; Olbers, D.; Ross, H.; Wolff-Gladrow, D. Potential vorticity constraints on the dynamics and hydrography of the Southern Ocean. J. Phys. Oceanogr. 1993, 23, 465–487. [Google Scholar] [CrossRef]
- Kartsen, R.H.; Marshall, J. Testing theories of the vertical stratification of the ACC against observations. Dyn. Atmos. Oceans 2002, 36, 233–246. [Google Scholar]
- Stommel, H. A survey of ocean current theory. Deep Sea Res. 1957, 4, 149–184. [Google Scholar] [CrossRef]
- Marshall, D.P.; Munday, D.R.; Allison, L.C.; Hay, R.J.; Johnson, H.L. Gill’s model of the Antarctic Circumpolar Current, revisited: The role of latitudinal variations in wind stress. Ocean Modell. 2016, 97, 37–51. [Google Scholar] [CrossRef]
- Killworth, P.D. An equivalent barotropic mode in the Fine Resolution Antarctic Model. J. Phys. Oceanogr. 1992, 22, 1379–1386. [Google Scholar] [CrossRef]
- Tailleux, R.; McWilliams, J.C. Acceleration, creation, and depletion of wind-driven, baroclinic Rossby waves over an ocean ridge. J. Phys. Oceanogr. 2000, 30, 2186–2213. [Google Scholar] [CrossRef]
- Tailleux, R.; McWilliams, J.C. Energy propagation of long extratropical Rossby waves over slowly varying zonal topography. J. Fluid Mech. 2002, 473, 295–319. [Google Scholar] [CrossRef]
- Smith, K.S.; Marshall, J. Evidence for enhanced eddy mixing at mid-depth in the Southern Ocean. J. Phys. Oceanogr. 2009, 39, 50–69. [Google Scholar] [CrossRef]
- Abernathey, R.; Marshall, J.; Mazloff, M.; Shuckburgh, E. Enhancement of Mesoscale Eddy Stirring at Steering Levels in the Southern Ocean. J. Phys. Oceanogr. 2010, 40, 170–184. [Google Scholar] [CrossRef]
- Meredith, M.P.; Woodworth, P.L.; Chereskin, T.K.; Marshall, D.P.; Allison, L.C.; Bigg, G.R.; Donahue, K.; Heywood, K.J.; Hughes, C.W.; Hibbert, A.; et al. Sustained monitoring of the Southern Ocean at Drake Passage: Past achievements and future priorities. Rev. Geophys. 2011, 49. [Google Scholar] [CrossRef]
- Held, I.M. Stationary and quasi-stationary eddies in the extratropical troposphere: Theory. In Large-Scale Dynamical Processes in the Atmosphere; Hoskins, B.J., Pearce, R.P., Eds.; Academic Press: Cambridge, MA, USA, 1983; pp. 127–168. [Google Scholar]
- Liu, Z.Y. Planetary waves in the thermocline: Non-Doppler-shift mode, advective mode and Green mode. Q. J. R. Met. Soc. 1999, 125, 1315–1339. [Google Scholar] [CrossRef]
- Colin de Verdiere, A.; Tailleux, R. The interaction of a baroclinic mean flow with long Rossby waves. J. Phys. Oceanogr. 2005, 35, 865–879. [Google Scholar] [CrossRef]
- Samelson, R. An effective-β vector for linear planetary waves on a weak mean flow. Ocean Modell. 2010, 32, 170–174. [Google Scholar] [CrossRef]
- Killworth, P.D.; Chelton, D.B.; de Szoeke, R.A. The speed of observed and theoretical long extratropical planetary waves. J. Phys. Oceanogr. 1997, 27, 1946–1966. [Google Scholar] [CrossRef]
- Dewar, W.K. On ‘too fast’ baroclinic planetary waves in the general circulation. J. Phys. Oceanogr. 1998, 28, 1739–1758. [Google Scholar] [CrossRef]
- De Szoeke, R.A.; Chelton, D.B. The modification of long planetary waves by homogeneous potential vorticity layers. J. Phys. Oceanogr. 1999, 29, 500–511. [Google Scholar] [CrossRef]
- Tansley, C.E.; Marshall, D.P. Flow past a cylinder on a β-plane, with application to Gulf Stream separation and the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2001, 31, 3274–3283. [Google Scholar] [CrossRef]
- Tansley, C.E.; Marshall, D.P. On the dynamics of wind-driven circumpolar currents. J. Phys. Oceanogr. 2001, 31, 3258–3272. [Google Scholar] [CrossRef]
- Hallberg, R.W.; Gnanadesikan, A. The role of eddies in determining the structure and response of the wind-driven Southern Hemisphere overturning: Results from the modeling eddies in the Southern Ocean (MESO) project. J. Phys. Oceanogr. 2006, 36, 2232–2252. [Google Scholar] [CrossRef]
- Salmon, R. Lectures on Geophysical Fluid Dynamics; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- De Szoeke, R.A.; Samelson, R.M. The duality between the Boussinesq and non-Boussinesq hydrostatic equations of motion. J. Phys. Oceanogr. 2002, 32, 2194–2203. [Google Scholar] [CrossRef]
- Losch, M.; Adcroft, A.; Campin, J.M. How Sensitive Are Coarse General Circulation Models to Fundamental Approximations in the Equations of Motion? J. Phys. Oceanogr. 2004, 34, 306–319. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Campin, J.M.; Hill, C. Atmosphere-Ocean Modeling Exploiting Fluid Isomorphisms. Mon. Weather Rev. 2004, 132, 2882–2894. [Google Scholar] [CrossRef]
- Charney, J.G. On the scale of atmospheric motions. Geofys. Publ. 1948, 17, 1–17. [Google Scholar]
- Eady, E.T. Long waves and cyclone waves. Tellus 1949, 1, 33–52. [Google Scholar] [CrossRef]
- Green, J.S.A. A problem in baroclinic instability. Quart. J. R. Meteor. Soc. 1960, 86, 237–251. [Google Scholar] [CrossRef]
- Bretheron, F.P. Critical layer instability in baroclinic flows. Quart. J. R. Meteor. Soc. 1966, 92, 325–334. [Google Scholar] [CrossRef]
- Treguier, A.M. Evaluating eddy mixnig coefficients from eddy-resolving ocean models: A case study. J. Mar. Res. 1999, 57, 89–108. [Google Scholar] [CrossRef]
- Cerovecki, I.; Plumb, R.A.; Heres, W. Eddy transport and mixing in a wind- and buoyancy-driven jet on the sphere. J. Phys. Oceanogr. 2009, 39, 1133–1149. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marshall, D.P. A Theoretical Model of Long Rossby Waves in the Southern Ocean and Their Interaction with Bottom Topography. Fluids 2016, 1, 17. https://doi.org/10.3390/fluids1020017
Marshall DP. A Theoretical Model of Long Rossby Waves in the Southern Ocean and Their Interaction with Bottom Topography. Fluids. 2016; 1(2):17. https://doi.org/10.3390/fluids1020017
Chicago/Turabian StyleMarshall, David P. 2016. "A Theoretical Model of Long Rossby Waves in the Southern Ocean and Their Interaction with Bottom Topography" Fluids 1, no. 2: 17. https://doi.org/10.3390/fluids1020017
APA StyleMarshall, D. P. (2016). A Theoretical Model of Long Rossby Waves in the Southern Ocean and Their Interaction with Bottom Topography. Fluids, 1(2), 17. https://doi.org/10.3390/fluids1020017